Numerical Investigation of Energy Saving Characteristic in Building Roof Coupled with PCM Using Lattice Boltzmann Method with Economic Analysis
Abstract
Featured Application
Abstract
1. Introduction
2. Mathematical Model for Conjugate Heat Transfer with Phase Change
3. Lattice Boltzmann Method and Comprehensive Incremental Benefit Model
3.1. Lattice Boltzmann Method
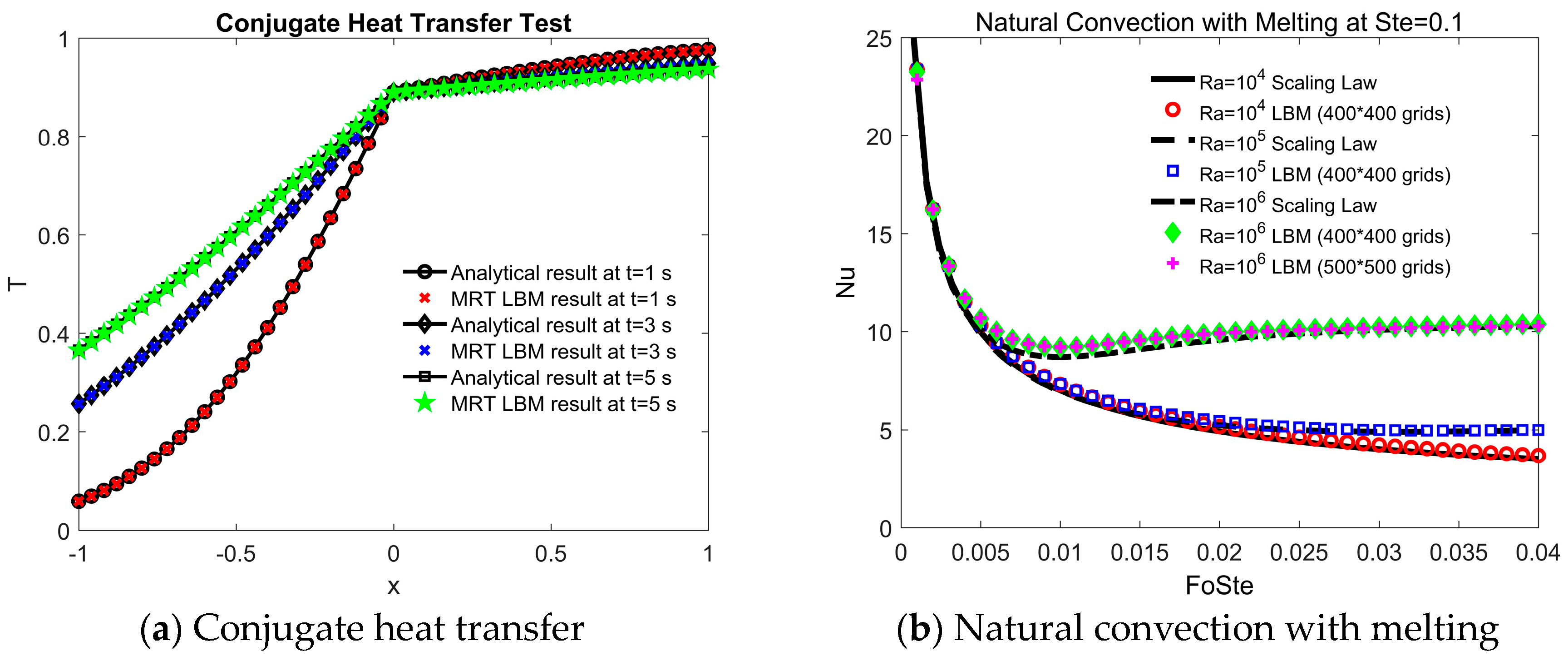
3.2. Code Validation
3.3. Comprehensive Incremental Benefit Model
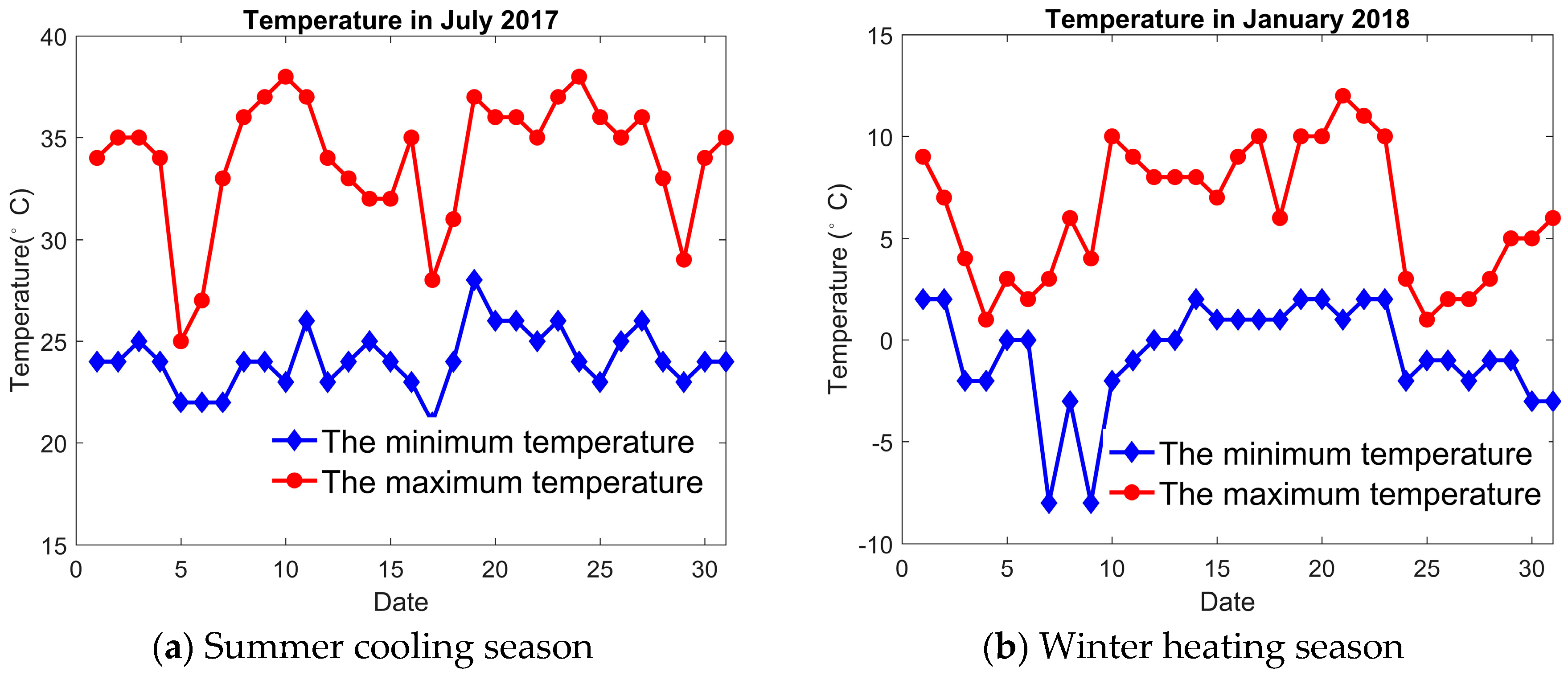
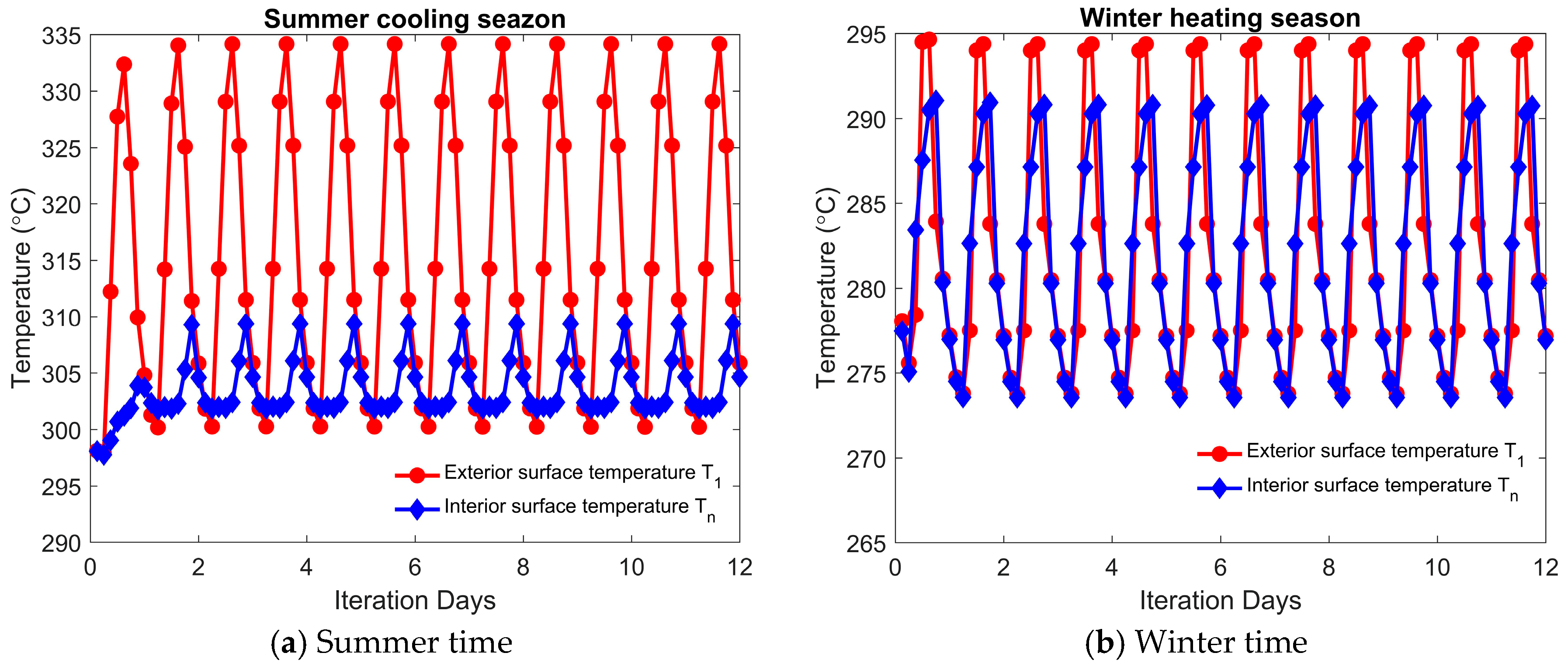
4. Results and Discussions
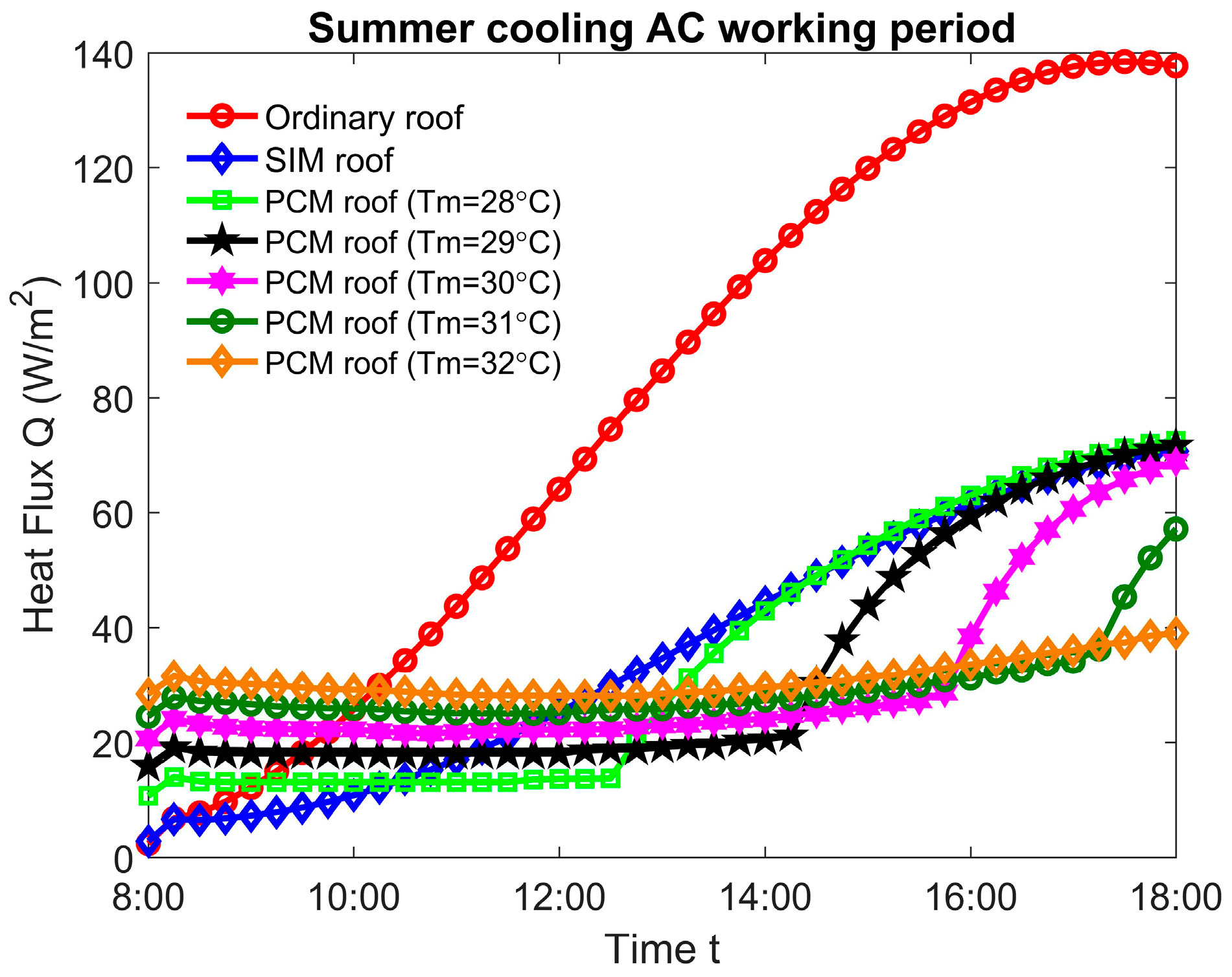
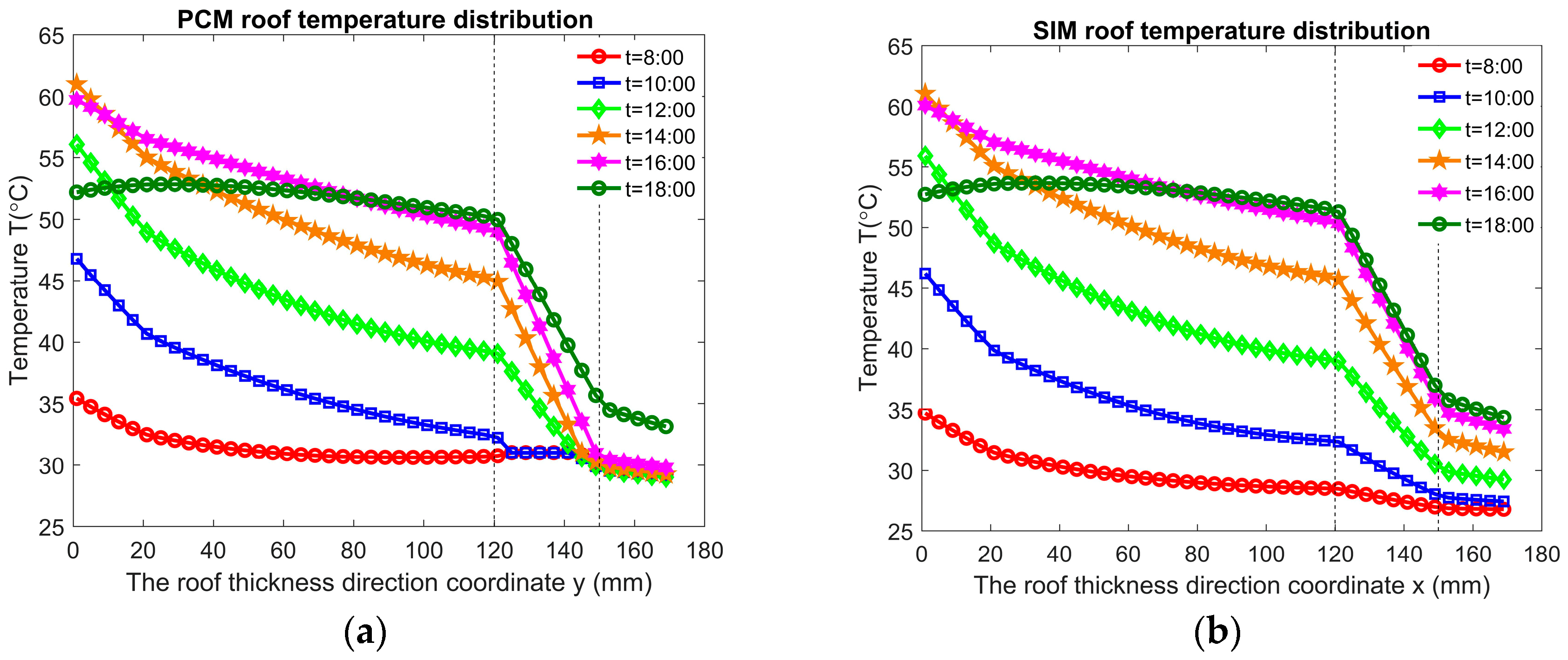
4.1. The Influence of Roof Type
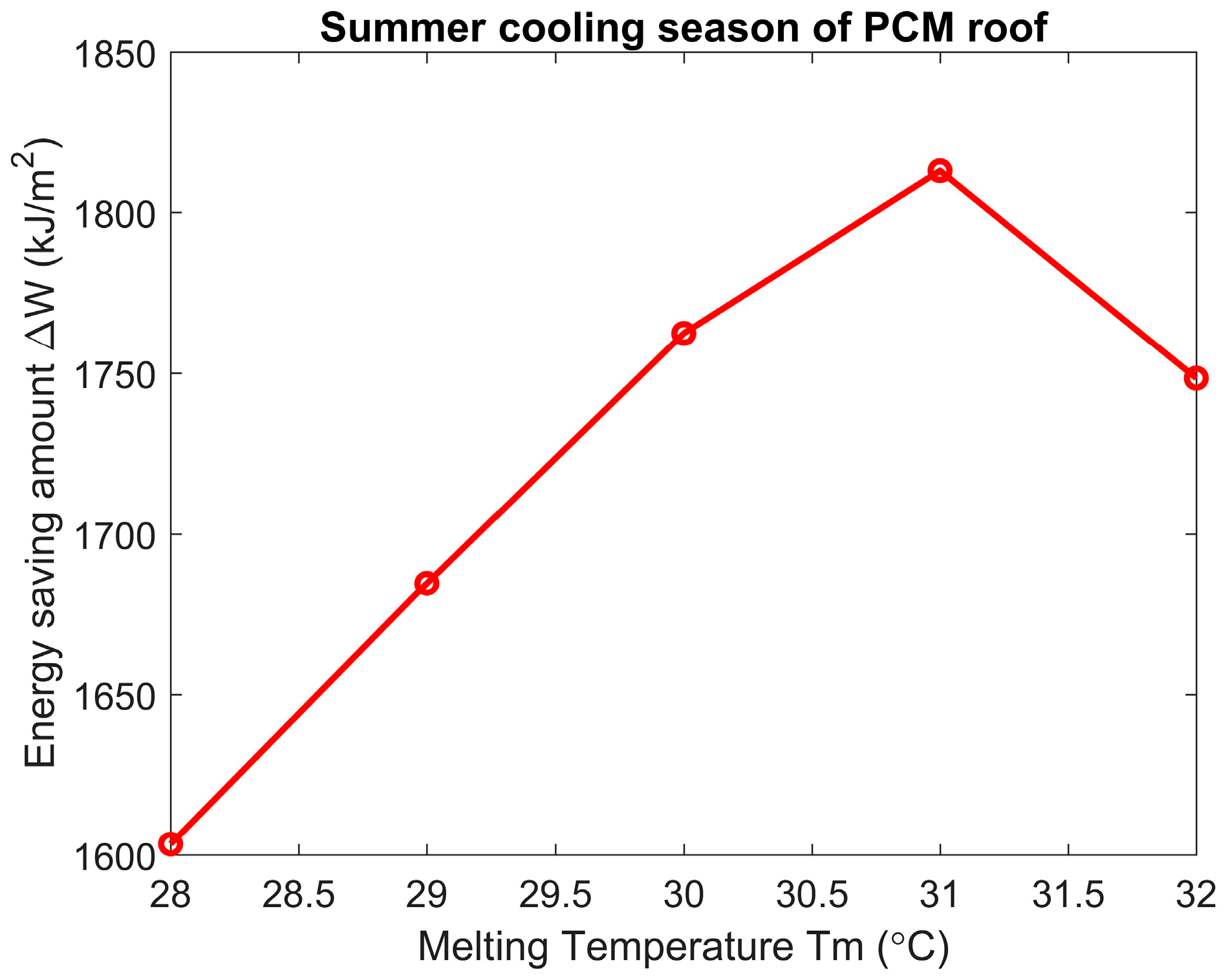
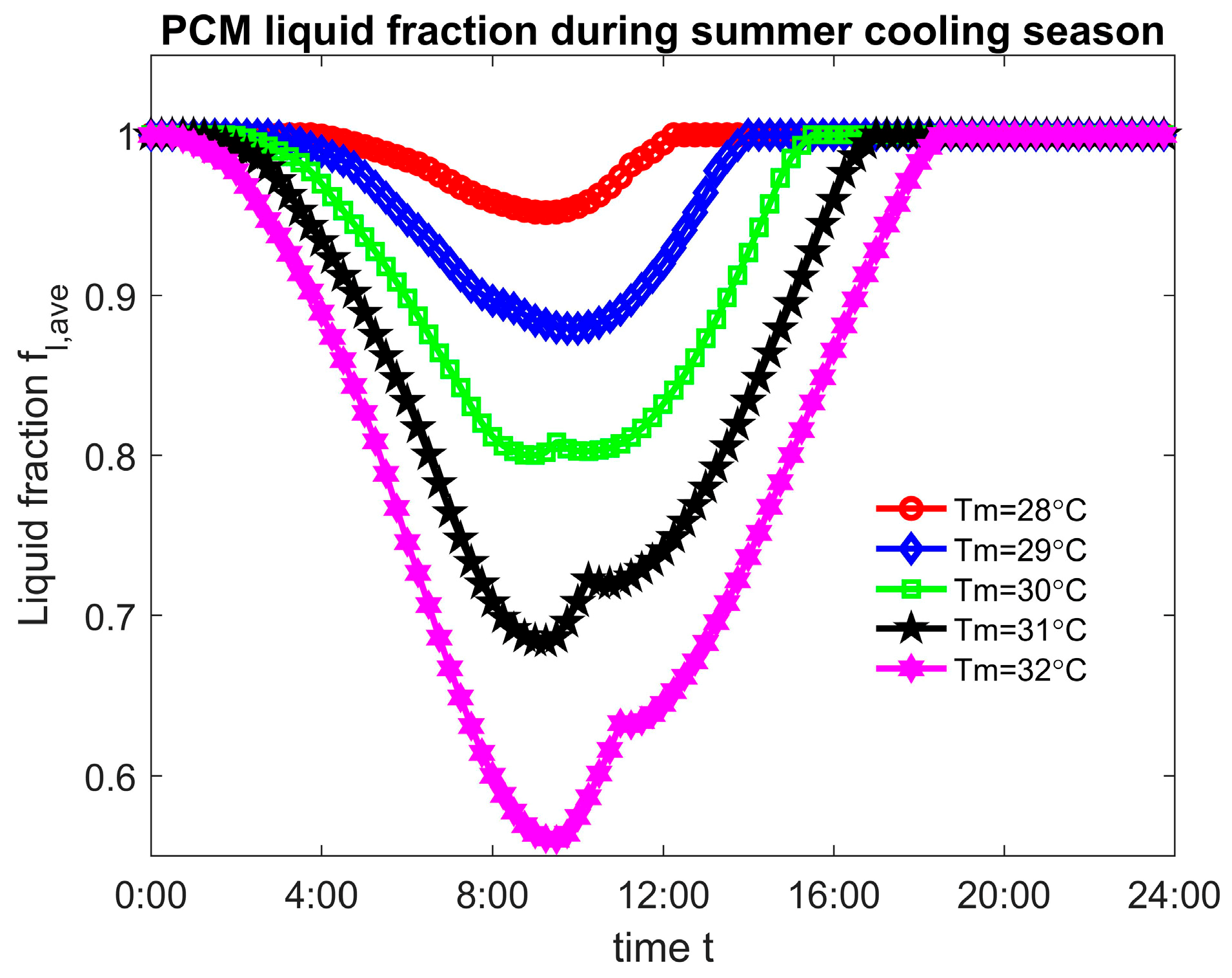
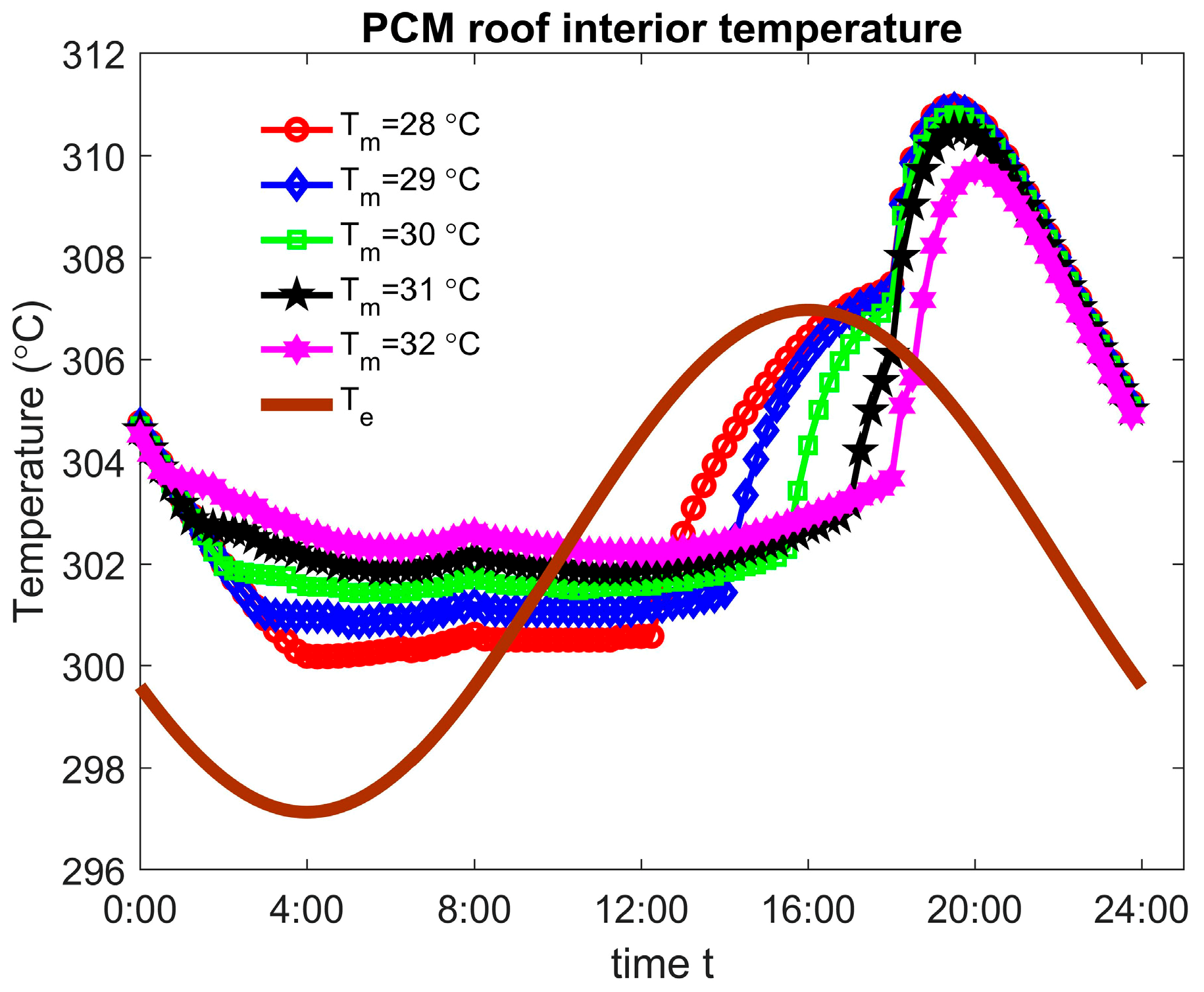
4.2. The Influence of PCM Melting Temperature
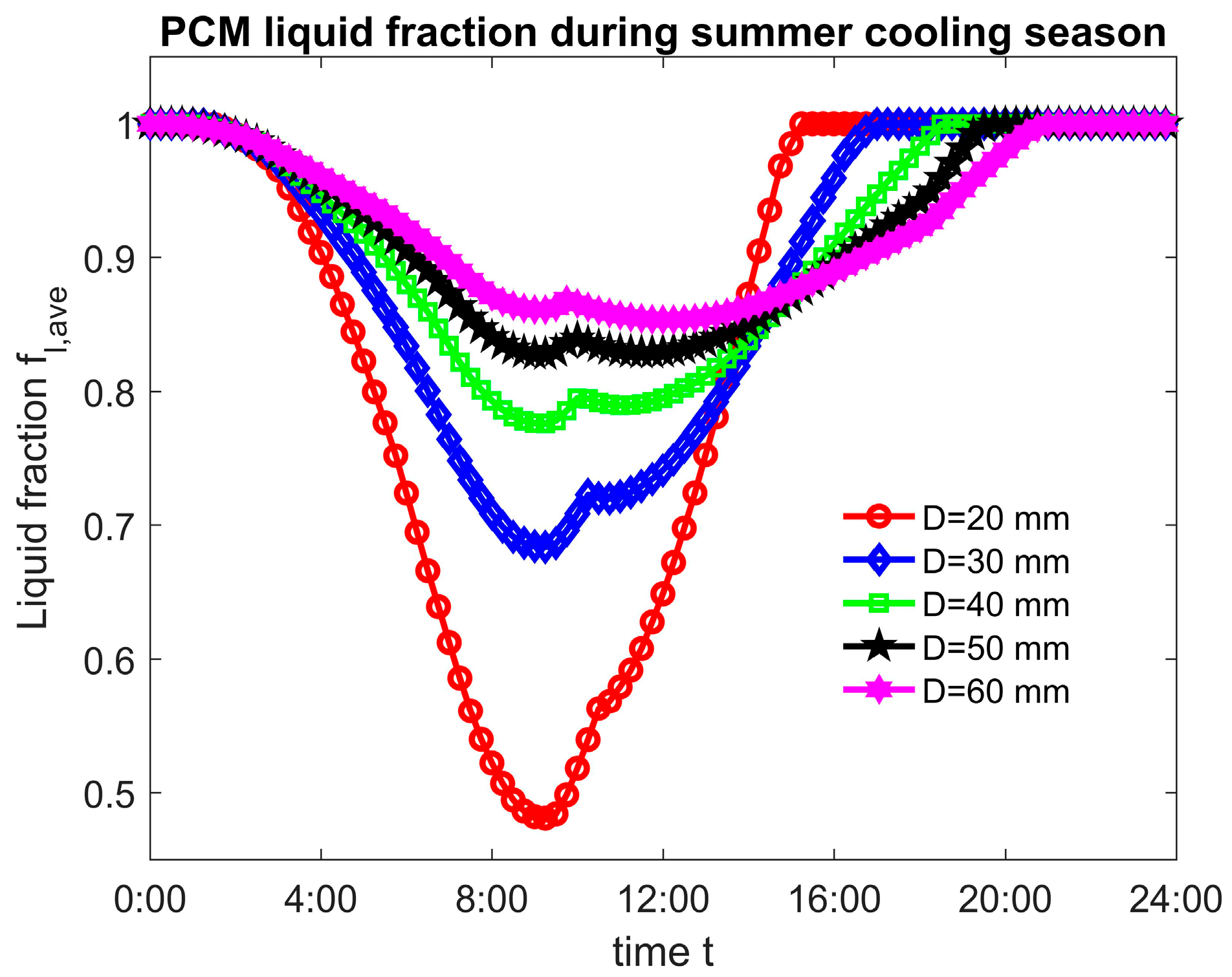
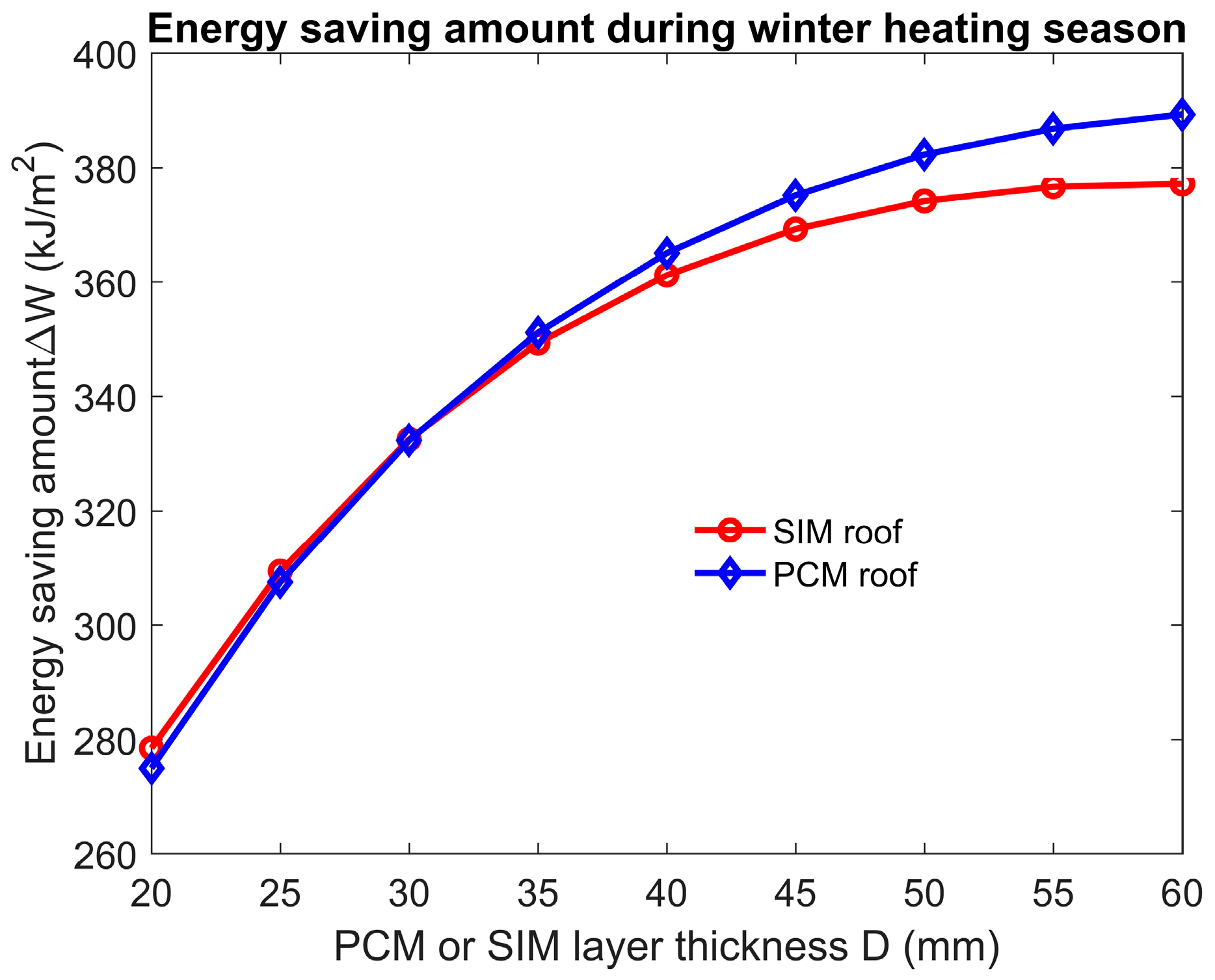
4.3. The Influence of PCM or SIM Layer Thickness
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Erdem, C.; Young, C.H.; Saffa, B.R. Performance investigation of heat insulation solar glass for low-carbon buildings. Energy Convers. Manag. 2014, 88, 834–841. [Google Scholar]
- Kong, X.; Lu, S.; Li, Y.; Huang, J.; Liu, S. Numerical study on the thermal performance of building wall and roof incorporating phase change material panel for passive cooling application. Energy Build. 2014, 81, 404–415. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Y.; Liu, C.; Wu, G. Numerical analysis on thermal performance of roof contained PCM of a single residential building. Energy Convers. Manag. 2015, 100, 147–156. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Phase change materials for building applications: A state-of-the-art review. Energy Build. 2010, 42, 1361–1368. [Google Scholar]
- Zhou, D.; Zhao, C.Y.; Tian, Y. Review on thermal energy storage with phase change materials (PCMs) in building applications. Appl. Energy 2012, 92, 593–605. [Google Scholar]
- Akeiber, H.; Nejat, P.; Majid, M.Z.A.; Wahid, M.A.; Jomehzadeh, F.; Famileh, I.Z.; Calautit, J.K.; Hughes, B.R.; Zaki, S.A. A review on phase change material (PCM) for sustainable passive cooling in building envelopes. Renew. Sustain. Energy Rev. 2016, 60, 1470–1497. [Google Scholar] [CrossRef]
- Al-Saadi, S.N.; Zhai, Z.J. Modeling phase change materials embedded in building enclosure: A review. Renew. Sustain. Energy Rev. 2013, 21, 659–673. [Google Scholar] [CrossRef]
- Izquierdo-Barrientos, M.A.; Belmonte, J.F.; Rodríguez-Sánchez, D.; Molina, A.E.; Almendros-Ibáñez, J.A. A numerical study of external building walls containing phase change materials (PCMs). Appl. Therm. Eng. 2012, 47, 73–85. [Google Scholar] [CrossRef]
- Zwanzig, S.D.; Lian, Y.; Brehob, E.G. Numerical simulation of phase change material composite wallboard in a multi-layered building envelope. Energy Convers. Manag. 2013, 69, 27–40. [Google Scholar] [CrossRef]
- Jin, X.; Medina, M.A.; Zhang, X. Numerical analysis for the optimal location of a thin PCM layer in frame walls. Appl. Therm. Eng. 2016, 103, 1057–1063. [Google Scholar] [CrossRef]
- Xie, J.; Wang, W.; Liu, J.; Pan, S. Thermal performance analysis of PCM wallboards for building application base on numerical simulation. Sol. Energy 2018, 162, 533–540. [Google Scholar] [CrossRef]
- Tokuç, A.; Başaran, T.; Yesügey, S.C. An experimental and numerical investigation on the use of phase change materials in building elements: The case of a flat roof in Istanbul. Energy Build. 2015, 102, 91–104. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, Y.; Li, D.; Meng, F.; Zheng, Y.; Liu, X. Numerical analysis on thermal performance of a PCM-filled double glazing roof. Energy Build. 2016, 125, 267–275. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Miller, W. The lattice Boltzmann method: A new tool for numerical simulation of the interaction of growth kinetics and melt flow. J. Cryst. Growth 2001, 230, 263–269. [Google Scholar] [CrossRef]
- Rasin, I.; Miller, W.; Succi, S. Phase-field lattice kinetic scheme for the numerical simulation of dendritic growth. Phys. Rev. E 2005, 72, 066705. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Wu, H. An immersed boundary-thermal lattice Boltzmann method for solid-liquid phase change. J. Comput. Phys. 2014, 277, 305–319. [Google Scholar] [CrossRef]
- Jiaung, W.S.; Ho, J.R.; Kuo, C.P. Lattice Boltzmann method for the heat conduction problem with phase change. Numer. Heat Transf. Part B Fundam. 2001, 39, 167–187. [Google Scholar]
- Eshraghi, M.; Felicelli, S.D. An implicit lattice Boltzmann model for heat conduction with phase change. Int. J. Heat Mass Transf. 2012, 55, 2420–2428. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H.; Cheng, P. A new lattice Boltzmann model for solid-liquid phase change. Int. J. Heat Mass Transf. 2013, 59, 295–301. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H. Phase interface effects in the total enthalpy-based lattice Boltzmann model for solid-liquid phase change. J. Comput. Phys. 2015, 294, 346–362. [Google Scholar] [CrossRef]
- Li, D.; Ren, Q.; Tong, Z.X.; He, Y.L. Lattice Boltzmann models for axisymmetric solid-liquid phase change. Int. J. Heat Mass Transf. 2017, 112, 795–804. [Google Scholar] [CrossRef]
- Li, D.; Tong, Z.X.; Ren, Q.; He, Y.L.; Tao, W.Q. Three-dimensional lattice Boltzmann models for solid-liquid phase change. Int. J. Heat Mass Transf. 2017, 115, 1334–1347. [Google Scholar] [CrossRef]
- Ren, Q.; Chan, C.L. Numerical study of double-diffusive convection in a vertical cavity with Soret and Dufour effects by lattice Boltzmann method on GPU. Int. J. Heat Mass Transf. 2016, 93, 538–553. [Google Scholar] [CrossRef]
- Ren, Q.; Meng, F.; Guo, P. A comparative study of PCM melting process in a heat pipe-assisted LHTES unit enhanced with nanoparticles and metal foams by immersed boundary-lattice Boltzmann method at pore-scale. Int. J. Heat Mass Transf. 2018, 121, 1214–1228. [Google Scholar] [CrossRef]
- Ren, Q. Investigation of pumping mechanism for non-Newtonian blood flow with AC electrothermal forces in a microchannel by hybrid boundary element method and immersed boundary-lattice Boltzmann method. Electrophoresis 2018, 39, 1329–1338. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.; He, Y.L.; Su, K.Z.; Chan, C.L. Investigation of the effect of metal foam chracteristics on the PCM melting performance in a latent heat thermal energy storage unit by pore-scale lattice Boltzmann modelling. Numer. Heat Transf. Part A Appl. 2017, 72, 745–764. [Google Scholar] [CrossRef]
- Ren, Q. Bioparticle delivery in physiological conductivity solution using AC electrokinetic micropump with castellated electrodes. J. Phys. D Appl. Phys. 2018. [Google Scholar] [CrossRef]
- Ren, Q.; Meng, F.; Chan, C.L. Cell transport and suspension in high conductivity electrothermal flow with negative dielectrophoresis by immersed boundary-lattice Boltzmann method. Int. J. Heat Mass Transf. 2019, 128, 1129–1244. [Google Scholar] [CrossRef]
- Ren, Q.; Chan, C.L. Natural convection with an array of solid obstacles in an enclosure by lattice Boltzmann method on a CUDA computation platform. Int. J. Heat Mass Transf. 2016, 93, 273–285. [Google Scholar] [CrossRef]
- Ren, Q.; Chan, C.L. GPU accelerated numerical study of PCM melting process in an enclosure with internal fins using lattice Boltzmann method. Int. J. Heat Mass Transf. 2016, 100, 522–535. [Google Scholar] [CrossRef]
- Jany, P.; Bejan, A. Scaling theory of melting with natural convection in an enclosure. Int. J. Heat Mass Transf. 1988, 31, 1221–1235. [Google Scholar] [CrossRef]
- Li, J.; Tian, Z. Incremental cost-benefit of life cycle green buildings. J. Eng. Manag. 2011, 5, 004. [Google Scholar]
- Ballim, Y. A numerical model and associated calorimeter for predicting temperature profiles in mass concrete. Cem. Concr. Compos. 2004, 26, 695–703. [Google Scholar] [CrossRef]


| Material | ||||
|---|---|---|---|---|
| Cement | ||||
| Concrete | - | |||
| Paraffin | ||||
| Perlite | 350 | |||
| Lime |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, B.; Du, X.; Ren, Q. Numerical Investigation of Energy Saving Characteristic in Building Roof Coupled with PCM Using Lattice Boltzmann Method with Economic Analysis. Appl. Sci. 2018, 8, 1739. https://doi.org/10.3390/app8101739
Shao B, Du X, Ren Q. Numerical Investigation of Energy Saving Characteristic in Building Roof Coupled with PCM Using Lattice Boltzmann Method with Economic Analysis. Applied Sciences. 2018; 8(10):1739. https://doi.org/10.3390/app8101739
Chicago/Turabian StyleShao, Bilin, Xingxuan Du, and Qinlong Ren. 2018. "Numerical Investigation of Energy Saving Characteristic in Building Roof Coupled with PCM Using Lattice Boltzmann Method with Economic Analysis" Applied Sciences 8, no. 10: 1739. https://doi.org/10.3390/app8101739
APA StyleShao, B., Du, X., & Ren, Q. (2018). Numerical Investigation of Energy Saving Characteristic in Building Roof Coupled with PCM Using Lattice Boltzmann Method with Economic Analysis. Applied Sciences, 8(10), 1739. https://doi.org/10.3390/app8101739






