Hard X-ray Generation from ZnO Nanowire Targets in a Non-Relativistic Regime of Laser-Solid Interactions
Abstract
1. Introduction
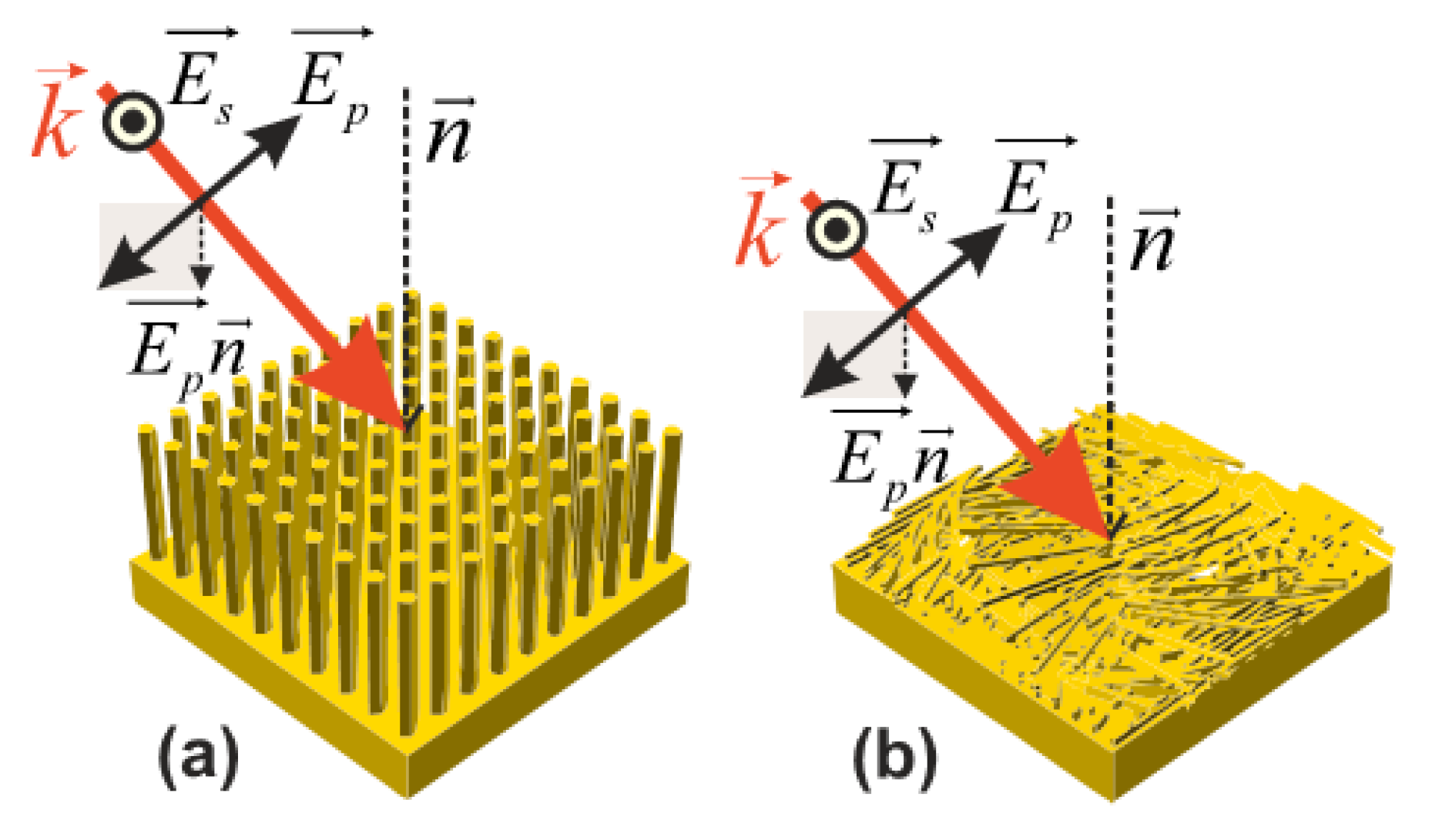
2. Materials and Methods
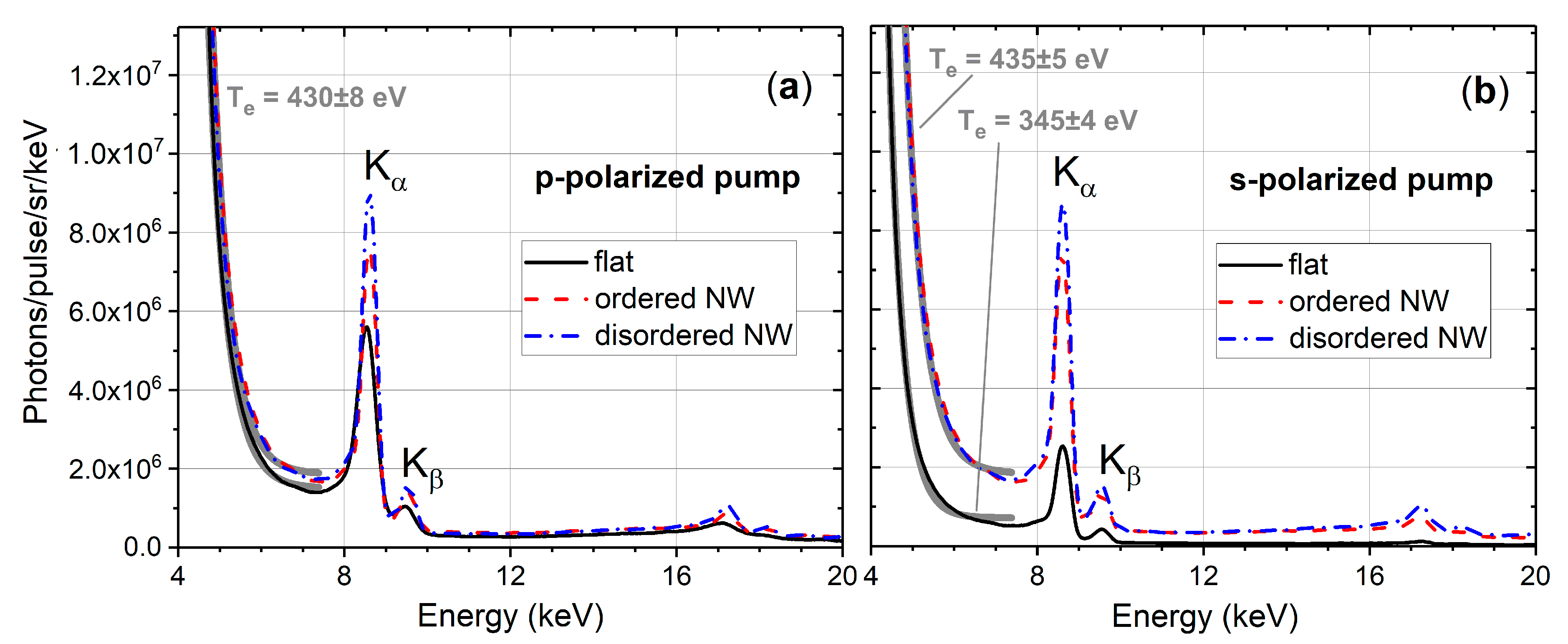
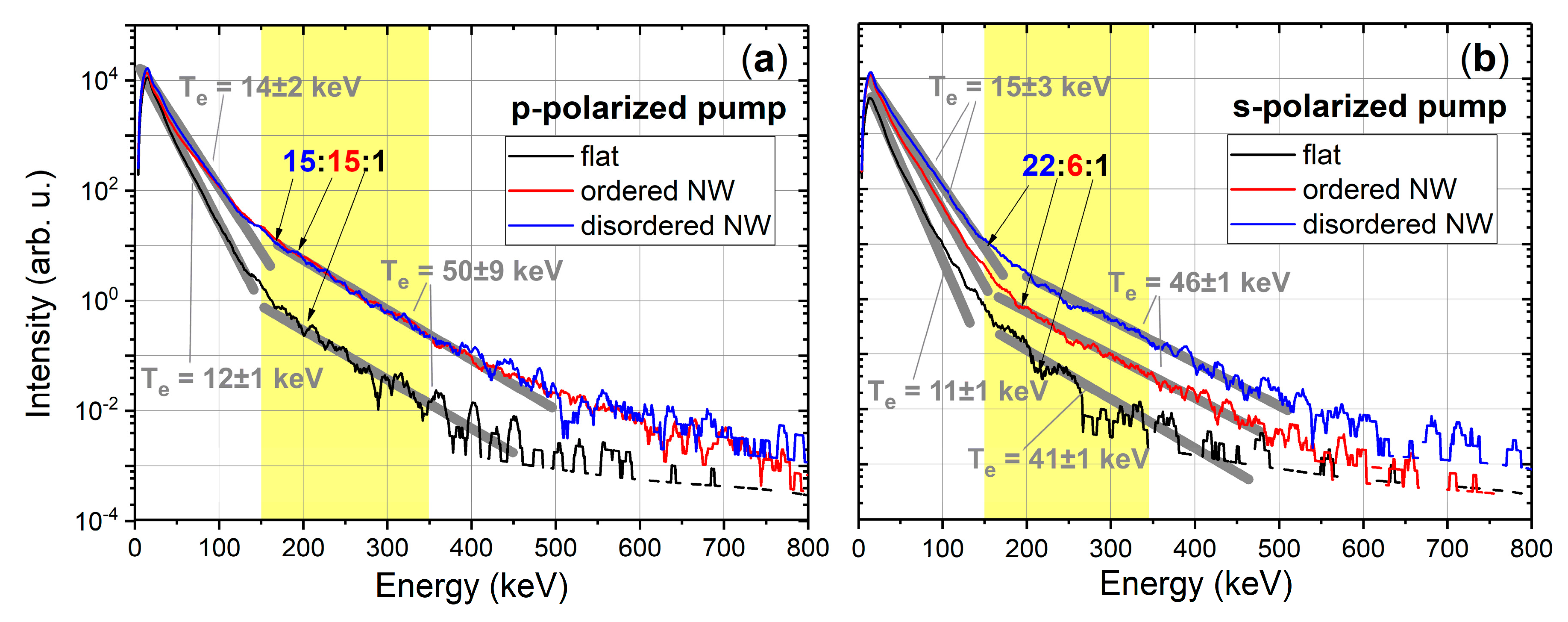
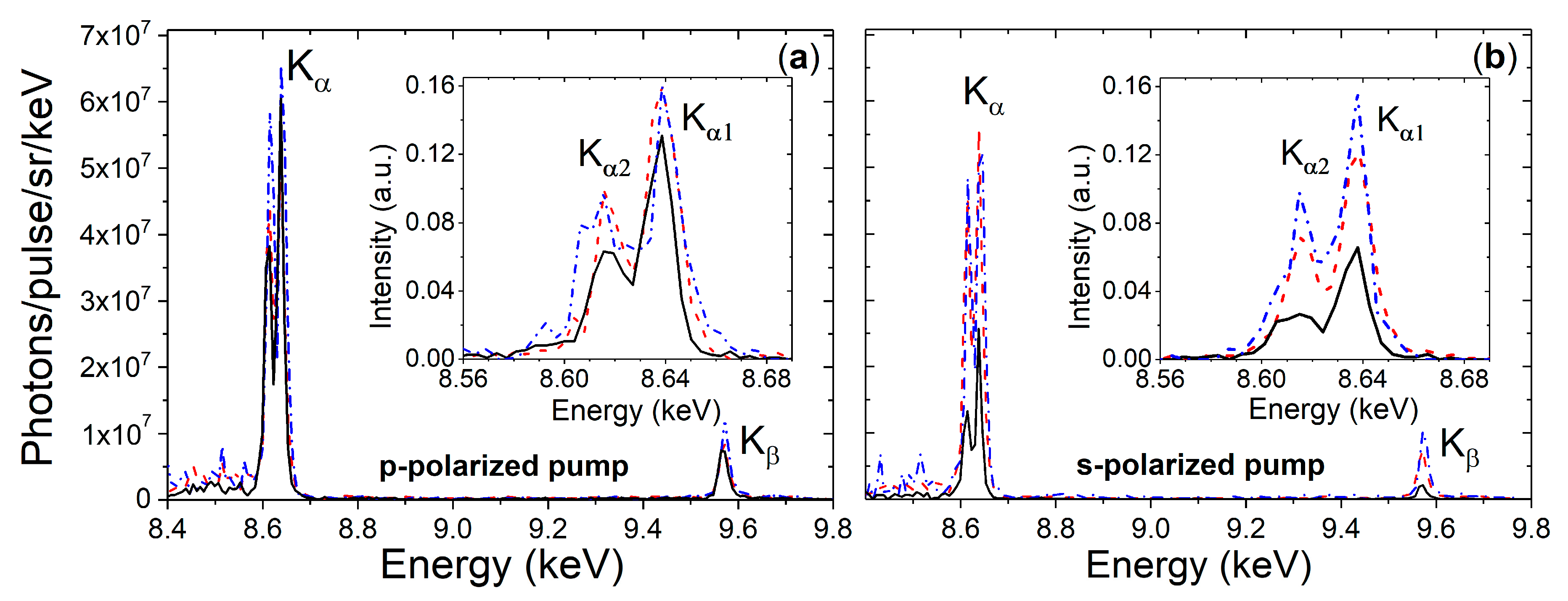
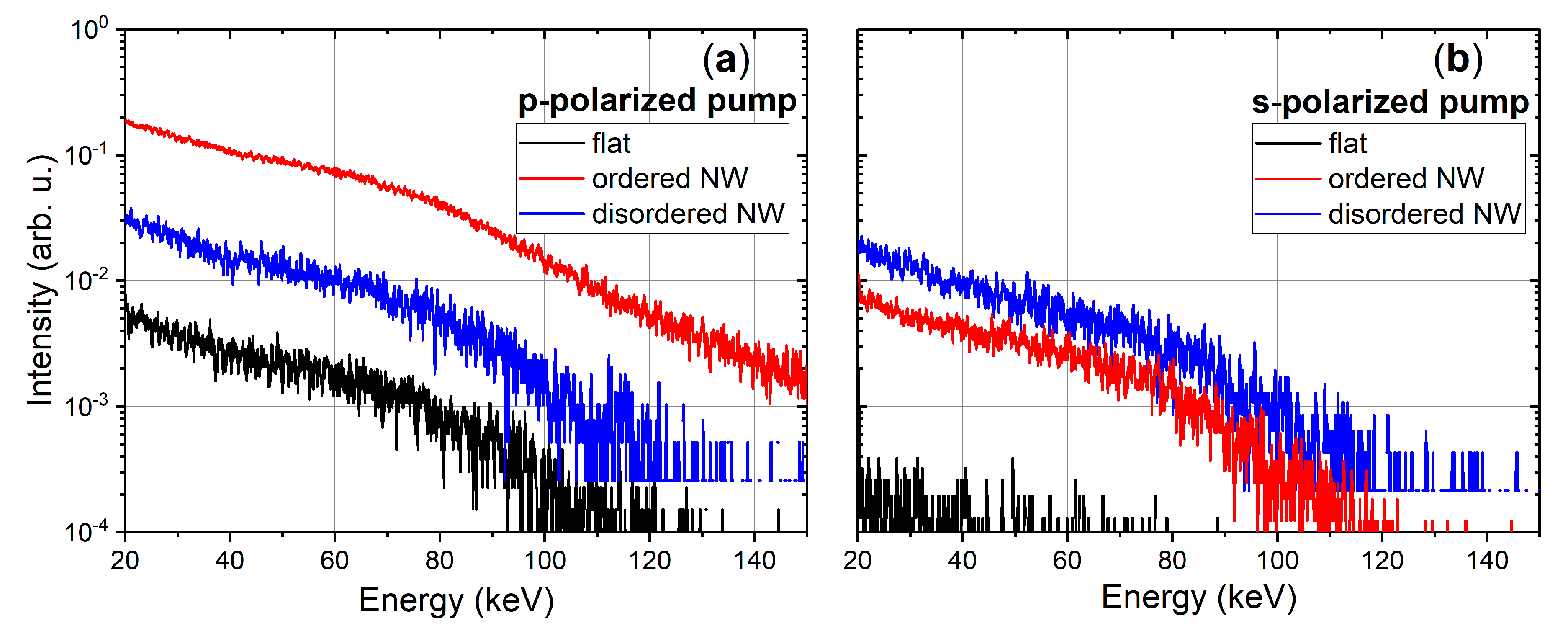
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rousse, A.; Rischel, C.; Gauthier, J.-C. Ultrafast X-ray sources and applications. Comptes Rendus de l’Académie des Sciences-Series IV-Physics 2000, 1, 305–315. [Google Scholar] [CrossRef]
- Umstadter, D. Relativistic laser–Plasma interactions. J. Phys. D Appl. Phys. 2003, 36, R151. [Google Scholar] [CrossRef]
- Beg, F.N.; Bell, A.R.; Dangor, A.E.; Danson, C.N.; Fews, A.P.; Glinsky, M.E.; Hammel, B.A.; Lee, P.; Norreys, P.A.; Tatarakis, M. A study of picosecond laser–Solid interactions up to 1019 W cm−2. Phys. Plasmas 1997, 4, 447–457. [Google Scholar] [CrossRef]
- Cowan, T.E.; Hunt, A.W.; Phillips, T.W.; Wilks, S.C.; Perry, M.D.; Brown, C.; Fountain, W.; Hatchett, S.; Johnson, J.; Key, M.H.; et al. Photonuclear fission from high energy electrons from ultraintense laser-solid interactions. Phys. Rev. Lett. 2000, 84, 903–906. [Google Scholar] [CrossRef] [PubMed]
- Schwoerer, H.; Gibbon, P.; Düsterer, S.; Behrens, R.; Ziener, C.; Reich, C.; Sauerbrey, R. MeV X rays and photoneutrons from femtosecond laser-produced plasmas. Phys. Rev. Lett. 2001, 86, 2317–2320. [Google Scholar] [CrossRef] [PubMed]
- Park, H.-S.; Chambers, D.M.; Chung, H.-K.; Clarke, R.J.; Eagleton, R.; Giraldez, E.; Goldsack, T.; Heathcote, R.; Izumi, N.; Key, M.H.; et al. High-energy Kα radiography using high-intensity, short-pulse lasers. Phys. Plasmas 2006, 13, 056309. [Google Scholar] [CrossRef]
- Fourmaux, S.; Kieffer, J.C. Laser-based Kα X-ray emission characterization using a high contrast ratio and high-power laser system. Appl. Phys. B 2016, 122, 162. [Google Scholar] [CrossRef]
- Hagedorn, M.; Kutzner, J.; Tsilimis, G.; Zacharias, H. High-repetition-rate hard X-ray generation with sub-millijoule femtosecond laser pulses. Appl. Phys. B 2003, 77, 49–57. [Google Scholar] [CrossRef]
- Zamponi, F.; Ansari, Z.; Korff Schmising, C.V.; Rothhardt, P.; Zhavoronkov, N.; Woerner, M.; Elsaesser, T.; Bargheer, M.; Trobitzsch-Ryll, T.; Haschke, M. Femtosecond hard X-ray plasma sources with a kilohertz repetition rate. Appl. Phys. A 2009, 96, 51–58. [Google Scholar] [CrossRef]
- Holtz, M.; Hauf, C.; Weisshaupt, J.; Salvador, A.-A.H.; Woerner, M.; Elsaesser, T. Towards shot-noise limited diffraction experiments with table-top femtosecond hard x-ray sources. Struct. Dyn. 2017, 4, 054304. [Google Scholar] [CrossRef]
- Silies, M.; Witte, H.; Linden, S.; Kutzner, J.; Uschmann, I.; Förster, E.; Zacharias, H. Table-top kHz hard X-ray source with ultrashort pulse duration for time-resolved X-ray diffraction. Appl. Phys. A 2009, 96, 59–67. [Google Scholar] [CrossRef]
- Höfer, S.; Kämpfer, T.; Förster, E.; Stöhlker, T.; Uschmann, I. The formation of rarefaction waves in semiconductors after ultrashort excitation probed by grazing incidence ultrafast time-resolved x-ray diffraction. Struc. Dyn. 2016, 3, 051101. [Google Scholar] [CrossRef] [PubMed]
- Park, H.-S.; Maddox, B.R.; Giraldez, E.; Hatchett, S.P.; Hudson, L.T.; Izumi, N.; Key, M.H.; Le Pape, S.; MacKinnon, A.J.; MacPhee, A.G.; et al. High-resolution 17–75 keV backlighters for high energy density experiments. Phys. Plasmas 2008, 15, 072705. [Google Scholar] [CrossRef]
- Remington, B.A.; Rudd, R.E.; Wark, J.S. From microjoules to megajoules and kilobars to gigabars: Probing matter at extreme states of deformation. Phys. Plasmas 2015, 22, 090501. [Google Scholar] [CrossRef]
- Benesch, F.; Lee, T.W.; Jiang, Y.; Rose-Petruck, C.G. Ultrafast laser-driven x-ray spectrometer for x-ray absorption spectroscopy of transition metal complexes. Opt. Lett. 2004, 29, 1028–1030. [Google Scholar] [CrossRef] [PubMed]
- Fullagar, W.; Harbst, M.; Canton, S.; Uhlig, J.; Walczak, M.; Wahlström, C.-G.; Sundström, V. A broadband laser plasma x-ray source for application in ultrafast chemical structure dynamics. Rev. Sci. Instrum. 2007, 78, 115105. [Google Scholar] [CrossRef] [PubMed]
- Kulcsár, G.; AlMawlawi, D.; Budnik, F.W.; Herman, P.R.; Moskovits, M.; Zhao, L.; Marjoribanks, R.S. Intense picosecond X-Ray pulses from laser plasmas by use of nanostructured “Velvet” targets. Phys. Rev. Lett. 2000, 84, 5149–5152. [Google Scholar] [CrossRef]
- Rajeev, P.P.; Banerjee, S.; Sandhu, A.S.; Issac, R.C.; Tribedi, L.C.; Kumar, G.R. Role of surface roughness in hard-X-ray emission from femtosecond-laser-produced copper plasmas. Phys. Rev. A 2002, 65, 052903. [Google Scholar] [CrossRef]
- Rajeev, P.P.; Taneja, P.; Ayyub, P.; Sandhu, A.S.; Ravindra Kumar, G. Metal nanoplasmas as bright sources of hard X-Ray pulses. Phys. Rev. Lett. 2003, 90, 115002. [Google Scholar] [CrossRef] [PubMed]
- Andreev, A.A.; Platonov, K.Y. Interaction of ultra high intensity laser pulse with structured target and fast particle generation in a stable mode. Contrib. Plasma Phys. 2013, 53, 173–178. [Google Scholar] [CrossRef]
- Purvis, M.A.; Shlyaptsev, V.N.; Hollinger, R.; Bargsten, C.; Pukhov, A.; Prieto, A.; Wang, Y.; Luther, B.M.; Yin, L.; Wang, S.; et al. Relativistic plasma nanophotonics for ultrahigh energy density physics. Nat. Photonics 2013, 7, 796–800. [Google Scholar] [CrossRef]
- Uschmann, I.; Kämpfer, T.; Zamponi, F.; Lübcke, A.; Zastrau, U.; Loetzsch, R.; Höfer, S.; Morak, A.; Förster, E. Investigation of fast processes in condensed matter by time-resolved x-ray diffraction. Appl. Phys. A 2009, 96, 91–98. [Google Scholar] [CrossRef]
- Borchers, C.; Stichtenoth, D.; Müller, S.; Schwen, D.; Ronning, C. Catalyst−Nanostructure interaction in the growth of 1-D ZnO nanostructures. J. Phys. Chem. B 2016, 110, 1656–1660. [Google Scholar] [CrossRef] [PubMed]
- Johannes, A.; Noack, S.; Paschoal, W., Jr.; Kumar, S.; Jacobsson, D.; Pettersson, H.; Samuelson, L.; Dick, K.A.; Martinez-Criado, G.; Burghammer, M.; et al. Enhanced sputtering and incorporation of Mn in implanted GaAs and ZnO nanowires. J. Phys. D 2014, 47, 394003. [Google Scholar] [CrossRef]
- Wagner, R.S.; Ellis, W.C. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett. 1964, 4, 89–90. [Google Scholar] [CrossRef]
- Yang, P.; Yan, H.; Mao, S.; Russo, R.; Johnson, J.; Saykally, R.; Morris, N.; Pham, J.; He, R.; Choi, H.-J. Controlled Growth of ZnO Nanowires and Their Optical Properties. Adv. Funct. Mater. 2002, 12, 323–331. [Google Scholar] [CrossRef]
- Hahn, C.; Weber, G.; Märtin, R.; Höfer, S.; Kämpfer, T.; Stöhlker, T. CdTe Timepix detectors for single-photon spectroscopy and linear polarimetry of high-flux hard x-ray radiation. Rev. Sci. Instrum. 2016, 87, 043106. [Google Scholar] [CrossRef]
- Sjögren, A.; Harbst, M.; Wahlström, C.-G.; Svanberg, S.; Olsson, C. High-repetition-rate, hard x-ray radiation from a laser-produced plasma: Photon yield and application considerations. Rev. Sci. Instrum. 2003, 74, 2300–2311. [Google Scholar] [CrossRef]
- Chen, C.D.; Patel, P.K.; Hey, D.S.; Mackinnon, A.J.; Key, M.H.; Akli, K.U.; Bartal, T.; Beg, F.N.; Chawla, S.; Chen, H.; et al. Bremsstrahlung and Kα fluorescence measurements for inferring conversion efficiencies into fast ignition relevant hot electrons. Phys. Plasmas 2009, 16, 082705. [Google Scholar] [CrossRef]
- Lötzsch, R.; Jäckel, O.; Höfer, S.; Kämpfer, T.; Polz, J.; Uschmann, I.; Kaluza, M.C.; Förster, E.; Stambulchik, E.; Kroupp, E.; et al. K-shell spectroscopy of silicon ions as diagnostic for high electric fields. Rev. Sci. Instrum. 2012, 83, 113507. [Google Scholar] [CrossRef]
- Livet, F.; Bley, F.; Mainville, J.; Caudron, R.; Mochrie, S.G.J.; Geissler, E.; Dolino, G.; Abernathy, D.; Grübel, G.; Sutton, M. Using direct illumination CCDs as high-resolution area detectors for X-ray scattering. Nucl. Instrum. Methods Phys. Res. A 2000, 451, 596–609. [Google Scholar] [CrossRef]
- McCall, G.H. Calculation of X-ray bremsstrahlung and characteristic line emission produced by a Maxwellian electron distribution. J. Phys. D 1982, 15, 823. [Google Scholar] [CrossRef]
- Rosmej, O.N.; Samsonova, Z.; Höfer, S.; Kartashov, D.; Arda, C.; Khaghani, D.; Schoenlein, A.; Zähter, S.; Hoffmann, A.; Loetzsch, R.; et al. Generation of keV hot near-solid density plasma states at high contrast laser-matter interaction. Phys. Plasmas 2018, 25, 083103. [Google Scholar] [CrossRef]
- Ivanov, K.; Shulyapov, S.; Turinge, A.; Brantov, A.; Uryupina, D.; Volkov, R.; Rusakov, A.; Djilkibaev, R.; Nedorezov, V.; Bychenkov, V.; et al. X-Ray Diagnostics of Ultrashort Laser-Driven Plasma: Experiment and Simulations. Contrib. Plasma Phys. 2013, 53, 116–121. [Google Scholar] [CrossRef]
- Sherlock, M. Universal scaling of the electron distribution function in one-dimensional simulations of relativistic laser-plasma interactions. Phys. Plasmas 2009, 16, 103101. [Google Scholar] [CrossRef]
- Burnett, N.H.; Enright, G.D. Hot-electron generation and transport in high-intensity laser interaction. Can. J. Phys. 1986, 64, 920–931. [Google Scholar] [CrossRef]
- Brunel, F. Not-so-resonant, resonant absorption. Phys. Rev. Lett. 1987, 59, 52–55. [Google Scholar] [CrossRef] [PubMed]
- Gibbon, P.; Bell, A.R. Collisionless absorption in sharp-edged plasmas. Phys. Rev. Lett. 1992, 68, 1535–1538. [Google Scholar] [CrossRef] [PubMed]
- Mulser, P.; Weng, S.M.; Liseykina, T. Analysis of the Brunel model and resulting hot electron spectra. Phys. Plasmas 2012, 19, 043301. [Google Scholar] [CrossRef]
- Liseykina, T.; Mulser, P.; Murakami, M. Collisionless absorption, hot electron generation and energy scaling in intense laser-target interaction. Phys. Plasmas 2015, 22, 033302. [Google Scholar] [CrossRef]
- Mondal, S.; Chakraborty, I.; Ahmad, S.; Carvalho, D.; Singh, P.; Lad, A.D.; Narayanan, V.; Ayyub, P.; Ravindra Kumar, G.; Zheng, J.; et al. Highly enhanced hard x-ray emission from oriented metal nanorod arrays excited by intense femtosecond laser pulses. Phys. Rev. B 2011, 83, 035408. [Google Scholar] [CrossRef]
- Salzmann, D.; Reich, C.; Uschmann, I.; Förster, E.; Gibbon, P. Theory of Kα generation by femtosecond laser-produced hot electrons in thin foils. Phys. Rev. E 2002, 65, 036402. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.J.; Coursey, J.S.; Zucker, M.A.; Chang, J. PSTAR, and ASTAR: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions (Version 1.2.3); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005; Volume 39. Available online: http://physics.nist.gov/Star (accessed on 10 July 2018).


| Flat | Ordered NW | Disordered NW | |
|---|---|---|---|
| p-polarization | 1 | 1.19 ± 0.04 | 1.31 ± 0.05 |
| s-polarization | 1 | 2.79 ± 0.11 | 3.18 ± 0.08 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samsonova, Z.; Höfer, S.; Hollinger, R.; Kämpfer, T.; Uschmann, I.; Röder, R.; Trefflich, L.; Rosmej, O.; Förster, E.; Ronning, C.; et al. Hard X-ray Generation from ZnO Nanowire Targets in a Non-Relativistic Regime of Laser-Solid Interactions. Appl. Sci. 2018, 8, 1728. https://doi.org/10.3390/app8101728
Samsonova Z, Höfer S, Hollinger R, Kämpfer T, Uschmann I, Röder R, Trefflich L, Rosmej O, Förster E, Ronning C, et al. Hard X-ray Generation from ZnO Nanowire Targets in a Non-Relativistic Regime of Laser-Solid Interactions. Applied Sciences. 2018; 8(10):1728. https://doi.org/10.3390/app8101728
Chicago/Turabian StyleSamsonova, Zhanna, Sebastian Höfer, Richard Hollinger, Tino Kämpfer, Ingo Uschmann, Robert Röder, Lukas Trefflich, Olga Rosmej, Eckhart Förster, Carsten Ronning, and et al. 2018. "Hard X-ray Generation from ZnO Nanowire Targets in a Non-Relativistic Regime of Laser-Solid Interactions" Applied Sciences 8, no. 10: 1728. https://doi.org/10.3390/app8101728
APA StyleSamsonova, Z., Höfer, S., Hollinger, R., Kämpfer, T., Uschmann, I., Röder, R., Trefflich, L., Rosmej, O., Förster, E., Ronning, C., Kartashov, D., & Spielmann, C. (2018). Hard X-ray Generation from ZnO Nanowire Targets in a Non-Relativistic Regime of Laser-Solid Interactions. Applied Sciences, 8(10), 1728. https://doi.org/10.3390/app8101728







