Live Load Distribution Factors for Skew Stringer Bridges with High-Performance-Steel Girders under Truck Loads
Abstract
1. Introduction
2. Finite Element Modeling and Verification
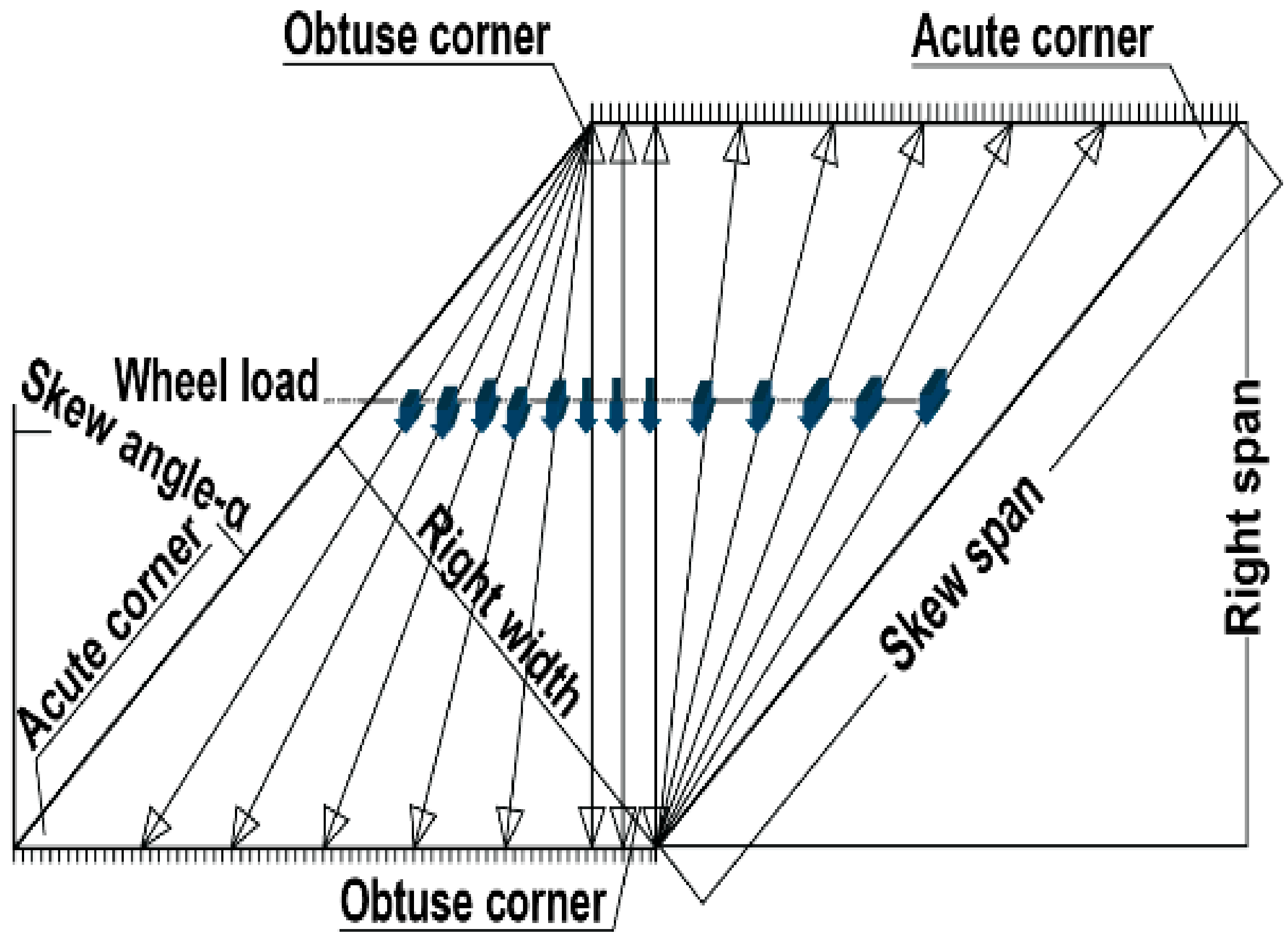
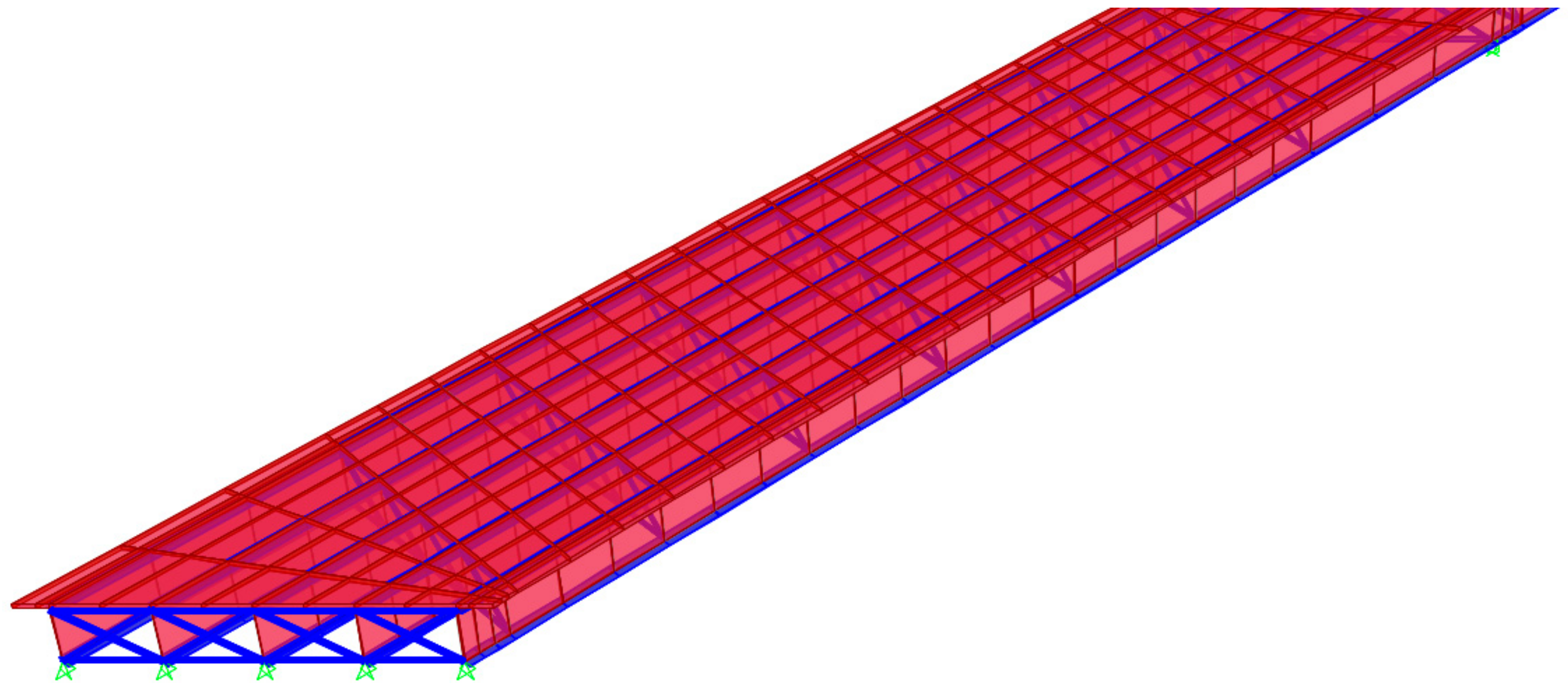
2.1. Bridge Section
2.2. Verification of Finite Element Models
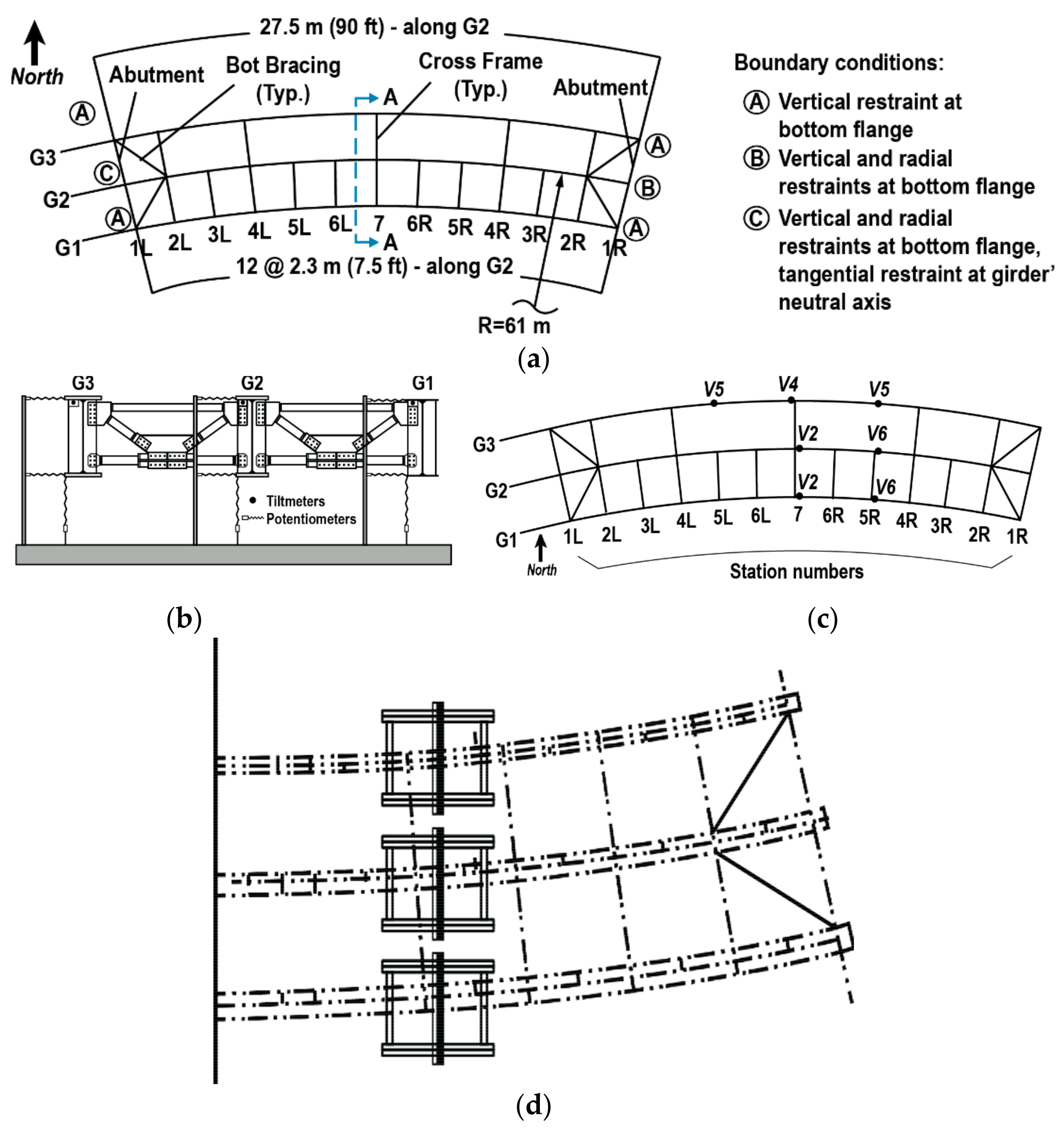
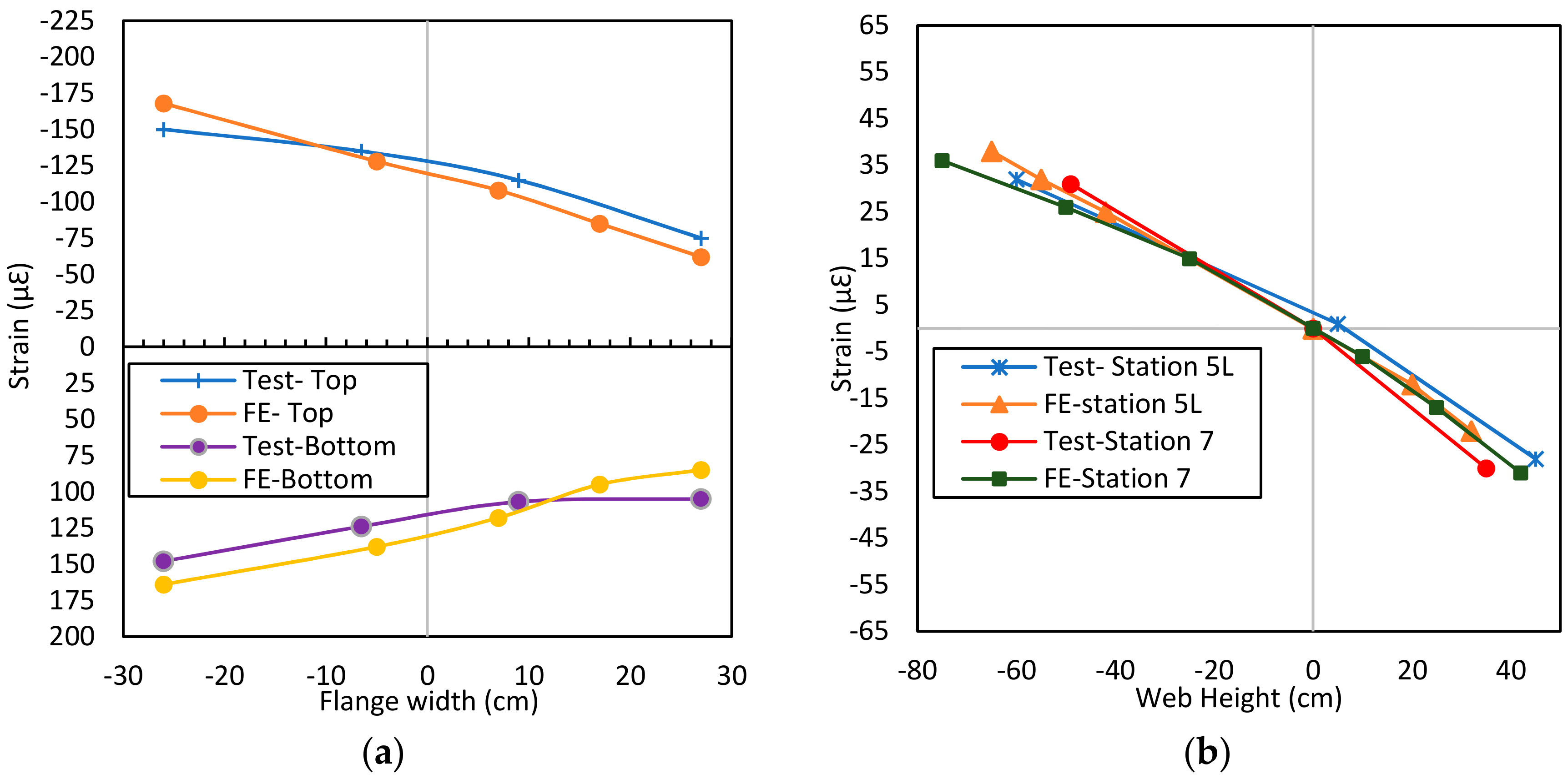
2.2.1. Laboratory Tests at the Turner-Fairbank Highway Research Center
2.2.2. Laboratory Test of a Quarter Scale Model Bridge
3. Bridge Superstructure Database
4. Sensitivity Analysis
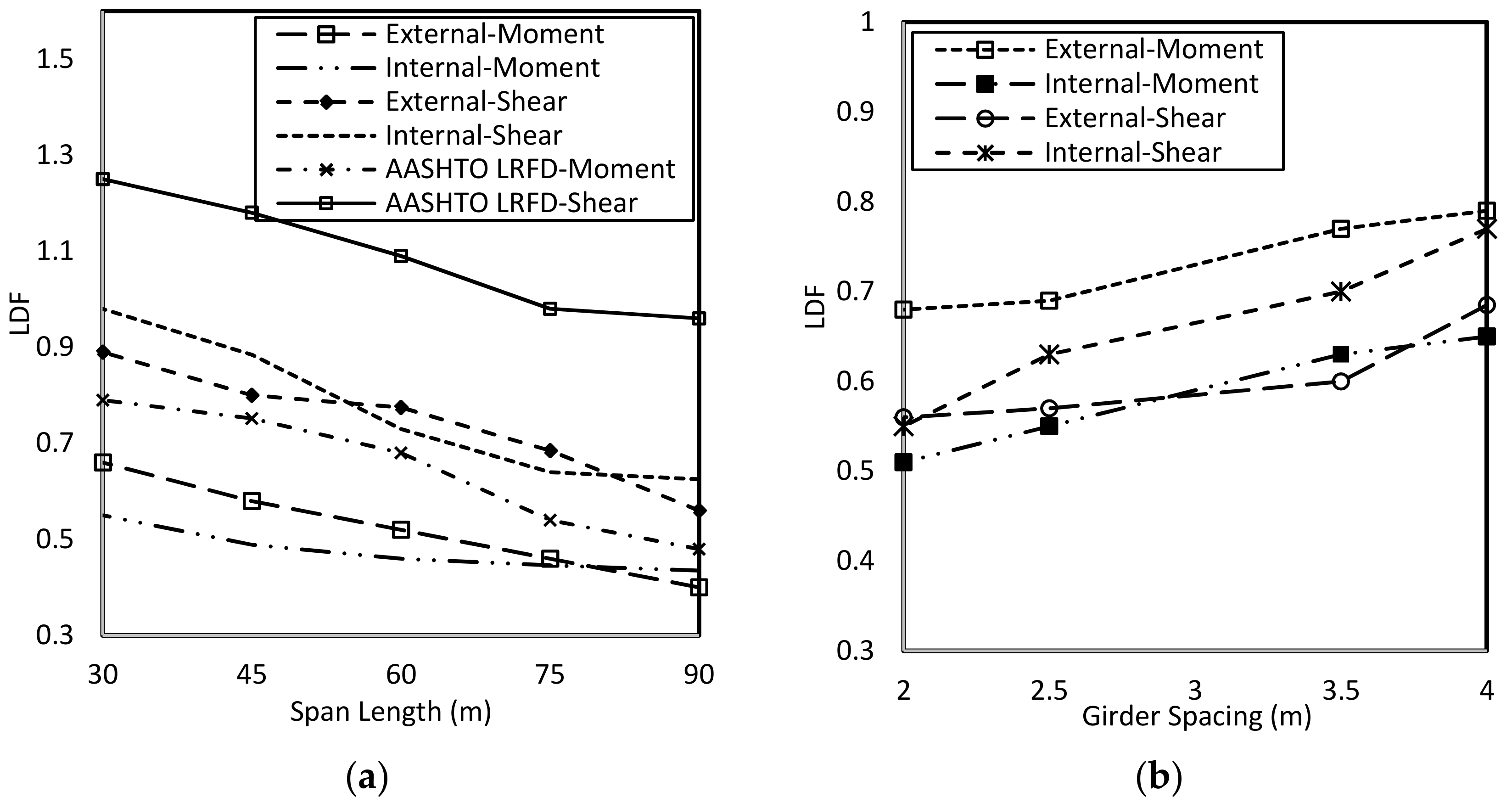
4.1. Effect of Span Length
4.2. Effect of Girder Spacing
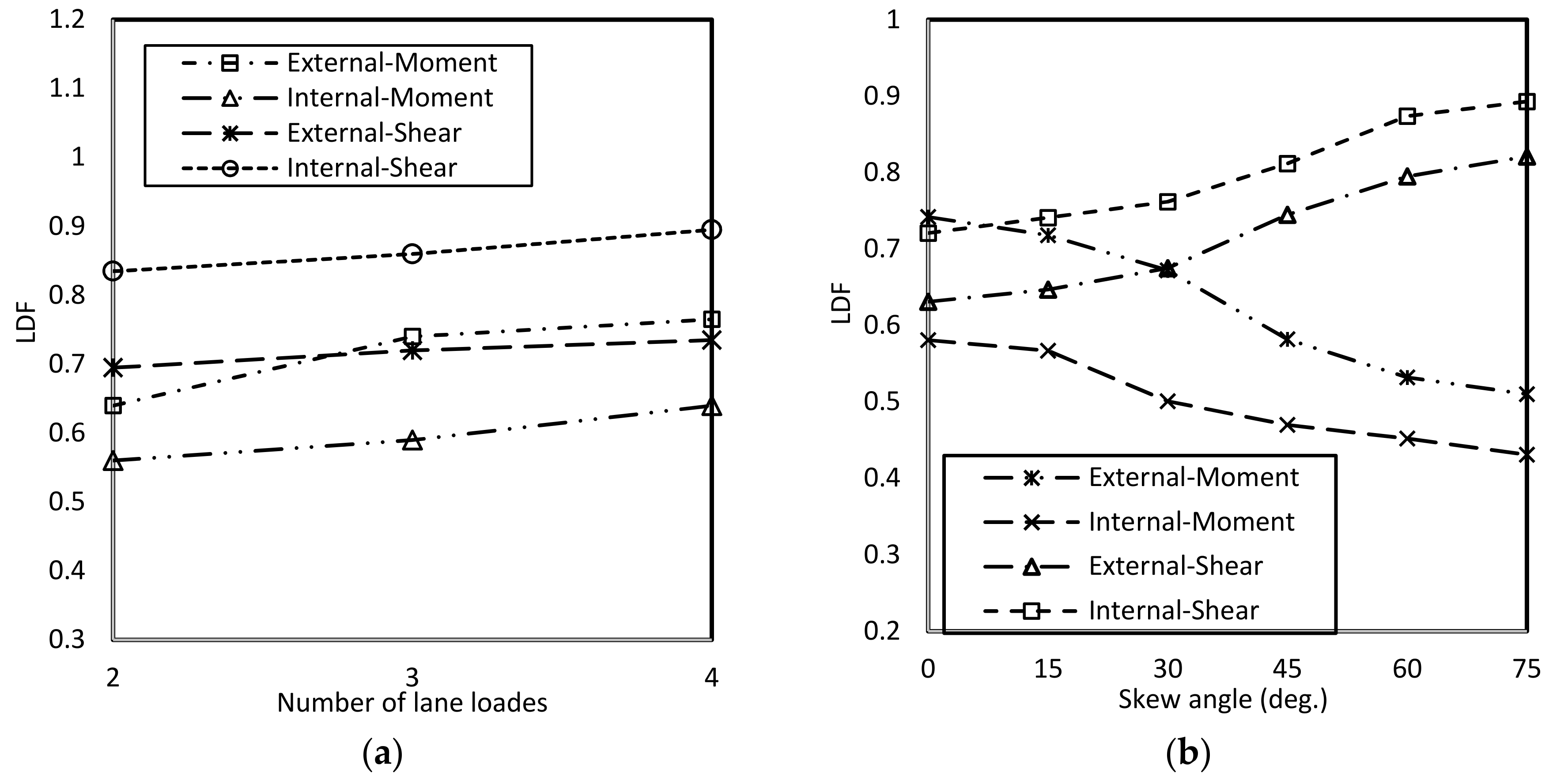
4.3. Effect of Number of Lane Loads
4.4. Effect of the Skew Angle
5. Development of New Equations for the Live Load Distribution Factors
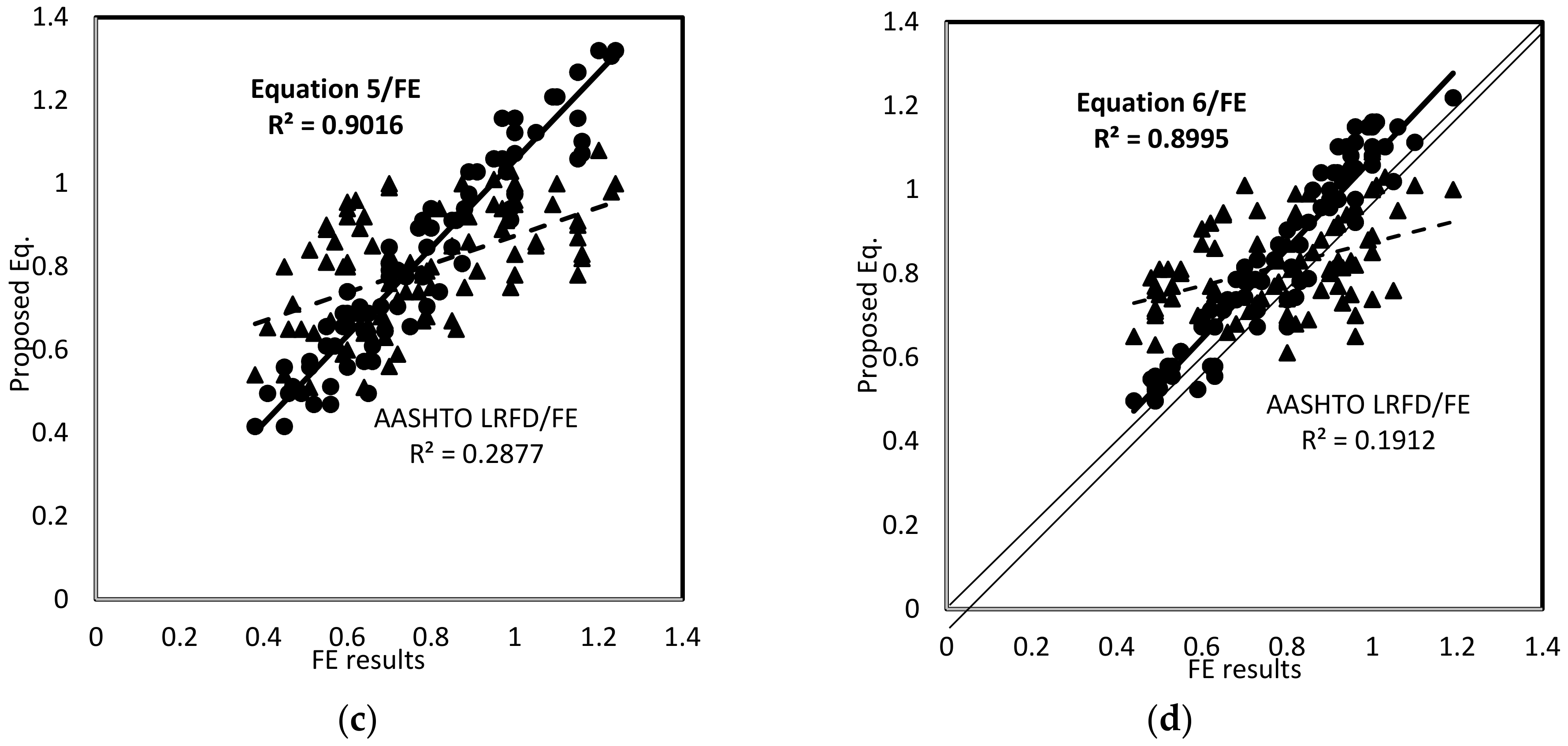
6. Verification of the Proposed Equations
7. Conclusions and Recommendations
- A good agreement in the structural responses was achieved between the 3-dimensional modeling of the prototype bridges and the results obtained experimentally, confirming that numerical models can reliably predict the responses of slab-on-girder bridges.
- The discrepancy between the finite element results and those calculated using the codified AASHTO LRFD equations revealed that the current LRFD specifications are not suitable for predicting the live load distribution factors for both the bending moment and the shear force for skewed composite bridge with HPS girders. It was therefore necessary to develop a new set of LDF equations for both shear and moment.
- Based on the results of the parametric study on prototype bridges, the span length, girder spacing, number of lane loaded, and skew angle were identified as the key parameters affecting the LDFs of skewed composite bridges. The LDFs for both shear force and bending moment decreased with increasing span length and number of lanes, and increased with increased girder spacing. Increasing the skew angle of the bridge superstructures increased the LDFs for shear force but decreased those for bending moment.
- Based on the statistical analysis, conducted for this study, a set of simplified expressions were developed for the LDFs for both shear force and bending moment. The slightly greater than unity average and low standard deviation and coefficient of variation for each of the proposed expressions indicate high reliabilities for these proposed expressions in estimating the LDFs for shear force and bending moment of skewed composite bridge with HPS girders.
- More studies can be carried to assess the dynamic interaction of these type of bridge and moving load due to traffic conditions. The simplified equations can be derived to determine dynamic impact factor of bridges with HPS steel.
- Analytical and computational approaches to study the seismic response characteristics of bridges are the most economically feasible methods. It is particularly important to investigate the performance of skewed bridges with HPS steel due to vertical ground motions. The study, therefore, would provide comprehensive results through including all the parameters interacting for a wide range of skew angles.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huo, X.S.; Zhang, Q. Effect of skewness on the distribution of live load reaction at piers of skewed continuous bridges. J. Bridge Eng. 2008, 13, 110–114. [Google Scholar] [CrossRef]
- Deng, Y.; Phares, B.; Lu, P. Lateral live-load distribution of dual-lane vehicles with nonstandard axle configurations. J. Bridge Eng. 2017, 22, 110–114. [Google Scholar] [CrossRef]
- Mohseni, I.; Khalim, A.R. Transverse load distribution of skew cast-in-place concrete multicell Box—Girder bridges subjected to traffic condition. Lat. Am. J. Solid Struct. 2013, 10, 247–262. [Google Scholar] [CrossRef]
- Nouri, G.H.; Ahmadi, Z. Influence of skew angle on continuous composite girder bridge. J. Bridge Eng. 2012, 17, 617–623. [Google Scholar] [CrossRef]
- Ebeido, T.; Kennedy, J.B. Girder moment in continuous skew composite bridge. J. Bridge Eng. 1996, 1, 37–45. [Google Scholar] [CrossRef]
- Hamby, G.; Clinton, G.; Nimis, R.; Lwin, M.M. High Performance Steel Designers’ Guide, 2nd ed.; U.S. Department of Transportation, FHWA: Washington, DC, USA, 2002.
- Mertz, D.R. Trends in design and construction of steel highway bridges in the United States. Prog. Struct. Eng. Mater. 2001, 3, 5–12. [Google Scholar] [CrossRef]
- Kim, S.H.; Heo, W.H.; You, D.W.; Choi, G.J. Vehicle loads for assessing the required load capacity considering the traffic environment. Appl. Sci. 2017, 7. [Google Scholar] [CrossRef]
- Kim, S.H.; Choi, G.J.; Heo, W.H.; You, D.W. Reliability evaluation of a PSC highway bridge based on resistance capacity degradation due to a corrosive environment. Appl. Sci. 2016, 6, 423. [Google Scholar] [CrossRef]
- Zokaie, T. AASHTO-LRFD live load distribution specifications. J. Bridge Eng. 2000, 10, 511–554. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). Standard Specifications for Design of Highway Bridges, 16th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1996. [Google Scholar]
- Hue, X.S.; Wasserman, E.P.; Iqbal, R.A. Simplified method for calculating lateral distribution factors for live load shear. J. Bridge Eng. 2005, 5, 131–138. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). LRFD Bridge Design Specifications, 8th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- Zokaie, T.; Imbsen, R.A. Distribution of Wheel Loads on Highway Bridges, National Cooperative Highway Research Program (Nchrp) 12-26 Project Report; Transportation Research Board, National Research Council: Washington, DC, USA, 1993. [Google Scholar]
- Tarhini, K.M.; Frederick, G.R. Wheel load distribution in I-girder highway bridges. J. Struct. Eng. 1992, 118, 1285–1294. [Google Scholar] [CrossRef]
- Mensah, S.A.; Durham, S. Live load distribution factors in two-girder bridge systems using precast trapezoidal U-girders. J. Bridge Eng. 2014, 19, 281–288. [Google Scholar] [CrossRef]
- Chung, W.; Phuvoravan, K.; Liu, J.; Sotelino, E. Applicability of the simplified load distribution factor equation to PSC girder bridges. KSCE J. Civ. Eng. 2005, 9, 313–319. [Google Scholar] [CrossRef]
- Huo, X.S.; Conner, S.O.; Iqbal, R. Re-Examination of the Simplified Method (Henry’s Method) of Distribution Factors for Live Load Moment and Shear; Project No. Tnspr-Res 1218; Tennessee Department of Transportation: Nashville, TN, USA, 2003. [Google Scholar]
- Mohseni, I.; Khalim, A.R. Development of the applicability of simplified Henry’s method for skewed multicell box-girder bridges under traffic loading conditions. J. Zhejiang Univ. Sci. A (Appl. Phys. Eng.) 2012, 13, 915–925. [Google Scholar] [CrossRef]
- Khaleel, M.A.; Itani, R.Y. Live-load moments for continuous skew bridges. J. Struct. Eng. 1990, 116, 2361–2373. [Google Scholar] [CrossRef]
- Menkulasi, F.; Wollmann, C.L.R.; Cousins, T. Live-load distribution factors for composite bridges with precast inverted T-beams. J. Perform. Constr. Facil. 2016, 30. [Google Scholar] [CrossRef]
- Suksawang, N.; Nassif, H.H. Development of live load distribution factor equation for girder bridges. TRB 2016, 2028, 9–18. [Google Scholar] [CrossRef]
- Mohseni, I.; Khalim, A.R.; Kang, J. Live load distribution factor at the piers of skewed continuous multicell box girder bridges subjected to moving loads. TRB 2015, 2522, 59–69. [Google Scholar] [CrossRef]
- Khaloo, A.R.; Mirzabozorg, H. Load distribution factors in simply supported skew bridges. J. Bridge Eng. 2003, 8, 241–244. [Google Scholar] [CrossRef]
- Mohseni, I.; Khalim, A.R.; Kang, J. Effect of intermediate diaphragm on lateral load distribution factor of multicell box-girder bridges. KSCE J. Civ. Eng. 2014, 18, 2128–2137. [Google Scholar] [CrossRef]
- Computers and Structures, Inc. CSIbridge, Version 20, Structural Software; Berkley: Hong Kong, China, 2018. [Google Scholar]
- Sennah, K.; Kennedy, J.B. Load distribution factors for composite multicell box girder bridges. J. Bridge Eng. 1999, 4, 71–78. [Google Scholar] [CrossRef]
- Bedon, C.; Dilena, M.; Morassi, A. Ambient vibration testing and structural identification of a cable-stayed bridge. Meccanica 2016, 51, 2777–2796. [Google Scholar] [CrossRef]
- Mohseni, I.; Ahn, Y.; Kang, J. Development of improved frequency expressions for composite horizontally curved bridges with high-performance steel girders. Arab. J. Sci. Eng. 2018. [CrossRef]
- Linzell, D.G. Studies of a Full-Scale Horizontally Curved Steel I-Girder Bridge System Under Self-Weight. Ph.D. Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 1999. [Google Scholar]
- Newmark, N.W.; Siess, C.P.; Penman, R.R. Studies of Slab and Beam Highway Bridges Part. I Tests of Simple-Span. Right I-Beam Bridges; Bulletin Series No. 363; The Engineering Experimental Station, The University of Illinois: Urbana, IL, USA, 1946. [Google Scholar]
- Wegmuller, A.W. Post elastic behavior of composite steel-concrete bridges. In Second International Conference on Finite Element Methods in Engineering; University of Adelaide: Adelaide, Australia, 1976. [Google Scholar]
- Zhang, Q. Development of Skew Correction Factors for Live Load Shear and Reaction Distribution in Highway Bridge Design. Ph.D. Dissertation, Tennessee Technological University, Cookeville, TN, USA, December 2008. [Google Scholar]
- Kashif, R.M. Load Distribution Factors for Skewed Composite Steel I-Girder Bridges. Ph.D. Dissertation, University of Windsor, Windsor, ON, Canada, December 2017. [Google Scholar]
- Erhan, S.; Dicleli, M. Live load distribution equations for integral bridge substructures. Eng. Struct. 2009, 1250–1264. [Google Scholar] [CrossRef]
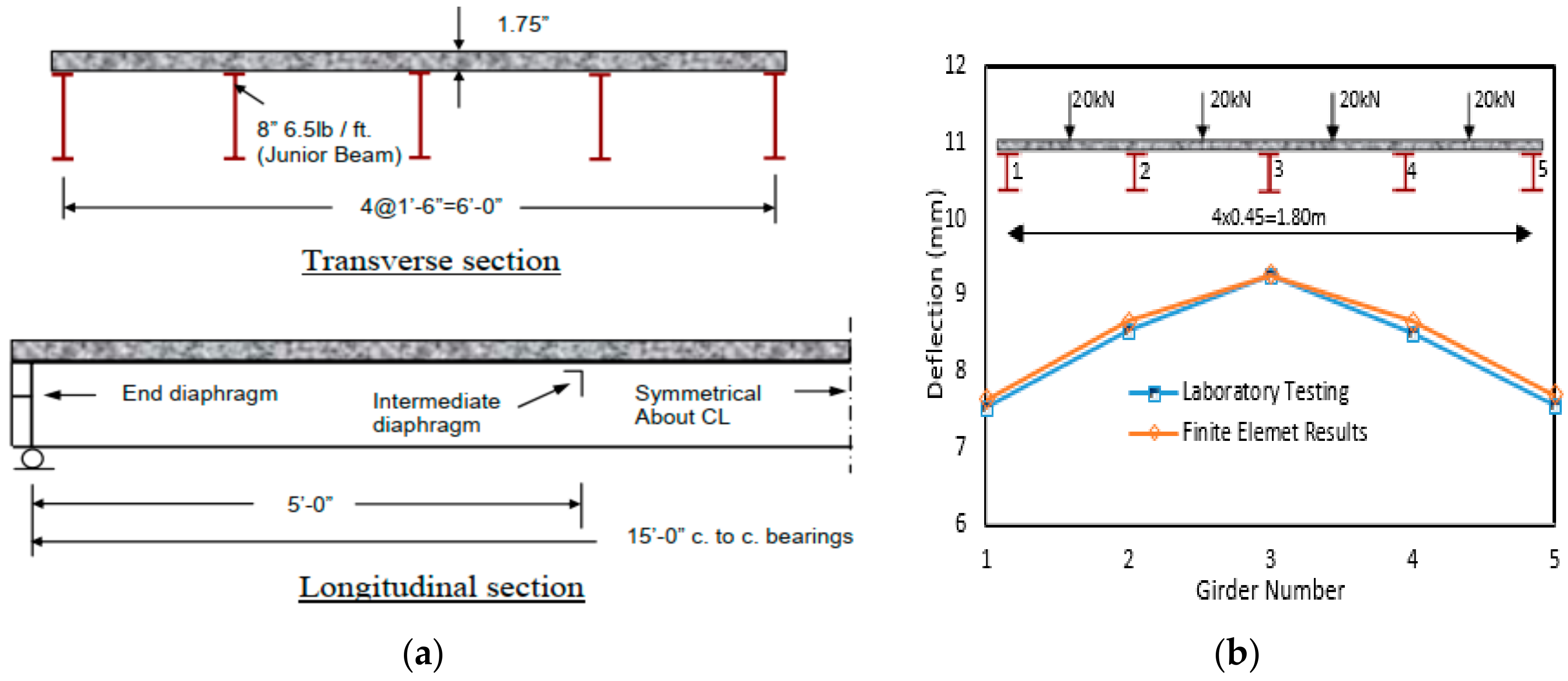


| Girder | Vertical Defl. (cm) | Web Rotat. (Degree) | ||||
|---|---|---|---|---|---|---|
| FE | Test | Error | FE | Test | Error | |
| G1 | 0.47 | 0.51 | 6.2 | 0.18 | 0.19 | 5.5 |
| G2 | 1.51 | 1.63 | 7.9 | 0.21 | 0.20 | 4.7 |
| G3 | 2.83 | 2.69 | 4.9 | 0.33 | 0.31 | 6.10 |
| Set | L (m) | HPS (w) | L/D | NL | Ng | S (m) | W (m) | θ (Deg.) |
|---|---|---|---|---|---|---|---|---|
| 1 | (30, 45, 60, 75, 90, 105) | (50, 70, 100) | 20 | 2,3 | 3,4,5 | (2, 2.5, 3.0, 3.5, 4) | 9.5 | (0, 15, 30, 45, 60, 75) |
| 2 | 25 | 2,3 | 3,4 | 13 | ||||
| 3 | 30 | 2,3 | 3,4 | 13 | ||||
| 4 | 25 | 2,3,4 | 3,4,5 | 15 |
| LDF | Girder Type | AVG. | SD. | COV. |
|---|---|---|---|---|
| MDFex | External | 1.065 | 0.076 | 0.071 |
| MDFin | Internal | 1.045 | 0.069 | 0.067 |
| CDFex | External | 1.072 | 0.082 | 0.076 |
| CDFin | Internal | 1.059 | 0.094 | 0.085 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohseni, I.; Cho, Y.K.; Kang, J. Live Load Distribution Factors for Skew Stringer Bridges with High-Performance-Steel Girders under Truck Loads. Appl. Sci. 2018, 8, 1717. https://doi.org/10.3390/app8101717
Mohseni I, Cho YK, Kang J. Live Load Distribution Factors for Skew Stringer Bridges with High-Performance-Steel Girders under Truck Loads. Applied Sciences. 2018; 8(10):1717. https://doi.org/10.3390/app8101717
Chicago/Turabian StyleMohseni, Iman, Yong Kwon Cho, and Junsuk Kang. 2018. "Live Load Distribution Factors for Skew Stringer Bridges with High-Performance-Steel Girders under Truck Loads" Applied Sciences 8, no. 10: 1717. https://doi.org/10.3390/app8101717
APA StyleMohseni, I., Cho, Y. K., & Kang, J. (2018). Live Load Distribution Factors for Skew Stringer Bridges with High-Performance-Steel Girders under Truck Loads. Applied Sciences, 8(10), 1717. https://doi.org/10.3390/app8101717





