Abstract
Virtual control surfaces for the optimization of steady and unsteady airloads on a compressor cascade are assessed numerically. The effects of mechanical surfaces are realized with plasma actuators, located both on the pressure and on the suction side of the blade trailing edge. Suction side plasma actuation is thought to reproduce the effects of mechanical wing spoilers, whereas pressure side plasma actuation is meant to act as a mechanical Gurney flap. Indeed, actuators are operated to generate an induced velocity field that is opposite relative to the direction of the freestream velocity. As a consequence, controlled recirculating flow areas are generated, which modify the effective mean line shape, as well as the position of the Kutta condition application point—and in turn the developed airloads. Proper triggering of pressure/suction side actuation is found to be effective in altering the blade loading, with effects comparable to those of mechanical control surfaces. Traveling wave mode simulations show that significant reductions in the peaks of the blade pitching moment can be achieved on the whole spectrum of interblade phase angles. It is proved that virtual control surfaces can provide effective load alleviation on the cascade, with potential remarkable reduction of fatigue phenomena.
1. Introduction
The demand for lighter and more efficient aero engines has significantly grown during the last few years. To address these issues, modern compressors have been conceived with increasingly larger pressure ratios per stage. Natural consequences of these solutions are an aggressive blade loading and high flutter sensitivity, especially for long and slim blades. Fatigue phenomena, due to large vibratory loads, are severely enhanced [1,2]. Blade design approaches aiming specifically to provide a reduction in vibratory loads and a delay of the flutter onset were proposed, e.g., in Refs. [3,4]. In addition, the aerodynamic performance is significantly affected on such highly loaded blades. Indeed, larger pressure gradients over the blade suction surface may accelerate the stall onset, therefore degrading the overall compressor performance. Several active flow control solutions have been proposed to optimize the aerodynamic response of heavily loaded blades. Tiedemann et al. [5] investigated experimentally the effect of steady and pulsed blowing through side wall actuators on a linear compressor cascade. They showed that both steady and pulsed jets are effective in suppressing three-dimensional secondary flow phenomena occurring on critically loaded blades. Matejka et al. [6] employed a synthetic jet located on the side wall at the level of the blade leading edge. A positive effect of such actuation on the flow field and on the loss coefficient was found. Similarly, a beneficial effect of side wall blowing on flow separation was found in Ref. [7]. Besides blowing, blade morphing has been extensively studied as a means to enhance the aerodynamic response of heavily loaded compressor and turbine blades. Monner et al. [8] employed piezo actuators to control the blade shape. The resulting deformed blade was found to affect the measured aerodynamic loads significantly. Hammer et al. [9] investigated different adaptive blade solutions with numerical computations and experimental tests. Specifically, they studied and compared four morphing solutions, i.e., blades with adjustable angle of attack, movable leading edge, Gurney flaps, and adaptive camber. Suman et al. assessed experimentally [10] and numerically [11] the effect of shape memory alloys for blade shape adaptation on a heavy-duty automotive cooling axial fan.
Large interest has been latterly addressed toward plasma actuation. The suitability of these actuators stems from their lightness and their almost negligible intrusiveness into the flow field. Additionally, the absence of mechanical parts avoids the risk of structural and operational failures, likely to occur under high centrifugal loads typical of aero engines. Vo et al. [12] carried out a computational assessment of plasma actuators installed on a transonic axial compressor. The capability of suppressing spike stall inception was assessed by taking into account several locations and strengths of the plasma actuators. The work of De Giorgi et al. [13] deals with the experimental and numerical characterization of plasma actuators in a compressor cascade. It was shown that properly tuned plasma actuation allows for an effective reduction of pressure losses on highly loaded compressor blades. Akcayoz et al. [14] performed numerical and experimental assessments of plasma actuators to control corner stall separation on a heavily loaded blade cascade. In this work, realistic operation conditions were simulated. It was found that a combination of plasma actuators placed on the suction surface is a very effective means to control flow separation and in turn pressure losses. Zhang et al. [15] carried out numerical investigations of plasma actuators to control flow separation on a high-speed compressor cascade. The effects of both endwall and suction side plasma actuators were studied.
The purpose of the present work is to assess numerically the effectiveness of plasma actuators for load alleviation on a compressor cascade. Here, plasma actuators are meant to reproduce qualitatively the effect of the mechanical L-tab investigated in Refs. [16,17,18,19,20] for rotorcraft vibration reduction. Specifically, plasma actuation is meant to develop vortical structures and recirculating flow areas similar to those generated by mechanical control surfaces (see, for instance, Ref. [21]). Plasma actuators are thought to be located on the pressure and on the suction side (PS and SS, respectively) of the three central blades in the targeted cascade. The plasma induced flow is conceived to be opposite relative to the freestream direction, with the specific aim to generate the aforementioned separated flow areas. Numerical computations performed on the clean blade configuration are validated with experimental data achieved on the wind tunnel facility of the Chair for Aero Engines at Technische Universität (TU) Berlin and with literature results [22,23,24] . Constant angle of attack configurations for the blade cascade are assessed first. It is shown that plasma affects significantly both local and resulting loads on the blade, including the pitching moment. At the same time, no remarkable drag rises are encountered. Traveling wave mode simulations are then performed with alternate PS/SS actuation. Within a traveling wave mode, the blades oscillate at the same frequency but at a certain—constant and uniform—phase lag referred to as Interblade Phase Angle (IBPA), see [25]. In this work, it is found that appropriate phasing the switch between PS and SS actuation allows for effectively manipulating the peaks of unsteady airloads, especially the pitching moment. As a result, mean and oscillating loads can be controlled, and fatigue phenomena can be alleviated. Additionally, the blade aeroelastic stability could also be improved. The manuscript is structured as follows. Section 2 presents the computational geometry, the set up of the simulations, as well as the numerical modeling for plasma. The comparison between numerical results achieved on the clean cascade and experimental measurements on the same geometry is also reported. Section 3 discusses the simulations carried out on the blades at constant angle of attack. The results of time-dependent computations performed at constant angle of attack are shown to prove the steadiness in the mean of the flow, both for the clean and for the plasma equipped configuration. The effects of PS and SS actuation on the airloads and on the flow field are reported. Section 4 describes the results obtained with traveling mode simulations. The triggering of alternate PS/SS actuation is presented first. The affection of plasma on the pitching moment oscillations is discussed as a second instance. Concluding remarks are provided in Section 5.
2. Numerical Modeling
2.1. Computational Geometry and Flow Solver
The compressor cascade is modeled with seven blades, as depicted in Figure 1. The blade section is an airfoil of the NACA 65 series. The chord length is 0.15 m. The pitch to chord ratio corresponds to 0.75. The cascade resembles the experimental facility for aeroelastic assessments of the Chair of Aero Engines at TU Berlin [22]. This allows for comparisons between numerical and experimental data for the clean configuration. Plasma actuators are applied on the three central blades of the cascade, in order to take into account the relative effects of plasma between the blades. Two-dimensional numerical simulations are performed, as the flow has been proved to have negligible three-dimensional effects, at least for the conditions considered here [22]. Additionally, plasma actuators are meant to cover the entire blade span when installed, so that their effects can be assumed as mostly two-dimensional.
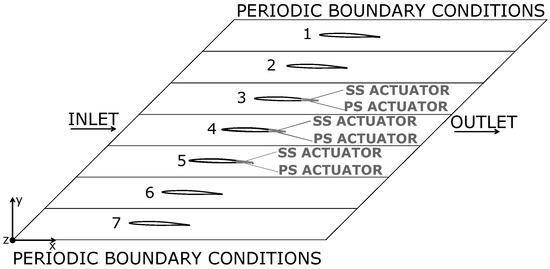
Figure 1.
Sketch of the computational geometry for the blade cascade.
A multiblock structured grid composed of 550,949 elements is realized by means of the commercial software Ansys ICEM CFD®(Version 17, Ansys, Canonsburg, PA, USA).The domain extends approximately two chords both upstream the leading edge and downstream the trailing edge. In order to reproduce correctly the main features of the boundary layer, a targeted O-grid is realized around the airfoil. The O-grid features 100 elements in the direction normal to the airfoil and 410 elements on the airfoil surface. Refinements are introduced in the area where the plasma is modeled, as well as on the leading edge and on the trailing edge. The height of first cell in the boundary layer is set to keep the y equal to one, for the Reynolds number of ∼10, based on the airfoil chord and on the freestream velocity. One block of the grid is realized specifically for the wake region. In this block, the grid is kept finer, compared to the other far field areas. This allows for capturing accurately the modifications in the airfoil circulation—and in turn on lift and moment—induced by the blade motion. With the aim to maximize the quality of the numerical solution, the elements of the boundary layer and of the wake are all kept approximately squared.
The results of grid sensitivity studies are presented in the following. Figure 2 is a detail of the computational grid around one blade with a blowing up of the trailing edge region.
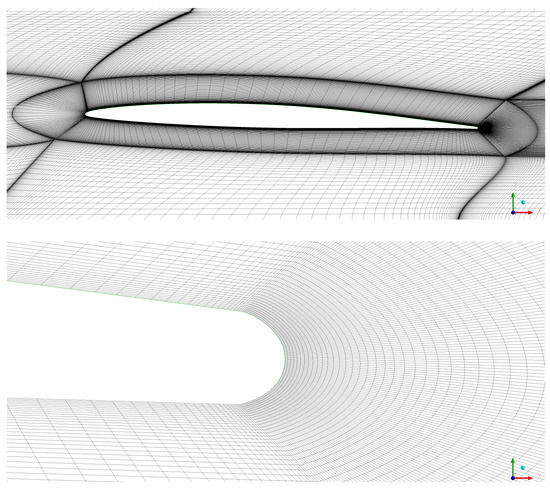
Figure 2.
Detail of the computational grid around one blade (top), and blowing up on the trailing edge area (bottom).
The angle of attack is set here to = 2 degrees. Freestream velocities of 34.36 m/s and 19.17 m/s are imposed as a boundary condition at the inlet, consistently with the experimental tests of Refs. [22,26]. An average static pressure condition of 101,325 Pa is imposed at the outlet. Periodic boundary conditions are applied on the top and on the bottom of the computational domain (see again Figure 1).
The finite volume solver Ansys CFX® is employed for the viscous computations on the present cascade. The advection terms are solved with a high resolution scheme, whereas a second order backward scheme is employed for the transient terms. The flow is assumed as fully turbulent, and the system of Reynolds-Averaged Navier Stokes (RANS) equations is closed with the SST k- Menter turbulence model [27]. Wall functions are employed close to the solid walls. In [28], the performance of different turbulence models in describing fully turbulent flows around oscillating airfoils in pre-stall and in deep-stall conditions was investigated. The contents shown in [28] shows that the k- SST model [27], the Spalart–Allmaras [29] model and the Baldwin–Barth [30] model are those that better capture the unsteady flow physics associated with airfoils in oscillating motion. The k- SST model [27] is employed here because it is appropriate to describe the flow around oscillating airfoils and because it allows to get a good accuracy both close to the walls and in external flow. This twofold capability is especially desired for the present application. Indeed, a good capturing of the plasma-induced effects close to the walls, as well as of the interaction between the neighbouring blades, is needed here. The SST k- Menter model combines the advantages of the k- and k-. By means of a blending function—unitary close to the wall and zero elsewhere—it is possible to switch between the k- and the k- models. Namely, the k- model, performing well close to the walls (chapter 11, [31]) is used near the blades. Conversely, the k-, which is more accurate for describing the external flow (chapter 11, [31]), is employed for the rest of the fluid domain. Notice that the k- SST Menter model is used in other numerical works dealing with turbomachinery cascades. Akcayoz et al. [14] used the same solver and the same modeling to perform RANS computations on a compressor cascade equipped with plasma actuators, employed to control corner stall separations. Keerthi et al. [2] used Ansys CFX® to carry out fully turbulent RANS computations closed with the k- SST Menter model on a linear cascade featuring blades oscillating in pitch.
For the present assessments, incompressible simulations are performed. This is consistent with the capabilities of the aeroelastic experimental rig of TU Berlin [22] and appropriate for the first assessments of the novel actuation system proposed here. Simulations in transonic conditions, closer to the actual flow in aero engine compressors, are scheduled as an outlook of this work. The temperature is set to 20 C and the reference pressure to 101,325 Pa. For traveling wave mode simulation, a periodic displacement is imposed to the blades. With this aim, a mesh deformation algorithm is employed. Specifically, the harmonic motion of the blade nodes is specified via an external text file. This latter contains: (i) the node coordinates for the blades at their initial positions; (ii) the node coordinates related to the blade maximum displacements—positive and negative. The frequency and the phase of the motion are set directly in the flow solver. The motion of all remaining nodes is determined by the Displacement Diffusion mesh deformation model, the only one currently available in Ansys CFX®. With this model, the displacements applied on domain boundaries or in subdomains are diffused to other mesh points by solving the diffusion equation , being the displacement relative to previous mesh locations and the mesh stiffness. This quantity determines the entity of the motion in different regions of the domain. In this work, the stiffness is defined as the reciprocal of the cell volumes, so that the mesh deforms less where cells are smaller, e.g., close to the boundary layer. The diffusion equation is solved at the start of every time step of the simulation. Notice that the displacement diffusion model preserves the element distribution of the initial mesh. That is, if the initial mesh is relatively fine in certain regions of the domain, e.g., the boundary layer, then it will remain relatively fine also after solving the displacement diffusion equation. Further details on the algorithm can be found in [32,33].
2.2. Plasma Modeling
Figure 3 shows a schematic of a single dielectric barrier discharge plasma actuator. Two electrodes are separated by a dielectric barrier material. One electrode is exposed to air, i.e., on the aerodynamic surface, and one is grounded within the dielectric material, inside the blade internal volume. When an alternate current voltage is applied between the electrodes, a plasma discharge is initiated. As a consequence, air is locally ionized in the area close to the electrodes and the flow momentum can be manipulated.
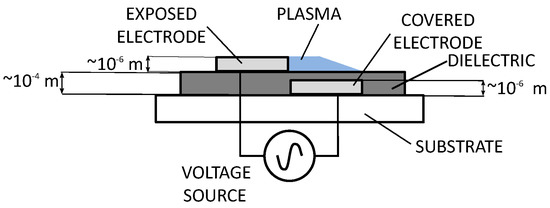
Figure 3.
Schematic of a plasma actuator with indicative sizes according to [13].
The essential effect of plasma actuators is to add momentum into the flow field and in turn to modify the local velocity profile (see, for instance, Ref. [34]). In the present work, a source term is in fact added to the momentum equations for modeling the plasma. Specifically, a uniform force per unit volume is applied over a limited region always bounded on one side by the airfoil wall. Notice that this approach is consistent with that of Refs. [35,36,37]. The plasma is here meant to act on a completely attached flow at Re ∼10, with x component opposite to the main freestream direction—the y component is set in order to keep the plasma always tangent to the airfoil. Therefore, the body force has to be larger compared to classical low Re applications. Consistently with the assessments of Ref. [14] and with the experiments of Ref. [38], a force per unit span of 300 mN/m is used in this work. Notice that this approach is employed also in Refs. [35,36,37,39]. According to [38], this body force is achieved with input voltages between 10 and 20 kV. Notice that, notwithstanding the voltage required to effectively operate plasma actuators is of the order of kV, the power requirements are usually limited to ∼10 W, the currents being employed of few mA [40,41]. The plasma region is modeled as a quadrangle 0.1 mm thick and 10 mm wide (see Figure 4). These sizes are the same used in Refs. [12,35] and representative of the experimental models of Refs. [14,42,43].
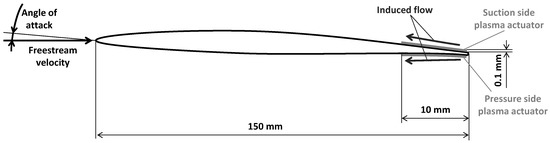
Figure 4.
Sketch of the blade section with the modeling of plasma actuators.
It is worth remarking that the present work is an exploratory investigation to assess whether plasma actuators could be suitable for load control in turbomachinery. The detailed design is planned for works to come and lies beyond the purposes of this manuscript. However, preliminary considerations on the practical implementation of plasma actuators on actual blades have been done. The actuators per se are very thin, as shown in the sketch of Figure 3. The overall thickness of an actuator is expected to be ∼10−4 m see Ref. [13]. Therefore, actuators could be installed also on quite thin trailing edges, by realizing appropriate hollows on the blade surface, both on the pressure and on the suction side. Optimization studies need to be performed to assess the optimal geometrical orientation of actuators. The first experimental studies envisaged in the near future will feature plasma actuators parallel to the chord and covering the whole span of the targeted linear cascade (see [22]). Successive studies are thought to be carried out on a rotating annulus, in order to investigate whether the transverse flow arising from the rotation requires orienting the actuators with a certain angle relative to the chord direction. There are different possible approaches to fit the cables into the blades. The selected configuration depends on the geometrical arrangement of the actuators along the blade span. In works to come, the optimal geometrical configuration for the actuators to control the blade loads will be assessed. If the actuators will cover the entire span, the cables will be connected at the level of the blade root, where there will be less problems in terms of space. Dedicated hollows will be realized to locate the cables. When employing plasma actuators on the compressor rotor, the transmission of the signal from the fixed to the rotating frame will be realized by means of devices like those produced by Jordil Technic Sárl, which have already been used in [44] for a piezo-actuated aero engine blisk. An alternative, which would avoid the transmission of electrical signals from a fixed to a rotating system, was proposed by Iwrey in [45]. Iwrey suggested exploiting the rotation to generate the required voltage, by using electromagnetic effects. The concept of [45] is targeted to plasma actuators employed to control the tip clearance flow on gas turbine engines. Therefore, it is suitable also for the application of the present work. Iwrey proposed locating one or more magnets on the casing of the engine and a magnet with a solenoid on each of the plasma actuated blades. The solenoid is connected to the electrodes of the plasma actuator. Due to the relative rotation of the blade and of the casing magnets, a voltage is generated on the solenoid. This voltage can indeed be used to feed the actuators, if an appropriate signal modulation is applied. A further path, which is currently pursued by the authors in cooperation with the University of Salento, consists of developing micro controllers and micro generators, small enough to be located in targeted hollows, realized internally to the blades. In order to avoid a possible interference of the electrodes on the pressure side with those on the suction side, proper electromagnetic shielding will be employed between the two actuators. This shield can be realised by means of e.g., metal screens, metal foams or metal sheets.
2.3. Grid Sensitivity Study and Comparison with Experimental Data
The reliability of the Computational Fluid Dynamic (CFD) simulations is checked first by assessing the sensitivity of the numerical solution to the spacial refinement. Namely, the steady state airloads computed with the reference grid—550,949 elements—are compared to those obtained with a finer and coarser mesh. The finer grid is composed of 1,138,921 elements, whereas the coarser grid features 274,946 elements. The clean cascade, as well as the configurations with PS/SS plasma, are considered. A low and a moderate angle of attack, i.e., = 2 deg. and = 8 deg., are taken into account. Table 1 and Table 2 show the percent difference between the airloads computed with the reference grid and with the finer or coarser spacial resolutions. The percent difference is depicted for both the non-actuated and the actuated configurations. Both for the actuated and the non-actuated case, the reference grid features small discrepancies with respect to the finer mesh. This occurs at deg. and at degrees. Namely, the percent differences in loads are always smaller than 1% beside two cases, in which the drag values differ by 1.2% and 3.1% for reference and finer mesh. This is regarded as acceptable, as an accurate quantification of drag is not the main focus of the paper. The assumption of fully turbulent flow, together with the employment of RANS computations adopted here, do not allow for predicting properly the drag coefficient. On the other hand, the coarser grid provides larger differences not only in terms of drag, but also in terms of lift and moment coefficients, already at deg. As a consequence, the reference grid is regarded as the best trade-off between accuracy of the solution and computational burden.

Table 1.
Percent difference between the aerodynamic loads computed on the reference grid and the counterparts achieved on the finer and on the coarser mesh; clean cascade, with PS the actuated cascade and SS the actuated cascade; Re ∼350,000; degrees.

Table 2.
Percent difference between the aerodynamic loads computed on the reference grid and the counterparts achieved on the finer and on the coarser mesh; clean cascade, with PS the actuated cascade and SS the actuated cascade; Re ∼350,000; degrees.
Figure 5 shows the pressure distribution achieved experimentally on the reference test rig of the Chair of Aero Engines at TU Berlin and the counterpart obtained with CFD simulations. Specifically, the pressure coefficient CP is displayed. A steady state configuration is considered, with angle of attack of 2 degrees, and freestream velocity of 34.36 m/s, yielding a chord/freestream velocity based Reynolds number of ∼350,000. A very good agreement is found between the numerical computations and the experiments, including the leading edge and the trailing edge area of the blade.
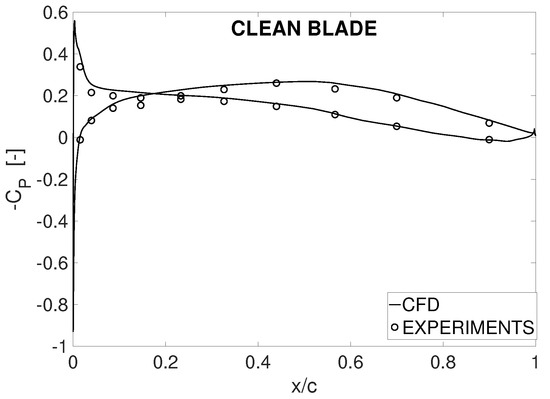
Figure 5.
Distribution of pressure coefficient CP. Experiments and CFD on the clean configuration; Re ∼350,000, degrees.
Figure 6 shows the results of time-resolved traveling wave mode simulations performed on the clean cascade and compared to the experimental counterpart, as well as to the measured data of Carta [23] and Sachs [24] on the same geometry. The comparison is performed for the blades oscillating at frequency of 5.25 Hz, corresponding to a reduced frequency —with the same inlet velocity used for the comparisons at constant angle of attack. The IBPA is equal to 0 degrees. The time step employed for the simulations is s, corresponding to 100 time steps per period. Three oscillation periods are simulated, in order to allow the flow to reach a fully developed periodic behaviour. Sensitivity studies to the time resolution and to the number of simulated periods—the latter shown in the following—have highlighted that these parameters give the best trade-off between accuracy and computational resources. Specifically, the real and imaginary parts of unsteady pressure are computed separately for the pressure and for the suction side of the central blade. The real part of the suction side is then subtracted to the counterpart of the pressure side, in order to get the displayed quantity . The same procedure is adopted for the imaginary part. The numerical results are found in good agreement with the experimental and literature data, in terms of both real and imaginary parts. Light differences are encountered just downstream of the leading edge, where, however, all the plotted data are remarkably scattered.
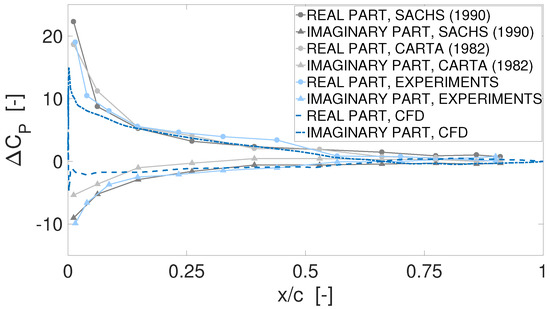
Figure 6.
Real and imaginary part of unsteady pressure distribution. Experiments and CFD on the clean configuration; Re ∼350,000; IBPA = 0 deg.; degrees; Hz; : time.
3. Results at Constant Angle of Attack
Simulations with the blades at constant angle of attack are performed on the blade cascade, in order to investigate the affection of plasma actuation on mean loads and flow field. Only results on the central blade of the cascade are discussed in the following. The counterparts on the remaining blades are not reported for brevity purposes. The freestream velocity is 34.36 m/s and the angle of attack is two degrees. The Reynolds number is again ∼350,000.
Figure 7 shows the time history of the airloads obtained with time-resolved simulations at fixed angle of attack. These simulations are meant to show that the flow can be assumed as steady in the mean, when the blades are kept at a constant angle of attack. The time step for the unsteady computations is set to s and 100 time steps are performed for each period. It is found that all the three airloads converge to a constant value, after a maximum of ∼0.015 s. Therefore, steady state computations can be performed to assess the affection of plasma actuators on the force coefficients and on the flow field.
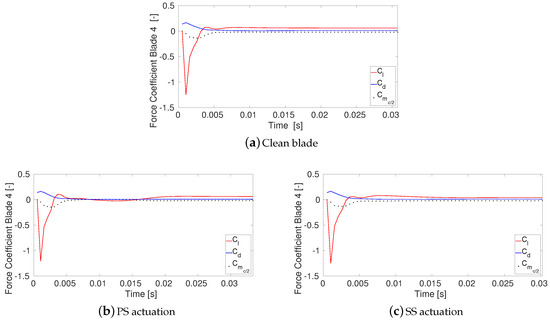
Figure 7.
Time history of unsteady lift , drag and mid-chord moment coefficient at constant angle of attack of two degrees; Re ∼350,000.
Figure 8 shows the normalized velocity and vorticity magnitude fields. The velocity is made dimensionless by the freestream velocity and the vorticity is made dimensionless by the ratio of chord over freestream velocity. A detail of the trailing edge is displayed for the clean blade and for the configurations with PS and SS actuation, respectively. A body force of 300 mN/m is applied on the pressure and on the suction side. Both actuations lead to the development of low speed recirculating flow areas, with a consequent modification of local and resulting loads. In particular, PS actuation yields a recirculating flow region on the pressure side trailing edge, in the area where the plasma is modeled. These locally developed vortical structures shift the application point of the Kutta condition downstream of the physical trailing edge. This is approximately equivalent to employing a longer and more cambered airfoil. Therefore, lift augmentations are expected to be a direct consequence of this phenomenon. The recirculating flow area generated by SS actuation causes an induced camber effect that is opposite relative to the SS counterpart. As a consequence, the resulting effect will be a reduction in the developed airloads. The flow fields of Figure 8 show that, as expected, the wake becomes thicker relative to the clean blade counterpart—the light blue low speed region is larger for the actuated configurations. This effect, which is consistent with the results of Refs. [18,19], may lead to possible drag increases compared to the baseline blade. Nevertheless, it will be hereinafter shown that no significant drag rises are encountered for both the actuated configurations. It is also worth noting that the recirculating flow area developed on the suction side is less extended, relative to the pressure side counterpart. This is probably due to the fact that higher velocity gradients are encountered on the suction side, near the trailing edge. Therefore, a larger body force is probably required on the suction side, in order to obtain almost equally extended recirculating flow areas on upper and on the lower side of the blade. It will be illustrated that a consistent asymmetry is encountered in terms of local and resulting airloads achieved with PS or SS actuation. On the basis of these results, the traveling wave mode simulations discussed in the following section are performed with a larger body force on the suction side and a smaller one on the pressure side.
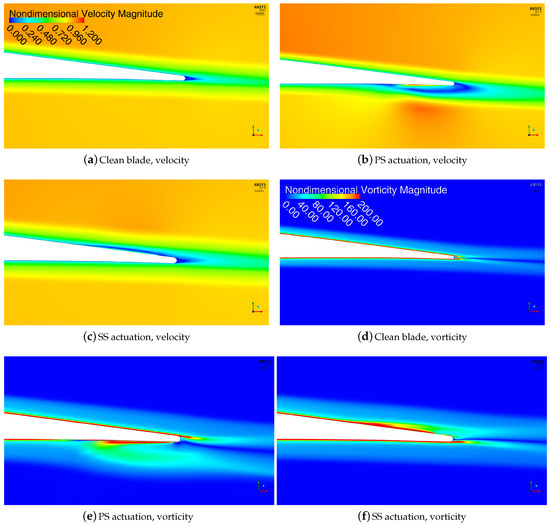
Figure 8.
Trailing edge detail of velocity magnitude, normalized by the freestream velocity, and of z-vorticity magnitude, normalized by the chord/freestream velocity ratio, for the clean cascade and with PS/SS actuation; Re ∼350,000; degrees.
Figure 9 shows the pressure coefficient distribution for the clean blade, compared to the configuration with PS and SS actuation, respectively. Consistently with the results achieved in terms of flow field, PS actuation yields a clearly visible negative peak in the plasma region. The opposite occurs for the SS actuation. The most influential effect induced by the actuation can be seen by looking at the pressure distribution upstream the actuation, up to the leading edge. Indeed, SS actuation yields an overall modification of the pressure distribution, characterized by a covered area that is smaller compared to the clean configuration. This causes an overall attenuation of blade loading. The opposite occurs with PS actuation. This latter induces a modification of the pressure distribution, such that the area covered by the curve is significantly larger relative to the clean configuration. As a consequence, an increase in blade loading is expected. It is worth remarking that these results are in qualitative agreement with the assessments of Refs. [16,17,18,19,20], where the same effects were obtained with a mechanical L-tab deflected downward or upward, installed on a helicopter blade section. Additionally, the computed flow fields are qualitatively consistent with the Particle Image Velocimetry measurements of Feng et al. [21] on a low-speed fixed wing section with PS plasma actuation opposite to the freestream direction.
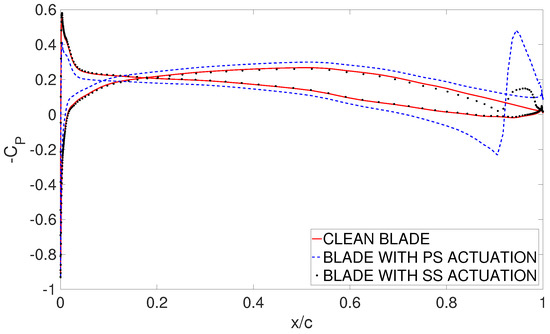
Figure 9.
Pressure coefficient distribution on the clean blade and with PS/SS actuation; Re ∼350,000; degrees.
Figure 10 shows an histogram of the aerodynamic loads, computed on the clean, PS- and SS-actuated configurations, at angles of attack ranging from 0 to 12 degrees. Namely, the lift coefficient , the drag coefficient and the mid-chord moment coefficient are reported. As anticipated, actuation yields a modification of the effective camber, opposite for PS and SS plasma, alongside a chord-wise shift of the Kutta condition downstream of the trailing edge. Both PS and SS actuations provide lift and pitching moment modifications, which are also quantitatively comparable to those of Refs. [16,17,18,19,20], achieved with a mechanical Gurney flap. In particular, PS actuation allows for increasing the lift coefficient without changing the blade angle of attack, and with no significant drawbacks in terms of drag. The moment coefficient—nose-down positive—increases in magnitude, relative to the non-actuated counterpart. That is, PS actuation has a stabilizing effect on the mean airfoil torsion (see [46]). On the other hand, SS actuation yields effects that are comparable to those exhibited by upward deflections of control surfaces. Namely, lift is reduced compared to the clean configuration, with potential benefits in counteracting stall phenomena [19]. A reduction of the pitching moment, relative to the clean configuration, is observed. Again, no major effects are encountered in terms of drag rise. The affection of the actuation on the pitching moment is regarded as particularly important for this work. Within this framework, it is worth remarking that the behavior of pitching moment according to PS/SS actuation is consistent with the results of several works in literature, dealing with mechanical trailing edge control surfaces, e.g., Refs. [19,47,48]. Additionally, the light reductions of drag coefficient relative to the clean blade—encountered with both pressure and SS actuation—are in agreement with other results found in literature on trailing edge devices (see e.g., Refs. [16,17,18,19,20,49]). It is also worth remarking that the present fully-turbulent RANS assessments can’t provide a quantitative evaluation of drag. The results presented here are meant to give only a qualitative overview on the affection of plasma on this quantity.
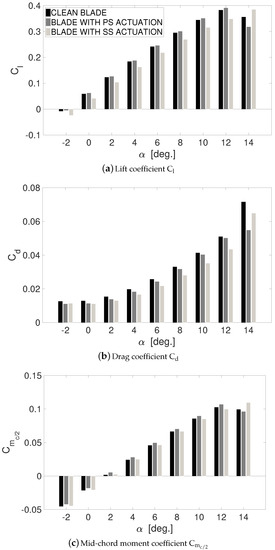
Figure 10.
Lift, drag and mid-chord moment coefficient on the clean blade and with PS/SS actuation; Re ∼350,000; degrees.
4. Results of Traveling Wave Mode Simulations
Traveling wave mode simulations are carried out on the clean and on the plasma equipped blade cascade. For these simulations, an alternate PS/SS actuation is imposed over the pitching oscillating cycle of the blade. The frequency of oscillation for the simulations presented hereinafter is f = 19.17 Hz, yielding a reduced frequency based on the semi-chord of = 0.4597—being the blade chord and = 19.65 m/s the freestream velocity. The mean angle of attack is set to two degrees and the oscillation amplitude is set to one degree. The motion law of the nth blade of the cascade reads: . Notice that these specific simulation parameters have been chosen because a significant rise in the vibratory loads—alongside a drop in the aeroelastic stability—was detected numerically at IBPA = deg. [22] and experimentally at IBPA ∼ deg. [26], on the same cascade in these conditions.
The blade displacement is achieved via a mesh adaptation algorithm implemented within the flow solver. One hundred time steps per oscillation cycle are employed for the numerical computations, yielding a time step size of ∼5.2 s. A total of three periods are simulated, in order to ensure the convergence of the numerical solution. The time histories of the unsteady loads for the plasma equipped cascade are illustrated in the following part of this section. Several IBPAs between −180 deg. and 180 deg. are considered, including degrees.
In order to maximize the actuation effectiveness, the triggering of PS/SS actuation during the oscillation period has to be set properly. To this aim, the phase of unsteady airloads relative to the blade pitching cycle for the clean cascade is evaluated for different IBPAs, at k = 0.4597. This allows to tune the triggering of PS/SS actuation in order to: (i) maximize the airloads when a minimum of the oscillating loads is observed; and (ii) minimize the airloads when a maximum in the oscillating airloads is encountered. Indeed—due to a combination of vortex shedding phenomena and inertial effects caused by the flow acceleration—the unsteady airloads are out of phase relative to the airfoil harmonic motion. The lead/lag phasing of loads is determined by the reduced frequency and by the thickness of the airfoil. A detailed discussion of these phenomena for an isolated airfoil is provided in Ref. [50]. Additional out of phasing effects may be caused by the mutual interaction of the blades. Figure 11a,b show the phase of the mid-chord moment and lift coefficient, computed at IBPAs between −180 and 180 degrees. Notice that the same out of phasing has been computed for the different blades of the cascade, at each of the interblade phase angles. Consistently with Ref. [50] and with Ref. [51], chapter 8, the computed phase is different for the two force coefficients. Only the phase of the moment coefficient—which has been proved to yield the most detrimental vibratory loads on the targeted cascade [26]—is used here to tune the actuation triggering. In fact, the main target of the conceived actuation is—at least for the present work—to manipulate the pitching moment. Indeed, the blade bending stiffness is much larger than the torsional counterpart, for the cascade under consideration [22,26]. Moreover, the experimental results of Sachs [24] showed that the torsional mode is the most critical for the cascade under consideration. Therefore, acting on the pitching moment, can have the further beneficial effect of increasing the aeroelastic stability of the cascade. Additionally, because the geometry of the reference cascade is span-wise uniform and meant to represent a blade section, the lift is not an accurate picture of the blade loading at the hub, which should be quantified with three-dimensional bladings. It is also worth noting that the choice of focusing on the pitching moment only and not on the lift is consistent with other works (see e.g., [2,23]). These works deal indeed with the unsteady aerodynamics and with the aeroelastic response of linear two-dimensional cascades.
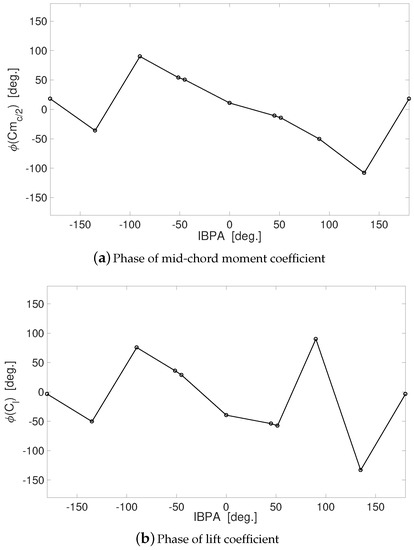
Figure 11.
Phase of mid-chord moment coefficient and of lift coefficient at different IBPAs; Re ∼195,000; degrees; Hz, .
The results at constant angle of attack presented in Section 3 show that a larger body force is required on the suction side, in order to obtain percentage gains similar to the PS counterpart. As a consequence, a body force equal to 75% of the reference 300 mN/m, i.e., 225 mN/m, is applied on the pressure side. On the other hand, a force equal to 150% of 300 mN/m, i.e., 450 mN/m, is applied on the suction side—this value being feasible for modern plasma actuators [38]. Therefore, the body force on the suction side is double relative to that applied on the pressure side. The body force is modeled as constant during the actuation-on cycle, hence its time history would be a squared wave. In order to avoid undesired peaks in the pressure distribution, an exponential law modulation is applied to the body force amplitude at the very beginning and end of the operating cycle. This allows a smooth transition between the non-actuated and actuated configuration and vice versa. The triggering of the PS/SS actuation is defined on the basis of Figure 11a. The previous section showed that PS actuation increases the positive nose-down pitching moment. Therefore, PS plasma should be operated when the pitching moment features negative oscillations, relative to the mean value. On the contrary SS actuation, which provides a reduction of the positive nose-up pitching moment, has to be operated when the Cm oscillations have positive amplitude. Because Figure 11a shows that the moment is out of phase relative to the motion, this lead/lag has to be accounted for, when setting the PS/SS actuation triggering. For an oscillation law in the form , the phase of the PS actuation on the nth blade is . Consistently, the phase of the SS actuation relative to the blade motion is .
Figure 12 shows the time history of lift, drag and moment coefficient on the central blade of the plasma-equipped cascade at IBPA = −51.43 degrees. In this case, four oscillation periods are simulated. Figure 12a depicts the four simulated periods, whereas Figure 12b is a blowing up on the second, third and fourth simulated periods, where the reaching of a well-established period regime can be better detected. Specifically, the transient results are deemed quasi-converged when the force coefficient relative difference between two consecutive periods falls below 0.02%. This condition must be achieved for all the force coefficients considered, i.e., lift, drag and moment. It is found that the difference in lift, drag and moment coefficient falls below the fixed threshold already between the second and the third oscillation period. Notice that also Keerthi et al. [2], who performed numerical computations on a cascade with pitching blades, found that their numerical solution reaches a good periodicity after two periods of oscillation. Namely, three oscillating cycles are simulated for small amplitude oscillations and four oscillating cycles for high amplitude oscillations are simulated in [2].
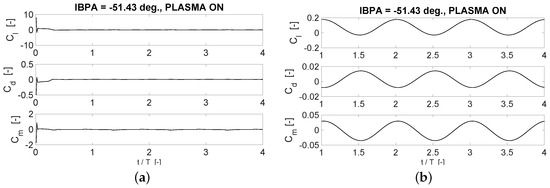
Figure 12.
Time history of lift, drag and moment coefficient for the complete simulation (a) and for the last three periods (b); Re ∼195,000; IBPA = −51.43 deg.; deg.; Hz, .
Figure 13 shows the velocity magnitude field, normalized by the freestream velocity, at four different instants of the pitching cycle. A detail of central blade trailing edge is depicted. Analogous results are obtained on the other two plasma-equipped blades of the cascade. The alternate switching of the PS and SS actuation is clearly visible. It is also worth noting that, differently from the assessments at a constant angle of attack, the recirculating flow areas on the pressure and on the suction side are almost equally extended. This is due to the application of a larger body force on the suction side, relative to the pressure side. It will be highlighted hereinafter that now the affection on the positive and negative oscillations in the pitching moment is almost symmetrical. This means that the effects provided by PS and SS actuation are expected to be more similar, when the SS body force is larger than the PS counterpart.
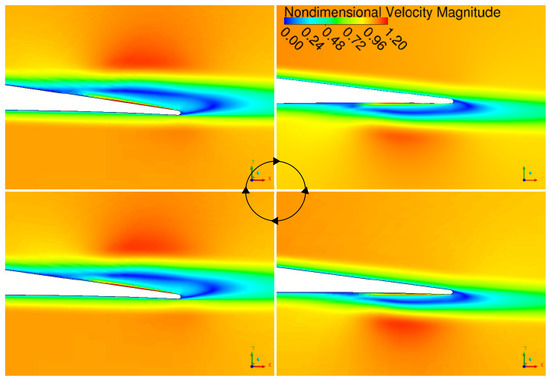
Figure 13.
Trailing edge detail of velocity magnitude, normalized by the freestream velocity, at four time instants of the oscillation cycle; plasma actuation on; Re ∼195,000; IBPA = −51.43 deg.; deg.; Hz, .
Figure 14, Figure 15 and Figure 16 show the fluctuation of the mid-chord pitching moment coefficient versus the non-dimensional time, for the last simulated period. Several IBPAs, ranging from −180 to 180 deg., are shown. The time on the x-axis is made dimensionless by the oscillation period of the blade. An effective reduction of the unsteady peaks on the pitching moment is observed for each of the interblade phase angles. As a result, two major benefits can be achieved: (i) vibratory loads, responsible for fatigue phenomena are alleviated; and (ii) the blade aeroelastic stability is potentially increased, as the energy transfer from the flow to the blade is reduced [23]. It is worth remarking that plasma seems to have a greater affection on the pitching moment for negative IBPAs than for positive values of the interblade phase angle. According to the convention employed in this work, for IBPA < 0, the pressure wave travels from the pressure side of a blade to the suction side of the neighbouring one. On the contrary, for IBPA > 0, the pressure wave travels from the suction side of a blade to the pressure side of the neighbouring one. A higher body force is employed on the SS for travelling wave mode simulations. Even though the recirculating flow areas generated on PS and SS with asymmetric actuation have comparable extensions, the affection on unsteady loads might be slightly higher on the suction side. This may be one of the causes for the better affection of the actuation for negative IBPAs which—according to [24,26]—feature lower aerodynamic damping, and therefore are the most critical. The differences in actuation effectiveness encountered among the negative IBPAs are probably due to local effects that are not detectable when integrating pressure to obtain the resulting loads. In Ref. [2], Keehrti et al. investigate the effects of the IBPA on the pressure distribution on a cascade of blades oscillating in pitch. The reduced frequency of oscillation is comparable to the ones of this work, therefore the findings of [2] can be considered valid also for this manuscript. Keehrti et al. [2] show that, whereas the phase of the pressure distribution along the chord on the suction side is close to zero for all the IBPAs, a large excursion of this quantity is observed on the pressure side. Specifically, they point out that the “average phase lead on the pressure surface varies [with the IBPA] in steps of 45 deg. for every 45 deg. change in [IBPA]” [2]. That is, the pressure peaks on the pressure side change remarkably their chord-wise location, according to the IBPA. This shifts change the interaction between blade-induced and plasma-induced pressure distribution. As a result, the plasma affection on the phase of the pitching moment varies with the IBPA. Overall, in order to further improve the effectiveness of the actuation for the diverse IBPAs, the amplitude and the phase of the pressure distribution should be accounted for together with the integral loads. This aspect will be taken under consideration and investigated in detail in future works, the present one being an exploratory study on the capabilities of plasma in controlling vibratory loads.
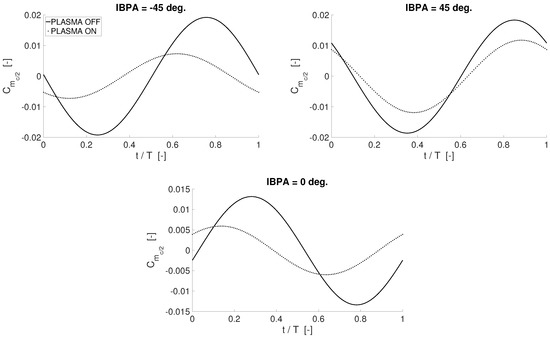
Figure 14.
Time history of the mid-chord pitching moment coefficient on the central blade for the last simulated period; Re ∼195,000; degrees; Hz, ; .
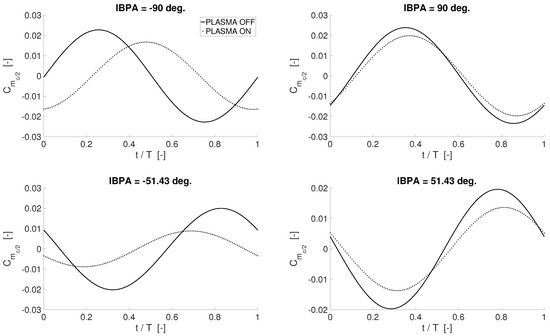
Figure 15.
Time history of the mid-chord pitching moment coefficient on the central blade for the last simulated period; Re ∼195,000; degrees; Hz, ; .
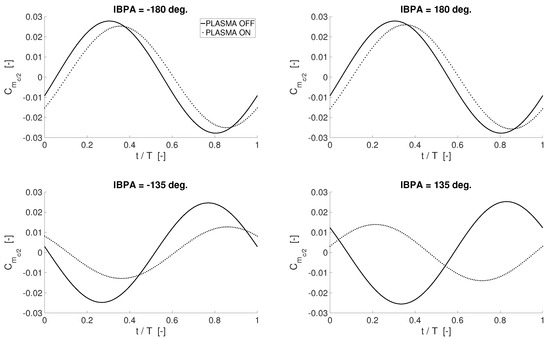
Figure 16.
Time history of the mid-chord pitching moment coefficient on the central blade for the last simulated period; Re ∼195,000; Hz, ; .
The unsteady lift curves are shown in Figure 17 for IBPA = [−180, −135, 135, 180] degrees. Overall, the lift coefficient is found to be less affected by actuation, compared to the moment, though the reduction in amplitude provided by the actuation is clearly visible. This discrepancy with respect to the moment coefficient is somehow expected because the phase of the lift coefficient for a pitching airfoil is different from the moment coefficient counterpart, consistently with Figure 11 and with Refs. [50,51]. Moreover, it is worth recalling that vibratory loads associated to the bending mode are expected to be less influential for fatigue phenomena—as well as for the aerostructural stability—of the targeted cascade compared to vibratory loads in pitch (see again Refs. [22,26]). The computed drag coefficient is not reported for brevity purposes. Indeed, the main concern of this work is to show the effect of plasma actuators on unsteady moment coefficient. Computations at constant angle of attack have shown that no significant drag rises have to be expected when employing plasma actuators. Additionally, as already mentioned, an accurate evaluation of plasma effects on the drag coefficient would require anyway more detailed and much more computationally demanding numerical simulations, which lie beyond the purposes of the present work. The assumption of fully turbulent flow, together with the numerical filtering associated with the Reynolds averaging operation, allows for getting only the qualitative behaviour of the drag.
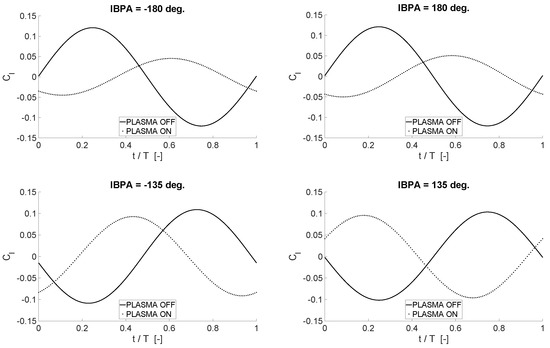
Figure 17.
Time history of the lift coefficient on the central blade for the last simulated period; Re ∼195,000; Hz, ; .
5. Conclusions
A computational fluid dynamic assessment of virtual control surfaces for load control on a compressor cascade is carried out. Virtual surfaces are realized by means of plasma actuators with induced flow against the freestream. As a result, controlled recirculating flow areas can be generated. By placing the actuators at the blade trailing edge—both on the pressure and on the suction side—effects comparable to those provided by Gurney flaps and wing spoilers can be achieved, respectively. The employment of plasma actuators in place of mechanical control surfaces is regarded as a powerful, fast responding, light and almost non-intrusive solution for load control. Moreover, as opposed to mechanical devices, plasma actuators are almost exempt from the risk of failure due to temperature and centrifugal fields encountered on aero engines. Plasma actuators are modeled numerically by introducing local source terms to the solved flow momentum equations. The intensity of the body force provided by the actuators is defined according to literature data. Computations at constant angle of attack are first performed, with the aim to characterize the affection of pressure or suction side actuation on the mean flow field and airloads. It is found that suction side actuation provides a decrease in the blade pitching moment and lift, whereas the opposite is encountered with PS actuation. Traveling wave pitch mode simulations are then carried out, with the blades oscillating in pitch at different interblade phase angles. Properly triggered alternate pressure/suction side actuations are shown to be capable of manipulating considerably the vibratory loads on the cascade. In particular, a remarkable attenuation in the peaks of the pitching moment—with potential beneficial effects also on the aeroelastic stability of the cascade—is observed. Because the triggering of the control is defined intentionally on the basis of the phase of the moment coefficient only, the oscillation amplitude of the lift coefficient is less affected by the actuation. By the way, the bending stiffness of the blade being much larger than the torsional counterpart, the resulting bending vibratory loads are expected to be affected only marginally. As a support to the findings of this work, it is worth remarking that the results achieved are qualitatively comparable to those obtained with mechanical control surfaces, both in fixed position and harmonically deflected. This confirms the potential suitability of the present actuation as a novel load control solution for heavily loaded compressor blades, but ultimately extensible to any lifting surface. Experimental tests of plasma actuators, operated as virtual control surfaces for load alleviation and enlargement of the flutter boundaries on the TU Berlin compressor cascade, are planned as an outlook to the present work.
Acknowledgments
The authors are grateful to Elisa Pescini and Maria Grazia De Giorgi for their useful support on the numerical modeling of plasma actuators. This research has been carried out within the framework and the support of the Collaborative Research Centre 1029 of Technische Universität Berlin (http://www.sfb1029.tu-berlin.de/menue/sfb_1029/parameter/en/).
Author Contributions
Valentina Motta carried out the researh work together with Leonie Malzacher. Dieter Peitsch is the Head of the Chair of Aero Engines and provides general support to all the activities of the research staff.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| c | blade chord, [m] |
| CFD | computational fluid dynamic(s) |
| Cd | drag coefficient, [-] |
| CP | pressure coefficient, [-] |
| Cl | lift coefficient, [-] |
| Cm | moment coefficient, at the mid-chord if not differently specified, [-] |
| Cmc/2 | mid-chord moment coefficient, [-] |
| f | blade oscillation frequency, [Hz] |
| k = | reduced frequency, [Hz] |
| IBPA | interblade phase angle, [deg.] |
| PS | pressure side |
| Re = U∞c/ | Reynolds number, [-] |
| SS | suction side |
| t | time, [s] |
| T | blade oscillation period, [s] |
| U | flow velocity, [m/s] |
| U∞ | freestream velocity, [m/s] |
| x | horizontal spacial coordinate, [m] |
| y | vertical spacial coordinate, [m] |
| blade angle of attack, [deg.] | |
| phase angle, [deg.] | |
| air kinematic viscosity at 20 C, [m2/s] |
References
- Im, H.; Zha, G. Investigation of Flow Instability Mechanism Causing Compressor Rotor-Blade Nonsynchronous Vibration. AIAA J. 2014, 52, 2019–2031. [Google Scholar] [CrossRef]
- Keerthi, M.C.; Shubham, S.; Kushari, A. Aerodynamic Influence of Oscillating Adjacent Airfoils in a Linear Compressor Cascade. AIAA J. 2017, 55, 4113–4126. [Google Scholar] [CrossRef]
- Panovski, J.; Kielb, R.E. A Design Method to Prevent Low Pressure Turbine Blade Flutter. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998. [Google Scholar]
- Huang, X.Q.; Bell, D.L. Influence of upstream stator on rotor flutter stability in a low pressure steam turbine stage. Proc. Inst. Mech. Eng. Part A 2006, 220, 23–35. [Google Scholar] [CrossRef]
- Tiedemann, C.; Heinrich, A.; Peitsch, D. A New Linear High Speed Compressor Stator Cascade for Active Flow Control Investigations. In Proceedings of the 6th AIAA Flow Control Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Matejka, M.; Popelka, L.; Safarik, P.; Nozicka, J. Influence of Active Methods of Flow Control on Compressor Blade Cascade Flow. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Trávníček, Z.; Cyrus, V.; Šimurda, D.; Luxa, M.; Lukač, J.; Kordik, J. Experimental Investigation of the Compressor Cascade under an Active Flow Control. EPJ Web Conf. 2013, 45. [Google Scholar] [CrossRef]
- Monner, H.P.; Huxdorf, O.; Riemenschneider, J.; Keimer, R. Design and manufacturing of morphing fan blades for experimental investigations in a cascaded wind tunnel. In Proceedings of the 23rd AIAA/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Hammer, S.; Phan, D.T.; Peter, J.; Werder, T.; Meyer, R.; Liebich, R.; Thamsen, P.U. Active flow control by adaptive blade systems in periodic unsteady flow conditions. In Proceedings of the Active Flow and Combustion Control, Berlin, Germany, 10–12 September 2014. [Google Scholar]
- Suman, A.; Fortini, A.; Aldi, N.; Merlin, M.; Pinelli, M. A Shape Memory Alloy-Based Morphing Axial Fan Blade: Part I—Blade Structure Design and Functional Characterization. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Suman, A.; Fortini, A.; Aldi, N.; Merlin, M.; Pinelli, M. A Shape Memory Alloy-Based Morphing Axial Fan Blade: Part II—Blade Shape and CFD Analyses. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Vo, H.D.; Cameron, J.D.; Morris, S.C. Control of Short Length-Scale Rotating Stall Inception on a High-Speed Axial Compressor with Plasma Actuation. In Proceedings of the Proceedings of ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- De Giorgi, M.G.; Pescini, E.; Marra, F.; Ficarella, A. Experimental and numerical analysis of a micro plasma actuator for active flow control in turbomachinery. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Akcayoz, E.; Huu, D.V.; Mahallati, A. Controlling Corner Stall Separation With Plasma Actuators in a Compressor Cascade. J. Turbomach. 2016, 138. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, X.; Liu, B.; Wu, Y.; Li, Y. Control of Corner Separation with Plasma Actuation in a High-Speed Compressor Cascade. Appl. Sci. 2017, 7, 465. [Google Scholar] [CrossRef]
- Motta, V.; Guardone, A.; Quaranta, G. Numerical investigation of an L-shaped deployable Gurney flap for rotorcraft vibration control. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics, Bristol, UK, 24–26 June 2013. [Google Scholar]
- Motta, V. Computational Fluid Dynamic Analysis of A L-shaped Gurney Flap for Vibration Control. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2015. Available online: http://hdl.handle.net/10589/100350 (accessed on 16 January 2018).
- Motta, V.; Quaranta, G. Linear Reduced-Order Model for Unsteady Aerodynamics of an L-Shaped Gurney Flap. J. Aircr. 2015, 52, 1887–1904. [Google Scholar] [CrossRef]
- Motta, V.; Zanotti, A.; Gibertini, G.; Quaranta, G. Numerical assessment of an L-shaped Gurney flap for load control. Proc. Inst. Mech. Eng. Part G 2016, 231, 951–975. [Google Scholar] [CrossRef]
- Motta, V.; Quaranta, G. A comparative assessment of vibration control capabilities of a L-shaped Gurney flap. Aeronaut. J. 2016, 120, 1812–1831. [Google Scholar] [CrossRef]
- Feng, L.; Choi, K.; Wang, J. Flow control over an airfoil using virtual Gurney flaps. J. Fluid Mech. 2015, 767, 595–626. [Google Scholar] [CrossRef]
- Malzacher, L.; Geist, S.; Peitsch, D.; Hennings, H. A low speed compressor test rig for flutter investigations. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 12–16 June 2016. [Google Scholar]
- Carta, F.O. An Experimental Investigation of Gapwise Periodicity and Unsteady Aerodynamic Response in an Oscillating Cascade; Contractor Report 3523; NASA, United Technologies Research Center: East Hartford, CT, USA, 1982.
- Sachs, W. Windkanal für Instationäre Gitter (WiG), Messstrecke für Instationäre Gitter (MiG). Phase 1: Bau und InbetriebnahmeWindkanal für Instationäre Gitter (WiG); Technical Report; DLR, Institute of Aeroelasticity: Göttingen, Germany, 1990. [Google Scholar]
- He, C.; Corke, T.C.; Patel, M.P. System Mode Shapes in the Flutter of Compressor Blade Rows. J. Aeronaut. Sci. 1956, 23, 54–66. [Google Scholar]
- Hennings, H. Flutter Investigations on a Finite Linear 2D Compressor Cascade in A Wind Tunnel in Incompressible Flow. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 1997. [Google Scholar]
- Garrick, I. Improved Two-Equation k–Omega Turbulence Models for Aerodynamic Flows; TR 93; NASA Ames Research Center: Moffett Field, CA, USA, 1992.
- Ekaterinaris, J.A.; Menter, F.R. Computation of Oscillating Airfoil Flows with One- and Two-Equation Turbulence Models. AIAA J. 1994, 32, 2359–2365. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Baldwin, B.S.; Barth, T.J. A One-Equation Turbulence Transport Model for High Reynolds Number Wall-Bounded Flows. In Proceedings of the 29th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 1991. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Botsch, M.; Sorkine, O. On Linear Variational Surface Deformation Methods. IEEE Trans. Vis. Comput. Graph. 2008, 14, 213–230. [Google Scholar] [CrossRef] [PubMed]
- ANSYS, Inc. ANSYS Academic Research, Release 17.1; ANSYS, Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Wang, J.; Choi, K.; Feng, L.; Jukes, T.; Whalley, R. Recent developments in DBD plasma flow control. Prog. Aerosp. Sci. 2013, 62, 52–78. [Google Scholar] [CrossRef]
- West, T.K.; Hosder, S. Numerical Investigation of Plasma Actuator Configurations for Flow Separation Control at Multiple Angles of Attack. Int. J. Flow Control 2013, 5, 169–174. [Google Scholar] [CrossRef]
- Aholt, J.; Finaish, F. Active Flow Control Strategy of Laminar Separation Bubbles Developed over Subsonic Airfoils at Low Reynolds Numbers. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Ibrahimoglu, B.; Yilmazoglu, M.Z.; Cücen, A. Numerical Analysis of Active Control of Flow on a DBD Plasma Actuator Integrated Airfoil. In Sustainable Aviation: Energy and Environmental Issues; Chapter 8; Springer International Publishing: Cham, Switzerland, 2016; pp. 363–374. [Google Scholar]
- Corke, T.C.; Post, M.L.; Orlov, D.M. SDBD plasma enhanced aerodynamics: Concepts, optimization and application. Prog. Aerosp. Sci. 2007, 43, 193–217. [Google Scholar] [CrossRef]
- Shyy, W.; Jayaraman, B.; Andersson, D. Modeling of glow discharge-induced fluid dynamics. J. Appl. Phys. 2002, 92, 6434–6443. [Google Scholar] [CrossRef]
- Pescini, E.; Martínez, D.S.; De Giorgi, M.G.; Ficarella, A. Optimization of micro single dielectric barrier discharge plasma actuator models based on experimental velocity and body force fields. Acta Astronaut. 2015, 116, 318–332. [Google Scholar] [CrossRef]
- Moreau, E. Airflow Control by Non-Thermal Plasma Actuators. J. Phys. D Appl. Phys. 2007, 40, 605–636. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L. Overview of Plasma Flow control: Concepts, Optimization and Applications. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- He, C.; Corke, T.C.; Patel, M.P. Plasma Flaps and Slats: An Application of Weakly Ionized Plasma Actuators. J. Aircr. 2009, 46, 864–873. [Google Scholar] [CrossRef]
- Belz, J.; May, M.; Siemann, J.; Seume, J.R.; Voigt, C.; Böhmer, H.; Grüber, B. Excited Blade Vibration for Aeroelastic Investigations of a Rotating Blisk Using Piezo-Electric Macro Fiber Composites. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Iwrey, B.M. Gas Turbine Engine with Rotor Blade Clearance Flow Control. U.S. Patent 2016/0177769 A1, 23 June 2016. [Google Scholar]
- Carta, F.O. An Analysis of the Stall Flutter Instability of Helicopter Rotor Blades. J. Am. Helicopter Soc. 1967, 12, 1–18. [Google Scholar] [CrossRef]
- Zanotti, A.; Grassi, D.; Gibertini, G. Experimental investigation of a trailing edge L-shaped tab on a pitching airfoil in deep dynamic stall conditions. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 2371–2382. [Google Scholar] [CrossRef]
- Abbott, I.; von Doenhoff, A. Theory of Wing Sections; Dover Publication, Inc.: New York, NY, USA, 1949. [Google Scholar]
- Giguère, P.; Lemay, J.; Dumas, G. Gurney Flap Effects and Scaling for Low-Speed Airfoils. In Proceedings of the 13th AIAA Applied Aerodynamic Conference, San Diego, CA, USA, 19–22 June 1995. [Google Scholar]
- Motta, V.; Guardone, A.; Quaranta, G. Influence of airfoil thickness on unsteady aerodynamic loads on pitching airfoils. J. Fluid Mech. 2015, 774, 460–487. [Google Scholar] [CrossRef]
- Leishman, J.G. Principle of Helicopter Aerodynamics; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).