Frequency Modulation and Erosion Performance of a Self-Resonating Jet
Abstract
1. Introduction
2. Research Method
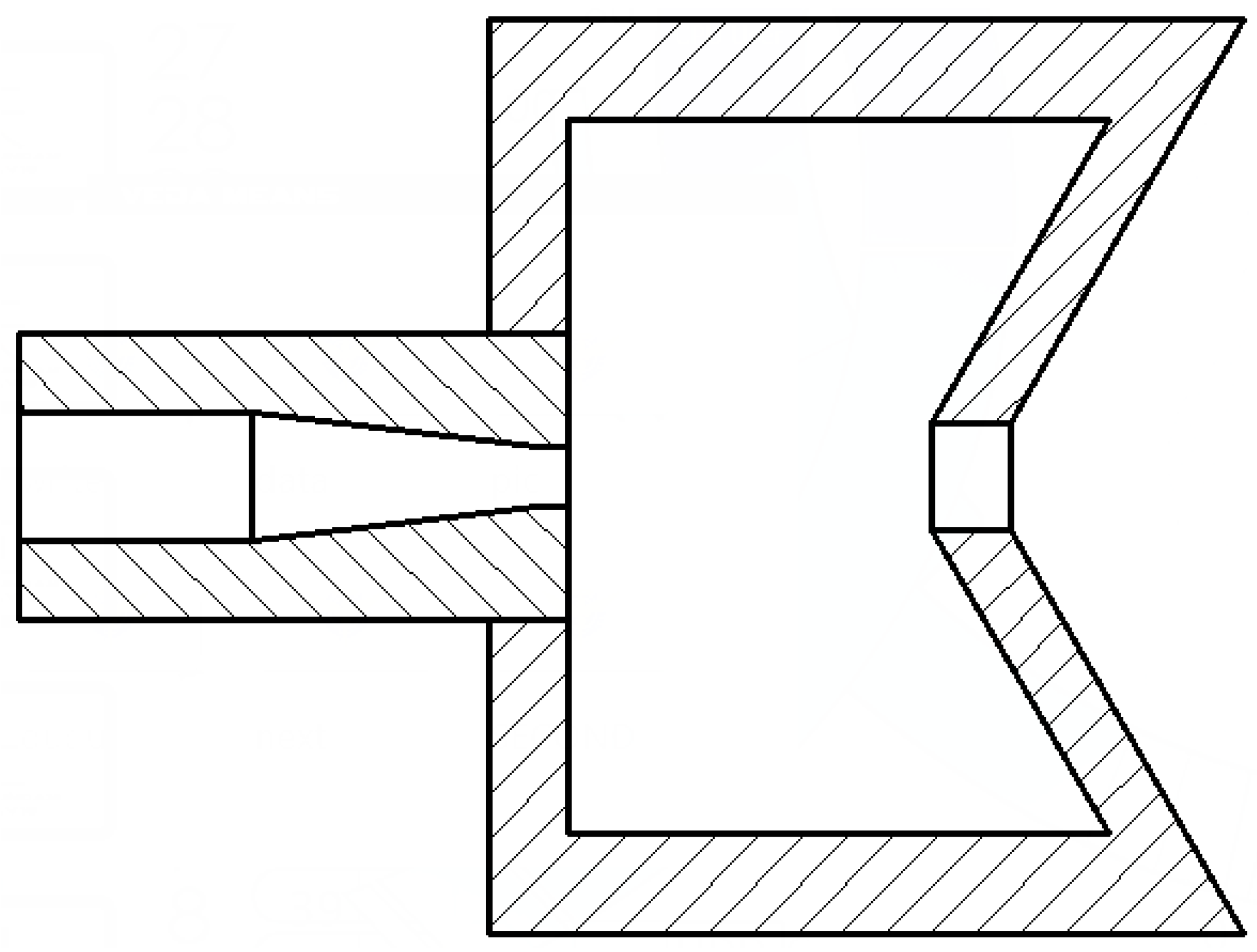
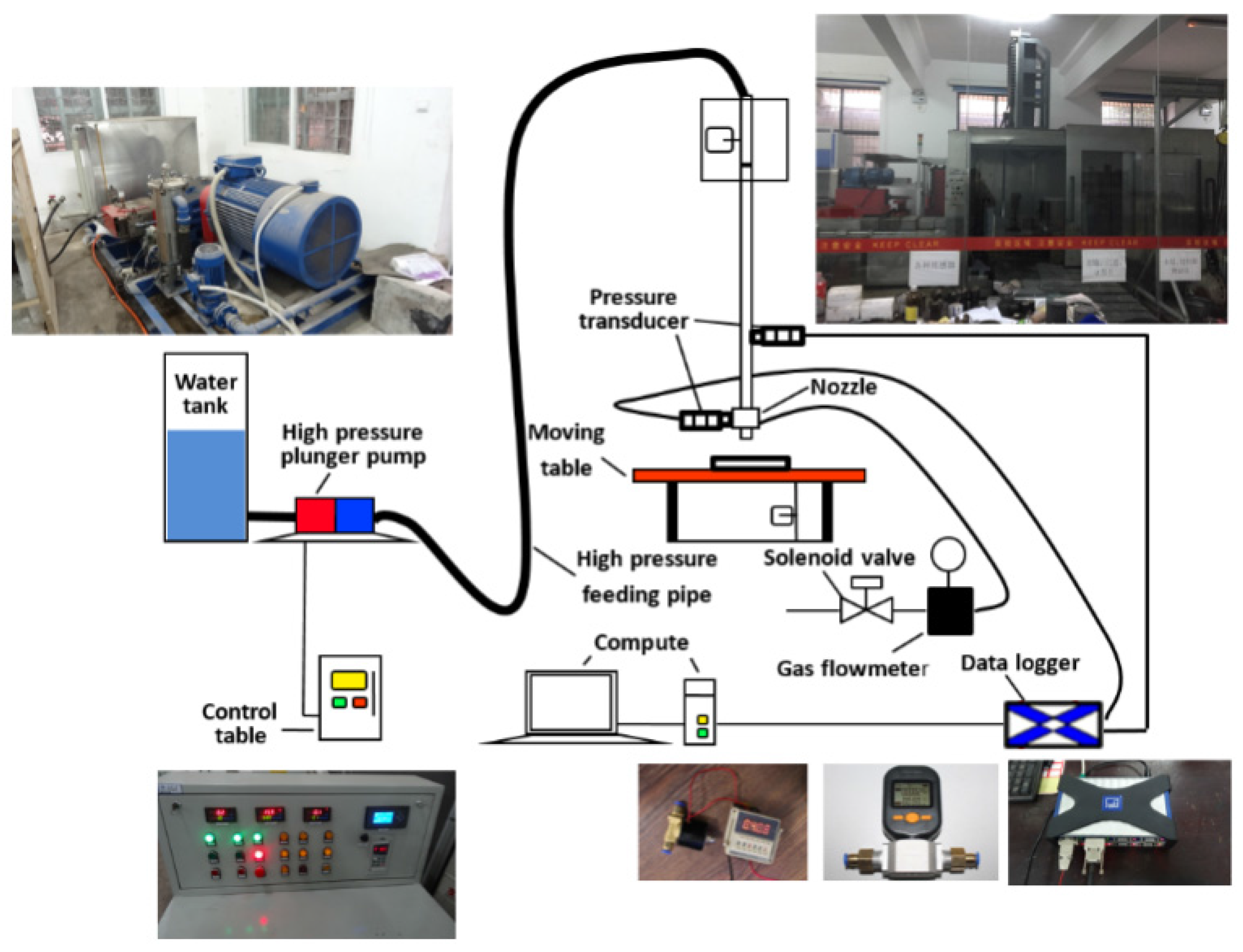
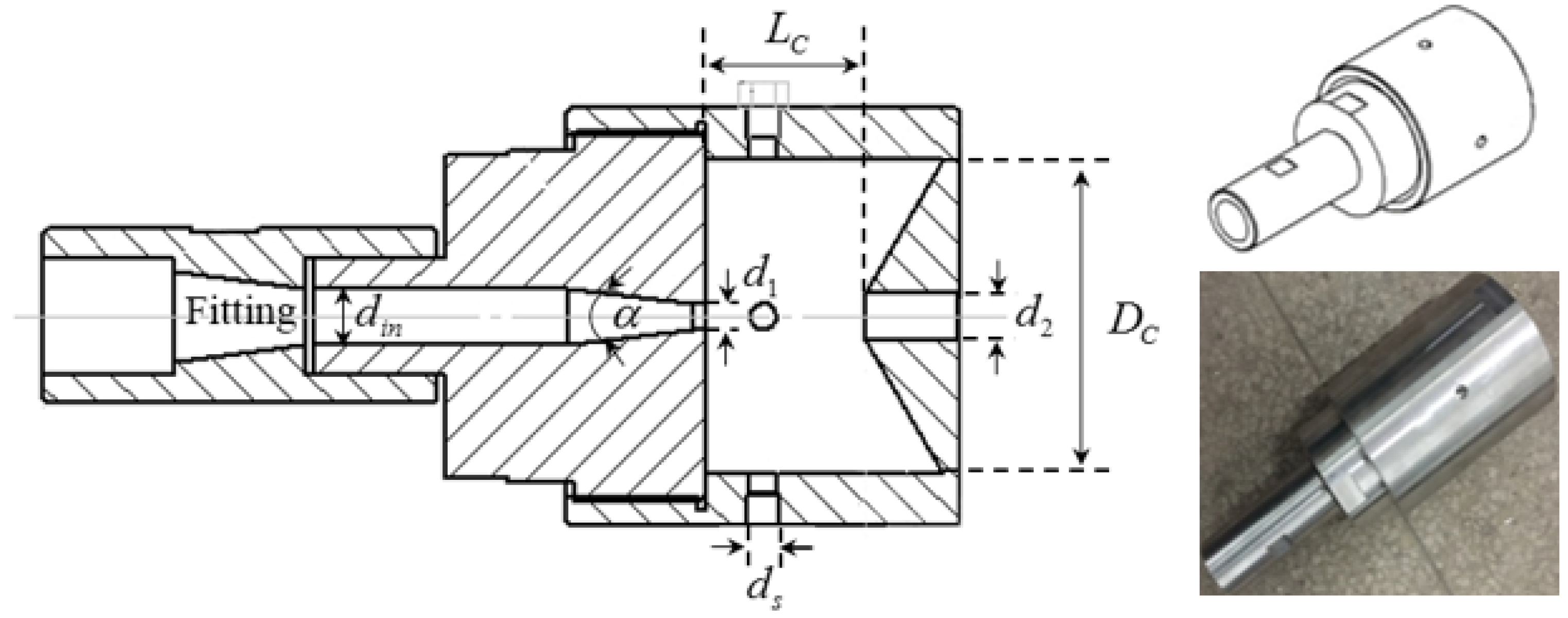
2.1. Experimental Method
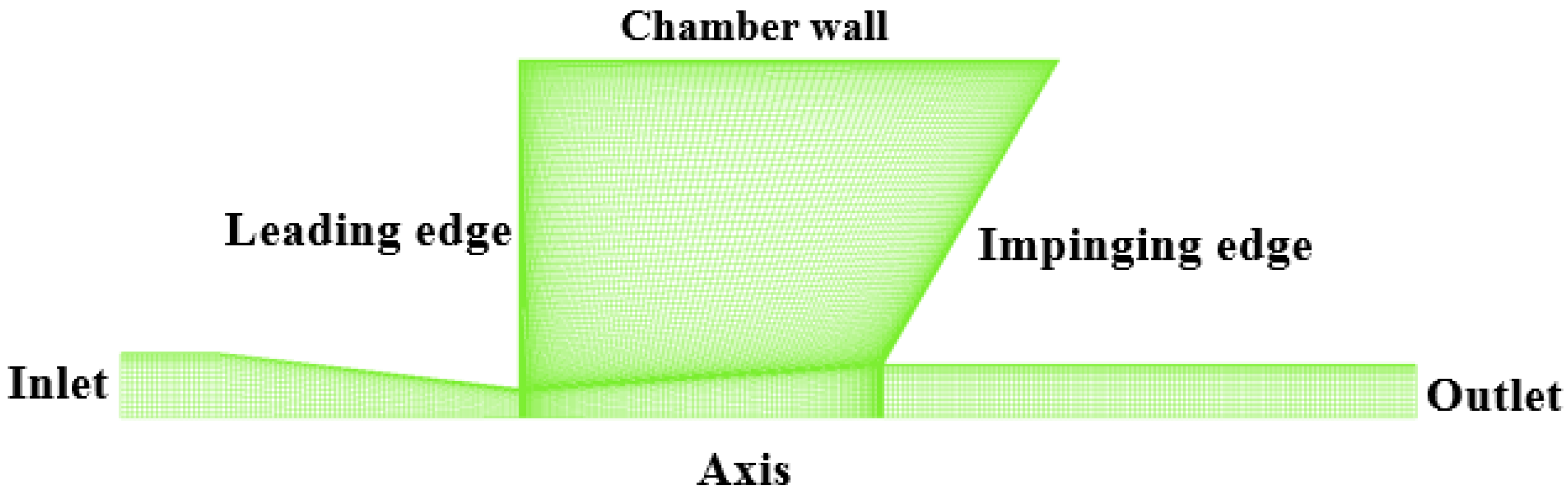
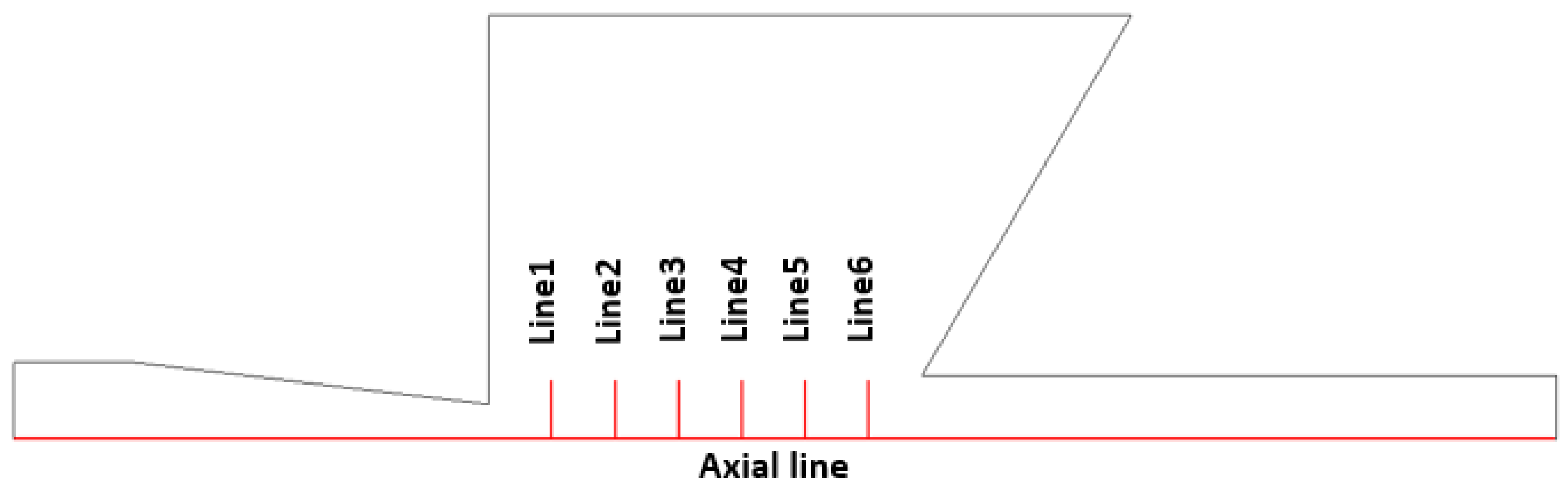
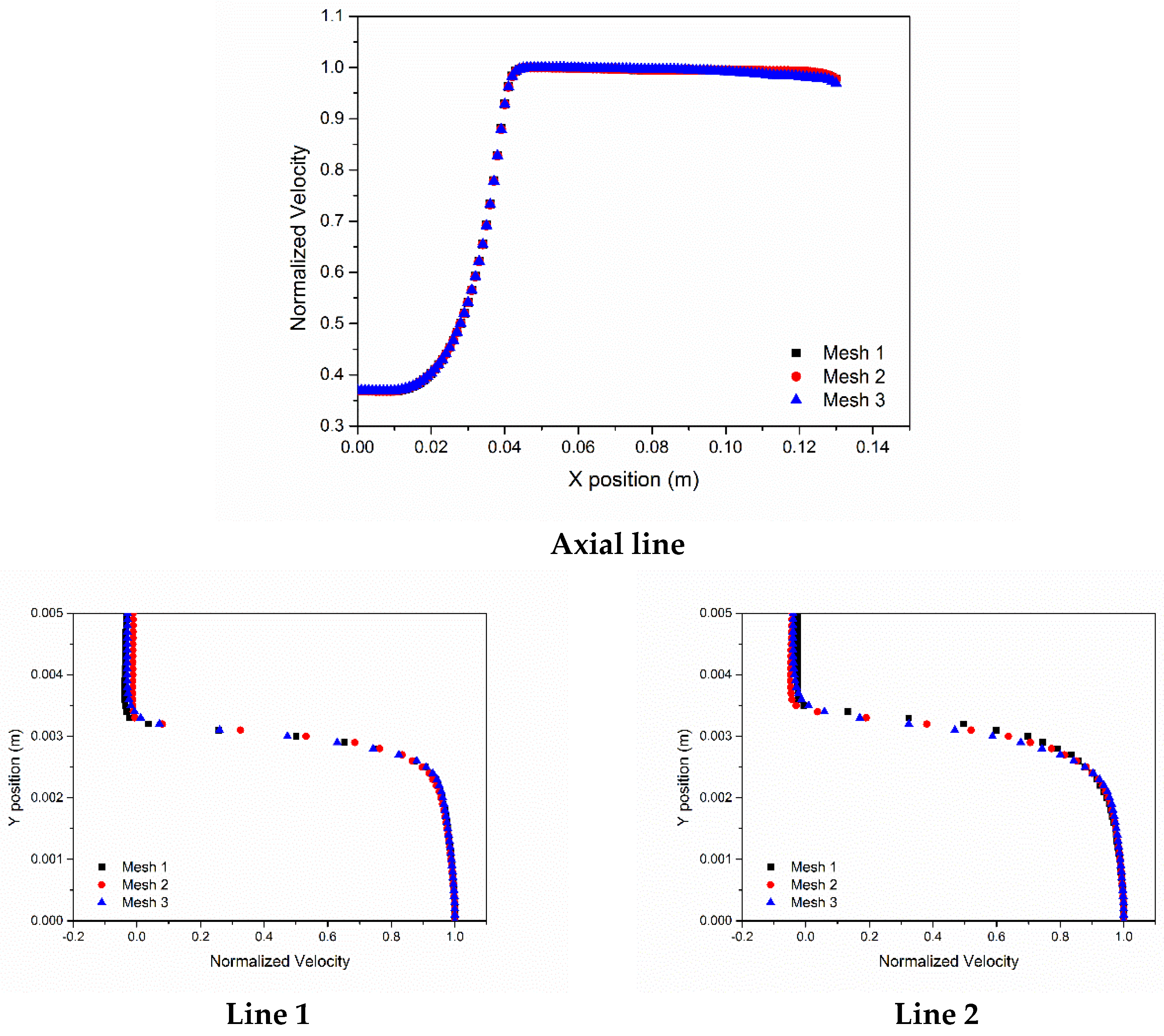
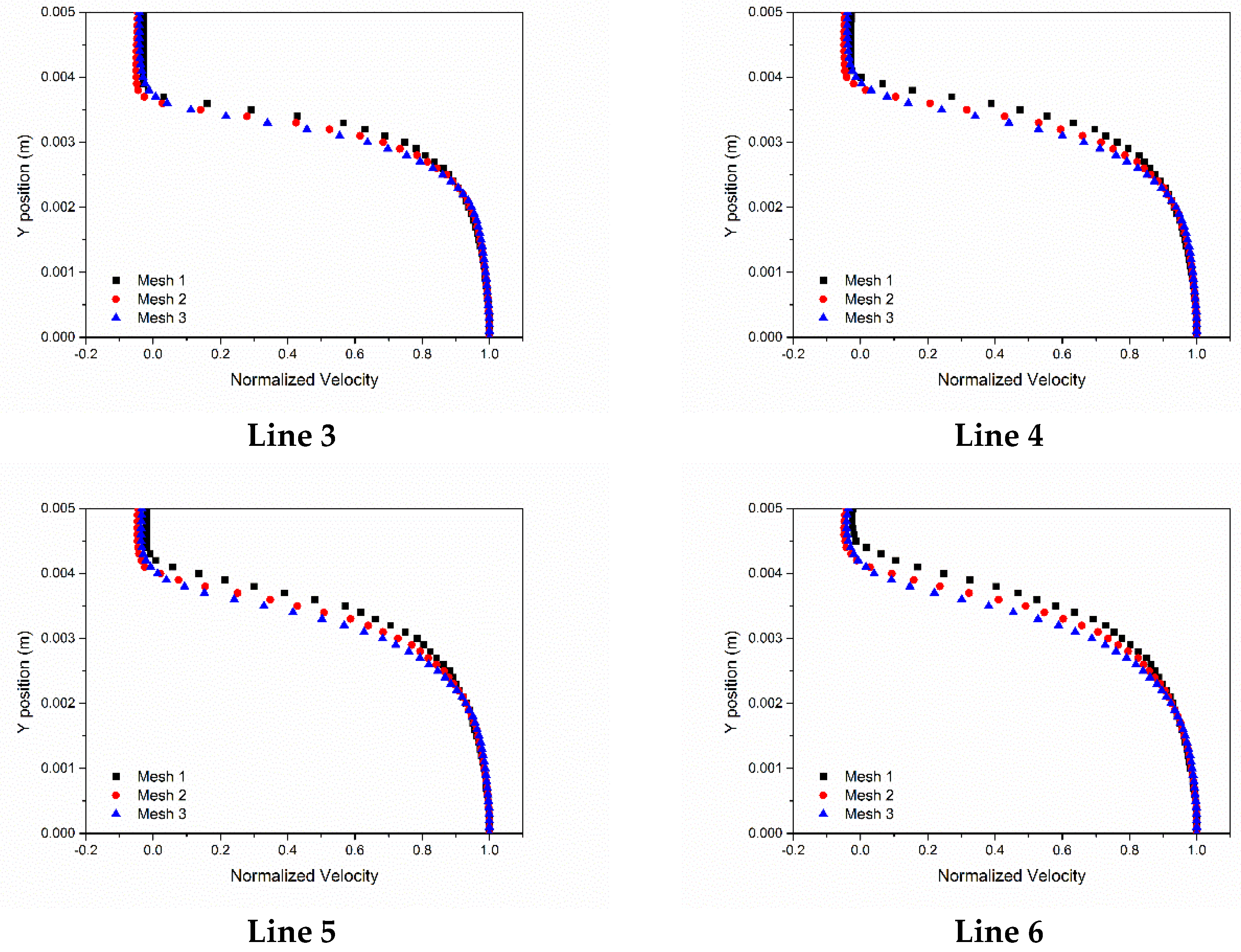
2.2. Numerical Simulation Setup
3. Results and Discussion
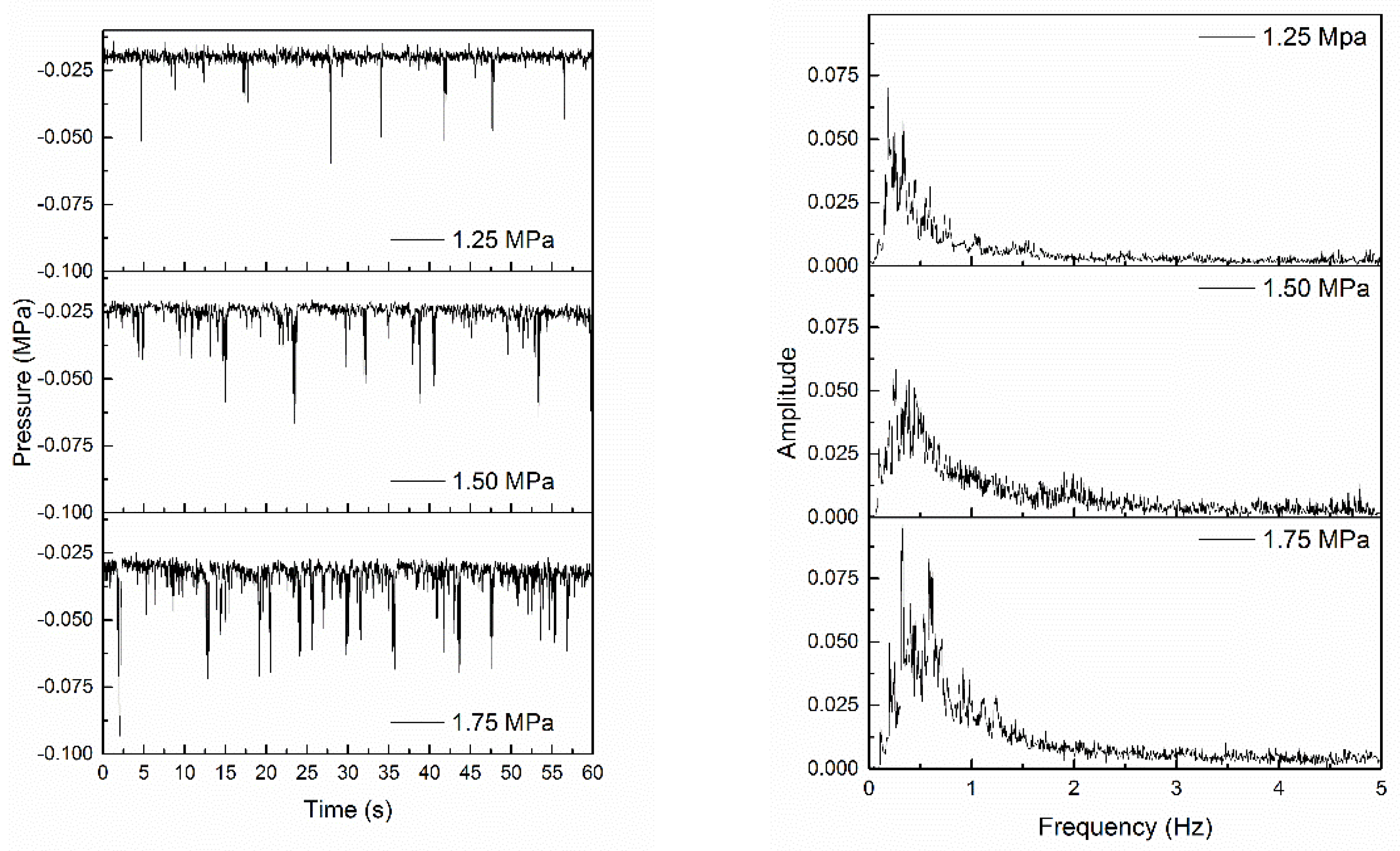
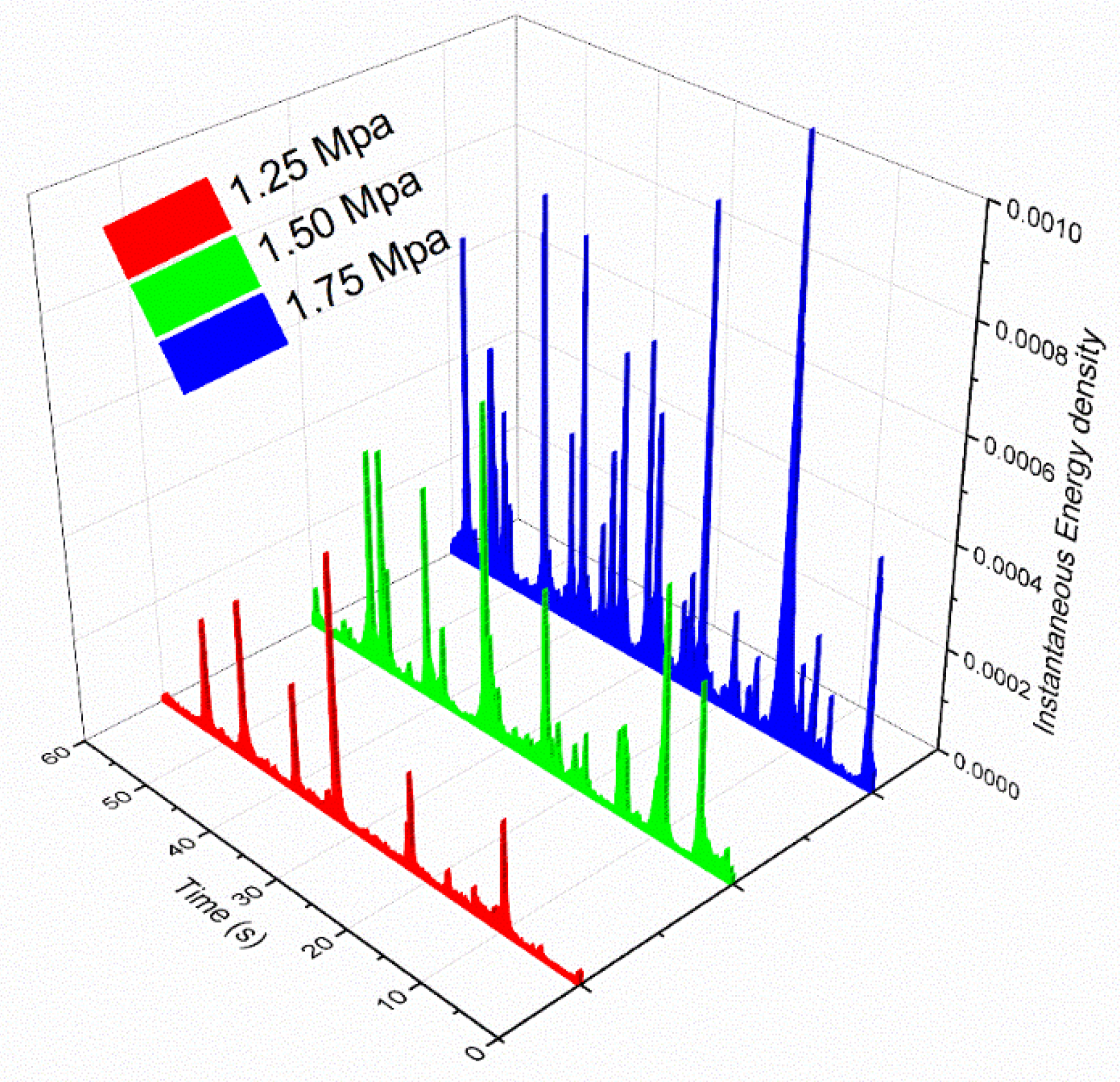
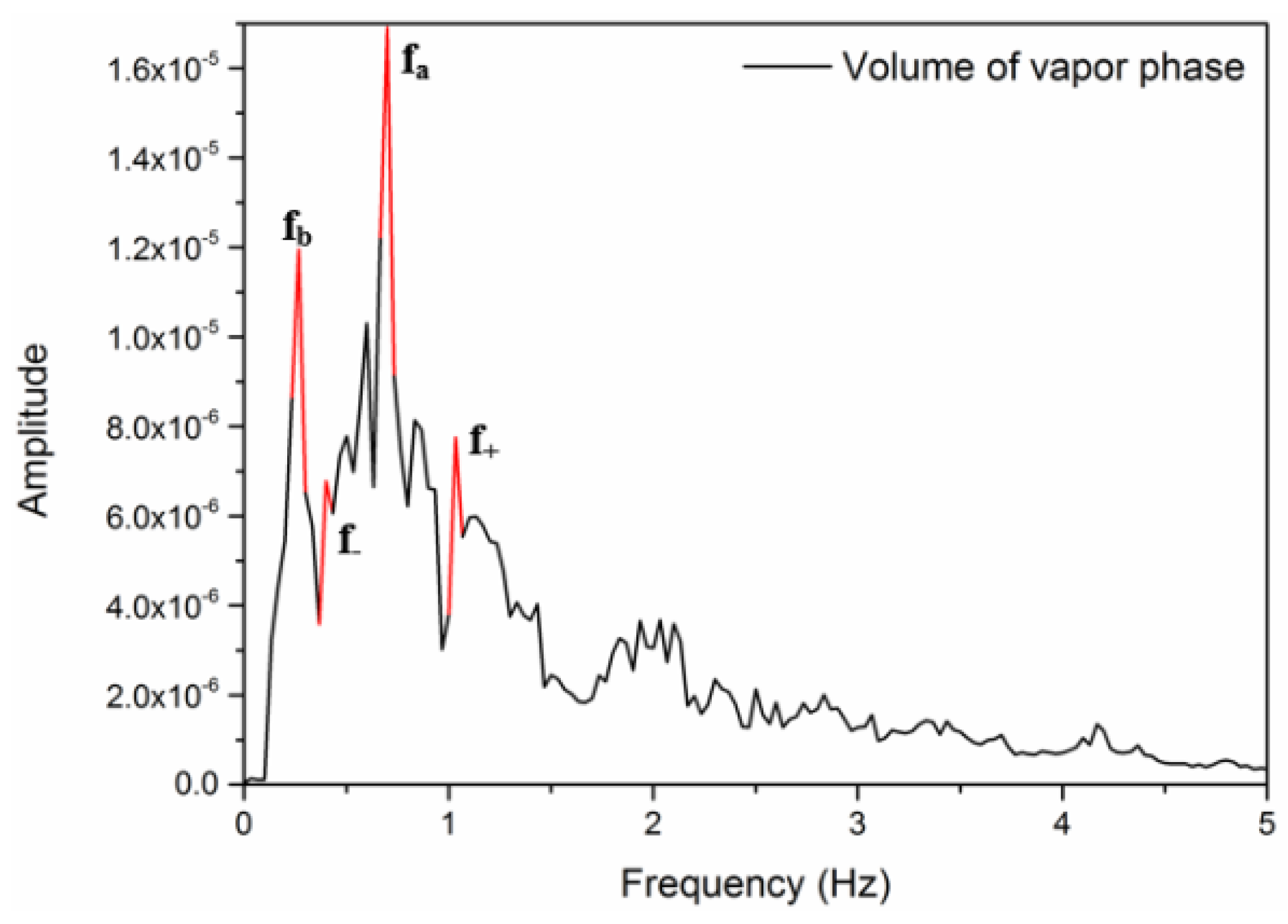
3.1. Gas-Spring Theory
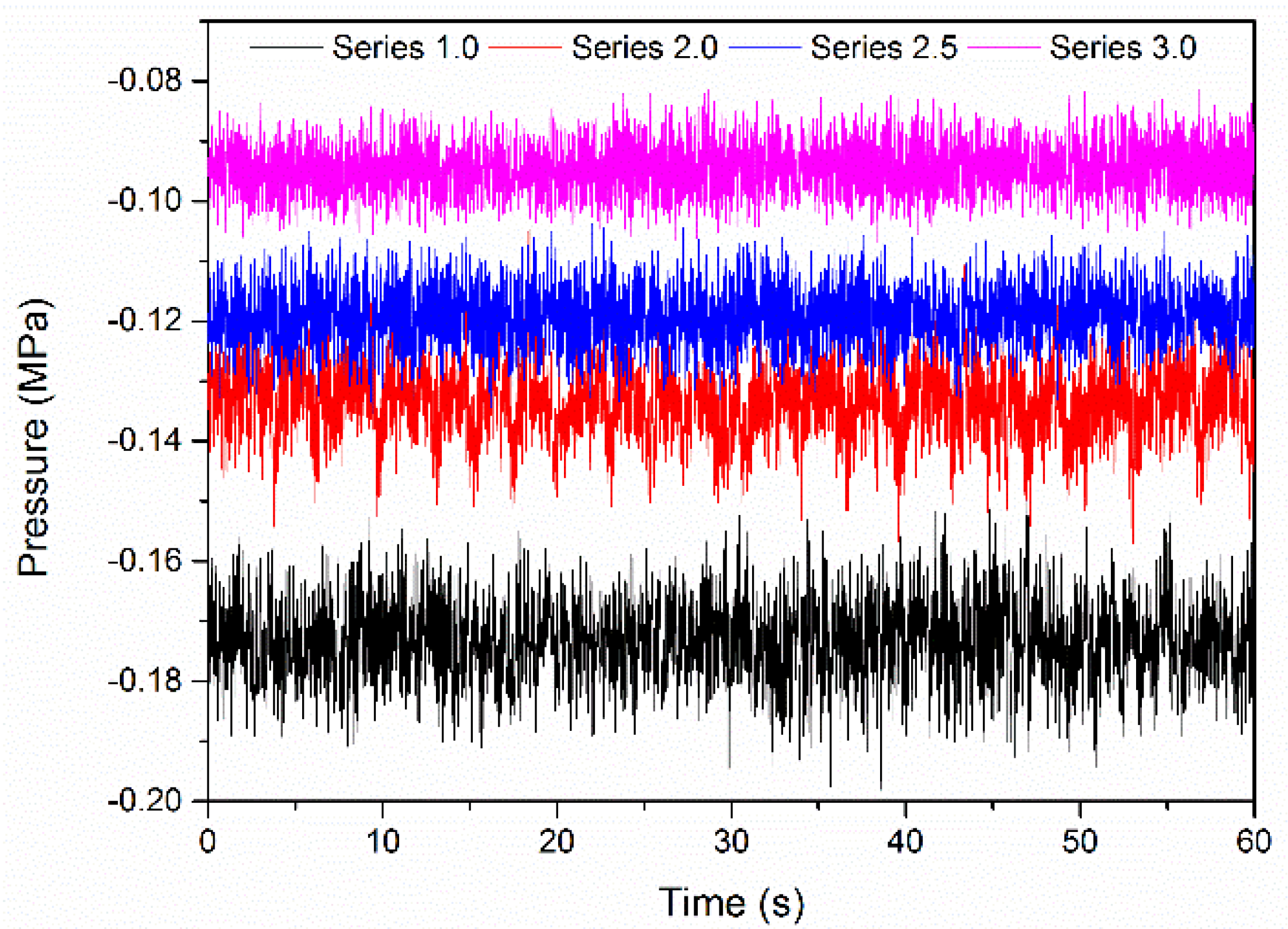
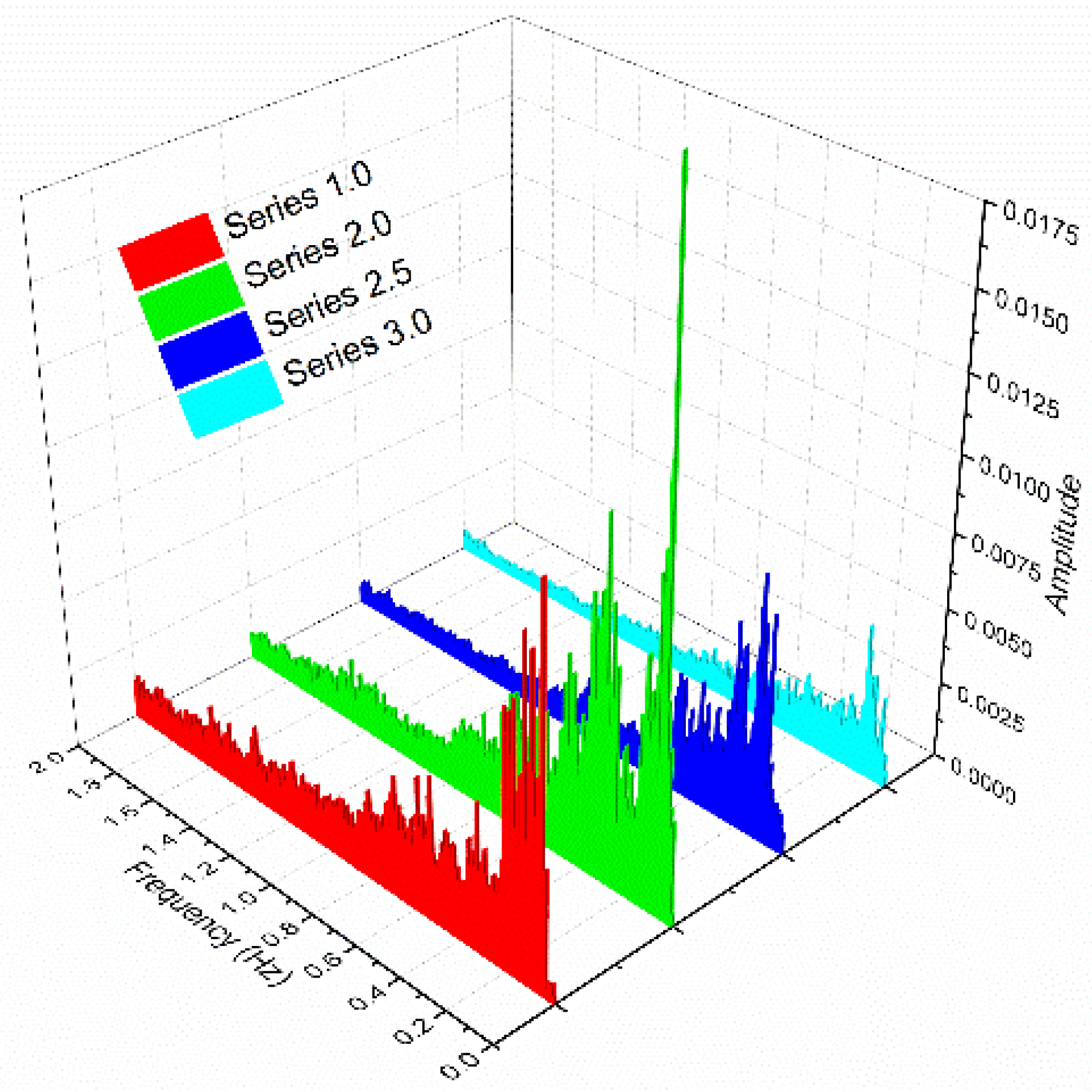
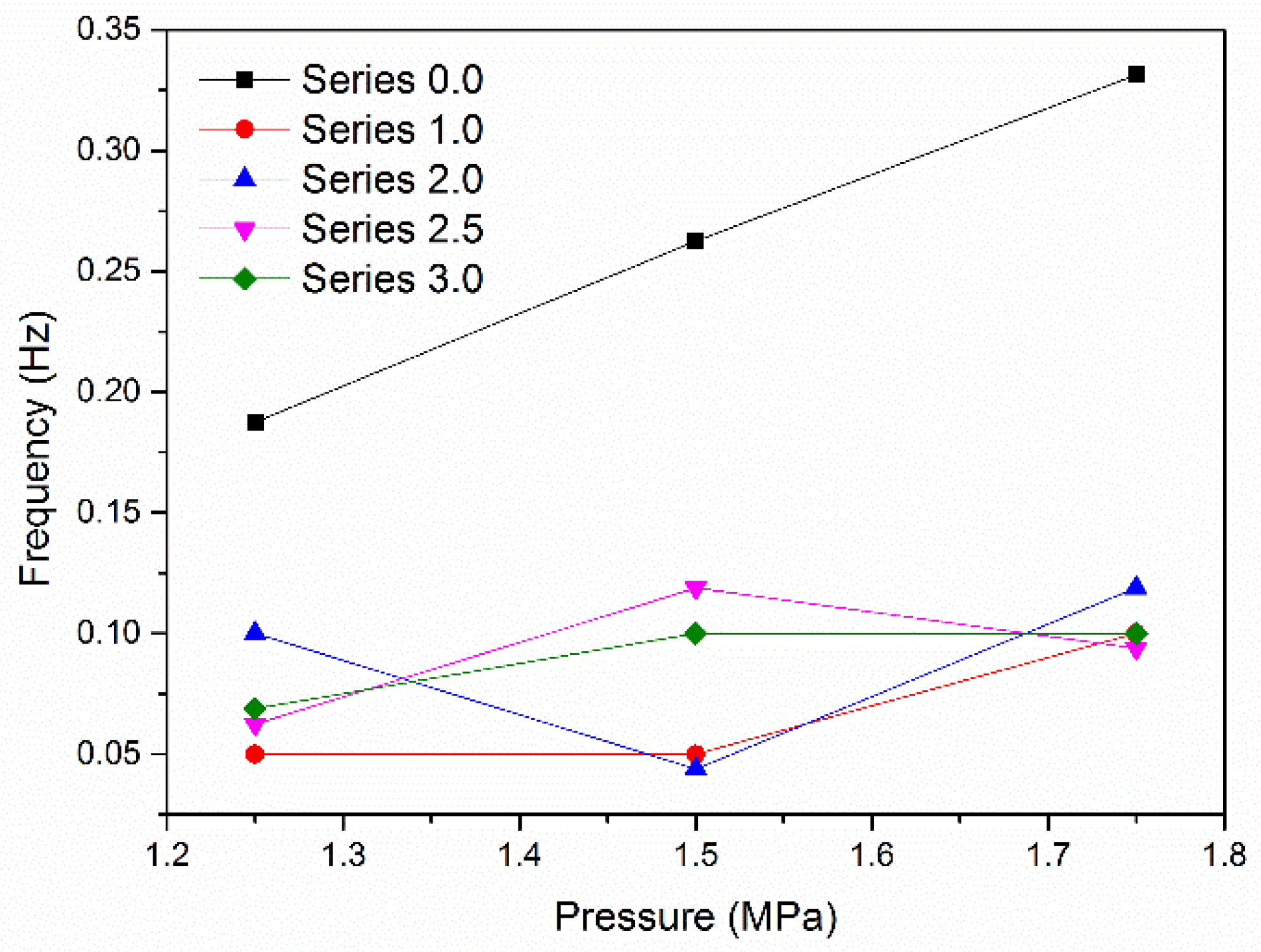
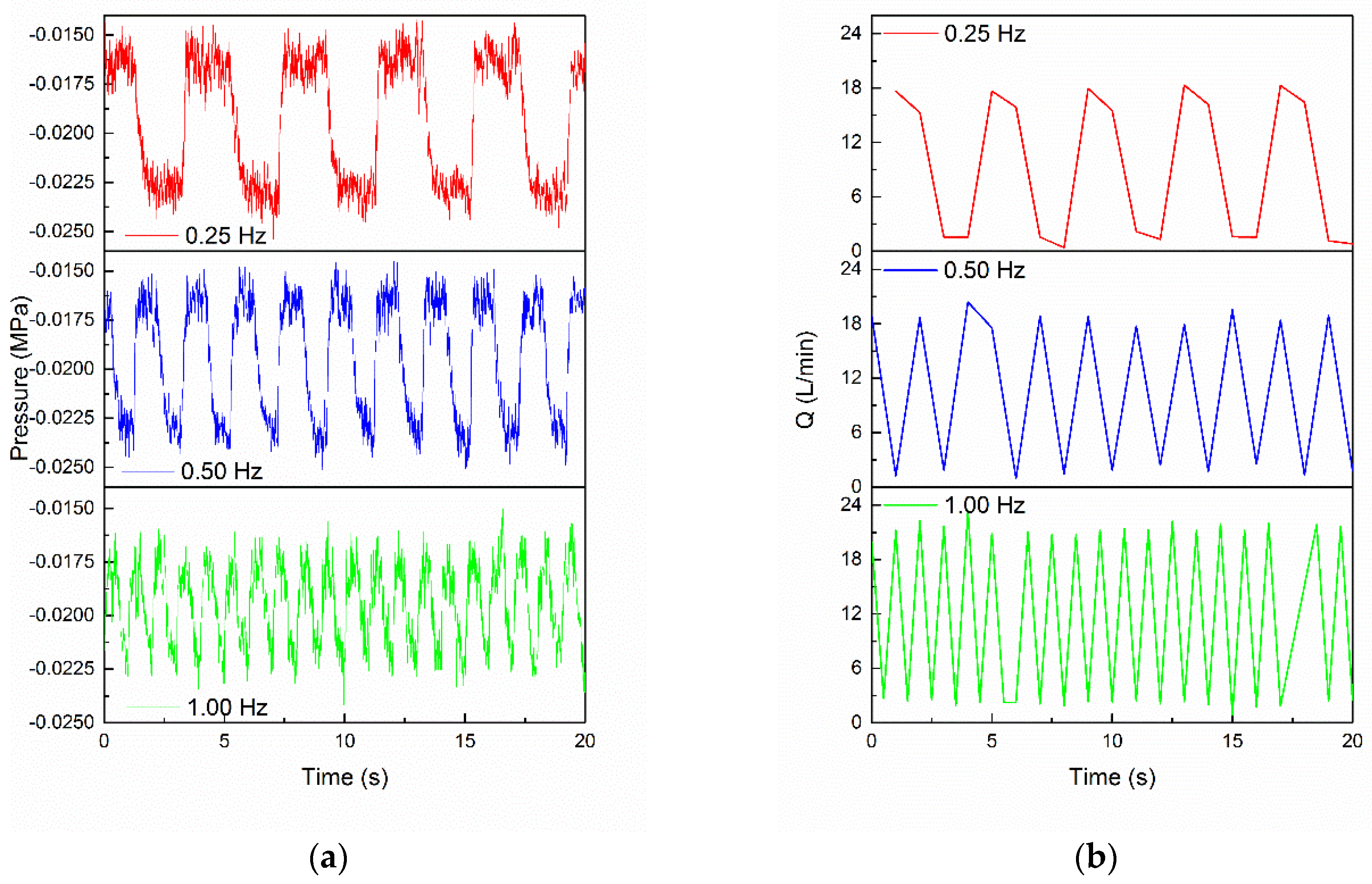
3.2. Frequency Modulation
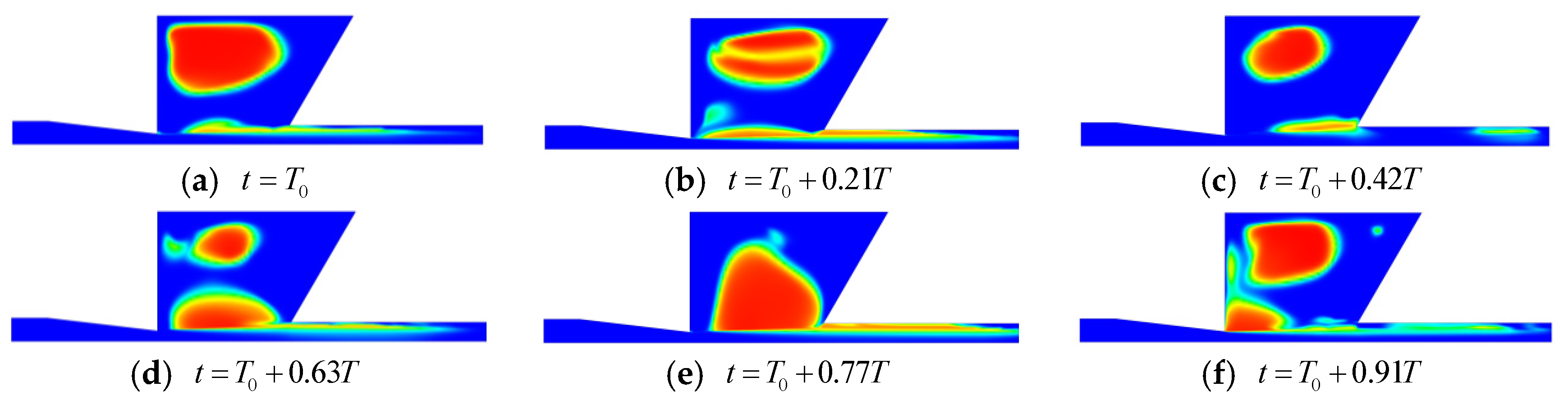
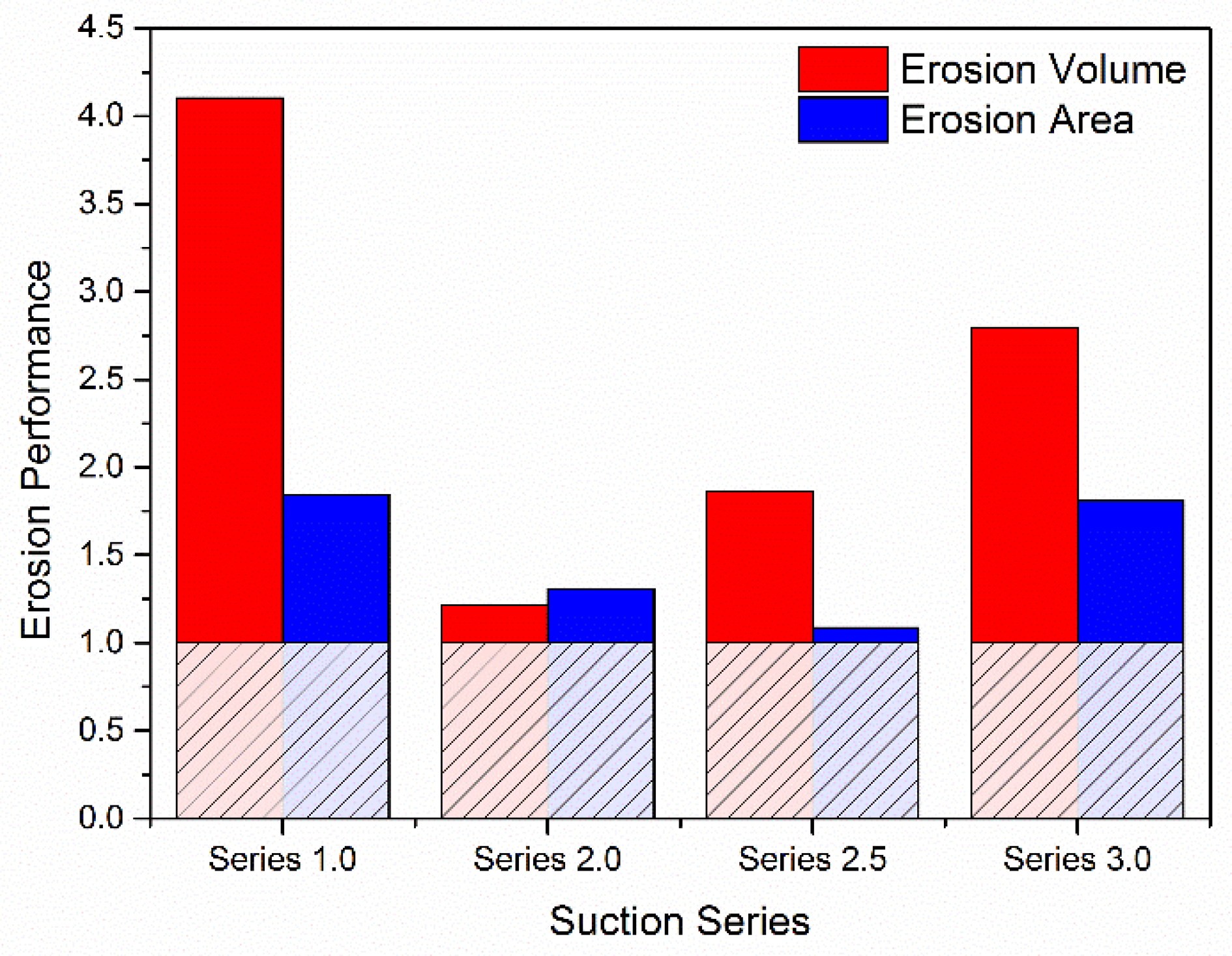
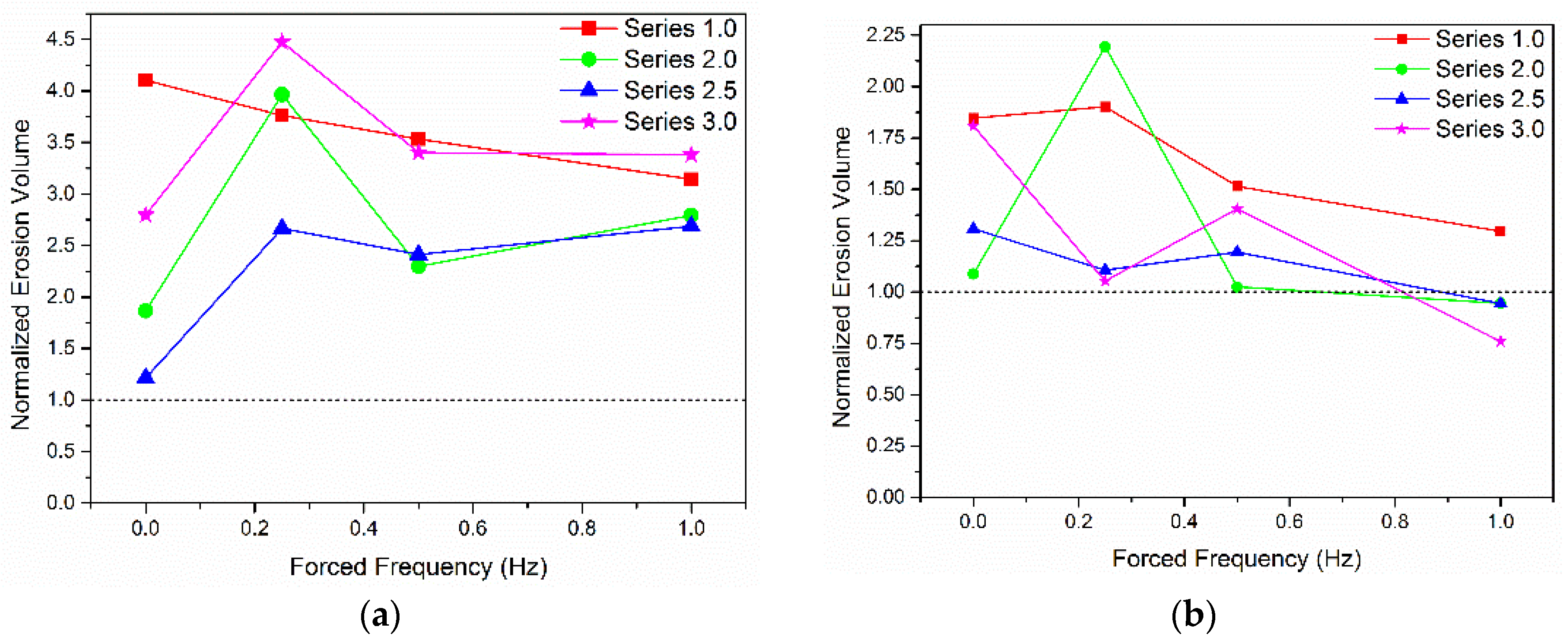
3.3. Erosion Performance
4. Conclusions
- The Gas-Spring Theory was verified by both the experiment and the numerical simulation. The cavitation cluster dominated the oscillating frequency in the LPHF nozzle and the non-linear interaction between the cavitation cluster and acoustic modulation should also be considered. The global structure of the spectral distribution can be viewed as the result of non-linear interactions and modulation processes.
- The mechanism of frequency modulation was different with/without air intake. When no air was entrained, the dominant frequency increased linearly with the increasing pressure declines due to the decreasing accumulated time for the cavity cluster. For the LPHF nozzle with suction holes, the frequency of each inspiratory method did not vary monotonically with the pressure decrease.
- For the LPHF nozzle with suction holes, frequency modulation could be achieved in a wide range by simply changing the number and distribution of the open suction holes. The modulation range was dependent on the pressure decrease.
- For the forced exciting condition, the oscillating frequency was totally determined by the forced frequency of entrained air. With the increasing forced frequency, the mean volume of entrained air increased due to the fierce entraining and momentum transportation.
- The removal rate was improved with the entrained air. The erosion performance was affected by both the volume of entrained air and the distribution of the air entry-path. The best erosion performance was achieved at the frequency closest to the fundamental oscillation frequency. Thus, it is necessary to consider various combinations of the number and distributions of suction holes in order to achieve the expected goal.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| diameter | |
| length | |
| diameter of chamber hole | |
| convergent angle | |
| density | |
| time | |
| pressure | |
| viscosity | |
| mass transfer rate | |
| vapor volume fraction | |
| water volume fraction | |
| bubble radius | |
| saturation vapor pressure | |
| bubble number density | |
| turbulent kinetic energy | |
| turbulent eddy dissipation | |
| exponential coefficient | |
| cross section area | |
| volume of chamber | |
| f | oscillation frequency |
| circular frequency | |
| vapor phase volume | |
| adiabatic exponent of air |
Subscripts
| parameters of chamber | |
| property of gas | |
| property of water | |
| turbulence |
References
- Conn, A.F.; Johnson, V.E.; Liu, H.L.; Frederick, G.S. Evaluation of CAVIJET cavitating jets for deep-hole rock cutting. Geotherm. Energy 1981. [Google Scholar] [CrossRef]
- Chahine, G.L.; Conn, A.F.; Johnson, V.E.; Frederick, G.S. Cleaning and Cutting with Self-Resonating Pulsed Water Jets. In Proceedings of the U.S. Water Jet Conference, Rolla, MO, USA, 24–26 May 1983; pp. 167–176. [Google Scholar]
- Zhang, X.; Peng, J.; Ge, D.; Bo, K.; Yin, K.; Wu, D. Performance Study of a Fluidic Hammer Controlled by an Output-Fed Bistable Fluidic Oscillator. Appl. Sci. 2016, 6, 305. [Google Scholar] [CrossRef]
- Johnson, J.V.E.; Chahine, G.L.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S.; Giac-Chino, J.G.J. Cavitating and Structered Jets for Mechanical Bits to Increase Drilling Rate. J. Energy Resour. Technol. 1982, 106, 289–294. [Google Scholar] [CrossRef]
- Johnson, V.E.; Chahine, G.L.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S.; Giacchino, G.J. The Development of Structured Cavitating Jets for Deep Hole Bits. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 26–29 September 1982. [Google Scholar]
- Johnson, V.E.; Conn, A.F.; Lindenmuth, W.T.; Chahine, G.L.; Frederick, G.S. Self-Resonating Cavitating Jets. In Proceedings of the International Symposium on Jet Cutting Technology presented at the International Symposium on Jet Cutting Technology, Surrey, England, 16 January 1982; p. 16. [Google Scholar]
- Johnson, V.E.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S. Feasibility study of tuned-resonator, pulsating cavitating water jet for deep-hole drilling. Petroleum 1981. [Google Scholar] [CrossRef]
- Morel, T. Experimental study of a jet-driven Helmholtz oscillator. J. Fluids Eng. 1978, 101, 383–390. [Google Scholar] [CrossRef]
- Liao, Z.F.; Tang, C.L. Theoretical analysis and experimental study of the selfexcited oscillation pulsed jet device. In Proceedings of the Fourth US Water Jet Conference, Berkeley, CA, USA, 26–28 August 1987. [Google Scholar]
- Rockwell, D.; Naudascher, E. Review—Self-Sustaining Oscillations of Flow Past Cavities. J. Fluids Eng. 1978, 100, 152–165. [Google Scholar] [CrossRef]
- Liao, Z.F.; Tang, C.L. Theoretical analysis and experimental study a self-excited oscillation pulsed jet device. J. China Coal Soc. 1989, 1, 90–100. [Google Scholar]
- Wang, X.M. Influence Factors Simulation Study of the Self-Excited Oscillation Pulsed Jet Device and Nozzle Structure Optimized Design. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
- Kubota, A.; Kato, H.; Yamaguchi, H. A new modelling of cavitating flows: A numerical study of unsteady cavitation on a hydrofoil section. J. Fluid Mech. 1992, 240, 59–96. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Reboud, J.L.; Delannoy, Y. Numerical simulation of the unsteady behaviour of cavitating flows. Int. J. Numer. Methods Fluids 2003, 42, 527–548. [Google Scholar]
- Delannoy, Y. Two Phase Flow Approach in Unsteady Cavitation Modelling. In Proceedings of the Cavitation and Multiphase Flow Forum, Toronto, ON, Canada, 4–7 June 1990. [Google Scholar]
- Merkle, C.L.; Feng, J.; Buelow, P.E.O. Computational modeling of the dynamics of sheet cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Habil, S.I. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. In Proceedings of the International Conference on Multiphase Flow (ICMF-2001), New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Ducoin, A.; Huang, B.; Yin, L.Y. Numerical Modeling of Unsteady Cavitating Flows around a Stationary Hydrofoil. Int. J. Rotat. Mach. 2012, 2012. [Google Scholar] [CrossRef]
- Frikha, S.; Coutierdelgosha, O.; Astolfi, J.A. Influence of the Cavitation Model on the Simulation of Cloud Cavitation on 2D Foil Section. Int. J. Rotat. Mach. 2014, 2008, 498–499. [Google Scholar] [CrossRef]
- Morgut, M.; Nobile, E.; Bilu, I. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil. Int. J. Multiph. Flow 2011, 37, 620–626. [Google Scholar] [CrossRef]
- Senocak, I.; Wei, S. Interfacial dynamics-based modelling of turbulent cavitating flows, Part-1: Model development and steady-state computations. Front. Public Health 2004, 2, 141. [Google Scholar] [CrossRef]
- Goncalvès, E.; Charrière, B. Modelling for isothermal cavitation with a four-equation model. Int. J. Multiph. Flow 2014, 59, 54–72. [Google Scholar] [CrossRef]
- Momber, A.W. Concrete failure due to air-water jet impingement. J. Mater. Sci. 2000, 35, 2785–2789. [Google Scholar] [CrossRef]
- Kollé, J.J. Coiled tubing drilling with supercritical carbon dioxide. In Proceedings of the SPE/CIM International Conference on Horizontal Well Technology, Calgary, AB, Canada, 6–8 November 2000. [Google Scholar]
- Hu, D.; Li, X.H.; Tang, C.L.; Kang, Y. Analytical and experimental investigations of the pulsed air–water jet. J. Fluids Struct. 2014, 54, 88–102. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Chi, C.T.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wang, J. Study on the Mechanism of Low-Frequency Self-Excited Pulse Jet Flow and the Frequency Modulation. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Zhou, Y.X. Experimental Study about Self-Excited Pulsed Suction Jet. Master’s Thesis, Wuhan University, Wuhan, China, 2016, unpublished. [Google Scholar]
- Reboud, J.L.; Stutz, B.; Coutier, O. Two-phase flow structure of cavitation: Experiment and modeling of unsteady effects. In Proceedings of the 3rd International Symposium on Cavitation CAV1998, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Cheng, H.; Long, X.; Ji, B.; Zhu, Y.; Zhou, J. Numerical investigation of unsteady cavitating turbulent flows around twisted hydrofoil from the Lagrangian viewpoint. J. Hydrodyn. 2016, 28, 709–712. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Fortes-Patella, R.; Reboud, J.L. Evaluation of the Turbulence Model Influence on the Numerical Simulations of Unsteady Cavitation. In Proceedings of the ASME FEDSM, New Orleans, LA, USA, 29 May–1 June 2001; pp. 38–45. [Google Scholar]
- Decaix, J.; Goncalvès, E. Compressible effects modeling in turbulent cavitating flows. Eur. J. Mech. 2013, 39, 11–31. [Google Scholar] [CrossRef]
- Long, X.P.; Liu, Q.; Ji, B.; Lu, Y.Y. Numerical investigation of two typical cavitation shedding dynamics flow in liquid hydrogen with thermodynamic effects. Int. J. Heat Mass Transf. 2017, 879–893. [Google Scholar] [CrossRef]
- Basley, J.; Pastur, L.R.; Lusseyran, F.; Faure, T.M.; Delprat, N. Experimental investigation of global structures in an incompressible cavity flow using time-resolved PIV. Exp. Fluids 2011, 50, 905–918. [Google Scholar] [CrossRef]
- Delprat, N. Rossiter’s formula: A simple spectral model for a complex amplitude modulation process. Phys. Fluids 2006, 18, 152. [Google Scholar] [CrossRef]
- Delprat, N. Low-frequency components and modulation processes in compressible cavity flows. J. Sound Vib. 2010, 329, 4797–4809. [Google Scholar] [CrossRef]
- Knisely, C.; Rockwell, D. Self-sustained low-frequency components in an impinging shear layer. J. Mech. 2006, 116, 157–186. [Google Scholar] [CrossRef]
- Lucas, M.; Rockwell, D. Self-excited jet—Upstream modulation and multiple frequencies. J. Fluid Mech. 2006, 147, 333–352. [Google Scholar] [CrossRef]
- Miksad, R.W.; Jones, F.L.; Powers, E.J. Measurements of nonlinear interactions during natural transition of a symmetric wake. Phys. Fluids 1983, 26, 1402–1409. [Google Scholar] [CrossRef]
- Luo, Z.C. Fluidic Networks; China Machine Press: Beijing, China, 1988. [Google Scholar]
- Wright, M.M.; Epps, B.; Dropkin, A.; Truscott, T.T. Cavitation of a submerged jet. Exp. Fluids 2013, 54, 1541. [Google Scholar] [CrossRef]



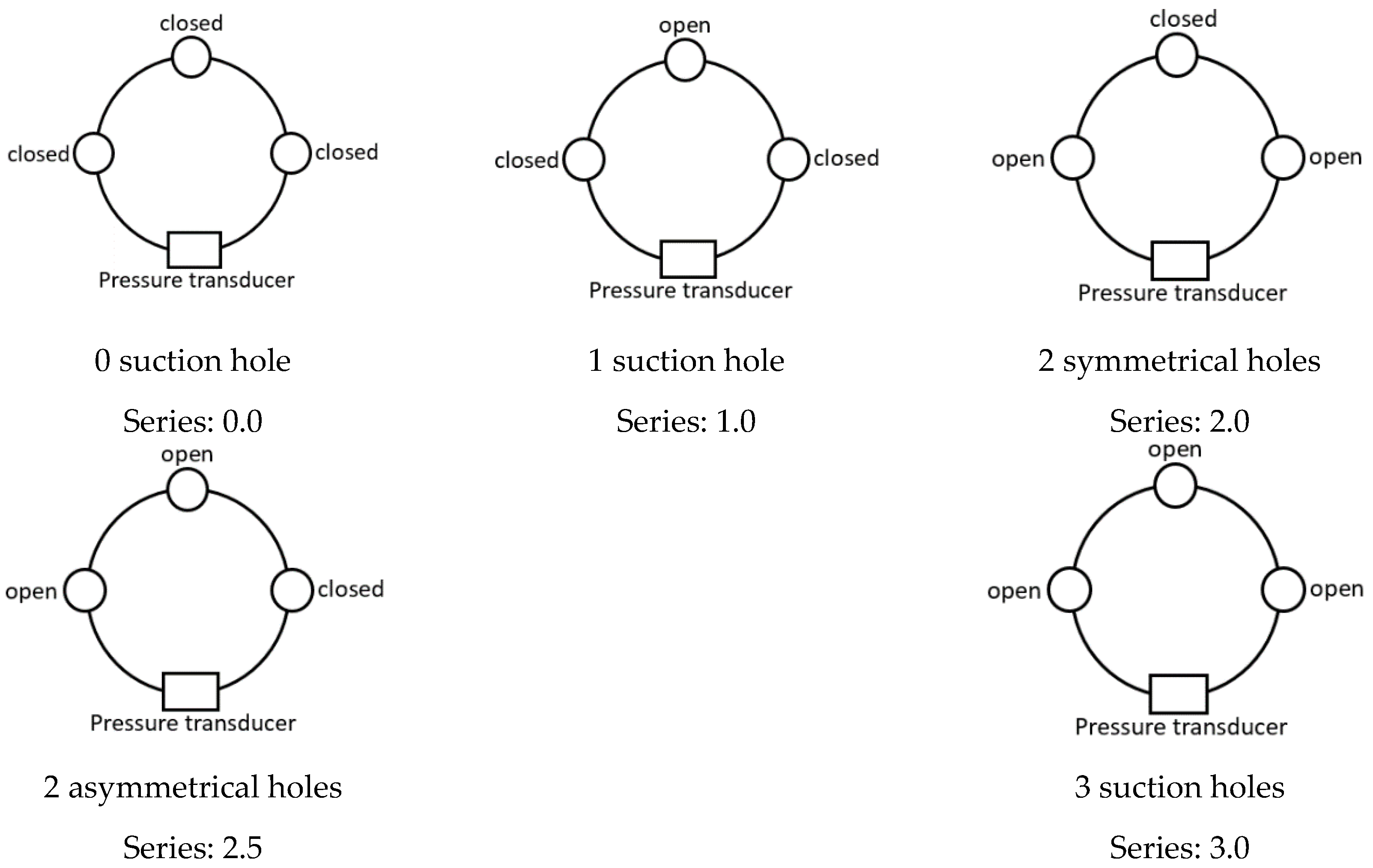

| Suction Series | Pressure Drop | Exciting Frequency |
|---|---|---|
| 0.0 | 1.25 MPa | 0 Hz |
| 1.0 | 1.50 MPa | 0.25 Hz |
| 2.0 | 1.75 MPa | 0.50 Hz |
| 2.5 | 1.00 Hz | |
| 3.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Kang, Y.; Zhang, M.; Zhou, Y.; Wang, X.; Li, D. Frequency Modulation and Erosion Performance of a Self-Resonating Jet. Appl. Sci. 2017, 7, 932. https://doi.org/10.3390/app7090932
Liu W, Kang Y, Zhang M, Zhou Y, Wang X, Li D. Frequency Modulation and Erosion Performance of a Self-Resonating Jet. Applied Sciences. 2017; 7(9):932. https://doi.org/10.3390/app7090932
Chicago/Turabian StyleLiu, Wenchuan, Yong Kang, Mingxing Zhang, Yongxiang Zhou, Xiaochuan Wang, and Deng Li. 2017. "Frequency Modulation and Erosion Performance of a Self-Resonating Jet" Applied Sciences 7, no. 9: 932. https://doi.org/10.3390/app7090932
APA StyleLiu, W., Kang, Y., Zhang, M., Zhou, Y., Wang, X., & Li, D. (2017). Frequency Modulation and Erosion Performance of a Self-Resonating Jet. Applied Sciences, 7(9), 932. https://doi.org/10.3390/app7090932







