Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point
Abstract
:1. Introduction
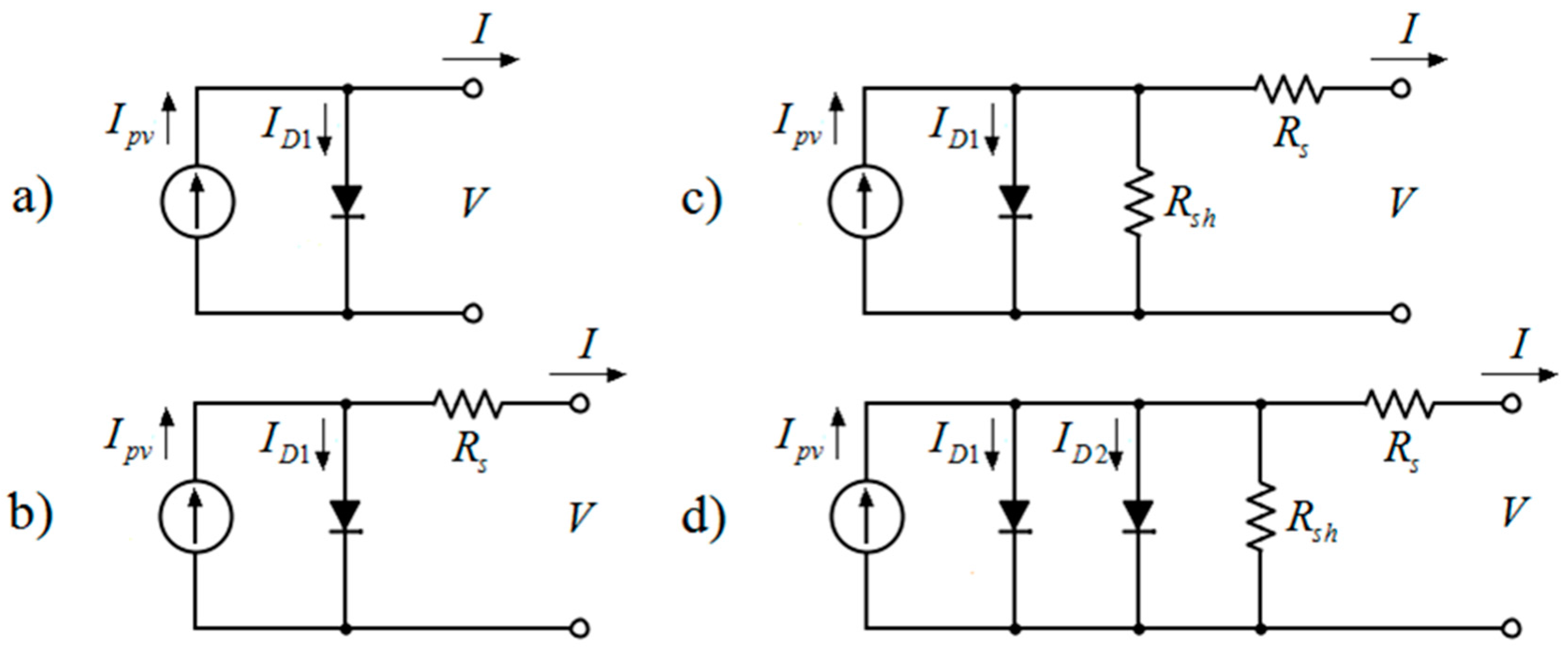
1.1. The Solar Cell/Panel Equivalent Circuit Models
- (1)
- The 1-diode model, whose equation to relate the output current, I, to the output voltage, V, is:where Ipv is the photocurrent delivered by the constant current source, I0 is the reverse saturation current corresponding to the diode, VT is the thermal voltage (VT = kT/q, where k is the Boltzmann constant, T the temperature expressed in kelvin, and q is the electron charge), a is the ideality factor that takes into account the deviation of the diodes from the Shockley diffusion theory, and N is the number of series-connected cells in the photovoltaic system to be analyzed (obviously, N = 1 in case of a single cell).
- (2)
- The 1-diode/1-resistor model, whose main equation is:where Rs is the series resistor.
- (3)
- The 1-diode/2-resistor model, whose main equation is:where Rsh is the shunt resistor.
- (4)
- And finally, the 2-diode/2-resistor model, whose main equation is:
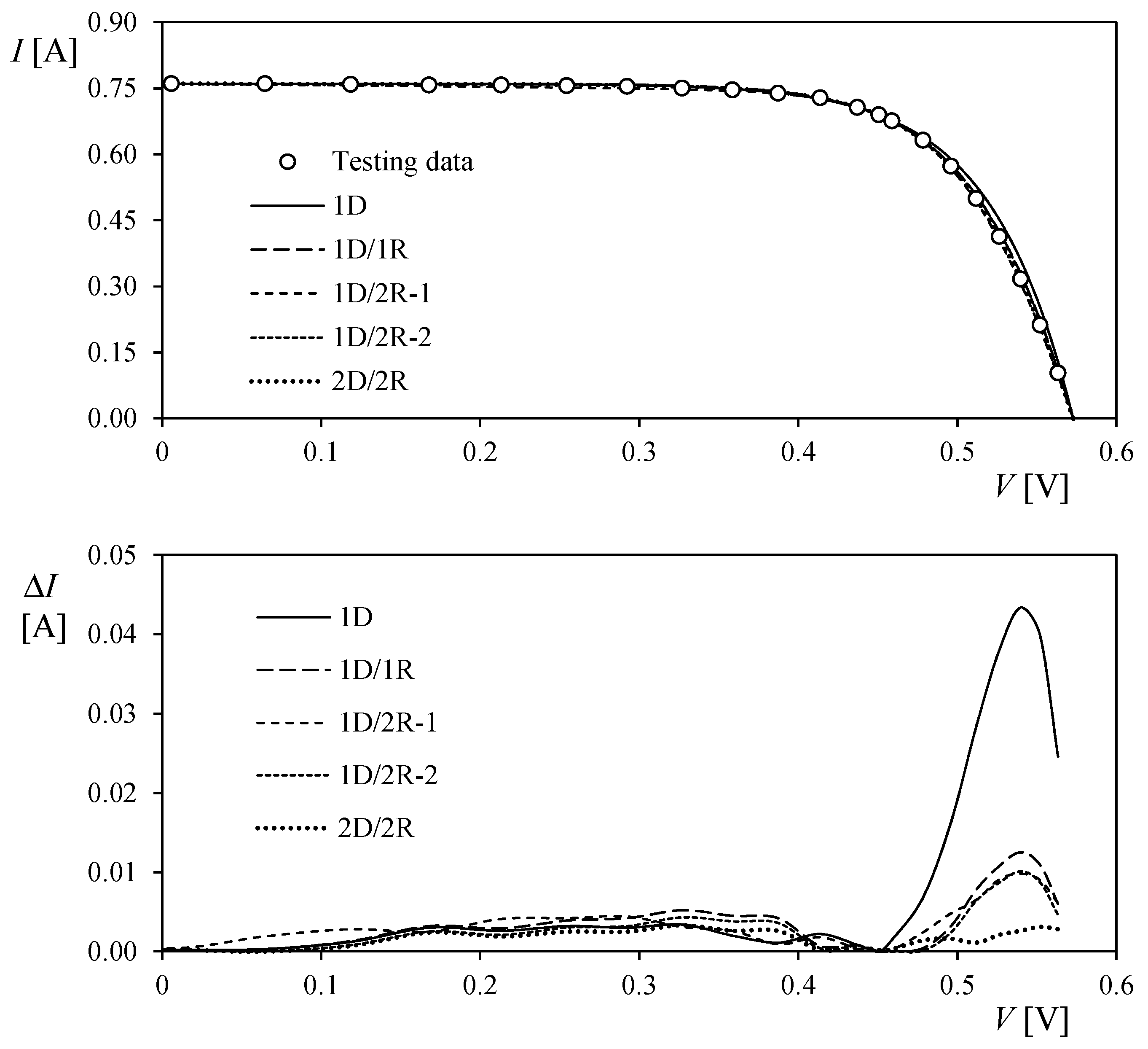
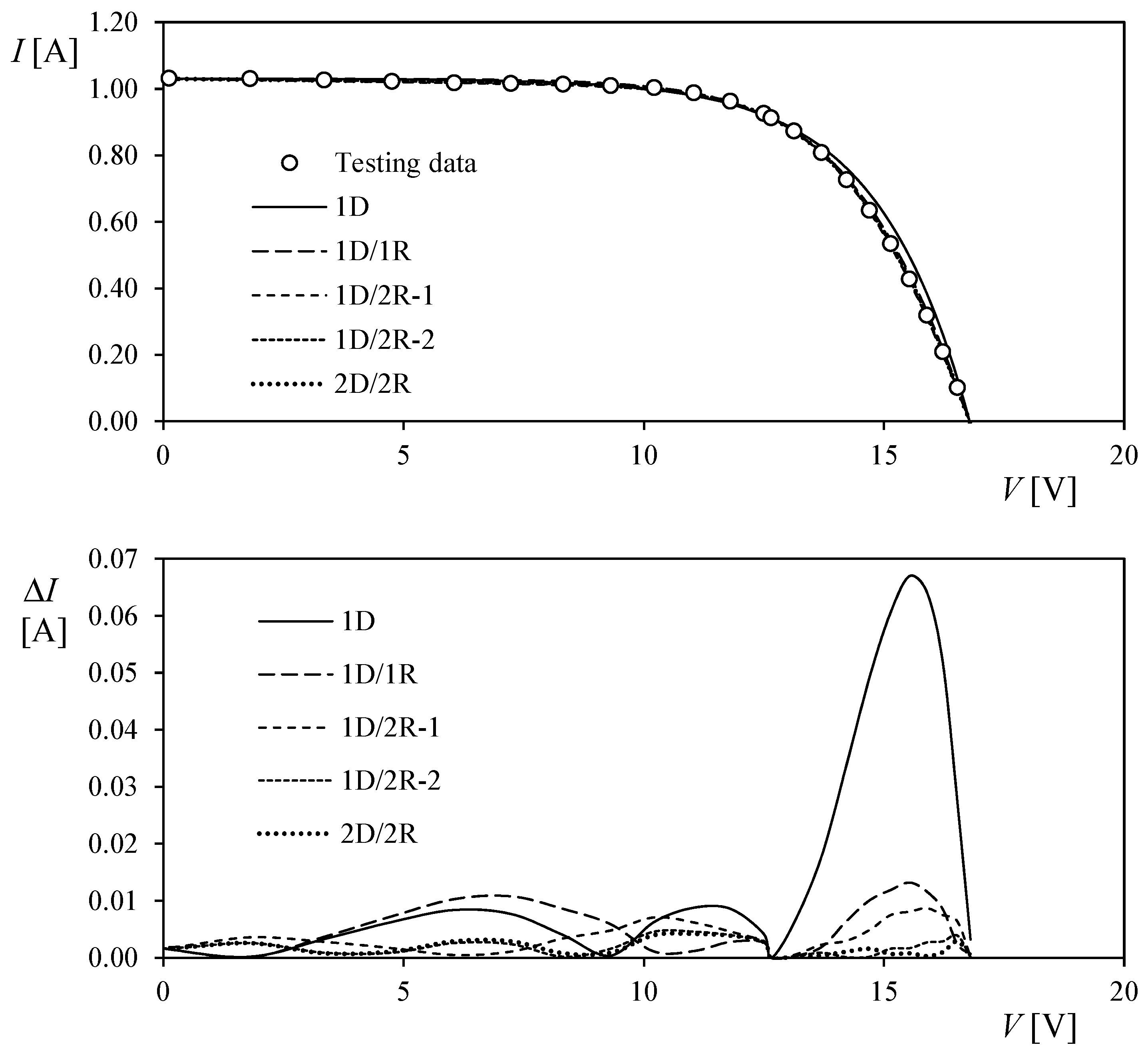
- 1-diode model (indicated as 1D in Figure 2 and Figure 3, and Table 2 and Table 3): the three characteristic points from the testing data (short circuit current, Isc, open circuit voltage, Voc, and current and voltage levels at maximum power point, Imp, Vmp), are used as the three conditions needed to extract the values of parameters Ipv, I0 and a in Equation (1). The I-V curve resulting from this model crosses the aforementioned maximum power point, but it is not assured that this condition is reached at this point.
- 1-diode/2-resistor model, two procedures are used in this case:
- (a)
- Four conditions procedure (indicated as 1D/2R-1 in Figure 2 and Figure 3, and Table 2 and Table 3): the three characteristic points and the slope of the I-V curve at maximum power point, together with a pre-established value of the ideality factor (reasonably, in the bracket from a = 1.1 to a = 1.3 [8]), are used as the four conditions needed to extract the values of parameters Ipv, I0, Rs and Rsh in Equation (3).
- (b)
- Five boundary conditions procedure (indicated as 1D/2R-2 in Figure 2 and Figure 3, and Table 2 and Table 3): the three characteristic points, the slope of the I-V curve at maximum power point, and the inverse of the slope of the I-V curve at the short-circuit point, Rsh0, are used as the five conditions needed to extract the values of parameters Ipv, I0, a, Rs and Rsh in Equation (3).
- 2-diode/2-resistor model (indicated as 2D/2R in Figure 2 and Figure 3, and Table 2 and Table 3): the three characteristic points, the slope of the I-V curve at maximum power point, and the inverse of the slope of the I-V curve at the short-circuit and open-circuit points, Rsh0 and Rs0, together with the pre-established value of the ideality factor corresponding to the second diode (a2 = 2.0), are used as the four conditions needed to extract the values of parameters Ipv, I01, I02, a1, Rs and Rsh in Equation (4).
1.2. The Problem of Determining the I-V Curve Maximum Power Point (MPP)
1.3. Methodology Proposed to Calculate the Maximum Power Point (MPP)
- Obtain the short circuit current, Isc, and the inverse of the I-V curve’s slope at that point, Rsh0, of the solar cell/panel as in MPPT offline methods (short circuiting the panel or with pilot cells).
- Obtain the open circuit voltage, Voc, of the solar cell/panel like in MPPT offline methods (opening the circuit or with pilot cells).
- Monitor the solar panel to obtain the instantaneous working point, that is, the operation point (Ii, Vi) and dI/dV|i.
- Extract the 1-diode/2-resistor equivalent circuit model parameters.
- Calculate the maximum power point Imp, Vmp.
2. Equations Proposed to Calculate the 1-Diode/2-Resistor Equivalent Circuit and the Maximum Power Point (MPP)
3. Results. Maximum Power Point (MPP) Determination
3.1. R.T.C. France Solar Cell and Photowatt PWP201 Solar Panel
- R.T.C. France solar cell. Point 1: (Vi, Ii) = (0.4137, 0.728), and Point 2: (Vi, Ii) = (0.4784, 0.632).
- Photowatt PWP201 solar panel. Point 1: (Vi, Ii) = (11.8018, 0.963), and Point 2: (Vi, Ii) = (13.1231, 0.8725).
- R.T.C. France solar cell (Point 1): (Vmp, Imp) = (0.4529, 0.6874), which implies a 0.197% error with regard to the maximum power supplied (Table 1).
- R.T.C. France solar cell (Point 2): (Vmp, Imp) = (0.4497, 0.6932), which implies a 0.329% error with regard to the maximum power supplied (Table 1).
- Photowatt PWP201 solar panel (Point 1): (Vmp, Imp) = (12.5249, 0.9212), which implies a 0.018% error with regard to the maximum power supplied (Table 1).
- Photowatt PWP201 solar panel (Point 2): (Vmp, Imp) = (12.6174, 0.9157), which implies a 0.155% error with regard to the maximum power supplied (Table 1).
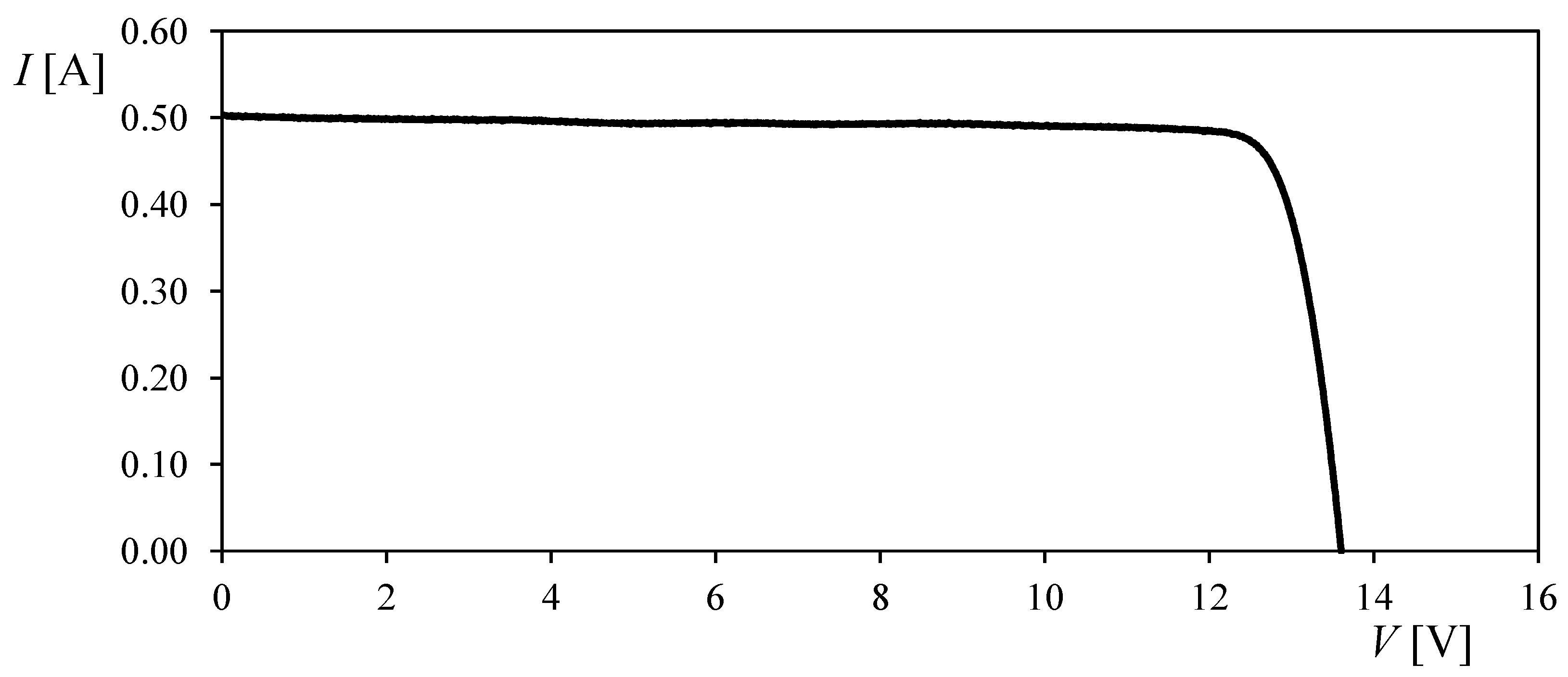
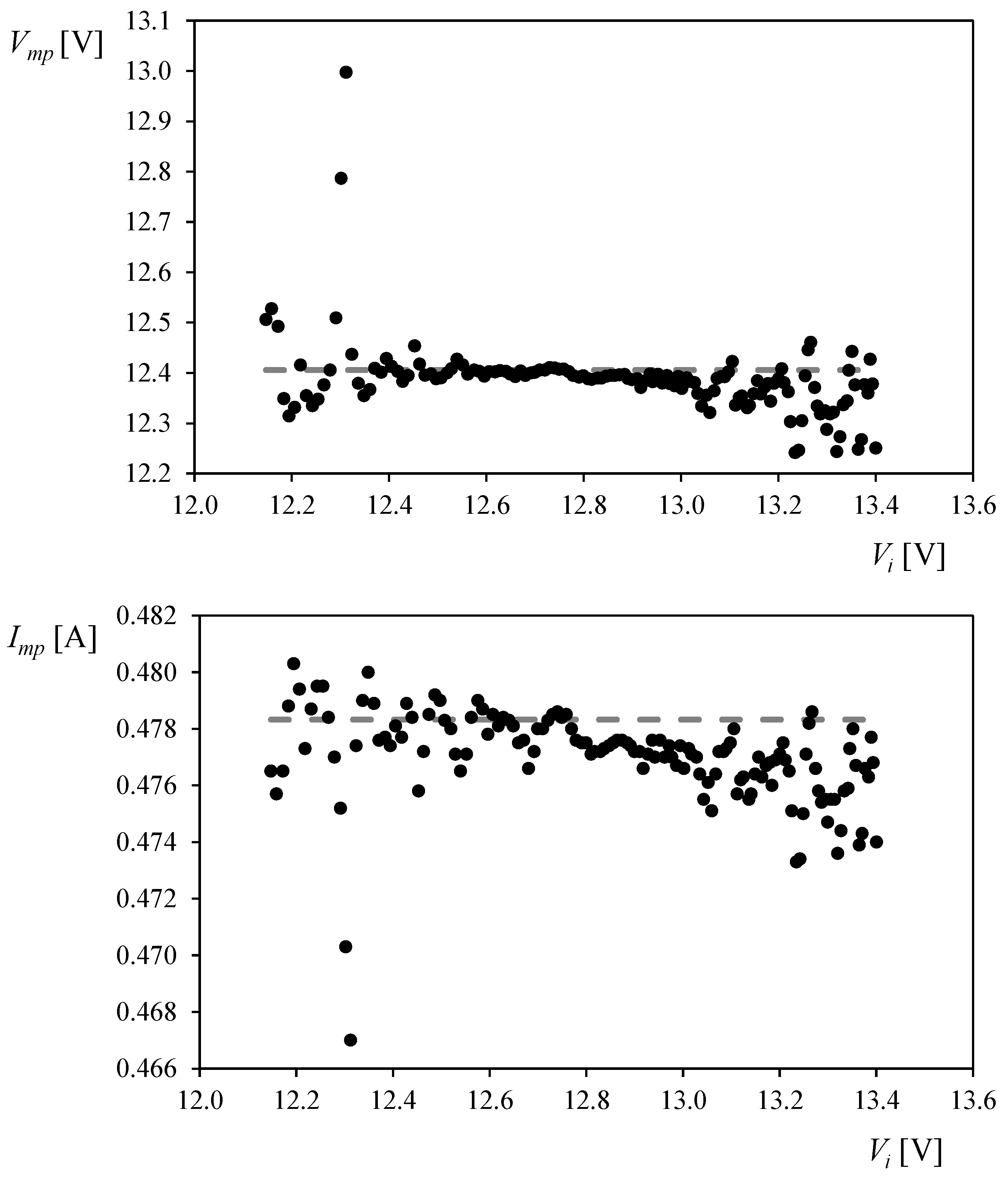
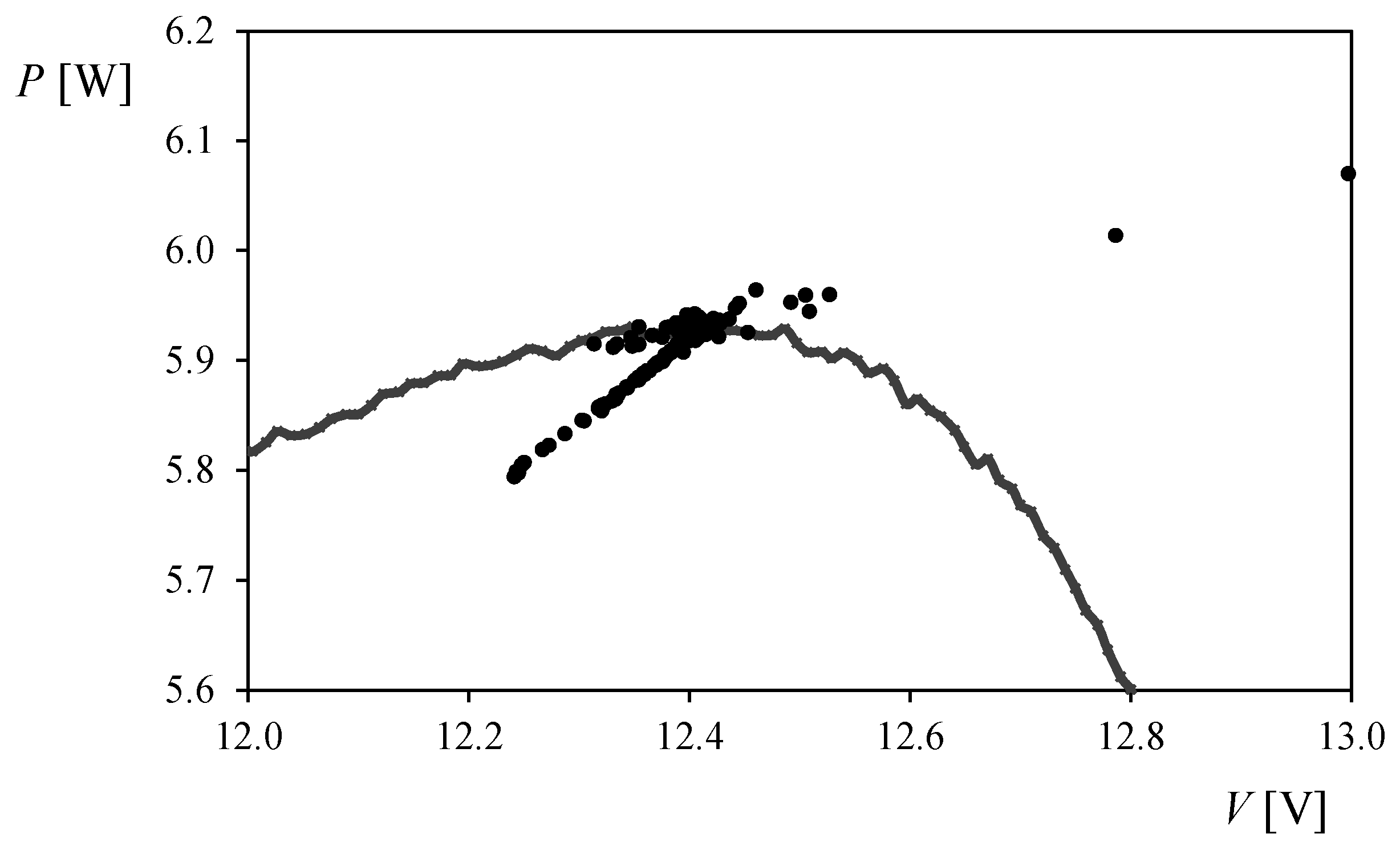
3.2. SELEX Galileo 5-Cell Photovoltaic Assembly
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jena, D.; Ramana, V.V. Modeling of photovoltaic system for uniform and non-uniform irradiance: A critical review. Renew. Sustain. Energy Rev. 2015, 52, 400–417. [Google Scholar] [CrossRef]
- Humada, A.M.; Hojabri, M.; Mekhilef, S.; Hamada, H.M. Solar cell parameters extraction based on single and double-diode models: A review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; Victoria, M. On the analytical approach for modeling photovoltaic systems behavior. J. Power Sources 2014, 247, 467–474. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; de Manuel, C. New method for analytical photovoltaic parameters identification: Meeting manufacturer’s datasheet for different ambient conditions. In International Congress on Energy Efficiency and Energy Related Materials (ENEFM2013); Oral, A.Y., Bahsi, Z.B., Ozer, M., Eds.; Springer International Publishing: Antalya, Turkey; Cham, Germany, 2014; pp. 161–169. [Google Scholar]
- Cubas, J.; Pindado, S.; Farrahi, A. New method for analytical photovoltaic parameter extraction. In Proceedings of the 2nd International Conference Renewable Energy Research Application (ICRERA 2013), Madrid, Spain, 20–23 October 2013; pp. 873–877. [Google Scholar]
- Pindado, S.; Cubas, J.; Sorribes-Palmer, F. On the harmonic analysis of cup anemometer rotation speed: A principle to monitor performance and maintenance status of rotating meteorological sensors. Measurement 2015, 73, 401–418. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Modeling and circuit-based simulation of photovoltaic arrays. In Proceedings of the 2009 Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; pp. 1244–1254. [Google Scholar]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 2013, 102, 943–949. [Google Scholar] [CrossRef]
- Lyden, S.; Haque, M.E. Maximum Power Point Tracking techniques for photovoltaic systems: A comprehensive review and comparative analysis. Renew. Sustain. Energy Rev. 2015, 52, 1504–1518. [Google Scholar] [CrossRef]
- Koutroulis, E.; Blaabjerg, F. Overview of maximum power point tracking techniques for photovoltaic energy production systems. Electr. Power Compon. Syst. 2015, 43, 1329–1351. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Shandilya, A.M.; Dash, S.K. Maximum power point tracking (MPPT) techniques: Recapitulation in solar photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Liu, L.; Meng, X.; Liu, C. A review of maximum power point tracking methods of PV power system at uniform and partial shading. Renew. Sustain. Energy Rev. 2016, 53, 1500–1507. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; Sanz-Andrés, Á. Accurate simulation of MPPT methods performance when applied to commercial photovoltaic panels. Sci. World J. 2015, 2015, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Laudani, A.; Riganti Fulginei, F.; Salvini, A. High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental I–V curves by using reduced forms. Sol. Energy 2014, 103, 316–326. [Google Scholar] [CrossRef]
- Garrigós, A.; Blanes, J.M.; Carrasco, J.A.; Ejea, J.B. Real time estimation of photovoltaic modules characteristics and its application to maximum power point operation. Renew. Energy 2007, 32, 1059–1076. [Google Scholar] [CrossRef]
- Toledo, F.J.; Blanes, J.M.; Garrigós, A.; Martínez, J.A. Analytical resolution of the electrical four-parameters model of a photovoltaic module using small perturbation around the operating point. Renew. Energy 2012, 43, 83–89. [Google Scholar] [CrossRef]
- Blanes, J.M.; Toledo, F.J.; Montero, S.; Garrigós, A. In-site real-time photovoltaic I–V curves and maximum power point estimator. IEEE Trans. Power Electron. 2013, 28, 1234–1240. [Google Scholar] [CrossRef]
- Pindado Carrion, S.; Andres, S.; Franchini, S.; Pérez Grande, M.I.; Alonso, G.; Pérez, J.; Sorribes Palmer, F.; Cubas Cano, J.; García, A.; Roibás-Millán, E.; et al. Master in space systems, An advanced Master’ s Degree in space engineering. In Proceedings of the Athens ATINER’S Conference Paper Series No ENGEDU2016-1953, Athens, Greece, 9–12 May 2016; pp. 1–16. [Google Scholar]
- Pindado Carrion, S.; Roibás-Millán, E.; Cubas Cano, J.; García, A.; Sanz Andres, A.P.; Franchini, S.; Pérez Grande, M.I.; Alonso, G.; Pérez-Álvarez, J.; Sorribes Palmer, F.; et al. The UPMSat-2 Satellite: An academic project within aerospace engineering education. In Proceedings of the 2nd Annual International Conference on Engineering Education & Teaching, Atenas, Greece, 5–8 June 2017. [Google Scholar]
- Pindado, S.; Roibas, E.; Cubas, J.; Sorribes-Palmer, F.; Sanz-Andrés, A.; Franchini, S.; Grande, I.P.; Zamorano, J.; de la Puente, J.A.; Pérez-Álvarez, J.; et al. MUSE. Master in Space Systems at Universidad Politécnica de Madrid (UPM). 2017. Available online: https://www.researchgate.net/project/MUSE-Master-in-Space-Systems-at-Universidad-Politecnica-de-Madrid-UPM (accessed on 24 July 2017).
- Pindado, S.; Cubas, J. Simple mathematical approach to solar cell/panel behavior based on datasheet information. Renew. Energy 2017, 103, 729–738. [Google Scholar] [CrossRef]
- Roibás-Millán, E.; Alonso-Moragón, A.; Jiménez-Mateos, A.; Pindado, S. On solar panels testing for small-size satellites. The UPMSAT-2 mission. Meas. Sci. Technol. 2017. [Google Scholar]
- Barbini, N.; Lughi, V.; Mellit, A.; Pavan, A.M.; Tessarolo, A. On the impact of photovoltaic module characterization on the prediction of PV plant productivity. In Proceedings of the 9th International Conference Ecological Vehicles and Renewable Energies( EVER 2014), Montecarlo, Monaco, 25–27 March 2014. [Google Scholar]
- AlRashidi, M.R.; AlHajri, M.F.; El-Naggar, K.M.; Al-Othman, A.K. A new estimation approach for determining the I–V characteristics of solar cells. Sol. Energy 2011, 85, 1543–1550. [Google Scholar] [CrossRef]
- El-Naggar, K.M.; AlRashidi, M.R.; AlHajri, M.F.; Al-Othman, A.K. Simulated Annealing algorithm for photovoltaic parameters identification. Sol. Energy 2012, 86, 266–274. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Parameter extraction of solar cell models using repaired adaptive differential evolution. Sol. Energy 2013, 94, 209–220. [Google Scholar] [CrossRef]
- Peng, L.; Sun, Y.; Meng, Z.; Wang, Y.; Xu, Y. A new method for determining the characteristics of solar cells. J. Power Sources 2013, 227, 131–136. [Google Scholar] [CrossRef]
- Phang, J.C.H.; Chan, D.S.H.; Phillips, J.R. Accurate analytical method for the extraction of solar cell model parameters. Electron. Lett. 1984, 20, 406–408. [Google Scholar] [CrossRef]
- Bouzidi, K.; Chegaar, M.; Bouhemadou, A. Solar cells parameters evaluation considering the series and shunt resistance. Sol. Energy Mater. Sol. Cells 2007, 91, 1647–1651. [Google Scholar] [CrossRef]
- Wei, H.; Cong, J.; Lingyun, X.; Deyun, S. Extracting solar cell model parameters based on chaos particle swarm algorithm. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 398–402. [Google Scholar]
- Silva, J.P.; Balenzategui, J.L.; Nieto, M.B. On the relationship between spectral reflectance and working temperature of PV modules. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 1–5 September 2008; pp. 2861–2864. [Google Scholar]
- Silva, J.P.; Nofuentes, G.; Munoz, J.V. Spectral reflectance patterns of photovoltaic modules and their thermal effects. J. Sol. Energy Eng. ASME 2010, 132, 13. [Google Scholar] [CrossRef]
- Balenzategui, J.L.; Rodríguez-Outón, I.; Chenlo, F. Calibration of crystalline silicon solar cells as reference devices for cell testers and sorters. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition/5th World Conference Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010; pp. 2642–2648. [Google Scholar]
- Balenzategui, J.L.; Cuenca, J.; Rodríguez-Outón, I.; Chenlo, F. Intercomparison and validation of solar cell I-V characteristic measurement procedures. In Proceedings of the 27th European Photovoltaic Solar Energy Conference and Exhibition, Frankfurt, Gerermany, 25–27 September 2012; pp. 1471–1476. [Google Scholar]


| Characteristic Data | R.T.C. France | Photowatt PWP201 |
|---|---|---|
| Isc (A) | 0.7603 | 1.0300 |
| Voc (V) | 0.5728 | 16.778 |
| Vmp (V) | 0.4507 | 12.649 |
| Imp (A) | 0.6894 | 0.9120 |
| Rsh0 (Ω) | 246.80 * | 689.13 * |
| Rs0 (Ω) | 0.0907 * | 2.5193 * |
| T (K) | 306.15 | 318.15 |
| N | 1 | 36 |
| Model | Rs (Ω) | Rsh (Ω) | Ipv (A) | I01 (A) | a1 | I02 (A) | a2 | ξ |
|---|---|---|---|---|---|---|---|---|
| 1D | - | - | 0.7603 | 1.12 × 10−5 | 1.9509 | - | - | 2.25 × 10−2 |
| 1D/1R | 0.0233 | - | 0.7603 | 2.07 × 10−6 | 1.6944 | - | - | 6.84 × 10−3 |
| 1D/2R-1 | 0.0481 | 28.931 | 0.7616 | 4.14 × 10−8 | 1.3 * | - | - | 5.95 × 10−3 |
| 1D/2R-2 | 0.0261 | 246.77 | 0.7604 | 1.44 × 10−6 | 1.6478 | - | - | 5.48 × 10−3 |
| 2D/2R | 0.0450 | 246.76 | 0.7604 | 1.54 × 10−9 | 1.1087 | 5.15 × 10−6 | 2.0 * | 2.50 × 10−3 |
| Model | Rs (Ω) | Rsh (Ω) | Ipv (A) | I01 (A) | a1 | I02 (A) | a2 | ξ |
|---|---|---|---|---|---|---|---|---|
| 1D | - | - | 1.0300 | 1.55 × 10−4 | 1.9319 | - | - | 2.87 × 10−2 |
| 1D/1R | 0.8884 | - | 1.0300 | 1.80 × 10−5 | 1.5520 | - | - | 6.70 × 10−3 |
| 1D/2R-1 | 1.4429 | 497.75 | 1.0330 | 7.04 × 10−7 | 1.2 * | - | - | 4.59 × 10−3 |
| 1D/2R-2 | 1.2829 | 687.85 | 1.0319 | 2.04 × 10−6 | 1.2968 | - | - | 2.31 × 10−3 |
| 2D/2R | 1.2004 | 687.93 | 1.0318 | 5.31 × 10−6 | 1.3882 | −1.96 × 10−5 | 2.0 * | 2.04 × 10−3 |
| Model | Rs (Ω) | Rsh (Ω) | Ipv (A) | I0 (A) | a | ξ |
|---|---|---|---|---|---|---|
| P.M. 1 * | 0.0459 | 246.78 | 0.7606 | 2.92 × 10−6 | 1.7407 | 1.24 × 10−2 |
| P.M. 2 ** | 0.0403 | 246.76 | 0.7606 | 5.02 × 10−7 | 1.5283 | 3.60 × 10−3 |
| Al-Rashidi et al. [26] | 0.0313 | 64.103 | 0.7617 | 9.98 × 10−7 | 1.6 | 2.509 × 10−2 |
| El-Naggar et al. [27] | 0.0345 | 43.103 | 0.762 | 4.767 × 10−7 | 1.5172 | 2.235 × 10−3 |
| Gong and Cai [28] | 0.0364 | 53.719 | 0.7608 | 3.23 × 10−7 | 1.4812 | 1.297 × 10−3 |
| Askarzadeh and Rezazadeh [9] | 0.0366 | 53.595 | 0.7607 | 3.05 × 10−7 | 1.4754 | 1.308 × 10−3 |
| Peng et al. [29] | 0.0364 | 54.054 | 0.7609 | 3.22 × 10−7 | 1.4837 | 4.659 × 10−3 |
| Askarzadeh and Rezazadeh [10] | 0.0366 | 52.290 | 0.7608 | 3.06 × 10−7 | 1.4758 | 1.303 × 10−3 |
| Laudani et al. [16] | 0.0368 | 49.9736 | 0.7611 | 2.0901 × 10−7 | 1.4701 | 1.163 × 10−3 |
| Model | Rs (Ω) | Rsh (Ω) | Ipv (A) | I0 (A) | a | ξ |
|---|---|---|---|---|---|---|
| P.M. 1 * | 1.7146 | 687.42 | 1.0343 | 3.105 × 10−7 | 1.1342 | 1.24 × 10−2 |
| P.M. 2 ** | 1.3995 | 687.73 | 1.0338 | 1.260 × 10−6 | 1.2512 | 4.00 × 10−3 |
| Phang et al. [30] | 0.0832 | 561.03 | 1.0319 | 6.405 × 10−5 | 1.7602 | 2.05 × 10−2 |
| Bouzidi et al. [31] | 1.2030 | 555.55 | 1.0339 | 3.076 × 10−6 | 13385 | 5.53 × 10−3 |
| Wei et al. [32] | 1.0755 | 1850.1 | 1.0286 | 8.301 × 10−6 | 1.4512 | 4.04 × 10−3 |
| Al-Rashidi et al. [26] | 1.1968 | 555.55 | 1.0441 | 3.436 × 10−6 | 1.3496 | 2.22 × 10−3 |
| El-Naggar et al. [27] | 1.1989 | 833.33 | 1.0331 | 3.664 × 10−6 | 1.3561 | 2.44 × 10−3 |
| Gong and Cai [28] | 1.2013 | 981.98 | 1.0305 | 3.482 × 10−6 | 1.3512 | 2.02 × 10−3 |
| Peng et al.[29] | 1.2132 | 625.00 | 1.0313 | 3.221 × 10−6 | 1.3423 | 7.49 × 10−3 |
| Cubas et al. [3] | 1.3535 | 559.68 | 1.0342 | 1.321 × 10−6 | 1.2554 | 2.86 × 10−3 |
| Laudani et al. [16] | 1.2241 | 689.32 | 1.3354 | 2.826 × 10−6 | 1.3294 | 2.09 × 10−3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cubas, J.; Pindado, S.; Sorribes-Palmer, F. Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point. Appl. Sci. 2017, 7, 870. https://doi.org/10.3390/app7090870
Cubas J, Pindado S, Sorribes-Palmer F. Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point. Applied Sciences. 2017; 7(9):870. https://doi.org/10.3390/app7090870
Chicago/Turabian StyleCubas, Javier, Santiago Pindado, and Felix Sorribes-Palmer. 2017. "Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point" Applied Sciences 7, no. 9: 870. https://doi.org/10.3390/app7090870
APA StyleCubas, J., Pindado, S., & Sorribes-Palmer, F. (2017). Analytical Calculation of Photovoltaic Systems Maximum Power Point (MPP) Based on the Operation Point. Applied Sciences, 7(9), 870. https://doi.org/10.3390/app7090870





