Global Analysis for an HIV Infection Model with CTL Immune Response and Infected Cells in Eclipse Phase
Abstract
:1. Introduction
2. Mathematical Analysis of the HIV Model
2.1. Existence and Local Stability
2.2. Global Stability Results
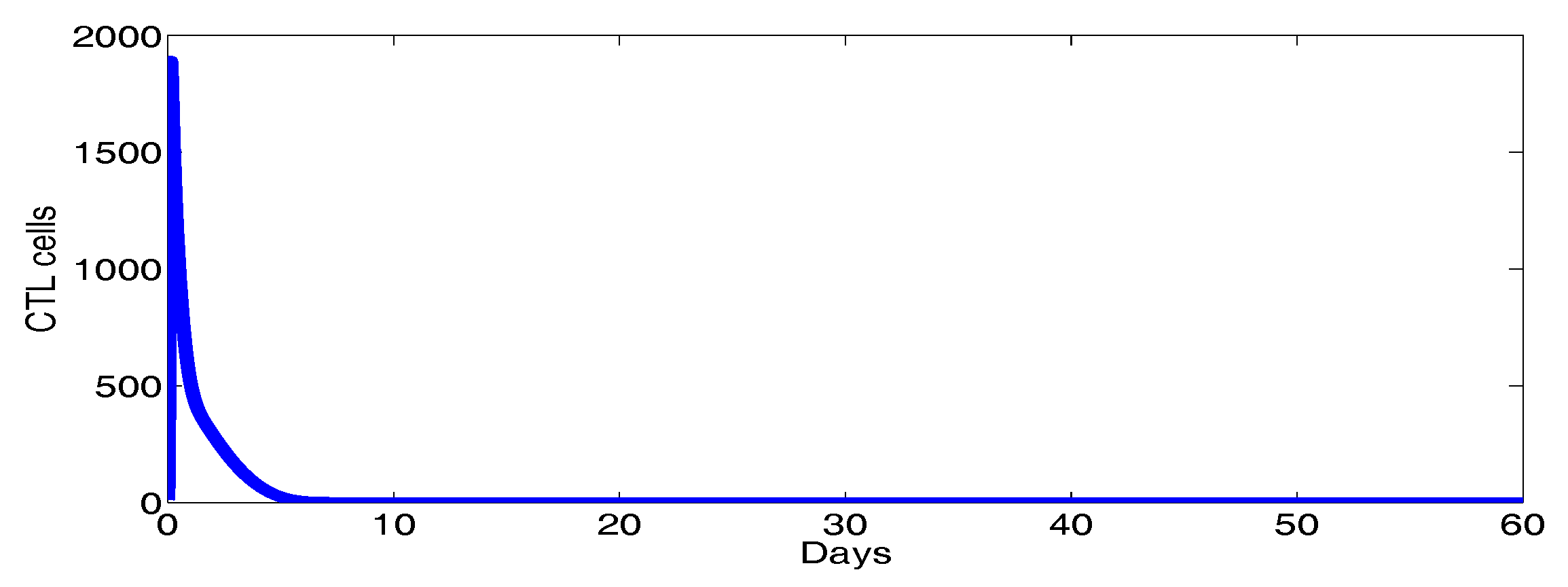
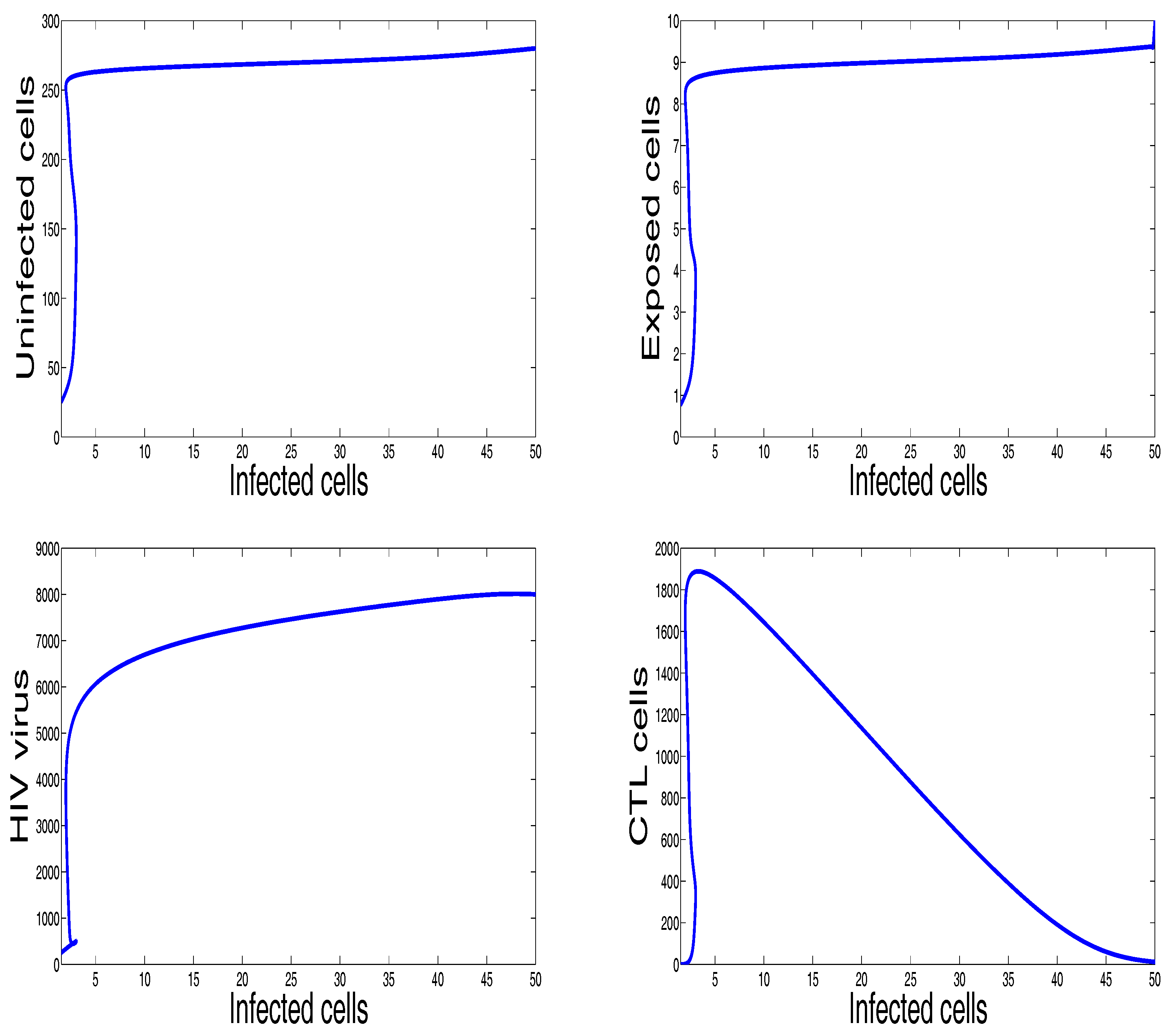
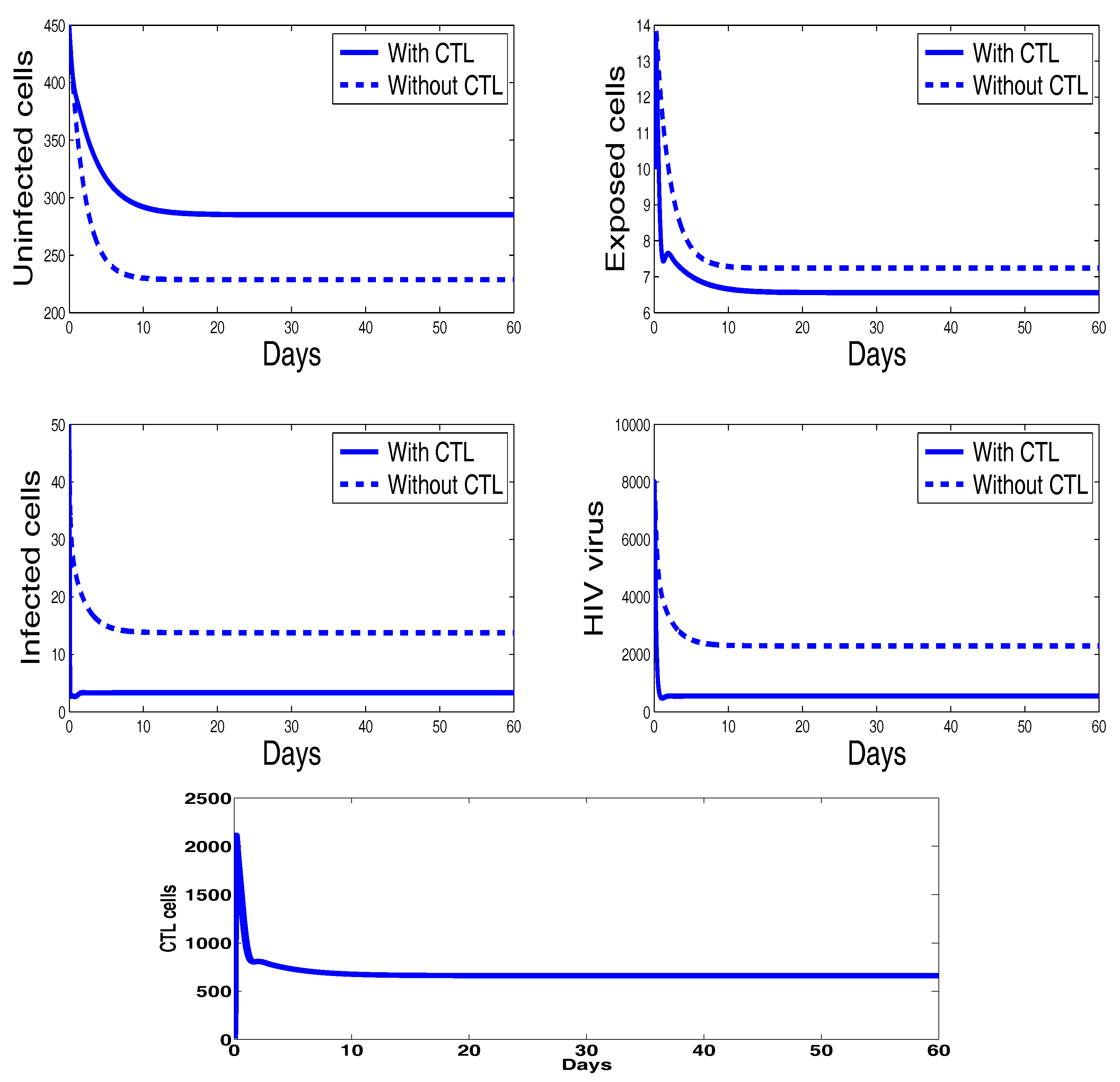
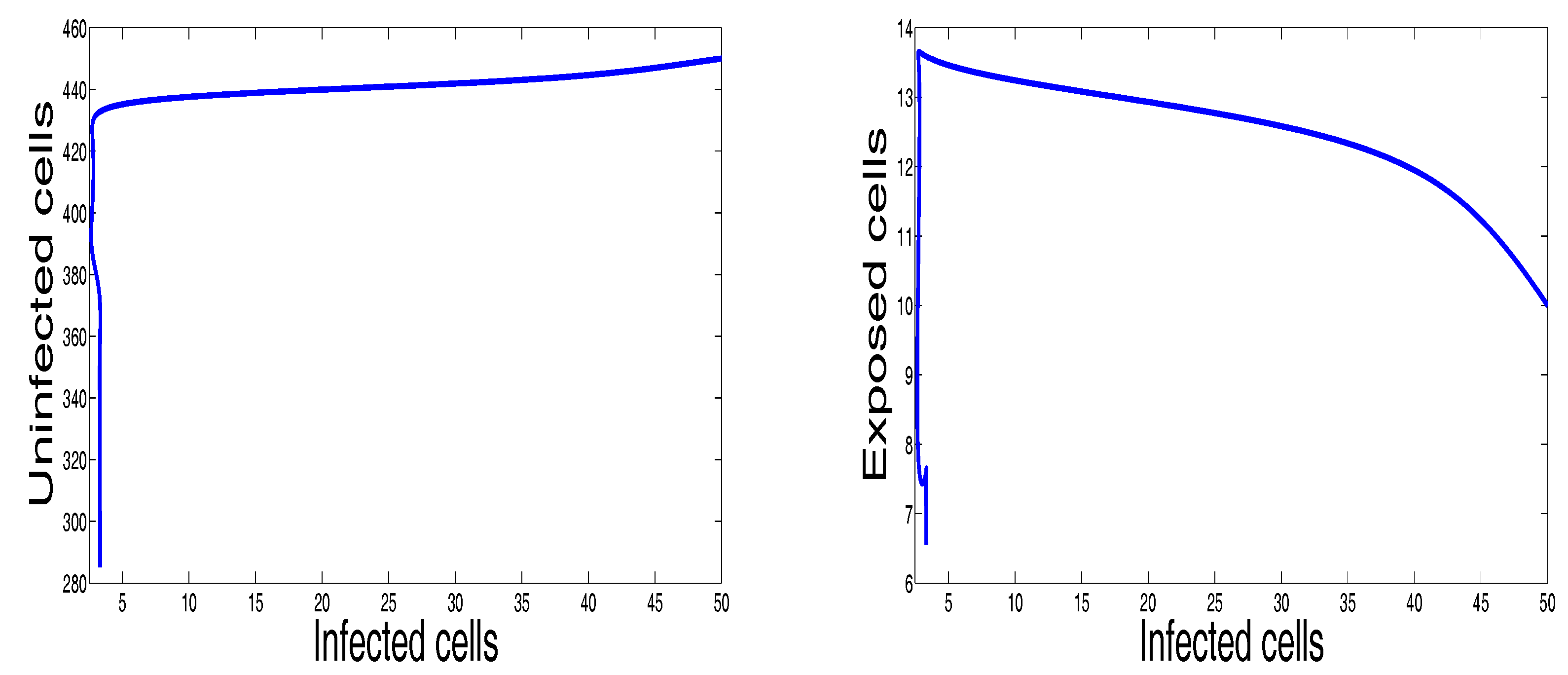
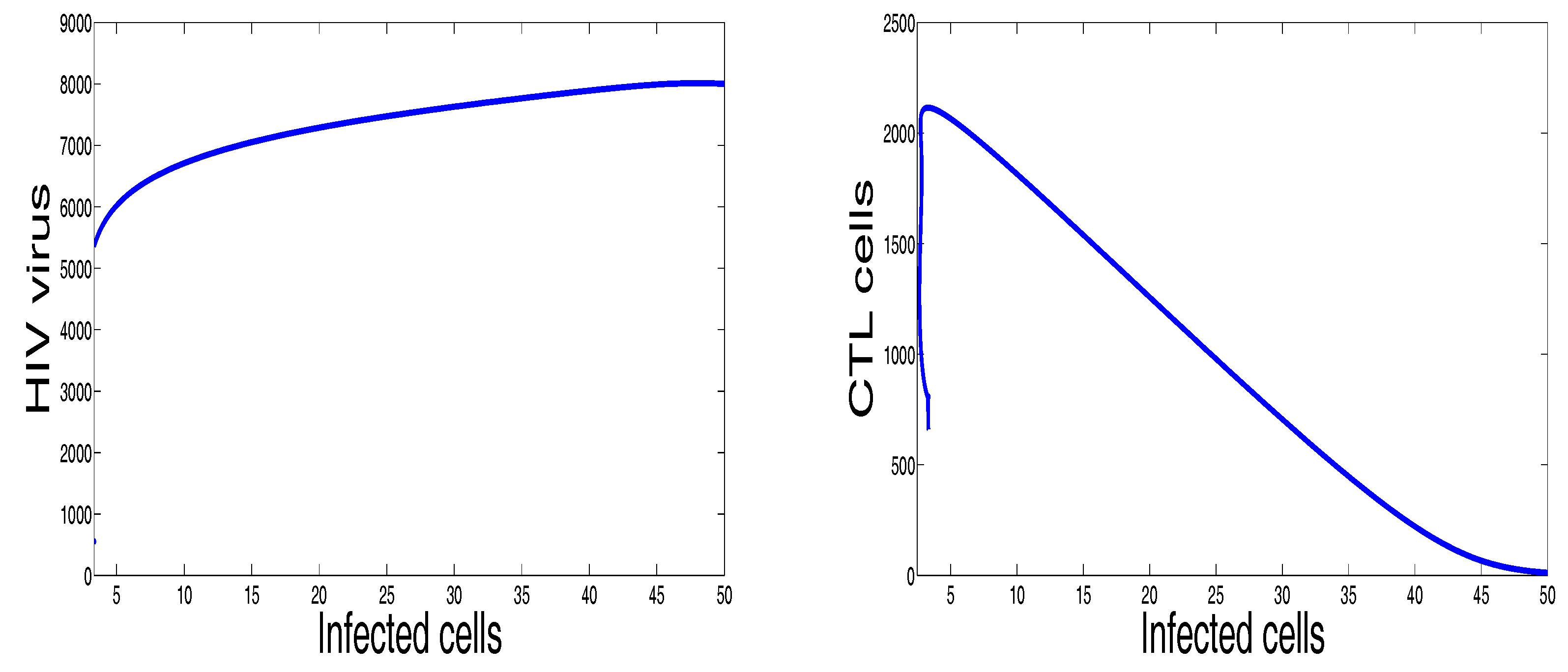
3. Numerical Results and Simulations
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Existence and Local Stability Results Proof
Appendix B. Global Stability Result Proof
References
- Blanttner, W.; Gallo, R.C.; Temin, H.M. HIV causes aids. Science 1988, 241, 515–516. [Google Scholar] [CrossRef]
- Weiss, R.A. How does HIV cause AIDS? Science 1993, 260, 1273–1279. [Google Scholar] [CrossRef] [PubMed]
- Saez-Cirion, A.; Lacabaratz, C.; Lambotte, O.; Versmisse, P.; Urrutia, A.; Boufassa, F.; Barre-Sinoussi, F.; Delfraissy, J.F.; Sinet, M.; Pancino, G.; et al. HIV controllers exhibit potent CD8 T cell capacity to suppress HIV infection ex vivo and peculiar cytotoxic T-lymphocyte activation phenotype. Proc. Natl. Acad. Sci. USA 2007, 104, 6776–6781. [Google Scholar] [CrossRef] [PubMed]
- Betts, M.R.; Nason, M.C.; West, S.M.; De Rosa, S.C.; Migueles, S.A.; Abraham, J.; Lederman, M.M.; Benito, J.M.; Goepfert, P.A.; Connors, M.; et al. HIV nonprogressors preferentially maintain highly functional HIV-specific CD8+ T-cells. Blood 2006, 107, 4781–4789. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Bangham, C.R.M. Population dynamics of immune responses to persistent viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Smith, H.L.; De Leenheer, P. Virus dynamics: A global analysis. SIAM J. Appl. Math. 2003, 63, 1313–1327. [Google Scholar] [CrossRef]
- Korobeinikov, A. Global properties of basic virus dynamics models. Bull. Math. Biol. 2004, 66, 879–883. [Google Scholar] [CrossRef] [PubMed]
- Daar, E.S.; Moudgil, T.; Meyer, R.D.; Ho, D.D. Transient highlevels of viremia in patients with primary human immunodeficiency virus type 1 infection. N. Engl. J. Med. 1991, 324, 961–964. [Google Scholar] [CrossRef] [PubMed]
- Kahn, J.O.; Walker, B.D. Acute human immunodeficiency virus type 1 infection. N. Engl. J. Med. 1998, 339, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, G.R.; Cunningham, P.; Kelleher, A.D.; Zauders, J.; Carr, A.; Vizzard, J.; Law, M.; Cooper, D.A. Patterns of viral dynamics during primary human immunodeficiency virus type 1 infection. J. Infect. Dis. 1998, 178, 1812–1815. [Google Scholar] [CrossRef] [PubMed]
- Schacker, T.; Collier, A.; Hughes, J.; Shea, T.; Corey, L. Clinical and epidemiologic features of primary HIV infection. Ann. Int. Med. 1996, 125, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Elaiw, A.; Song, X. Global properties of a delayed HIV infection model with CTL immune response. Appl. Math. Comput. 2012, 218, 9405–9414. [Google Scholar] [CrossRef]
- Wang, X.; Tao, Y.; Song, X. Global stability of a virus dynamics model with Beddington-DeAngelis incidence rate and CTL immune response. Nonlinear Dyn. 2011, 66, 825–830. [Google Scholar] [CrossRef]
- Sun, Q.; Min, L.; Kuang, Y. Global stability of infection-free state and endemic infection state of a modified human immunodeficiency virus infection model. IET Syst. Biol. 2015, 9, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Min, L. Dynamics Analysis and Simulation of a Modified HIV Infection Model with a Saturated Infection Rate. Comput. Math. Methods Med. 2014, 2014, 145162. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, Y.; Wu, J.; Heffernan, J. Oscillatory viral dynamics in a delayed HIV pathogenesis model. Math. Biosci. 2009, 219, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Luo, Y.; Chen, M. Stability and Hopf bifurcation of a HIV infection model with CTL-response delay. Comput. Math. Appl. 2011, 62, 3091–3102. [Google Scholar] [CrossRef]
- De Boer, R.J.; Perelson, A.S. Target cell limited and immune control models of HIV infection: A comparison. J. Theor. Biol. 1998, 190, 201–214. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.M.; Perelson, A.S. Post-treatment control of HIV infection. Proc. Natl. Acad. Sci. USA 2015, 112, 5467–5472. [Google Scholar] [CrossRef] [PubMed]
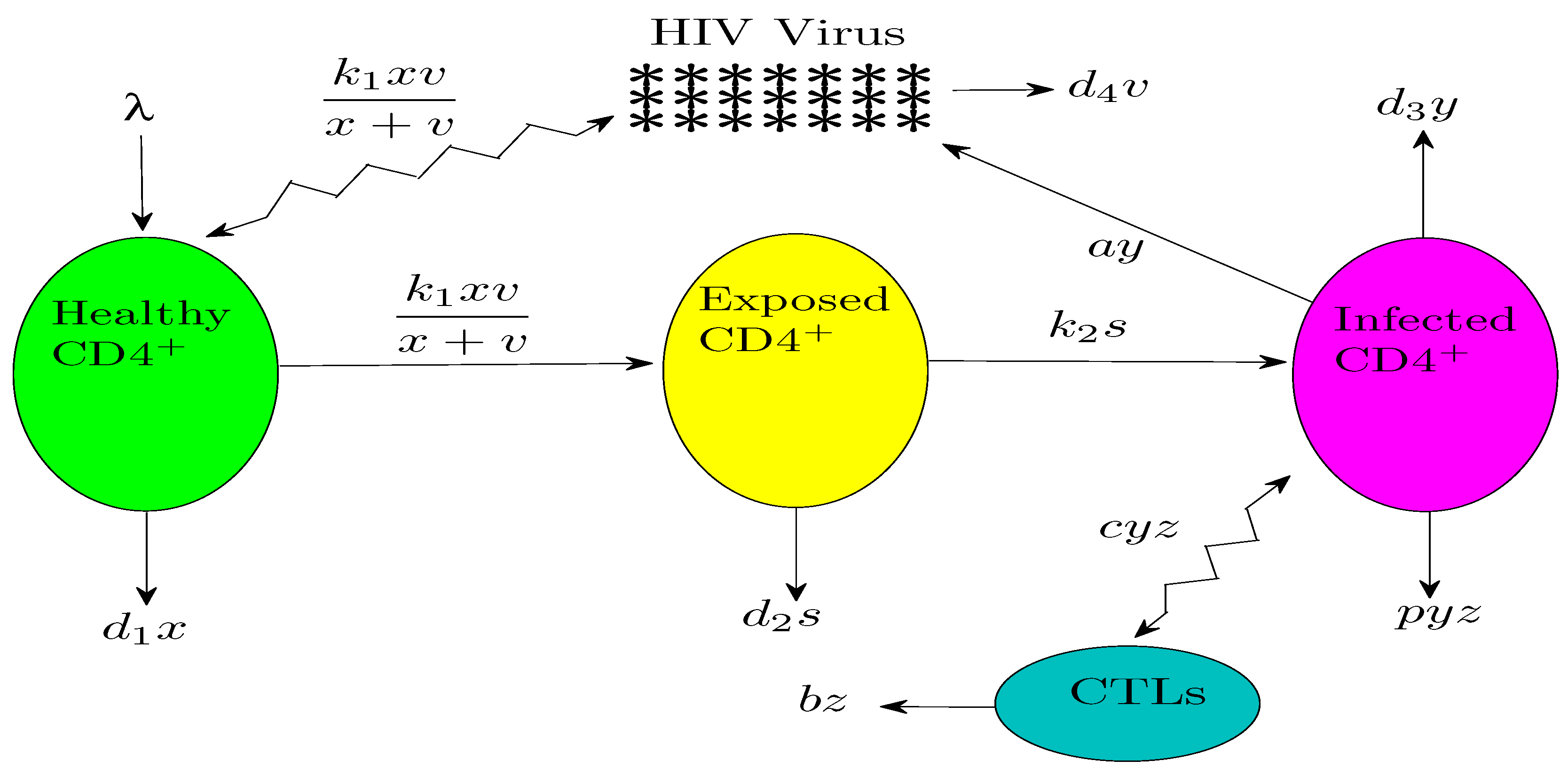
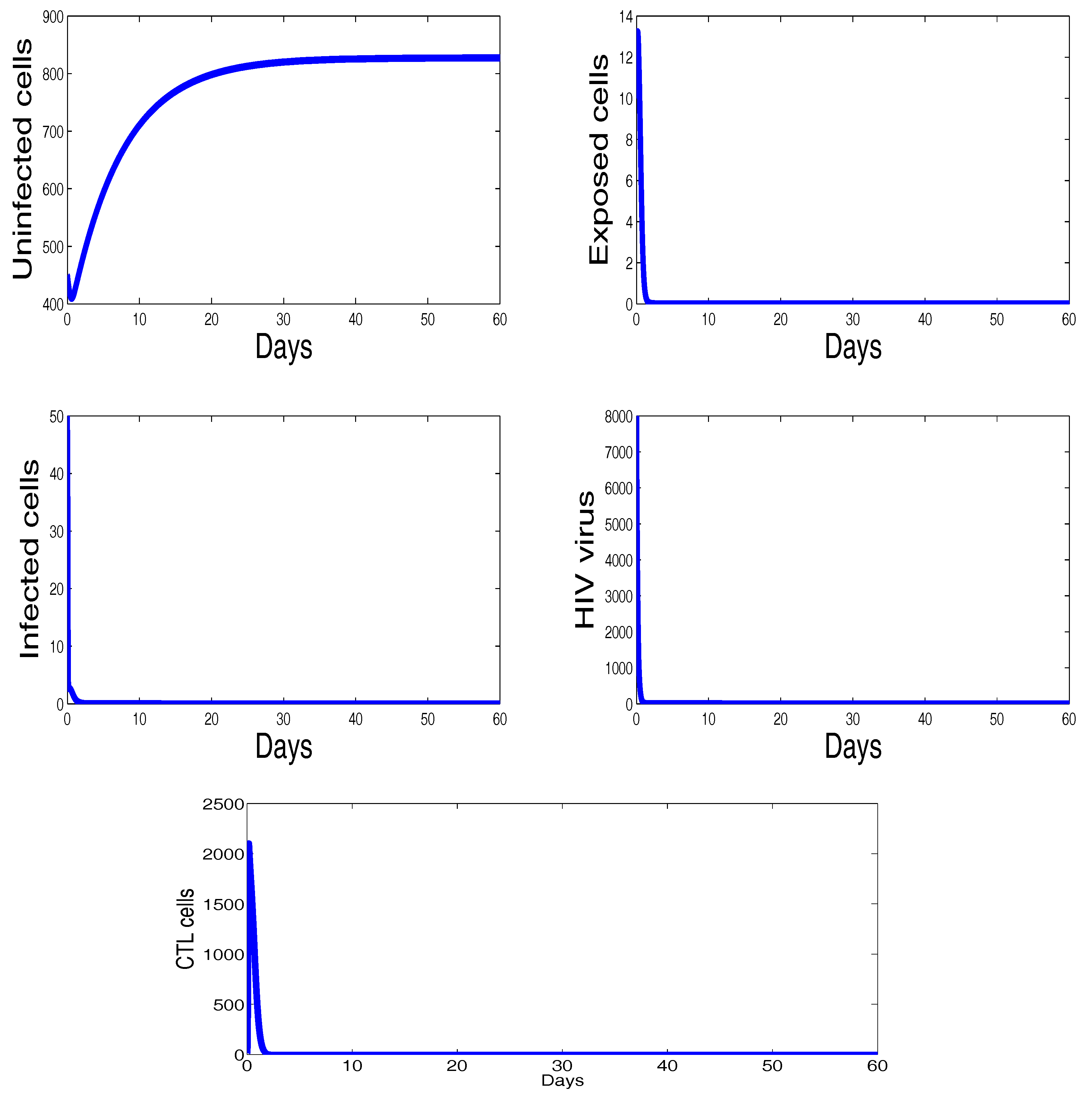
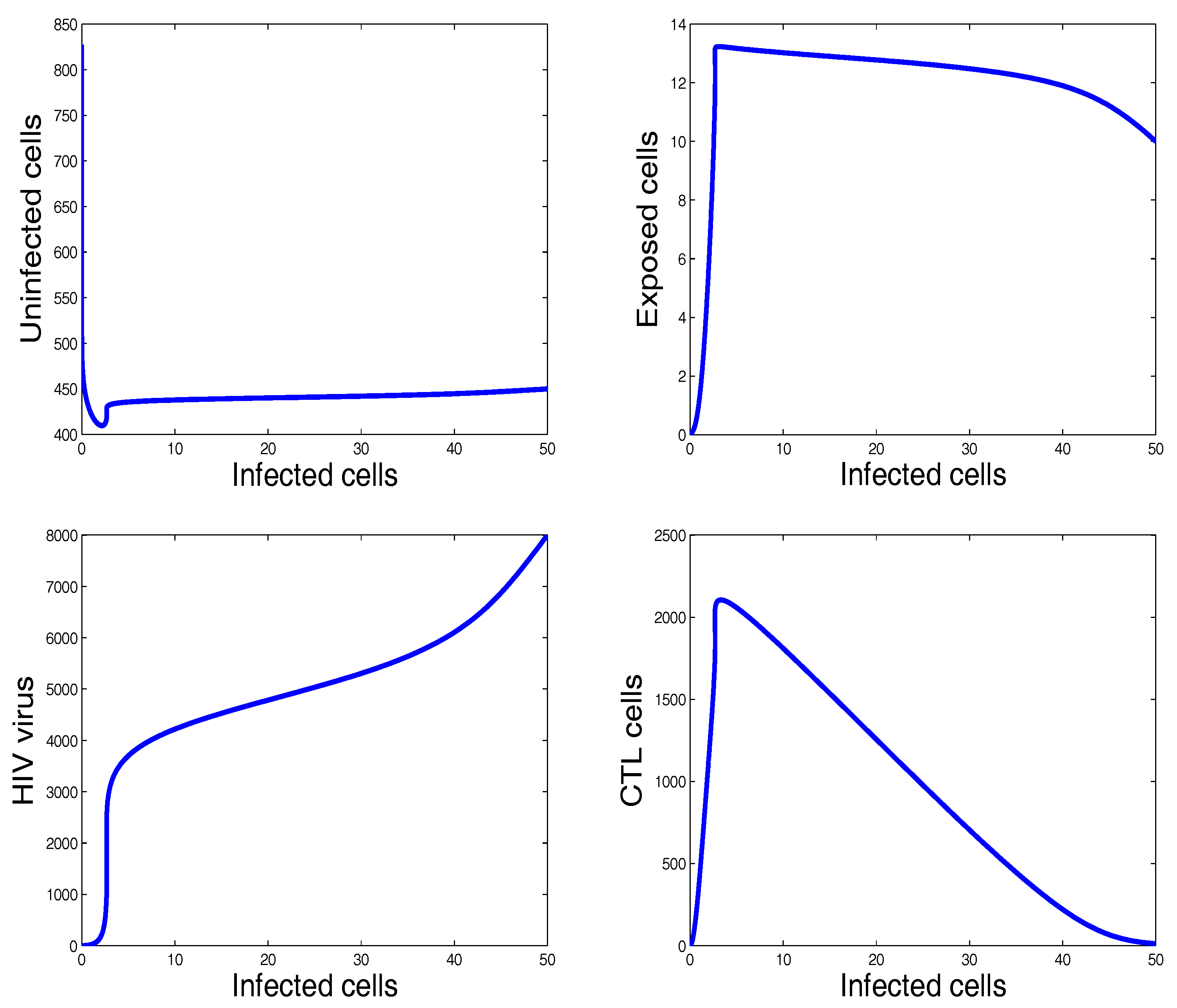
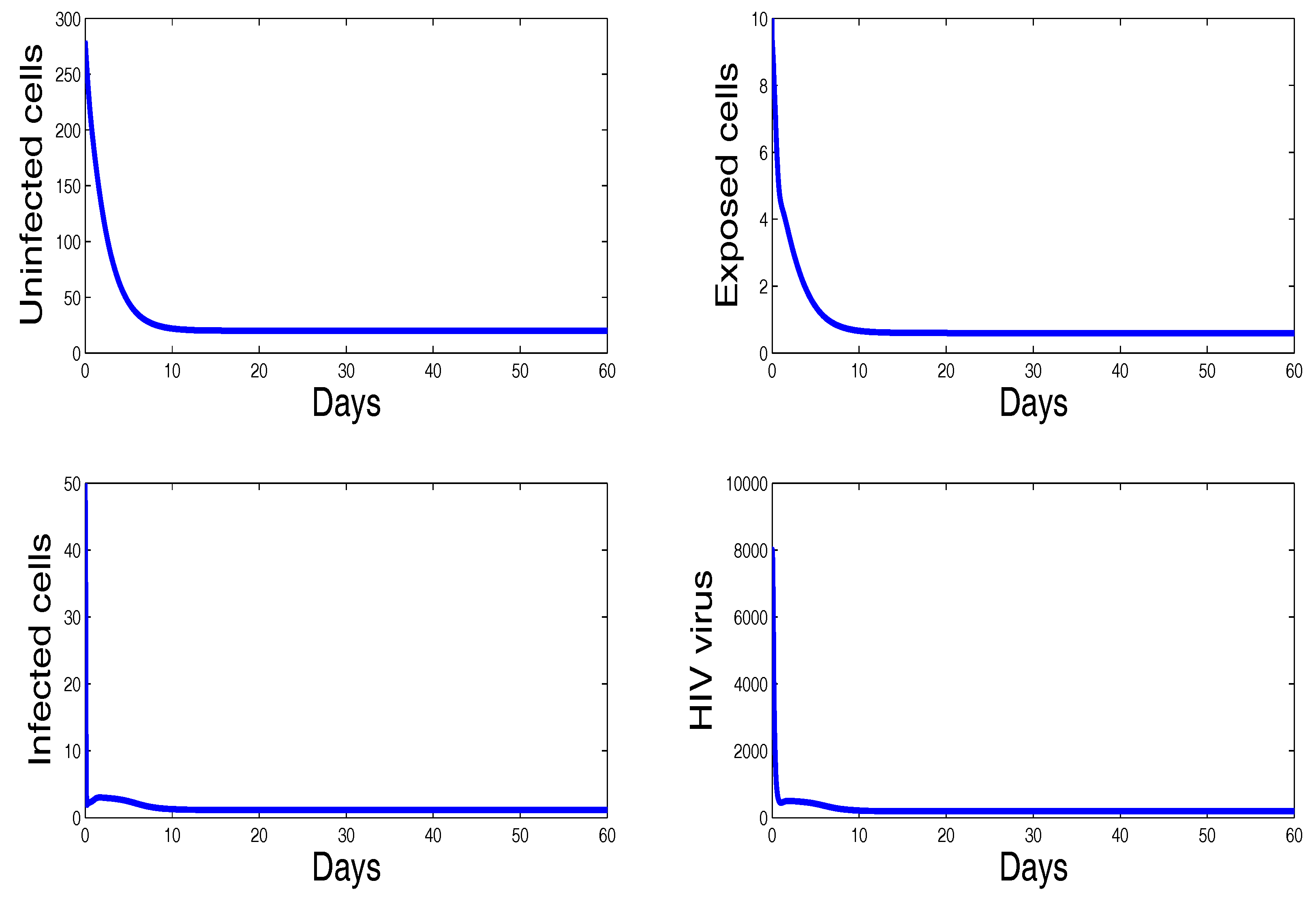
| Parameters | Meaning | Value | References |
|---|---|---|---|
| Source rate of CD4 T cells | [16] | ||
| Average of infection | [14] | ||
| Decay rate of healthy cells | [14] | ||
| Death rate of exposed CD4 T cells | [14] | ||
| The rate that exposed become infected CD4 T cells | [14] | ||
| Death rate of infected CD4 T cells, not by CTL killing | [14] | ||
| a | The rate of production the virus by infected CD4 T cells | [14] | |
| Clearance rate of virus | [14] | ||
| p | Clearance rate of infection | [17] | |
| c | Activation rate CTL cells | [17] | |
| b | Death rate of CTL cells | [17] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allali, K.; Danane, J.; Kuang, Y. Global Analysis for an HIV Infection Model with CTL Immune Response and Infected Cells in Eclipse Phase. Appl. Sci. 2017, 7, 861. https://doi.org/10.3390/app7080861
Allali K, Danane J, Kuang Y. Global Analysis for an HIV Infection Model with CTL Immune Response and Infected Cells in Eclipse Phase. Applied Sciences. 2017; 7(8):861. https://doi.org/10.3390/app7080861
Chicago/Turabian StyleAllali, Karam, Jaouad Danane, and Yang Kuang. 2017. "Global Analysis for an HIV Infection Model with CTL Immune Response and Infected Cells in Eclipse Phase" Applied Sciences 7, no. 8: 861. https://doi.org/10.3390/app7080861
APA StyleAllali, K., Danane, J., & Kuang, Y. (2017). Global Analysis for an HIV Infection Model with CTL Immune Response and Infected Cells in Eclipse Phase. Applied Sciences, 7(8), 861. https://doi.org/10.3390/app7080861







