FE Model and Operational Modal Analysis of Lower Limbs
Abstract
:Featured Application
Abstract
1. Introduction
2. Method
2.1. Measurement
2.2. Modal Parameters
2.3. FE Model
3. Results
3.1. Modal Identification
3.2. FE Model Results
3.3. Model Update
4. Discussions
Author Contributions
Conflicts of Interest
References
- Gómez-Cabello, A.; González-Agüero, A.; Morales, S.; Ara, I.; Casajús, J.A.; Vicente-Rodríguez, G. Effects of a short-term whole body vibration intervention on bone mass and structure in elderly people. J. Sci. Med. Sport 2014, 17, 160–164. [Google Scholar] [CrossRef] [PubMed]
- Madou, K.H.; Cronin, J.B. The Effects of Whole Body Vibration on Physical and Physiological Capability in Special Populations. Hong Kong Physiother. J. 2008, 26, 24–38. [Google Scholar] [CrossRef]
- Matute-Llorente, Á.; González-Agüero, A.; Gómez-Cabello, A.; Vicente-Rodríguez, G.; Casajús Mallén, J.A. Effect of Whole-Body Vibration Therapy on Health-Related Physical Fitness in Children and Adolescents With Disabilities: A Systematic Review. J. Adolesc. Health 2014, 54, 385–396. [Google Scholar] [CrossRef] [PubMed]
- Carlsöö, S. The effect of vibration on the skeleton, joints and muscles. A review of the literature. Appl. Ergon. 1982, 13, 251–258. [Google Scholar] [CrossRef]
- Wang, Y.J.; Huang, X.L.; Yan, J.W.; Wan, Y.N.; Wang, B.X.; Tao, J.H.; Chen, B.; Li, B.Z.; Yang, G.J.; Wang, J. The association between vibration and vascular injury in rheumatic diseases: A review of the literature. Autoimmunity 2015, 48, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.J.; Norris, S.R.; Smith, D.J.; Herzog, W. Vibration Training: An Overview of the Area, Training Consequences, and Future Considerations. J. Strength Cond. Res. 2005, 19, 459. [Google Scholar] [CrossRef] [PubMed]
- Gurram, R. A Study of Vibration Response Characteristics of the Human Hand-Arm System. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 1993. [Google Scholar]
- Munera, M.; Chiementin, X.; Crequy, S.; Bertucci, W. Physical risk associated with vibration at cycling. Mech. Ind. 2014, 15, 535–540. [Google Scholar] [CrossRef]
- Fridén, J. Vibration damage to the hand: Clinical presentation, prognosis and length and severity of vibration required. J. Hand Surg. 2001, 26, 471–474. [Google Scholar] [CrossRef] [PubMed]
- Ayari, H.; Thomas, M.; Doré, S.; Serrus, O. Evaluation of lumbar vertebra injury risk to the seated human body when exposed to vertical vibration. J. Sound Vib. 2009, 321, 454–470. [Google Scholar] [CrossRef]
- Grassi, L.; Väänänen, S.; Ristinmaa, M.; Jurvelin, J.S.; Isaksson, H. How accurately can subject-specific finite element models predict strains and strength of human femora? Investigation using full-field measurements. J. Biomech. 2016, 49, 802–806. [Google Scholar] [CrossRef] [PubMed]
- Adewusi, S.; Thomas, M.; Vu, V.; Li, W. Modal parameters of the human hand-arm using finite element and operational modal analysis. Mech. Ind. 2014, 15, 541–549. [Google Scholar] [CrossRef]
- Hostens, I.; Ramon, H. Descriptive analysis of combine cabin vibrations and their effect on the human body. J. Sound Vib. 2003, 266, 453–464. [Google Scholar] [CrossRef]
- Kitazaki, S.; Griffin, M.J. Resonance behaviour of the seated human body and effects of posture. J. Biomech. 1998, 31, 143–149. [Google Scholar] [CrossRef]
- Hobatho, M.C.; Darmana, R.; Pastor, P.; Barrau, J.J.; Laroze, S.; Morucci, J.P. Development of a three-dimensional finite element model of a human tibia using experimental modal analysis. J. Biomech. 1991, 24, 371–383. [Google Scholar] [CrossRef]
- Munera, M.; Chiementin, X.; Murer, S.; Bertucci, W. Model of the risk assessment of hand-arm system vibrations in cycling: Case of cobblestone road. Proc. Inst. Mech. Eng. Part P 2015, 229, 231–238. [Google Scholar] [CrossRef]
- Thuong, O.; Griffin, M.J. The vibration discomfort of standing persons: 0.5–16 Hz fore-and-aft, lateral, and vertical vibration. J. Sound Vib. 2011, 330, 816–826. [Google Scholar] [CrossRef]
- Wakeling, J.M.; Liphardt, A.M.; Nigg, B.M. Muscle activity reduces soft-tissue resonance at heel-strike during walking. J. Biomech. 2003, 36, 1761–1769. [Google Scholar] [CrossRef]
- Lafortune, M.A.; Lake, M.J.; Hennig, E.M. Differential shock transmission response of the human body to impact severity and lower limb posture. J. Biomech. 1996, 29, 1531–1537. [Google Scholar] [CrossRef]
- Peeters, B.; Van Der Auweraer, H. Polymax: A revolution in operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 26–27 April 2005. [Google Scholar]
- Van der Auweraer, H.; Guillaume, P.; Verboven, P.; Vanlanduit, S. Application of a Fast-Stabilizing Frequency Domain Parameter Estimation Method. J. Dyn. Syst. Meas. Control 2001, 123, 651. [Google Scholar] [CrossRef]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing; Katholieke Universiteit Leuven, Faculty of Engineering, Department of Mechanical Engineering, Division of Production Engineering, Machine Design and Automation: Leuven, Belgium, 1998. [Google Scholar]
- Afnor. ISO 2631-1:1997—Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements; ISO: Geneva, Switzerland, 1997. [Google Scholar]
- Beillas, P.; Papaioannou, G.; Tashman, S.; Yang, K. A new method to investigate in vivo knee behavior using a finite element model of the lower limb. J. Biomech. 2004, 37, 1019–1030. [Google Scholar] [CrossRef] [PubMed]
- De Mendonça, M.C. Estimation of height from the length of long bones in a Portuguese adult population. Am. J. Phys. Anthropol. 2000, 112, 39–48. [Google Scholar] [CrossRef]
- Atilla, B.; Oznur, A.; Cağlar, O.; Tokgözoğlu, M.; Alpaslan, M. Osteometry of the femora in Turkish individuals: A morphometric study in 114 cadaveric femora as an anatomic basis of femoral component design. Acta Orthop. Traumatol. Turc. 2007, 41, 64–68. [Google Scholar] [PubMed]
- Beauthier, J.; Mangin, P.; Hédouin, V. Traité de Médecine Légale. De Boeck: Bruxelles, Belgique, 2011. [Google Scholar]
- Schmidt, W.; Reyes, M.; Fischer, F.; Geesink, R.; Nolte, L.; Racanelli, J.; Reimers, N. Quantifying human knee anthropometric differences between ethnic groups and gender using shape analysis techniques. In Proceedings of the Annual Meeting American Society of Biomechanics, State College, PA, USA, 26–29 August 2009. [Google Scholar]
- NASA. Volume I: Man-Systems Integration Standards (MSIS); Chapter Anthropometry and Biomechanics; NASA: Washington, DC, USA, 1995. [Google Scholar]
- Giladi, M.; Milgrom, C.; Simkin, A.; Stein, M.; Kashtan, H.; Margulies, J.; Rand, N.; Chisin, R.; Steinberg, R.; Aharonson, Z. Stress fractures and tibial bone width. A risk factor. J. Bone Jt. Surg. Br. Vol. 1987, 69, 326–329. [Google Scholar]
- Radzi, S.; Uesugi, M.; Baird, A.; Mishra, S.; Schuetz, M.; Schmutz, B. Assessing the bilateral geometrical differences of the tibia—Are they the same? Med. Eng. Phys. 2014, 36, 1618–1625. [Google Scholar] [CrossRef] [PubMed]
- Ozden, H.; Balci, Y.; Demirüstü, C.; Turgut, A.; Ertugrul, M. Stature and sex estimate using foot and shoe dimensions. Forensic Sci. Int. 2005, 147, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Kanaani, J.; Mortazavi, S.B.; Khavanin, A.; Mirzai, R.; Rasulzadeh, Y.; Mansurizadeh, M. Foot Anthropometry of 18–25 Years Old Iranian Male Students. Asian J. Sci. Res. 2010, 3, 62–69. [Google Scholar] [CrossRef]
- Pionteck, A.; Munera, M.; Chiementin, X. Modélisation 2D des Membres Inférieurs et Comportement Modale Face aux Paramètres Biomécaniques; 22ème Congrès Français de Mécanique, Lyon, France (FR); AFM, Association Française de Mécanique: Courbevoie, France, 2015. [Google Scholar]
- Cornelissen, P.; Cornelissen, M.; Van der Perre, G.; Christensen, A.B.; Ammitzbøll, F.; Dyrbye, C. Assessment of tibial stiffness by vibration testing in situ–II. Influence of soft tissues, joints and fibula. J. Biomech. 1986, 19, 551–561. [Google Scholar] [CrossRef]
- Dumas, R.; Camomilla, V.; Bonci, T.; Cheze, L.; Cappozzo, A. Generalized mathematical representation of the soft tissue artefact. J. Biomech. 2014, 47, 476–481. [Google Scholar] [CrossRef] [PubMed]
- Munera, M.; Bertucci, W.; Duc, S.; Chiementin, X. Transmission of whole body vibration to the lower body in static and dynamic half-squat exercises. Sports Biomech. 2016, 15, 409–428. [Google Scholar] [CrossRef] [PubMed]
- Kiiski, J.; Heinonen, A.; Järvinen, T.L.; Kannus, P.; Sievänen, H. Transmission of Vertical Whole Body Vibration to the Human Body. J. Bone Miner. Res. 2008, 23, 1318–1325. [Google Scholar] [CrossRef] [PubMed]
- Van der Perre, G.; Cornelissen, P. On the mechanical resonances of a human tibia in vitro. J. Biomech. 1983, 16, 549–552. [Google Scholar] [CrossRef]
- Taylor, W.R.; Roland, E.; Ploeg, H.; Hertig, D.; Klabunde, R.; Warner, M.D.; Hobatho, M.C.; Rakotomanana, L.; Clift, S.E. Determination of orthotropic bone elastic constants using FEA and modal analysis. J. Biomech. 2002, 35, 767–773. [Google Scholar] [CrossRef]
- Kumar, A.; Jaiswal, H.; Garg, T.; Patil, P.P. Free Vibration Modes Analysis of Femur Bone Fracture Using Varying Boundary Conditions based on FEA. Procedia Mater. Sci. 2014, 6, 1593–1599. [Google Scholar] [CrossRef]
- Gupta, A.; Ming Tse, K. Finite Element Analysis on Vibration Modes of Femur Bone. In Proceedings of the International Conference on Advances in Mechanical Engineering, NCR-Delhi Region, India, December 2013. [Google Scholar]
- Tsuchikane, A.; Nakatsuchi, Y.; Nomura, A. The influence of joints and soft tissue on the natural frequency of the human tibia using the impulse response method. Proc. Inst. Mech. Eng. Part H 1995, 209, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Tseng, J.G.; Huang, B.W.; Liang, S.H.; Yen, K.T.; Tsai, Y.C.; Tseng, J.G. Normal Mode Analysis of a Human Fibula. Life Sci. J. 2014, 11, 711–718. [Google Scholar]
- Kassab, G.; Sacks, M. Structure-Based Mechanics of Tissues and Organs; Springer: New York, NY, USA, 2016. [Google Scholar]
- Gruber, A.H.; Boyer, K.A.; Derrick, T.R.; Hamill, J. Impact shock frequency components and attenuation in rearfoot and forefoot running. J. Sport Health Sci. 2014, 3, 113–121. [Google Scholar] [CrossRef]
- Taiar, R.; Chiementin, X. Ergonomics and biomechanics on the impact of mats on decreasing whole body vibration. In Proceedings of the 8th International Conference on Applied Human Factors and Ergonomics, Los Angeles, CA, USA, 7–17 July 2017. [Google Scholar]
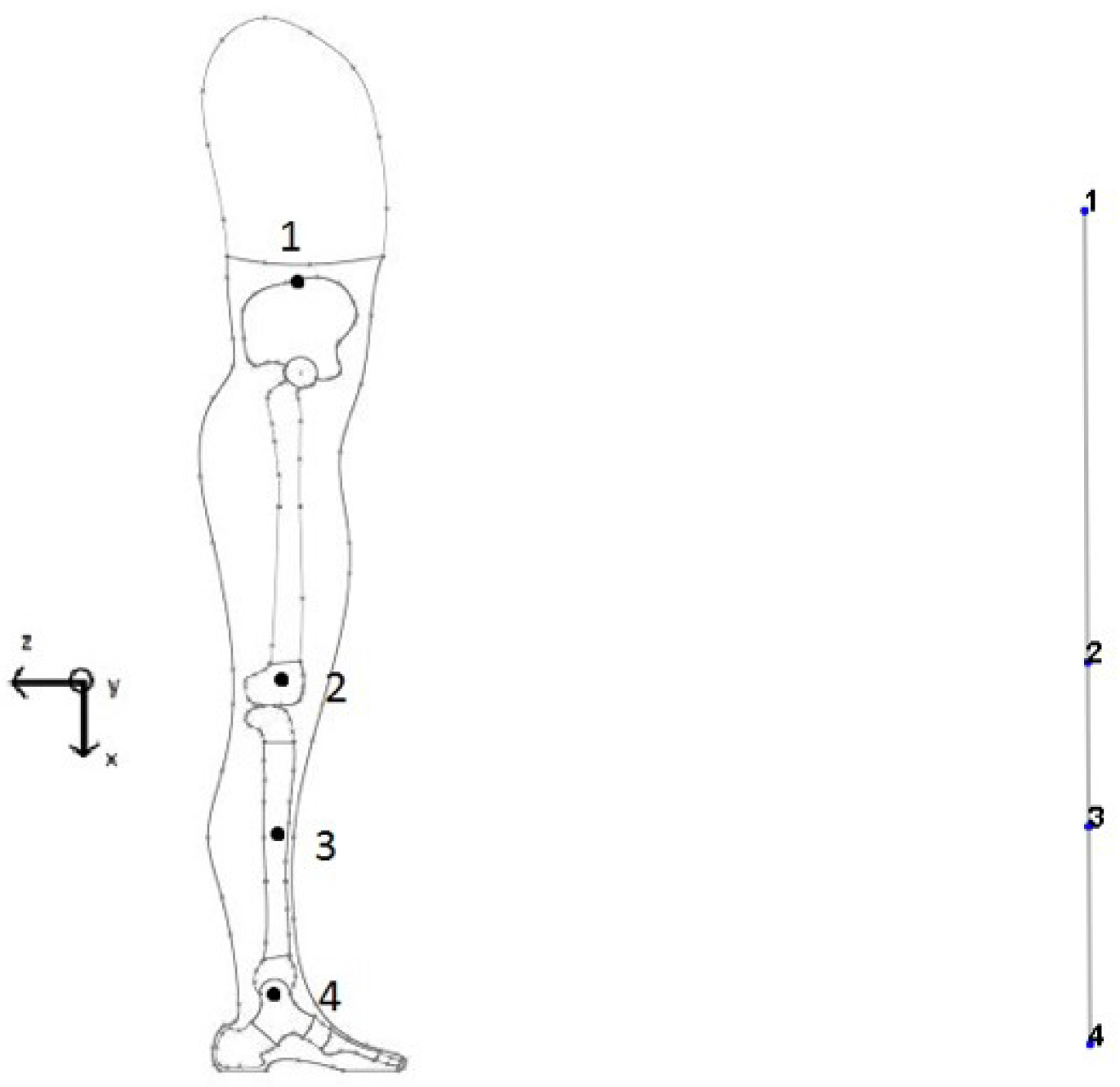
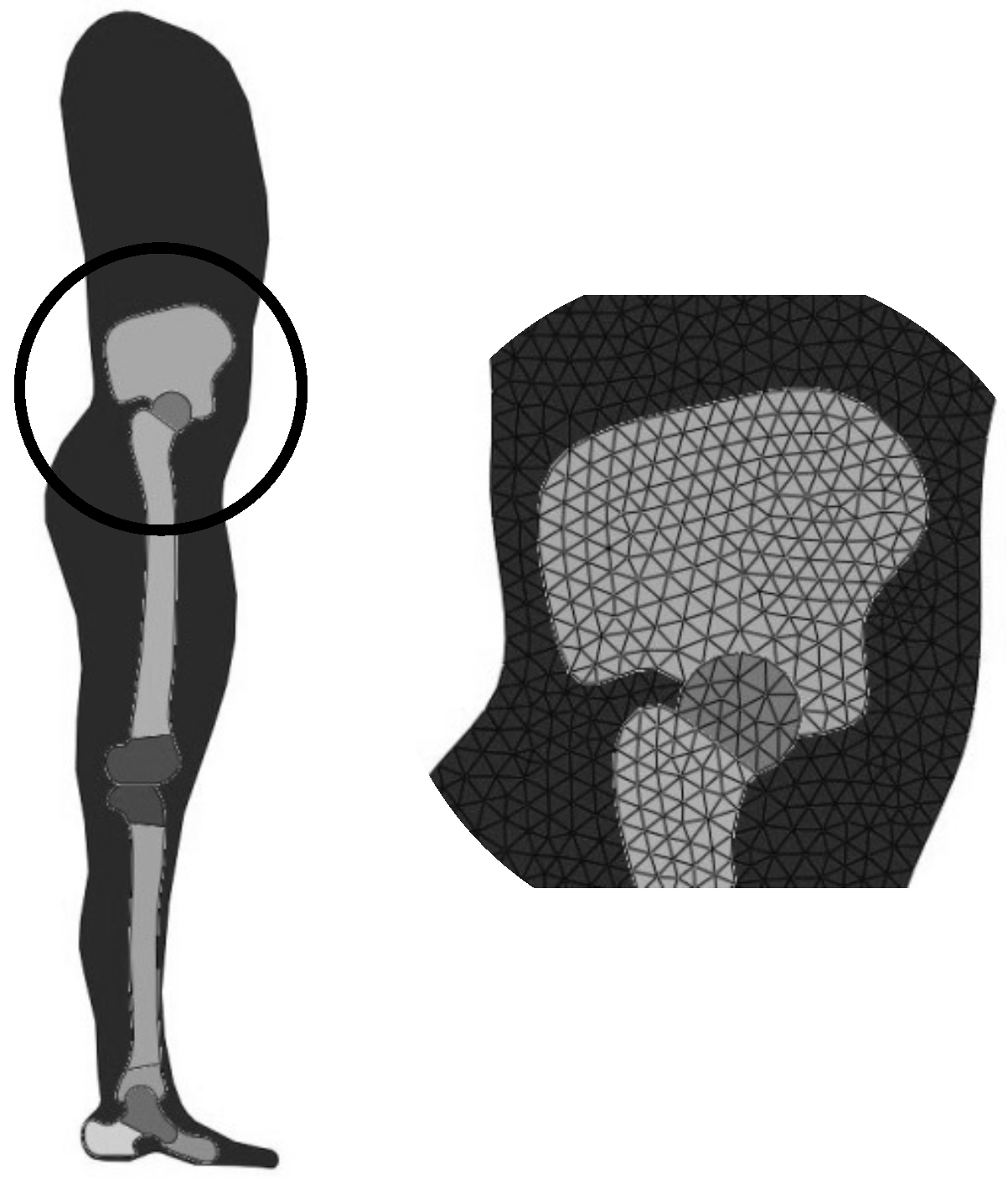
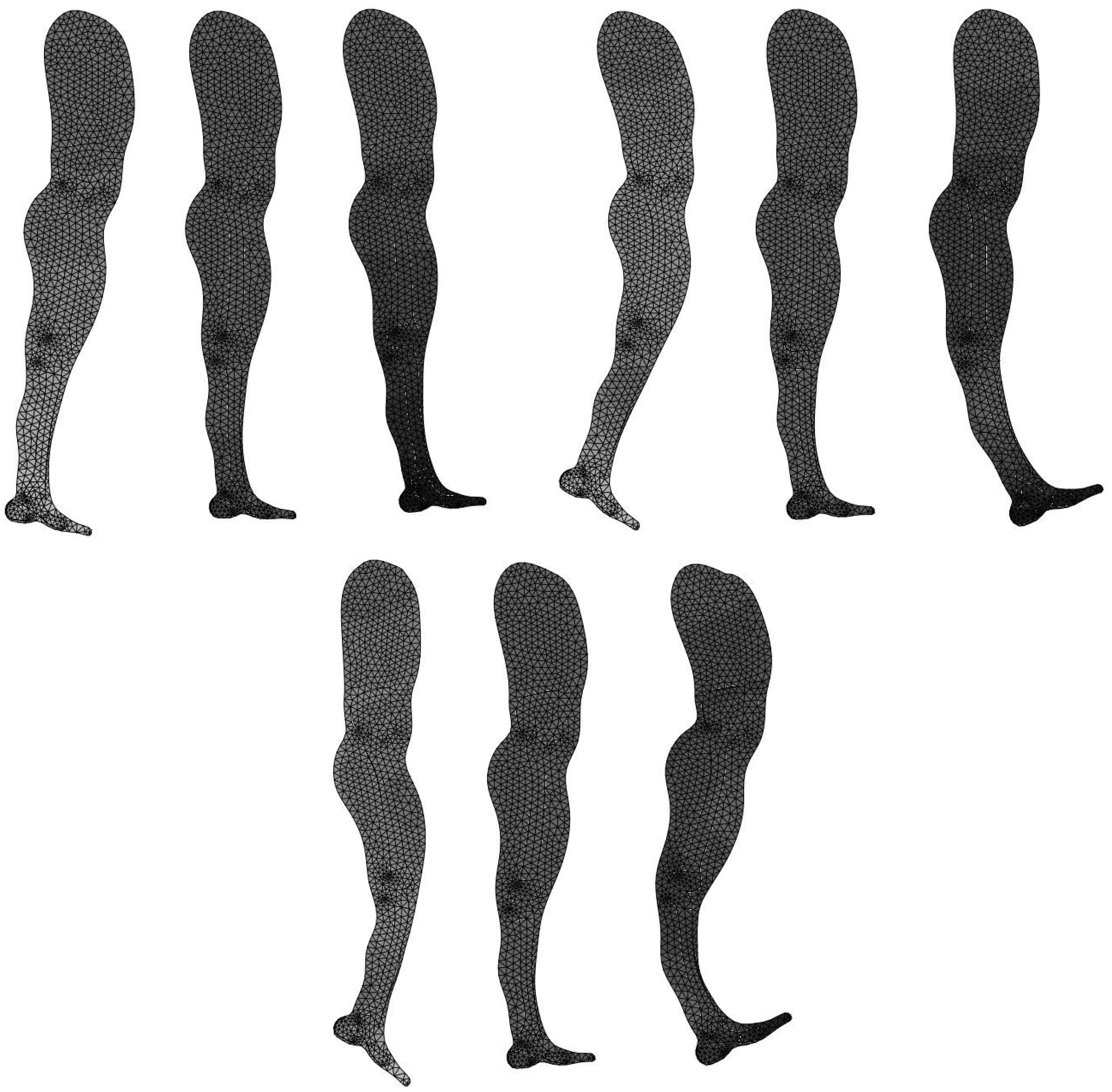
| Parameters | Ranges | Mean | STD |
|---|---|---|---|
| Age (years) | 22–34 | 25.90 | 2.81 |
| Height () | 1.68–1.84 | 1.78 | 0.04 |
| Weight () | 65.30–84.70 | 73.52 | 4.93 |
| Body Mass Index (BMI) | 20.73–27.04 | 23.34 | 2.09 |
| Hip-knee () | 50.00–60.00 | 53.73 | 3.88 |
| Knee-tibia () | 15.00–21.07 | 17.29 | 1.09 |
| Tibia-ankle () | 20.00–27.93 | 22.89 | 1.52 |
| Total length () | 80.00–107.00 | 93.91 | 5.72 |
| Segment | Parameters | Dimension () |
|---|---|---|
| Thigh | Femoral length [25] | 482.0 |
| Femoral head diameter [26] | 46.1 | |
| Neck width of the femoral head [26] | 24.1 | |
| Femoral diaphysiswidth [27] | 30.0 | |
| Femoral condyles width [28] | 81.4 | |
| Thigh diameter [29] | 191.0 | |
| Knee radius [29] | 125.4 | |
| Leg | Tibia length [28] | 383.4 |
| Tibia width ( above ankle) [30] | 28.2 | |
| Tibia proximal epiphysis width [31] | 60.1 | |
| Tibia distal epiphysis width [31] | 43.6 | |
| Calf radius [29] | 119.7 | |
| Foot | Foot length [32] | 260.0 |
| Foot height [33] | 81.2 | |
| Ankle height [33] | 127.9 |
| Body Zones | Initial | Updated | ||
|---|---|---|---|---|
| E | D | E | D | |
| Trunk | 600 | 1.00 | 600 | 1.30 |
| Cortical | 17,500 | 2.10 | 17,500 | 2.10 |
| Trabecular | 450 | 1.80 | 450 | 1.80 |
| Soft tissues | 345 | 1.20 | 615 | 1.11 |
| Mode | Score | Frequency () m ± std (CV%) | Damping % m ± std (CV%) |
|---|---|---|---|
| 1 | 100% | 36.82 ± 0.98 (2.7) | 10.03 ± 1.73 (17.2) |
| 2 | 60% | 42.26 ± 2.02 (4.8) | 7.5 4± 3.29 (43.7) |
| 3 | 100% | 49.48 ± 1.23 (2.5) | 7.04 ± 1.74 (24.7) |
| 4 | 90% | 62.51 ± 2.68 (4.3) | 7.78 ± 2.19 (28.2) |
| 5 | 30% | 71.30 ± 1.26 (1.8) | 4.81 ± 2.40 (49.9) |
| 6 | 80% | 82.14 ± 2.60 (3.2) | 7.82 ± 1.26 (16.2) |
| 7 | 100% | 98.26 ± 3.16 (3.2) | 7.53 ± 2.33 (31.0) |
| 8 | 90% | 122.89 ± 1.07 (0.9) | 2.58 ± 0.76 (29.3) |
| Mode | Frequency () m ± std (CV%) | Damping % m ± std (CV%) |
|---|---|---|
| 1 | 35.66 ± 1.00 (2.8) | 1.39 ± 0.97 (69.8) |
| 2 | 43.24 ± 2.09 (4.8) | 7.28 ± 2.36 (32.4) |
| 3 | 52.54 ± 2.05 (3.9) | 6.41 ± 2.35 (36.8) |
| 4 | 61.99 ± 1.67 (2.7) | 5.16 ± 2.28 (44.2) |
| 5 | 70.40 ± 1.60 (2.3) | 4.73 ± 1.57 (33.1) |
| 6 | 84.06 ± 3.71 (4.4) | 4.46 ± 1.34 (30.1) |
| 7 | 100.38 ± 3.71 (3.7) | 3.52 ± 2.12 (60.1) |
| 8 | 118.94 ± 2.70 (2.3) | 1.60 ± 0.76 (47.7) |
| Frequencies | Mode 3 | Mode 8 |
|---|---|---|
| Mean experimental frequencies () | 52.54 | 118.94 |
| Confidence interval () | 51.17–53.91 | 117.13–120.75 |
| Initial model () | 54.55 | 126.85 |
| Updated model () | 51.17 | 120.70 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pionteck, A.; Chiementin, X.; Munera, M.; Murer, S.; Chadefaux, D.; Rao, G. FE Model and Operational Modal Analysis of Lower Limbs. Appl. Sci. 2017, 7, 853. https://doi.org/10.3390/app7080853
Pionteck A, Chiementin X, Munera M, Murer S, Chadefaux D, Rao G. FE Model and Operational Modal Analysis of Lower Limbs. Applied Sciences. 2017; 7(8):853. https://doi.org/10.3390/app7080853
Chicago/Turabian StylePionteck, Aymeric, Xavier Chiementin, Marcela Munera, Sébastien Murer, Delphine Chadefaux, and Guillaume Rao. 2017. "FE Model and Operational Modal Analysis of Lower Limbs" Applied Sciences 7, no. 8: 853. https://doi.org/10.3390/app7080853
APA StylePionteck, A., Chiementin, X., Munera, M., Murer, S., Chadefaux, D., & Rao, G. (2017). FE Model and Operational Modal Analysis of Lower Limbs. Applied Sciences, 7(8), 853. https://doi.org/10.3390/app7080853







