Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Microgrid
Abstract
1. Introduction
2. Optimization Model of Stand-Alone MG
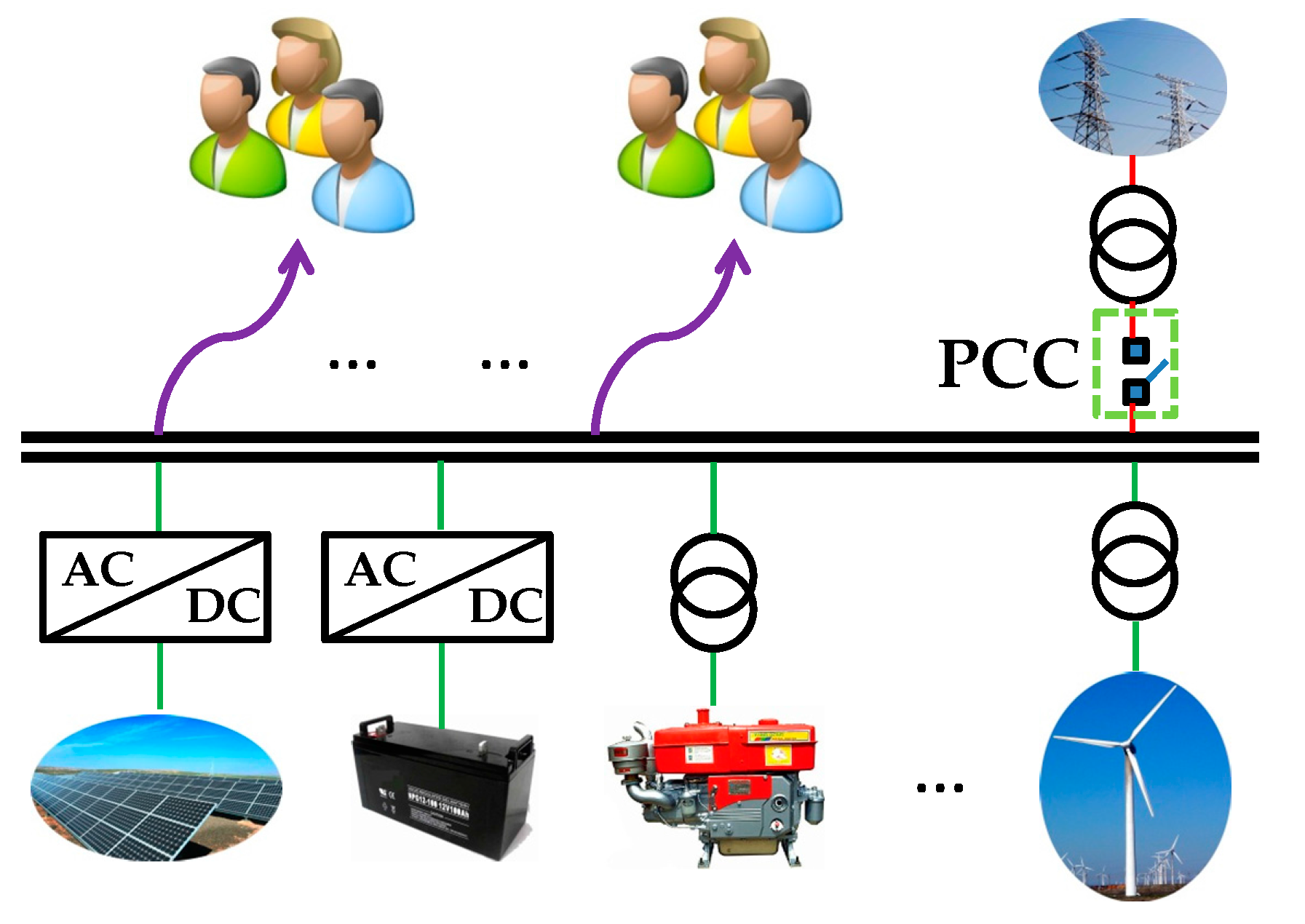
2.1. An Overview of MG
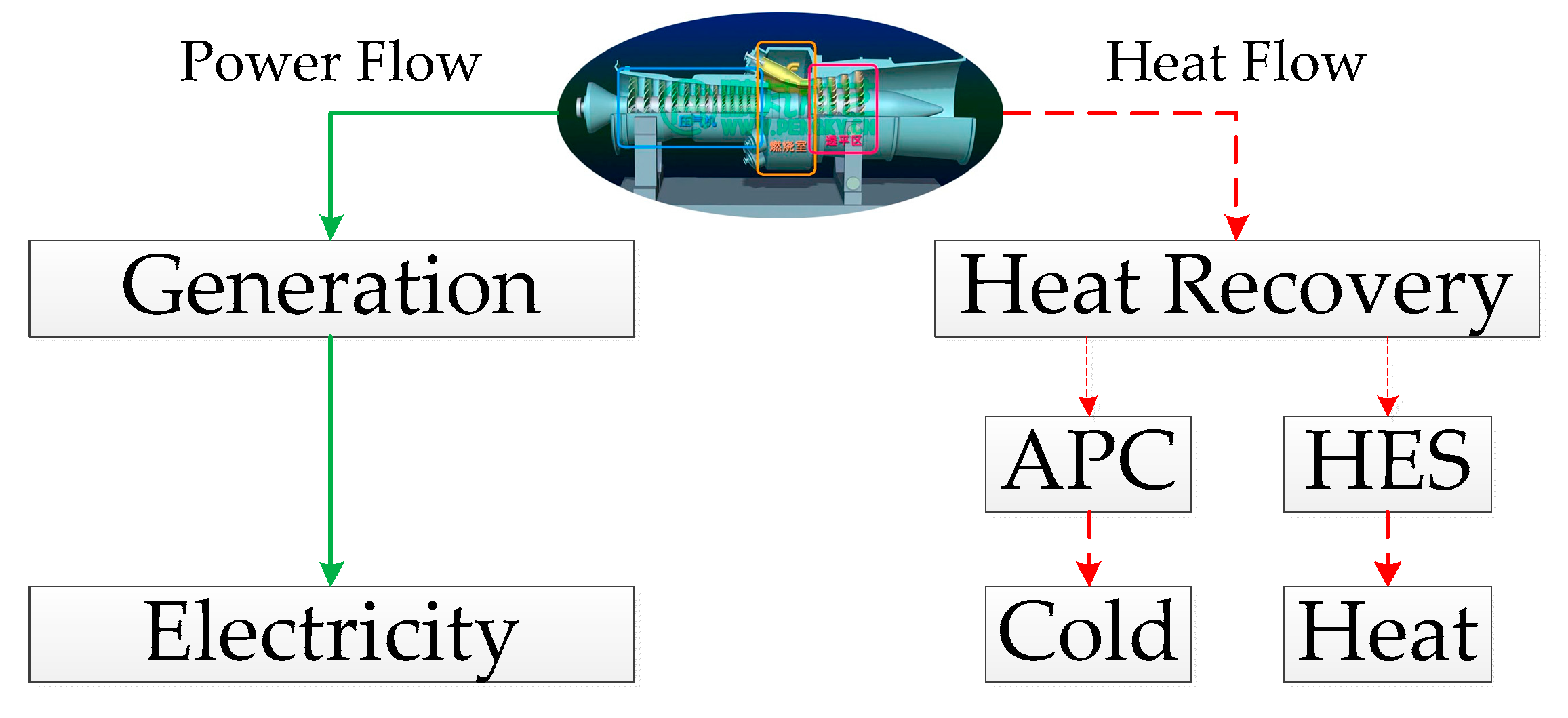
2.2. The CCHP Model of MT
2.3. Objective Function
2.3.1. Operation and Maintenance Cost
2.3.2. Pollutant Disposal Cost
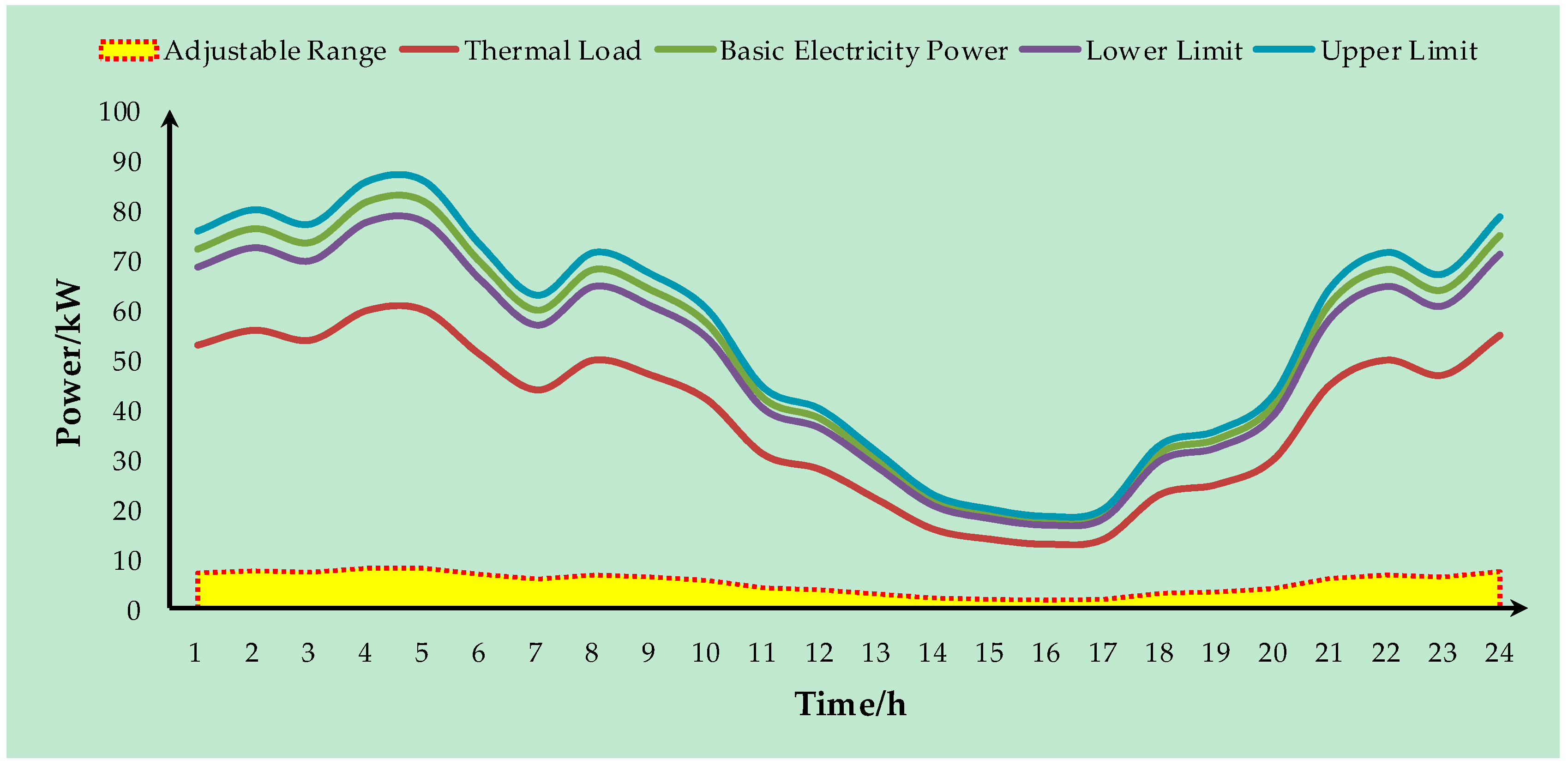
2.3.3. Load Cut Compensation
2.4. Operation Constraint
2.4.1. Power Balance Constraint
2.4.2. Output Constraint
2.4.3. Ramp Up/Down Rate Constraint
2.4.4. Battery Operation Constraint
2.4.5. Load Cut Constraint
2.5. Modified CCHP Dispatch Strategy
3. Modified Chaos Particle Swarm Optimization
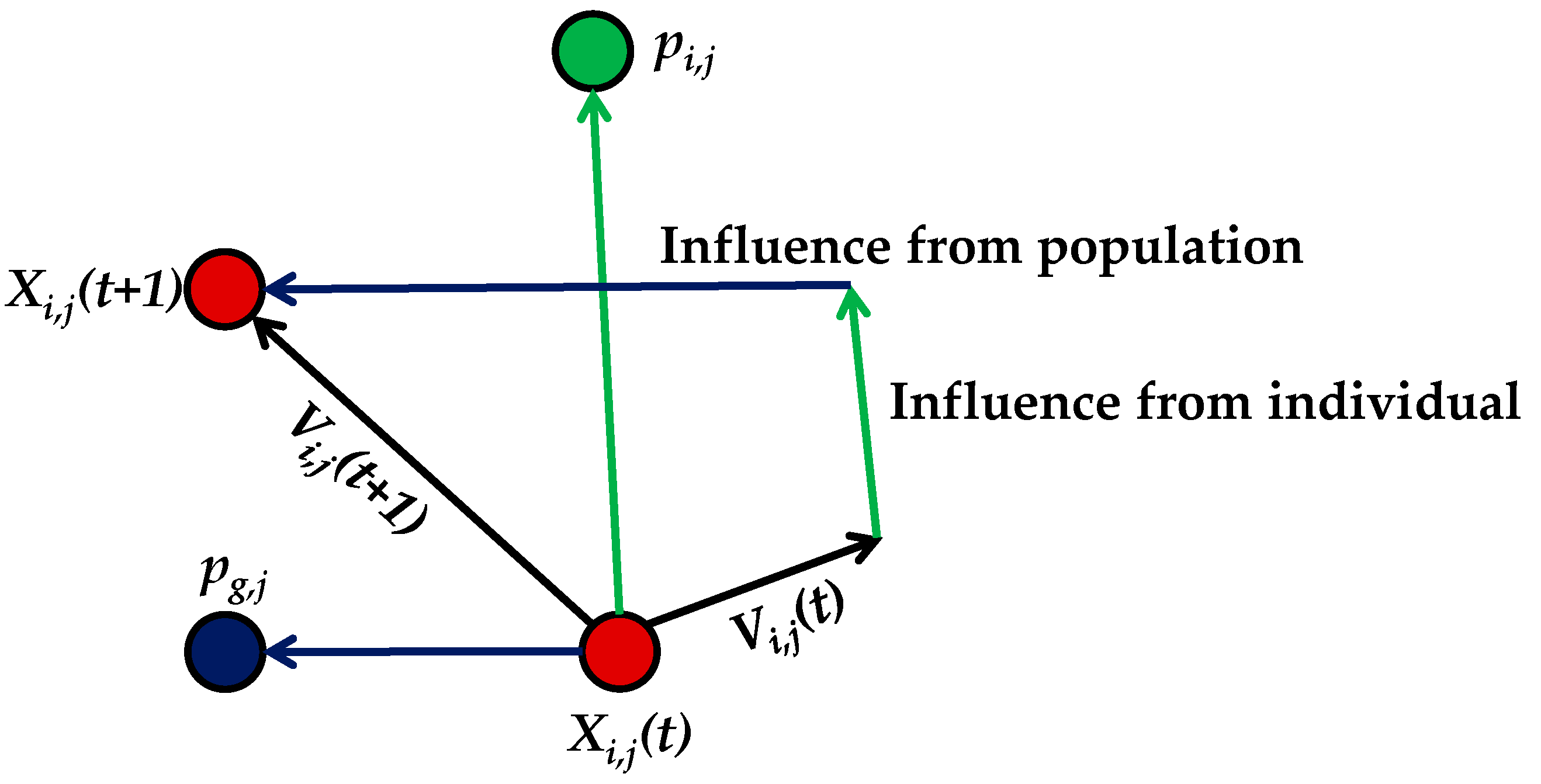
3.1. Basic PSO
3.2. Chaotic Optimization
- (1)
- Assume h = 0, and map the decision variables zjh, j = 1, 2, …, m into chaotic variables between 0 and 1 for every dimension of the solution, where zmax,j and zmin,j represent the upper and lower search bounds of the jth dimension, m is the dimension number of solution.
- (2)
- Calculate the chaotic variables of next iteration by the following formula:
- (3)
- Transform chaotic variables chjh+1 into decision variable
- (4)
- Evaluate the new solution according to decision variable . If the new solution is better than the initial or the chaotic search has reached the maximum iterations, the new solution will be the result of chaos search, otherwise, set h = h + 1 and turn to the second step.
3.3. Elite Retention Strategy
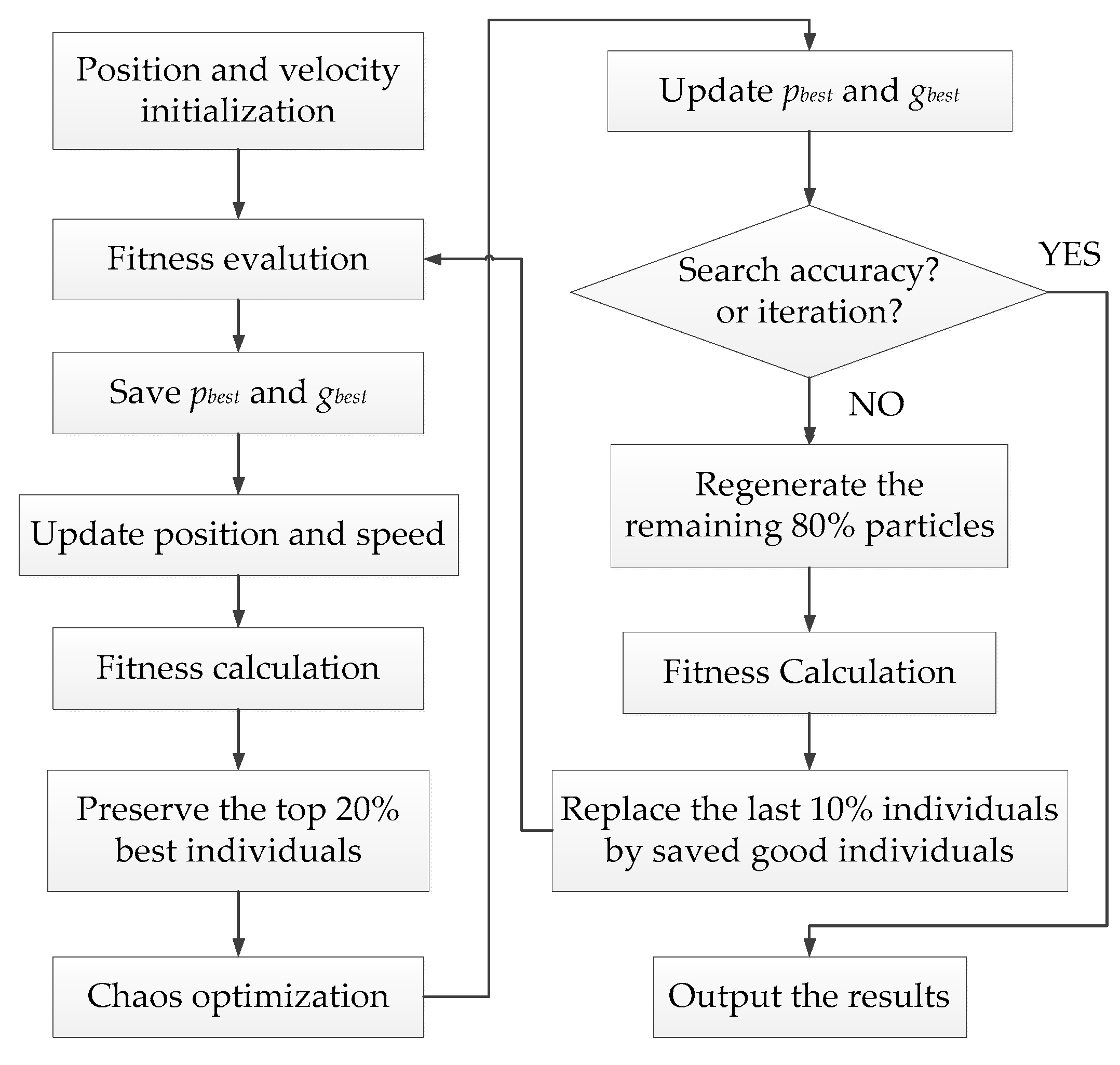
3.4. Steps of MCPSO
- (1)
- Initialize the position and velocity of each particle in the population.
- (2)
- Evaluate the fitness of each particle; save current particles’ positions and fitness values into pbest of each particle; save the position and fitness value of the optimal individual in current population into gbest.
- (3)
- Update the position and the speed of each particle.
- (4)
- Calculate the objective function value of each particle; preserve the top 20% of the best individuals with the best fitness values.
- (5)
- Search the selected particles with chaos optimization; update pbest and gbest of the population.
- (6)
- If the search accuracy is satisfied or the iteration number is reached, stop the search and output the result, otherwise, turn to step 7.
- (7)
- Regenerate the remaining 80% of the particles; calculate the fitness values and replace the last 10% of the individuals with the worst fitness by the top 10% of the good individuals obtained in step 4 and transfer to step 2 then.
4. Case Studies
4.1. The Framework of Stand-Alone MG
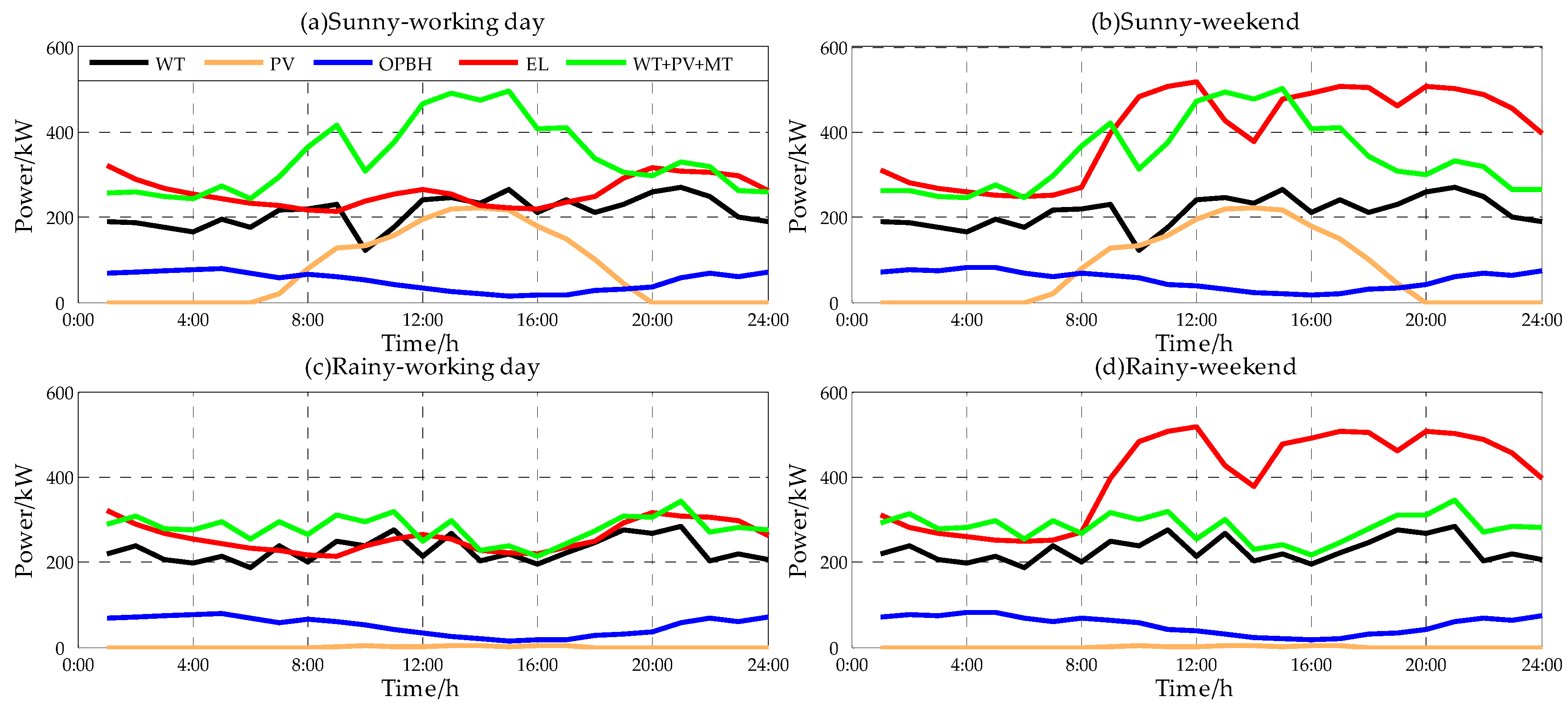
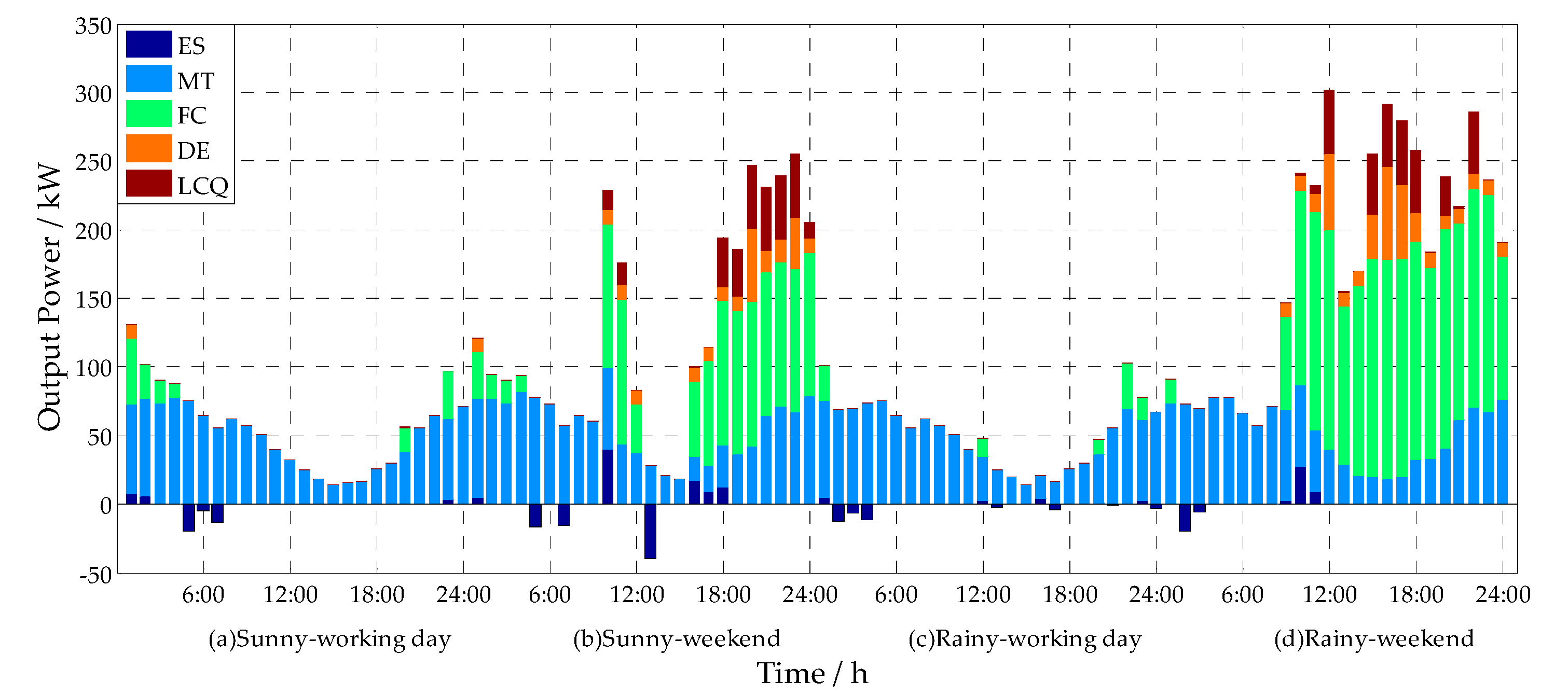
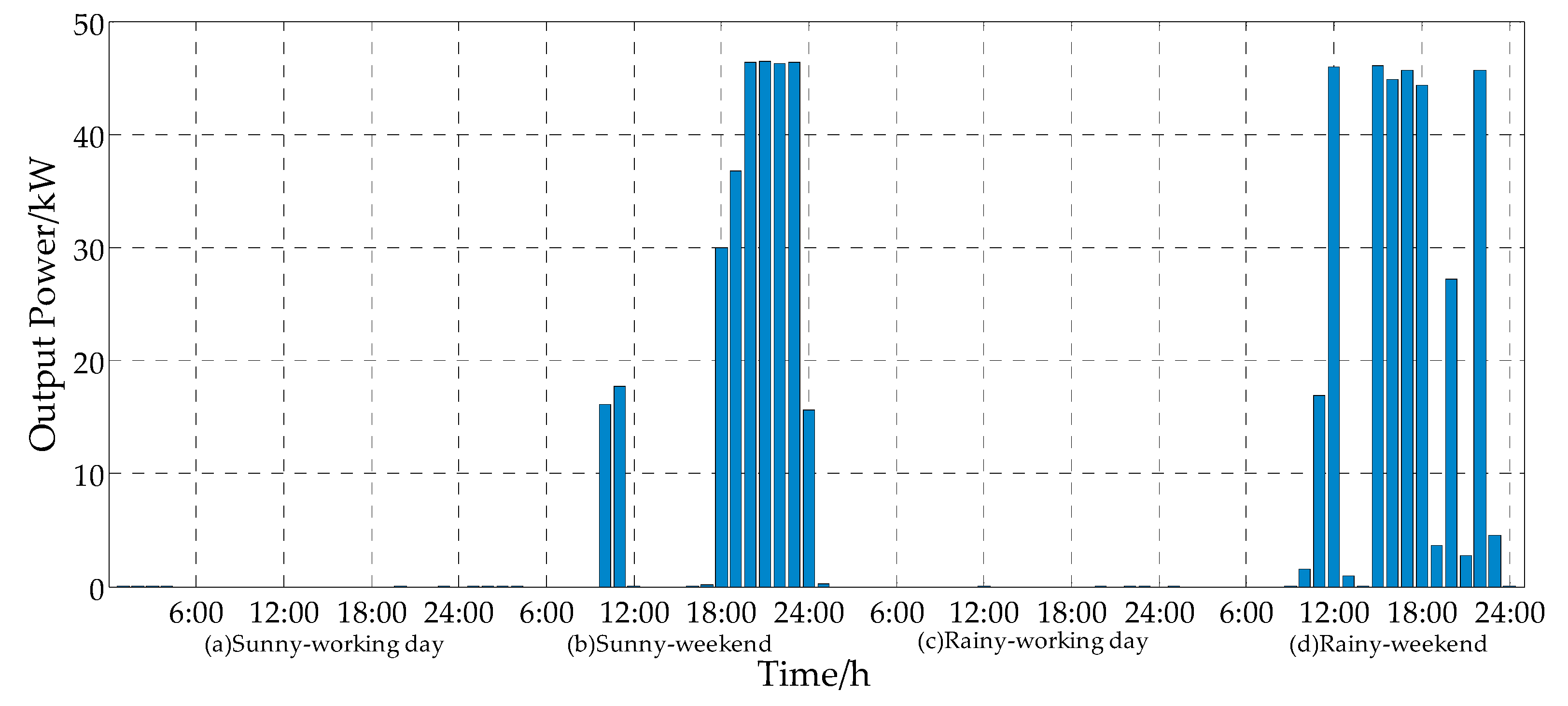
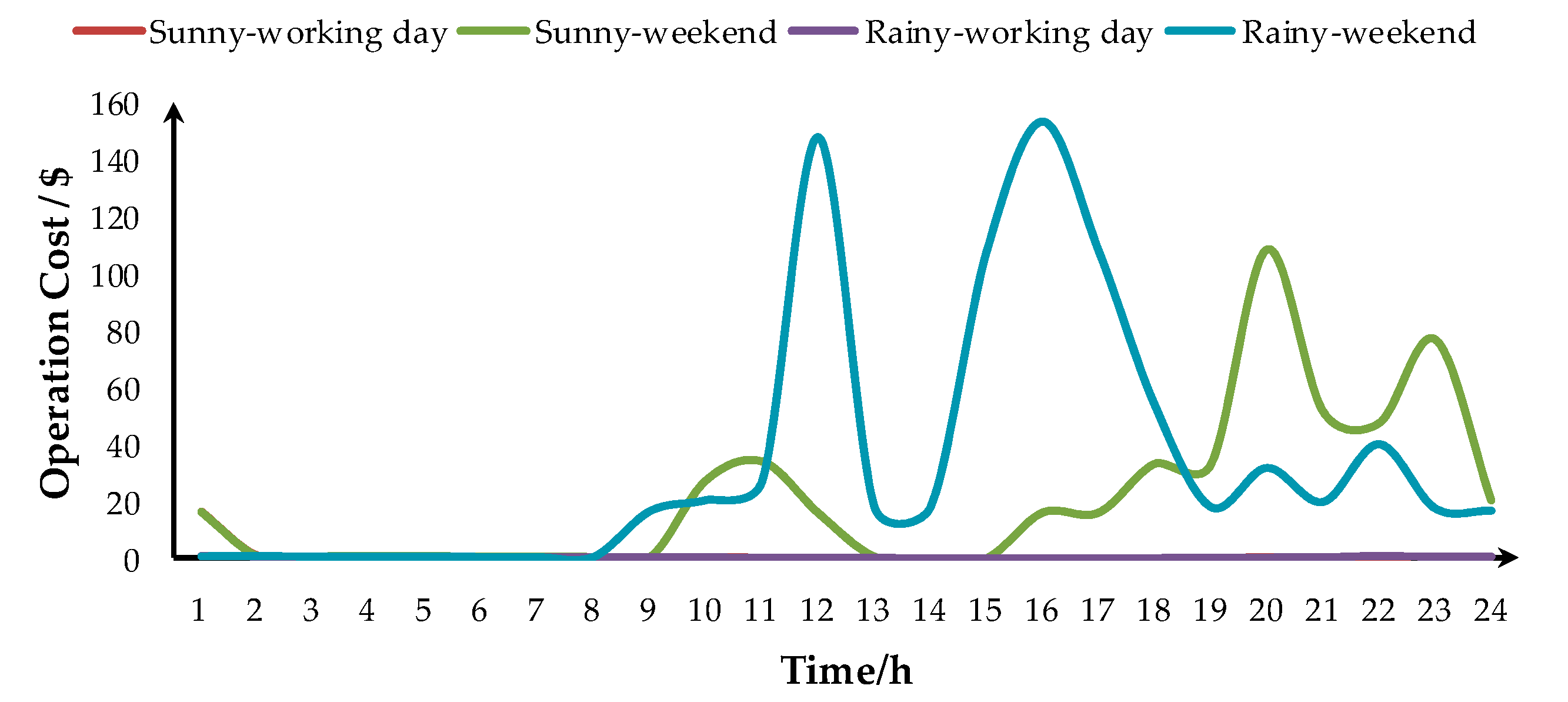
4.2. Results Analysis
4.3. Comparison Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct Quantile Regression for Nonparametric Probabilistic Forecasting of Wind Power Generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Yu, K.; Ai, Q.; Wang, S.; Ni, J.; Lv, T. Analysis and Optimization of Droop Controller for Microgrid System Based on Small-Signal Dynamic Model. IEEE Trans. Smart Grid 2016, 7, 695–705. [Google Scholar] [CrossRef]
- Pouresmaeil, E.; Mehrasa, M.; Catalão, J.P.S. A Multifunction Control Strategy for the Stable Operation of DG Units in Smart Grids. IEEE Trans. Smart Grid 2015, 6, 598–607. [Google Scholar] [CrossRef]
- Fuangfoo, P.; Meenual, T.; Lee, W.J.; Chompoo-inwai, C. PEA Guidelines for Impact Study and Operation of DG for Islanding Operation. IEEE Trans. Ind. Appl. 2008, 44, 1348–1353. [Google Scholar] [CrossRef]
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition1. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Senjyu, T.; Miyazato, Y.; Yona, A.; Urasaki, N.; Funabashi, T. Optimal Distribution Voltage Control and Coordination with Distributed Generation. IEEE Trans. Power Deliv. 2008, 23, 1236–1242. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting Power Output of Photovoltaic Systems Based on Weather Classification and Support Vector Machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Mi, Z.; Sun, H.; Su, S.; Yang, G. Solar irradiance feature extraction and support vector machines based weather status pattern recognition model for short-term photovoltaic power forecasting. Energy Build. 2015, 86, 427–438. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-term Solar Irradiance Forecasting Model Based on Artificial Neural Network Using Statistical Feature Parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Song, Y.; Xu, Z.; Yang, G. Probabilistic Forecasting of Photovoltaic Generation: An Efficient Statistical Approach. IEEE Trans. Power Syst. 2017, 32, 2471–2472. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Optimal Offering Strategies for Wind Power Producers Considering Uncertainty and Risk. IEEE Syst. J. 2012, 6, 270–277. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Mendes, V.M.F. Influence of Environmental Constraints on Profit-Based Short-Term Thermal Scheduling. IEEE Trans. Sustain. Energy 2011, 2, 131–138. [Google Scholar] [CrossRef]
- Fang, X.; Li, F.; Wei, Y.; Cui, H. Strategic scheduling of energy storage for load serving entities in locational marginal pricing market. IET Gen. Transm. Distrib. 2016, 10, 1258–1267. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic Forecasting of Wind Power Generation Using Extreme Learning Machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, C.; Wang, Y.; Yang, X.; Zhang, X.; Wu, C.; Chen, Y. Relay Protection Coordination Integrated Optimal Placement and Sizing of Distributed Generation Sources in Distribution Networks. IEEE Trans. Smart Grid 2016, 7, 55–65. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Li, X.; Liu, H.; Chen, F.; Liu, B. S-shaped droop control method with secondary frequency characteristics for inverters in microgrid. IET Gener. Transm. Distrib. 2016, 10, 3385–3392. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.D.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Li, H.; McLellan, B.C.; Chen, S.; Li, Y.; Tian, Y. Study on the promotion impact of demand response on distributed PV penetration by using non-cooperative game theoretical analysis. Appl. Energy 2017, 185 Pt 2, 1869–1878. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Tian, R.; Li, H. Combined Impacts of RTP and FIT on Optimal Management for a Residential Micro-Grid. Energy Procedia 2015, 75, 1666–1672. [Google Scholar] [CrossRef]
- Ross, M.; Abbey, C.; Bouffard, F.; Jos, G. Multiobjective Optimization Dispatch for Microgrids with a High Penetration of Renewable Generation. IEEE Trans. Sustain. Energy 2015, 6, 1306–1314. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.; Xu, T.; Li, K.; Shafie-khah, M.; Catalão, J.P.S. The values of market-based demand response on improving power system reliability under extreme circumstances. Appl. Energy 2017, 193, 220–231. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, F.; Hodge, B.M.; Zhang, J.; Li, Z.; Shafie-khah, M.; Catalao, J.P.S. Dynamic Price Vector Formation Model Based Automatic Demand Response Strategy for PV-assisted EV Charging Station. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Vahedi, H.; Noroozian, R.; Hosseini, S.H. Optimal management of MicroGrid using differential evolution approach. In Proceedings of the 7th International Conference on the European Energy Market, Madrid, Spain, 23–25 June 2010; pp. 1–6. [Google Scholar]
- Bao, Z.; Zhou, Q.; Yang, Z.; Yang, Q.; Xu, L.; Wu, T. A Multi Time-Scale and Multi Energy-Type Coordinated Microgrid Scheduling Solution—Part I: Model and Methodology. IEEE Trans. Power Syst. 2015, 30, 2257–2266. [Google Scholar] [CrossRef]
- Li, P.; Xu, D.; Zhou, Z.; Lee, W.J.; Zhao, B. Stochastic Optimal Operation of Microgrid Based on Chaotic Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2016, 7, 66–73. [Google Scholar] [CrossRef]
- Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Scheduling of demand side resources using binary particle swarm optimization. IEEE Trans. Power Syst. 2009, 24, 1173–1181. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R. Power Management Strategies for a Microgrid with Multiple Distributed Generation Units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Abbes, D.; Martinez, A.; Champenois, G. Eco-design optimisation of an autonomous hybrid wind-photovoltaic system with battery storage. IET Renew. Power Gener. 2012, 6, 358–371. [Google Scholar] [CrossRef]
- Azmy, A.M.; Erlich, I. Online optimal management of PEM Fuel cells using neural networks. IEEE Trans. Power Deliv. 2005, 20, 1051–1058. [Google Scholar] [CrossRef]
- Noroozian, R.; Vahedi, H. Optimal management of MicroGrid using Bacterial Foraging Algorithm. In Proceedings of the 18th Iranian Conference on Electrical Engineering, Isfahan, Iran, 11–13 May 2010; pp. 895–900. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Kaddoum, G. Wireless Chaos-Based Communication Systems: A Comprehensive Survey. IEEE Access 2016, 4, 2621–2648. [Google Scholar] [CrossRef]
- Kocarev, L.; Szczepanski, J.; Amigo, J.M.; Tomovski, I. Discrete Chaos-I: Theory. IEEE Trans. Circuits Syst. I 2006, 53, 1300–1309. [Google Scholar] [CrossRef]
- Diaf, S.; Diaf, D.; Belhamel, M.; Haddadi, M.A. Louche, A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy 2007, 35, 5708–5718. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Willingham, M.; Rahman, S. Implications of on-site distributed generation for commercial/industrial facilities. IEEE Trans. Power Syst. 2005, 20, 206–212. [Google Scholar] [CrossRef]
- Bernow, S.; Marron, D. Valuation of Environmental Externalities for Energy Planning and Operations; Tellus Institute Report 90-SB01; Tellus Institute: Boston, MA, USA, May, 1990. [Google Scholar]

| Type | Pe (kW) | Pmax/Pmin (kW) | Rup/Rdown (kW/min) | K ($/kWh) |
|---|---|---|---|---|
| DE | 155 | 180/10 | 20 | 0.01258 |
| FC | 135 | 160/10 | 10 | 0.00419 |
| MT | 100 | 125/10 | 10 | 0.00587 |
| ES | 25 | - | - | 0.01241 |
| Type | Disposal Cost ($/lb) | DE (lb/kWh) | FC (lb/kWh) | MT (lb/kWh) |
|---|---|---|---|---|
| NOx | 4.2 | 2.18 × 10−2 | 3 × 10−5 | 4.4 × 10−4 |
| SO2 | 0.99 | 4.54 × 10−4 | 6 × 10−6 | 8 × 10−6 |
| CO2 | 0.014 | 1.43 × 10−3 | 1.078 × 10−3 | 1.596 × 10−3 |
| Scenario | (a) | (b) | (c) | (d) |
|---|---|---|---|---|
| Modified Strategy ($) | 28.926 | 506.816 | 13.043 | 824.484 |
| Traditional Strategy ($) | 30.201 | 521.794 | 13.639 | 844.073 |
| Decreased Percentage (%) | 4.22 | 2.87 | 4.37 | 2.32 |
| Initial Load Demand (kW) | 1201.761 | 1268.601 | 1201.761 | 1268.601 |
| Actual Power Output (kW) | 1159.959 | 1273.904 | 1156.716 | 1266.460 |
| Decreased Percentage (%) | 3.48 | 0.42 | 3.75 | 0.17 |
| Algorithms | Total Cost | Average Convergence Time/s | |
|---|---|---|---|
| Average Cost/$ | Standard Deviation/$ | ||
| PSO | 851.146 | 1.972 | 254.84 |
| CPSO | 833.564 | 1.496 | 267.35 |
| MCPSO | 824.732 | 0.358 | 243.28 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhou, L.; Wang, B.; Wang, Z.; Shafie-khah, M.; Catalão, J.P.S. Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Microgrid. Appl. Sci. 2017, 7, 754. https://doi.org/10.3390/app7080754
Wang F, Zhou L, Wang B, Wang Z, Shafie-khah M, Catalão JPS. Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Microgrid. Applied Sciences. 2017; 7(8):754. https://doi.org/10.3390/app7080754
Chicago/Turabian StyleWang, Fei, Lidong Zhou, Bo Wang, Zheng Wang, Miadreza Shafie-khah, and João P. S. Catalão. 2017. "Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Microgrid" Applied Sciences 7, no. 8: 754. https://doi.org/10.3390/app7080754
APA StyleWang, F., Zhou, L., Wang, B., Wang, Z., Shafie-khah, M., & Catalão, J. P. S. (2017). Modified Chaos Particle Swarm Optimization-Based Optimized Operation Model for Stand-Alone CCHP Microgrid. Applied Sciences, 7(8), 754. https://doi.org/10.3390/app7080754








