Abstract
The optimized dispatch of different distributed generations (DGs) in stand-alone microgrid (MG) is of great significance to the operation’s reliability and economy, especially for energy crisis and environmental pollution. Based on controllable load (CL) and combined cooling-heating-power (CCHP) model of micro-gas turbine (MT), a multi-objective optimization model with relevant constraints to optimize the generation cost, load cut compensation and environmental benefit is proposed in this paper. The MG studied in this paper consists of photovoltaic (PV), wind turbine (WT), fuel cell (FC), diesel engine (DE), MT and energy storage (ES). Four typical scenarios were designed according to different day types (work day or weekend) and weather conditions (sunny or rainy) in view of the uncertainty of renewable energy in variable situations and load fluctuation. A modified dispatch strategy for CCHP is presented to further improve the operation economy without reducing the consumers’ comfort feeling. Chaotic optimization and elite retention strategy are introduced into basic particle swarm optimization (PSO) to propose modified chaos particle swarm optimization (MCPSO) whose search capability and convergence speed are improved greatly. Simulation results validate the correctness of the proposed model and the effectiveness of MCPSO algorithm in the optimized operation application of stand-alone MG.
1. Introduction
Under the dual pressures of global energy crisis and environmental pollution [1], distributed generations (DGs) have received more and more attention for its advantages of low pollution, high efficiency and flexible installation site [2,3,4]. DGs include micro-gas turbine (MT), diesel engine (DE), fuel cell (FC), photovoltaic (PV), wind turbine (WT), small hydropower and some energy-saving technologies, such as flywheels, super capacitors and accumulators [5]. However, the uncontrollability and fluctuation of DGs have caused certain impact to the connected distribution network [6], especially the renewable power generation, such as PV [7,8,9,10] and WT [11,12,13,14]. With the growing penetration of DGs, the negative impact on power grid operation is also increasingly prominent [15].
Microgrid (MG) is an autonomous system that can realize self-control, self-protection and self-management. It could operate interconnected with the utility grid or in an islanded mode [16] managing all kinds of DGs effectively at the same time [17]. MGs create a good environment for DGs’ development with the abilities to improve the power quality and reduce the loss of high-voltage network.
To decrease the economic costs and improve the environmental benefits, the optimal dispatch has gained more and more attention [18]. Different optimization models were proposed for MGs with diverse constitutions [19]. Michael Ross put forward a dispatch model with consideration of cost, reliability of service, power fluctuation, peak loading and greenhouse gas emissions [20], but the CL was not considered while demand side is receiving increasing concerns with the development of demand response (DR) these years [21,22]. H. Vahedi applied the optimization model in a certain scenario and got the power output of every micro resource in each period [23]. However, the basic data from various operation environments would impact the performance of algorithm and model. Consequently, single scenario cannot verify the adaptation of the algorithm and model. Zhejing Bao established a day-ahead scheduling model, which combined MT’s combined cooling-heating-power (CCHP) mode with ice-storage air-conditioners [24]. The electricity power output of MTs is only decided by the thermal or cooling load. To make full use of the CCHP to improve the whole benefit of the MG system, this paper proposed a modified strategy for MT to operate in a more economical way. The MG in this paper consists of six different kinds of DGs since the structure with multi-type micro resources could further enhance the complementarity between various types of energy.
Particle swarm optimization (PSO) is a stochastic, population-based evolutionary algorithm and has embraced popularity in the optimized operation of MG because of their advantages of few constraints on fitness function, simple principle, easy coding and rapid convergence speed [25]. However, basic PSO algorithm is easy to fall into local optimum due to the problem of premature [26]. In order to overcome the problems of premature and poor local search performance in PSO, this paper introduced chaotic optimization and elite retention strategy into PSO to present modified chaos particle swarm optimization (MCPSO). The validity and feasibility of the proposed algorithm were proved by simulation results.
The rest part of this paper is organized as follows. In Section 2, the optimization model of MG is presented in detail. In Section 3, the proposed MCPSO is presented and the steps of the algorithm are listed step by step. In Section 4, the case study is conducted to verify the proposed model and algorithm, while at the same time the simulation results are discussed. Finally, the conclusion is given in Section 5.
2. Optimization Model of Stand-Alone MG
2.1. An Overview of MG
MG could be defined as an integrated distribution system composed of various DGs, different types of loads and other protection or management modules [27]. Figure 1 shows a typical structure of MG, which connects to the external grid through the point of common coupling (PCC). If the PCC operates on connected status, the system is called grid-connected MG that is able to exchange electricity power with external bulk grid. Otherwise, the system is called a stand-alone MG whose power balance must be maintained by itself. The AC bus contacts the DGs (PV, WT, DE and energy storage (ES) in this MG) and the electric equipment in this system, ensuring the power generation and consumption. Usually, ES system and controllable DGs such as DE, MT and FC should be integrated into the MG except the renewable power generation in order to guarantee the crucial loads to be powered under extreme situations where the renewable energy output is very low or a fault occurs in external grid.
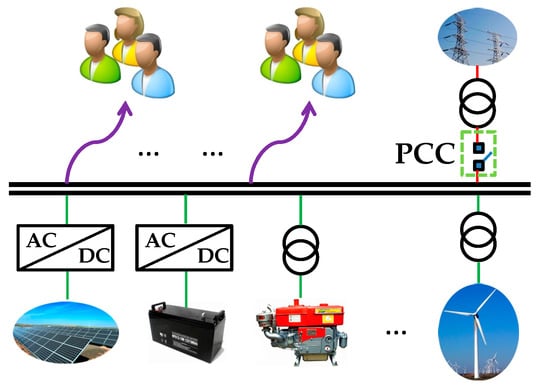
Figure 1.
Typical structure of a microgrid (MG). PCC: point of common coupling.
2.2. The CCHP Model of MT
Generally, MT is inefficient unless operating in CCHP mode. The model adopted in this paper for MT is:
where CMT is the fuel cost of MT in operation time, Cnl is the natural gas price to supply MT, PMT represents the electrical power produced by MT and ηMT stands for the efficiency of MT.
CCHP system is consisted of generation module and heat recovery module, and the latter is further divided into absorption chiller (APC) and heat-exchanging system (HES). The generation, APC and HES modules export electricity, cold and heat energy, respectively. The structure is shown in Figure 2.
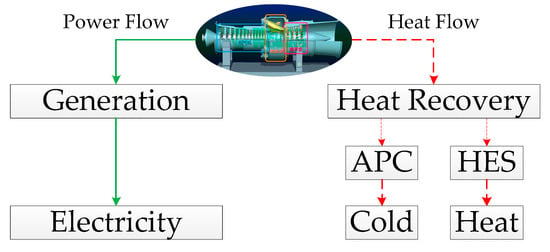
Figure 2.
The structure of micro-gas turbine’s (MT’s) combined cooling-heating-power (CCHP) mode. APC: absorption chiller; HES: heat-exchanging system.
The energy relationship contained in the heat recovery module could be described by Formulas (2)–(4).
where QMT.E, QH and QC represent the residual heat of exhaust, heating and cooling capacity provided by the residual heat of exhaust severally, ηl is the heat loss factor of CCHP system, ηH.REC and ηC.REC stand for the heating and cooling efficiency while ωH and ωC are the heating and refrigeration coefficient.
Models of PV, WT, FC, DE and ES refer to [28,29,30].
2.3. Objective Function
The optimized operation of MG is a multi-objective and multi-constraint optimization problem. This paper adopted the daily scheduling model which divided one day into 24 periods equally, and the load and renewable energy output were assumed to be constant in each dispatch period.
2.3.1. Operation and Maintenance Cost
The operation and maintenance cost is assumed to be proportional to the output of micro resources. Assuming that the WT and PV module have little operation and maintenance cost, the sub-objective can be expressed by:
where S1(t) is the operation and maintenance cost of the whole MG, Pm(t) and Cm(Pm(t)) are the electricity output and fuel cost of micro resource m in the tth dispatch period respectively. Km, KH, KC are the maintenance factors of micro resource m, HES and APC modules, PH(t) and PC(t) are the heat power generated by HES and the cooling power generated by AC severally, ∆t is the dispatch interval time, which is 1 h in this paper.
2.3.2. Pollutant Disposal Cost
MT, DE and FC would discharge NOX, CO2, SO2 and other environmental pollutants in the generation process. Emission coefficients of pollutants are diverse for different generation units while different pollutants will cause various environmental impacts. In this paper, the environmental benefit was considered by the following conversion formulation:
where S2(t) is the pollutant disposal cost of the whole MG, ξn represents the conversion coefficient for different pollutants (NOX, CO2, SO2), Amn is the discharge quantity of pollutant n when micro resource m lets out unit electricity power, P is the number of pollutant types while Q is the number of generation units.
2.3.3. Load Cut Compensation
To make use of demand side and further improve the operation reliability, CL was taken into account, which could also act as an auxiliary adjustment means for power balance in emergency circumstances. The load cut compensation corresponds to the reliability cost of MG. Generally, it is measured by the product of the expected energy not supplied (EENS) and unit interruption cost (UIC). In this study, the EENS was the load cut quantity which had considered the actual operation economy and reliability conditions of the whole MG, the corresponding compensatory costs S3(t) can be expressed by:
where PEL.c(t) is the actual load cut power in different dispatch period and c(t) is the UIC of MG.
Therefore, the established multi-objective optimization model could be described as:
Since all the sub-goals have been transformed into cost, the multi-objective model could be converted to a single-objective model:
The optimization model aims to develop a 24-h dispatching scheme of various distributed resources in the stand-alone MG to minimize the total cost while meeting the electricity, heat and cooling demand of customers.
2.4. Operation Constraint
Constraints such as security, reliability and power quality must be achieved in the optimized operation of MG.
2.4.1. Power Balance Constraint
2.4.2. Output Constraint
2.4.3. Ramp Up/Down Rate Constraint
2.4.4. Battery Operation Constraint
2.4.5. Load Cut Constraint
2.5. Modified CCHP Dispatch Strategy
Generally, the electric power output from MT is determined by the thermal or cooling load of the whole MG. In this case, the output of MT is transformed from a decision variable to a constant value. Therefore, the optimization model is simplified and the effect produced by MT to operation performance is weakened. Based on the fact that little variation (5% in this paper) in environmental parameters will not have a great impact on people’s comfort feeling, this paper proposed a modified dispatch strategy for MT’s CCHP mode, which is shown in Figure 2 (Take the situation of thermal load for example). The basic electricity power is determined by thermal load (TL), while the upper limit increases 5% and lower limit decreases 5% since the variation margin in environmental parameters. The column in Figure 3 represents the adjustable range of MT’s electric power.
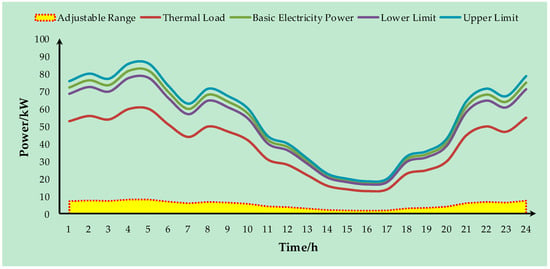
Figure 3.
Modified dispatch strategy for MT’s CCHP mode.
3. Modified Chaos Particle Swarm Optimization
For multi-objective optimization problem, it is best to find the absolute optimal solution. However, sub-goals are often contradictory and the absolute optimal solution does not exist. Considering that the model has been transformed into single-objective optimization, this paper proposed MCPSO to solve the model.
3.1. Basic PSO
PSO is a metaheuristic intelligence algorithm based on population search [31]. Figure 4 shows the optimization search principle of PSO. Individuals update their velocity vectors according to their own speed, individual optimal solution pbest and population optimal solution gbest converge to global optimal solution during iteration. The jth dimension of the velocity and position for particle i at moment t are updated as follows:
where g is the inertia weight representing the velocity component inherited from the original velocity, s1 and s2 are learning factors while rand1 and rand2 are random numbers between 0~1, d is the dimension of the optimization model, pi,j and pg,j stand for the individual and population optimal solution, respectively.
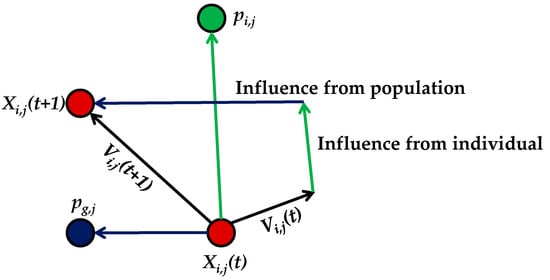
Figure 4.
The schematic diagram of particle swarm optimization (PSO) algorithm.
PSO can approach the optimal solution at a relatively fast convergence speed, because the individuals can make full use of their experience and the group’s experience. In this paper, load control and multi-scenario were considered. More decision variables and constraints, and intricate data in variable scenarios made the model complicated. As a result, for PSO, the problems of premature, poor local research ability and slow convergence speed in the later iteration appeared. However, the optimized scheduling of MG requires not only a faster running speed to meet dispatch timeliness, but also the global convergence capacity to satisfy the dispatch accuracy. Reasonable modification is urgent to be adopted to improve the performance of basic PSO.
3.2. Chaotic Optimization
Generally, the random state of motion obtained from deterministic equations is called chaos. The chaotic state widely exists in natural and social phenomenon, especially in nonlinear system, with its behaviors being complex and similar to random. However, the seemingly chaotic process is not completely chaotic, there is a fine internal regularity [32]. Chaos optimization is novel because the randomness and ergodicity of chaos could realize local deep search by searching the space near superior individuals even without requirement for the continuity and differentiable properties of the objective function. Consequently, the premature phenomenon will be prevented in this case. The basic idea for chaos to avoid falling into local optimum is to map the chaotic variables linearly into the space of the optimal variables [33]. Also, the traversal range of the chaotic motion is enlarged to the range of the optimization variables. Then the optimization search is completed by the generated chaotic variables. The chaotic search steps in this paper are listed as follows:
- (1)
- Assume h = 0, and map the decision variables zjh, j = 1, 2, …, m into chaotic variables between 0 and 1 for every dimension of the solution, where zmax,j and zmin,j represent the upper and lower search bounds of the jth dimension, m is the dimension number of solution.
- (2)
- Calculate the chaotic variables of next iteration by the following formula:
- (3)
- Transform chaotic variables chjh+1 into decision variable
- (4)
- Evaluate the new solution according to decision variable . If the new solution is better than the initial or the chaotic search has reached the maximum iterations, the new solution will be the result of chaos search, otherwise, set h = h + 1 and turn to the second step.
3.3. Elite Retention Strategy
Elite retention strategy preserves the optimal individual or part of excellent individuals in each iteration, and replaces the worst individuals after next iteration. After this process, the optimal solution is reserved, and the algorithm’s convergence speed is accelerated while the diversity of particles is guaranteed.
In this paper, elite retention strategy was introduced into PSO. The first 20% of the best individuals in each iteration will be chaos searched so as to further excavate the adaptability of excellent individuals and enhance the local search ability. Then the top 10% of the best individuals will be reserved in each iteration and replace the last 10% of the population in next-generation individuals. The proportion of the relatively better individuals in the population is ensured.
3.4. Steps of MCPSO
Steps of the proposed MCPSO in this paper are given as follows while Figure 5 is the flowchart of the algorithm:
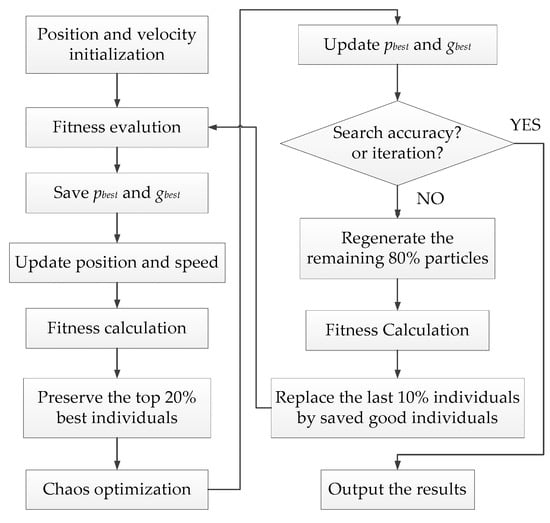
Figure 5.
The flowchart of proposed modified chaos particle swarm optimization (MCPSO) algorithm.
- (1)
- Initialize the position and velocity of each particle in the population.
- (2)
- Evaluate the fitness of each particle; save current particles’ positions and fitness values into pbest of each particle; save the position and fitness value of the optimal individual in current population into gbest.
- (3)
- Update the position and the speed of each particle.
- (4)
- Calculate the objective function value of each particle; preserve the top 20% of the best individuals with the best fitness values.
- (5)
- Search the selected particles with chaos optimization; update pbest and gbest of the population.
- (6)
- If the search accuracy is satisfied or the iteration number is reached, stop the search and output the result, otherwise, turn to step 7.
- (7)
- Regenerate the remaining 80% of the particles; calculate the fitness values and replace the last 10% of the individuals with the worst fitness by the top 10% of the good individuals obtained in step 4 and transfer to step 2 then.
4. Case Studies
4.1. The Framework of Stand-Alone MG
Figure 6 shows the structure of stand-alone MG adopted in this study. The total capacity of battery is 50 kWh and the initial SOC is 50% of the total capacity. Other parameters for battery refer to [34]. PV’s and WT’s rated power are assumed as 250 kW and 300 kW, respectively. Other parameters such as rated power and maximal/minimal power of various DGs are listed in Table 1. The disposal cost for different types of pollutants and the emission factors of MT, DE and FC are summarized in Table 2 [35,36]. It should be noted that the whole simulation takes the situation of thermal load for example.
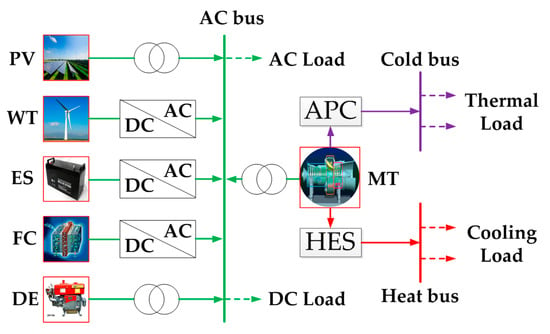
Figure 6.
The structure of stand-alone MG; photovoltaic (PV), wind turbine (WT), MT and energy storage (ES), fuel cell (FC), diesel engine (DE).

Table 1.
Parameters of different distributed generations (DGs); MT: micro-gas turbine.

Table 2.
Pollutant discharge coefficient.
4.2. Results Analysis
Considering the influence from the scenarios, this paper designed four types of scenarios: sunny-working day, sunny-weekend, rainy-working day and rainy-weekend. Diverse characteristics from diverse categories result in the data differences. Working day and weekend mainly cause the differences in load demand because of people’s life style, while the weather property mainly affects the output of WT and PV. The predicted load demand and renewable energy output in four scenarios are shown in Figure 7. It is obvious that the load demand is higher on weekends because of more activities and no work, and the output of PV in rainy days is evidently lower than that of sunny days due to the weak sunshine. In comparison, the output of WT is not as regular as PV whose output concentrates in a certain period (8:00 a.m. to 6:00 p.m. usually) and not such influenced by weather conditions. In other words, there are more fluctuations of WT’s power generation.
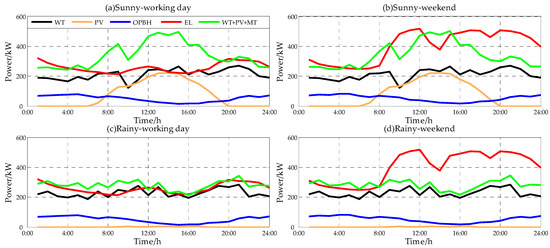
Figure 7.
The load demand and output prediction of renewable energy in four scenarios. OPBH: ordering power by heat; EL: electric load.
MCPSO’s parameters setting are: the iteration of chaos search and MCPSO are 10 and 200, respectively, the particle number is 30, inertia weight is 0.5 and the learning factors are both 2. For renewable energy generations: PV module adopted maximum power point tracking (MPPT) technology in all the dispatch periods. When the sum output of PV, WT and MT (ordering power by heat, OPBH) are greater than the electric load demand, and the battery capacity has reached the upper limit, WT was adjusted to track the actual electric load. For other situations, the WT module also applied MPPT. The four models were solved severally to see the adaptation of the proposed algorithm. The optimization results in different scenarios are shown in Figure 8. Apart from renewable energy generations, the ES, MT, DE, FC and load demand were all dispatched as decision variables in the optimized operation.
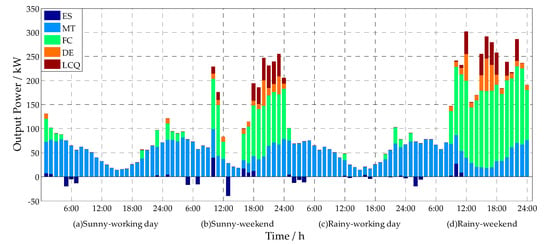
Figure 8.
The dispatch optimization results for MG in each period for four scenarios; LCQ: load cut quantity.
The proposed multi-objective model took load control into account for optimized operation. Figure 9 displays the load control which corresponds to the load cut quantity (LCQ) in detail for different scenarios. From the results, it could be found that the load control in sunny-working day and rainy-working day scenarios concentrates in 1:00~7:00 and 19:00~24:00 periods for the most time. Compared with the load demand and renewable energy output in Figure 7, it can be found that the load control mainly occurs in the period when the renewable power was lacking or the load demand was relatively high. The reason is that for stand-alone MG, controllable DGs such as DE, FC and MT are started to satisfy the load demand when the clean energy is insufficient in order to keep the power balance. If the load compensation was lower than the generation cost of DGs and there were loads that could participate in DR, the energy management system would cut off part of the unimportant load under the guidance of the economic purpose. In contrast, the load control in sunny-weekend and rainy-weekend scenarios was more common, because the load demand on weekend increases and renewable energy could not satisfy the load demand at most times. In addition, low PV output in rainy-weekend further expanded the gap between the load demand and renewable energy output.
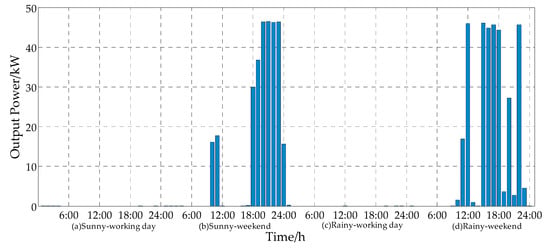
Figure 9.
The LCQ dispatch optimization results for MG in each period for four scenarios.
The SOC variation of ES is related to the total output of renewable energy system and electric load (EL). From Figure 8, it could be seen that the battery were prior to be used in initial period, because it is more economical compared with other micro-sources. After that, the SOC change of battery depends on whether the electric power is surplus when the load demand is ensured. It can be found that sunny-working day, sunny-weekend and rainy-working day scenarios in Figure 7 exist in the condition where the sum of renewable energy and basic output (decided by TL) of MT was greater than the EL demand. Accordingly, the battery output was negative at these times, which represents the charge of battery. For rainy-weekend scenario, the EL was high and PV’s output was low, which led to a situation that the EL was always higher than the sum of renewable energy and basic output of MT, so there was no charge condition after the beginning discharge period.
Figure 8 also reveals that the FC was prior dispatched to the DE within a certain range, because the model took the economic and environmental benefits into account and the FC was more ecofriendly than DE, which was proved by the parameters in Table 2.
According to the optimization strategy, the operation costs of four scenarios at different times for each day are shown in Figure 10. When the sum of renewable energy and basic output of MT was greater or closer to the load demand, the operation cost was relatively low. Otherwise, the cost would increase because of the expenditure from other generation units. Comparing the four scenarios, the costs of sunny-weekend and rainy-weekend were significantly higher than the working days because the load demand was higher on weekend. And the cost of rainy-weekend was higher than sunny-weekend, because the PV output was lower on rainy days.
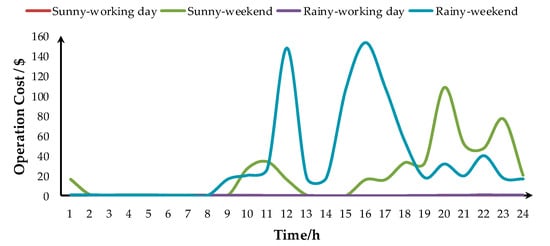
Figure 10.
Operation cost of each period in four scenarios.
4.3. Comparison Analysis
This paper proposed a modified dispatch strategy for CCHP mode without influencing the essential demand and comfort feeling. In order to verify the effectiveness of the modified strategy, simulations with completely same conditions except the strategy of CCHP in four scenarios were conducted and the operation costs were shown in Table 3.

Table 3.
Comparison of the modified and traditional strategy for CCHP.
Through the above comparison, it is obvious that the economic and environmental benefits of MG were improved in the four scenarios while the comfort and primary demand were not destroyed with the modified CCHP dispatch strategy. For example, in the rainy-weekend scenario, the total cost decreased 2.32% at the expense of 0.17% thermal load change. The improved effect was more evident in the weekend scenario because of the wider changeable range resulted from higher load demand.
With the purpose of comparing the effectiveness and overcoming the randomness of different algorithms, PSO, CPSO and MCPSO algorithms were applied to solve the entirely same models in the rainy-weekend scenario for 20 times, and the statistic results are shown in Table 4.

Table 4.
Statistics of different algorithms’ 20 operating results.
From Table 4, it can be seen that the proposed MCPSO obtained the lowest average total cost in 20 times, which indicated the better searching performance and the more excellent convergence ability. The next was the CPSO while the last was PSO. This is because elite retention and chaos search further excavate the best individuals in each iteration. The lowest standard deviation of MCPSO indicated that the algorithm was stable and had a stronger robustness. It is really a great advantage in optimization. MCPSO also had some advantages on average convergence time, because the elite retention strategy could help particles realize the accuracy requirement more quickly.
5. Conclusions
This paper studied the optimized operation problem of a stand-alone MG consisted of WT, PV, MT, FC, DE and ES with the consideration of CL and various scenarios. Based on the CCHP mode of MT, a multi-objective optimization model was established to dispatch the DGs effectively and economically considering four different operation scenarios. A modified dispatch strategy for CCHP was proposed to further strengthen the economy of MG. To solve the optimization model, the chaotic optimization and elite retention strategy were introduced into PSO so as to improve the global search ability and accelerate the convergence speed. Simulation results validated that the presented model and MCPSO could effectively solve the optimization problem for stand-alone MG in different scenarios and the modified strategy could further improve the economic and environmental benefits.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China (grant No. 51577067), the Beijing Natural Science Foundation of China (grant No. 3162033), the Hebei Natural Science Foundation of China (grant No. E2015502060), the State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (grant No. LAPS16007, LAPS16015), the Science & Technology Project of State Grid Corporation of China (SGCC), the Open Fund of State Key Laboratory of Operation and Control of Renewable Energy & Storage Systems (China Electric Power Research Institute) (No. 5242001600FB), the China Scholarship Council. M. Shafie-khah and João P. S. Catalão acknowledge the support by FEDER funds through COMPETE 2020 and by Portuguese funds through FCT, under Projects SAICT-PAC/0004/2015-POCI-01-0145-FEDER-016434, POCI-01-0145-FEDER-006961, UID/EEA/50014/2013, UID/CEC/50021/2013, and UID/EMS/00151/2013, and also funding from the EU 7th Frame-work Programme FP7/2007–2013 under GA No. 309048.
Author Contributions
Fei Wang and Lidong Zhou conceived and designed the experiments; Lidong Zhou, Miadreza Shafie-khah and Zheng Wang performed the experiments; Fei Wang, Lidong Zhou and Bo Wang analyzed the data; Lidong Zhou and Zheng Wang contributed reagents/materials/analysis tools; Lidong Zhou, Fei Wang and João P. S. Catalão wrote the paper.
Conflicts of Interest
The authors declare that the grant, scholarship and/or funding mentioned in the Acknowledgments section do not lead to any conflict of interest. Additionally, the authors declare that there is no conflict of interest regarding the publication of this manuscript.
References
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct Quantile Regression for Nonparametric Probabilistic Forecasting of Wind Power Generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Yu, K.; Ai, Q.; Wang, S.; Ni, J.; Lv, T. Analysis and Optimization of Droop Controller for Microgrid System Based on Small-Signal Dynamic Model. IEEE Trans. Smart Grid 2016, 7, 695–705. [Google Scholar] [CrossRef]
- Pouresmaeil, E.; Mehrasa, M.; Catalão, J.P.S. A Multifunction Control Strategy for the Stable Operation of DG Units in Smart Grids. IEEE Trans. Smart Grid 2015, 6, 598–607. [Google Scholar] [CrossRef]
- Fuangfoo, P.; Meenual, T.; Lee, W.J.; Chompoo-inwai, C. PEA Guidelines for Impact Study and Operation of DG for Islanding Operation. IEEE Trans. Ind. Appl. 2008, 44, 1348–1353. [Google Scholar] [CrossRef]
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition1. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Senjyu, T.; Miyazato, Y.; Yona, A.; Urasaki, N.; Funabashi, T. Optimal Distribution Voltage Control and Coordination with Distributed Generation. IEEE Trans. Power Deliv. 2008, 23, 1236–1242. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting Power Output of Photovoltaic Systems Based on Weather Classification and Support Vector Machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Mi, Z.; Sun, H.; Su, S.; Yang, G. Solar irradiance feature extraction and support vector machines based weather status pattern recognition model for short-term photovoltaic power forecasting. Energy Build. 2015, 86, 427–438. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-term Solar Irradiance Forecasting Model Based on Artificial Neural Network Using Statistical Feature Parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Song, Y.; Xu, Z.; Yang, G. Probabilistic Forecasting of Photovoltaic Generation: An Efficient Statistical Approach. IEEE Trans. Power Syst. 2017, 32, 2471–2472. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Optimal Offering Strategies for Wind Power Producers Considering Uncertainty and Risk. IEEE Syst. J. 2012, 6, 270–277. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Mendes, V.M.F. Influence of Environmental Constraints on Profit-Based Short-Term Thermal Scheduling. IEEE Trans. Sustain. Energy 2011, 2, 131–138. [Google Scholar] [CrossRef]
- Fang, X.; Li, F.; Wei, Y.; Cui, H. Strategic scheduling of energy storage for load serving entities in locational marginal pricing market. IET Gen. Transm. Distrib. 2016, 10, 1258–1267. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic Forecasting of Wind Power Generation Using Extreme Learning Machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, C.; Wang, Y.; Yang, X.; Zhang, X.; Wu, C.; Chen, Y. Relay Protection Coordination Integrated Optimal Placement and Sizing of Distributed Generation Sources in Distribution Networks. IEEE Trans. Smart Grid 2016, 7, 55–65. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Li, X.; Liu, H.; Chen, F.; Liu, B. S-shaped droop control method with secondary frequency characteristics for inverters in microgrid. IET Gener. Transm. Distrib. 2016, 10, 3385–3392. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.D.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Li, H.; McLellan, B.C.; Chen, S.; Li, Y.; Tian, Y. Study on the promotion impact of demand response on distributed PV penetration by using non-cooperative game theoretical analysis. Appl. Energy 2017, 185 Pt 2, 1869–1878. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Tian, R.; Li, H. Combined Impacts of RTP and FIT on Optimal Management for a Residential Micro-Grid. Energy Procedia 2015, 75, 1666–1672. [Google Scholar] [CrossRef]
- Ross, M.; Abbey, C.; Bouffard, F.; Jos, G. Multiobjective Optimization Dispatch for Microgrids with a High Penetration of Renewable Generation. IEEE Trans. Sustain. Energy 2015, 6, 1306–1314. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.; Xu, T.; Li, K.; Shafie-khah, M.; Catalão, J.P.S. The values of market-based demand response on improving power system reliability under extreme circumstances. Appl. Energy 2017, 193, 220–231. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, F.; Hodge, B.M.; Zhang, J.; Li, Z.; Shafie-khah, M.; Catalao, J.P.S. Dynamic Price Vector Formation Model Based Automatic Demand Response Strategy for PV-assisted EV Charging Station. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Vahedi, H.; Noroozian, R.; Hosseini, S.H. Optimal management of MicroGrid using differential evolution approach. In Proceedings of the 7th International Conference on the European Energy Market, Madrid, Spain, 23–25 June 2010; pp. 1–6. [Google Scholar]
- Bao, Z.; Zhou, Q.; Yang, Z.; Yang, Q.; Xu, L.; Wu, T. A Multi Time-Scale and Multi Energy-Type Coordinated Microgrid Scheduling Solution—Part I: Model and Methodology. IEEE Trans. Power Syst. 2015, 30, 2257–2266. [Google Scholar] [CrossRef]
- Li, P.; Xu, D.; Zhou, Z.; Lee, W.J.; Zhao, B. Stochastic Optimal Operation of Microgrid Based on Chaotic Binary Particle Swarm Optimization. IEEE Trans. Smart Grid 2016, 7, 66–73. [Google Scholar] [CrossRef]
- Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Scheduling of demand side resources using binary particle swarm optimization. IEEE Trans. Power Syst. 2009, 24, 1173–1181. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R. Power Management Strategies for a Microgrid with Multiple Distributed Generation Units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Abbes, D.; Martinez, A.; Champenois, G. Eco-design optimisation of an autonomous hybrid wind-photovoltaic system with battery storage. IET Renew. Power Gener. 2012, 6, 358–371. [Google Scholar] [CrossRef]
- Azmy, A.M.; Erlich, I. Online optimal management of PEM Fuel cells using neural networks. IEEE Trans. Power Deliv. 2005, 20, 1051–1058. [Google Scholar] [CrossRef]
- Noroozian, R.; Vahedi, H. Optimal management of MicroGrid using Bacterial Foraging Algorithm. In Proceedings of the 18th Iranian Conference on Electrical Engineering, Isfahan, Iran, 11–13 May 2010; pp. 895–900. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Kaddoum, G. Wireless Chaos-Based Communication Systems: A Comprehensive Survey. IEEE Access 2016, 4, 2621–2648. [Google Scholar] [CrossRef]
- Kocarev, L.; Szczepanski, J.; Amigo, J.M.; Tomovski, I. Discrete Chaos-I: Theory. IEEE Trans. Circuits Syst. I 2006, 53, 1300–1309. [Google Scholar] [CrossRef]
- Diaf, S.; Diaf, D.; Belhamel, M.; Haddadi, M.A. Louche, A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy 2007, 35, 5708–5718. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Willingham, M.; Rahman, S. Implications of on-site distributed generation for commercial/industrial facilities. IEEE Trans. Power Syst. 2005, 20, 206–212. [Google Scholar] [CrossRef]
- Bernow, S.; Marron, D. Valuation of Environmental Externalities for Energy Planning and Operations; Tellus Institute Report 90-SB01; Tellus Institute: Boston, MA, USA, May, 1990. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).