Discrimination of Aortic and Pulmonary Components from the Second Heart Sound Using Respiratory Modulation and Measurement of Respiratory Split
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
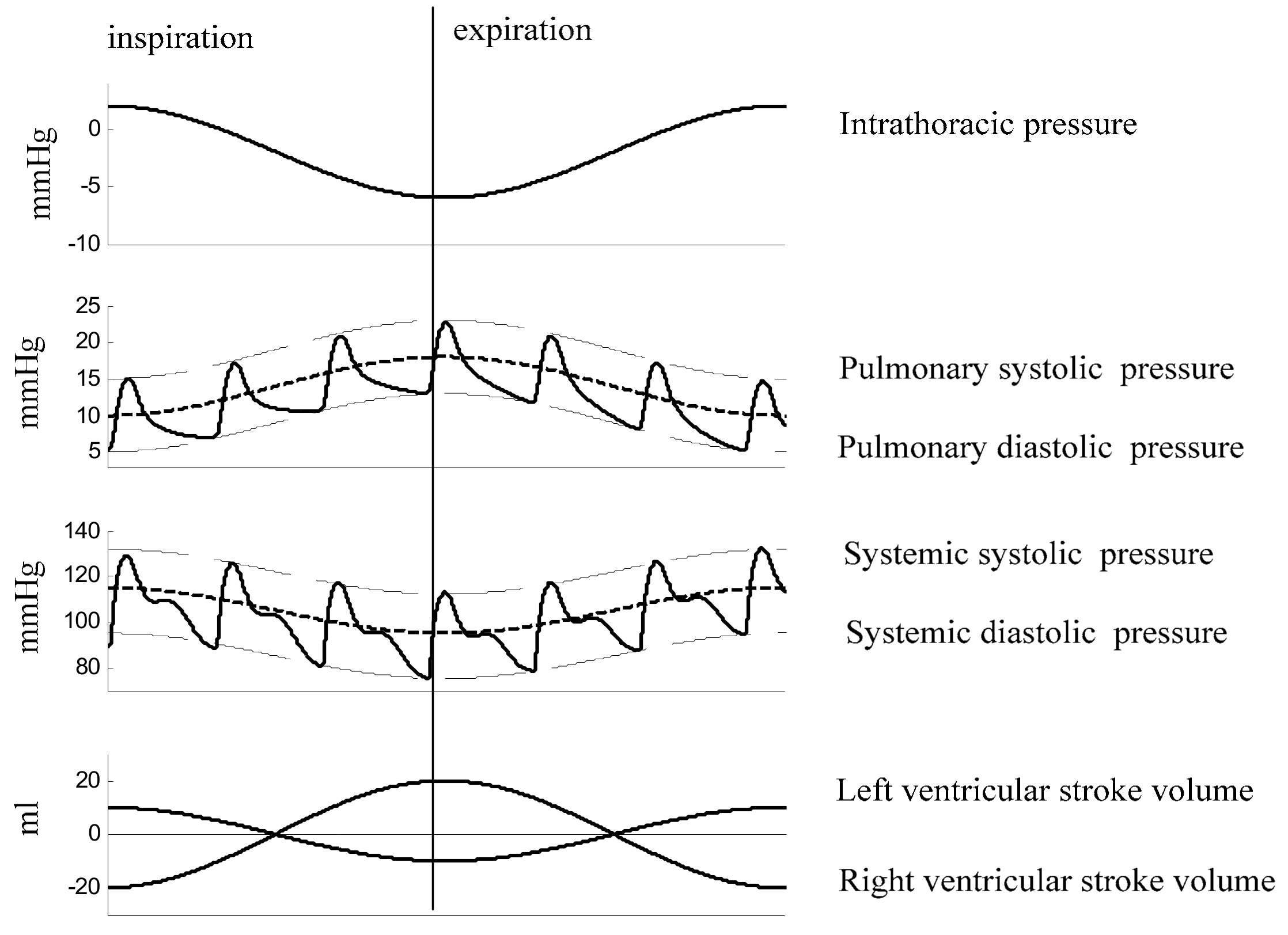
2.1. Physiology of Respiratory Split in S2
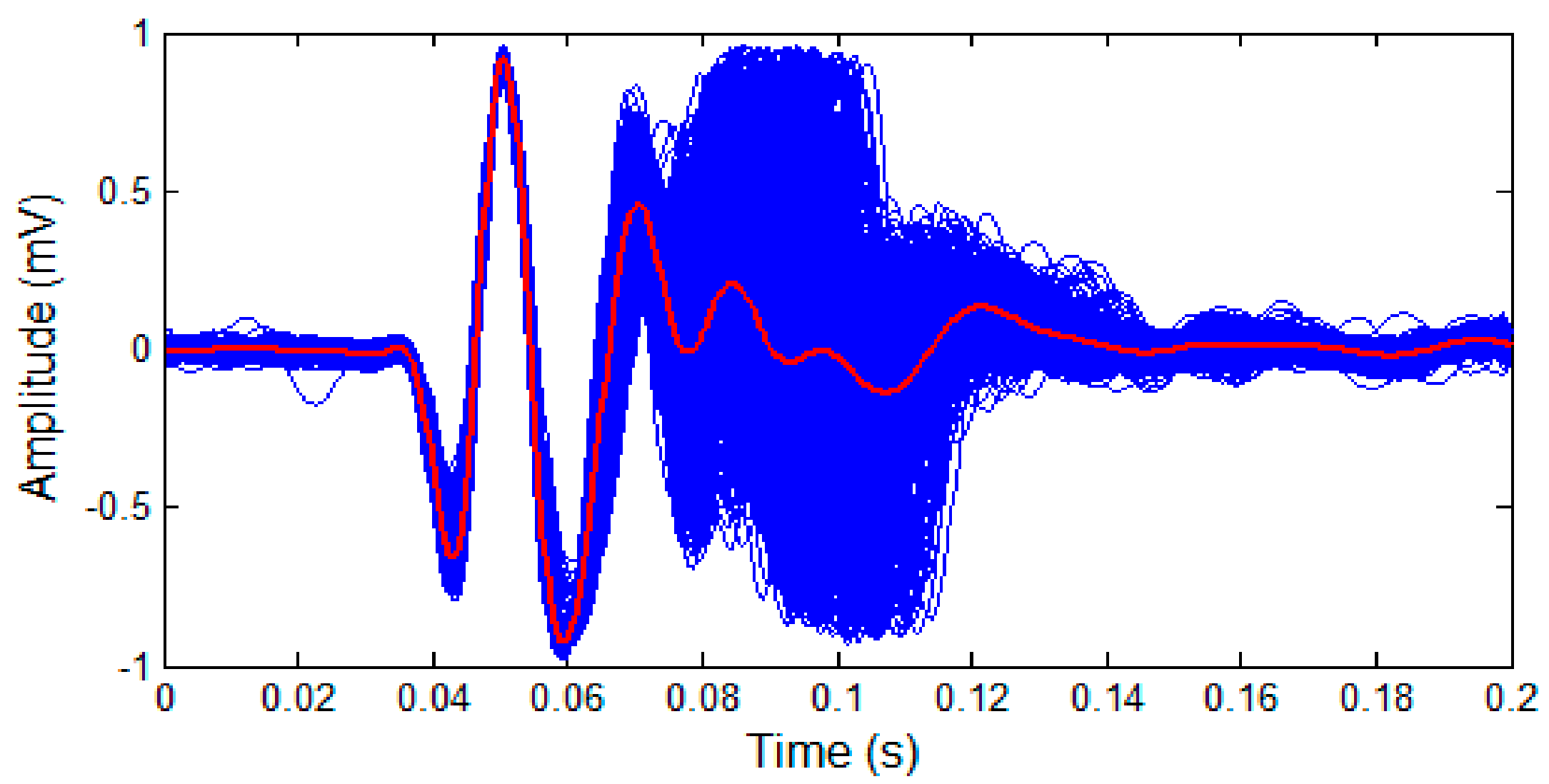
2.2. Data Collection
2.3. System Overview
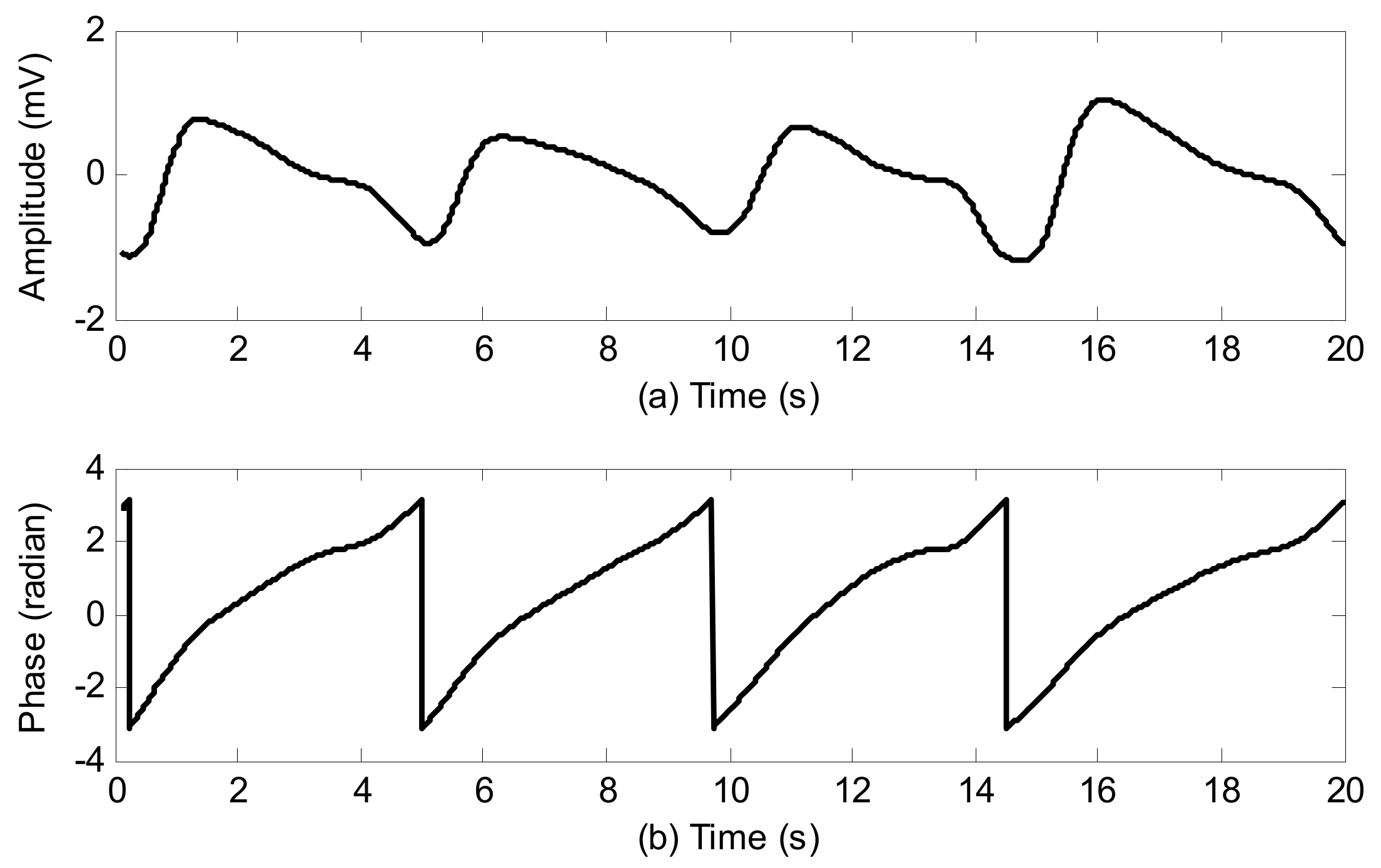
2.4. Respiratory Phase
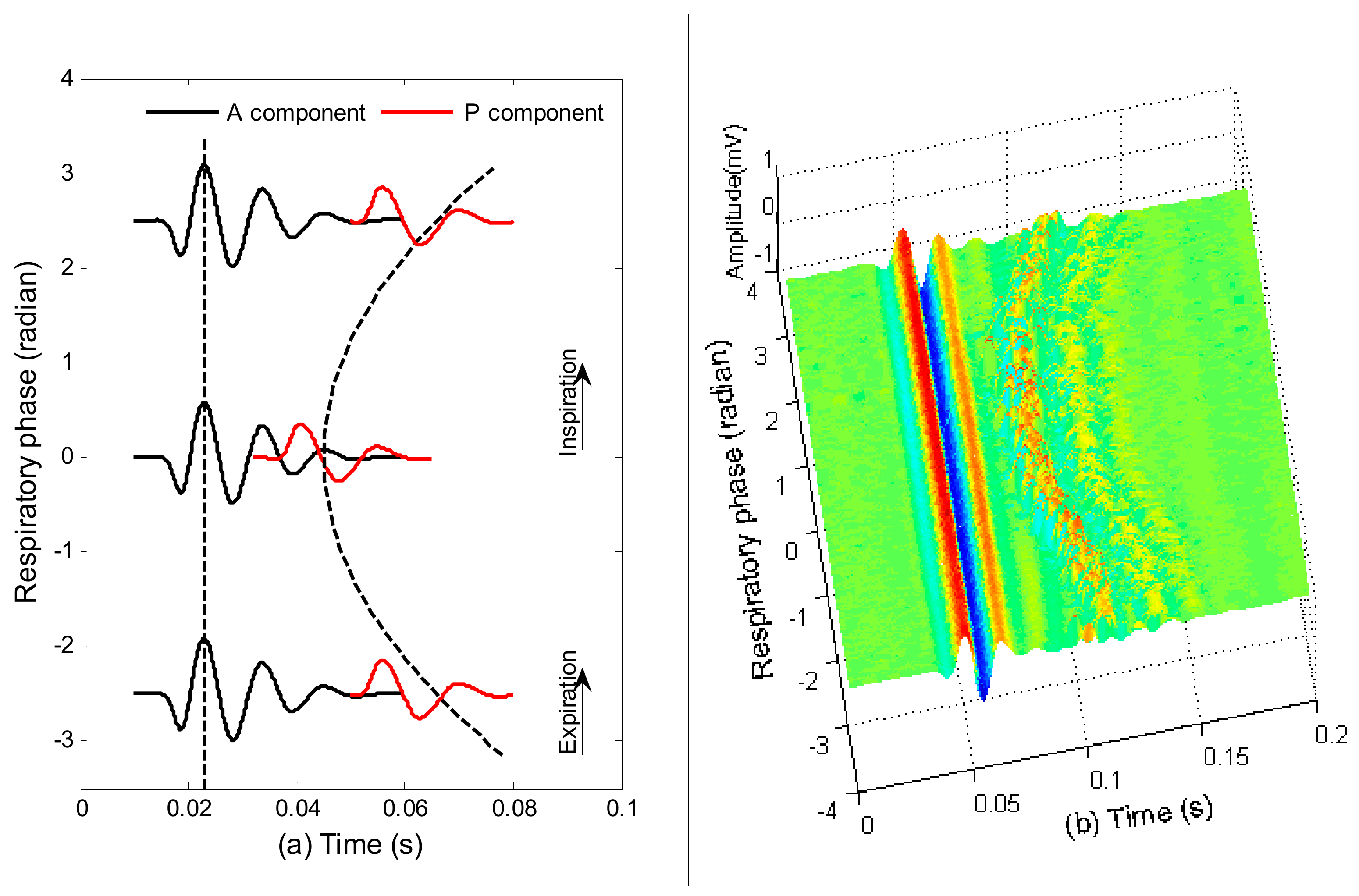
2.5. Investigation on S2 Waveform Changing Modulated by Respiration
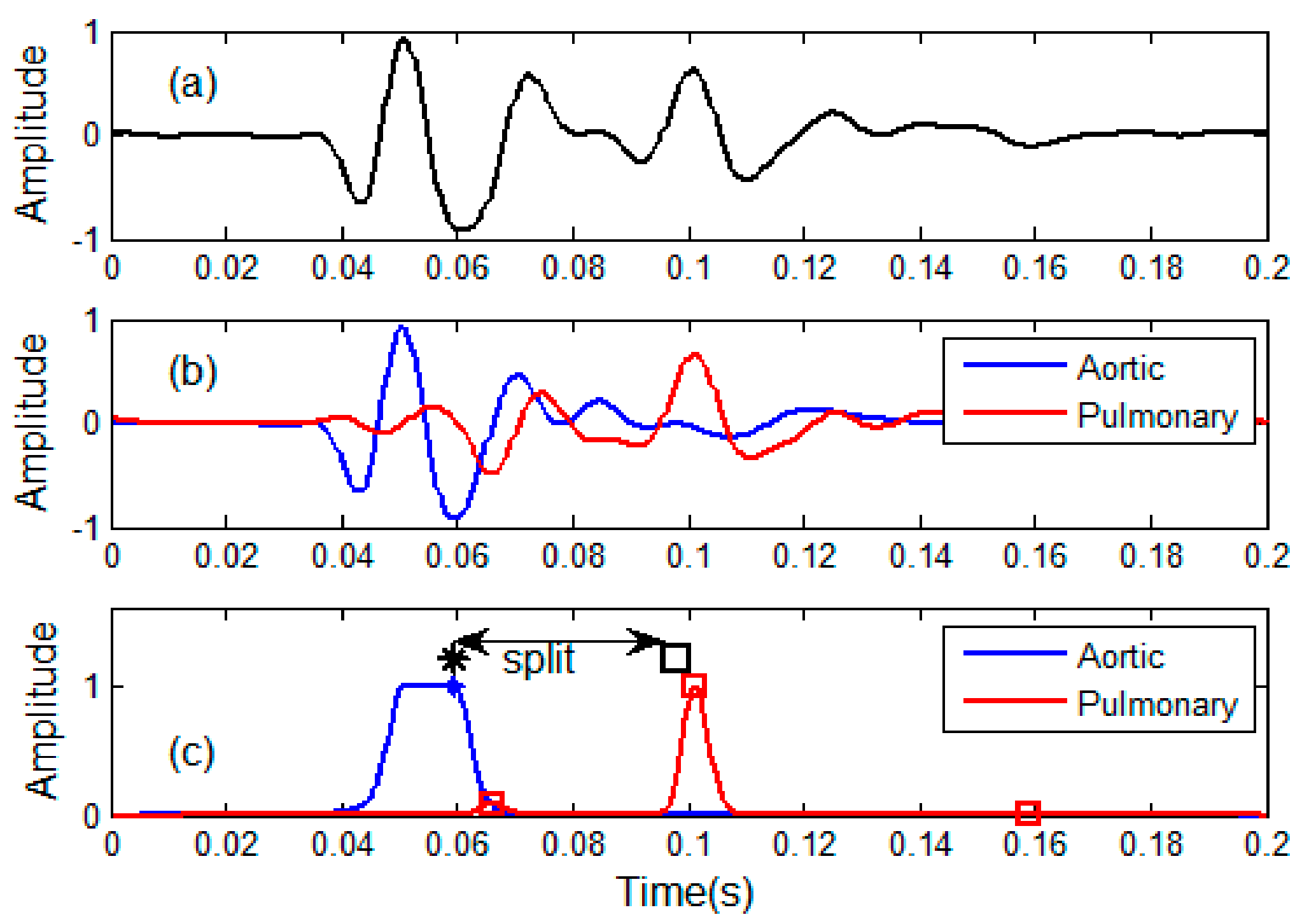
2.6. Discrimination of Aortic and Pulmonary Component
- (1)
- is assumed to have a fixed waveform over the respiratory phase, as can been seen in Figure 6.
- (2)
- is the time shifted version of . It is a delayed pulmonary component caused by respiration.
- (3)
- is assumed to be zero mean both over time and over respiratory phase, i.e., and . It may be colored, non-Gaussian and non-stationary.
2.7. Estimation of Time Indices
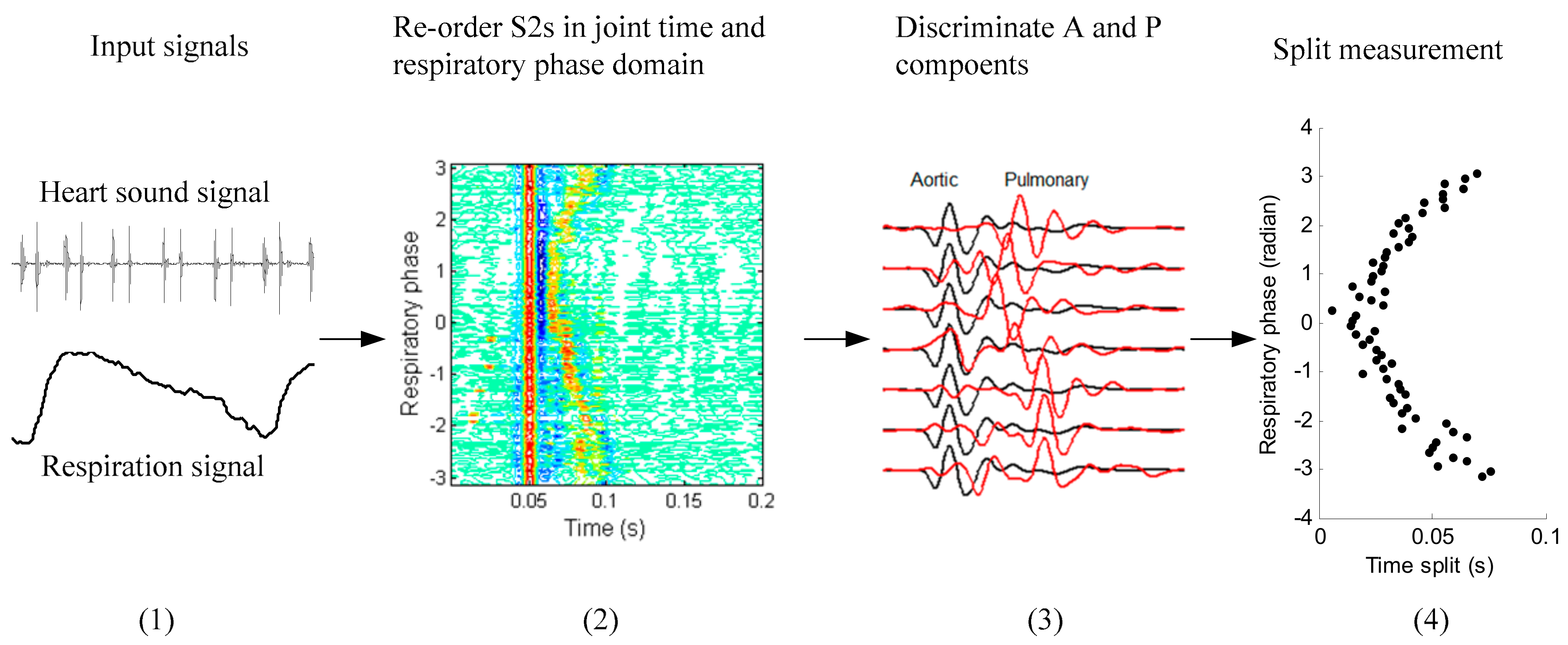
2.8. Steps to Implement the Method
- (1)
- Heart sound signal, respiratory signal and lead-II ECG signal are synchronously collected from a subject.
- (2)
- Extracted respiratory phase from the respiratory signal as given in Section 2.4.
- (3)
- Segmented all S2s from the heart sound signal and looked up the associated respiratory phase for each S2.
- (4)
- The S2s are re-ordered with respiratory phase in ascending order in joint time and respiratory phase domain.
- (5)
- The S2s are re-aligned in time domain.
- (6)
- Estimated the aortic component by average operation as shown in Section 2.6.
- (7)
- Estimated the pulmonary components by subtracting.
- (8)
- Estimated the split by weighted peak positions as given in Section 2.7.
3. Experiments and Discussions
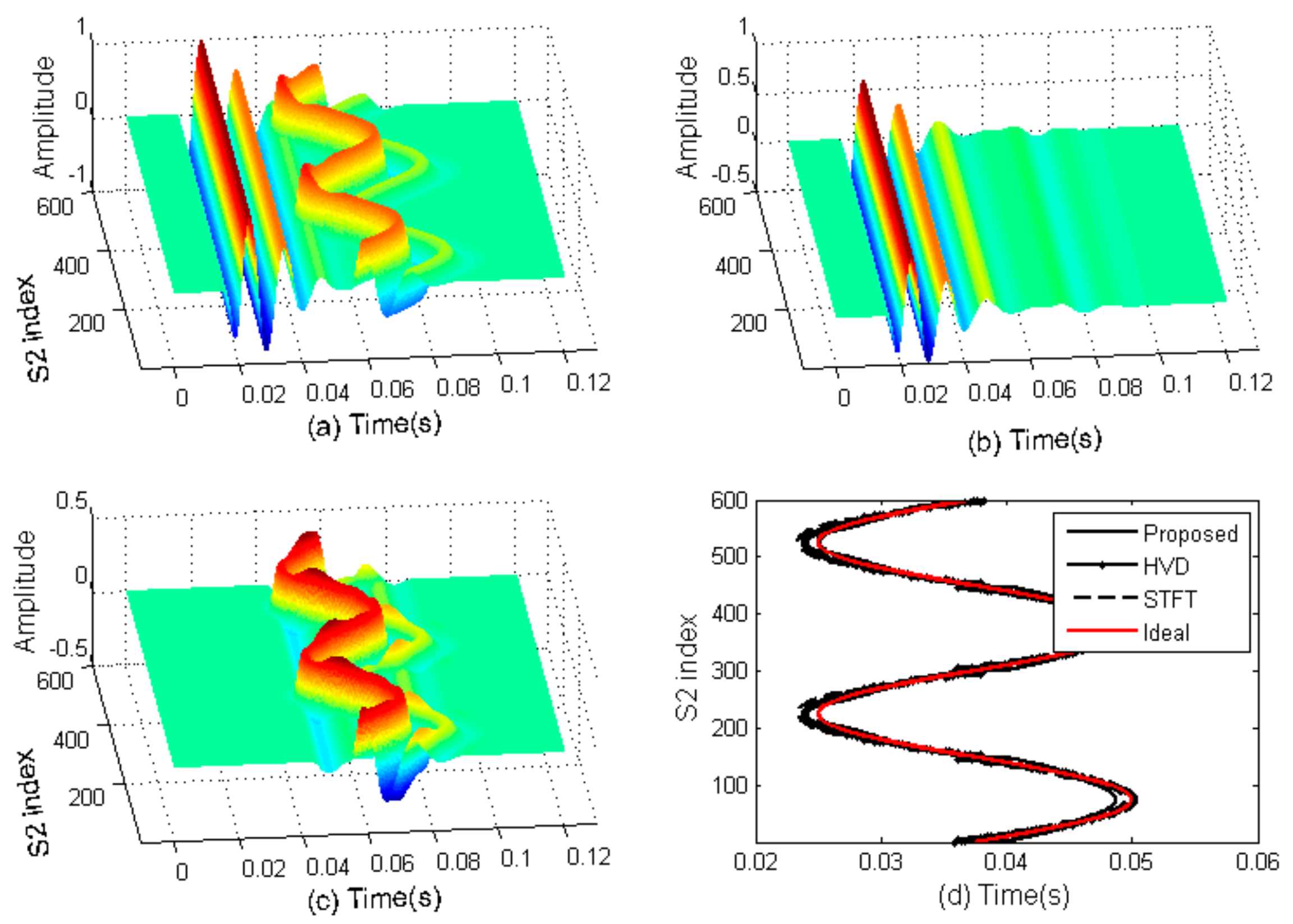
3.1. Computer Simulation
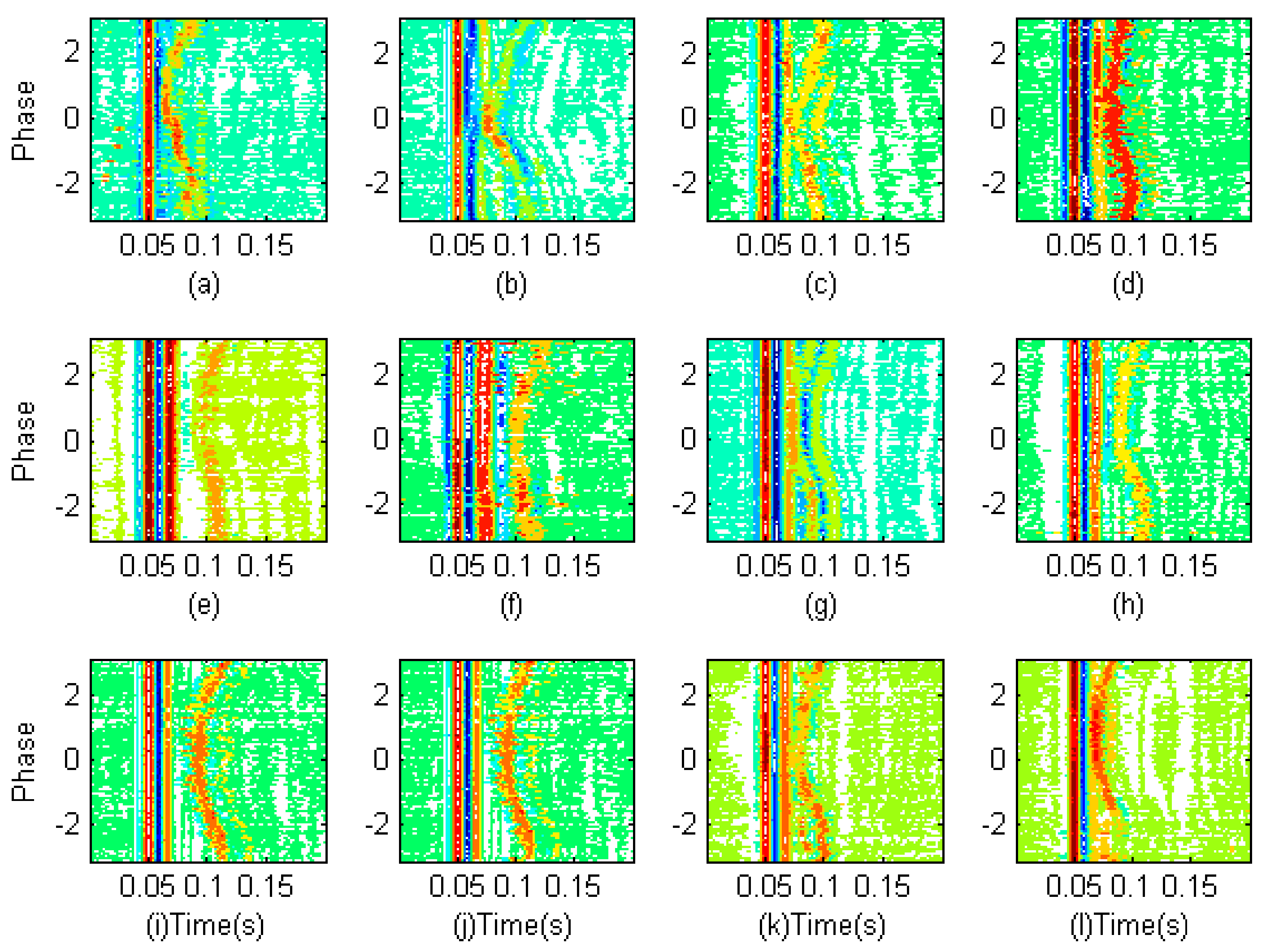
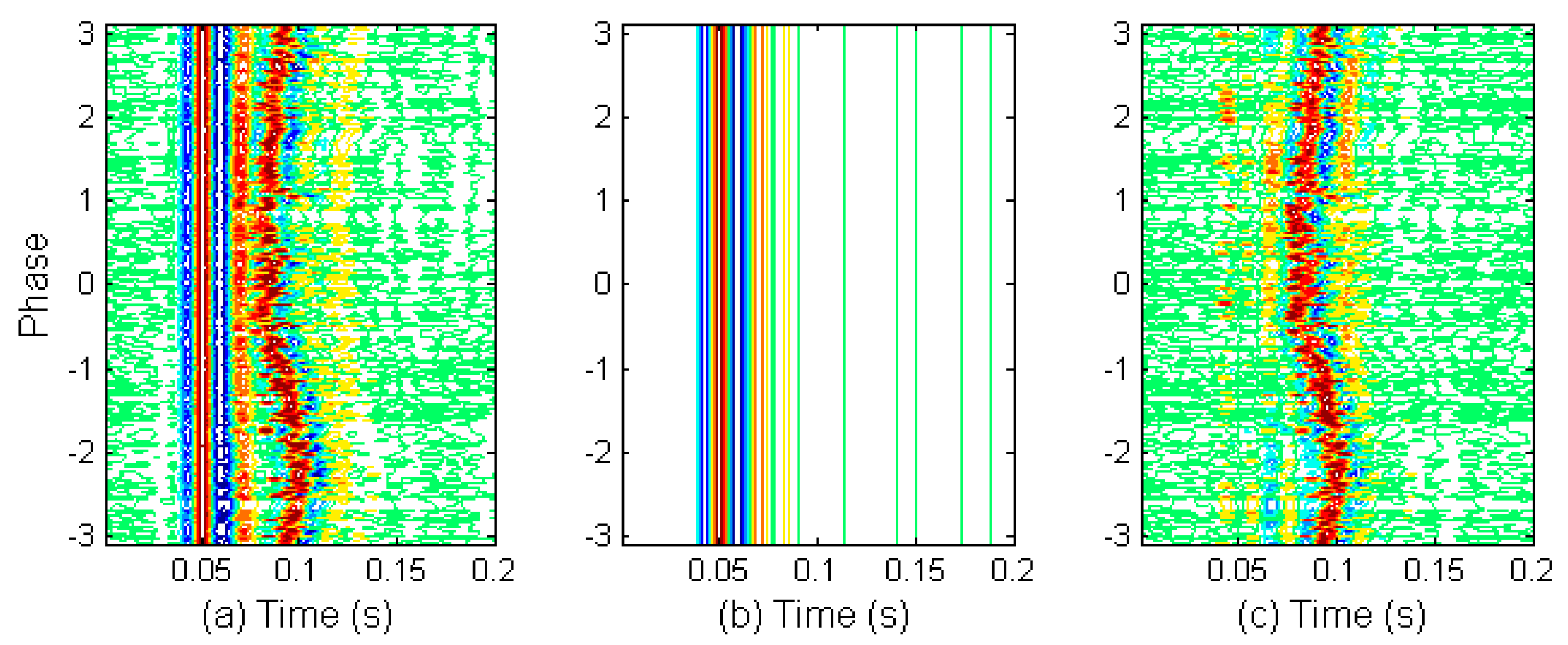
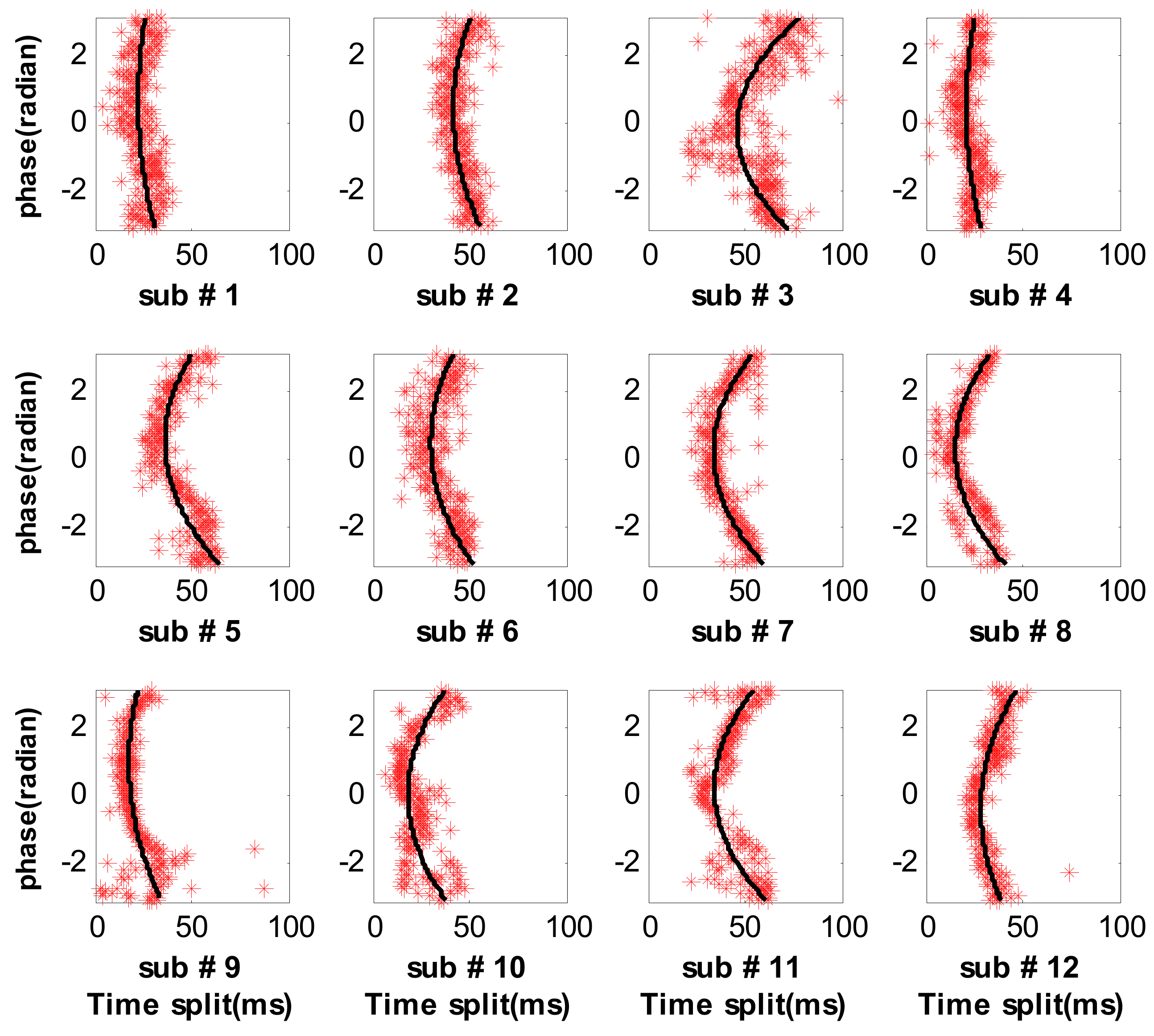
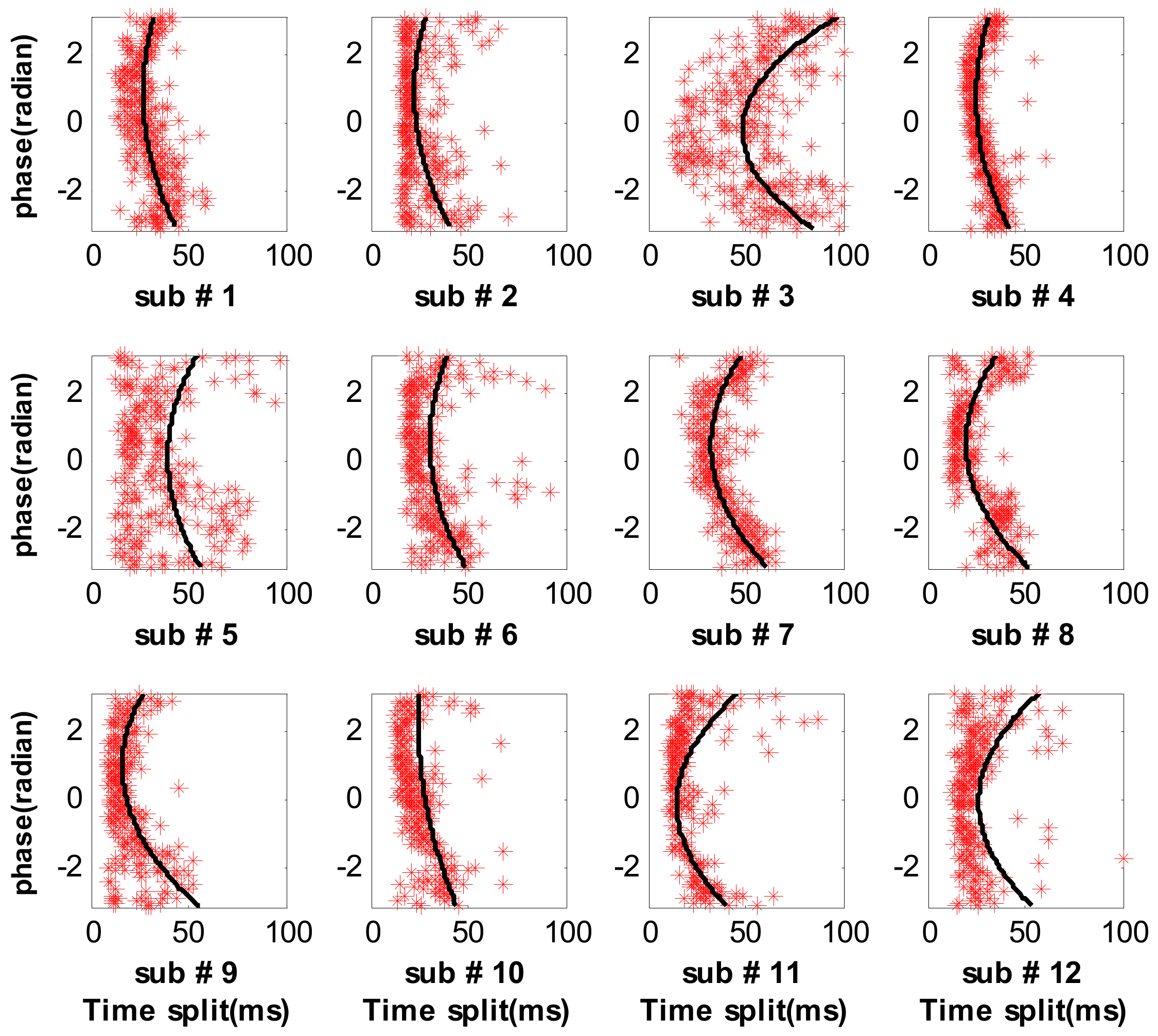
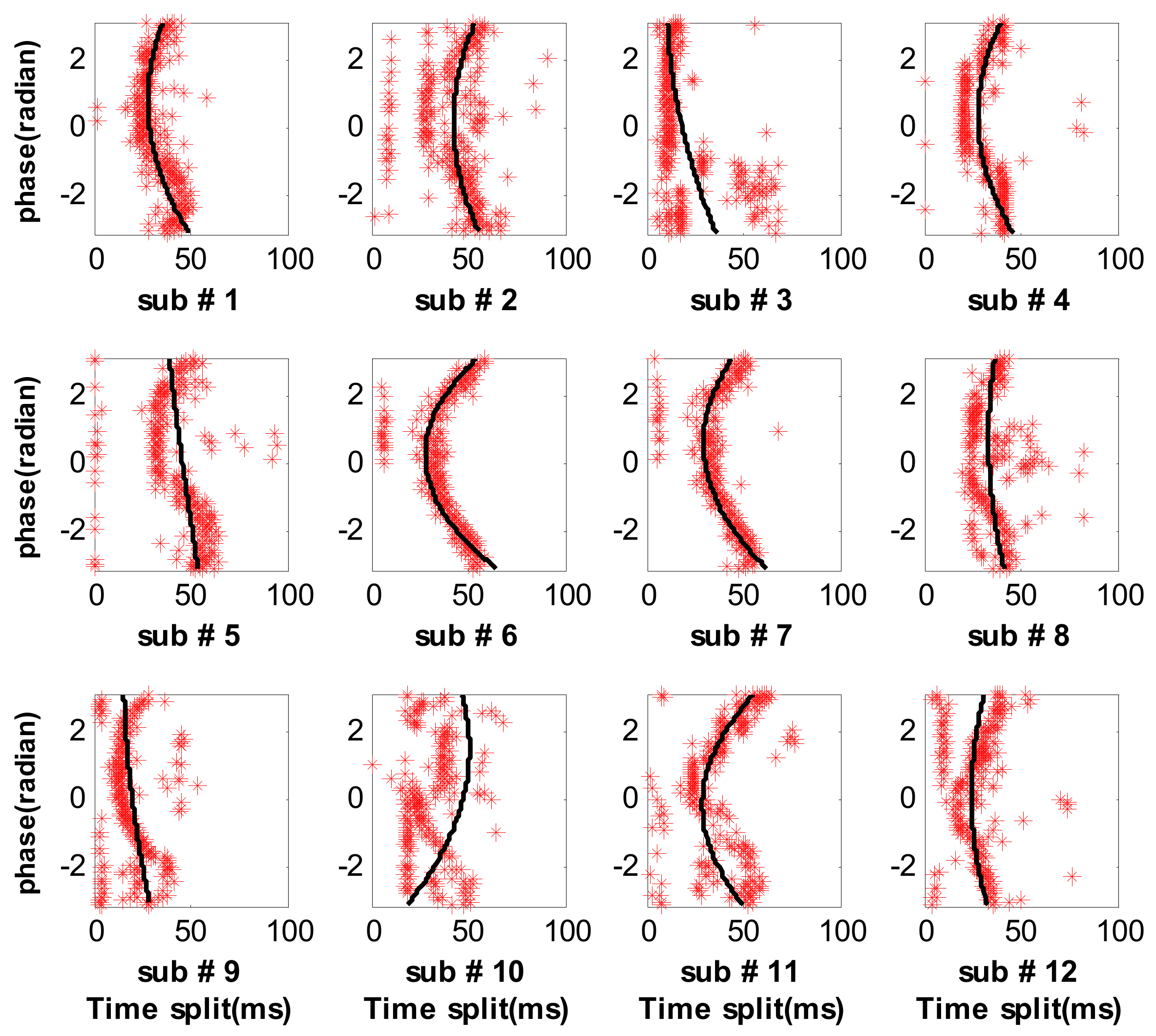
3.2. Measure Respiratory Variations for Human Subjects by the Proposed Method
3.3. Measure Respiratory Variations for Human Subjects by the Previous Methods
3.4. Effect of the Number of S2s
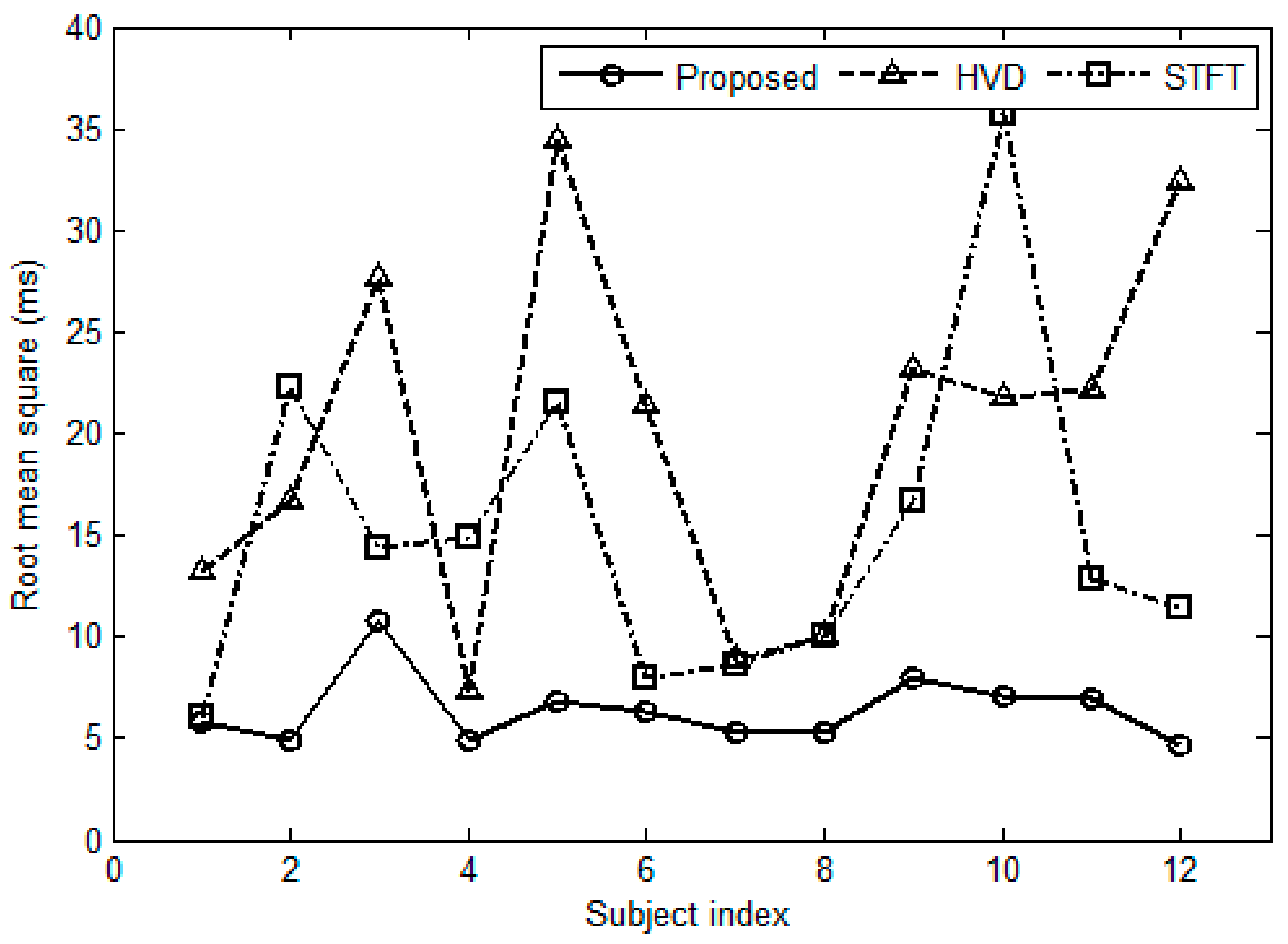
3.5. Comparisons in Computation Complexity
3.6. Limitations of the Proposed Method
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Luisada, A.A.; Liu, C.K.; Aravanis, C.; Testelli, M.; Morris, J.; Chicago, B.A. On the mechanism of production of the heart sounds. Am. Heart J. 1958, 55, 383–399. [Google Scholar] [CrossRef]
- Piemme, T.E.; Barnett, G.O.; Dexter, L. Relationship of heart sounds to acceleration of blood flow. Circ. Res. 1966, 18, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Durand, L.-G.; Pibarot, P. Extraction of the aortic and pulmonary components of the second heart sound using a nonlinear transient chirp signal model. IEEE Trans. Biomed. Eng. 2001, 48, 277–283. [Google Scholar] [PubMed]
- Leung, T.S.; White, P.R.; Cook, J.; Collis, W.B.; Brown, E.; Salmon, A.P. Analysis of the second heart sound for diagnosis of pediatric heart disease. IEE Proc.-Sci. Meas. Technol. 1998, 145, 285–290. [Google Scholar] [CrossRef]
- Djebbari, A.; Reguig, F. Smoothed pseudo wigner-ville distribution of normal and aortic stenosis heart sounds. J. Mech. Med. Biol. 2005, 5, 415–428. [Google Scholar] [CrossRef]
- Djebbari, A.; Bereksi-Reguig, F. Detection of the valvar split within the second heart sound using the reassigned smoothed pseudo Wigner-Ville distribution. Biomed. Eng. Online 2013, 12, 37–57. [Google Scholar] [CrossRef] [PubMed]
- Barma, S.; Chen, B.; Man, K.L.; Wang, J. Quantitative measurement of split of the second heart sound. IEEE Trans. Comput. Biol. Bioinform. 2015, 12, 851–860. [Google Scholar] [CrossRef] [PubMed]
- Feldman, M. Hilbert Transform Application in Mechanical Vibration; John Wiley Sons, Ltd.: West Sussex, UK, 2011; pp. 23–28. [Google Scholar]
- Augen, F.; Flandrin, P.; Lin, Y.; Mclaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H. Time-frequency reassignment and synchrosqueezing. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Castle, P.F.; Jones, K. The mechanism of respiratory variation in splitting of the second heart sound. Circulation 1961, 24, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, K.; Tamura, T. Study of respiratory influence on the intensity of heart sound in normal subjects. Angiology 1979, 30, 750–755. [Google Scholar] [CrossRef] [PubMed]
- Amit, G.; Gavriely, N.; Intrator, N. Cluster analysis and classification of heart sounds. Biomed. Signal Process. Control 2009, 4, 26–36. [Google Scholar] [CrossRef]
- Amit, G.; Shukha, K.; Gavriely, N.; Intrator, N. Respiratory modulation of heart sound morphology. Am. J. Physiol. Heart Circ. Physiol. 2009, 296, H796–H805. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Gao, J.; Ruan, C.; Qiu, T.; Park, Y. Modeling of heart sound morphology and analysis of the morphological variations induced by respiration. Comput. Boil. Med. 2013, 43, 1637–1644. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Lukkarimen, S.; Hartimo, I. Heart sound segmentation algorithm based on heart sound envelogram. Comput. Cardiol. 1997, 24, 105–108. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 454, 903–995. [Google Scholar] [CrossRef]

| Subject No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Num. of Cardiac cycles | 344 | 331 | 360 | 367 | 290 | 311 |
| Subject No. | 7 | 8 | 9 | 10 | 11 | 12 |
| Num. of Cardiac cycles | 299 | 281 | 312 | 285 | 286 | 301 |
| Subject Index | Indicator | HVD Method [7] (ms) | STFT Method [4] (ms) | Proposed Method (ms) |
|---|---|---|---|---|
| 1 | mean | (−1.40, 1.40) | (−0.64, 0.64) | (−0.61, 0.61) |
| std | (12.30, 14.29) | (5.60, 6.50) | (5.36, 6.23) | |
| 2 | mean | (−1.80, 1.80) | (−2.40, 2.40) | (−0.52, 0.52) |
| std | (15.48, 18.04) | (20.66, 24.08) | (4.50, 5.25) | |
| 3 | mean | (−2.85, 2.85) | (−1.48, 1.48) | (−1.11, 1.11) |
| std | (25.70, 29.76) | (13.38, 15.49) | (10.05, 11.64) | |
| 4 | mean | (−0.75, 0.75) | (−1.52, 1.52) | (−0.50, 0.50) |
| std | (6.78, 7.83) | (13.80, 15.95) | (4.52, 5.23) | |
| 5 | mean | (−3.97, 3.97) | (−2.48, 2.48) | (−0.78, 0.78) |
| std | (31.78, 37.42) | (19.84, 23.37) | (6.25, 7.35) | |
| 6 | mean | (−2.37, 2.37) | (−0.88, 0.88) | (−0.70, 0.70) |
| std | (19.76, 23.13) | (7.33, 8.58) | (5.85, 6.85) | |
| 7 | mean | (−1.01, 1.01) | (−0.97, 0.97) | (−0.60, 0.60) |
| std | (8.20, 9.66) | (7.93, 9.31) | (4.93, 5.80) | |
| 8 | mean | (−1.18, 1.18) | (−1.17, 1.17) | (−0.62, 0.62) |
| std | (9.25, 10.93) | (9.18, 10.85) | (4.88, 5.76) | |
| 9 | mean | (−2.58, 2.58) | (−1.86, 1.86) | (−0.88, 0.88) |
| std | (21.47, 25.13) | (15.45, 18.09) | (7.34, 8.59) | |
| 10 | mean | (−2.52, 2.52) | (−4.14, 4.14) | (−0.83, 0.83) |
| std | (20.01, 23.60) | (32.84, 38.73) | (6.57, 7.75) | |
| 11 | mean | (−2.57, 2.57) | (−1.49, 1.49) | (−0.81, 0.81) |
| std | (20.41, 23.60) | (11.86, 13.98) | (6.46, 7.61) | |
| 12 | mean | (−3.67, 3.67) | (−1.28, 1.29) | (−0.53, 0.53) |
| std | (29.94, 35.15) | (10.55, 12.39) | (4.33, 5.09) |
| Subject Index | Number of S2s | HVD Method [7] | STFT Method [4] | Proposed Method | |||
|---|---|---|---|---|---|---|---|
| CPUtime (s) | RMSerror (ms) | CPUtime (s) | RMSerror (ms) | CPUtime (s) | RMSerror (ms) | ||
| 1 | 344 | 942.1 | 13.2 | 11.5 | 6.0 | 1.3 | 5.8 |
| 2 | 331 | 948.1 | 16.7 | 11.4 | 22.3 | 1.2 | 4.9 |
| 3 | 360 | 971.4 | 27.7 | 11.6 | 14.3 | 1.2 | 10.8 |
| 4 | 367 | 981.1 | 7.3 | 13.1 | 14.8 | 1.1 | 4.9 |
| 5 | 290 | 830.1 | 34.5 | 10.1 | 21.5 | 0.9 | 6.8 |
| 6 | 311 | 843.3 | 21.4 | 10.6 | 7.9 | 1.0 | 6.3 |
| 7 | 299 | 799.3 | 8.9 | 10.2 | 8.6 | 0.9 | 5.4 |
| 8 | 281 | 773.5 | 10.1 | 9.5 | 10.0 | 0.9 | 5.3 |
| 9 | 312 | 847.3 | 23.2 | 10.4 | 16.7 | 0.9 | 7.9 |
| 10 | 285 | 776.7 | 21.7 | 9.7 | 35.7 | 0.9 | 7.1 |
| 11 | 286 | 765.3 | 22.2 | 10.4 | 12.9 | 0.9 | 7.0 |
| 12 | 301 | 804.2 | 32.4 | 10.2 | 11.4 | 1.0 | 4.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, H.; Chen, H.; Li, T. Discrimination of Aortic and Pulmonary Components from the Second Heart Sound Using Respiratory Modulation and Measurement of Respiratory Split. Appl. Sci. 2017, 7, 690. https://doi.org/10.3390/app7070690
Tang H, Chen H, Li T. Discrimination of Aortic and Pulmonary Components from the Second Heart Sound Using Respiratory Modulation and Measurement of Respiratory Split. Applied Sciences. 2017; 7(7):690. https://doi.org/10.3390/app7070690
Chicago/Turabian StyleTang, Hong, Huaming Chen, and Ting Li. 2017. "Discrimination of Aortic and Pulmonary Components from the Second Heart Sound Using Respiratory Modulation and Measurement of Respiratory Split" Applied Sciences 7, no. 7: 690. https://doi.org/10.3390/app7070690
APA StyleTang, H., Chen, H., & Li, T. (2017). Discrimination of Aortic and Pulmonary Components from the Second Heart Sound Using Respiratory Modulation and Measurement of Respiratory Split. Applied Sciences, 7(7), 690. https://doi.org/10.3390/app7070690






