1. Introduction
Long-span structures, e.g., footbridges, have become prevalent all over the world, and the excessive dynamic vibrations induced by locomotive crowds are a crucial maintenance concern for their life span. Full-scale dynamic measurements on service structures has shown that humans can change structural vertical dynamic properties [
1,
2], which has also been confirmed by a measurement experiment on a beam bearing different numbers of persons in Shahabpoor et al. [
3]. To explain the vibration mechanism induced by humans, some human-structure models have been proposed, including a one-person model [
4,
5] and a crowd model [
6,
7,
8,
9]. Zhou et al. [
6,
7] studied vertical dynamic characteristics of structure under a modeled human oscillator. Caprani and Ahmadi [
8] proposed a moving oscillator to simulate walking pedestrians and further studied the influence of structure frequency and damping variations. It is noted that crowd size may significantly affect variation of the dynamic properties of footbridges. Some crowd-structure interaction models have also been proposed to explore this mechanism. Nimmen et al. [
9] proposed two reduced-order models to approximate the dynamic behavior of a full-order coupled crowd-structure interaction system. Alonso et al. [
10] also recommended a vertical crowd-structure interaction model to analyze the effect of modal properties variations of a footbridge. To consider gait details, a human-structure interaction with bipedal pedestrian model was proposed by Qin et al. [
4,
5]. Gao and Yang [
11,
12,
13] extended this model to a crowd-structure interaction, based on a stability improvement technique. Although the bipedal pedestrian model is successfully applied for crowd-structure interaction in Gao and Yang [
11,
12,
13], the theoretical mechanisms between crowd size and structural modal properties by using this model have not yet been reported. Shahabpoor et al. [
3] studied the effect of crowd size on vertical modal parameters of an occupied structure by extensive Frequency Response Function (FRF)-based modal identification tests. Although they quantitatively researched the impact of the number of occupants on structural dynamic properties, one applicable formula which includes human dynamic properties for vibrational control between crowd scale and structural modal characteristics, is absent. Considering that the dynamic properties of humans are crucial to elucidating the variation of structural modal properties, it is therefore imperative to provide a quantitative estimation between crowd size and modal properties of structure.
In this paper, the theoretical formulae between crowd size and vertical modal properties are proposed as an extension of the study in Gao and Yang [
11,
12,
13]. Firstly, the dynamic equilibrium equation of a structure is established by considering the vertical interaction between bipedal crowd and structure. Secondly, an assumed uniform distribution of a walking crowd is used to calculate the crowd size by Taylor Expansion. Thirdly, the theoretical modal property formulas are derived, based on the assumption of a synchronous movement behavior. Finally, a numerical example is used to analyze the effect of crowd size on structural modal properties.
2. Dynamic Excitation Mechanism
The bipedal pedestrian structure system [
13] is shown in
Figure 1. The left end of the beam is defined as the origin of a planar coordinate system
x-0-
z;
LB is span length;
is the lump mass of the bipedal model; the superscript “
q” means the ordinal number of pedestrians;
and
are longitudinal and vertical displacements of the center of mass (CoM), respectively;
and
are the trialing and leading footholds positions, respectively;
and
are structural vertical displacements in the leading and trialing footholds, respectively.
By only considering the first modal property, the dynamic Equation (8a) from the study [
13] can be rewritten as:
where
is modal mass of structure;
and
are the damping ratio and circular frequency of structure, respectively;
,
and
are general displacement, velocity and acceleration, respectively;
and
are the structural modal [
13]. The tensor symbols
and
are shown as
The leading and trailing leg damping coefficients are shown as
where
and
are the leading and trialing leg damping, respectively;
and
are the leading and trialing leg lengths, respectively. The expressions of
,
,
and
can be found in the study [
13]. The tensor product
is shown as:
where
and
are given by
and
are the stiffness of leading and trialing legs, respectively.
is the relaxed length of the leg. Substituting Equations (2)–(7) into Equation (1), the dynamic equation of a crowd-structure system can be expressed as:
where
and
are the damping ratio and circular frequency of the structure induced by humans;
is the structure frequency induced by humans;
is the excited force. These are obtained by:
where
and
are fundamental frequency and damping of structure without including the crowd effect;
and
are given by Equation (12).
In general, the most unfavorable excitation induced by humans is that all pedestrians simultaneously walk with a uniform gait. It is very important for engineers to work out how to resist excessive vibration under this excitation. Calculating the dynamic properties induced by uniform excitation is necessary to control the excessive vibration of the structure. A further simplification is made in following section, so that the qualitative relationships between crowd size and modal properties can be estimated.
3. Excitation Assumption
All pedestrians are assumed to be uniformly distributed on a footbridge deck, without an overlap, as shown in
Figure 2. Additionally, pedestrians are assumed to be moving with consistent walking behavior and that they have the same dynamic properties. For simplicity, the superscript “(
q)” is omitted in the following contents. Each pedestrian is assumed to walk in a fixed position, as shown in
Figure 3. To be more specific, each pedestrian’s walking behavior is similar to the movement on a treadmill. The numbers of pedestrians in longitudinal and lateral directions are
Nx and
Ny, respectively. The total number of pedestrians can be obtained with
.
Considering the step length
is much less than the structure span
, the models of two footholds are approximated as:
Without considering leg compression, the lengths of two legs are kept as the original length. Based on the above assumption, the damping parameters
can be approximated by:
where
is the damping of leg. The
in Equation (10) is calculated by
where
is vertical vibration amplitude of CoM and
is leg stiffness.
,
and
are calculated by Equations (18)–(20), respectively.
The
is simplified by employing the Taylor expansion as:
Similarly, the
is approximated as:
Substituting Equations (16) and (21) into Equation (9), the system damping ratio induced by the crowd can be estimated as:
Similarly, by substituting Equations (17) and (21) into Equation (10), the system frequency induced by crowd is:
By substituting Equations (18)–(20) and (22) into Equation (11), the system excitation force induced by the crowd is calculated by:
Longitudinal movement velocity of the CoM is approximated to follow cosine [
14]. The velocity of the CoM is at its highest when the CoM is approximately located at the mid-position between two footholds. In this study, longitudinal velocity of the CoM is defined as:
where
is the period of stepping;
is the varying amplitude of the CoM velocity around mean velocity. Longitudinal displacement of the CoM can be obtained by Equation (27) after integration with Equation (26)
When the supporting leg is upright in the single stance phase, the CoM reaches the summit in the vertical direction. When the CoM is located at the mid-position between two footholds, it reaches the lowest place in the vertical direction [
14]. The vertical movement trajectory of the CoM is approximately sinusoidal and its expression is defined as:
where
is the compression deformation of the leg, induced by gravitational effect;
is the vertical change amplitude of the CoM. The vertical vibration amplitude of the CoM
can be obtained by:
Vertical velocity of the CoM can be obtained after a derivative operation to Equation (30) as:
Substituting Equations (26)–(30) into Equations (23)–(25), the damping ratio, frequency and excitation of the structure induced by the crowd can be expressed as:
where
is step frequency.
The damping ratio of Equation (31) shows that crowd size has a positive effect on structural damping. The larger crowd size induces the larger damping of the structure. However, the effect of crowd size on structural frequency is the opposite, as shown in Equation (32). Increase of crowd size causes a decrease of structural frequency. In addition, structural modal characteristics are also related to the movement of pedestrians. The term can disturb the effect of crowds on structural dynamic properties.
4. Numerical Validation
A simply supported beam [
15] with a span of 40 m is used for the simulation. Its mass per meter is
. Vertical flexural stiffness is
. Damping ratio is
. Fundamental frequency of the beam is 2.0 Hz. Parametric values of pedestrians are listed in
Table 1.
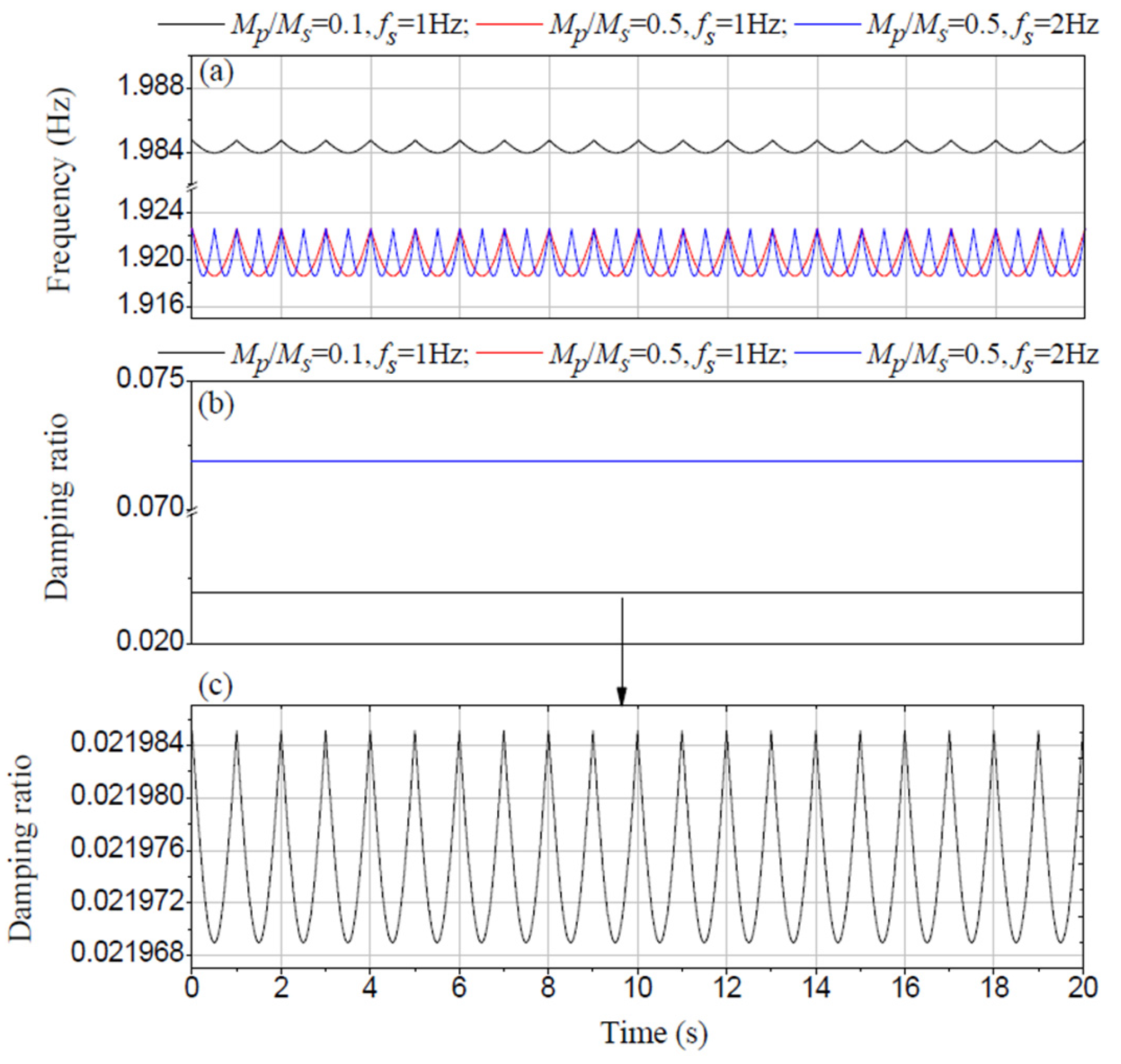
To contrast the effect of crowd size and step frequency, the dynamic properties under different crowd sizes and step frequencies are analyzed. When the mass ratio
Mp/
Ms between crowd and structure increases from 0.1 to 0.5 under same step 1 Hz in
Figure 4, the frequency approximately decreases from 1.985 Hz to 1.92 Hz and the damping ratio also shows an obvious change in
Figure 4b. However, the change of step frequency under the same mass ratio
Mp/
Ms = 0.5 has a smaller effect on the model parameters.
Figure 4c gives the detail of damping ratio under the
Mp/
Ms = 0.1 and
fs = 1 Hz, which shows that the structure damping ratio is periodically changed along with walking gait. The frequency in
Figure 4a also shows this effect and model property is disturbed by periodic walking gaits. The crowd size has a more significant impact on model properties than the walking excitation frequency.
The dynamic responses in mid-span are given in
Figure 5. Under the same walking frequency
fs = 1.0 Hz, the change of mass ratio between crowd and structure has a tiny effect on vibration amplitude. However, the variation of step frequency has an obvious impact on structural responses. Under the walking frequency
fs = 2.0 Hz, which is the same as the structural natural frequency, the acceleration response is rapidly amplified, as shown in
Figure 5b. This demonstrates that significantly varying the frequency of excitation from the structural natural frequency is a more efficient method for alleviating excessive vibration, than by limiting the crowd size.
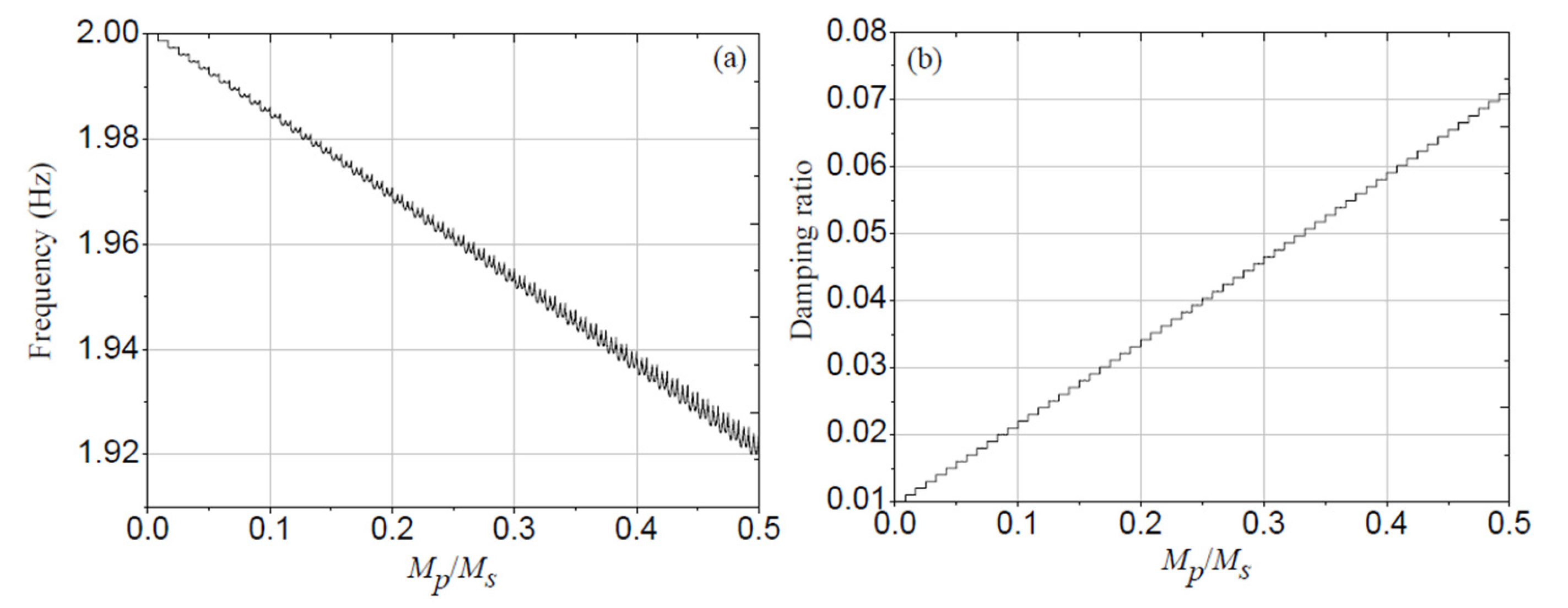
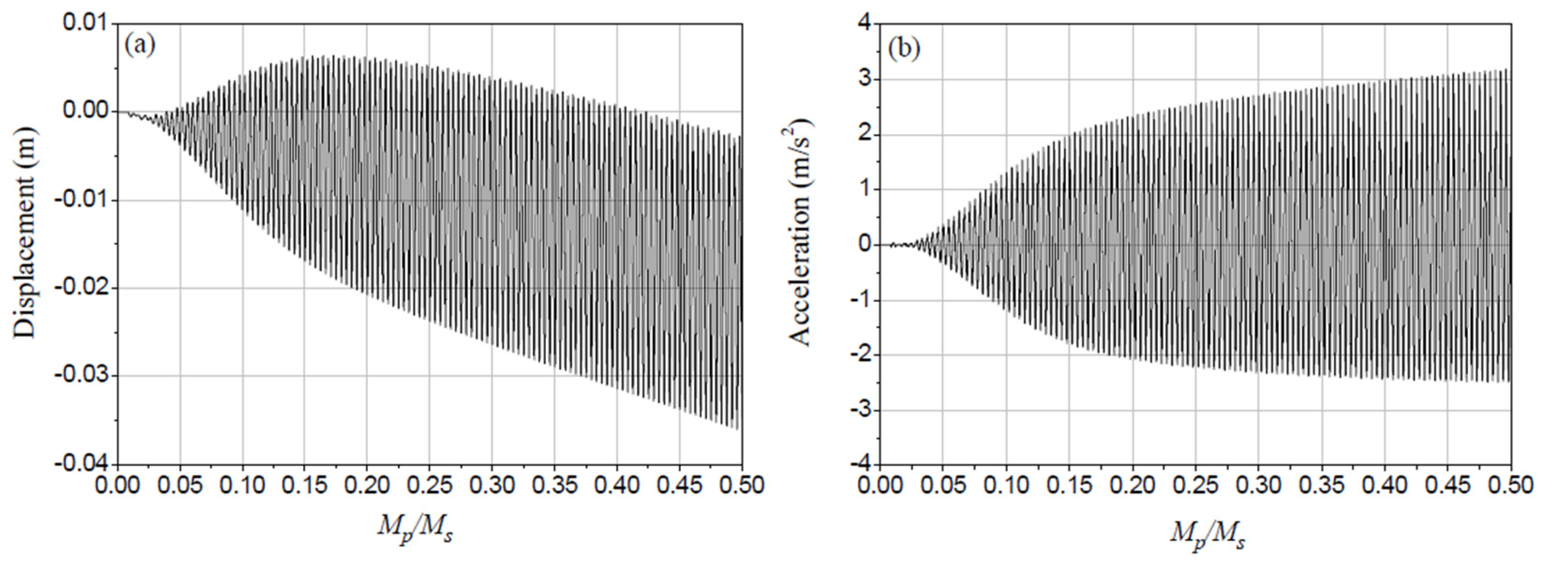
In order to explore the effect of crowd size, crowd mass was linearly increased from zero to half of the structure mass over 60 s.
Figure 6 gives the frequency and damping ratio under the resonance excitation frequency
fs = 2.0 Hz. Along with the increase of mass ratio between crowd and structure, crowd induced frequency approximately decreases from 2 Hz to 1.92 Hz and damping ratio approximately increases from 1% to 7%. It is noted that the both dynamic response displacement and acceleration amplitudes (
Figure 7) increase along with the increase of mass ratio between crowd and structure under resonance excitation frequency. Thus it can be seen that the increase of crowd size under resonance excitation has the most prominent effect on structural dynamic properties.
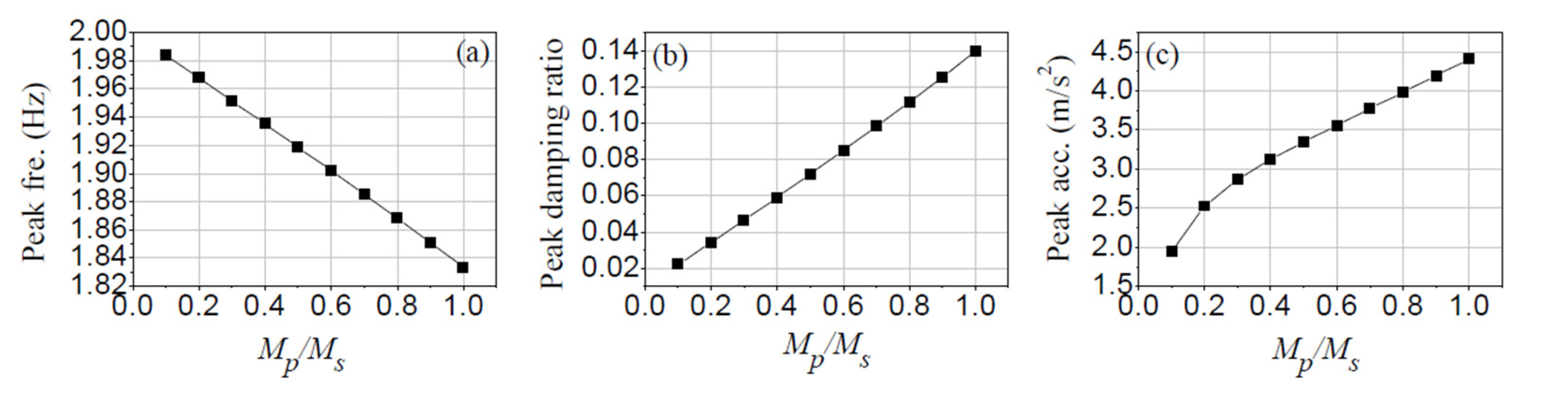
To further study the effect of crowd size, dynamic property peaks, including the frequency minimum peak, damping ratio maximum peak, and acceleration maximum peak were plotted, as shown in
Figure 8. Along with the increase of mass ratio between crowd and structure, the frequency peak approximately decreases linearly, as shown in
Figure 8a, which also happens to the damping ratio peak, as shown in
Figure 8b. In
Figure 8c, the acceleration peak shows a faster increase when the mass ratio
Mp/
Ms is less than 0.3. When the
Mp/
Ms is larger than 0.3, the acceleration approximately increases along with the increase of
Mp/
Ms. The influence of crowd size on model characteristics is consistent with measurement results [
3].
The model property formulas induced by crowd are obtained under the assumption that all pedestrians move consistently and that they follow a uniform distribution on the structure, which is also the most unfavorable situation for the control of structural vibration. However, the above descriptions do not happen frequently in real walking behaviors. Additionally, interactions between pedestrians may alleviate the worst situation. The proposed model formulas caused by crowds may give a more significant indication of human behaviors. Thus, a reduction coefficient needs to be incorporated into the model formulas and its definition needs experimentation, with the dynamic measurement of structure under the walking crowd in further research.