1. Introduction
Inventory inaccuracy refers to the discrepancy between the inventory record in the information system and the actual inventory [
1]. Misplacement errors are the primary cause of inventory inaccuracy in retail stores. Misplaced inventory occurs when employees put products on shelves that are not accessible to customers, or when customers take items from one shelf and leave them on another shelf [
2]. The misplaced items cannot meet the customer demand until they are replaced by the employees. Ton and Raman [
3] reported that misplaced inventory is prevalent in retail stores and 4% of Amazon’s warehouse inventory was misplaced. Because of misplaced inventory, the number of products available for sale is smaller than the inventory records, and this may result in “phantom stockouts” [
4]. Phantom stockouts have severe impacts on retailers since customers may delay the purchase or buy the products from other retailers. In the meantime, the retailers have to bear the extra holding cost of misplaced inventory. As a consequence, the retailer’s profit may be reduced by up to 10% [
5].
The consequence of an inaccurate inventory record is not only inefficient inventory management at the retailer level. It has been found that the information distortion will propagate through the supply chain, as seen in the bullwhip effect [
6,
7]. Inventory inaccuracy often results in the overall poor performance of the supply chain, especially when information asymmetry exists between the supplier and the retailer [
8]. IBM Business Consulting Services conducted an investigation on seven distinct supply chains and reported that inventory inaccuracy led to 1.75% of revenue loss for retailers and 0.22–0.73% of revenue loss for suppliers [
9]. This study specifically considers the misplaced inventory problem in a two-level supply chain, including an upstream supplier and a downstream retailer.
Traditionally, retailers conduct physical inventory audits to replace misplaced items and to correct inventory records in the information system. Recently, emerging Radio-Frequency Identification (RFID) technology is expected to address this problem. An RFID system includes tags and readers, where tags provide the unique identification numbers for products and readers detect the products as they flow through the reader points [
10]. RFID improves inventory visibility and therefore eliminates misplaced inventory in a timely manner [
11]. Several research projects have provided evidence for the fact that an RFID-enabled inventory control system outperforms a traditional replenishment process that relies on cycle counting [
12,
13]. Moreover, RFID enables the synchronization of information flow along with product flow in a supply chain, and thereby provides a high level of information integration among supply chain participants [
14]. There has been a growing need for supply chain management to achieve collaboration among supply chain participants in terms of information integration, synchronized planning, etc. [
15]. Besides tackling the inventory inaccuracy problem, RFID application is also expected to support these supply chain collaboration processes. Despite the great advantages, RFID implementation also imposes considerable costs and investment risks on supply chain participants, which become major obstacles in the diffusion of RFID technology in supply chain management [
16]. Consequently, a trade-off among the costs, risks, and benefits of adopting RFID technology becomes a crucial issue for supply chain participants. Another crucial issue in applying RFID is how the costs and benefits are distributed among supply chain participants. We therefore utilize game theory, which is widely used to model interactions among different stakeholders with various objectives, to analyze the decision making of the supply chain participants.
Most previous research on inventory inaccuracy has postulated risk-neutral decision makers who behave rationally and try to maximize expected profits, without accounting for the variance of the expected profit. In reality, however, decision makers usually show a risk-averse attitude and make decisions based on conservative objectives, i.e., they may lower their expectation of profits in order to reduce the variance of profits [
17]. Many empirical and theoretical studies have demonstrated that the actual decisions systematically deviate from those that maximize expected profits [
18,
19]. These results highlight the importance of incorporating risk-averse factors into the analysis of the decision making process for better modeling of real-life situations. On the other hand, misplaced inventory leads to high risks of overstock, as well as stockouts for retailers who rely on the inventory records to make ordering decisions [
20]. Moreover, the retailers are also exposed to investment risk when implementing RFID to eliminate misplaced inventory.
Motivated by these investigations, this study incorporates the retailer’s risk aversion attitude into the analysis of inventory inaccuracy. We compare different strategies for tackling the inventory inaccuracy problem to illustrate the benefits of information sharing and RFID implementation. A supply chain coordination scheme is proposed to synchronize the supplier and retailer’s incentives in RFID implementation. The objective of this study is to investigate the impact of a risk aversion attitude on a supply chain’s decision policies in terms of information sharing, RFID adoption, and supply chain coordination.
The contribution of this paper is threefold: (i) A risk aversion attitude is incorporated into the decision policies of a two-level supply chain subject to misplaced inventory; (ii) Explicit analytical expressions for the benefits of RFID implementation are derived considering different RFID effectiveness in eliminating inventory inaccuracy and the corresponding variable cost and fixed cost; and (iii) A supply chain coordination scheme is proposed based on the revenue sharing policy and the expense sharing scheme on RFID costs.
2. Literature Review
The inventory inaccuracy problem has received considerable attention in recent years. There are two main streams of literature dealing with the inventory inaccuracy problem. One stream has focused on optimal decision making when subject to inventory inaccuracy [
1,
11,
12,
21]. Specifically, these studies have dealt with the inventory errors from different sources, such as temporary shrinkage [
22,
23], transaction errors [
24], and misplaced inventory [
25,
26]. The other stream mainly investigates the effect of inventory inaccuracy on supply chain performance [
27,
28,
29], among which several studies have analyzed the effect of inventory inaccuracy on collaborative Supply Chains [
6,
30,
31]. This study belongs to the first stream of literature and focuses on the misplaced inventory problem.
Some studies have quantified the retailer’s benefits from RFID implementation in terms of reducing misplaced inventory. Rekik et al. [
25] presented an analytical model of a single-period retailer subject to misplacement errors. They showed the impact of misplacement errors on ordering decisions and explored the benefits of implementing the RFID technology. The analytical expression of the RFID tag cost which makes its deployment cost effective was derived in their study. Wang et al. [
26] explored the impact of inventory inaccuracy on the retailer with inventory-dependent demand. They considered the impact of inventory inaccuracy on the retailer’s profits under different demand sensitivity and demand uncertainty. The threshold RFID tag cost which makes the adoption of RFID profitable was also explored. However, the significant fixed cost of RFID implementation was not taken into account in the above studies, leading to an underestimation of the RFID critical tag price and overestimation of the benefits of RFID in reducing inventory inaccuracy.
This study is closely related to the literature that analytically dealt with the inventory inaccuracy problem in a supply chain framework. Camdereli and Swaminathan [
32] studied both centralized and decentralized supply chains subject to misplacement errors. They showed that the incentives of the parties for investing in RFID are not perfectly aligned in the existence of the fixed cost of investment. Heese [
33] investigated the effect of inventory inaccuracy on supply chain performance and the impact of double marginalization on the parties’ incentives for RFID adoption. They showed that RFID adoption improves supply chain coordination and a decentralized supply chain can benefit more from RFID technology. Cannella et al. [
34] analyzed the impact of inventory inaccuracy on the performance of supply chains under a variety of operational factors such as the error magnitude, inventory audits frequency, and lead time variability. They found that the detrimental effects of inventory inaccuracy on supply chain performance are exacerbated by the supply chain structural complexity and lead time variability. In most of the existing literature, RFID is assumed to have a 100% ability in eliminating inventory errors. The relationship between different scales of RFID investment and its effectiveness in eliminating inventory inaccuracy was not considered. Cui et al. [
21] first considered that different types of RFID possess unequal technique features and analyzed the cost-effectiveness of different RFIDs for the optimal decisions of supply chain participants. They illustrated the relationships between the variable cost of RFID and its non-full ability to decrease the stochastic inventory errors. However, the fixed cost of RFID is not considered in their study.
Risk analyses of the supply chain have been extensively studied in the literature. Many evaluation criteria (or analysis tools) have been introduced by previous studies, such as the mean–variance approach [
35], value-at-risk (VaR) approach [
36], and CVaR approach [
37]. CVaR was originally developed to measure the risk of possible losses in portfolio selections, and its use has recently been expanded to the field of supply chain management. Wu et al. [
38] introduced the concept of CVaR as the evaluation criterion in a supply contract context. They specifically showed that CVaR has advantages over mean-variance and VaR in both theory and practice, such as its coherent, sub-additive, positively homogeneous, and translation invariant characteristics. Moreover, the CVaR approach avoids the computational difficulties encountered by using the VaR approach and the mean–variance approach, and can thus obtain a closed-form solution which offers an explicit relationship between the decision maker’s risk attitude and the optimal decisions.
We therefore model the retailer’s risk aversion by adopting the CVaR decision criterion. There exist some studies applying CVaR to the newsvendor problem. Gotoh and Takano [
39] first adopted CVaR minimization in a newsvendor problem with a risk averse retailer. They showed the good computational characteristics of CVaR such that the CVaR minimization problem can be represented as a linear program. Dai and Meng [
40] utilized CVaR as the retailer’s objective in a newsvendor model where the demand depended on the marketing effort level and the price. Chen et al. [
41] investigated the combined order quantity and price decisions of a risk-averse retailer under the CVaR framework, and established the conditions under which the optimal policy uniquely exists. A supply chain contract under the CVaR framework has recently attracted considerable attention. Yang et al. [
42] studied the coordination of the supply chain involving a risk-neutral supplier and a risk-averse retailer with the CVaR criterion. They showed that the supply chain can be coordinated with the revenue-sharing, buy-back, two-part tariff, and quantity flexibility contracts. Caliskan-Demirag et al. [
43] analyzed a supply chain rebates contract problem and measured the retailer’s risk aversion attitude with CVaR. Li et al. [
44] considered a dual channel supply chain consisting of a risk-averse retailer and a risk-neutral supplier under the CVaR framework. A risk-sharing contract is proposed to coordinate the dual-channel supply chain. Although all of these studies incorporate a risk aversion attitude into the decision making process, they do not consider the discrepancy between the actual physical inventory and the recorded inventory information, which is quite a realistic problem in supply chain management.
Zhu et al. [
45] also utilized CVaR to explore the optimal ordering policy of a risk-averse retailer subject to inventory inaccuracy. However, the research only analyzed the problem from the retailer’s perspective, and focused on the retailer’s incentive for RFID adoption. It has been pointed out that RFID should be implemented in the entire supply chain to improve the supply chain performance [
46]. On the other hand, one of the major barriers for RFID implementation in a supply chain is the free-rider problem, which is the phenomenon where the retailer can take advantage of RFID without bearing any cost once RFID tags are attached to the products by the upstream supplier. Consequently, this study extends the previous work by analyzing the inventory inaccuracy problem in a two-level supply chain framework, focusing on synchronizing the incentives of both partners in RFID implementation and deciding how the costs and benefits should be distributed between them.
The remainder of this paper is organized as follows. In
Section 3, we describe the problem and investigate the decision policies of two cases: (1) information asymmetry about inventory errors exists; and (2) the retailer shares information about inventory errors with the supplier. We further explore the benefits of information sharing by comparing the two cases.
Section 4 presents another case when RFID is implemented in the supply chain to enable information integration, as well as to reduce inventory errors. The supply chain participants’ benefits as a result of RFID implementation are derived. In
Section 5, we propose a revenue and cost sharing contract to coordinate the supply chain.
Section 6 conducts a numerical analysis and
Section 7 provides managerial insights for managers to invest in RFID. Finally,
Section 8 concludes the paper.
3. Decision Policies of the Supply Chain with Information Asymmetry
3.1. Problem Description
We consider a two-level supply chain which consists of a supplier and a retailer subject to misplaced inventory. The supplier produces seasonal products and sells the products to the retailer. The retailer then sells the products to the end customers. The supplier decides a wholesale price for the product and the retailer decides the order quantity from the supplier. Therefore, a Stackelberg game, which is a method employed to model the hierarchical decision process, is proposed to model the interaction between the supplier and the retailer. As the Stackelberg leader, the supplier determines the wholesale price based on its impact on the retailer’s order quantity, while the retailer decides his order quantity based on the demand and the wholesale price.
The following notations and assumptions are used in this paper:
| Unit production cost |
| Unit selling price |
| Unit salvage price |
| Random demand |
| Probability density function (PDF) of D |
| Cumulative distribution function (CDF) of D |
| Ratio of items that are misplaced among the total physical inventory |
| Risk factor that reflects the degree of risk aversion |
| Unit variable RFID tag cost |
| Fixed RFID investment cost |
| Information sharing cost |
| Expected profit |
| The retailer’s share of revenue |
| The retailer’s share of RFID cost |
| Decision Variables | |
| Order quantity |
| w | Unit wholesale price |
| ε | Scale of RFID investment |
Assumption 1. Assume that β portion of items are misplaced instantaneously at the beginning of the season and cannot be found until the end of the season. Normally, misplacement occurs gradually over time in real-life situations. However, this assumption is widely used in the literature of misplaced inventory for analytical tractability [25,32]. Therefore, only (1 − β)Q amount of items are available for customers. At the end of the period, the whole unsold quantity (misplaced items and items on shelves) is salvaged. Assumption 2. To obtain closed-form analytical expressions, we assume that customer demand is uniformly distributed on [0, Dmax], which is commonly adopted in inventory management literature [25,45]. Assumption 3. The effectiveness of RFID in eliminating misplaced inventory is not 100%. Most previous studies consider RFID as a perfect technology which has a 100% ability to eliminate inventory errors. However, this assumption does not hold in reality and the effectiveness of RFID for the reduction of inventory errors can be quite different [47]. The effectiveness of RFID in eliminating misplaced inventory is considered as a function of the scale of RFID investment in this study. Assumption 4. Assume that the retailer is risk-averse and the supplier is risk-neutral. The risk neutrality assumption of the supplier is based on the fact that, in practice, the supplier is able to diversify her risk by serving a number of independent retailers [48]. The risk-neutral supplier makes decisions to maximize her profit, whereas the CVaR measure is considered as the risk-averse retailer’s objective. Throughout the remainder of this study, superscripts are used to indicate the concerned supply chain level (S, supplier; R, retailer; SC, supply chain), and subscripts (1–3) are used to distinguish between three cases (Case 1, information asymmetry about inventory errors exists; Case 2, the retailer shares information about inventory errors with the supplier; Case 3, RFID is implemented in the supply chain).
3.2. The Optimal Decisions in Case 1: Information Asymmetry about Inventory Errors Exists
When there is no information sharing, the retailer realizes the inventory inaccuracy problem and conducts physical inventory audits to estimate the errors, whereas the supplier has no information about the errors. In this situation, the retailer makes his ordering decision by taking the errors into account, whereas the supplier still decides the wholesale price based on the situation of accurate inventory.
With misplacement errors, the retailer’s profit is given by:
We obtain the expected profit function of the retailer as follows:
The retailer adopts CVaR as the decision criterion, and his objective function is given by (see Zhu et al. [
45] for a brief description of CVaR and its application in a newsvendor problem):
Note that denotes the retailer’s performance under the CVaR criterion and η denotes the degree of risk aversion. Retailers become more risk-averse as η decreases. Meanwhile, η = 1 indicates risk neutrality, which can be considered a special case of risk aversion.
The risk-neutral supplier’s objective function is given by:
where
Q0 is the order quantity of a retailer who has accurate inventory records.
Theorem 1. When the retailer has private information about inventory errors, the supplier sets her wholesale price as: Based on the wholesale price, the retailer decides the order quantityto maximize his performance under the CVaR criterion. The retailer maximizes his performance, which is , and the supplier maximizes her expected profit, which is .
3.3. The Optimal Decisions in Case 2: The Retailer Shares Information about Inventory Errors with the Supplier
It is well known that information sharing between the partners is beneficial to a supply chain [
49]. It is also generally acknowledged that providing additional information to suppliers would offer some benefits to the suppliers [
50]. In order to justify the information sharing action, such a benefit must be at least greater in value than the cost [
51]. In this section, we quantify the value of information with a consideration of the information sharing cost, which is born by the supplier and denoted as
E.
With information sharing, both parties make decisions based on the information about inventory errors, thus their expected profit functions can be expressed as:
Theorem 2. When the supply chain has public information about inventory errors, the supplier sets her wholesale price as:while the retailer decides his optimal order quantity as: The proof is similar to Theorem 1 and hence omitted.
The supplier’s expected profit decreases in the cost of information, which is , whereas the retailer’s performance is independent of this cost, which is .
The corollary below follows directly from Theorems 1 and 2.
Corollary 1. We get the following results for a supply chain consisting of a risk-averse retailer and a risk-neutral supplier:
- (1)
the retailer orders less if he is more risk-averse,
- (2)
the supplier obtains less profits if the retailer is more risk-averse.
Proof. It is straightforward to show that () has a positive relationship with η. Since η = 1 indicates risk neutrality, we infer that risk-averse retailers always order less than risk-neutral retailers, no matter whether information is shared or not. From and , we get the second result.
3.4. The Benefits of Information Sharing
Even though information sharing is beneficial to the centralized supply chain, the supplier may have no incentive to induce the retailer to share information about inventory errors. By Proposition 1, we quantify the benefits of information sharing for the supply chain participants.
Proposition 1. Compared with the case of information asymmetry, information sharing on inventory errors leads to the following results:
- (1)
the supplier lowers her wholesale price, i.e., ;
- (2)
the retailer orders more, i.e., ;
- (3)
the retailer always benefits from information sharing, i.e., ;
- (4)
the supplier benefits from information sharing if and only if:where .
Proof. From Equations (A3) and (10), we obtain:
It is obvious that , indicating that the retailer orders more after information sharing. Moreover, we observe that the retailer has a high tendency to stop ordering (i.e., ) when he has private information about inventory errors, whereas he can bear a higher level of inventory inaccuracy (i.e., ) after sharing information to the supplier.
Moreover, Equation (9) shows that decreases in , where indicates the situation of no inventory errors. Therefore, we infer that the supplier charges a lower wholesale price when she has public information about inventory errors. Since the wholesale price is decreased and the order quantity is increased after information sharing, the performance of the risk-averse retailer is improved from information sharing. Meanwhile, it is straightforward to obtain from Equation (12), which means that the retailer always benefits from information sharing.
Even though the supplier receives more orders from the retailer, she may not benefit from information sharing due to its cost, E. We define as the supplier’s benefit from information sharing, where . From , we derive the conditions under which the supplier can benefit from information sharing.
Obviously, the supplier cannot benefit from information sharing when the retailer has serious inventory errors (i.e., ). In this situation, the retailer will stop placing orders and thereby the supplier will avoid the additional cost of information sharing. When the inventory errors are not serious (), the supplier is motivated by a higher order quantity and is willing to induce the retailer to share information, as long as the benefits exceeds the costs. Since the supplier benefits less from information sharing when the magnitude of inventory errors becomes smaller, supply chain participants may not share information when there are few inventory errors.
4. Decision Policies of the Supply Chain with RFID Implementation
RFID provides a high level of information integration (sharing of information about production, inventory level, delivery) between supply chain participants. With RFID implementation, accurate and timely information about inventory errors can be transferred to the supplier; meanwhile, the retailer can benefit from the reduction of inventory errors. Since both the retailer and the supplier are direct beneficiaries through RFID implementation, it is reasonable to adopt RFID technology along the supply chain [
11].
4.1. The Optimal Decisions in Case 3: RFID Is Implemented in the Supply Chain
Currently, RFID is not extensively used because of its associated high costs, which includes variable tag costs and fixed costs (such as hardware and software costs, training costs, and infrastructure maintenance and upgrade costs). In the market, various types of RFID systems are available: e.g., RFID tags may cost as much as 100 dollars or as little as 7 cents, depending on the type of tag (passive tag or active tag), its efficiency, and its applications. Most of the previous studies consider RFID as a perfect technology which can eliminate all of the inventory errors. However, this assumption does not hold in reality and the effectiveness of RFID for the reduction of inventory errors can be quite different.
Therefore, the trade-off between the benefits and costs of RFID investment becomes a critical issue for decision makers. In this study, we explore the supply chain’s optimal scale for RFID when it has misplacement errors.
The effectiveness of RFID in eliminating misplaced inventory is considered as a function of the scale of RFID investment. For a given scale
ε (
),
εβQ items are prevented from misplacement and become available to meet customers’ demand. The variable cost of RFID investment is denoted as
tε, and the fixed cost for the retailer (supplier) is denoted as
LR (
LS). We set
tε =
φε2 and
LR =
ψRε2 (
LS =
ψSε2), where
φ,
ψR and
ψS are investment parameters. This quadratic assumption is widely used in the literature to describe the decreasing returns of investment [
52,
53]. We consider the situation when the variable cost of RFID investment is incurred by the supplier and the two parties bear their fixed costs respectively. This is a prevailing situation when RFID is implemented in the supply chain. For example, in 2005, Wal-Mart required its top 100 suppliers to tag all their pallets and cases and to bear the variable tag cost. RFID implementation also leads to large gains for the suppliers, boosts a long term partner relationship with the retailer, provides timely and accurate information, and helps to speed up the operational processes [
46].
The supplier decides the wholesale price and the scale of RFID investment, by taking into account their influences on the order quantity of the retailer.
Theorem 3. When the supply chain invests in RFID for the reduction of inventory errors, there exists an optimal scale of RFID investment, , and the corresponding wholesale price is . Thus, the order quantity of the retailer is given by: Using the optimality properties of Theorem 3, a simple searching algorithm may be employed to obtain the optimal scale of RFID investment, .
With RFID implementation, the retailer’s performance is , and the supplier’s expected profit is .
4.2. The Benefits of RFID Implementation
We derive the benefits of RFID implementation by comparing them with the case when information is shared among supply chain participants. We specify the cost thresholds at which RFID adoption is more profitable for supply chain participants. Let’s define as the cost threshold for the retailer (supplier). It is only profitable for the supplier (the retailer) to adopt RFID when the actual RFID costs t is no greater than ().
Proposition 2. The retailer has stronger incentives for RFID adoption compared with the supplier, i.e., .
The retailer benefits more from RFID technology even though he is the follower in the supply chain. In the situation when , RFID adoption is a win-win strategy for both parties. When , the retailer can benefit from RFID deployment; however, from the supplier’s perspective, it is not cost-effective. In other words, the cost savings from RFID implementation are not symmetrically distributed among supply chain participants.
5. Supply Chain Coordination
In this section, we analyze how the cost savings from RFID implementation should be allocated among supply chain participants by a revenue and cost sharing contract. We also show that, under this contract, the supply chain is coordinated and both parties are better off. In this section, the subscript “Co” is used to indicate the decision policies when the supply chain is coordinated.
Under a standard revenue sharing contract [
54], the retailer keeps
k portion of all revenue (
), while the supplier takes (1 −
k) portion of the retailer’s revenue and offers a low wholesale price, which is
w =
kc, in order to induce the retailer to place an order that maximizes the supply chain’s profit (i.e.,
). With RFID implementation, the additional RFID costs also need to be shared. Hence, we propose a revenue and cost sharing contract
to coordinate the supply chain. The variable cost is shared between the two parties using an arbitrary proportion, while the supplier bears (1 −
k) portion of the retailer’s fixed cost for RFID adoption. The retailer shares
θ portion of the variable RFID costs and the supplier pays (1 −
θ) portion of the variable RFID costs. We investigate how the revenue sharing policy, together with the expense sharing scheme on RFID costs, can coordinate the supply chain.
Under the revenue and cost sharing contract
, the expected profit functions of the two parties are given by:
Thus, we get the supply chain’s expected profit function, which is:
When it is cost-effective for the supply chain to adopt RFID technology, we get
. The decisions of the supply chain are equivalent to that of a centralized system, where the supplier and the retailer seek to jointly maximize their total profit. We derive the optimal order quantity and the expected profit of the centralized supply chain as follows:
Theorem 4. With RFID implementation, a revenue and cost sharing contract can coordinate the supply chain consisting of a risk-averse retailer and a risk-neutral supplier, where the parameters satisfy:where . Proof. From Equation (14), it is worth noting that when (i.e., ), the retailer will always benefit from each ordering and thereby he tends to order as much as possible, even beyond the optimal order quantity of the supply chain.
Therefore, we consider two cases of η:
- (1)
. From Equation (14), we get the retailer’s optimal order quantity, as follows:
When
, we have
, which means that the optimal decision of the centralized system is adopted. Substituting Equation (19) into (15), we obtain the supplier’s expected profit after coordination, as follows:
Comparing with , we derive the upper bound of k, , which ensures that the supplier benefits from coordination. Similarly, we derive the lower bound of k, , which ensures that the retailer benefits from coordination. Since the performance of the decentralized supply chain is always improved through coordination, the supplier is able to allocate the profits so that both parties are better off (i.e., ). Thus, coordination is achieved through the contract.
- (2)
. In this case, the optimal order quantity of the retailer is infinite. As the Stackelberg leader, the supplier can limit the retailer’s order quantity to the supply chain’s optimal order quantity (i.e., ), and negotiate with the retailer about the values of k and θ to make sure that the retailer benefits from coordination. In this situation, coordination is also achieved.
There exist multiple sets of (w, k, θ) that satisfy the required condition. In reality, the specific values of k and θ are decided depending on the bargaining power between the retailer and the supplier. It is worth noting that when θ = k and η = 1, the proposed cost and revenue sharing contract given by Equation (22) is specialized as the standard revenue sharing contract. In this sense, our results extend the supply chain coordination problem to the context of risk aversion and RFID costs sharing.
From Theorem 4, we obtain the following corollary.
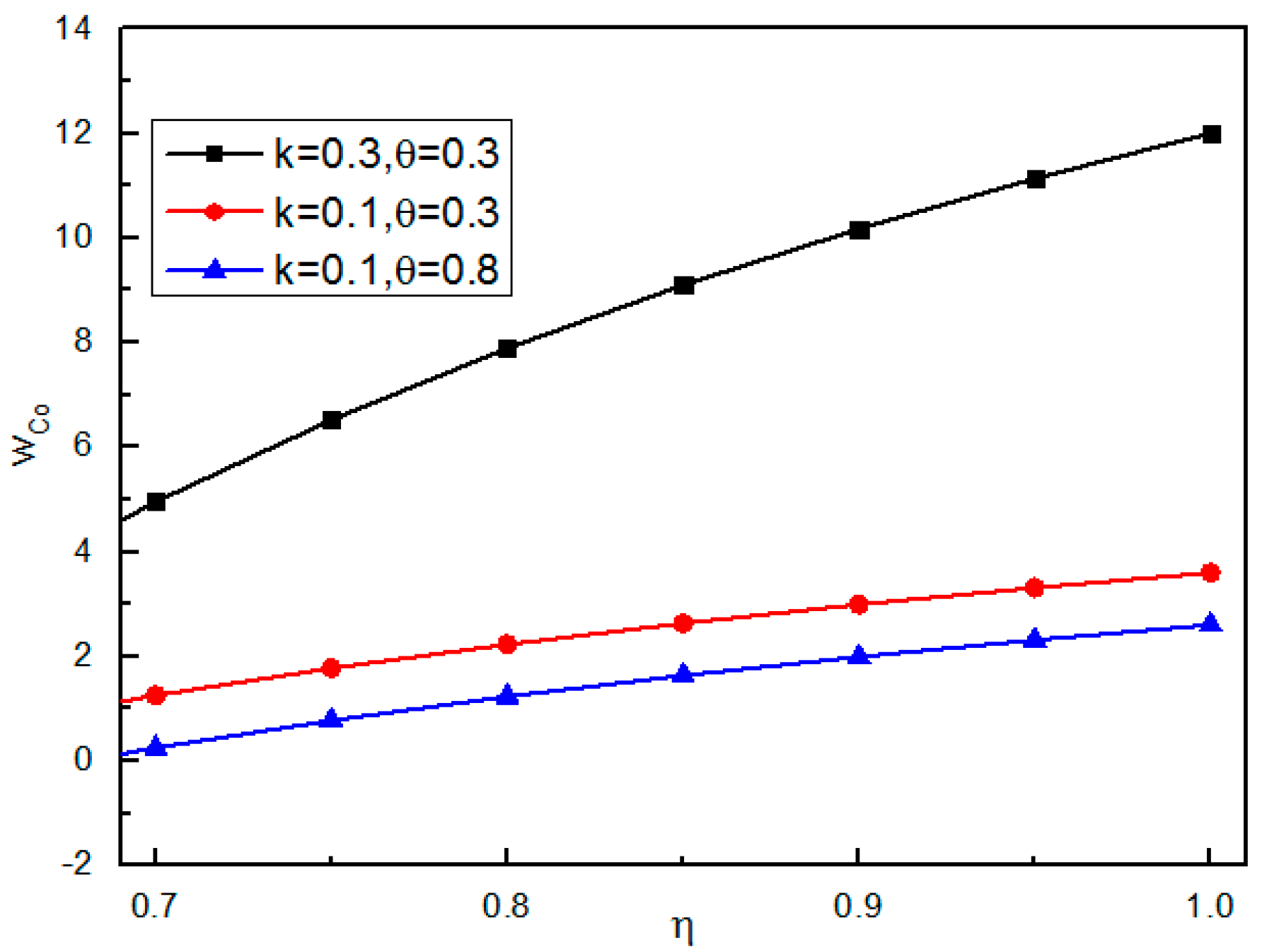
Corollary 2. Under the CVaR criterion, the revenue and cost sharing contract (w, k, θ) is relevant to the retailer’s degree of risk aversion, where η: wCo and k are increasing in η.
Proof. From Equation (19), it is straightforward that wCo increases in η. We can also derive that both the upper bound and lower bound of k are increasing in η from Equation (20).
Corollary 2 shows that when the retailer is more risk-averse (smaller η), he desires to share a higher portion of revenue (smaller k) to the supplier, in order to obtain a lower wholesale price (smaller w) in return. The reason for this is that the retailer’s risk increases as the holding cost increases, where the holding cost is denoted as h and h = w − s. Thus, the more risk-averse the retailer becomes, the lower wholesale price he desires in order to avoid the risk.
We also observe that for a given η, the wholesale price increases in k and decreases in θ, which is intuitive and useful when the participants negotiate the contract. For illustration, we consider a numerical example in the next section and show the impact of risk aversion on supply chain coordination.
6. Numerical Analysis
In this section, we conduct a numerical analysis to explore the impact of inventory inaccuracy and risk aversion on decision making in terms of information sharing, RFID adoption, and supply chain coordination. We consider the situation when a supplier sells its products to multiple retailers. The retailers are subject to different magnitudes of misplacement errors and have different risk attitudes. In the numerical example, we set the values of the parameters involved as
p = 100,
c = 40,
s = 20, and
Dmax = 300 following the setting used in previous studies [
25,
45]. Based on observations of empirical studies [
3,
4], we assume the range of
β is from 0 to 0.08.
Figure 1 shows how the supplier’s benefit from information sharing is affected by the magnitude of inventory errors and the retailer’s degree of risk aversion. The supplier’s benefit from information sharing is positively related to the magnitude of inventory errors. In other words, the supplier can benefit more when there exist serious inventory errors in the retail store. However, the supplier may suffer a loss from information sharing (
) when the magnitude of inventory errors is relatively low (
). The supplier’s benefit from information sharing is negatively affected by the retailer’s degree of risk aversion. When the retailer is less risk-averse (a higher
), the supplier can benefit more from information sharing, and thus has a stronger desire for information sharing.
Using
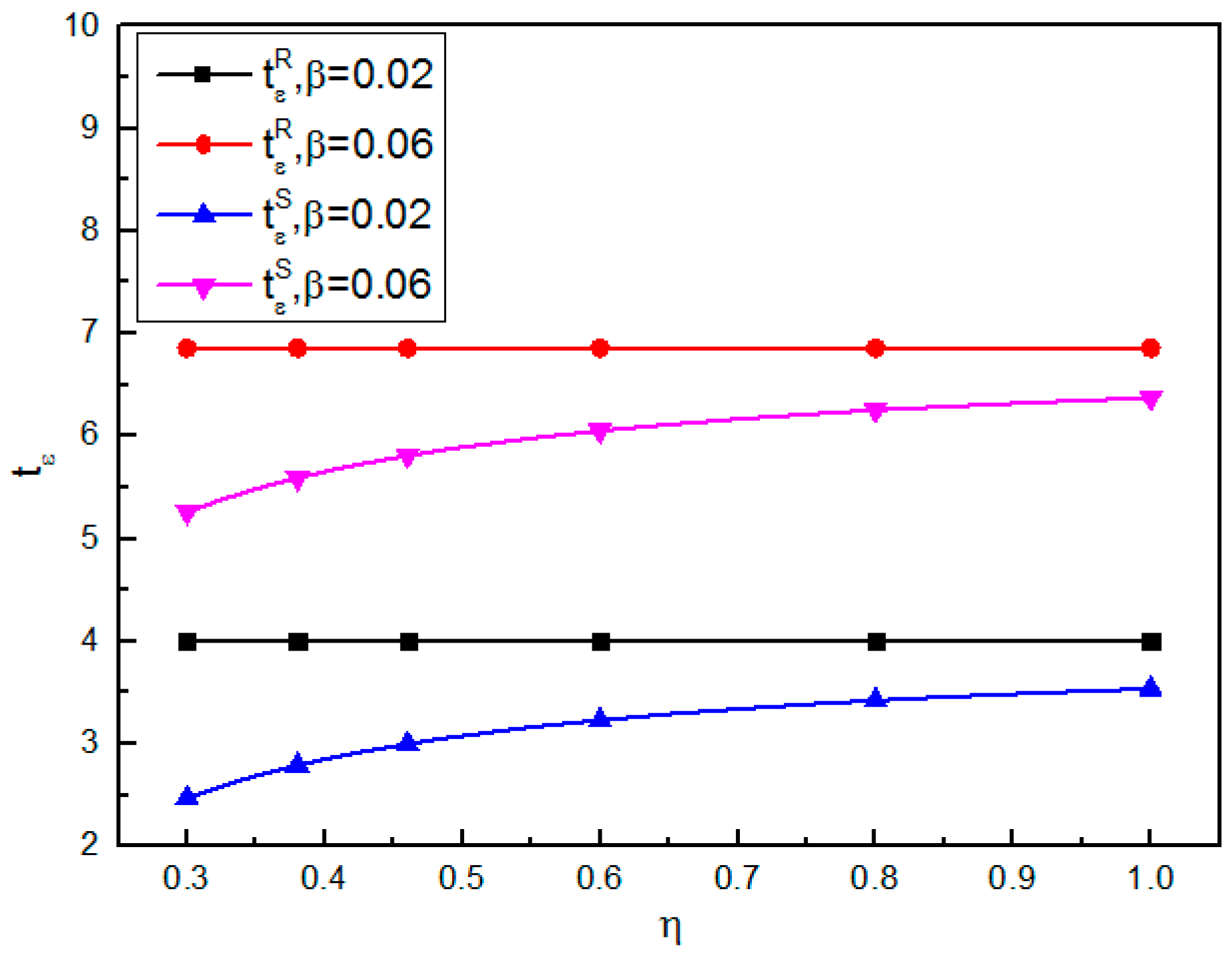
Figure 2, we illustrate the supply chain’s incentive to adopt RFID technology when the retailer is risk-averse.
Figure 2 shows that both parties tolerate higher RFID costs when the inventory errors become serious. From
Figure 2, we can also observe that the supplier’s incentive to invest in RFID is decreasing in the retailer’s degree of risk aversion. Moreover,
Figure 2 verifies that the cost savings from RFID implementation are not symmetrically distributed among supply chain participants: the retailer benefits more from RFID compared with the supplier.
Figure 3 verifies the observation that a risk-averse retailer is willing to share a high portion of his revenue to the supplier, in order to obtain a low wholesale price for avoidance of the risk. This is consistent with the definition of risk-averse, which states that risk-averse decision makers are willing to give up some profits to avoid possible losses.
The results shown in
Table 1 also confirm that a supply chain can always benefit from coordination (
). In particular, the supply chain is expected to benefit more when the retailer is more risk-averse.
7. Managerial Insights for Decision Makers
Inventory inaccuracy is prevalent in various industries all around the world. In this section, we provide managerial insights for the managers to deal with the inventory inaccuracy problem based on the theoretical results and the numerical results.
It is well known that the supplier can benefit from additional information provided by the retailer, such as inventory information and demand information. However, such a benefit needs to be justified by comparing it with the costs of investing in the information systems and processes. When the inventory errors occur, it is vital for the supplier to decide whether or not to ask the risk-averse retailer to share the inventory information, so as to reduce the negative effect of inventory inaccuracy. Our study finds that the supplier’s benefit from information sharing is affected by the magnitude of inventory errors, as well as the retailer’s degree of risk aversion. On one hand, the supplier can benefit more from information sharing when she selects less risk-averse retailers. On the other hand, the supplier should not induce the retailer to share information when there are few inventory errors. Moreover, when the retailer is subject to serious inventory errors, RFID implementation is preferred to information sharing. This is because information sharing only ensures that both parties make decisions by taking inventory errors into consideration; whereas RFID enables information integration and reduces inventory errors, thus generating more profits.
How the costs and benefits are distributed among supply chain participants has been a hot issue in RFID application in the supply chain. Our results show that the retailer benefits more from RFID compared with the supplier when dealing with the inventory inaccuracy problem. The reason for this is that, once RFID tags are attached to the products by the upstream supplier, the supplier can benefit from the information integration enabled by RFID; meanwhile, the downstream retailer can benefit from the reduction of inventory errors without any variable cost. This could cause a one-sided free-rider problem in the absence of any cost sharing scheme. Hence, from the supplier’s perspective, she may have no incentive to adopt RFID due to its high costs. In this situation, it is necessary for the retailer to bear a portion of the RFID costs in order to enable the implementation of RFID along the supply chain. On the other hand, the supplier is encouraged to extend the RFID efforts into other parts of her business, i.e., add values on RFID implementation. For example, a traceability system can be implemented in the perishable food supply chain to track food ‘from farm to fork’, and thereby improve food safety. Furthermore, the supplier can integrate the traceability system with the production process and the quality management process to improve the manufacturing efficiency.
It is also crucial for the managers to take into consideration the fact that RFID implementations are not static over time. Both technology improvements and cost savings are expected to increase the benefits of RFID implementation for supply chain applications. Moreover, our study shows that the maximum benefits from RFID application can be achieved through supply chain coordination.
8. Conclusions
In this study, we incorporated the risk aversion attitude into the decision policies of a supply chain subject to misplaced inventory. Our analytical and numerical results imply some managerial insights for a supply chain consisting of a risk-neutral supplier and a risk-averse retailer. First, the risk-averse retailer always orders less than the risk-neutral retailer, no matter whether information is shared or not; while the supplier obtains less profits if the retailer is more risk-averse. Second, the retailer benefits from RFID implementation for the reduction of inventory errors, whereas the supplier benefits from RFID implementation due to the public information on inventory errors. However, the cost savings from RFID implementation are not symmetrically distributed among supply chain partners: the retailer has stronger incentives for RFID adoption compared with the supplier. Therefore, the retailer induces the supplier to deploy RFID by bearing a portion of RFID costs. On the other hand, the supplier is encouraged to add values on RFID implementation, such as deploying an RFID-enabled traceability system. Last but not least, we proposed a revenue and cost sharing contract to allocate the cost savings from RFID implementation among supply chain participants. We found that a risk-averse retailer is willing to share a high portion of his revenue to the supplier, in order to obtain a low wholesale price in return.