Modified Godard Timing Recovery for Non Integer Oversampling Receivers
Abstract
:1. Introduction
- Most analog receivers rely on a phase locked loop (PLL). Here, the received signal is multiplied with a reference clock and the low pass filtered product is used to drive a voltage-controlled oscillator (VCO). This way, the reference clock, which is the output of the VCO, is converging to the transmitter clock. This synchronized clock is used to process the signal. The concept of the PLL can be extended to a Costas loop, which has increased sensitivity and therefore reduced jitter in the estimate.
- Next generation receivers mainly operate in the digital domain. A number of digital processing techniques have been developed. These techniques can be classified into three categories: pure time domain, combined time and frequency domain, and pure frequency domain. Pure time domain techniques typically observe the shape of the received waveform. These techniques process the time domain signal and shift the sampling time towards the maximum eye opening. The most common candidate of this group is the Gardner method [1]. Here, two samples per symbol are acquired, and the samples are shifted in such a way that the zero crossings occur right in between the samples that correspond to the symbols. Another common technique is the early-late gate synchronization (also called the Alexander phase detector) [2]. Three samples are acquired and compared. The correct sampling phase is reached when the early and the late samples have a similar amplitude and the optimum sample in between is located at the maximum of the pulse. In addition, techniques that use symbol decisions in a decision directed approach are proposed in the literature. One example of such a structure is the Mueller and Müller algorithm [3]. Combined time and frequency domain techniques process a time signal and calculate a frequency domain coefficient corresponding to the clock tone of the signal. This clock tone then contains the sampling phase information. Two commonly known examples are the Order and Meyer technique [4] and the Lee technique [5]. Both are flexible with respect to oversampling (the Order and Meyer technique requires more than two samples per symbol), but are rather computationally heavy. In the pure frequency domain technique, the domain coefficients of the signal can be used to calculate the clock tone directly with the Godard [6] algorithm. Here, a twofold oversampled signal is processed in the frequency domain.
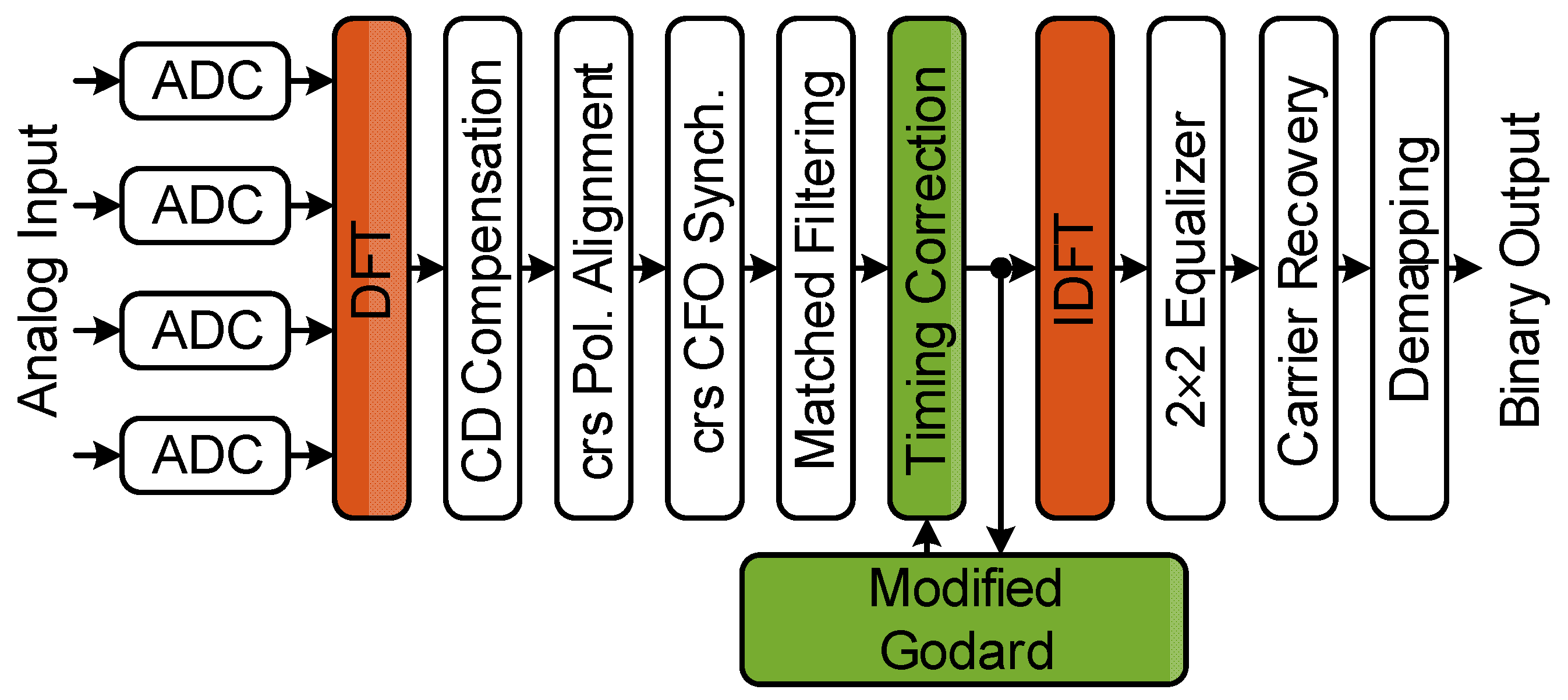
2. Non-Integer Oversampling Receiver Architecture in the Frequency Domain
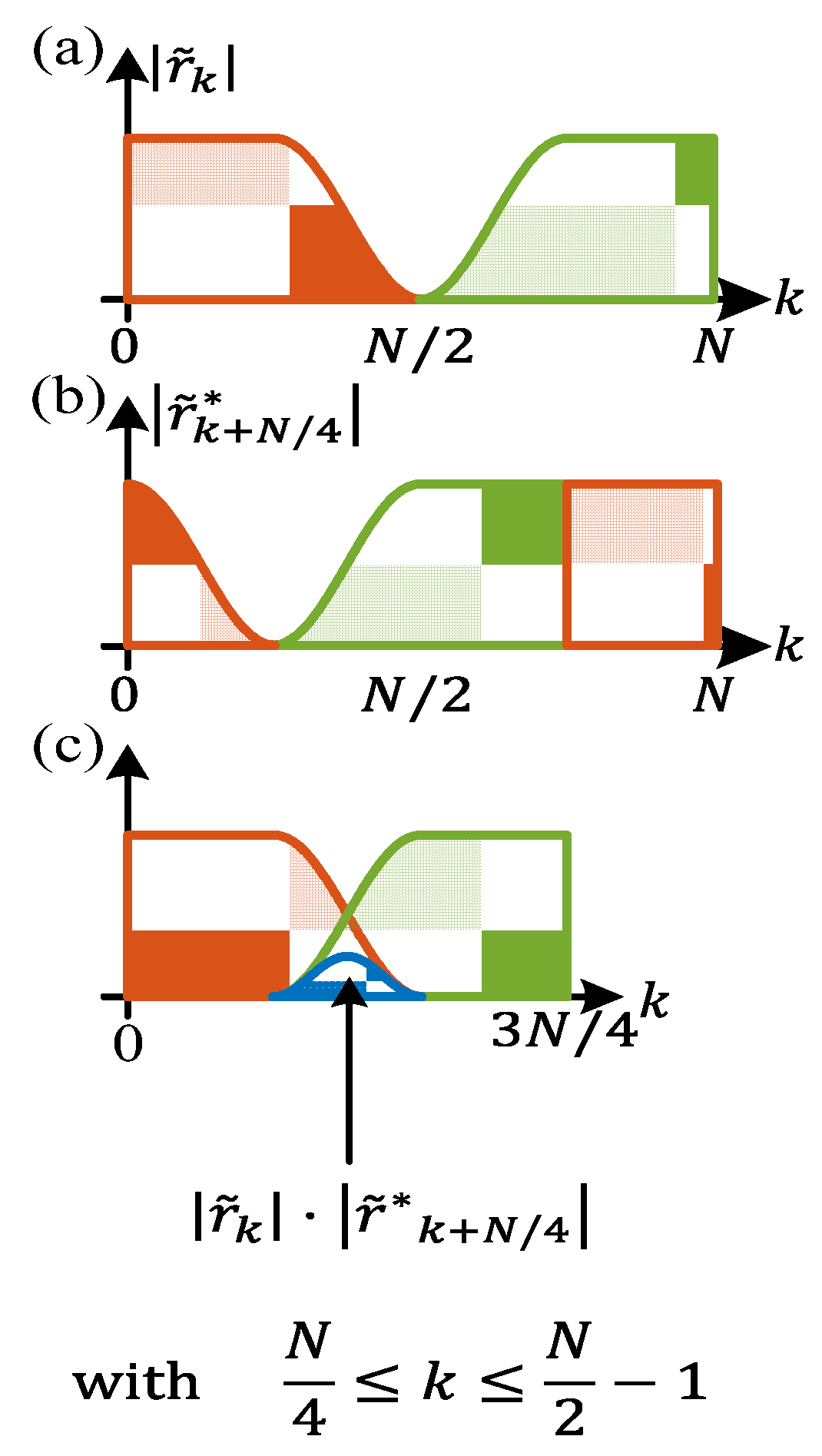
3. Multiplier-Free Modified Godard Timing Recovery
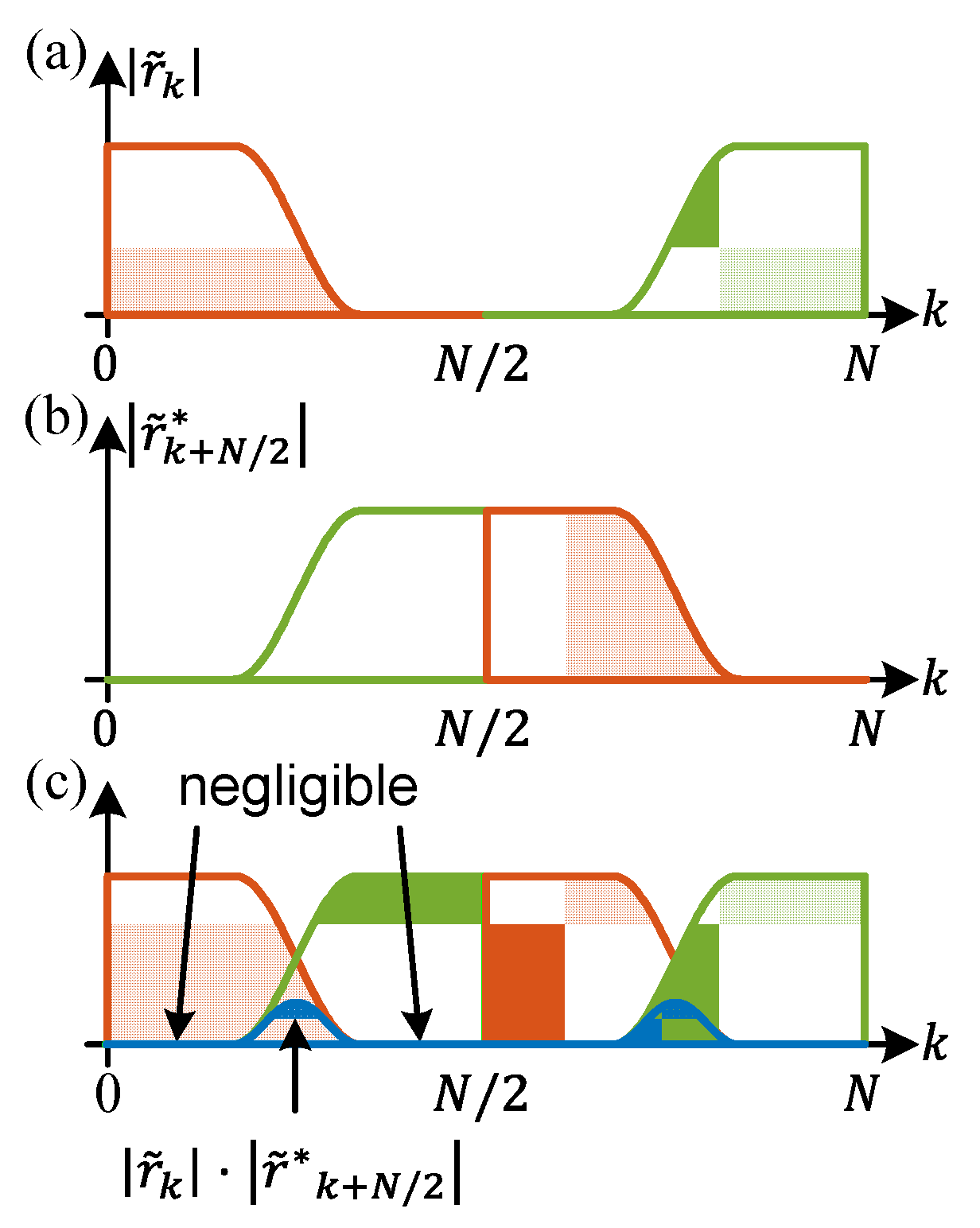
3.1. Modified Godard Algorithm for Simplified Clock Tone Calculation
3.2. Multiplier-Free Modified Godard Algorithm
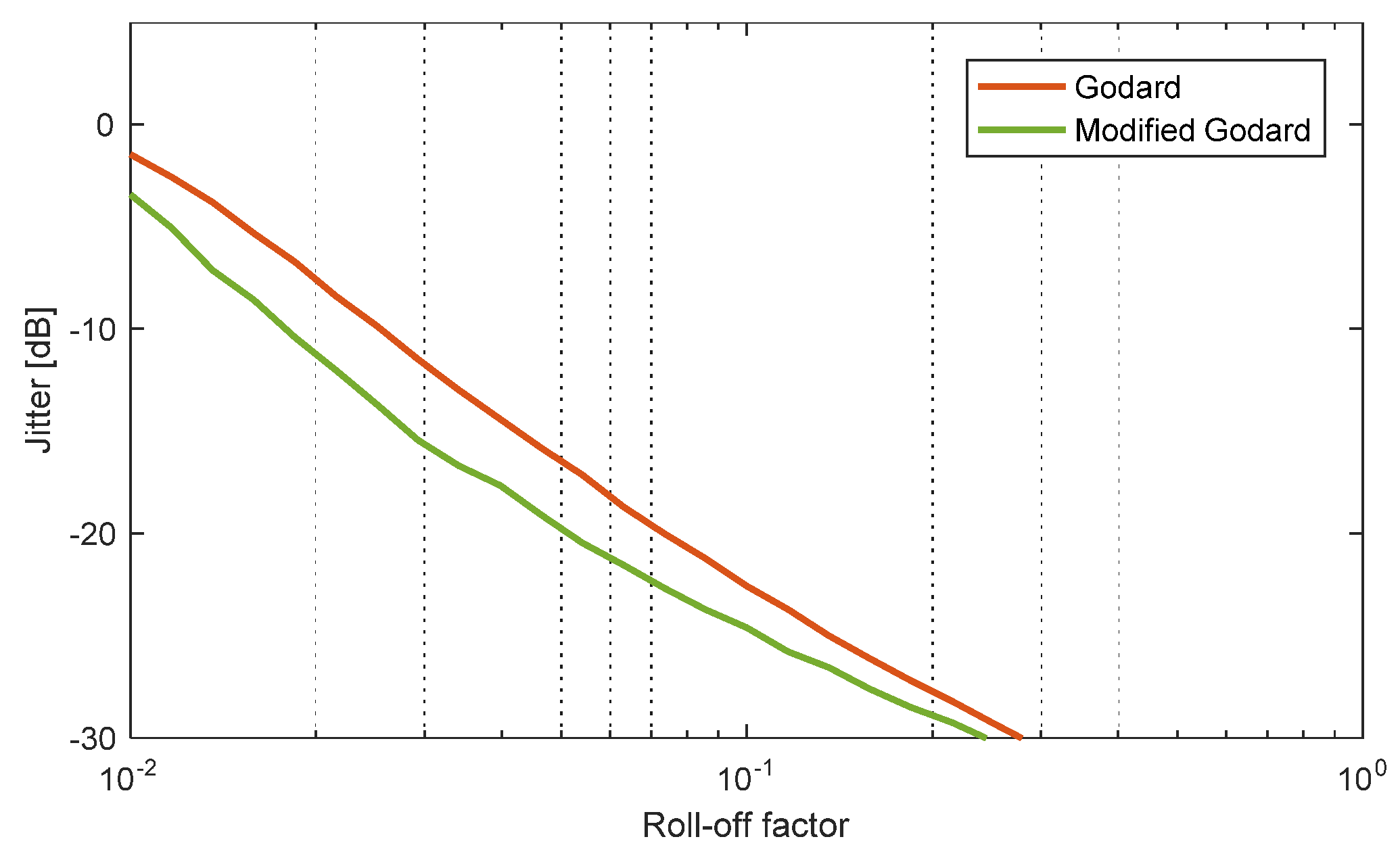
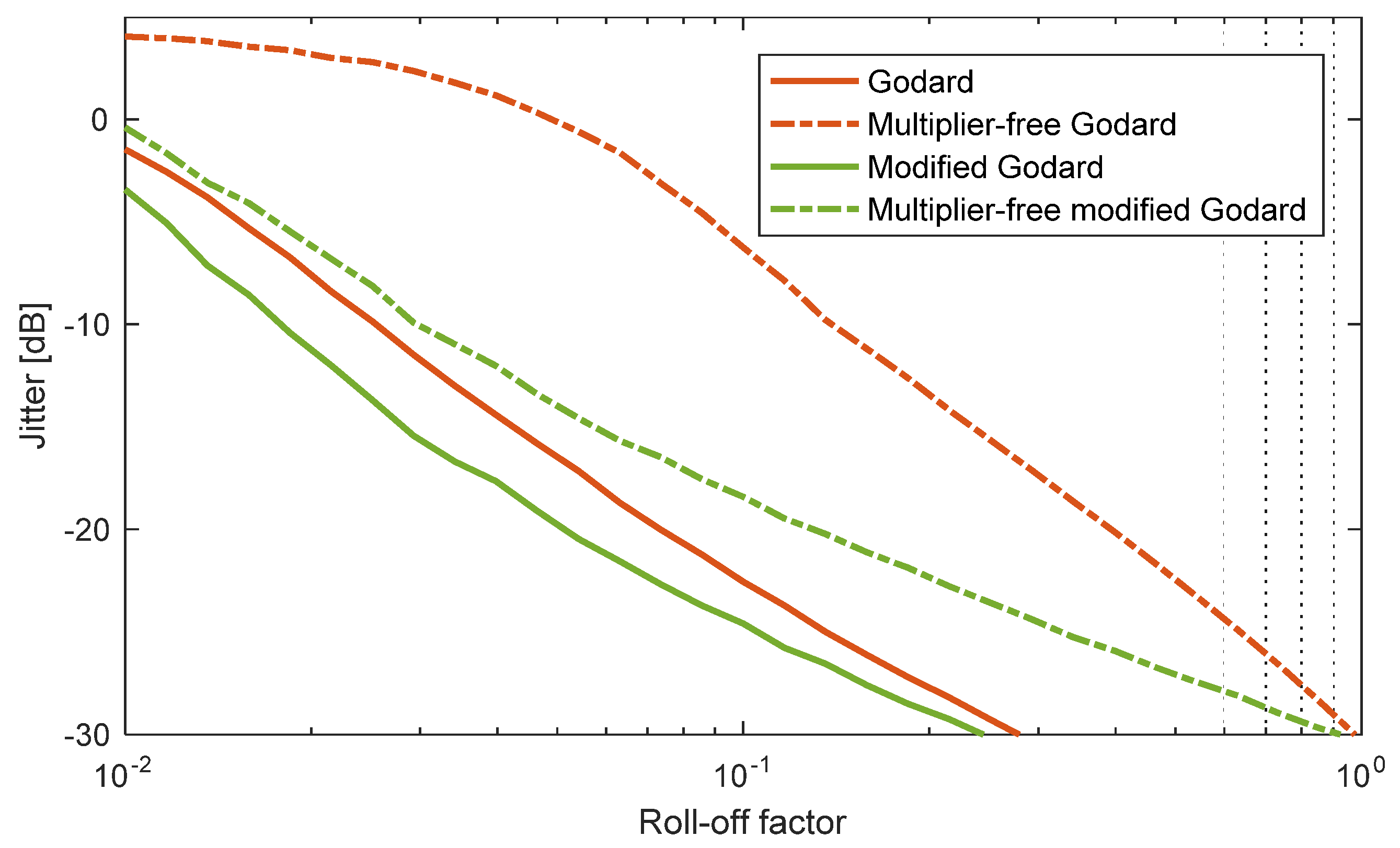
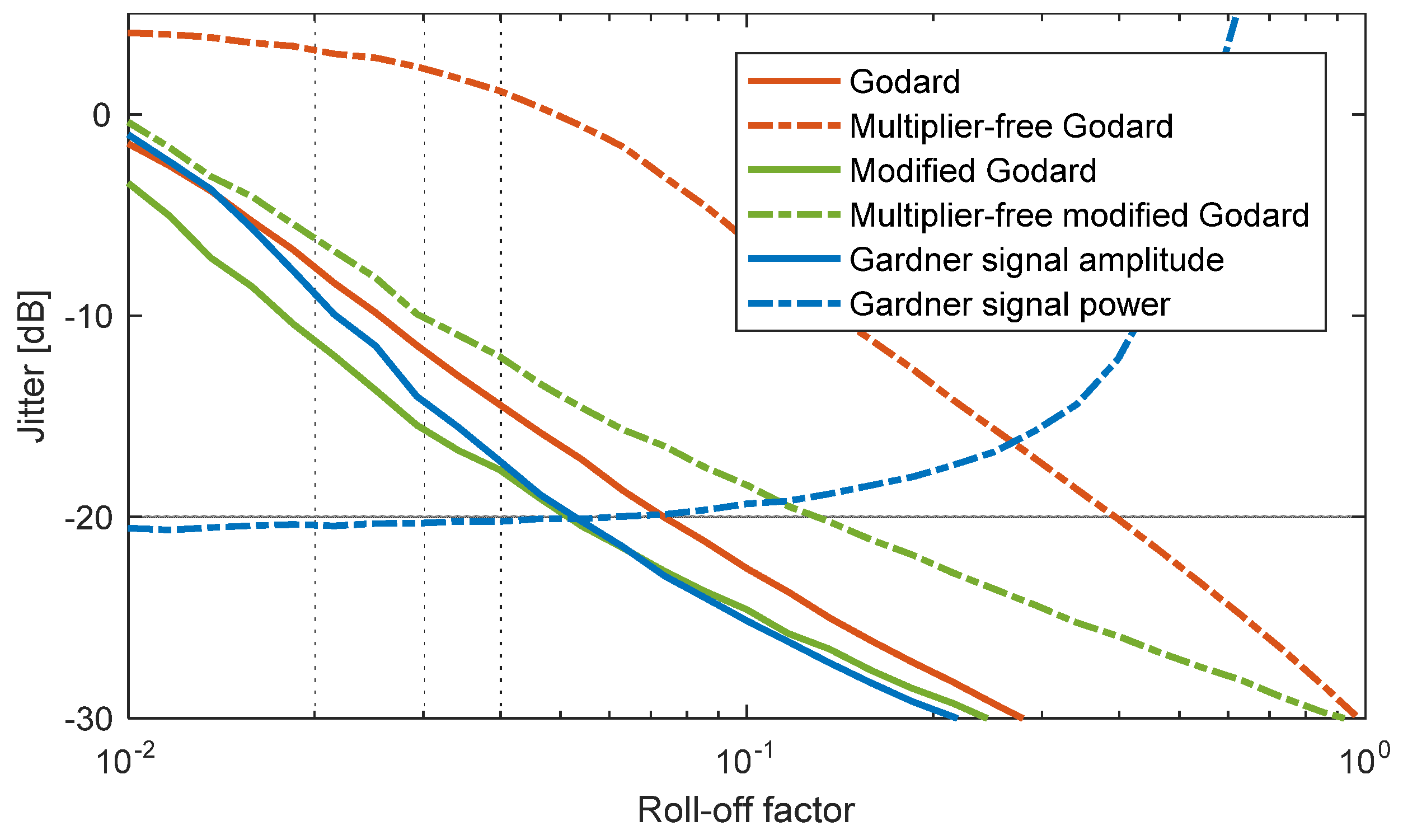
4. Comparison of the Modified Godard Algorithm to the Gardner Algorithm
5. Realization of Multiplier-Free Modified Godard on Real-Time Platform
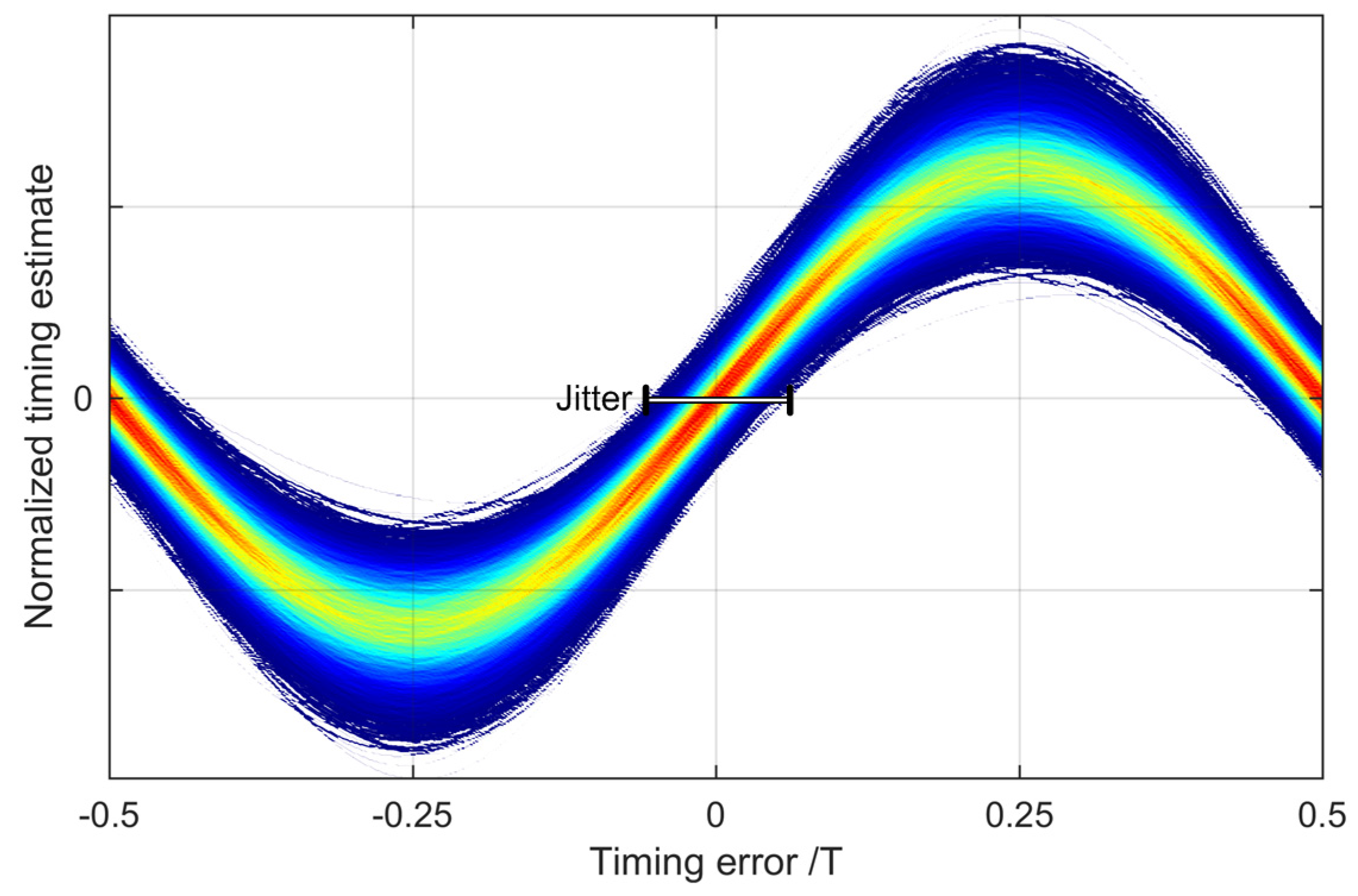
6. Performance Evaluation in Experiment
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gardner, F.M. A bpsk/qpsk timing-error detector for sampled receivers. IEEE Trans. Commun. 1986, 34, 423–429. [Google Scholar] [CrossRef]
- Alexander, J.D.H. Clock recovery from random binary signals. Electron. Lett. 1975, 11, 541–542. [Google Scholar] [CrossRef]
- Mueller, K.; Muller, M. Timing recovery in digital synchronous data receivers. IEEE Trans. Commun. 1976, 24, 516–531. [Google Scholar] [CrossRef]
- Oerder, M.; Meyr, H. Digital filter and square timing recovery. IEEE Trans. Commun. 1988, 36, 605–612. [Google Scholar] [CrossRef]
- Seung Joon, L. A new non-data-aided feedforward symbol timing estimator using two samples per symbol. IEEE Commun. Lett. 2002, 6, 205–207. [Google Scholar] [CrossRef]
- Godard, D. Passband timing recovery in an all-digital modem receiver. IEEE Trans. Commun. 1978, 26, 517–523. [Google Scholar] [CrossRef]
- Huang, L.; Wang, D.; Lau, A.P.T.; Lu, C.; He, S. Performance analysis of blind timing phase estimators for digital coherent receivers. Opt. Express 2014, 22, 6749–6763. [Google Scholar] [CrossRef] [PubMed]
- Josten, A.; Baeuerle, B.; Dornbierer, E.; Boesser, J.; Abrecht, F.; Hillerkuss, D.; Leuthold, J. Multiplier-Free Real-Time Timing Recovery Algorithm in the Frequency Domain Based on Modified Godard. In Proceedings of the Signal Processing in Photonic Communications, Boston, MA, USA, 27 June–1 July 2015; Optical Society of America: Boston, MA, USA, 2015. [Google Scholar]
- Zhou, X. Efficient clock and carrier recovery algorithms for single-carrier coherent optical systems: A systematic review on challenges and recent progress. IEEE Signal Process. Mag. 2014, 31, 35–45. [Google Scholar] [CrossRef]
- Farrow, C.W. A continuously variable digital delay element. In Proceedings of the IEEE International Symposium on Circuits and Systems, Espoo, Finland, 7–9 June 1988; IEEE: New York, NY, USA, 1988; Volume 2643, pp. 2641–2645. [Google Scholar]
- Diaz-Carmona, J.; Dolecek, G.J. Applications of Matlab in Science and Engineering—Fractional Delay Digital Filters; INTECH Open Access Publisher: Rijeka, Croatia, 2011. [Google Scholar]
- Mitra, S. Digital Signal Processing; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Josten, A.; Baeuerle, B.; Song, M.; Pincemin, E.; Hillerkuss, D.; Leuthold, J. Modified Godard algorithm applied on a fractional oversampled signal to correct cd, polarization, and cfo. In Proceedings of the Signal Processing in Photonic Communications, Vancouver, BC, Canada, 18–20 July 2016; Optical Society of America: Boston, MA, USA, 2016. [Google Scholar]
- Sun, H.; Wu, K.-T. A novel dispersion and pmd tolerant clock phase detector for coherent transmission systems. In Proceedings of the Optical Fiber Communication Conference and Exposition (OFC/NFOEC), Los Angeles, CA, USA, 6–10 March 2011. [Google Scholar]
- Stojanovic, N.; Chuan, H. Clock recovery in coherent optical receivers. In Proceedings of the Photonic Networks, 12. ITG Symposium, Leipzig, Germany, 2–3 May 2011; Optical Society of America: Los Angeles, CA, USA, 2012. [Google Scholar]
- Li, J.; Tipsuwannakul, E.; Eriksson, T.; Karlsson, M.; Andrekson, P.A. Approaching nyquist limit in wdm systems by low-complexity receiver-side duobinary shaping. J. Lightwave Tech. 2012, 30, 1664–1676. [Google Scholar] [CrossRef]
- Volder, J.E. The cordic trigonometric computing technique. IRE Trans. Electron. Comput. 1959, 8, 330–334. [Google Scholar] [CrossRef]
- Yan, M.; Tao, Z.; Dou, L.; Li, L.; Zhao, Y.; Hoshida, T.; Rasmussen, J.C. Digital clock recovery algorithm for nyquist signal. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference 2013, Anaheim, CA, USA, 17–21 March 2013; Optical Society of America: Los Angeles, CA, USA, 2013. [Google Scholar]
- Kikuchi, N.; Yano, T.; Riu, H.R. Fpga prototyping of single-polarization 112-gb/s transceiver for optical multilevel signaling with intensity and delay detection. J. Lightwave Tech. 2016, 34, 1762–1769. [Google Scholar] [CrossRef]
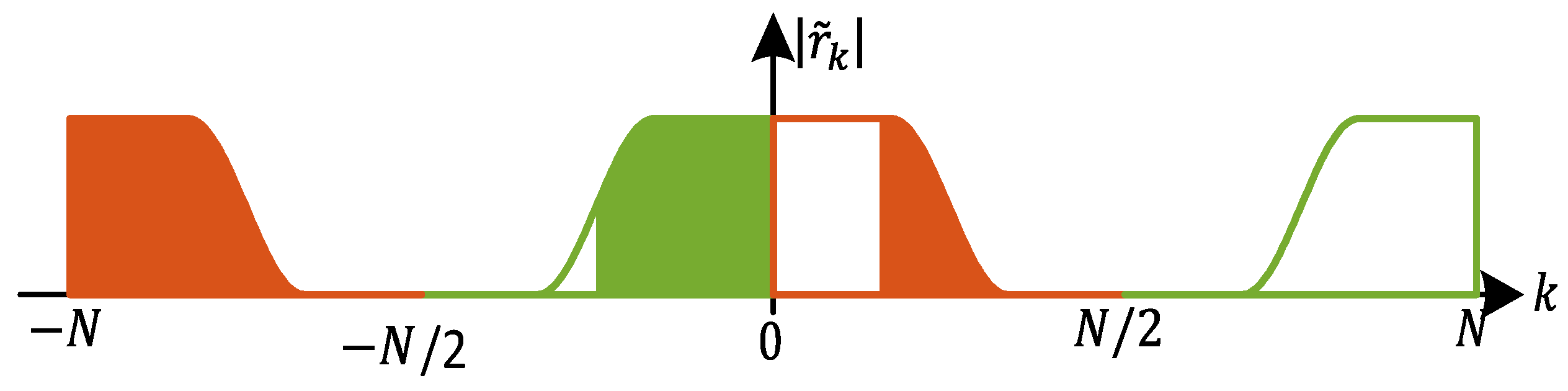
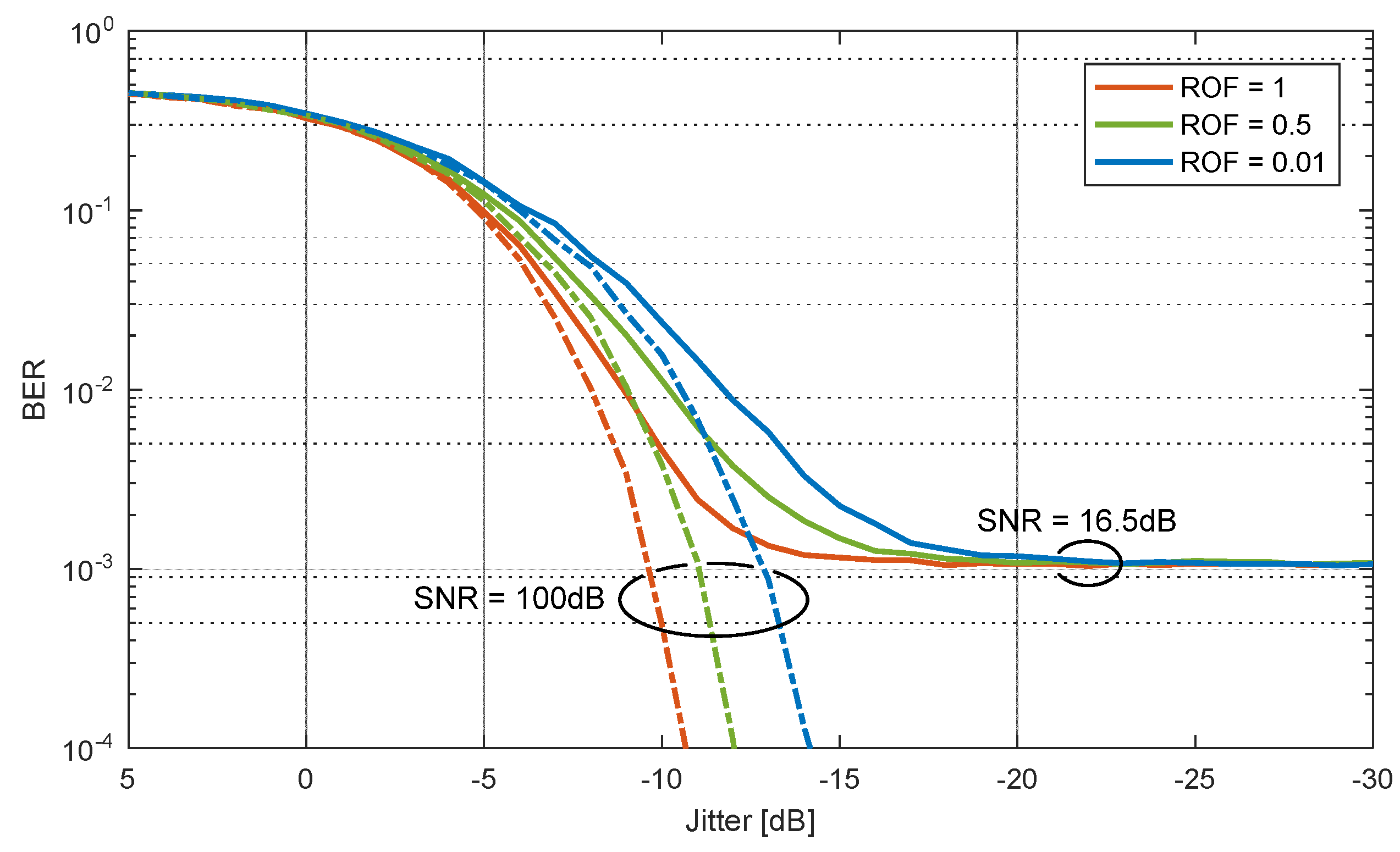
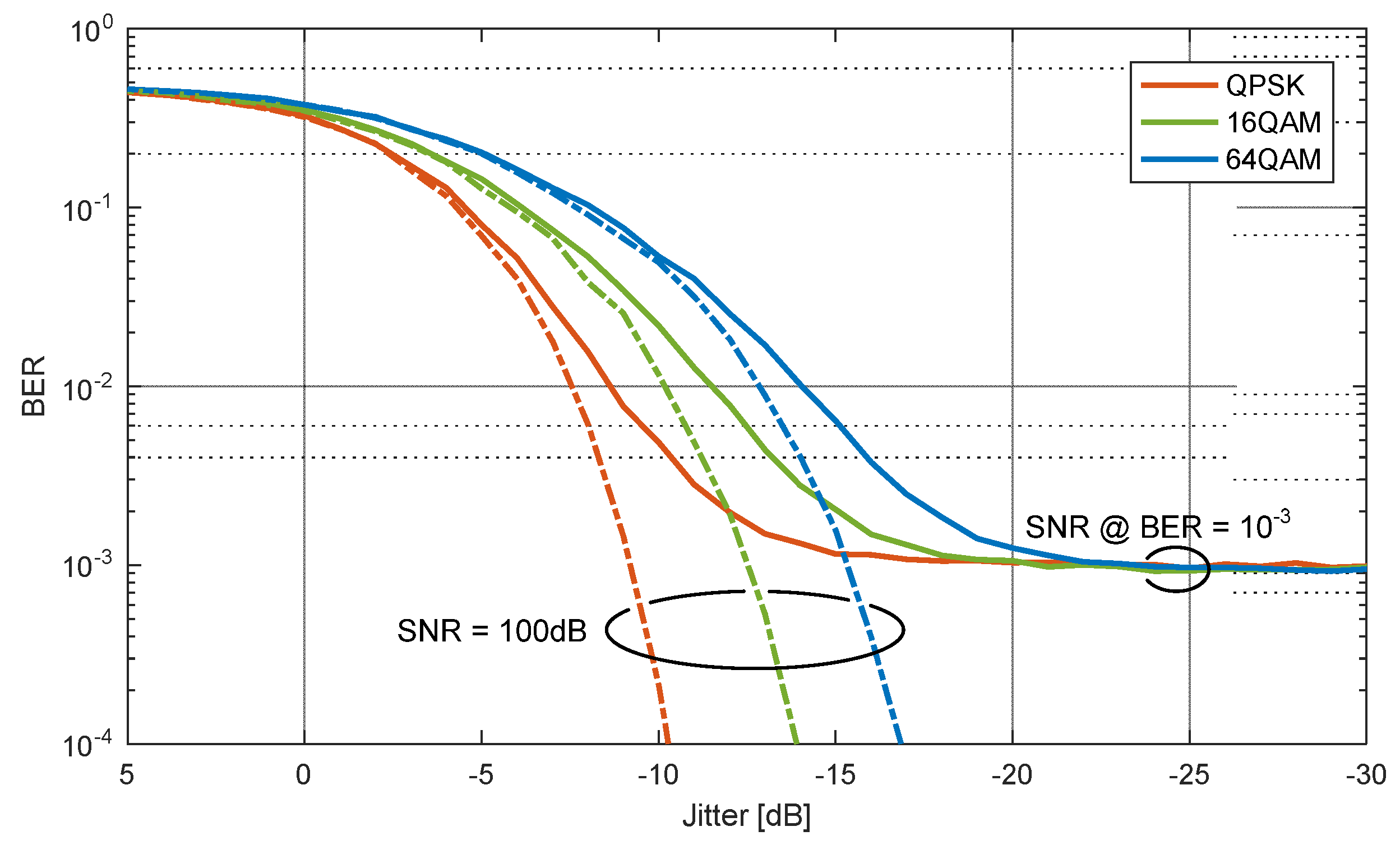



| Algorithm | Gardner | Modified Godard | ||
|---|---|---|---|---|
| Estimation | Correction | Estimation | Correction | |
| Lookup tables | 1435 (<1%) | 35,652 (8%) | 694 (<1%) | 1612 (<1%) |
| Flip-flops | 1932 (<1%) | 78,280 (9%) | 871 (<1%) | 11,641 (1%) |
| DSP | 97 (3%) | 2016 (56%) | 0 (0%) | 0 (0%) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Josten, A.; Baeuerle, B.; Dornbierer, E.; Boesser, J.; Hillerkuss, D.; Leuthold, J. Modified Godard Timing Recovery for Non Integer Oversampling Receivers. Appl. Sci. 2017, 7, 655. https://doi.org/10.3390/app7070655
Josten A, Baeuerle B, Dornbierer E, Boesser J, Hillerkuss D, Leuthold J. Modified Godard Timing Recovery for Non Integer Oversampling Receivers. Applied Sciences. 2017; 7(7):655. https://doi.org/10.3390/app7070655
Chicago/Turabian StyleJosten, Arne, Benedikt Baeuerle, Edwin Dornbierer, Jonathan Boesser, David Hillerkuss, and Juerg Leuthold. 2017. "Modified Godard Timing Recovery for Non Integer Oversampling Receivers" Applied Sciences 7, no. 7: 655. https://doi.org/10.3390/app7070655
APA StyleJosten, A., Baeuerle, B., Dornbierer, E., Boesser, J., Hillerkuss, D., & Leuthold, J. (2017). Modified Godard Timing Recovery for Non Integer Oversampling Receivers. Applied Sciences, 7(7), 655. https://doi.org/10.3390/app7070655





