1. Introduction
Aerodynamic design of helicopter rotors is a challenging task, especially when designing it for its optimal performance in both hover and forward flight conditions. There are two primary reasons for the trade-off problem between hover and forward flight: (1) the major two causes of rotor power loss—induced power loss and profile power loss—have different characteristics in different flight conditions. In hover and low advance ratio flight, the induced power loss dominates; while profile power loss rises with flight speed increases, and gradually becomes the major part; and (2) some rotor parameters have opposite effects on the two forms of power loss. For example, a large disk area benefits hover FM (figure of merit), but incurs a performance penalty in forward flight. The blade needs to have a large negative value for improving hover FM, while a large negative twist may cause forward flight performance to deteriorate [
1]. It is also known that a reduced rotor speed is advantageous in reducing rotor power requirements at moderate flight speeds, while a large rotor speed is necessary to maintain a high take-off capacity for the helicopter.
In recent years, many research studies have been published that solve such trade-off. Le Pape [
2] implemented three optimization algorithms in the 7A rotor and ERATO (Etude d’un Rotor A
roacoustique Technologiquement Optimis
) rotor aerodynamic designs. Constraint methods and weighting of objective functions (WOF) were applied to hover FM and forward flight rotor shaft torque balance. A genetic algorithm was implemented to optimize the ERATO rotor in three points: hover, 0.2 advance, and 0.4 advance. Léon et al. [
3] adopted the Nash game method for the ERATO blade to optimize blade planform, twist and chord distribution. A bi-objective strategy was composed, with hover FM maximization and rotor power minimization in a 0.334 advance ratio. The power was shown to decrease by 1% and the hover FM was shown to increase by 2% in the last Nash equilibrium point. A WOF (weighting of objective functions) method to consider both hover and forward flight performances was carried out by Imiela [
4], and weight analysis was done at a 0.4 advance ratio. The contribution of this study was to couple Computational Fluid Dynamics (CFD) and Computational Structural Dynamics (CSD) methods, providing a high-fidelity optimization framework. However, it should be noted that applying high-fidelity modeling methods to the optimization of an entire envelope leads to an expensive time-consumption problem. Leusink et al. [
5] carried out a multi-fidelity optimization. The low-fidelity model was utilized to reduce parameter space, and the high-fidelity surrogate model from CFD results was implemented in the optimization procedure. The set of Pareto optimal solutions with respect to hover and flight performances was found out through genetic algorithm. Bailly et al. [
6] recently studied the effects of blade twist and tip anhedral on required power. They demonstrated that the induced power loss could be reduced by 18.4% with an optimal blade twist, and by 18.8% with an optimal blade twist and anhedral.
Variable blade technology has been a focus over recent decades. It has been demonstrated to be a promising way of improving rotor performance [
7,
8]. In general, variable blade technology can be classified into variable blade geometry and variable rotor speed. The variable-speed rotor adopts a transmission system or wide speed range engine to change revolution, ensuring that operation is optimal in different conditions. Reduced rotor speed is advantageous to improving hover FM, saving energy in forward flight and extending the helicopter flight envelope [
9,
10]. Boeing applied an optimum rotor system (ORS) to unmanned aerial vehicles (UAV) A160/A160T in the last century, which achieved continuous flight for 18.7 h in 2008. The maximum flight speed reached up to 263 km/h in a real flight test. Guo [
11] modeled UH-60A; and optimized rotor speed at different forward velocities, rotor required power, and torque were investigated in this study. A power reduction of up to 15% was confirmed with the optimal rotor speed, while a 14% increase of shaft torque was obtained. Garavello and Benini [
12] combined the UH-60A and GE-T700 models to reveal benefits and drawbacks of a variable-speed helicopter, and found that a wide speed range turboshaft engine may be required in order to save energy in an ORS-helicopter. Han and Barakos [
13] examined the benefits from variable tail rotor speed, which concluded the fact that optimal tail rotor speed could achieve greater power saving in cruise than in hover, and a high advance ratio. The maximum power reduction was up to 30% of the baseline tail rotor.
Variable blade geometry usually includes variable span, blade twist and chord extension. Because variable blade geometry allows the rotor to change to an optimal state based on flight conditions, it is the preferred way of balancing hover and forward flight performances. Khoshlahjeh and Gandhi [
7] examined the benefits attained through chord extension morphing and variable rotor speed in a Black Hawk UH-60A helicopter. It was found that the required power could be reduced by 19.5% at sea level with 16,000 lbs gross weight, and by 13.4% at sea level with 183,000 lbs, with rotor speed set to 85% of the baseline. Ramanujam and Abhishek [
14] applied a particle swarm optimization for the UH-60A rotor blade, improving power consumption by employing variable radius, chord, twist, revolution and trailing-edge plate extension.
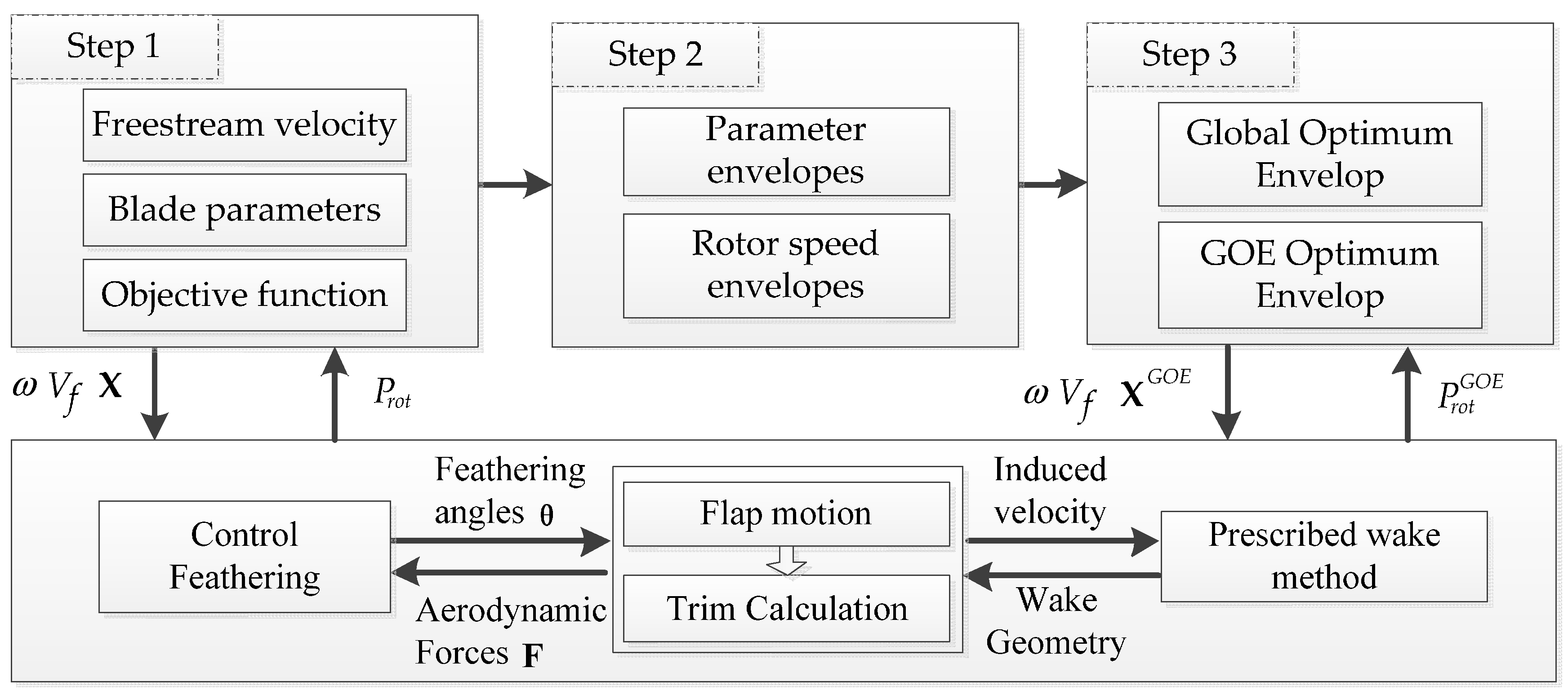
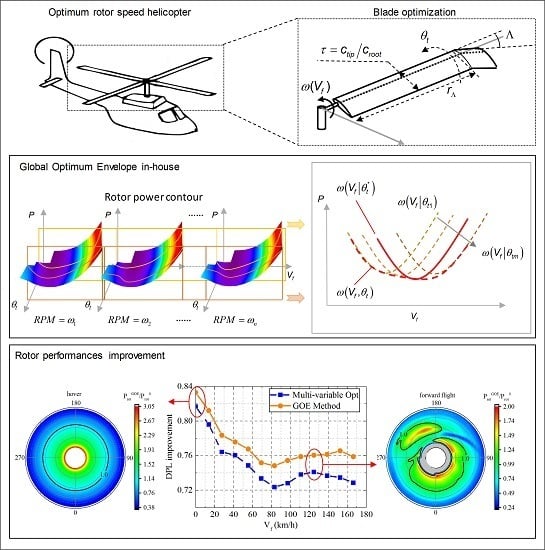
The main purpose of this study is to determine the optimal blade parameters in an ORS-helicopter through an aerodynamic design considering hover FM and forward flight performance simultaneously. The design variables include blade twist, taper ratio, blade tip sweep, and rotor speed. The quasi-static solutions of flap motion and prescribed wake are adopted in this study. The main contribution of this study is to establish a novel design method called Global Optimum Envelope (GEO) for blade optimization across the entire flight condition. The proposed GOE method integrates with a comprehensive helicopter code developed in-house, making the design procedure more efficient. It separates aerodynamic design into a global optimization step, allowing parameters to change with freestream velocities; and a secondary-optimization step, searching for the solution closest to the global optimization: First, a multi-variable hypersurface representing the relationships among objective, blade parameters and freestream velocities is established, and section lines of the objective corresponding to different rotor speeds are found. Second, the minimal objective value is obtained by rotor speed optimization at each of the given blade parameters. Finally, a global optimized objective with freestream velocity is identified at the envelope, with all blade parameters included; and the parameters with optimal rotor speed are determined as those optimal for the ORS-helicopter by minimizing the deviation between objective values and global optimized values with respect to freestream velocities. Another contribution of this study is to derive rotor power loss based on blade element theory, picking out the parts related to blade parameters and forming an objective function in rotor optimization. The effects of blade variations on rotor performance are investigated in this study. A multi-variable optimization is implemented for overall freestream velocities. The results of the GOE method and its comparison with variable blade technology are given.
3. Validation
An ultra-light helicopter is used as the baseline for the GOE method in this study. The helicopter parameters are listed in
Table 1.
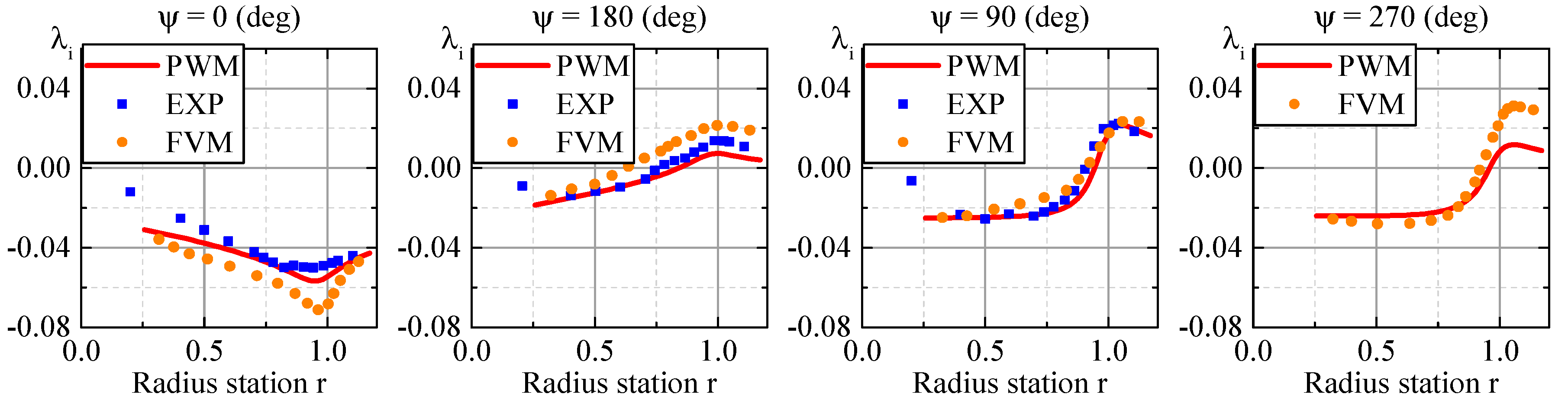
Since there is a lack of wake data, the 2MRTS wake experiment [
19,
20] is adopted to validate the prescribed wake method (PWM) used in this study. The following conditions are implemented in the validation: thrust coefficient
, advance ratio
, and rotor shaft
. The induced velocity is computed on a plane one-chord above TPP, the same as the experiment setting. Time-average induced velocity is shown in
Figure 3. Comparing with experimental data (EXP) [
19] and free vortex method (FVM) [
21], it is well understood that the prescribed wake method (PWM) is able to capture the non-uniform distribution of induced velocity, especially in the blade tip region. Slight deviations can be seen in the root region, which may be due to ignoring the root cut-out effect in this study, where root vortices may exist [
20]. The strongest downwash presents near the tip for a rotating blade; hence, non-uniform distribution and rotor performance estimation are a major responsibility in induced velocity.
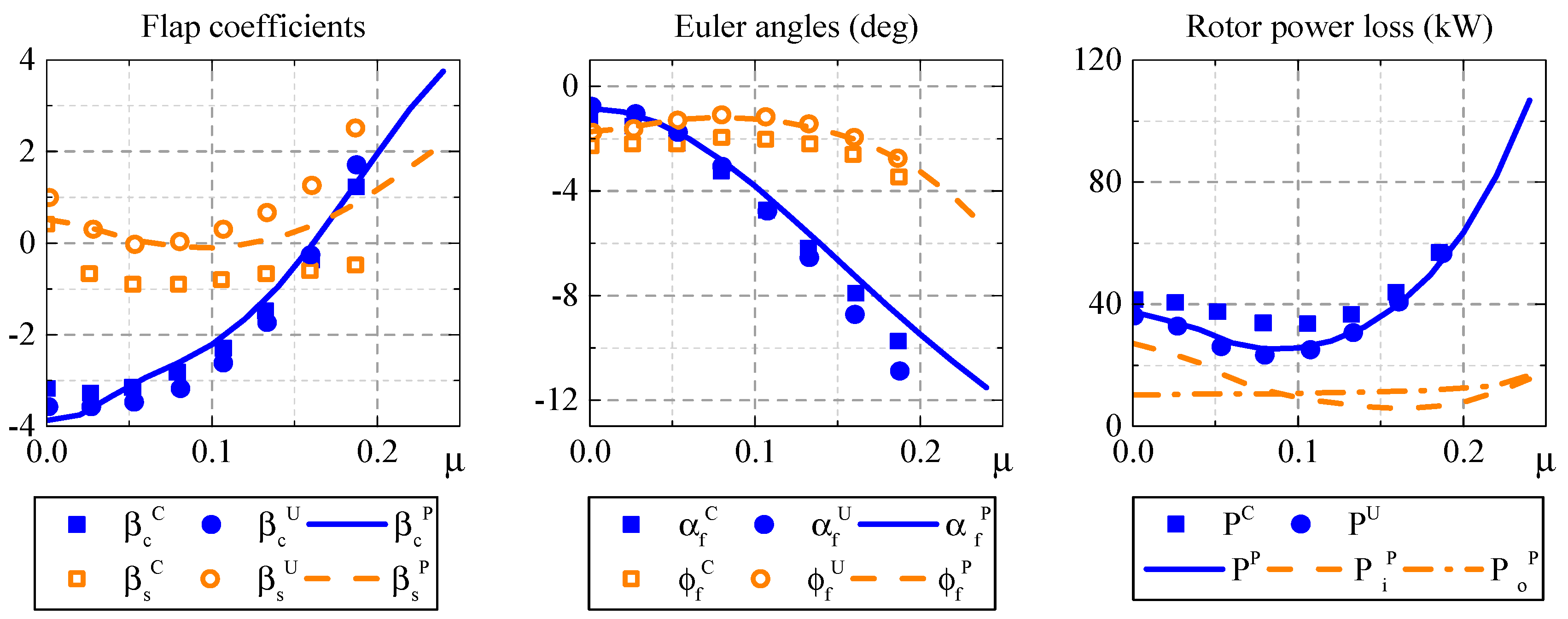
Figure 4 shows the trim results of the ultra-light helicopter, comparing with UMARC and CAMRAD II results from Shen et al. [
22]. With the increase in flight speed, the longitudinal flap coefficient
increases, providing propulsive force through the tilted TPP. The lateral trim results at present have the same trends as UMARC and CAMRAD II. With an increase in flight speed, a steady deviation of about 1 degree between present simulation and CAMRAD II always exists, the same as in the UMARC result. This may be caused by the inflow model, as Shen, Chopra and Johnson [
22] have mentioned. With a high advance ratio, the lateral flap coefficient
rises more slowly than UMARC, and may benefit from the prescribed wake method. As for rotor power loss, minimal consumption is achieved with the medium advance ratio, due to a reduction of induced power
and an increase of profile power
as flight speed rises. With flight speed increases,
is lower than in hover, which is because there is more mass flux contributed by freestream in forward flight, a bit of induced inflow can produce adequate thrust for the entire helicopter. Therefore, it can be seen that
is larger than
in forward flight, and becomes the bottleneck in performance improvement.
Figure 5 depicts the time history of
and
of a blade. In hover, the time histories of both power losses are steady, because of the symmetric aerodynamic environment; whereas in forward flight,
reduces from 0-degree azimuth to 180-degree azimuth, and becomes negative when the induced flow is upwash. The larger
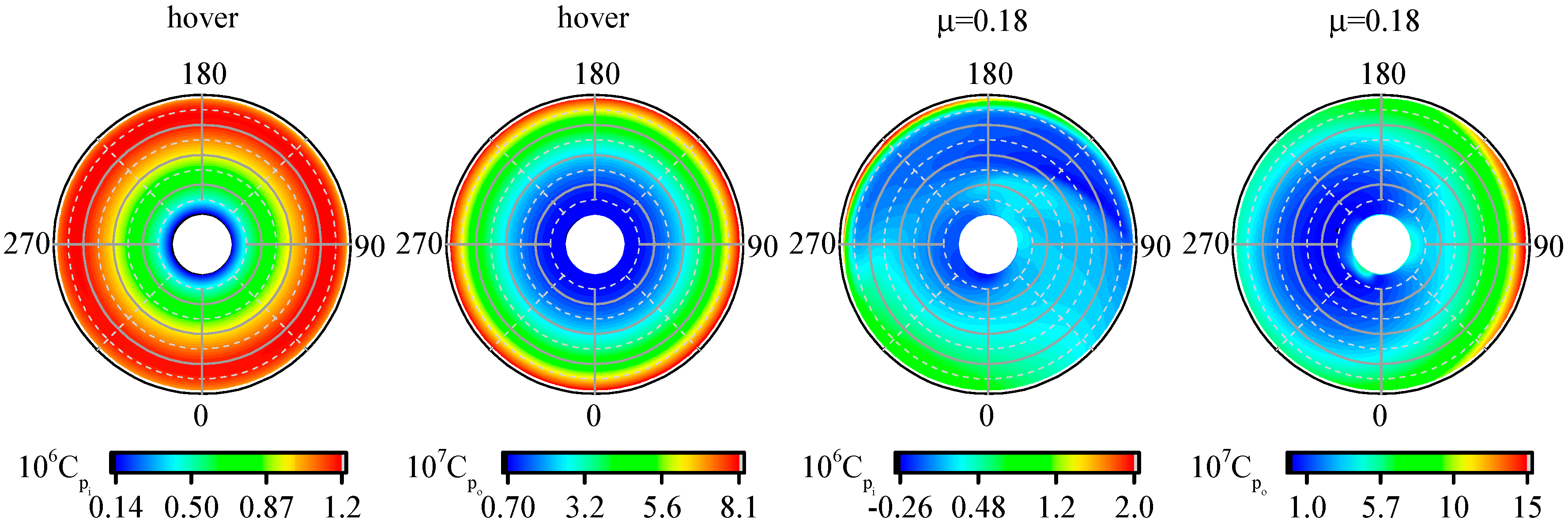
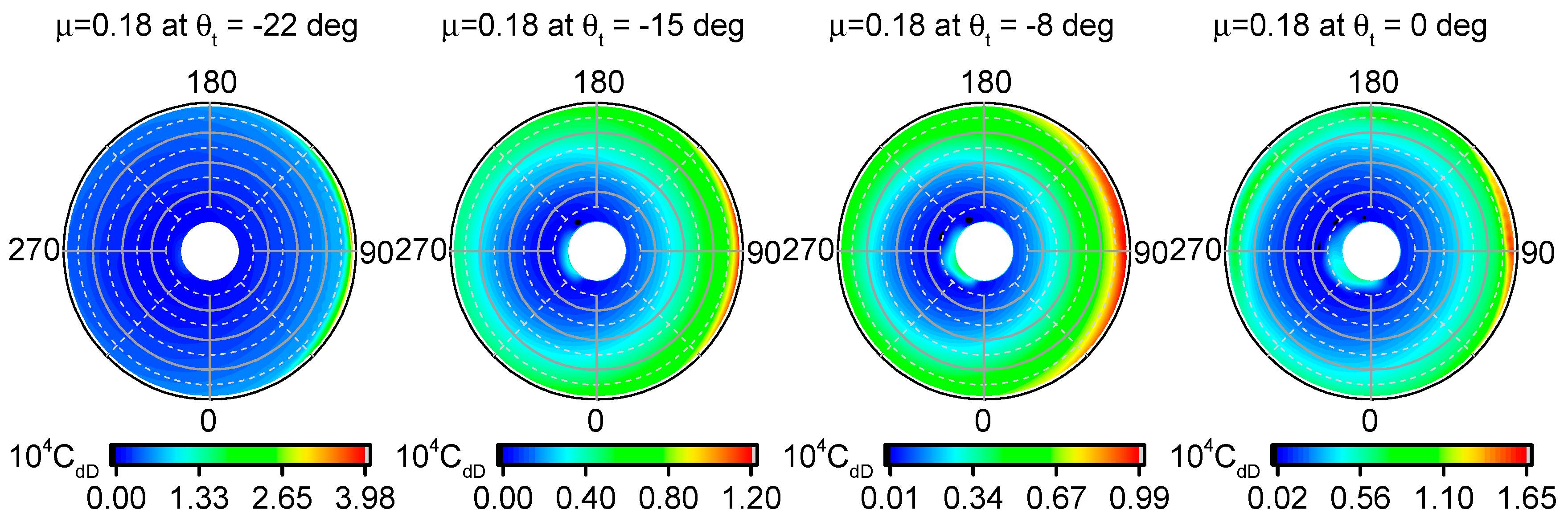
is consumed near the blade tip, especially in the advancing blade when dynamic pressure is highest. Therefore, a tapered or tip swept blade could be implemented to reduce rotor profile power loss in this study.
5. Conclusions
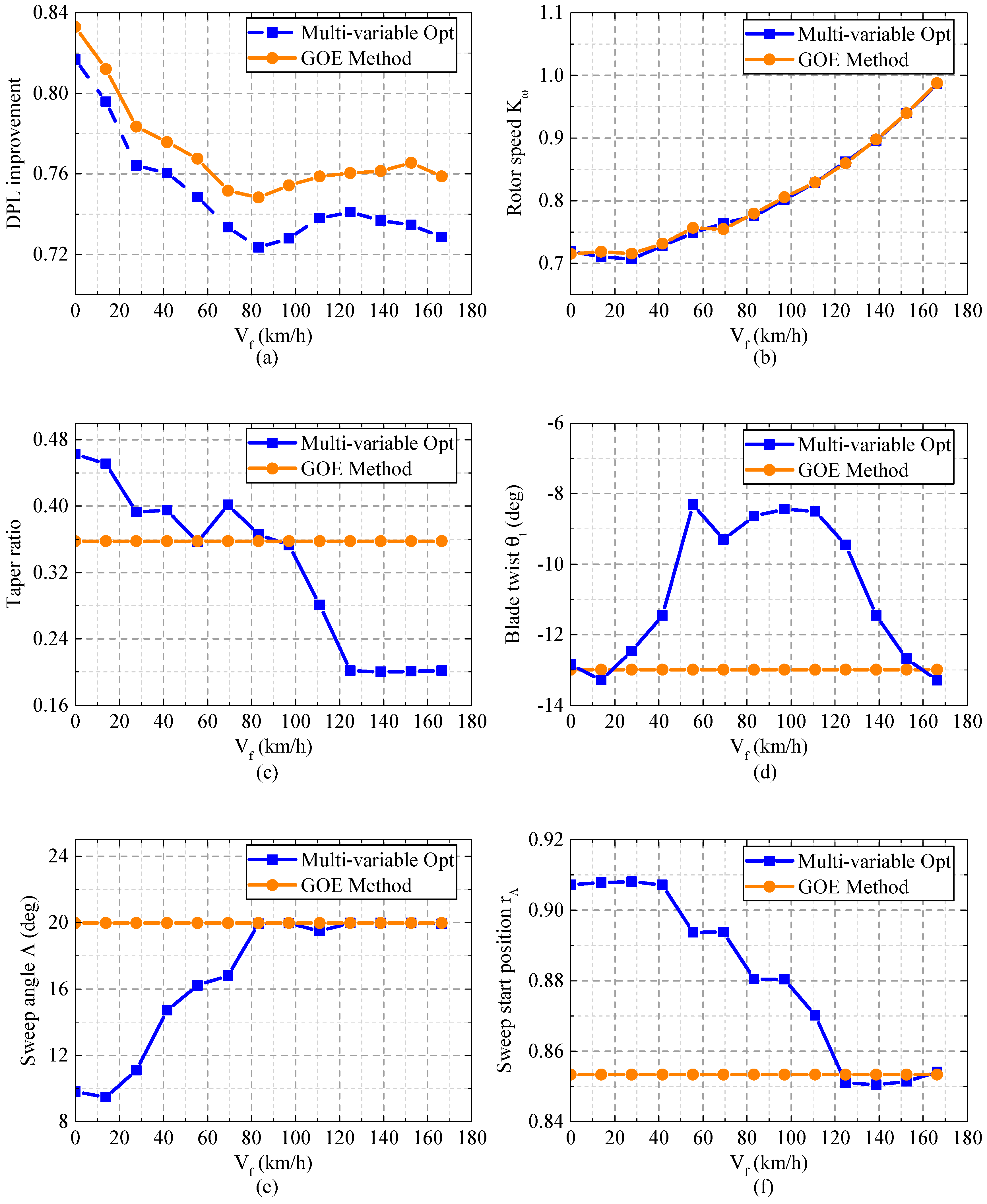
This study proposes a novel blade optimization method in ORS-helicopters, called GOE, achieving hover and forward flight balance at different freestream velocities. The GOE method integrates with an in-house developed rotorcraft comprehensive code, and is developed to optimize blade twist, taper ratio, tip sweep and rotor speed in ORS-helicopters. The proposed GOE method separates the design procedure into a global optimization step and a secondary optimization step. The global step solves the optimized blade parameters and rotor speed in different freestream velocity conditions, and the secondary step solves the fixed blade parameters and varied rotor speed, with the corresponding objective function closest to the global solution. This study derives the rotor power loss based on blade element theory, and defines DPL as an objective function, which is demonstrated to represent a direct measure of rotor performance. It is also shown to advantageously represent hover and forward flight performances.
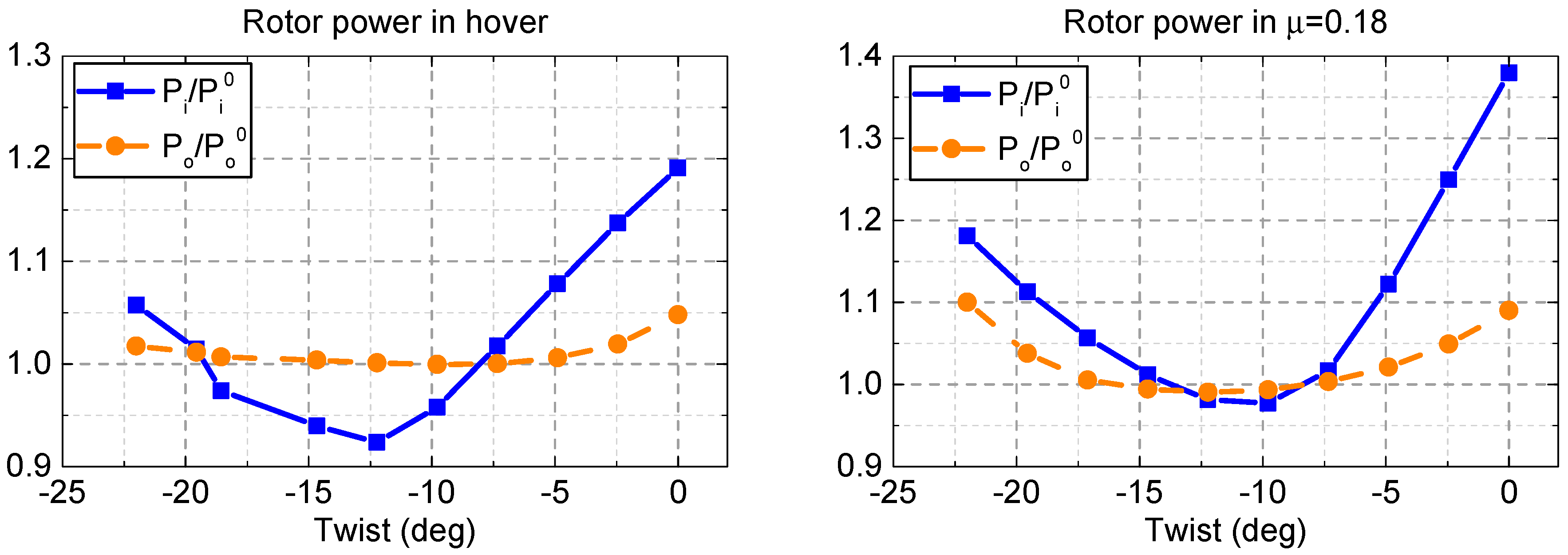
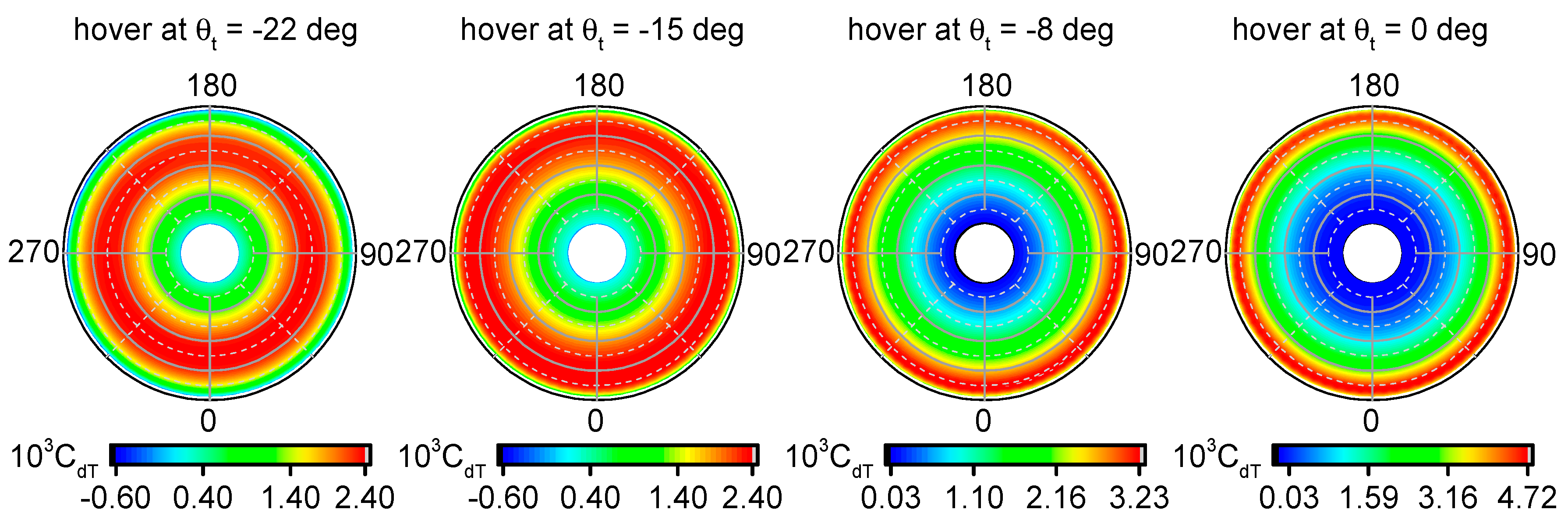
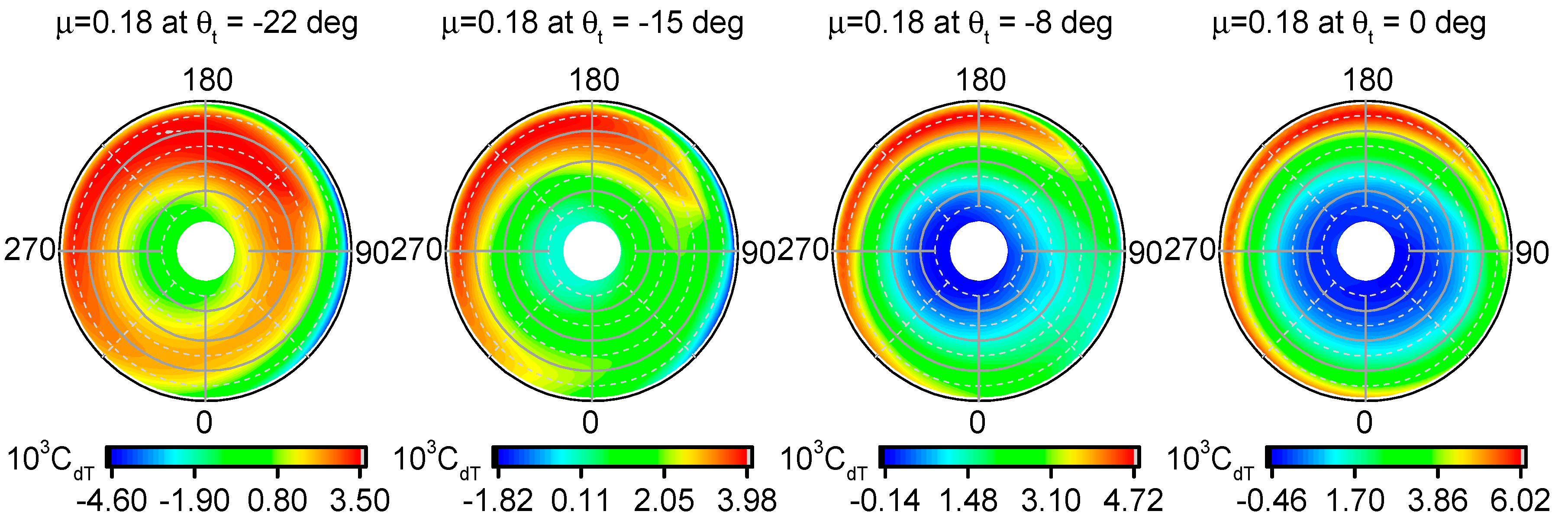
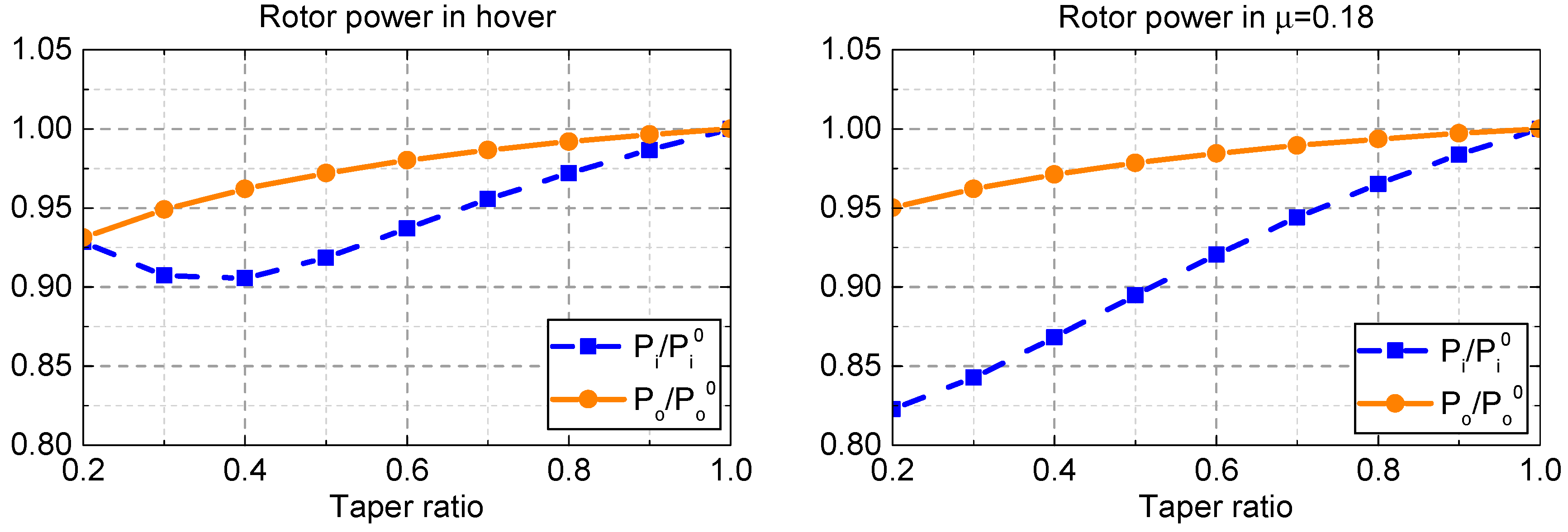
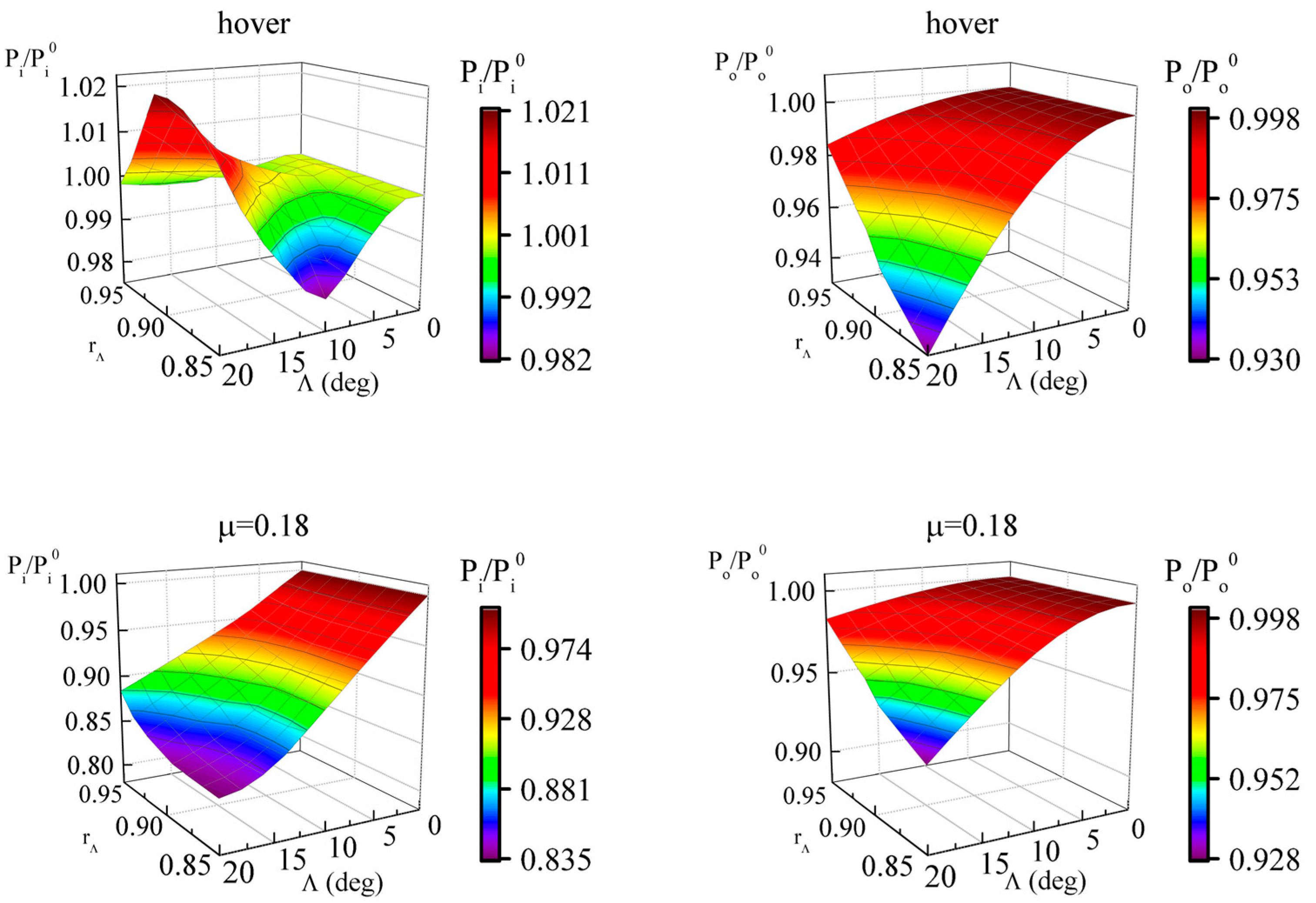
This study investigates the effects of blade parameters and rotor speed on induced power and profile power respectively. It reveals that induced power loss is sensitive to blade twist both in hover and forward flight. The region of large blade section lift moves inboard when twist becomes more negative, which makes its distribution close to uniform. A minimal induced power loss with moderate twist is obtained with the synthesized effect of induced inflow and blade section lift. However, profile power dominates in forward flight, and a more twisted blade will induce larger drag coefficients at the blade tip, damaging rotor performance. The blade taper ratio is also investigated in this study. For eliminating the effect of rotor solidity, the study constrains the thrust-weighted solidity to remain unchanged in the GOE scheme. It is concluded that a tapered blade is of benefit to rotor performance. The small tip chord reduces aerodynamic lift and drag near the blade tip. With a slightly elongated chord near the blade root, in accordance with the thrust-weighted solidity condition, only a small portion of profile power loss occurs in the region. It is concluded that significant benefit is attained through the swept back in the blade tip. The sweep angle is limited to within 20 degrees, and the start point is forced to between 0.85 and 0.95 radius station. With an increase in sweep angle, the chord in the blade tip effectively becomes lower. It reduces aerodynamic lift in the tip region and benefits induced power loss in most conditions. Similar characteristics can be observed in sweep start variations. A greater contribution to rotor performance is attained by the tip sweep in forward flight. A reduced Mach number as a result of sweeping the tip backward could weaken the compressibility effect in an advance blade, and decrease drag coefficients and the profile power consumed. The reduction of induced power loss is up to 16.5%, and of profile power loss is up to 7.2% in , for a blade with 20-degree sweep from a 0.85 radius station.
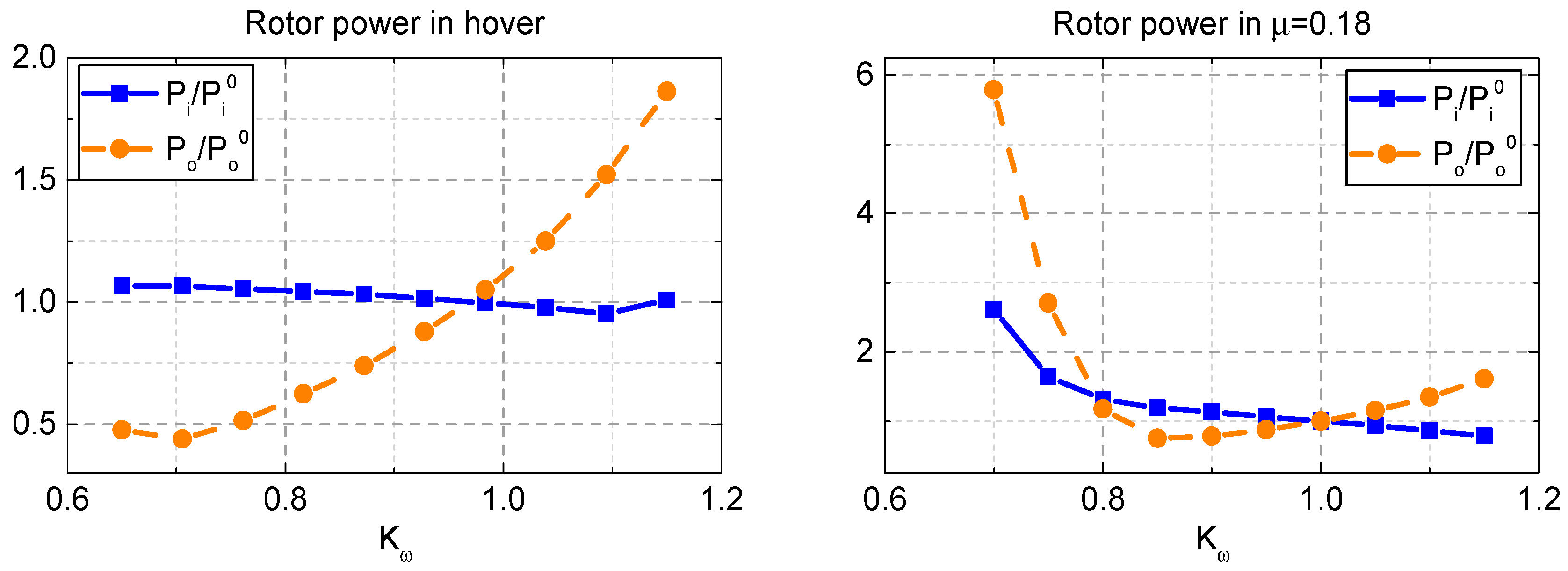
It is concluded that profile power loss is more sensitive to rotor speed than induced power loss. In hover, about a 56.1% improvement is achieved in profile power loss at a rotor speed of 70.5% of baseline. In forward flight in this study, profile power is reduced to 75.3% at 85% rotor speed. It is concluded that a variable rotor speed can provide great performance improvement in both hover and forward flight. There are two opposite impacts of rotor speed on performance. On one hand, profile power loss becomes lower with dynamic pressure decreases as a result of a reduced rotor speed. On the other hand, a larger drag coefficient arises for a reduced revolution rotor as a consequence of requiring a higher feathering angle to trim. A dramatic rise of profile power loss is encountered in stall. Therefore, the possible rotor speed range becomes narrower in forward flight.
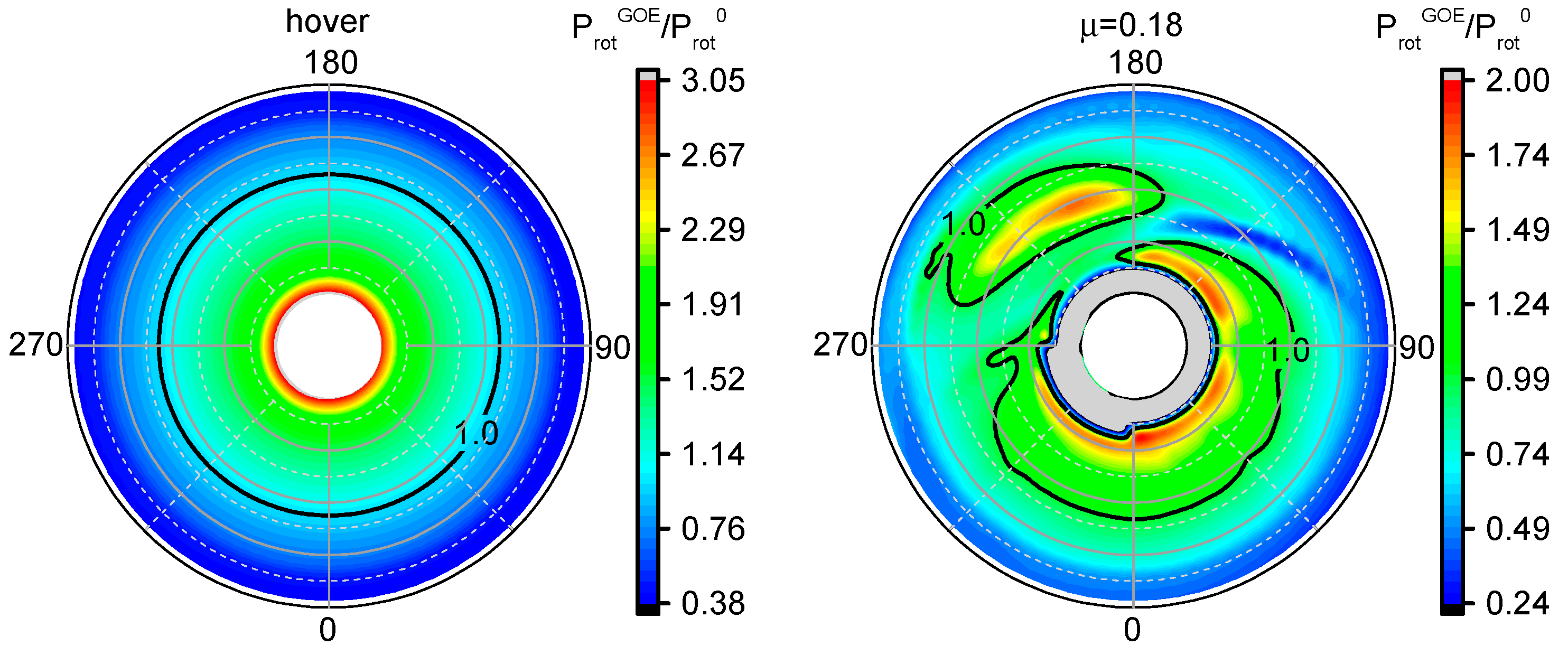
A multivariable optimization is implemented as the first two steps of the GOE method. DPL improves at different freestream velocities, and the minimum improvement is of 18.3% in hover conditions. It can be concluded variable blade technology is of great significance in improving rotor performance. However, it has so far been difficult to put it into production. The proposed GOE method is implemented for designing a rotor blade for an ORS-helicopter. Through the GOE method, the rotor performance significantly improves. The minimum improvement is by 16.7% in hover. With an increase in freestream velocity, a rotor designed using the GOE method achieves better improvement as a result of tip sweep design. In cruise flight and maximum flight, the improvement in DPL is about 24%. It is concluded that a rotor designed by the GOE method balances hover and forward flight better.
The proposed GOE design scheme is demonstrated to be effective at determining the optimal blade parameters in an ORS-helicopter, and balance the hover and forward flight performances. We firmly believe the concept of the GOE method could be beneficial to solving the multi-parameter optimization design problems of complex systems. Additionally, there is a relationship among rotor speed, required power and shaft torque. We will extend the GOE method into multi-objective optimization design problems in the future, such as the balance of shaft torque, required power and rotor speed in an ORS-helicopter.