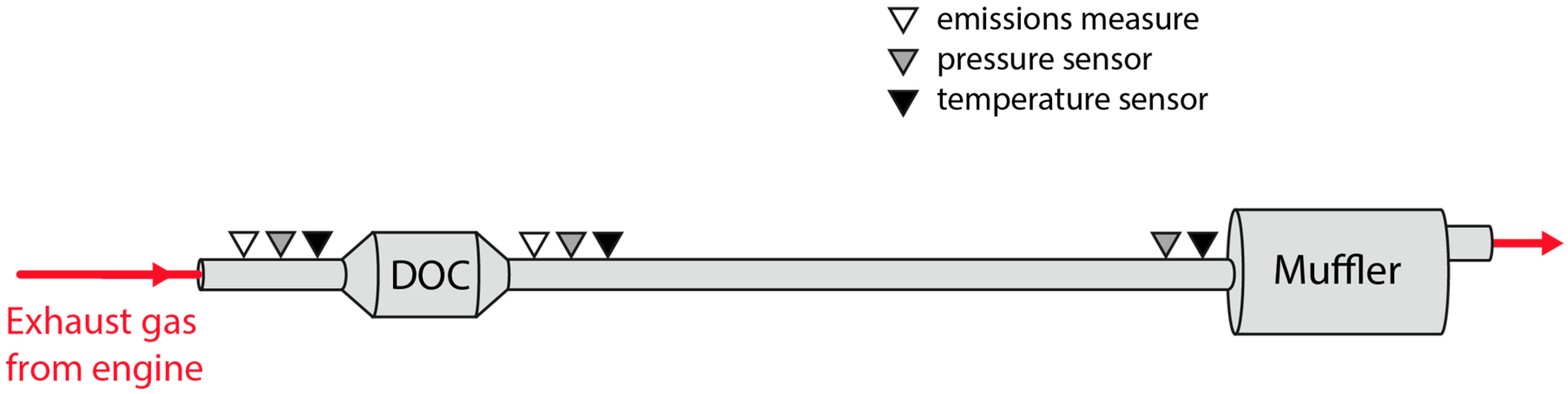
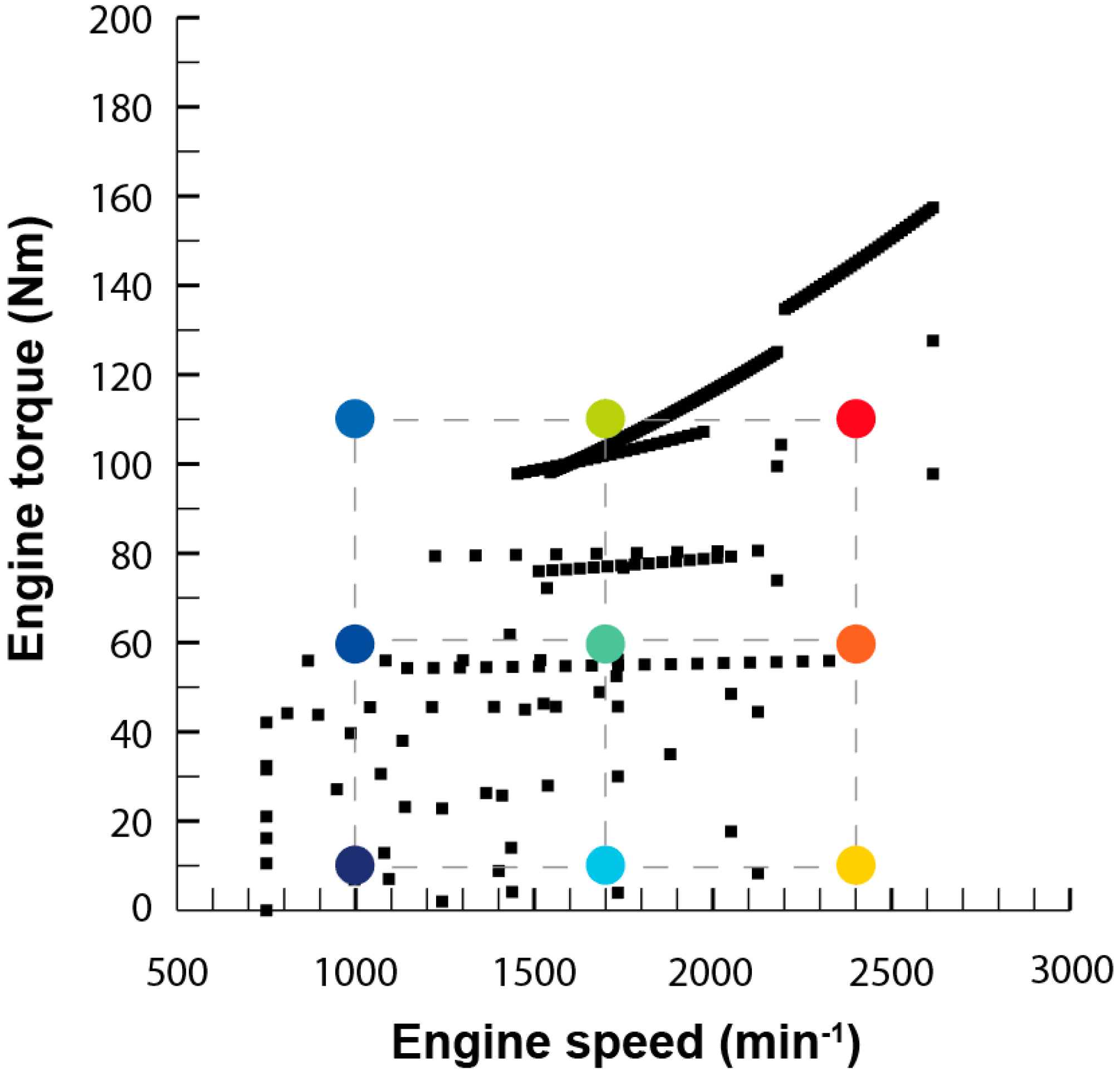
1. Introduction
Around a third of the fuel energy in a light-duty diesel engine is wasted through the exhaust system [
1]. Rising awareness of environmental issues together with the fuel economy have encouraged research on energy recovery [
1,
2] from exhaust gas. An obvious first step for energy recovery is evaluating the heat source. The nature of exhaust flow changes during engine operation. Hence, there is a need for models that allow evaluating exhaust gas in a cost- and time-efficient manner under different engine conditions.
Computational fluid dynamics (CFD) is becoming a very popular tool for numerical predictions in the automotive industry. CFD models are employed in five major areas: vehicle aerodynamics, thermal management (cooling and climate control), cylinder combustion, engine lubrication and exhaust system performance. The main applications of CFD in exhaust systems are: flow distribution in the front of the monolith, pressure loss through exhaust system, skin temperature prediction, heat loss analyses and emission-related studies [
3].
High levels of energy lost through engine exhaust have brought attention to heat transfer in exhaust systems and how to model associated phenomena.
In Konstantinidis et al. [
4], the status of knowledge regarding heat transfer phenomena in automotive exhaust systems was summarized, and a transient model covering diverse exhaust piping configurations was presented. Using this model, Kandylas et al. [
5] studied heat transfer in automotive exhaust pipes for steady and transient conditions. It is stated that the code is suitable to support a complete and efficient methodology for design optimization.
Not only are exhaust heat transfer and temperature models important for energy recovery, but also for on-board control and diagnosis of the after-treatment system. In the work of Guardiola et al. [
6], diesel oxidation catalyst (DOC) inlet temperature was modelled depending on fuel mass flow and engine speed using an engine map look-up table.
Traditionally, one-dimensional (1D) simulations using in-house or commercial codes have been used to study exhaust flow. In Shayler et al. [
7], a 1D model of system thermal behavior was developed. The exhaust system is modelled as connected pipe and junction elements with lumped thermal capacities. Heat transfer correlations for quasi-steady and transient conditions were investigated. The computational model supports studies of exhaust and after-treatment system design, the investigation of thermal conditions, and performance characteristics. Model predictions and experimental data were in good agreement.
In Kapparos et al. [
8], a 1D heat transfer model in an automotive diesel exhaust is presented. The external natural convective heat transfer coefficient was given by Churchill and Chu’s correlation. A sensitivity analysis of the main variables (heat transfer coefficient, external pipe emissivity and others) affecting heat transfer in exhaust pipes was carried out. Fu et al. [
9] developed a 1D model of an exhaust pipe (without the catalytic converter). Apart from typical variables studied, effects of pipe geometry and flow regime were investigated.
One-dimensional tools have the advantage of shorter computational time, but the accuracy of the results is limited by their inability to simulate 3D flow effects in regions such as the inlet and outlet cone. Usually strong turbulent flow exists when angled and asymmetrical cones are presented [
3].
Three different approaches were used in Fortunato et al. [
10] to simulate the exhaust and underbody of the car: 1D, 3D finite elements and 3D complete thermo-fluid-dynamics. Both 3D models allowed to detect the most critical points in terms of higher temperatures
In Chuchnowski et al. [
11], temperature distribution and heat flow analyses on the exhaust system of a mining diesel engine to determine technical parameters of a heat recuperation system are presented. Three-dimensional numerical simulations show it is possible to develop a suitable design of an energy recovery device.
Simulations in a coupled three-dimensional thermal model including the underhood, underbody and exhaust systems of a vehicle were conducted by Guoquan et al. [
12]. Pulsating flow and steady flow effects were compared. Pulsating exhaust showed an enhancement of more than a 10% in heat transfer. Influence of this effect was higher at the final components of the exhaust, such as the muffler.
Research has also been focused on finding optimal position for exhaust components. Durat et al. [
13] compared experimental and CFD heat transfer results in an exhaust system of a spark-ignition engine. An optimal position of a close-coupled catalytic converter in terms of light-off time was found using the CFD model. Liu [
14] developed a 3D exhaust model to study the optimal position of a heat recovery device. Three different simulations were carried out varying the position of a thermoelectric generator along the system. Higher surface temperature and lower backpressure were obtained when the recovery device was placed between catalytic converter and muffler. The influence of materials and insulation on heat transfer in catalytic converters has also been discussed employing a 3D model [
15].
In the same way preceding authors have employed CFD simulations successfully to find an optimal position for exhaust components or to assist in their design, CFD can also be used to gain knowledge of the relevant characteristics of the flow in terms of its usage in energy recovery. Previous works [
16] state that knowledge of heat transfer within the gas is critical to enhance harvested energy.
In exhaust systems, not only should heat transfer to surroundings be reproduced but also chemical reactions in catalytic processes, since after-treatment devices can modify gas temperature. Most mathematical kinetics models rely on the Langmuir-Hinshelwood expressions derived on pellet-type Pt catalysts for the CO and HC oxidation with modified parameters (activation energies and activity factors), best suited to the case modeled. This approach is widely employed because it provides acceptable accuracy in the most common automobile range of operation.
Measurements on pellet-type platinum-alumina catalysts have been processed [
17] to derive kinetic rate expressions for the oxidation reactions of CO and C
3H
6 under oxygen-rich conditions for a better understanding of platinum oxidation catalysts in automotive emission control systems. Terms accounting for CO, C
3H
6 and NO inhibition were included. The isothermal reactor approach in a numerical integration-optimization method was used to fit the kinetic parameters. These expressions, especially as written by Oh et al. [
18], have been widely used [
19,
20,
21,
22]. This approach has also been used to build simpler kinetic models over a range of interest [
23].
Detailed kinetics for a Pt/Rh three-way catalyst were described in Chatterjee et al. [
24]. The model consists of 60 elementary reaction steps and one global reaction step, involving 8 gas species and 23 site species. It considers the steps of adsorption of the reactants on the surface, reaction of the adsorbed species, and desorption of the reaction products. This approach includes a mechanism of C
3H
6 oxidation on Pt/Al
2O
3, a mechanism of NO reduction on Pt, and a mechanism for NO reduction and CO oxidation on Rh. This model has been used when more accuracy is required, as in Kumar et al. [
25].
Nevertheless, due to the variety of washcoat materials and loadings of the monoliths and to ageing effects of after-treatment devices, the kinetic parameters published have difficulties in fitting to conditions or catalytic converters different from the study cases. To overcome the difficulty of finding kinetic parameters fitted to their application, it would be of interest to have a simple method for researchers to develop their own kinetic constants for CFD exhaust models.
The real physical space of a full-size monolith converter contains thousands of tiny channels and could present an extremely time-consuming problem to solve. There are several approaches to modeling the monolith of a catalytic converter. For simulations of the converter performance, most models use a volume-averaging method and treat the monolith as a continuous porous medium [
23,
24,
25,
26]. With the porous medium, approach channels are not simulated but a macroscopic understanding of the flow is achieved while keeping the computational requirements affordable.
The scope of this work is to develop a combined theoretical and experimental methodology to build an exhaust model to obtain information about temperature and heat losses along the system. Results were used to provide an insight into those flow characteristics that must be taken into account when harvesting energy, especially but not exclusively for thermoelectric modules. The model does not only intend to reproduce the behavior of the exhaust system at a single operation point but in the whole most-used part of the engine map. This information is needed to evaluate the exhaust gas energy available for recovery under real operating conditions.
4. Discussion
4.1. Accuracy of the Model
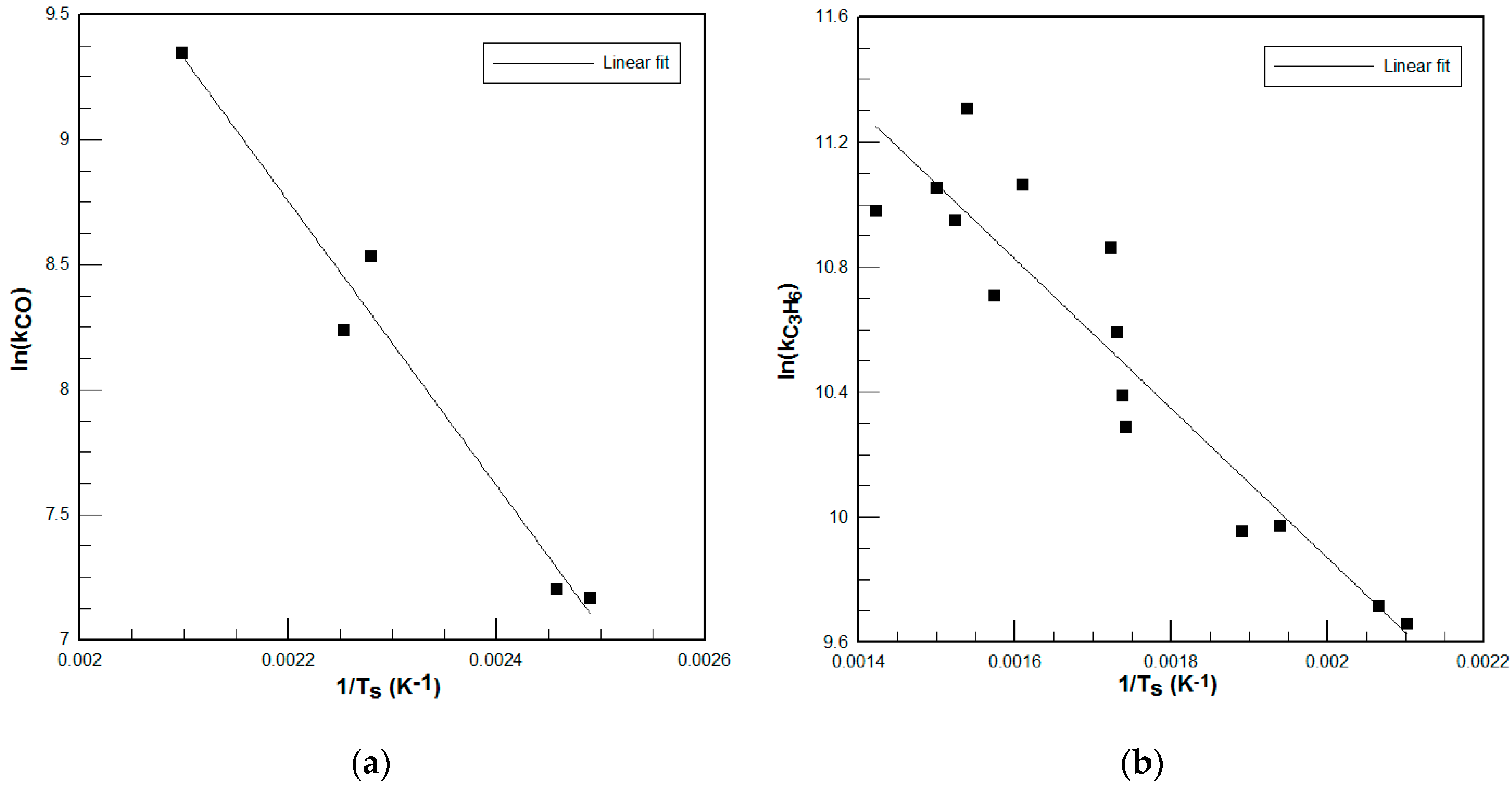
As can be seen, maximum error in chemical conversion was 11.58% and 11.81% for the CO model and the C3H6 model, respectively. Notice also that at relative low temperature modes with very low conversion rates, the model shows a 0% conversion. This is due to exclusion of near-to-zero points while developing the kinetic model, in order to better predict the whole operating range. Similarly, the CO kinetic model tends to show near total conversion for all high conversion modes, since these points were excluded when developing it for the same reason as above.
As can be seen, the maximum error at calibrating points was 4% in outlet temperature and 4.4% in heat losses. Out of training conditions, the maximum error in outlet was 5.9% in outlet temperature and 5.4% in heat losses.
It is difficult to find published kinetic parameters that fit the performance of a particular DOC, due mainly to the different washcoat materials and loadings of the monoliths and also to ageing effects of the DOC. A method to develop tailored kinetic parameters in the area of interest using numerical simulations was presented. The results show that although error in chemical conversion predictions reaches almost 12%, the error in the overall performance of the thermal model is lower. This is due to the low concentration of reactant species in the exhaust gas (see
Table 4): small errors in conversion do not involve big changes in total generated enthalpy of chemical reactions in the DOC. It can be concluded that the model shows good agreement with empirical data.
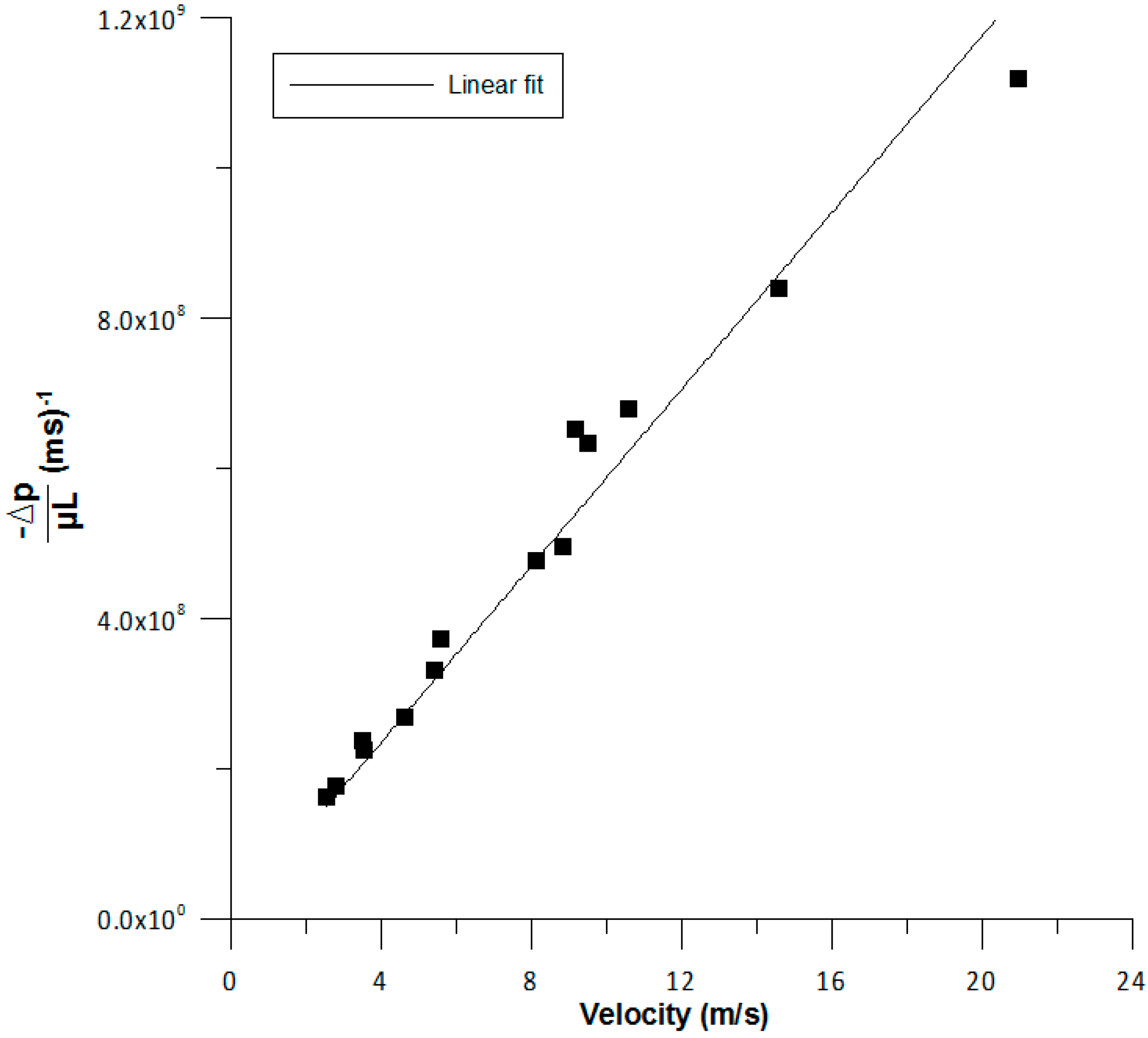
Regarding pressure drop, the linear correlation fits the data appropriately but for high velocities, the deviation can be larger (as seen in
Figure 9).
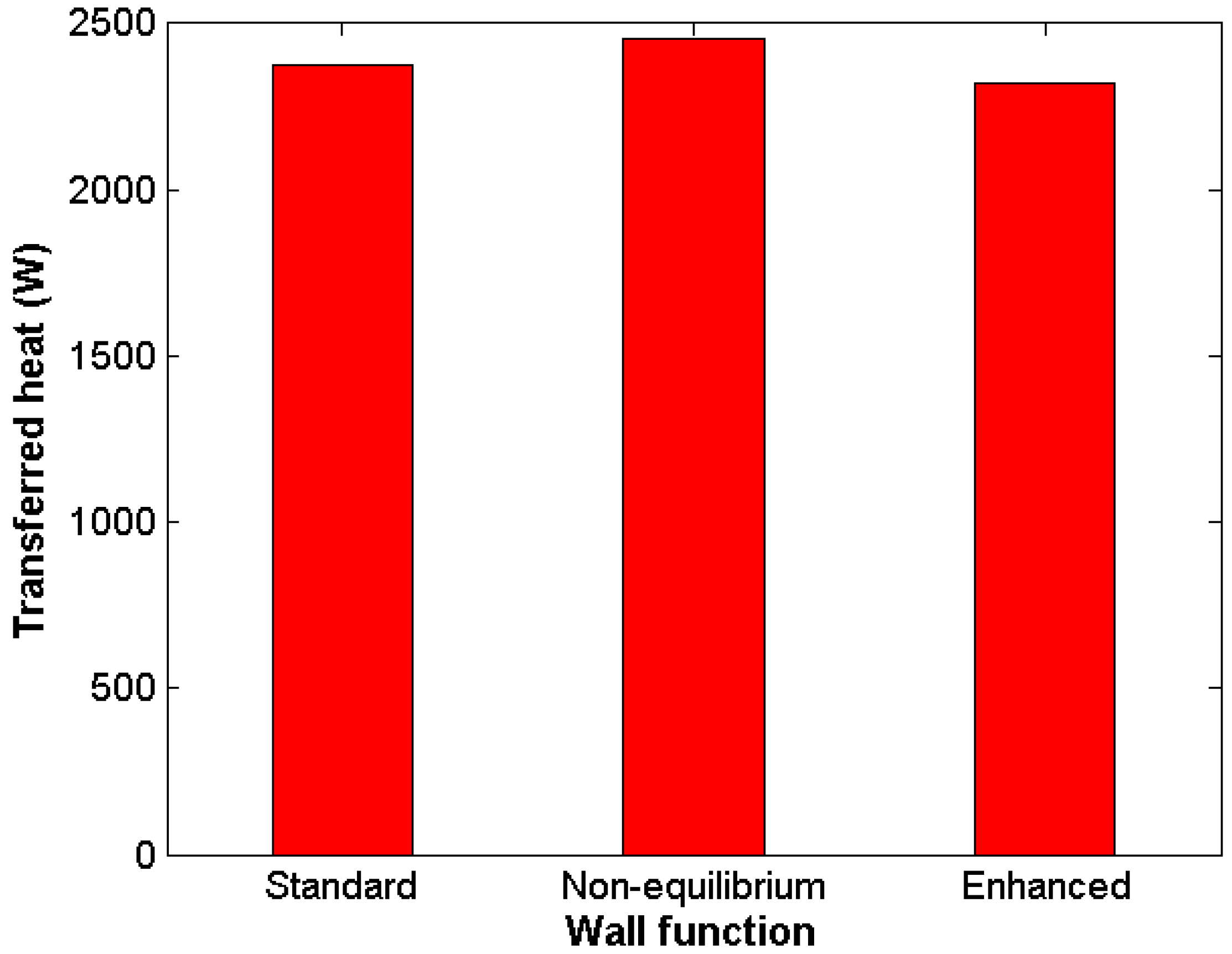
Complex numerical schemes and boundary layer refinement were proven not necessary to obtain reliable results. Standard wall-functions showed good results in comparison with other, more demanding approaches.
4.2. Energy Recovery Considerations for Exhaust Systems
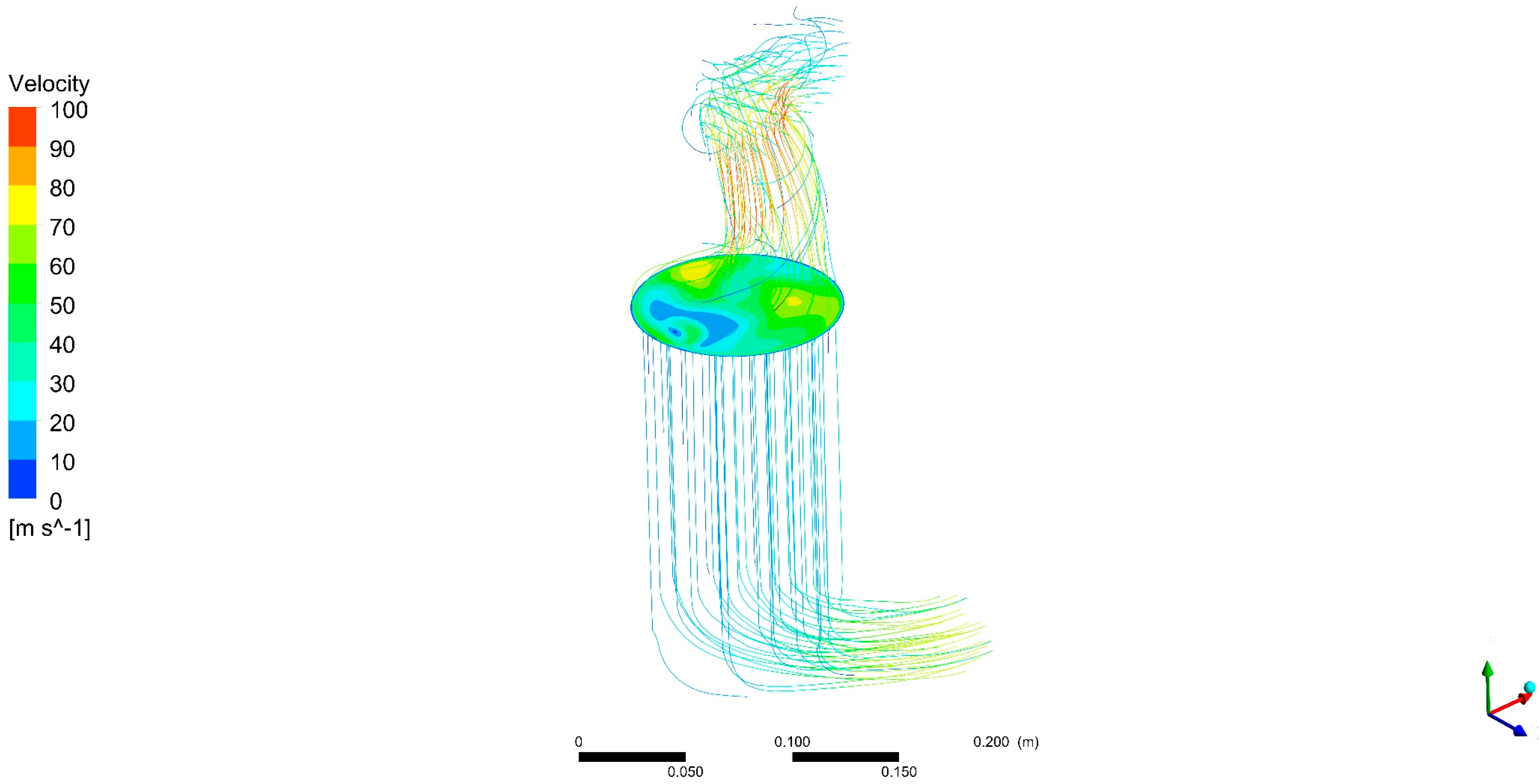
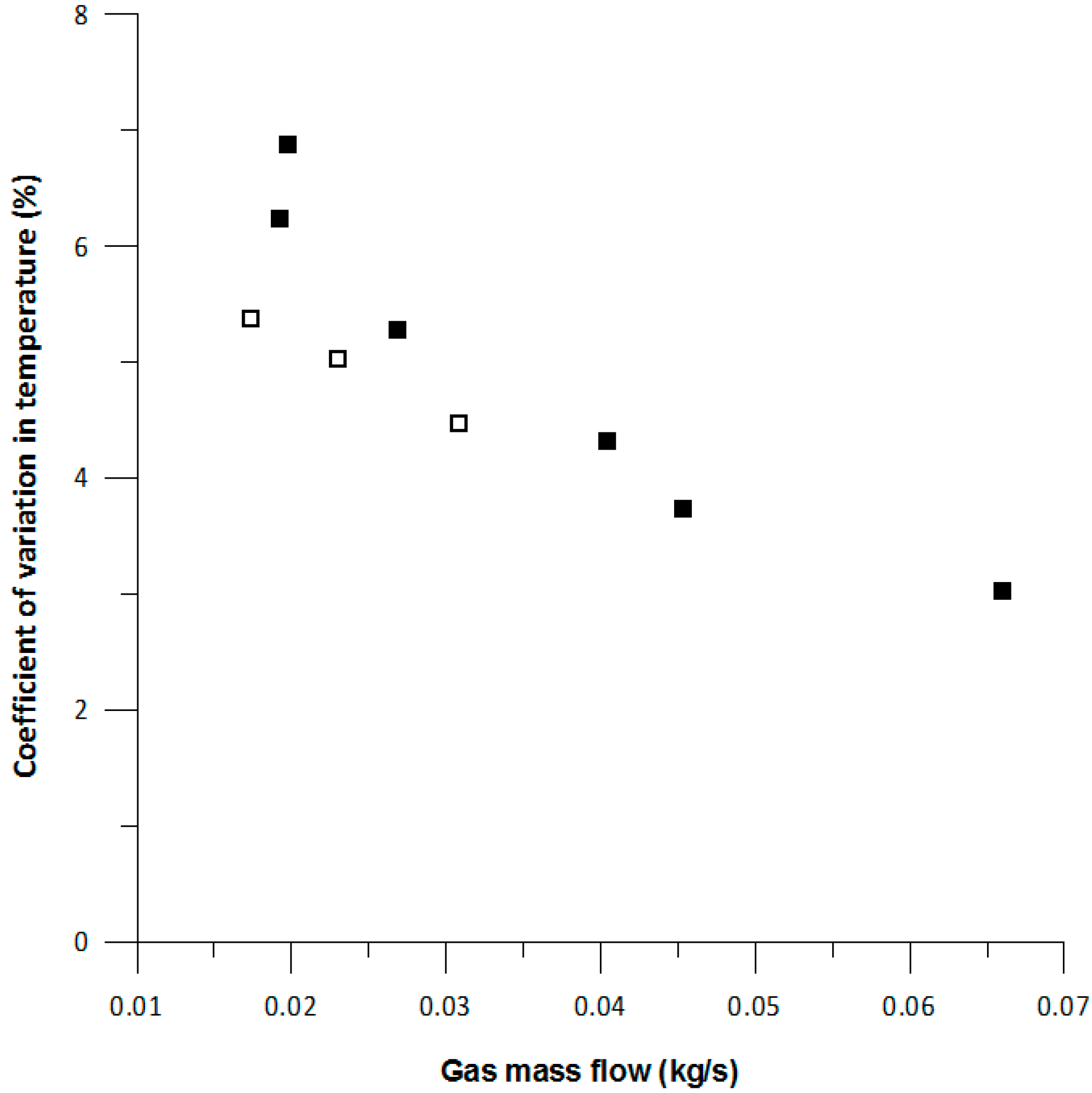
DOC outlet flow analysis showed that modules in thermoelectric generator devices placed after catalytic converters may have different performances not only because of the internal design of the devices but also because of the nature of the exhaust flow. It was found that the smaller the flow, the more uneven the flow temperature distribution is.
This can affect recovery devices being placed in the exhaust system. For instance, modules in a thermoelectric generator expected to have the same behaviour (for instance, upper and lower part thermoelectric modules in a flat-shaped, symmetrical design) may show a different performance due to exhaust flow structures.
Awareness of this effect be used to allow for electrical connections between modules depending on differences in voltage output from modules caused by variations in temperature. Even various types of modules can be selected in each zone to optimize the power output result for the different ranges of temperature.
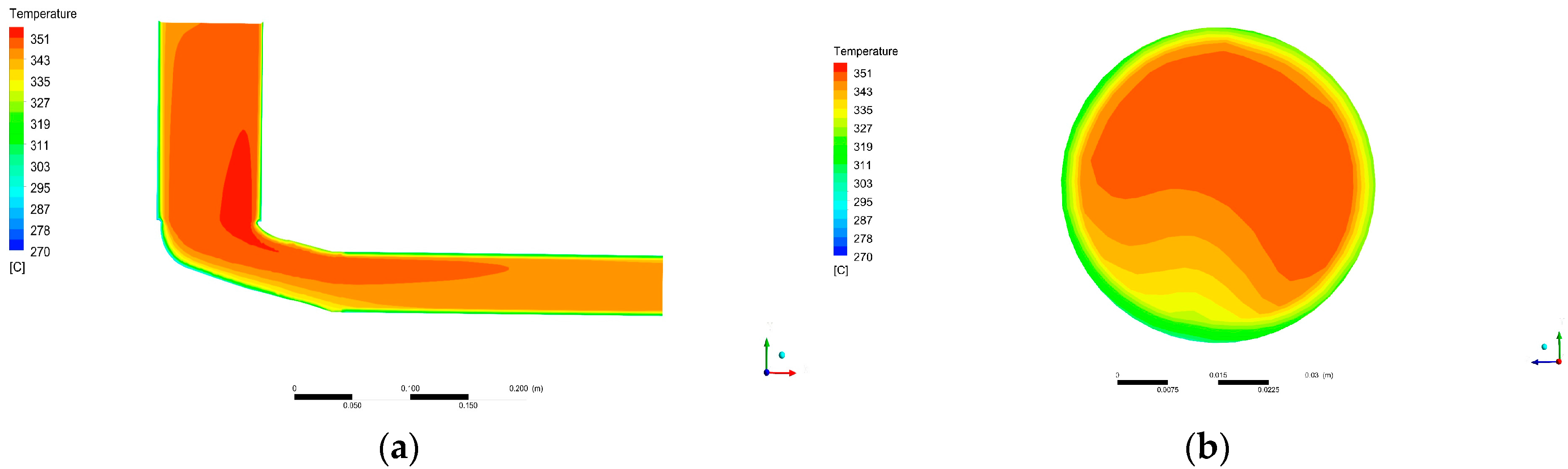
Loss in gas temperature with distance from DOC outlet was quantified. This will help to assess the trade-off between placing the recovery device near after-treatment systems (higher temperatures) or not (easiness in installation). Notice that temperature falls fast in a relatively short distance, reducing the amount of achievable harvested power.
5. Conclusions
Experimental exhaust data obtained for most common light-duty diesel engines was used to construct a 3D model. A complete methodology to build 3D CFD exhaust models is presented, including how to estimate main parameters needed and numerical approaches. A 2D axi-symmetrical complementary model was shown to be useful to overcome the necessity of chemical parameters fitted to a specific model of catalytic converter.
A computational model incorporating these findings will lead to accurate and faster numerical calculations of analysis of recoverable energy in exhaust systems. This will allow more designs to be explored in a given time.
It has been pointed out that the particular nature of the exhaust flow leaving catalytic converters has to be taken into account for energy-harvesting calculations, since the end of after-treatment systems is the indicated position to place energy recovery devices.
Furthermore, temperature losses caused by placing the recovery device distant from the DOC were evaluated. This information can be used in the evaluation process of the position of a recovery device in an automotive exhaust system. Since temperature falls promptly, it is advised to place the device as close as possible.
In works regarding simulations of recovery devices, if not enough experimental information is available, it is encouraged to include upstream elements of the exhaust that could alter the flow significantly in order to better predict their performance when installed in vehicles.