Photon Propagation through Linearly Active Dimers
Abstract
:1. Introduction
2. Quantum Model and Configurations
3. Spontaneous Generation of Photons
4. Photon Bunching in Spontaneous Generation
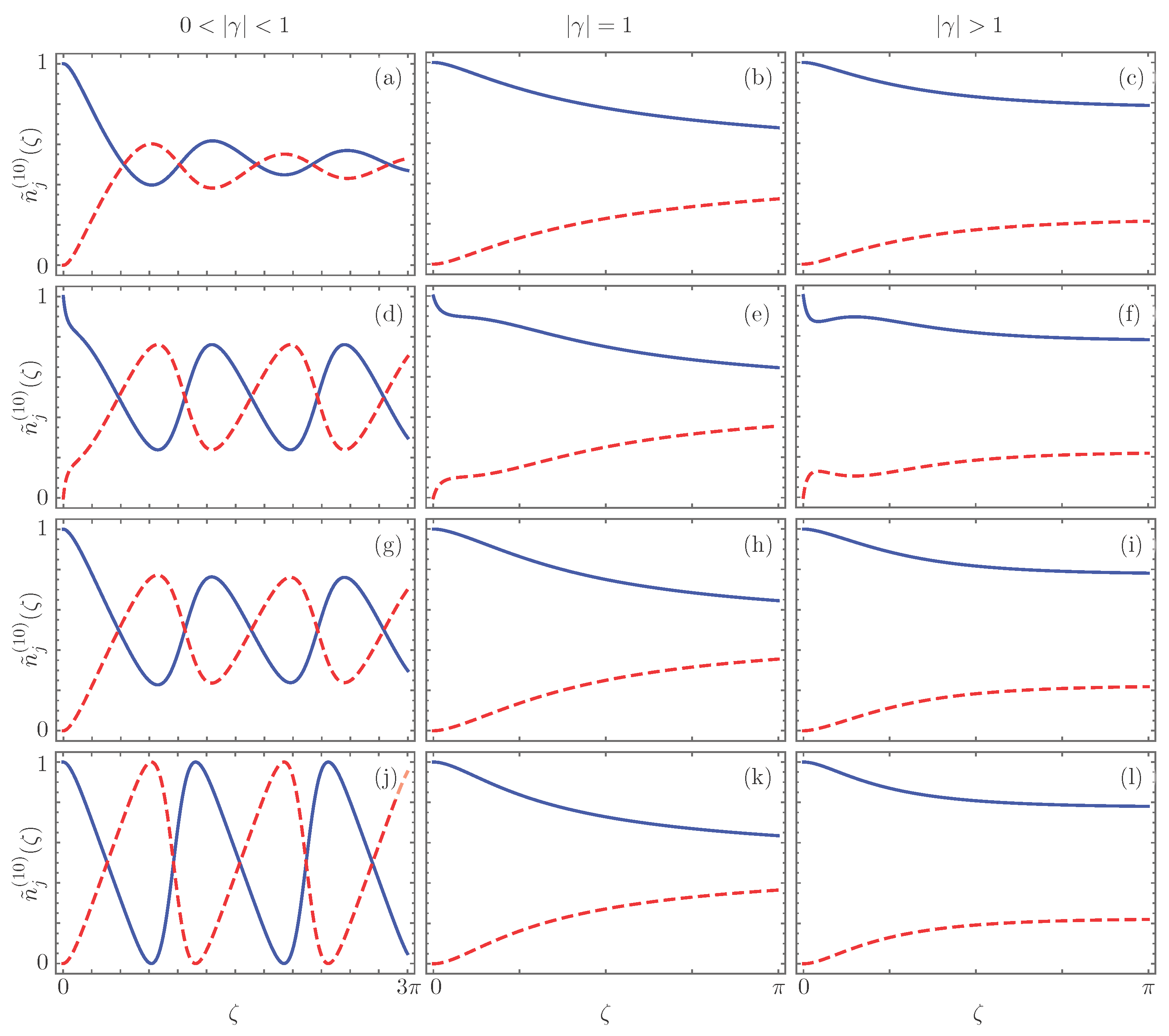
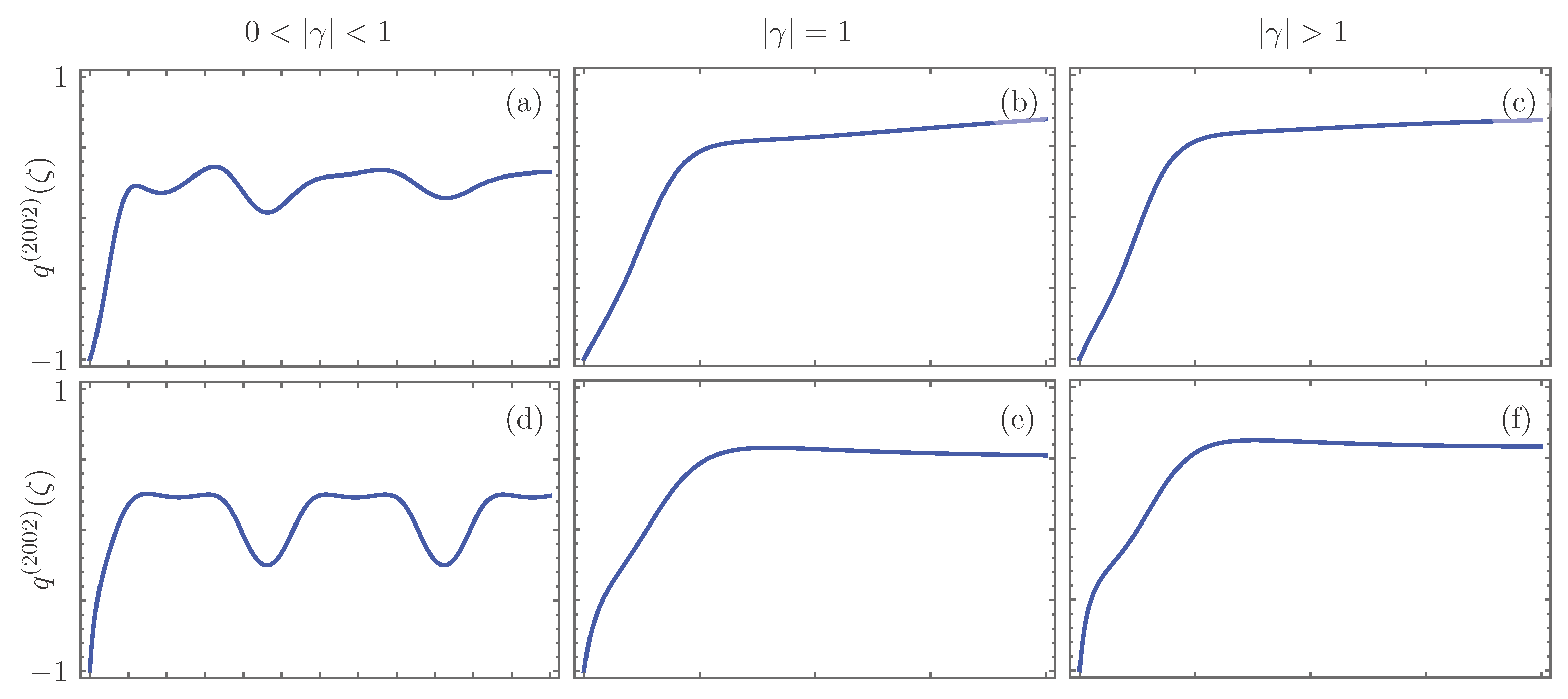
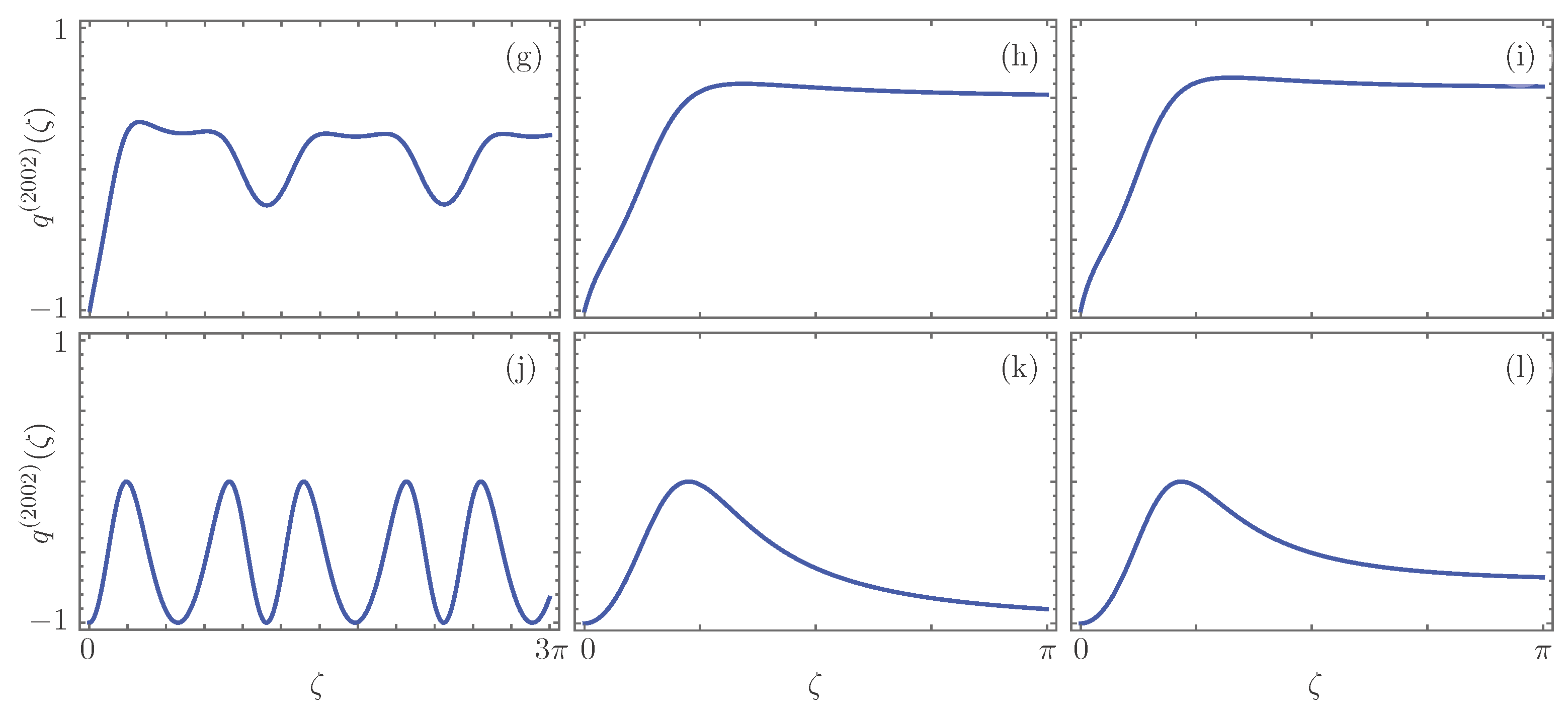
5. Photon Propagation
6. Photon Bunching and Anti-Bunching in Photon Propagation
7. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute. |
| Parity-Time. | |
| and | Real and imaginary parts of a complex number , in that order. |
| CONACYT | Consejo Nacional de Ciencia y Tecnología |
References
- Huerta Morales, J.D.; Guerrero, J.; Lopez-Aguayo, S.; Rodríguez-Lara, B.M. Revisiting the optical -symmetric dimer. Symmetry 2016, 8, 83. [Google Scholar] [CrossRef]
- Somekh, S.; Garmire, E.; Yariv, A.; Garvin, H.L.; Hunsperger, R.G. Channel optical waveguide directional couplers. Appl. Phys. Lett. 1973, 22, 46–47. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Delgado, F.; Muga, J.G. Physical realization of -symmetric potential scattering in a planar slab waveguide. J. Phys. A Math. Gen. 2005, 38, L171–L176. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Christodoulides, D.N.; Musslimani, Z.H. Theory of coupled optical -symmetric structures. Opt. Lett. 2007, 32, 2632–2634. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of -symmetry breaking in complex optical potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [PubMed]
- Ornigotti, M.; Szameit, A. Quasi -symmetry in passive photonic lattices. J. Opt. 2014, 16, 065501. [Google Scholar] [CrossRef]
- Peng, B.; Ozdemir, S.K.; Lei, F.C.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.H.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time-symmetric microring lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef] [PubMed]
- Schindler, J.; Lin, Z.; Lee, J.M.; Ramezani, H.; Ellis, F.M.; Kottos, T. -symmetric electronics. J. Phys A Math. Theor. 2012, 45, 444029. [Google Scholar] [CrossRef]
- Politi, A.; Cryan, M.J.; Rarity, J.G.; Yu, S.; O’Brien, J.L. Silica-on-Silicon waveguide quantum circuits. Science 2008, 320, 646–649. [Google Scholar] [CrossRef] [PubMed]
- Bromberg, Y.; Lahini, Y.; Morandotti, R.; Silberberg, Y. Quantum and Classical Correlations in Waveguide Lattices. Phys. Rev. Lett. 2009, 102, 253904. [Google Scholar] [CrossRef] [PubMed]
- Peruzzo, A.; Lobino, M.; Matthews, J.C.F.; Matsuda, N.; Politi, A.; Poulios, K.; Zhou, X.Q.; Lahini, Y.; Ismail, N.; Wörhoff, K.; et al. Quantum Walks of Correlated Photons. Science 2010, 329, 1500–1503. [Google Scholar] [CrossRef] [PubMed]
- Joglekar, Y.N.; Thompson, C.; Scott, D.D.; Vemuri, G. Optical waveguide arrays: Quantum effects and symmetry breaking. Eur. Phys. J. Appl. Phys. 2013, 63, 30001. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Qu, K. Spontaneous generation of photons in transmission of quantum fields in -symmetric optical systems. Phys. Rev. A 2012, 85, 031802. [Google Scholar] [CrossRef]
- Gräfe, M.; Heilmann, R.; Keil, R.; Eichelkraut, T.; Heinrich, M.; Nolte, S.; Szameit, A. Correlations of indistinguishable particles in non-Hermitian lattices. New J. Phys. 2013, 15, 033008. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Rodríguez-Lara, B.M.; Guerrero, J. Optical finite representation of the Lorentz group. Opt. Lett. 2015, 40, 5682–5685. [Google Scholar] [CrossRef] [PubMed]
- Mandel, L. Sub-Poissonian photon statistics in resonance fluorescence. Opt. Lett. 1979, 4, 205–207. [Google Scholar] [CrossRef] [PubMed]
- Lepert, G.; Trupke, M.; Hartmann, M.J.; Plenio, M.B.; Hinds, E.A. Arrays of waveguide-coupled optical cavities that interact strongly with atoms. New. J. Phys. 2011, 13, 113002. [Google Scholar] [CrossRef]
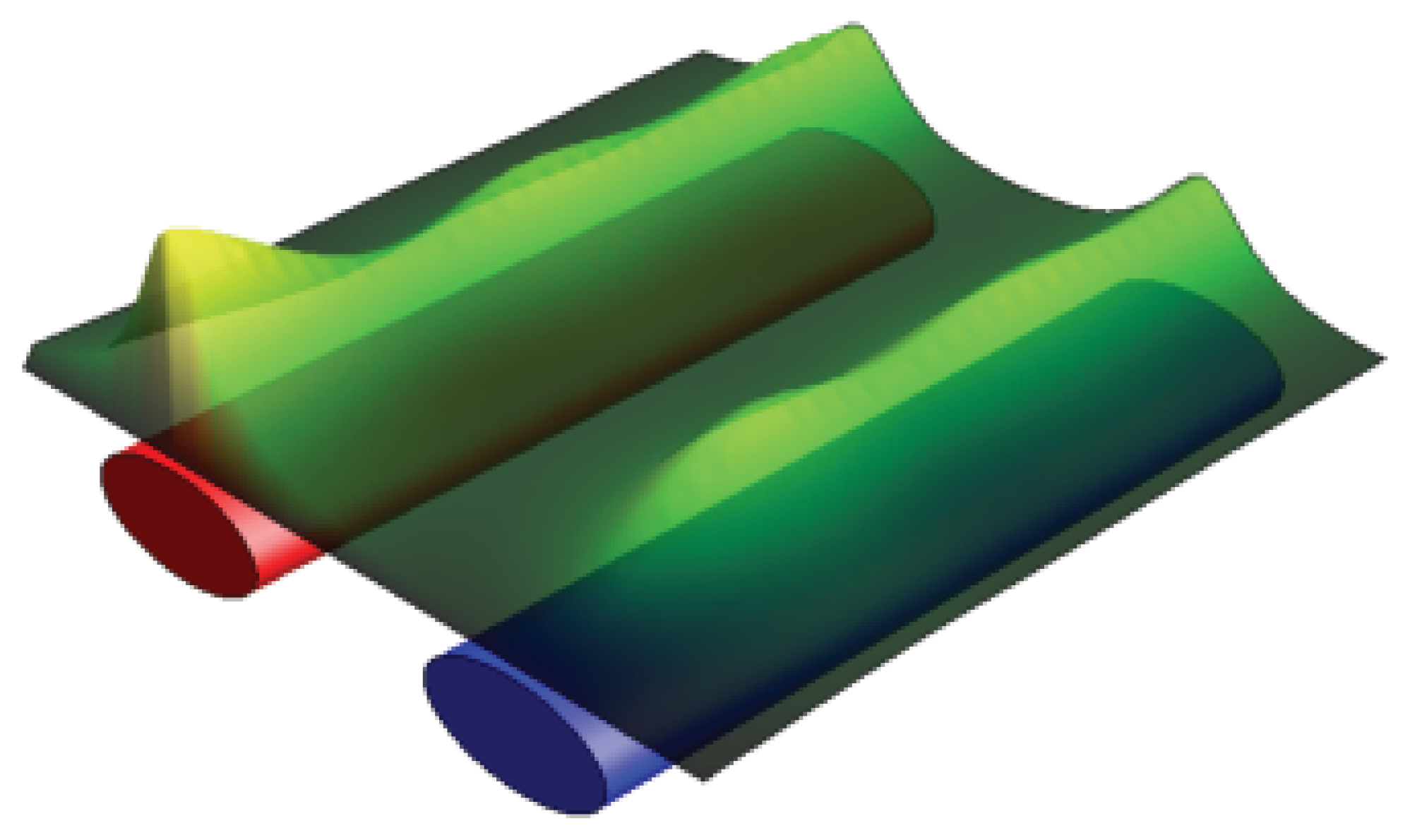
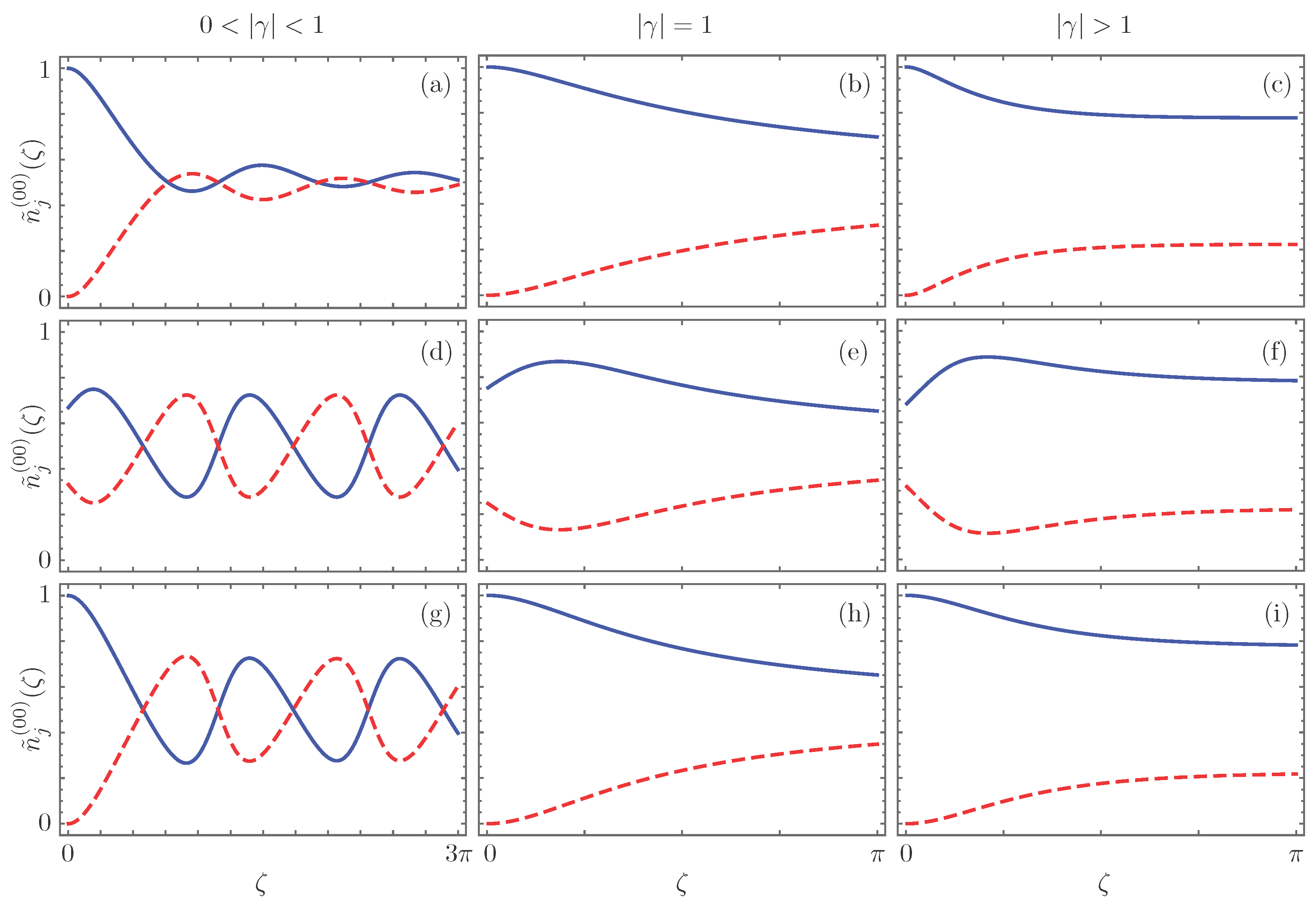
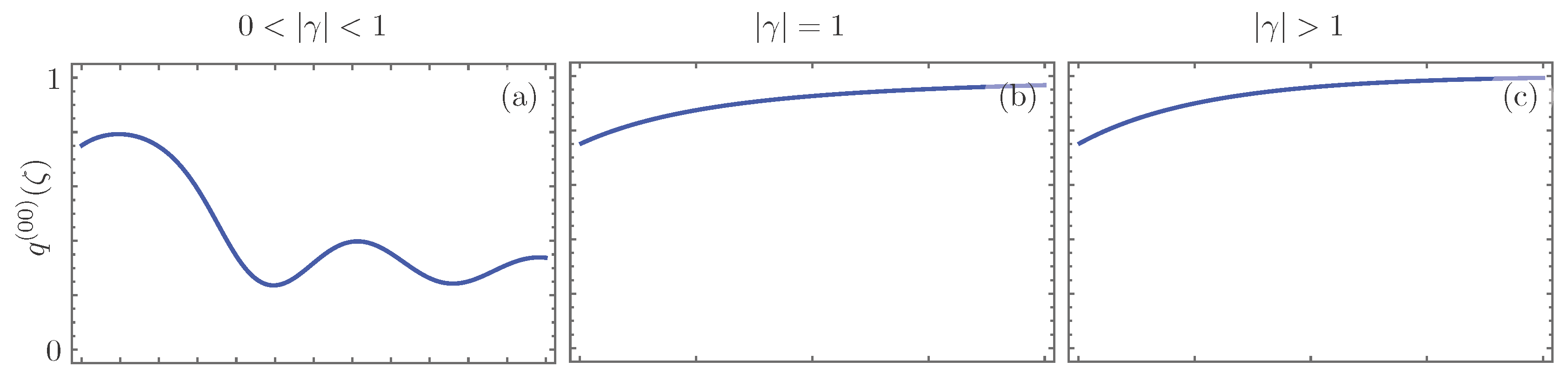
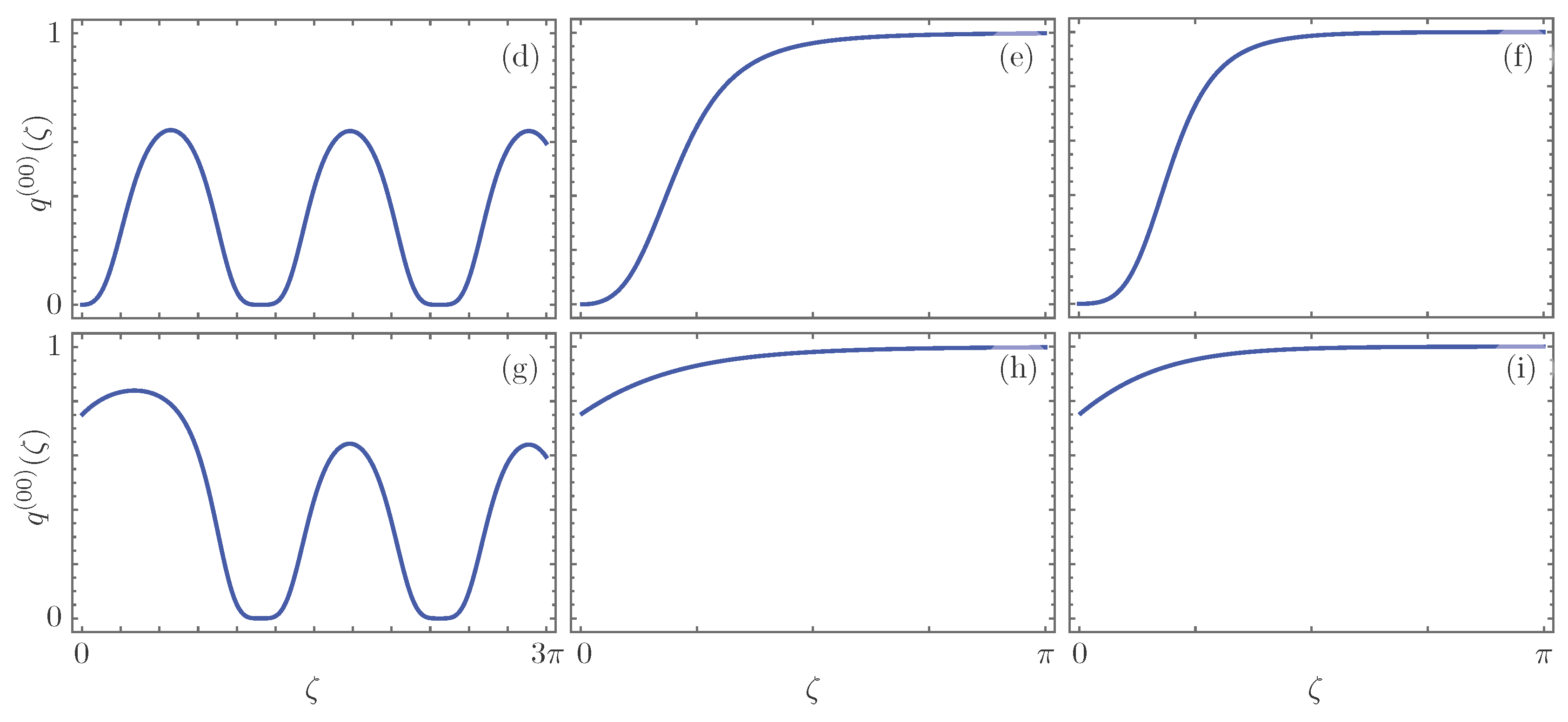
| Realization | n | |||||
|---|---|---|---|---|---|---|
| Gain-loss | 0 | |||||
| Gain-gain | ||||||
| Gain-passive | ||||||
| Passive-loss | ||||||
| Loss-loss |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huerta Morales, J.D.; Rodríguez-Lara, B.M. Photon Propagation through Linearly Active Dimers. Appl. Sci. 2017, 7, 587. https://doi.org/10.3390/app7060587
Huerta Morales JD, Rodríguez-Lara BM. Photon Propagation through Linearly Active Dimers. Applied Sciences. 2017; 7(6):587. https://doi.org/10.3390/app7060587
Chicago/Turabian StyleHuerta Morales, José Delfino, and Blas Manuel Rodríguez-Lara. 2017. "Photon Propagation through Linearly Active Dimers" Applied Sciences 7, no. 6: 587. https://doi.org/10.3390/app7060587
APA StyleHuerta Morales, J. D., & Rodríguez-Lara, B. M. (2017). Photon Propagation through Linearly Active Dimers. Applied Sciences, 7(6), 587. https://doi.org/10.3390/app7060587





