Split-And-Delay Unit for FEL Interferometry in the XUV Spectral Range
Abstract
:1. Introduction
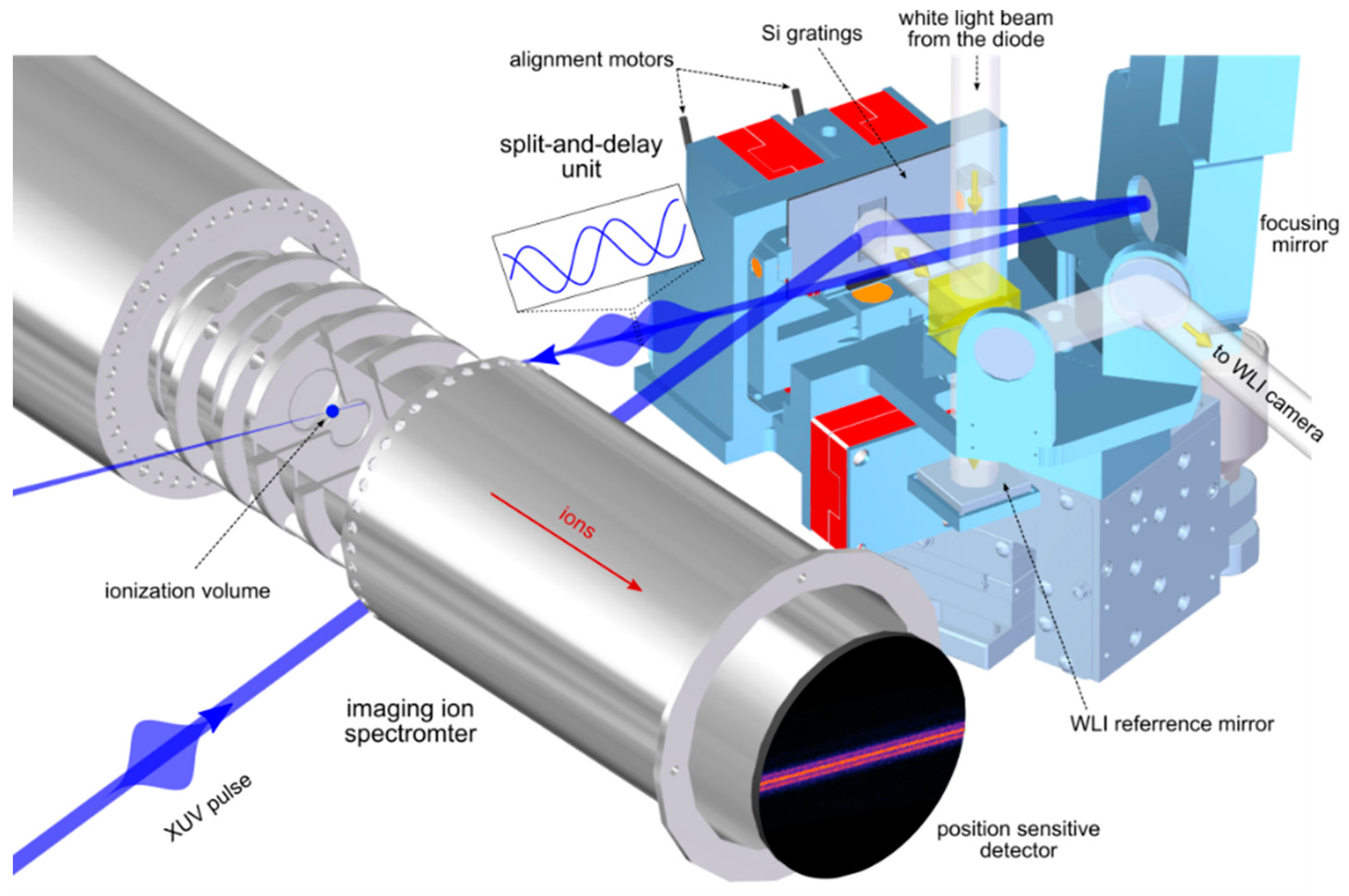
2. Split-And-Delay Unit for XUV Interferometry
Experimental Design of the SDU
3. White Light Interferometer for Time Delay Diagnostics
Experimental Design of the WLI
4. Results and Discussion
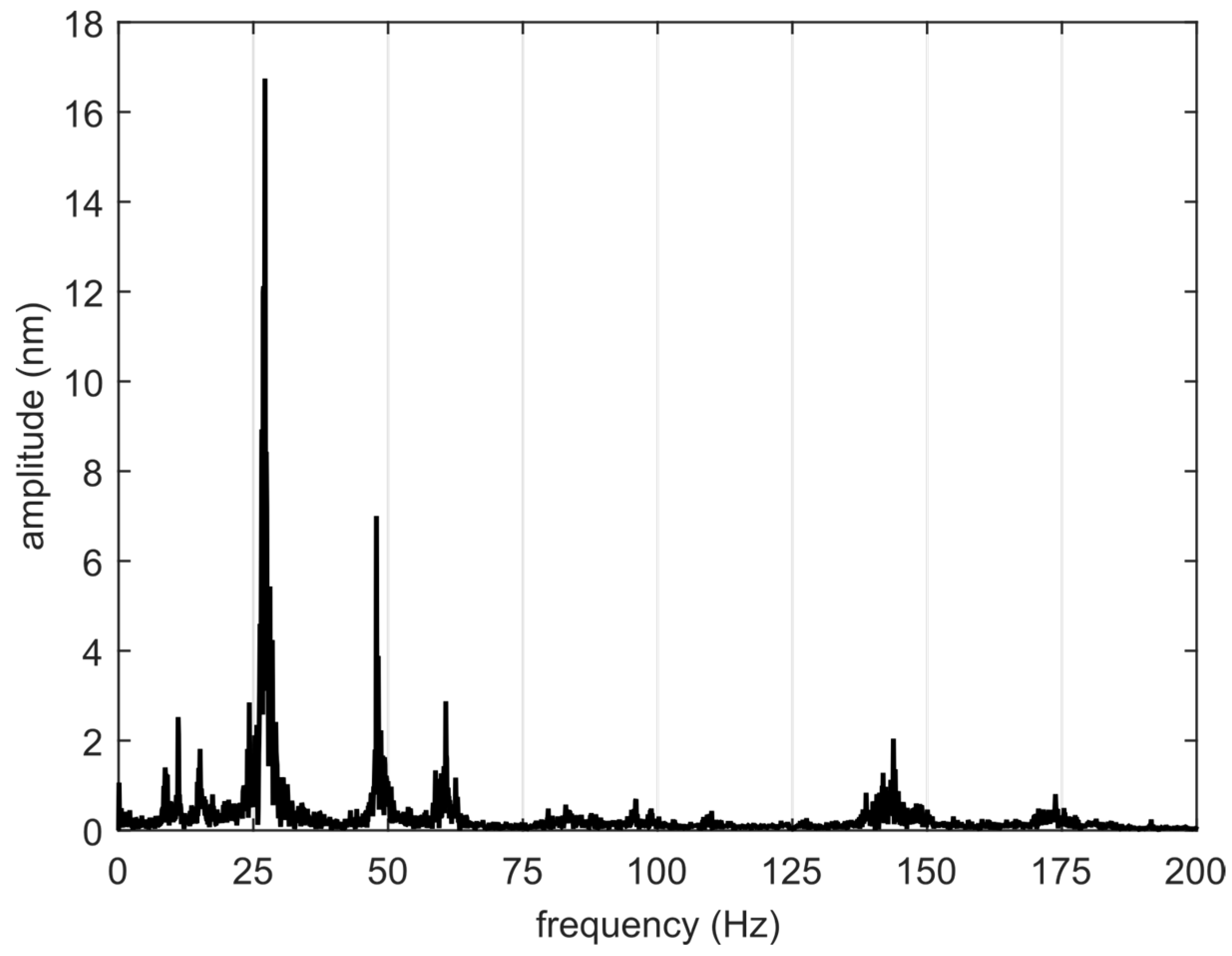
4.1. Analysis of the SDU Displacement Jitter
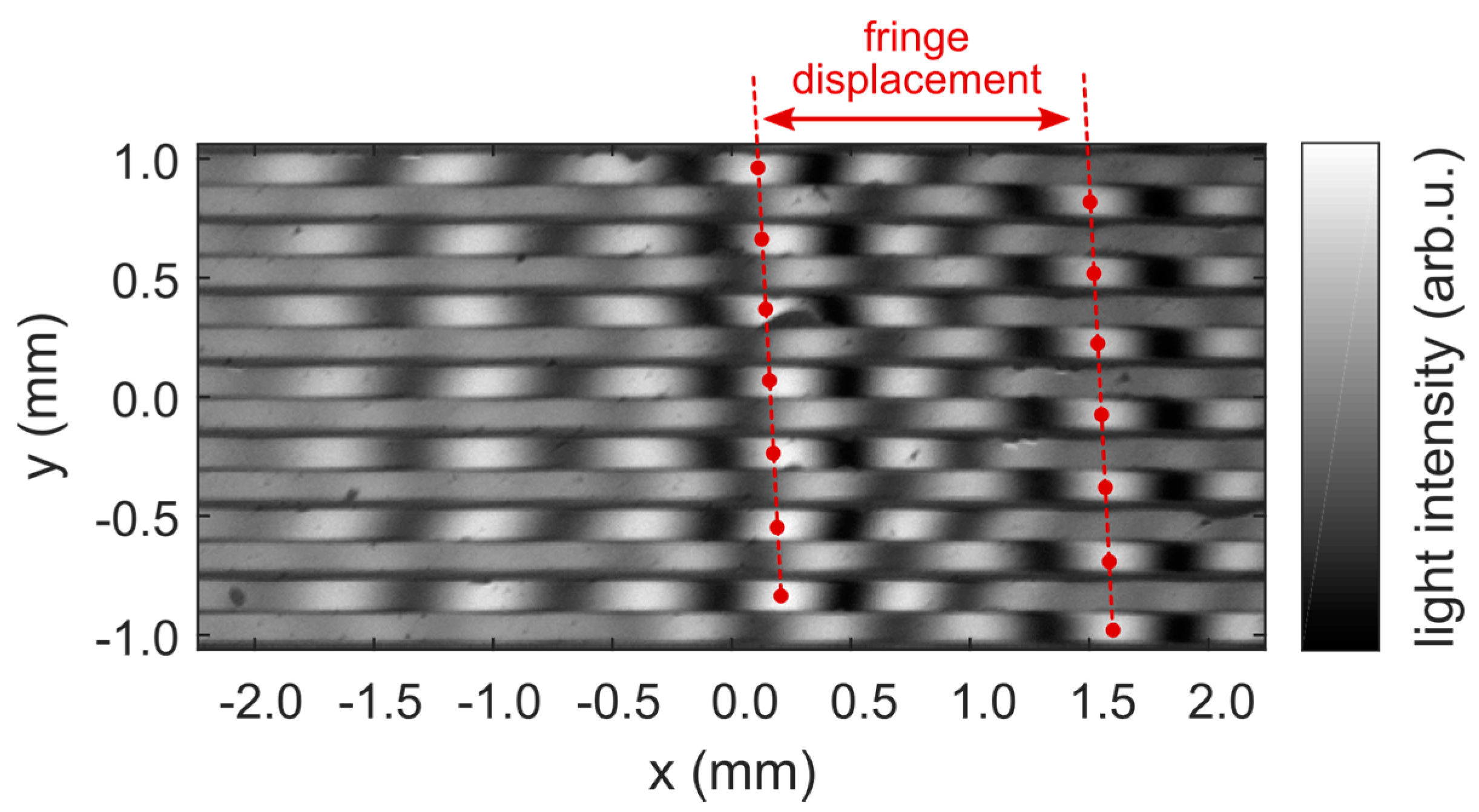
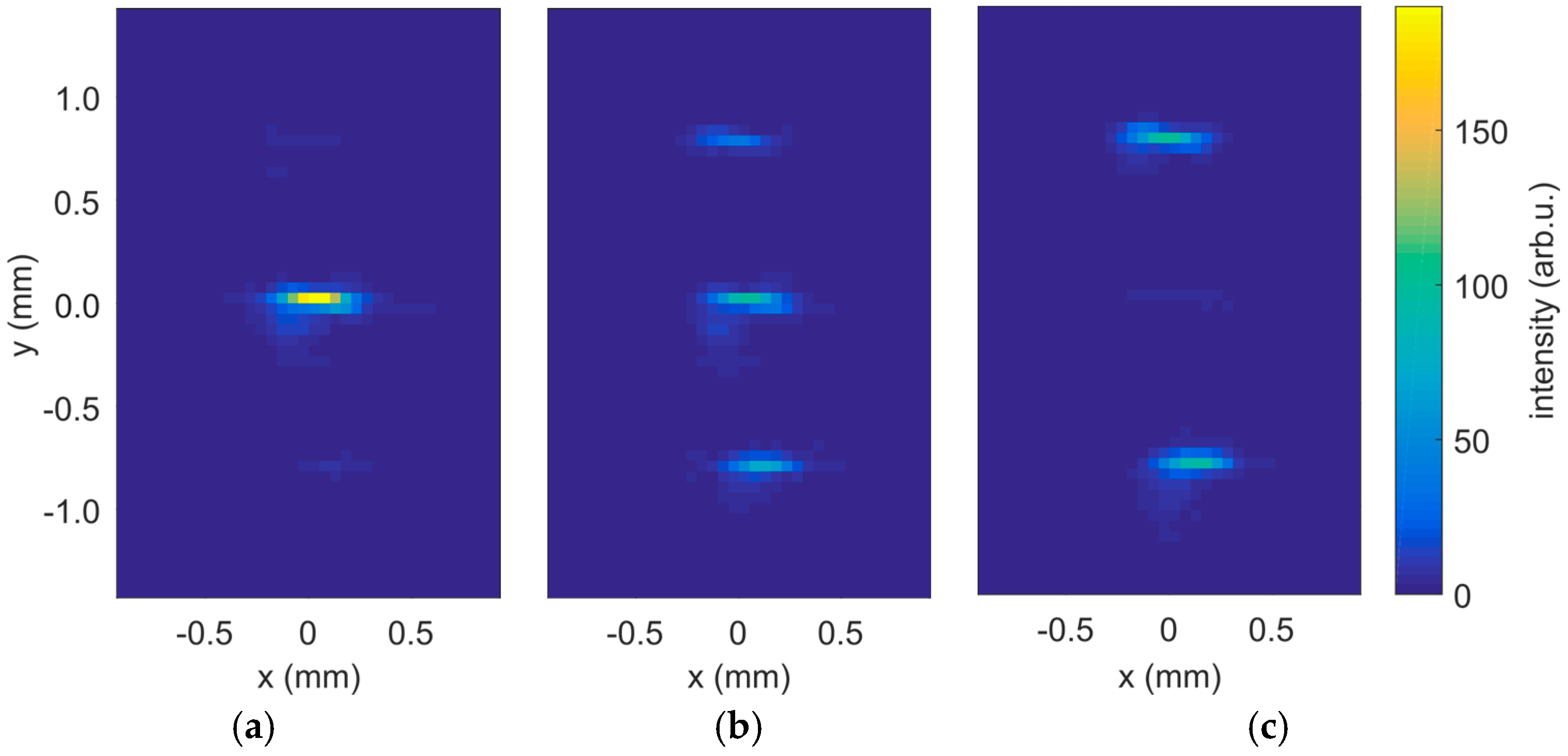
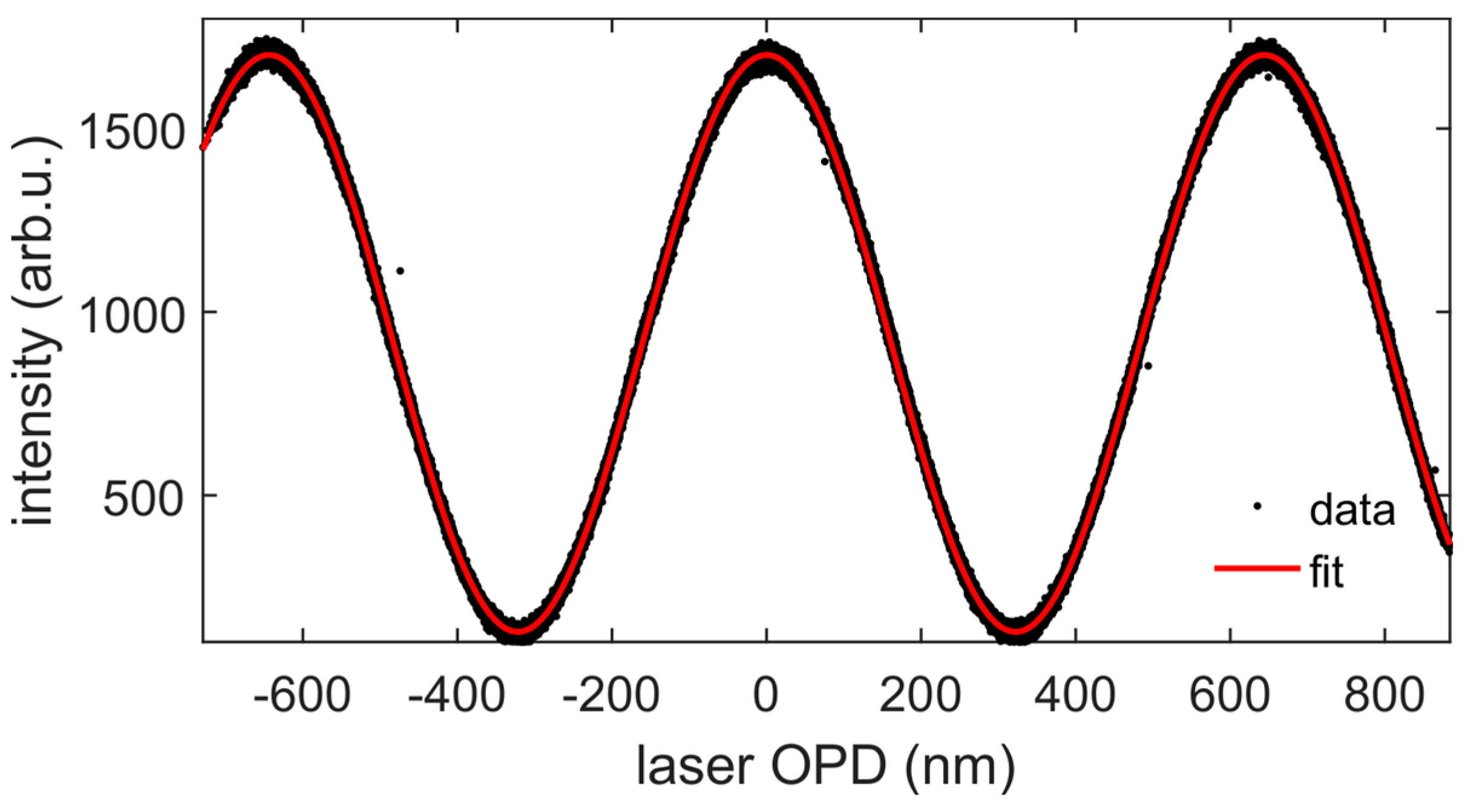
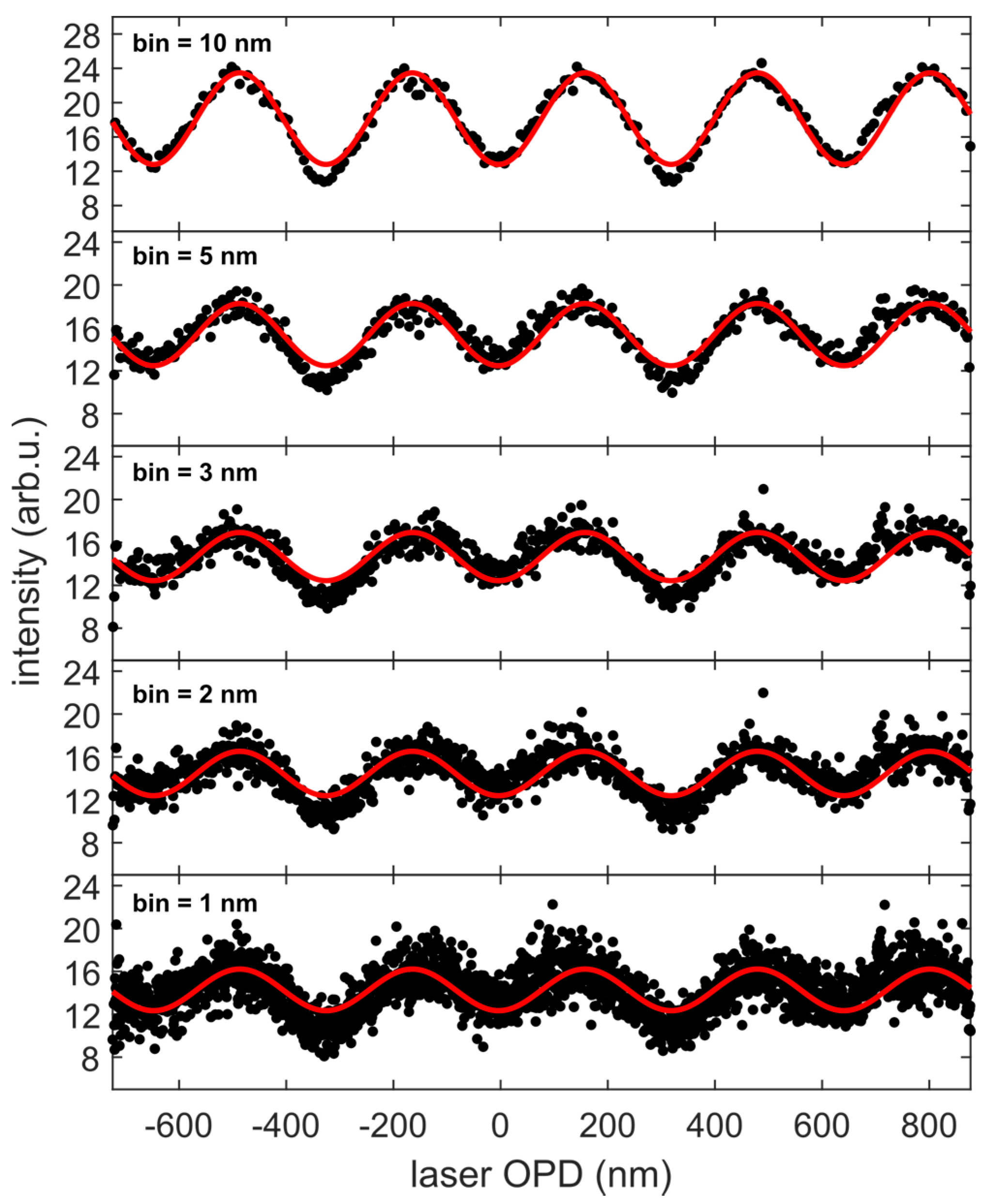
4.2. WLI Single-Shot Precision Determination
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Kohler, M.C.; Pfeifer, T.; Hatsagortsyan, K.Z.; Keitel, C.H. Frontiers of Atomic High-Harmonic Generation. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2012; Volume 61, pp. 159–208. [Google Scholar]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bähr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 2007, 1, 336–342. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.-J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 699–704. [Google Scholar] [CrossRef]
- Cundiff, S.T.; Mukamel, S. Optical multidimensional coherent spectroscopy. Phys. Today 2013, 66, 44–49. [Google Scholar] [CrossRef]
- Adams, B.W.; Buth, C.; Cavaletto, S.M.; Evers, J.; Harman, Z.; Keitel, C.H.; Pálffy, A.; Picón, A.; Röhlsberger, R.; Rostovtsev, Y.; et al. X-ray quantum optics. J. Mod. Opt. 2013, 60, 2–21. [Google Scholar] [CrossRef]
- Bencivenga, F.; Cucini, R.; Capotondi, F.; Battistoni, A.; Mincigrucci, R.; Giangrisostomi, E.; Gessini, A.; Manfredda, M.; Nikolov, I.P.; Pedersoli, E.; et al. Four-wave mixing experiments with extreme ultraviolet transient gratings. Nature 2015, 520, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Prince, K.C.; Allaria, E.; Callegari, C.; Cucini, R.; Ninno, G.D.; Mitri, S.D.; Diviacco, B.; Ferrari, E.; Finetti, P.; Gauthier, D.; et al. Coherent control with a short-wavelength free-electron laser. Nat. Photonics 2006, 10, 985–990. [Google Scholar] [CrossRef]
- Gauthier, D.; Ribič, P.R.; Ninno, G.D.; Allaria, E.; Cinquegrana, P.; Danailov, M.B.; Demidovich, A.; Ferrari, E.; Giannessi, L. Generation of phase-locked pulses from a seeded free-electron laser. Phys. Rev. Lett. 2016, 116, 024801. [Google Scholar] [CrossRef] [PubMed]
- Sorgenfrei, F.; Schlotter, W.F.; Beeck, T.; Nagasono, M.; Gieschen, S.; Meyer, H.; Foehlisch, A.; Beye, M.; Wurth, W. The extreme ultraviolet split and femtosecond delay unit at the plane grating monochromator beamline PG2 at FLASH. Rev. Sci. Instrum. 2010, 81, 043107. [Google Scholar] [CrossRef] [PubMed]
- Wöstmann, M.; Mitzner, R.; Noll, T.; Roling, S.; Siemer, B.; Siewert, F.; Eppenhoff, S.; Wahlert, F.; Zacharias, H. The XUV split-and-delay unit at beamline BL2 at FLASH. J. Phys. B 2013, 46, 164005. [Google Scholar] [CrossRef]
- Campi, F.; Coudert-Alteirac, H.; Miranda, M.; Rading, L.; Manschwetus, B.; Rudawski, P.; L’Huillier, A.; Johnsson, P. Design and test of a broadband split-and-delay unit for attosecond XUV-XUV pump-probe experiments. Rev. Sci. Instrum. 2016, 87, 023106. [Google Scholar] [CrossRef]
- Mashiko, H.; Suda, A.; Midorikawa, K. All-reflective interferometric autocorrelator for the measurement of ultra-short optical pulses. Appl. Phys. B 2003, 76, 525–530. [Google Scholar] [CrossRef]
- Faucher, O.; Tzallas, P.; Benis, E.P.; Kruse, J.; Conde, A.P.; Kalpouzos, C.; Charalambidis, D. Four-dimensional investigation of the 2nd order volume autocorrelation technique. Appl. Phys. B 2009, 97, 505–510. [Google Scholar] [CrossRef]
- Tzallas, P.; Charalambidis, D.; Papadogiannis, N.A.; Witte, K.; Tsakiris, G.D. Direct observation of attosecond light bunching. Nature 2003, 426, 267. [Google Scholar] [CrossRef] [PubMed]
- Strong, J.; Vanasse, G.A. Lamellar grating far-infrared interferometer. J. Opt. Soc. Am. 1960, 50, 113. [Google Scholar] [CrossRef]
- Hall, R.T.; Vrabec, D.; Dowling, J.M. A high-resolution, far infrared double-beam lamellar grating interferometer. Appl. Opt. 1966, 5, 1147. [Google Scholar] [CrossRef] [PubMed]
- Milward, R.C. A small lamellar grating interferometer for the very far-infrared. Infrared Phys. 1969, 9, 59–74. [Google Scholar] [CrossRef]
- Henry, R.L.; Tanner, D.B. A lamellar grating interferometer for the far-infrared. Infrared Phys. 1979, 19, 163–174. [Google Scholar] [CrossRef]
- Gebert, T.; Rompotis, D.; Wieland, M.; Karimi, F.; Azima, A.; Drescher, M. Michelson-type all-reflective interferometric autocorrelation in the VUV regime. New J. Phys. 2014, 16, 239–310. [Google Scholar] [CrossRef]
- Usenko, S.; Przystawik, A.; Jakob, M.; Lazzarino, L.L.; Brenner, G.; Toleikis, S.; Haunhorst, C.; Kip, D.; Laarmann, T. Attosecond interferometry with self-amplified spontaneous emission of a free-electron laser. Nat. Commun. 2017, 8, 15626. [Google Scholar]
- Flournoy, P.A.; McClure, R.W.; Wyntjes, G. White-light interferometric thickness gauge. Appl. Opt. 1972, 11, 1907. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.S.; Strand, T.C. Profilometry with a coherence scanning microscope. Appl. Opt. 1990, 29, 3784–3788. [Google Scholar] [CrossRef] [PubMed]
- Chim, S.S.C.; Kino, G.S. Correlation microscope. Opt. Lett. 1990, 15, 579. [Google Scholar] [CrossRef] [PubMed]
- Kino, G.S.; Chim, S.S.C. Mirau correlation microscope. Appl. Opt. 1990, 29, 3775–3783. [Google Scholar] [CrossRef] [PubMed]
- Danielson, B.L.; Boisrobert, C.Y. Absolute optical ranging using low coherence interferometry. Appl. Opt. 1991, 30, 2975. [Google Scholar] [CrossRef] [PubMed]
- Dresel, T.; Häusler, G.; Venzke, H. Three-dimensional sensing of rough surfaces by coherence radar. Appl. Opt. 1992, 31, 919–925. [Google Scholar] [CrossRef] [PubMed]
- Thorne, A. Fourier transform spectrometry in the vacuum ultraviolet: Applications and progress. Phys. Scr. 1996, T65, 31–35. [Google Scholar] [CrossRef]
- Ronchi, V. Forty years of history of a grating interferometer. Appl. Opt. 1964, 3, 437. [Google Scholar] [CrossRef]
- Munnerlyn, C.R. A Simple Laser Interferometer. Appl. Opt. 1969, 8, 827. [Google Scholar] [CrossRef] [PubMed]
- Goulielmakis, E.; Nersisyan, G.; Papadogiannis, N.A.; Charalambidis, D.; Tsakiris, G.D.; Witte, K. A dispersionless Michelson interferometer for the characterization of attosecond pulses. Appl. Phys. B 2002, 74, 197–206. [Google Scholar] [CrossRef]
- Papadogiannis, N.A.; Nersisyan, G.; Goulielmakis, E.; Rakitzis, T.P.; Hertz, E.; Charalambidis, D.; Tsakiris, G.D.; Witte, K. Temporal characterization of short-pulse third-harmonic generation in an atomic gas by a transmission-grating Michelson interferometer. Opt. Lett. 2002, 27, 1561. [Google Scholar] [CrossRef] [PubMed]
- Möller, K.D. Wavefront dividing interferometers. Infrared Phys. 1991, 32, 321–331. [Google Scholar] [CrossRef]
- Yin, H.; Wang, M.; Ström, M.; Nordgren, J. Study of a wave-front-dividing interferometer for Fourier transform spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. A 2000, 451, 529–539. [Google Scholar] [CrossRef]
- Schultze, M.; Bergüs, B.; Schroeder, H.; Krausz, F.; Kompa, K.L. Spatially resolved measurement of ionization yields in the focus of an intense laser pulse. New J. Phys. 2011, 13, 033001. [Google Scholar] [CrossRef]
- Bosselmann, T.; Ulrich, R. High-accuracy position-sensing with fiber-coupled white-light interferometers. In Proceedings SPIE 0514; Kersten, R.T., Kist, R., Eds.; SPIE: Bellingham, WA, USA, 1984; pp. 361–364. [Google Scholar]
- Chen, S.; Meggitt, B.T.; Rogers, A.J. Electronically scanned optical-fiber Young’s white-light interferometer. Opt. Lett. 1991, 16, 761. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usenko, S.; Przystawik, A.; Lazzarino, L.L.; Jakob, M.A.; Jacobs, F.; Becker, C.; Haunhorst, C.; Kip, D.; Laarmann, T. Split-And-Delay Unit for FEL Interferometry in the XUV Spectral Range. Appl. Sci. 2017, 7, 544. https://doi.org/10.3390/app7060544
Usenko S, Przystawik A, Lazzarino LL, Jakob MA, Jacobs F, Becker C, Haunhorst C, Kip D, Laarmann T. Split-And-Delay Unit for FEL Interferometry in the XUV Spectral Range. Applied Sciences. 2017; 7(6):544. https://doi.org/10.3390/app7060544
Chicago/Turabian StyleUsenko, Sergey, Andreas Przystawik, Leslie Lamberto Lazzarino, Markus Alexander Jakob, Florian Jacobs, Christoph Becker, Christian Haunhorst, Detlef Kip, and Tim Laarmann. 2017. "Split-And-Delay Unit for FEL Interferometry in the XUV Spectral Range" Applied Sciences 7, no. 6: 544. https://doi.org/10.3390/app7060544
APA StyleUsenko, S., Przystawik, A., Lazzarino, L. L., Jakob, M. A., Jacobs, F., Becker, C., Haunhorst, C., Kip, D., & Laarmann, T. (2017). Split-And-Delay Unit for FEL Interferometry in the XUV Spectral Range. Applied Sciences, 7(6), 544. https://doi.org/10.3390/app7060544





