Artwork Identification for 360-Degree Panoramic Images Using Polyhedron-Based Rectilinear Projection and Keypoint Shapes
Abstract
:1. Introduction
2. Research Background
3. Map Projection
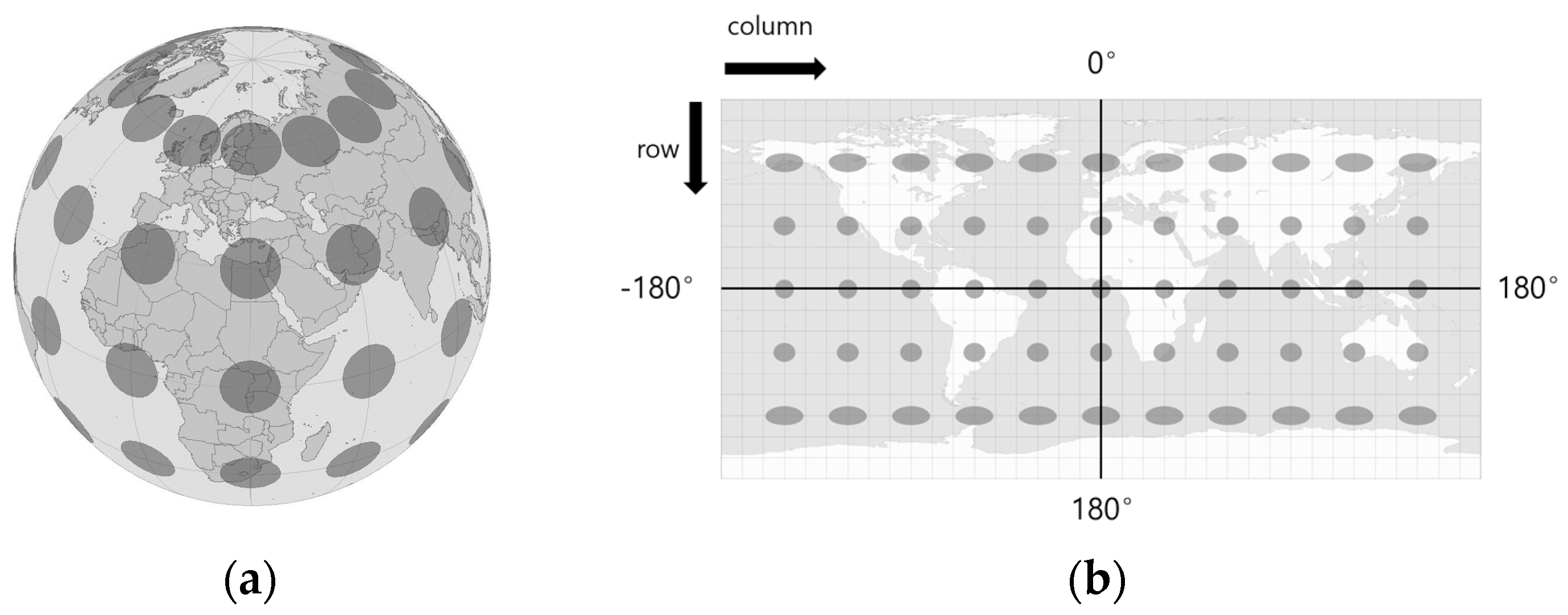
3.1. Equirectangular Projection
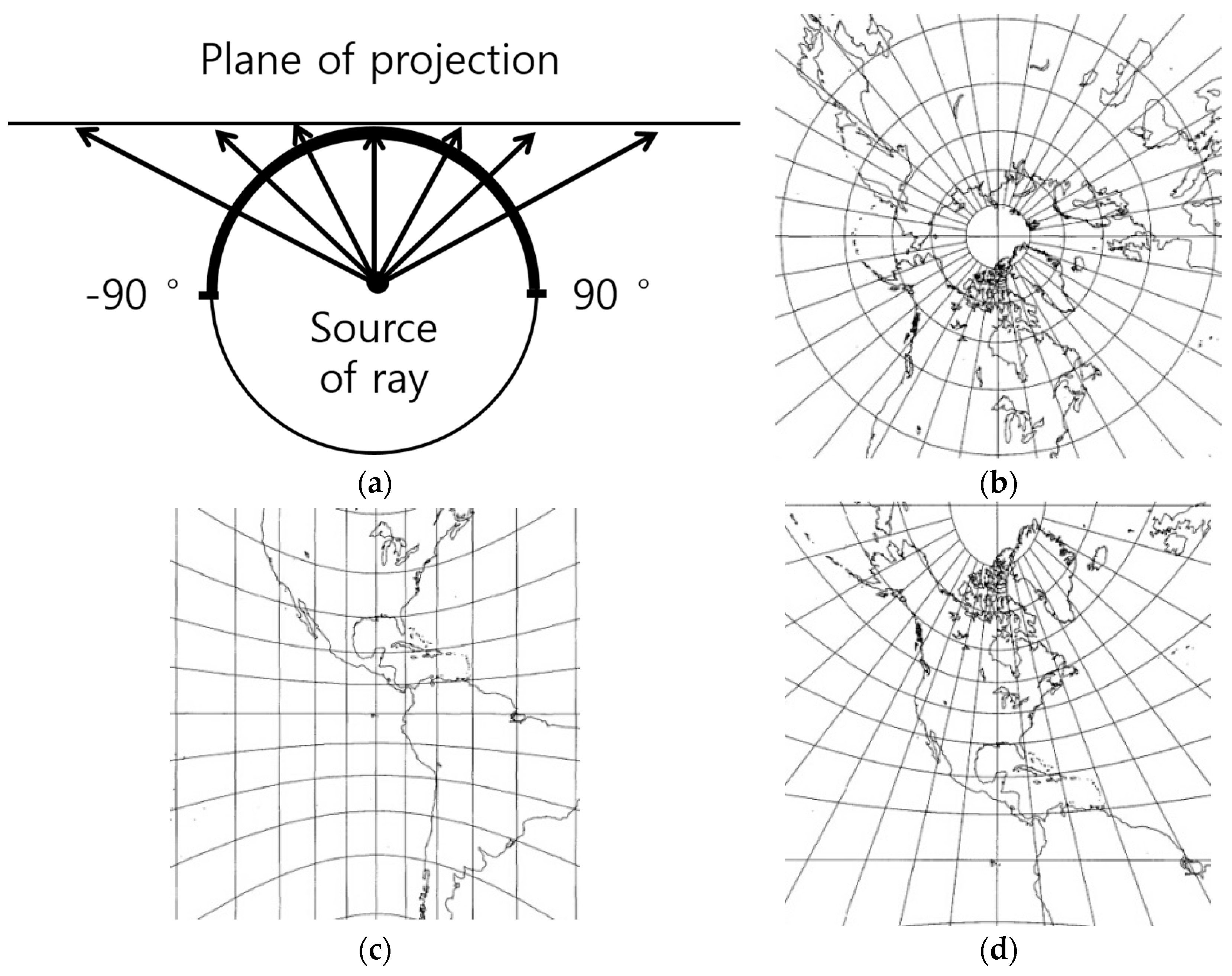
3.2. Rectilinear Projection
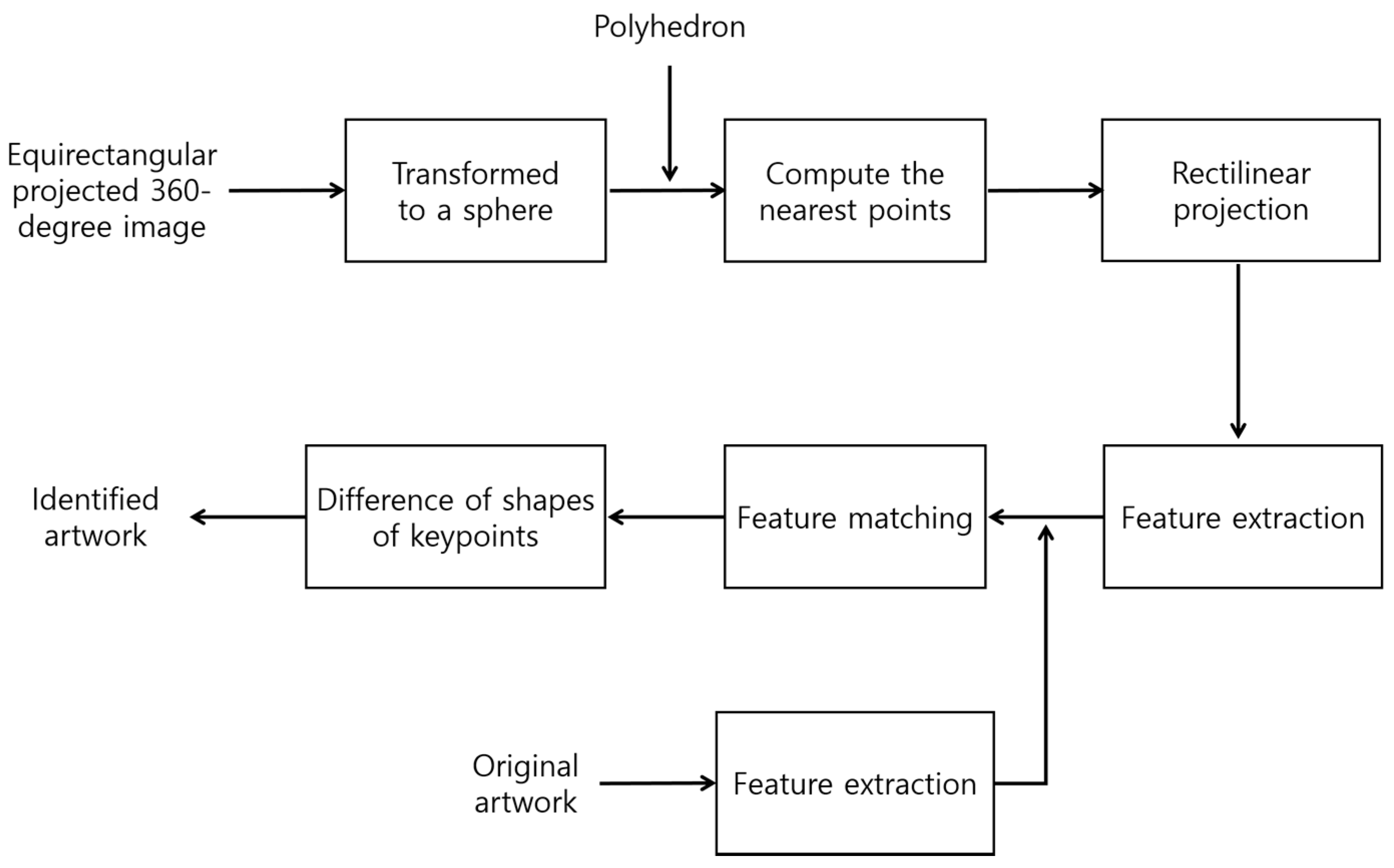
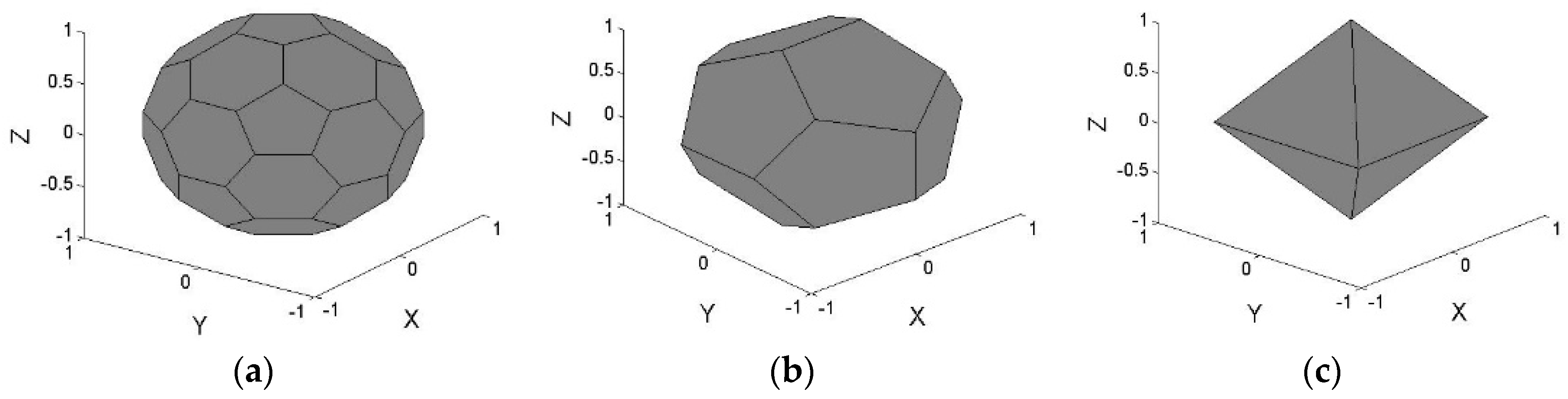
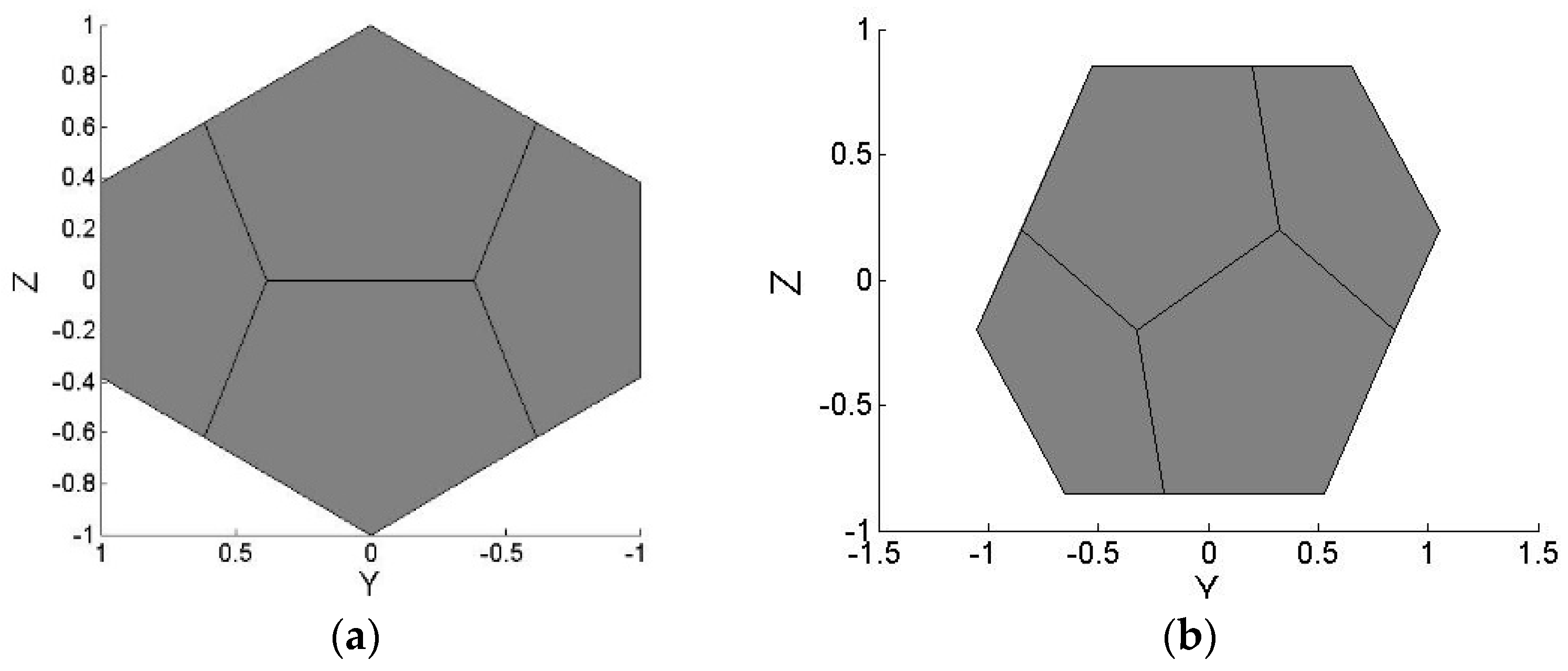
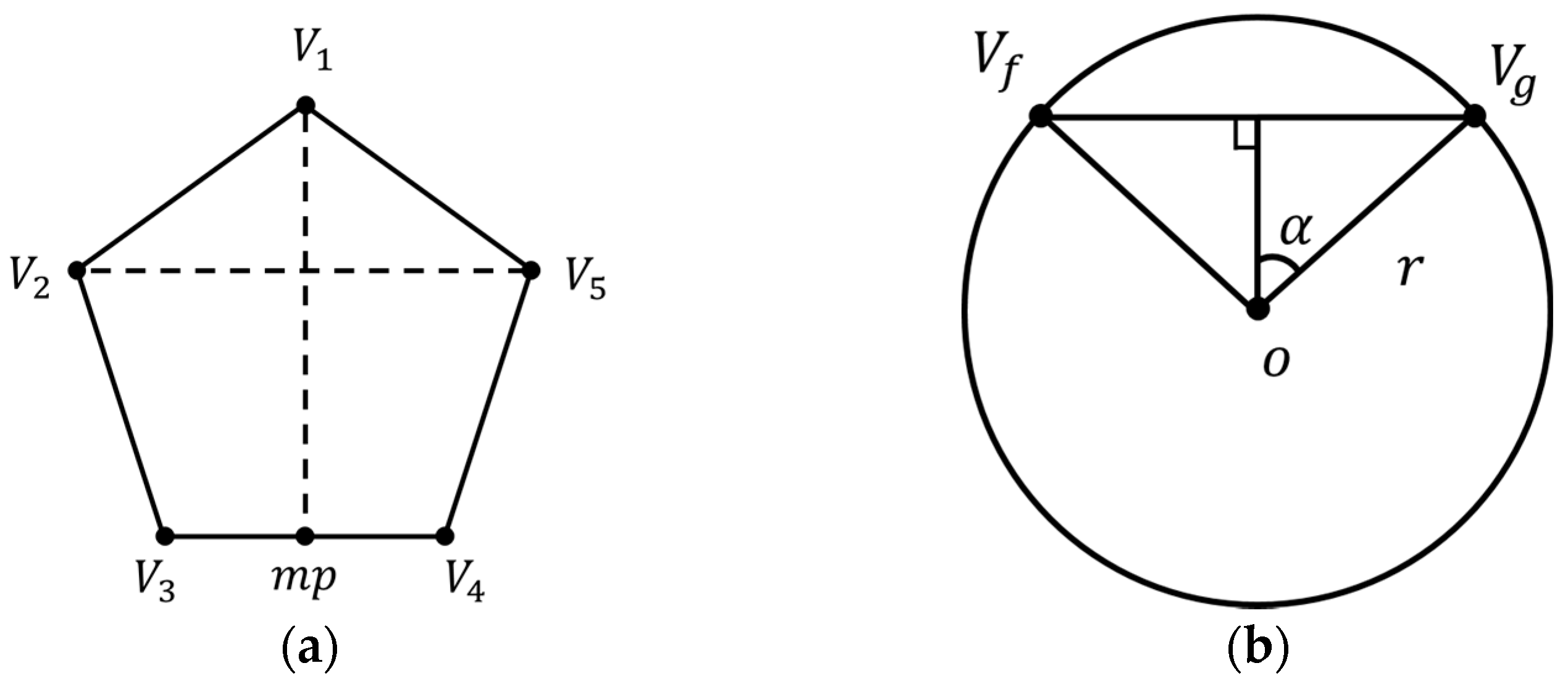
4. Polyhedron-Based Rectilinear Projection
5. Feature Extraction and Matching
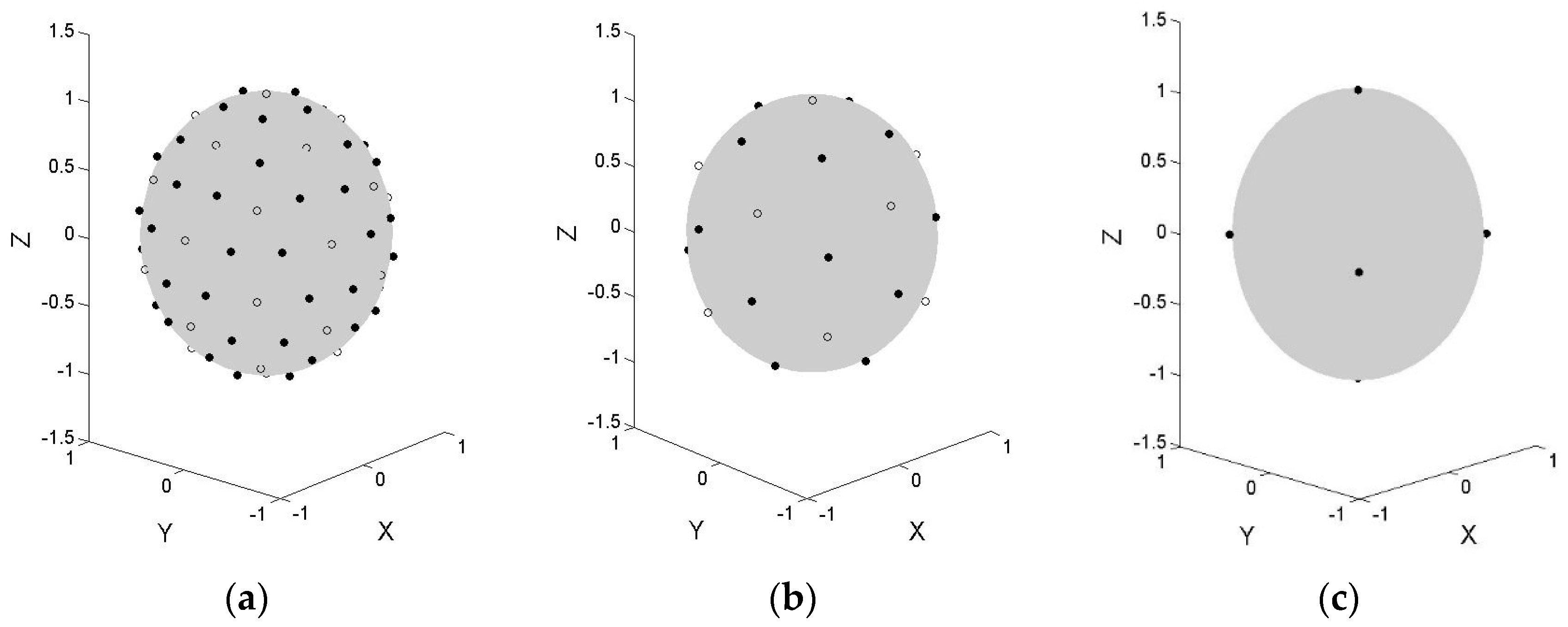
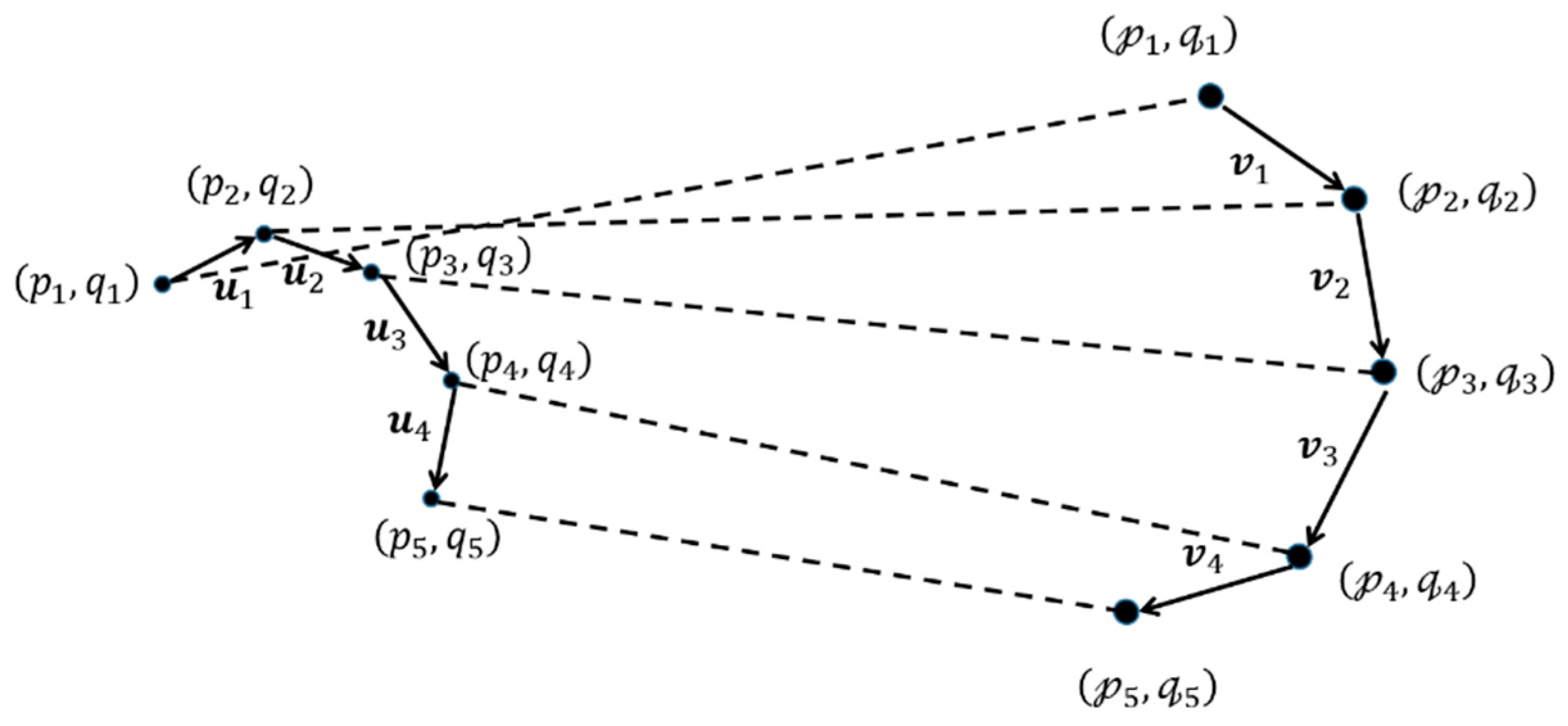
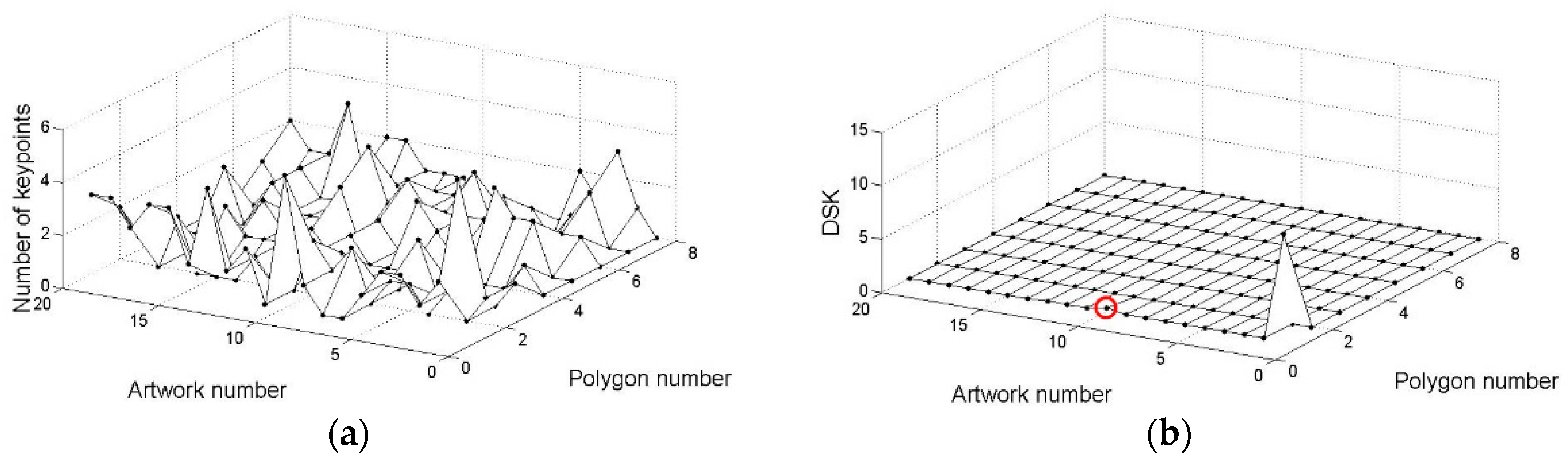
6. Differences in the Shapes of the Keypoints
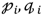 ), , and those in the rectilinear projected image are defined as . Each pair of keypoints with the same index constitutes the matched two keypoints, such as (
), , and those in the rectilinear projected image are defined as . Each pair of keypoints with the same index constitutes the matched two keypoints, such as ( 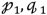 ) and . The keypoints are connected one by one in ascending order of as shown in Figure 10. Then, for each group of keypoints, vectors are generated to represent the keypoint’s shape.
) and . The keypoints are connected one by one in ascending order of as shown in Figure 10. Then, for each group of keypoints, vectors are generated to represent the keypoint’s shape.7. Performance Evaluation
7.1. Experimental Data and Platform
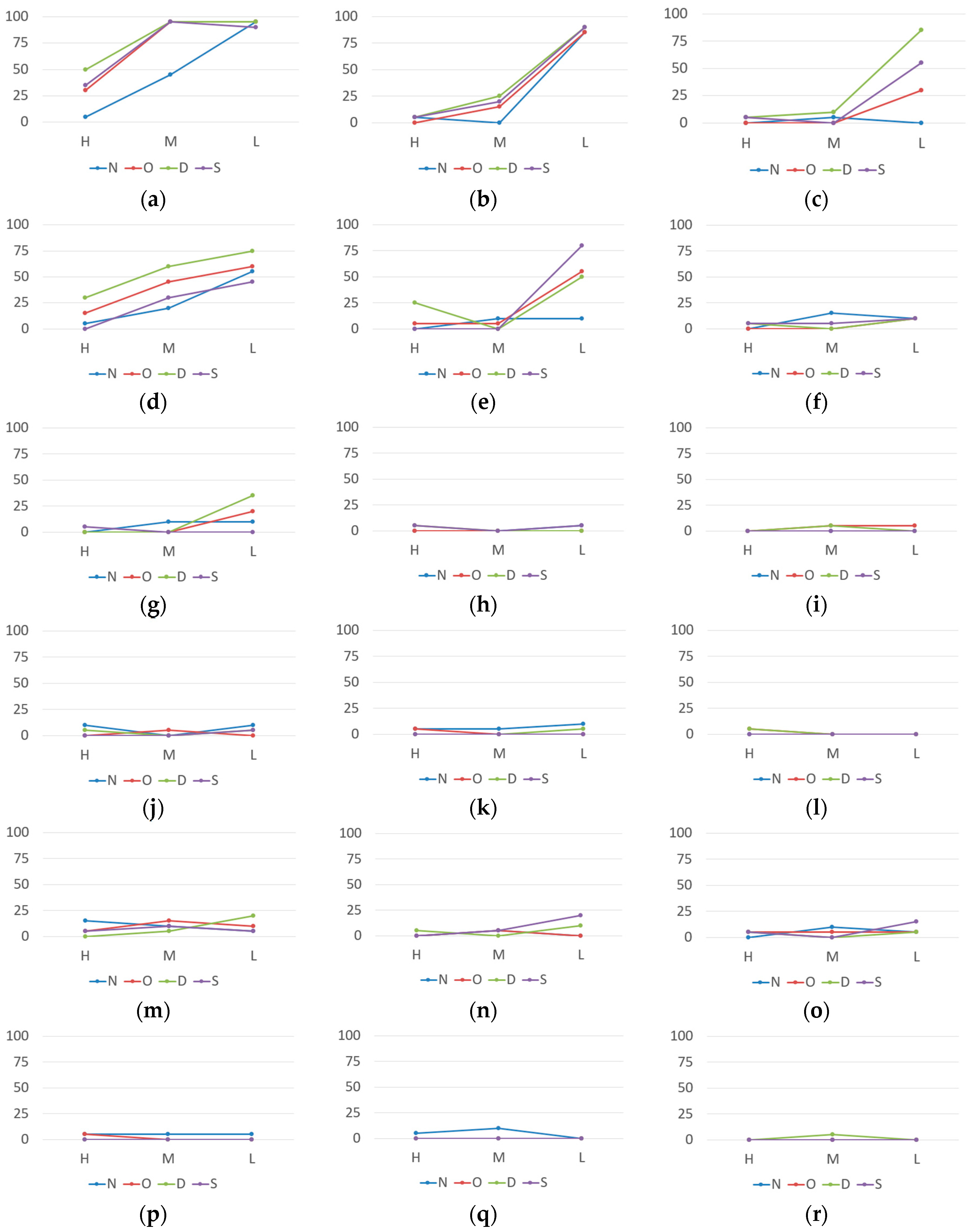
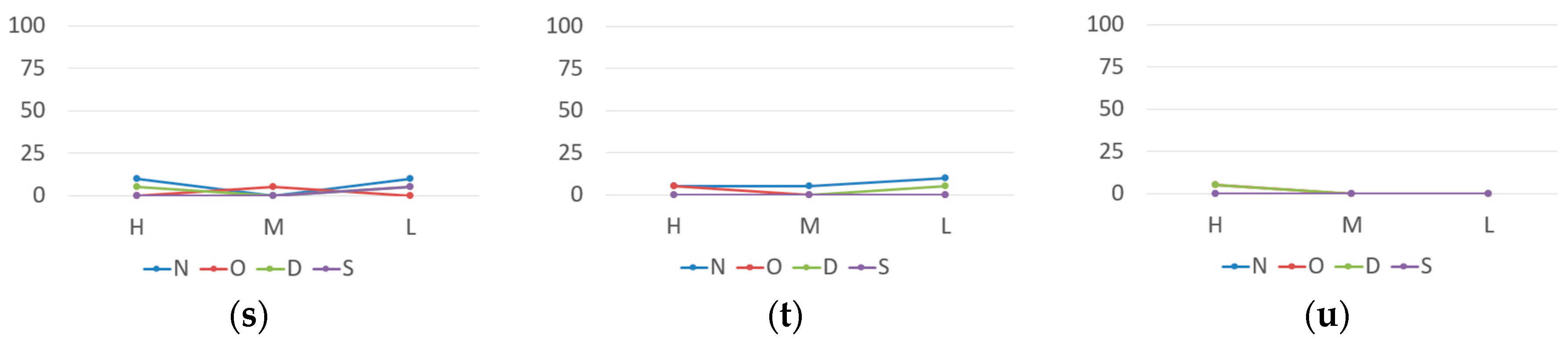
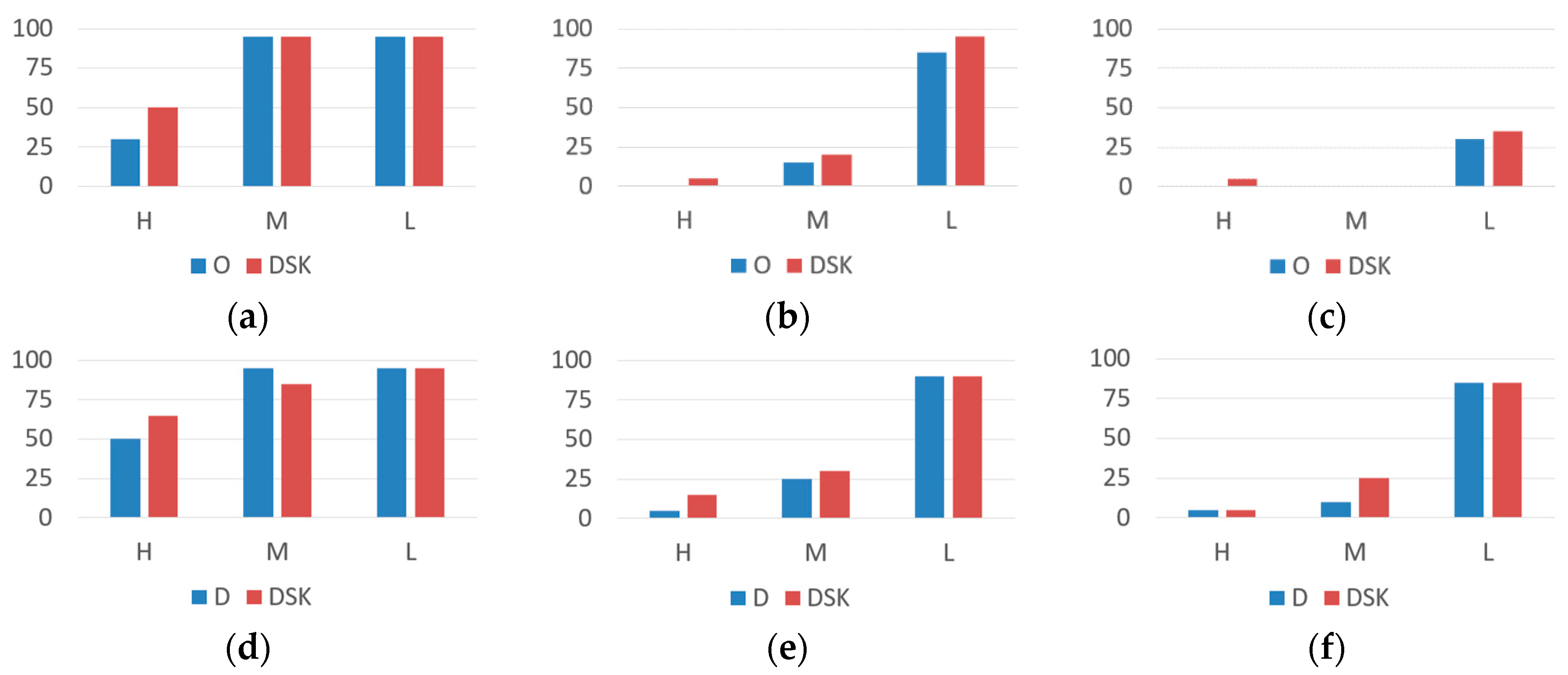
7.2. Experimental Results
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kelion, L. Technology News of BBC. Available online: http://www.bbc.com/news/technology-36073009 (accessed on 3 November 2016).
- McDowell, M. Business News Media of WWD. Available online: http://wwd.com/business-news/media/facebook-users-can-now-share-view-360-degree-photos-10449295/ (accessed on 3 November 2016).
- Loncomilla, P.; Ruiz-del-Solar, J.; Martinez, L. Object recognition using local invariant features for robotic applications: A survey. Pattern Recognit. 2016, 60, 499–514. [Google Scholar] [CrossRef]
- Kashif, M.; Deserno, T.M.; Haak, D.; Jonas, S. Feature description with SIFT, SURF, BRIEF, BRISK, or FREAK? A general question answered for bone age assessment. Comput. Biol. Med. 2016, 68, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Andreopoulos, A.; Tsotsos, J.K. 50 Years of Object Recognition: Directions Forward. Comput. Vis. Image Underst. 2013, 117, 827–891. [Google Scholar] [CrossRef]
- Ragland, K.; Tharcis, P. A Survey on Object Detection, Classification and Tracking Methods. Int. J. Eng. Res. Technol. 2014, 3, 622–628. [Google Scholar]
- Prasad, D.K. Survey of the Problem of Object Detection in Real Images. Int. J. Image Proc. 2012, 6, 441–466. [Google Scholar]
- Sukanya, C.M.; Gokul, R.; Paul, V. A Survey on Object Recognition Methods. Int. J. Comput. Sci. Eng. Technol. 2016, 6, 48–52. [Google Scholar]
- Shantaiya, S.; Verma, K.; Mehta, K. A Survey on Approaches of Object Detection. Int. J. Comput. Appl. 2013, 65, 14–20. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Kisku, D.R.; Gupta, P.; Sing, J.K. Face Recognition using SIFT Descriptor under Multiple Paradigms of Graph Similarity Constraints. Int. J. Multimedia Ubiquitous Eng. 2010, 5, 1–18. [Google Scholar]
- Sadeghipour, E.; Sahragard, N. Face Recognition Based on Improved SIFT Algorithm. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 548–551. [Google Scholar] [CrossRef]
- Krizaj, J.; Struc, V.; Pavesic, N. Adaptation of SIFT Features for Robust Face Recognition. In Image Analysis and Recognition; Campiho, A., Kamel, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 394–404. [Google Scholar]
- Pan, D.; Shi, P. A method of TV Logo Recognition based on SIFT. In Proceedings of the 3rd International Conference on Multimedia Technology; Springer: Berlin, Germany, 2013; pp. 1571–1579. [Google Scholar]
- Berretti, S.; Amor, B.B.; Daoudi, M.; Bimbo, A.D. 3D facial expression recognition using SIFT descriptors of automatically detected keypoints. Vis. Comput. 2011, 27, 1021–1036. [Google Scholar] [CrossRef]
- Lenc, L.; Kral, P. Novel Matching Methods for Automatic Face Recognition using SIFT. Artif. Intell. Appl. Innov. 2012, 381, 254–263. [Google Scholar]
- Choudhury, R. Recognizing Pictures at an Exhibition Using SIFT. Available online: https://web.stanford.edu/class/ee368/Project_07/reports/ee368group11.pdf (accessed on 3 November 2016).
- Ali, N.; Bajwa, K.B.; Sablatnig, R.; Chatzichristofis, S.A.; Iqbal, Z.; Rashid, M.; Habib, H.A. A Novel Image Retrieval Based on Visual Words Integration of SIFT and SURF. PLoS ONE 2016, 11, e0157428. [Google Scholar] [CrossRef] [PubMed]
- Bakar, S.A.; Hitam, M.S.; Yussof, W.N.J.H.W. Content-Based Image Retrieval using SIFT for binary and greyscale images. In Proceedings of the 2013 IEEE International Conference on Signal and Image Processing Applications, Melaka, Malaysia, 8–10 October 2013; pp. 83–88. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-Up Robust Features (SURF). Comput. Vis. Imag. Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Alfanindya, A.; Hashim, N.; Eswaran, C. Content Based Image Retrieval and Classification using speeded-up robust features (SURF) and grouped bag-of-visual-words (GBoVW). In Proceedings of the International Conference on Technology, Informatics, Management, Engineering and Environment, Bandung, Indonesia, 23–26 June 2013; pp. 77–82. [Google Scholar]
- Du, G.; Su, F.; Cai, A. Face recognition using SURF features. Proc. SPIE 2009, 7496, 1–7. [Google Scholar]
- Carro, R.C.; Larios, J.A.; Huerta, E.B.; Caporal, R.M.; Cruz, F.R. Face Recognition Using SURF, In Intelligent Computing Theories and Methodologies; Huang, D., Bevilacqua, V., Premaratne, P., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 316–326. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In Computer Vision ECCV; Daniilidis, K., Maragos, P., Paragios, N., Eds.; Springer: Berlin, Germany, 2010; pp. 778–792. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust Invariant Scalable Keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Washington, DC, USA, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Parnav, G.S. Registration of Face Image Using Modified BRISK Feature Descriptor. Master’s Thesis, Department of Electrical Engineering, National Institute of Technology, Rourkela, Niort, France, 2016. [Google Scholar]
- Mazzeo, P.L.; Spagnolo, P.; Distante, C. BRISK Local Descriptors for Heavily Occluded Ball Recognition. In Image Analysis and Processing; Murino, V., Puppo, E., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 172–182. [Google Scholar]
- Xiao, T.; Zhao, D.; Shi, J.; Lu, M. High-speed Recognition Algorithm Based on BRISK and Saliency Detection for Aerial Images. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 5469–5473. [Google Scholar]
- Oh, J.H.; Eoh, G.; Lee, B.H. Appearance-Based Place Recognition Using Whole-Image BRISK for Collaborative Multi-Robot Localization. Int. J. Mech. Eng. Robot. Res. 2015, 4, 264–268. [Google Scholar]
- Kim, M. Person Recognition using Ocular Image based on BRISK. J. Korea Multimedia Soc. 2016, 19, 881–889. [Google Scholar] [CrossRef]
- Iglesias, F.S.; Buemi, M.E.; Acevedo, D.; Berlles, J.J. Evaluation of Keypoint Descriptors for Gender Recognition. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications; Corrochano, E.B., Hancock, E., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 564–571. [Google Scholar]
- Paek, K.; Yao, M.; Liu, Z.; Kim, H. Log-Spiral Keypoint: A Robust Approach toward Image Patch Matching. Comput. Intell. Neurosci. 2015, 2015, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- Ren, H.; Li, Z.N. Object detection using edge histogram of oriented gradient. In Proceedings of the 2014 IEEE International Conference on Image Processing, Paris, France, 27–30 October 2014; pp. 4057–4061. [Google Scholar]
- Stefanou, S.; Argyros, A.A. Efficient Scale and Rotation Invariant Object Detection based on HOGs and Evolutionary Optimization Techniques. Adv. Vis. Comput. 2012, 7431, 220–229. [Google Scholar]
- Zhang, B. Offline signature verification and identification by hybrid features and Support Vector Machine. Int. J. Artif. Intell. Soft Comput. 2011, 2, 302–320. [Google Scholar] [CrossRef]
- Tsolakidis, D.G.; Kosmopoulos, D.I.; Papadourakis, G. Plant Leaf Recognition Using Zernike Moments and Histogram of Oriented Gradients. In Artificial Intelligence: Methods and Applications; Likas, A., Blekas, K., Kalles, D., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 406–417. [Google Scholar]
- Ebrahimzadeh, R.; Jampour, M. Efficient Handwritten Digit Recognition based on Histogram of Oriented Gradients and SVM. Int. J. Comput. Appl. 2014, 104, 10–13. [Google Scholar] [CrossRef]
- Carcagni, P.; Coco, M.D.; Leo, M.; Distante, C. Facial expression recognition and histograms of oriented gradients: A comprehensive study. SpringerPlus 2015, 4, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Torrione, P.A.; Morton, K.D.; Sakaguchi, R.; Collins, L.M. Histograms of Oriented Gradients for Landmine Detection in Ground-Penetrating Radar Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1539–1550. [Google Scholar] [CrossRef]
- Yan, G.; Yu, M.; Yu, Y.; Fan, L. Real-time vehicle detection using histograms of oriented gradients and AdaBoost classification. Optik-Int. J. Light Electron Opt. 2016, 127, 7941–7951. [Google Scholar] [CrossRef]
- Rybski, P.E.; Huber, D.; Morris, D.D.; Hoffman, R. Visual Classification of Coarse Vehicle Orientation using Histogram of Oriented Gradients Features. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 1–8. [Google Scholar]
- Beiping, H.; Wen, Z. Fast Human Detection Using Motion Detection and Histogram of Oriented Gradients. J. Comput. 2011, 6, 1597–1604. [Google Scholar] [CrossRef]
- Zhu, Q.; Avidan, S.; Yeh, M.; Cheng, K. Fast Human Detection Using a Cascade of Histograms of Oriented Gradients. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–23 June 2006; pp. 1491–1498. [Google Scholar]
- Kobayashi, T.; Hidaka, A.; Kurita, T. Selection of Histograms of Oriented Gradients Features for Pedestrian Detection. In Neural Information Processing; Ishikawa, M., Doya, K., Miyamoto, H., Yamakawa, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 598–607. [Google Scholar]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust Wide Baseline Stereo from Maximally Stable Extremal Regions. In Proceedings of the 2002 British Machine Vision Conference, Cardiff, UK, 2–5 September 2002; pp. 384–393. [Google Scholar]
- Tian, S.; Lu, S.; Su, B.; Tan, C.L. Scene Text Segmentation with Multi-level Maximally Stable Extremal Regions. In Proceedings of the 2014 International Conference on Pattern Recognition, Lanzhou, China, 13–16 July 2014; pp. 2703–2708. [Google Scholar]
- Oh, I.-S.; Lee, J.; Majumber, A. Multi-scale Image Segmentation Using MSER. In Computer Analysis of Images and Patterns; Wilson, R., Hancock, E., Bors, A., Smith, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 201–208. [Google Scholar]
- Zhu, H.; Sheng, J.; Zhang, F.; Zhou, J.; Wang, J. Improved maximally stable extremal regions based method for the segmentation of ultrasonic liver images. Multimedia Tools Appl. 2016, 75, 10979–10997. [Google Scholar] [CrossRef]
- Adlinge, G.; Kashid, S.; Shinde, T.; Dhotre, V. Text Extraction from image using MSER approach. Int. Res. J. Eng. Technol. 2016, 3, 2453–2457. [Google Scholar]
- Lee, S.; Yoo, C.D. Robust video fingerprinting based on affine covariant regions. In Proceedings of the 2008 International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008. [Google Scholar]
- Zhang, L.; Dai, G.J.; Wang, C.J. Human Tracking Method Based on Maximally Stable Extremal Regions with Multi-Cameras. Appl. Mech. Mater. 2011, 44, 3681–3686. [Google Scholar] [CrossRef]
- Obdrzalek, S.; Matas, J. Object Recognition Using Local Affine Frames on Maximally Stable Extremal Regions. In Toward Category-Level Object Recognition; Ponce, J., Hebert, M., Schmid, C., Zisserman, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 83–104. [Google Scholar]
- Rosten, E.; Drummond, T. Machine Learning for High-Speed Corner Detection. In Computer Vision-European Conference on Computer Vision; Leonardis, A., Bischof, H., Pinz, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 430–443. [Google Scholar]
- Rosten, E.; Drummond, T. Fusing Points and Lines for High Performance Tracking. In Proceedings of the 2005 IEEE International Conference on Computer Vision, Beijing, China, 15–21 October 2005; pp. 1508–1515. [Google Scholar]
- Lu, H.; Zhang, H.; Zheng, Z. A Novel Real-Time Local Visual Feature for Omnidirectional Vision Based on FAST and LBP. In RoboCup 2010: Robot Soccer World Cup XIV; Ruiz-del-Solar, J., Chown, E., Ploger, P.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 291–302. [Google Scholar]
- Pahlberg, T.; Hagman, O. Feature Recognition and Fingerprint Sensing for Guiding a Wood Patching Robot. In Proceedings of the 2012 World Conference on Timber Engineering, Auckland, New Zealand, 15–19 July 2012. [Google Scholar]
- Bharath, R.; Rajalakshmi, P. Fast Region of Interest detection for fetal genital organs in B-mode ultrasound images. In Proceedings of the 2014 Biosignals and Biorobotics Conference on Biosignals and Robotics for Better and Safer Living, Bahia, Brazil, 26–28 May 2014. [Google Scholar]
- Olaode, A.A.; Naghdy, G.; Todd, C.A. Unsupervised Region of Interest Detection Using Fast and Surf. In Proceedings of the 2015 International Conference on Signal, Image Processing and Pattern Recognition, Delhi, India, 23–25 May 2015; pp. 63–72. [Google Scholar]
- Alahi, A.; Ortiz, R.; Vandergheynst, P. FREAK: Fast Retina Keypoint. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 510–517. [Google Scholar]
- Yaghoubyan, S.H.; Maarof, M.A.; Zainal, A.; Rohani, M.F.; Oghaz, M.M. Fast and Effective Bag-of-Visual-Word Model to Pornographic Images Recognition Using the FREAK Descriptor. J. Soft Comput. Decis. Support Syst. 2015, 2, 27–33. [Google Scholar]
- Caetano, C.; Avila, S.; Schwartz, W.R.; Guimaraes, S.J.F.; Araujo, A.A. A mid-level video representation based on binary descriptors: A case study for pornography detection. Neurocomputing 2016, 213, 102–114. [Google Scholar] [CrossRef]
- Gomez, C.H.; Medathati, K.; Kornprobst, P.; Murino, V.; Sona, D. Improving FREAK Descriptor for Image Classification. In Computer Vision Systems; Nalpantidis, L., Kruger, V., Eklundh, J., Gasteratos, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 14–23. [Google Scholar]
- Strat, S.T.; Benoit, A.; Lambert, P. Retina Enhanced Bag of Words Descriptors for Video Classification. In Proceedings of the 2014 European Signal Processing Conference, Lisbon, Portugal, 1–5 September 2014; pp. 1307–1311. [Google Scholar]
- Chen, Y.; Xu, W.; Piao, Y. Target Matching Recognition for Satellite Images Based on the Improved FREAK Algorithm. Math. Probl. Eng. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Ju, M.H.; Kang, H.B. Stitching Images with Arbitrary Lens Distortions. Int. J. Adv. Robot. Syst. 2014, 11, 1–11. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic Panoramic Image Stitching using Invariant Features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Oh, S.H.; Jung, S.K. Vanishing Point Estimation in Equirectangular Images. In Proceedings of the 2012 International Conference on Multimedia Information Technology and Applications, Beijing, China, 8–10 December 2012; pp. 1–3. [Google Scholar]
- Bildirici, I.O. Quasi indicatrix approach for distortion visualization and analysis for map projections. Int. J. Geogr. Inf. Sci. 2015, 29, 2295–2309. [Google Scholar] [CrossRef]
- Snyder, J.P.; Voxland, P.M. An Album of Map Projections; USGS Professional Paper 1453; U.S. Government Printing Office: Washington, DC, USA, 1989.
- Temmermans, F.; Jansen, B.; Deklerck, R.; Schelkens, P.; Cornelis, J. The Mobile Museum Guide: Artwork Recognition with Eigenpaintings and SURF. In Proceedings of the International Workshop on Image Analysis for Multimedia Interactive Services, Delft, The Netherlands, 13–15 April 2011. [Google Scholar]
- Morel, J.M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Boussias-Alexakis, E.; Tsironis, V.; Petsa, E.; Karras, G. Automatic Adjustment of Wide-Base Google Street View Panoramas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 639–645. [Google Scholar] [CrossRef]
- Apollonio, F.I.; Ballabeni, A.; Gaiani, M.; Remondino, F. Evaluation of feature-based methods for automated network orientation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-5, 47–54. [Google Scholar] [CrossRef]
- Jin, X.; Kim, J. ArtWork recognition in 360-degree image using 32-hedron based rectilinear projection and scale invariant feature transform. In Proceedings of the 2016 IEEE International Conference on Electronic Information and Communication Technology, Harbin, China, 20–22 August 2016; pp. 356–359. [Google Scholar]








| No. | Name | Image Size | File Size |
|---|---|---|---|
| 1 | Cafe Terrace at Night | 1761 × 2235 (300 DPI) | 641 KB |
| 2 | Lady with an Ermine | 3543 × 4876 (300 DPI) | 3.33 MB |
| 3 | Family of Saltimbanques | 1394 × 1279 (180 DPI) | 233 KB |
| 4 | Flowers in a Blue Vase | 800 × 1298 (96 DPI) | 385 KB |
| 5 | Joan of Arc at the Coronation of Charles | 1196 × 1600 (96 DPI) | 460 KB |
| 6 | The Apotheosis of Homer | 1870 × 1430 (300 DPI) | 3.1 MB |
| 7 | Romulus’ Victory over Acron | 2560 × 1311 (72 DPI) | 384 KB |
| 8 | The Annunciation | 4057 × 1840 (72 DPI) | 7.52 MB |
| 9 | The Last Supper | 5381 × 2926 (96 DPI) | 3.19 MB |
| 10 | Mona Lisa | 7479 × 11146 (72 DPI) | 89.9 MB |
| 11 | The Soup | 1803 × 1510 (240 DPI) | 359 KB |
| 12 | The Soler Family | 2048 × 1522 (72 DPI) | 1.91 MB |
| 13 | The Red Vineyard | 2001 × 1560 (240 DPI) | 4.12 MB |
| 14 | Flowering orchard, surrounded by cypress | 2514 × 1992 (600 DPI) | 2.89 MB |
| 15 | Flowering Orchard | 3864 × 3036 (600 DPI) | 5.94 MB |
| 16 | Woman Spinning | 1962 × 3246 (600 DPI) | 3.79 MB |
| 17 | Wheat Fields with Stacks | 3864 × 3114 (600 DPI) | 6.01 MB |
| 18 | Bedroom in Arles | 767 × 600 (96 DPI) | 40.9 KB |
| 19 | The Starry Night | 1879 × 1500 (300 DPI) | 761 KB |
| 20 | A Wheat Field, with Cypresses | 3112 × 2448 (72 DPI) | 7.22 MB |
| Features | Feature Extraction Time (s) | Feature Matching Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| O | D | SP | SH | O | D | SP | SH | |
| SIFT | 1.192 | 1.256 | 1.561 | 2.225 | 0.027 | 0.029 | 0.049 | 0.061 |
| SURF | 0.941 | 0.975 | 1.125 | 1.630 | 0.002 | 0.003 | 0.002 | 0.002 |
| MSER | 1.026 | 1.050 | 1.161 | 1.689 | 0.002 | 0.002 | 0.001 | 0.001 |
| FAST | 0.926 | 0.958 | 1.108 | 1.597 | 0.004 | 0.003 | 0.002 | 0.002 |
| BRISK | 0.929 | 0.962 | 1.113 | 1.601 | 0.002 | 0.002 | 0.002 | 0.002 |
| HOG | 1.161 | 1.147 | 1.163 | 1.748 | 0.003 | 0.002 | 0.001 | 0.001 |
| FREAK | 0.925 | 0.958 | 1.109 | 1.595 | 0.002 | 0.002 | 0.002 | 0.002 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Kim, J. Artwork Identification for 360-Degree Panoramic Images Using Polyhedron-Based Rectilinear Projection and Keypoint Shapes. Appl. Sci. 2017, 7, 528. https://doi.org/10.3390/app7050528
Jin X, Kim J. Artwork Identification for 360-Degree Panoramic Images Using Polyhedron-Based Rectilinear Projection and Keypoint Shapes. Applied Sciences. 2017; 7(5):528. https://doi.org/10.3390/app7050528
Chicago/Turabian StyleJin, Xun, and Jongweon Kim. 2017. "Artwork Identification for 360-Degree Panoramic Images Using Polyhedron-Based Rectilinear Projection and Keypoint Shapes" Applied Sciences 7, no. 5: 528. https://doi.org/10.3390/app7050528
APA StyleJin, X., & Kim, J. (2017). Artwork Identification for 360-Degree Panoramic Images Using Polyhedron-Based Rectilinear Projection and Keypoint Shapes. Applied Sciences, 7(5), 528. https://doi.org/10.3390/app7050528






