Uniaxial Compressive Strength and Fracture Mode of Lake Ice at Moderate Strain Rates Based on a Digital Speckle Correlation Method for Deformation Measurement
Abstract
:1. Introduction
2. Experimental Methods
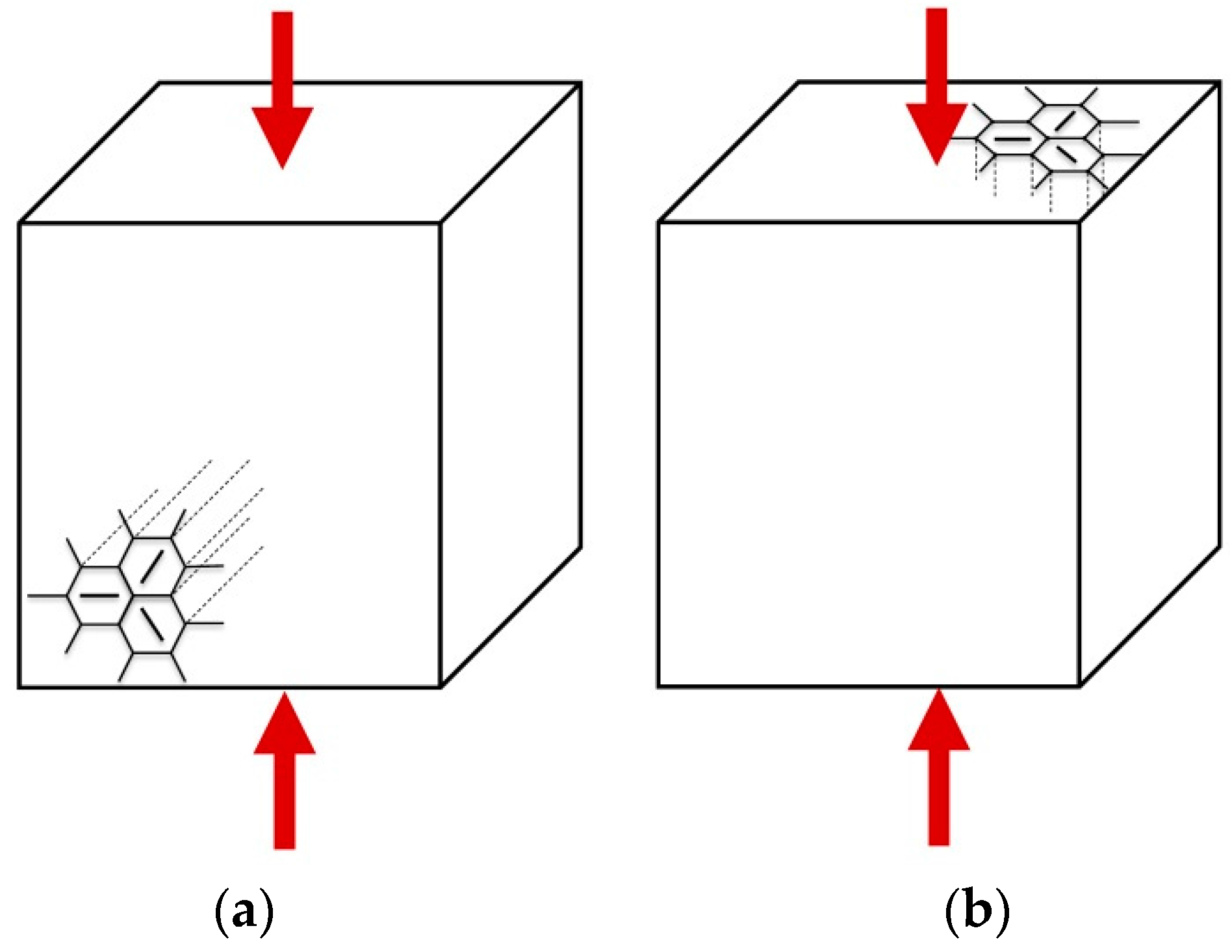
2.1. Ice Specimens
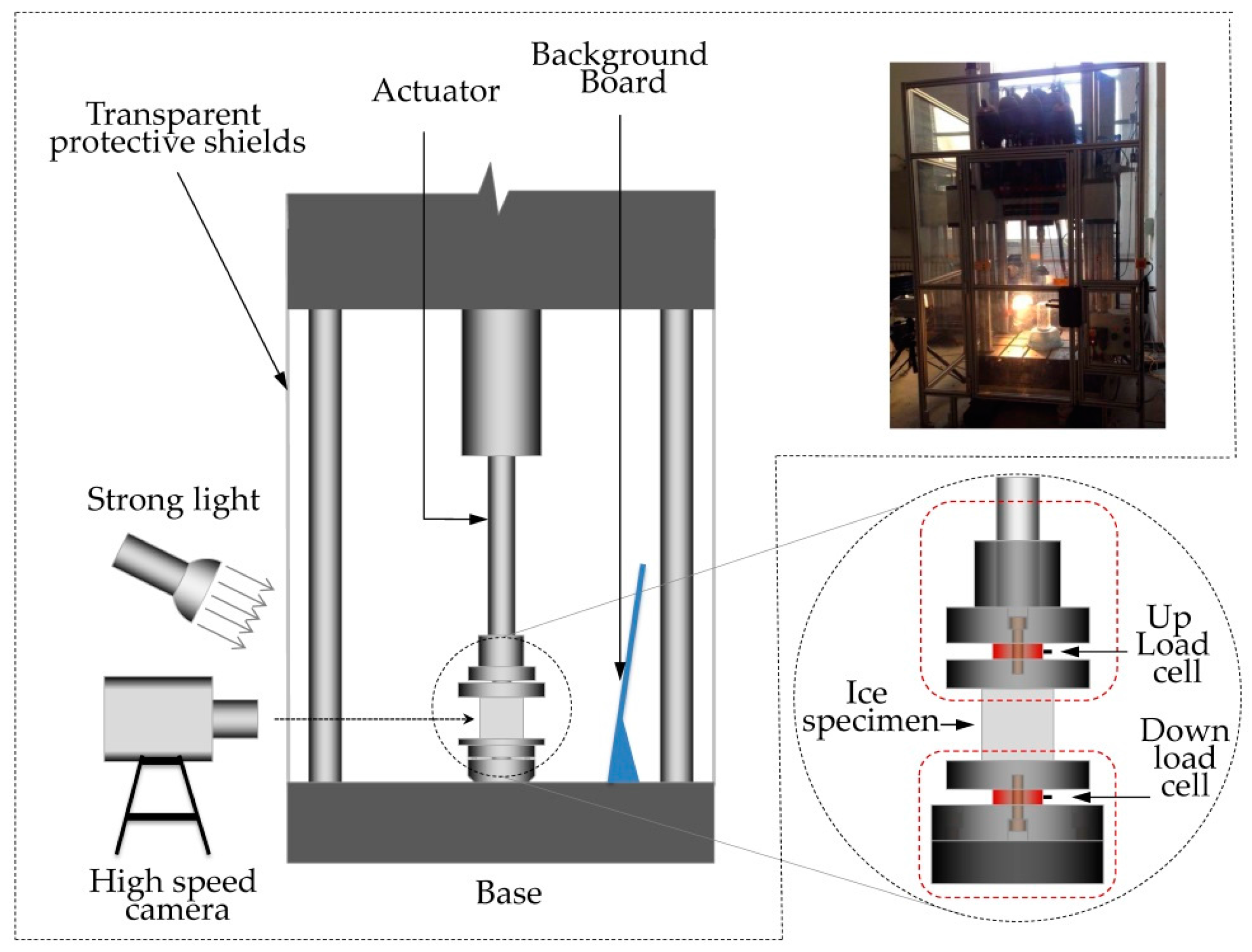
2.2. High-Speed Loading Machine with Two Load Cells for Dynamic Force Measurement
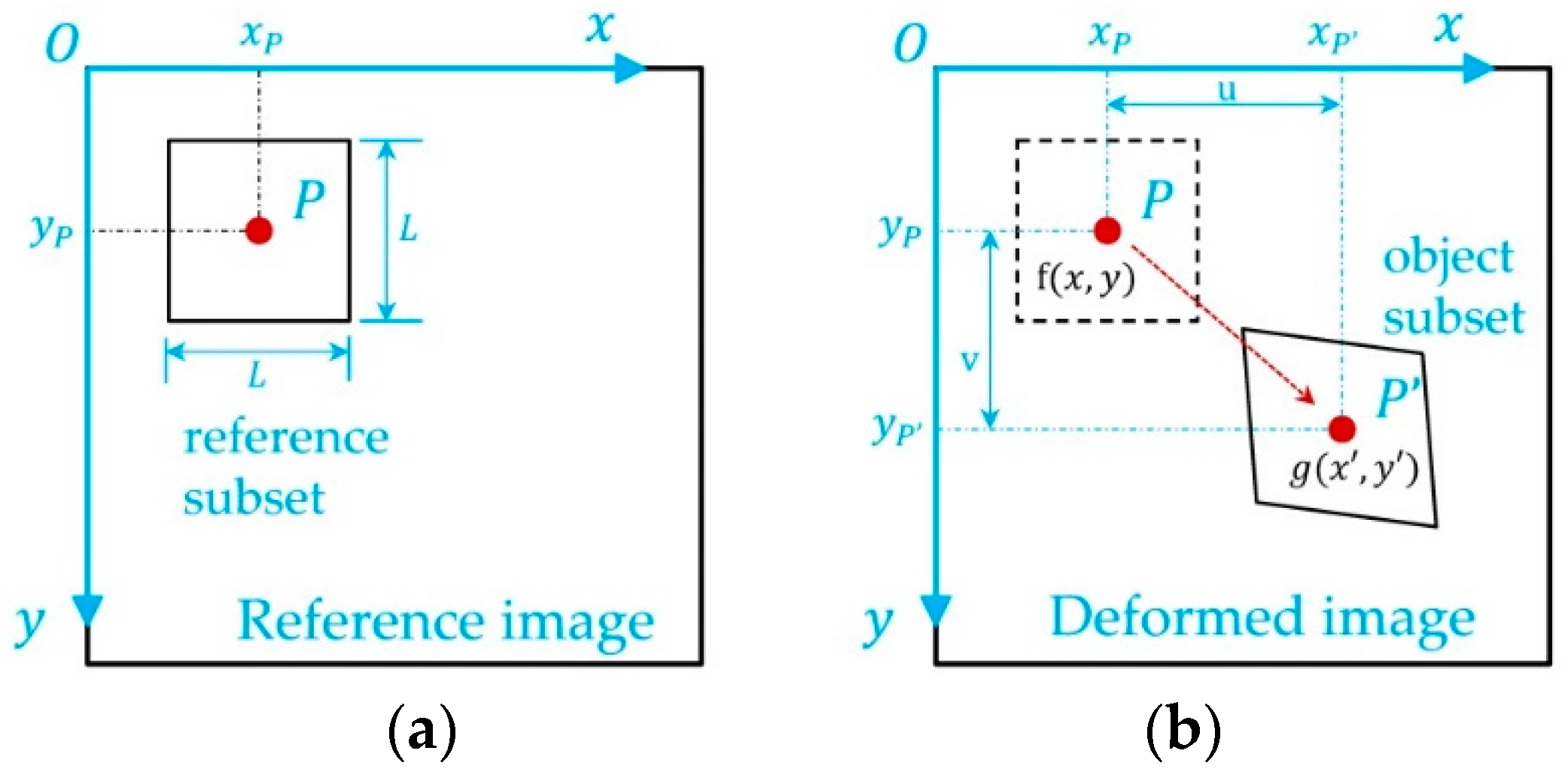
2.3. Digital Speckle Correlation Method for Deformation Measurement
3. Experimental Results
3.1. Results of Dynamic Uniaxial Compression Tests on Hard Ice
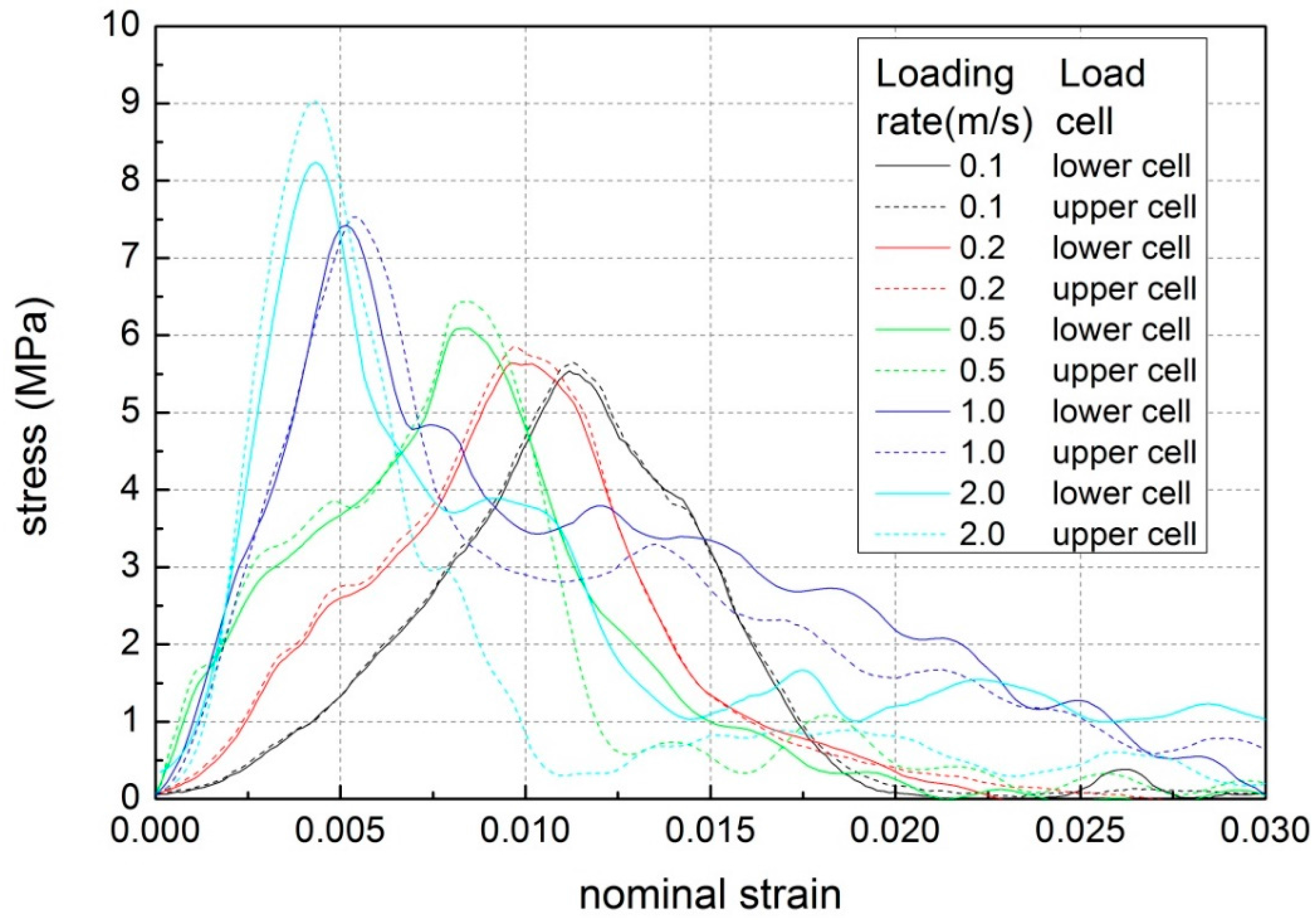
3.1.1. Uniaxial Compressive Strength of Hard Ice
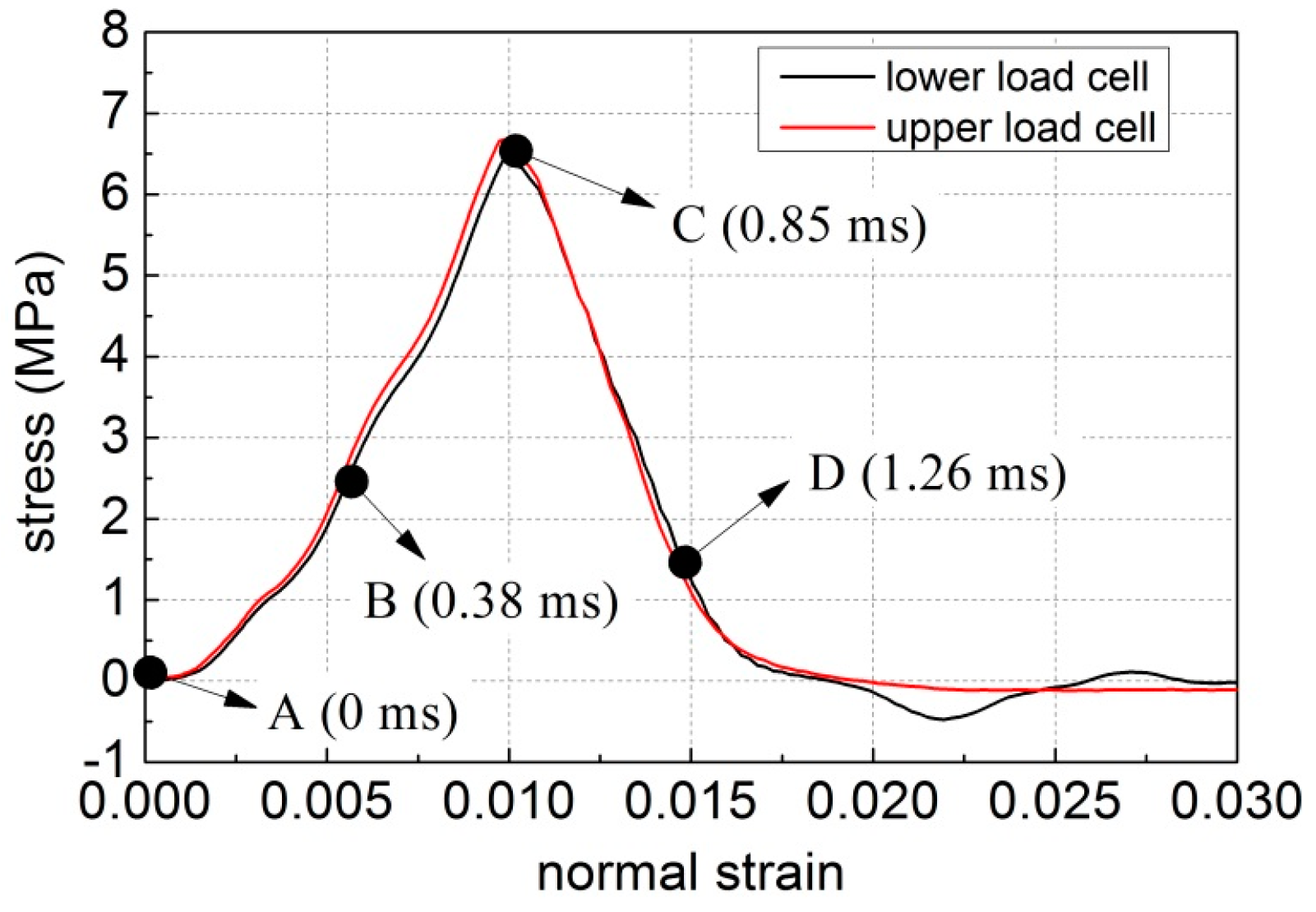
3.1.2. Fracture Mode of Hard Ice
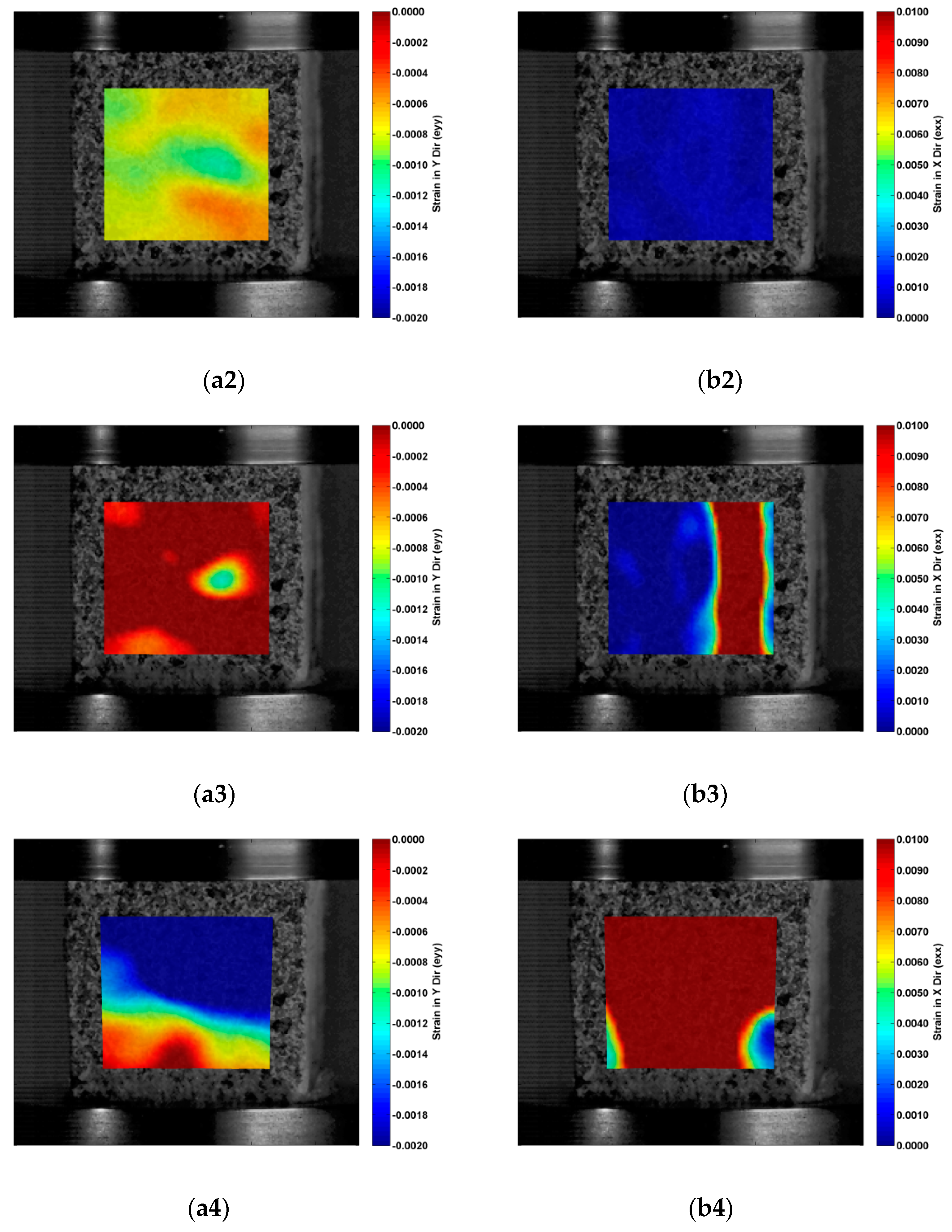
3.1.3. Dynamic Deformation Measurement by DSCM
3.2. Results of Dynamic Uniaxial Compression Tests on Soft Ice
3.2.1. Uniaxial Compressive Strength of Soft Ice
3.2.2. Fracture Mode of Soft Ice
3.2.3. Dynamic Deformation Measurement by DSCM
4. Summary of Results and Discussion
4.1. Dynamic Deformation of Ice Samples at Moderate Rates
4.2. Relationship between Compressive Strength and Strain-Rate, Air Porosity, Loading Direction as Well as Temperature in Moderate Strain-Rate Range
4.3. Fracture Mode of Ice at Moderate Strain Rates
4.4. Crack Propagation Velocity
5. Conclusions
- (1)
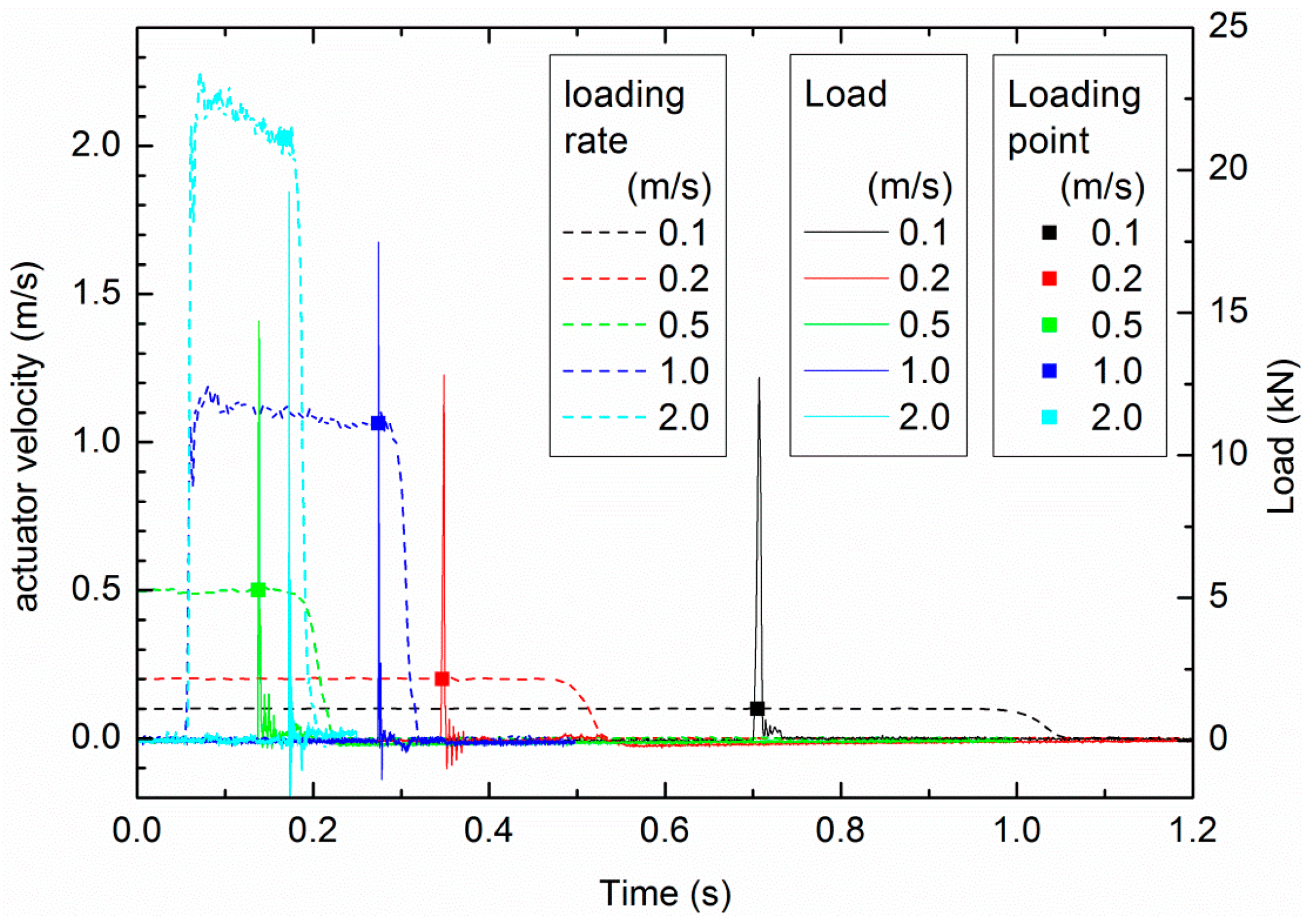
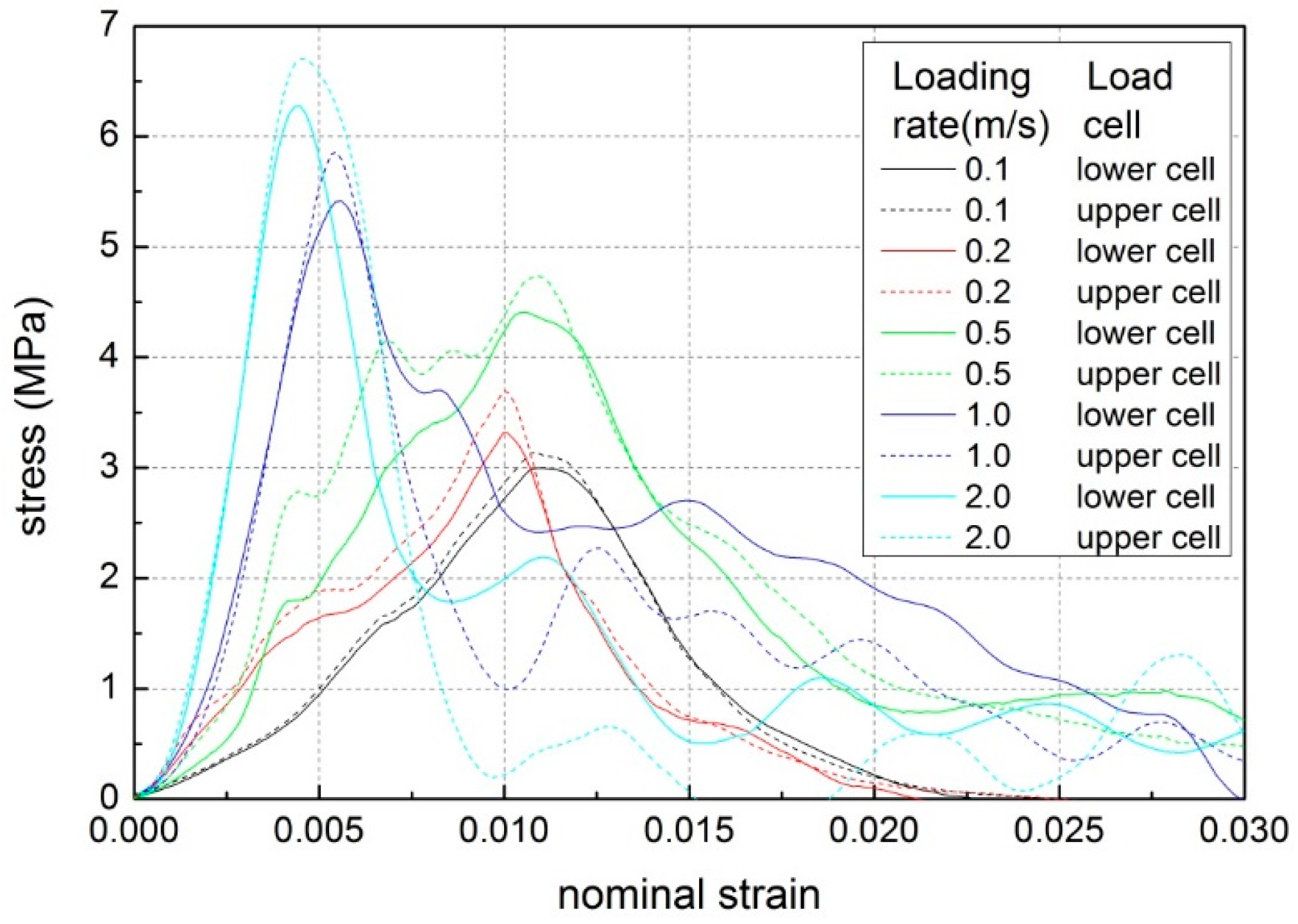
- When loading rate is not greater than 2.0 m·s−1, the forces obtained at the two ends of a five-centimeter-high ice specimen are balanced or approximately balanced. Therefore, the difference in forces between the upper-end and the lower-end, resulting from the inertial effect, could be ignored.
- (2)
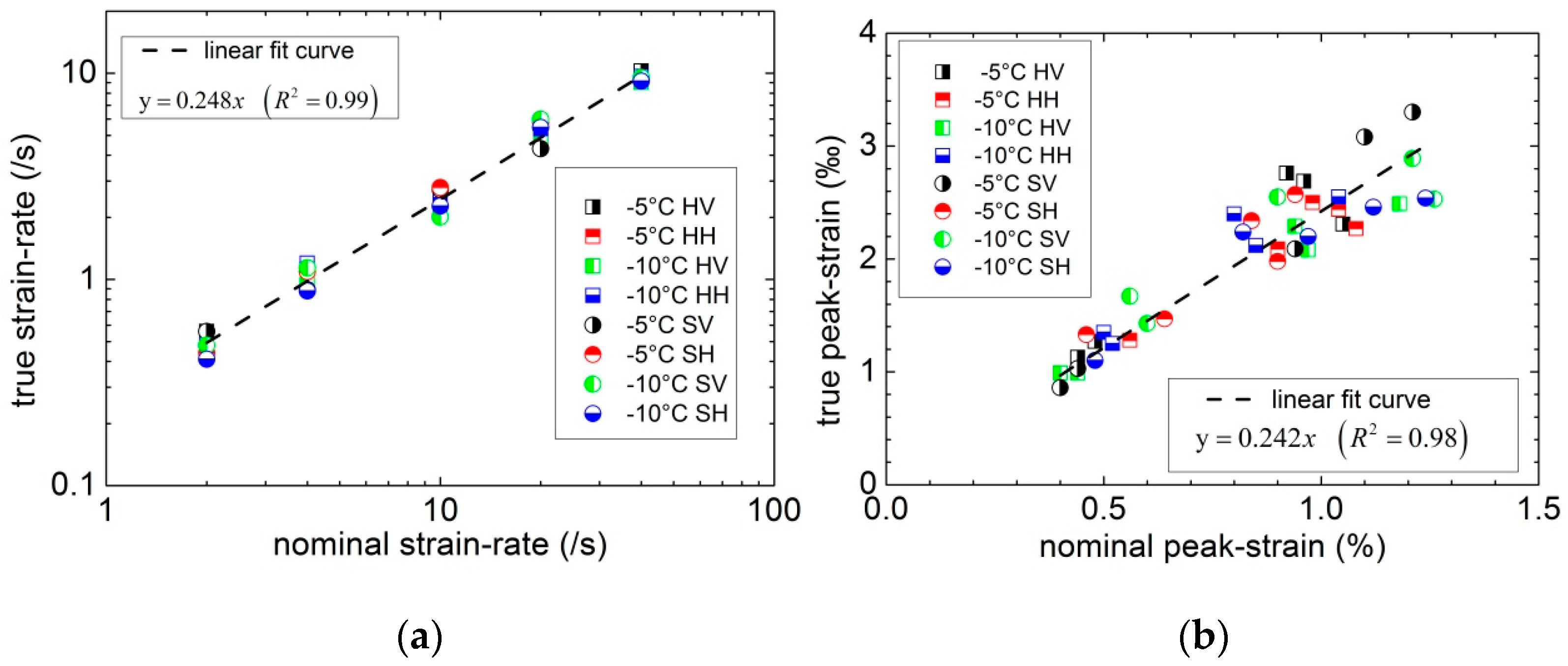
- In ice dynamic compression experiments, there may exist a significant difference between true deformation and nominal deformation, so it is not recommended to regard nominal strain-rate and nominal ultimate strain directly as true strain-rate and true ultimate strain.
- (3)
- By constructing an artificial speckle on ice surface, it is feasible to measure the deformation of ice specimen under dynamic compression tests through the digital speckle correlation method.
- (4)
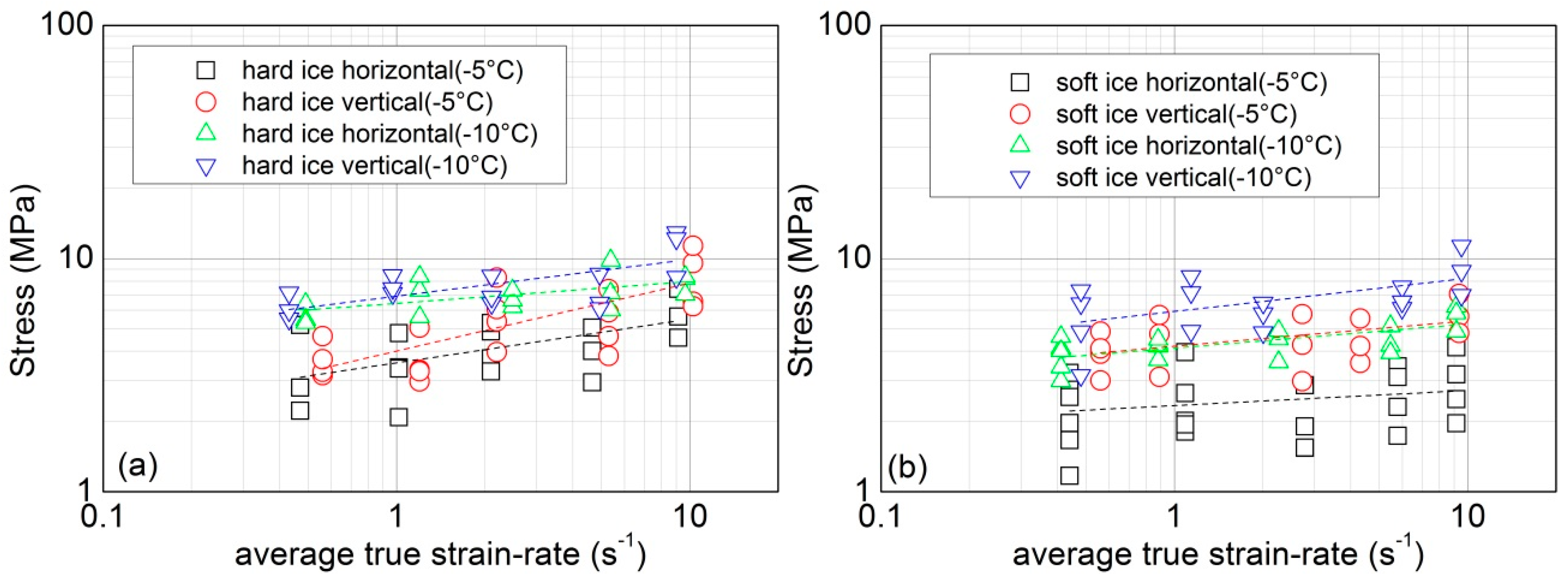
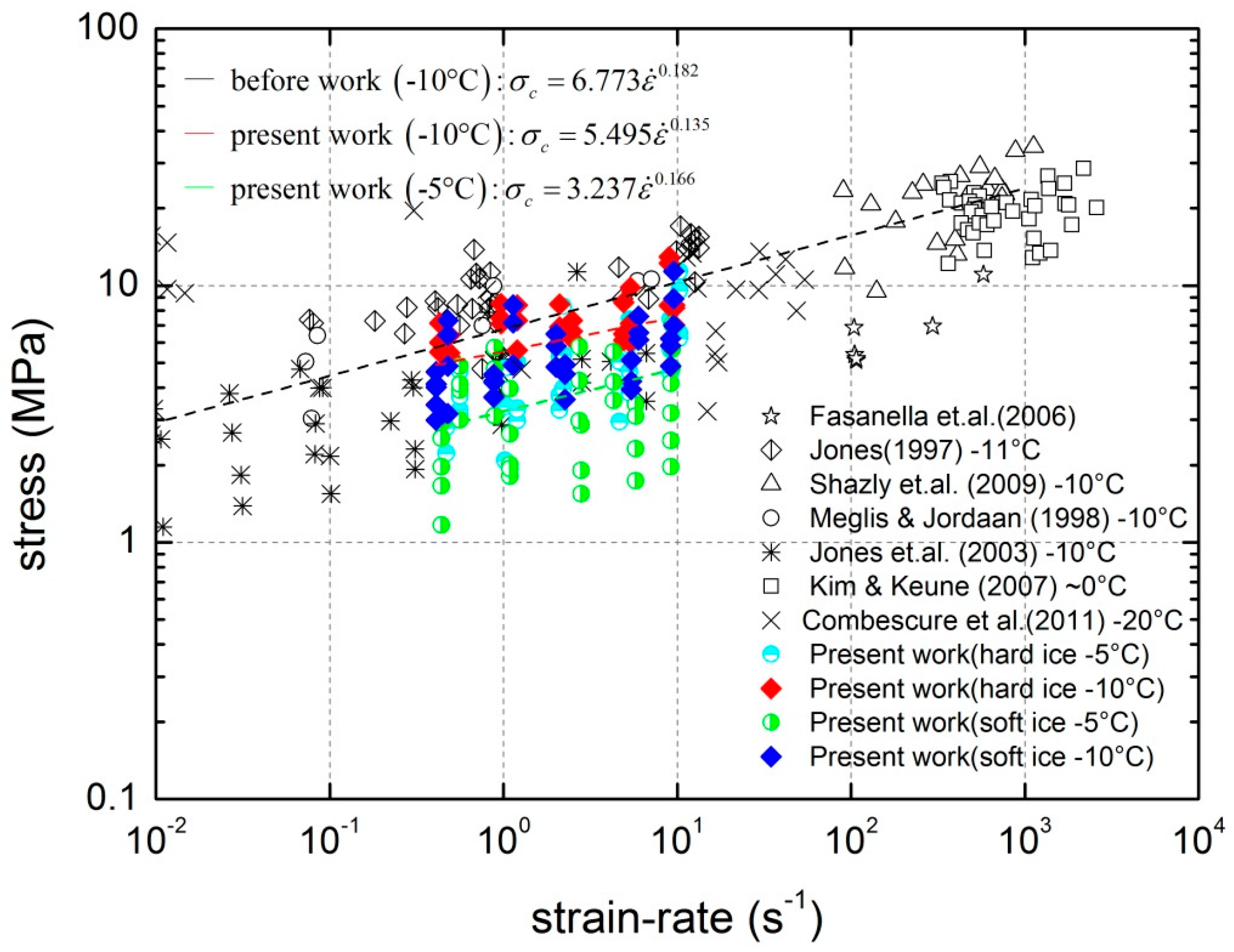
- In the employed strain-rate range (0.4–10 s−1), the relationships between uniaxial compressive strength of natural lake ice and its influencing factors, such as strain-rate, temperature, loading direction, as well as air porosity, are almost similar to that under quasi-static conditions. The compressive strength increases with increasing strain-rate, and they obey a power-law relationship with the power exponent of 0.14–0.17. Temperature has a significant effect on the compressive strength, no matter whether the air porosity in ice is low or high and whether the loading direction is horizontal or vertical. The compressive strength shows an increasing trend with decreasing temperature. The strength at −10 °C is about 1.4–1.8 times that at −5 °C. Moreover, the vertical compressive strength is slightly greater than the horizontal compressive strength.
- (5)
- In the employed strain-rate range, the fracture mode of ice is not sensitive to the loading rate and loading direction. Failure of ice specimen exhibits features of longitudinal splitting failure, accompanied with feature of forming a large number of small fragments, just like that in crushing failure mode. The fracture mode is a combination of splitting failure and crushing failure.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
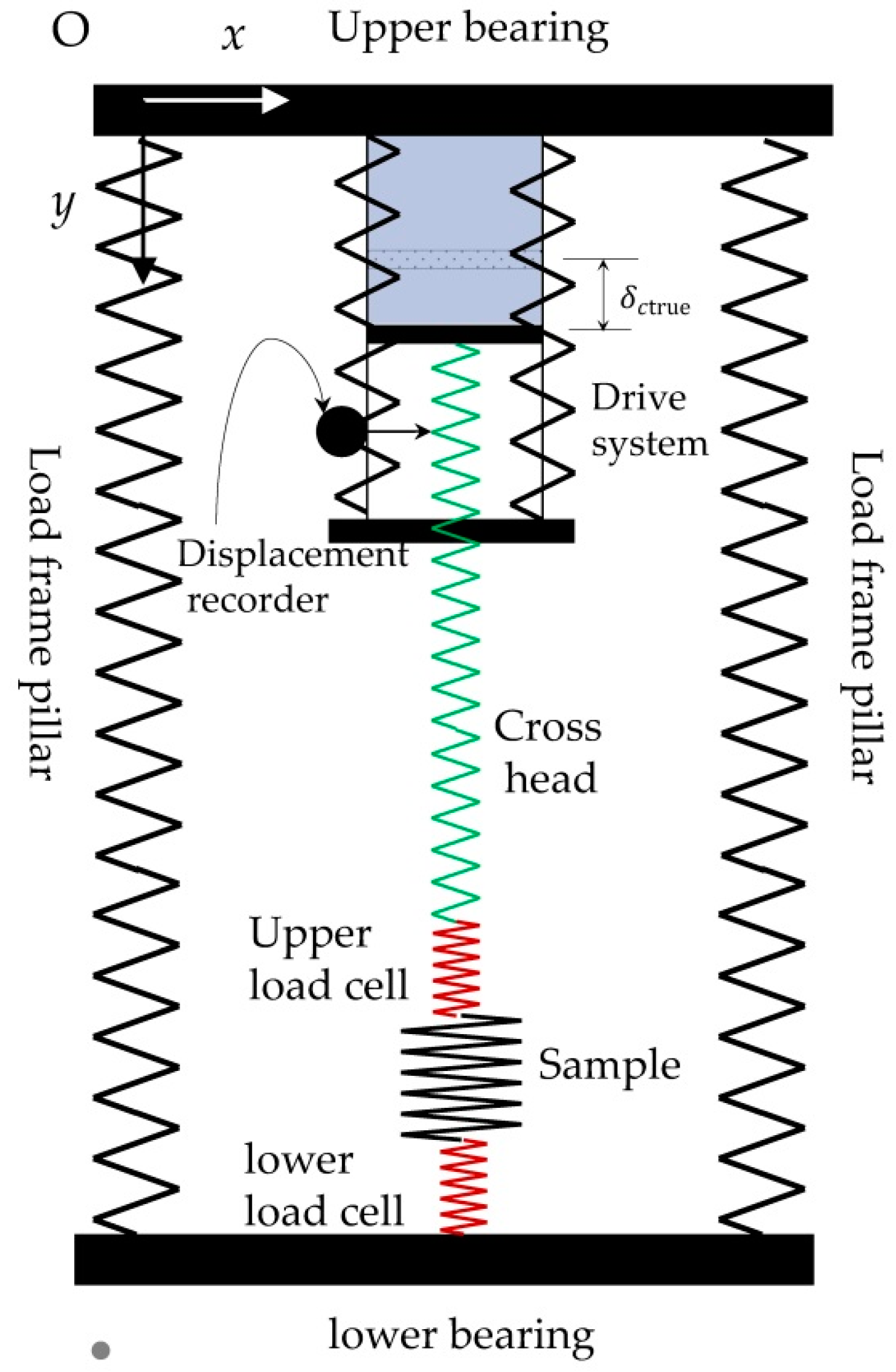
| Components | Deformation | Stiffness |
|---|---|---|
| Sample | ||
| Actuator | ||
| Load frames | ||
| Drive system | ||
| Load cell | ||
| Test fixtures | ||
| Contact interfaces |
References
- Michel, B. Ice Mechanics; University of Laval Press: Quebec, QC, Canada, 1978. [Google Scholar]
- Dempsey, J.P. Research trends in ice mechanics. Int. J. Solids Struct. 2000, 37, 131–153. [Google Scholar] [CrossRef]
- Cole, D.M. The microstructure of ice and its influence on mechanical properties. Eng. Fract. Mech. 2001, 68, 1797–1822. [Google Scholar] [CrossRef]
- Schulson, E.M.; Duval, P. Creep and Fracture of Ice; Cambridge University Press: Cambridge, UK, 2009; Volume 1. [Google Scholar]
- Jones, S.J. High strain-rate compression tests on ice. J. Phys. Chem. B 1997, 101, 6099–6101. [Google Scholar] [CrossRef]
- Meglis, I.; Jordaan, I. High Speed Testing of Freshwater Granular Ice; Technical Report; National Research Council Canada, Institute for Marine Dynamics: St. John’s, NL, Canada, 1998. [Google Scholar]
- Jones, S.J.; Gagnon, R.; Derradji, A.; Bugden, A. Compressive strength of iceberg ice. Can. J. Phys. 2003, 81, 191–200. [Google Scholar] [CrossRef]
- Dutta, P.K.; Cole, D.M.; Schulson, E.M.; Sodhi, D.S. A fracture study of ice under high strain rate loading. Int. J. Offshore Polar Eng. 2004, 14, 182–188. [Google Scholar]
- Kim, H.; Keune, J.N. Compressive strength of ice at impact strain rates. J. Mater. Sci. 2007, 42, 2802. [Google Scholar] [CrossRef]
- Shazly, M.; Prakash, V.; Lerch, B.A. High strain-rate behavior of ice under uniaxial compression. Int. J. Solids Struct. 2009, 46, 1499–1515. [Google Scholar] [CrossRef]
- Combescure, A.; Chuzel-Marmot, Y.; Fabis, J. Experimental study of high-velocity impact and fracture of ice. Int. J. Solids Struct. 2011, 48, 2779–2790. [Google Scholar] [CrossRef]
- Wu, X.; Prakash, V. Dynamic strength of distill water and lake water ice at high strain rates. Int. J. Impact Eng. 2015, 76, 155–165. [Google Scholar] [CrossRef]
- Wu, X.; Prakash, V. Dynamic compressive behavior of ice at cryogenic temperatures. Cold Reg. Sci. Technol. 2015, 118, 1–13. [Google Scholar] [CrossRef]
- Fasanella, E.L.; Boitnott, R.L.; Kellas, S. Test and Analysis Correlation of High Speed Impacts of Ice Cylinders. In Proceedings of the 9th International LS-DYNA Users Conference, Dearborn, MI, USA, 4–6 June 2006. [Google Scholar]
- Pernas-Sánchez, J.; Artero-Guerrero, J.A.; Varas, D.; López-Puente, J. Analysis of ice impact process at high velocity. Exp. Mech. 2015, 55, 1669–1679. [Google Scholar] [CrossRef]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Iliescu, D.; Baker, I.; Cullen, D. Preliminary microstructural and microchemical observations on pond and river accretion ice. Cold Reg. Sci. Technol. 2002, 35, 81–99. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Michel, B.; Ramseier, R. Classification of river and lake ice. Can. Geotech. J. 1971, 8, 36–45. [Google Scholar] [CrossRef]
- Jones, S.J. A review of the strength of iceberg and other freshwater ice and the effect of temperature. Cold Reg. Sci. Technol. 2007, 47, 256–262. [Google Scholar] [CrossRef]
- Pan, H.; Render, P. Effects of target curvature on the impact characteristics of simulated hailstones. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 1997, 211, 81–90. [Google Scholar] [CrossRef]
- Samanta, S. Dynamic deformation of aluminium and copper at elevated temperatures. J. Mech. Phys. Solids 1971, 19, 117–135. [Google Scholar] [CrossRef]
- Gorham, D. Specimen inertia in high strain-rate compression. J. Phys. D Appl. Phys. 1989, 22, 1888–1893. [Google Scholar] [CrossRef]
- Chu, T.; Ranson, W.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Davis, L.A.; Stewart, S.E.; Carsten, C.G.; Snyder, B.A.; Sutton, M.A.; Lessner, S.M. Characterization of fracture behavior of human atherosclerotic fibrous caps using a miniature single edge notched tensile test. Acta Biomater. 2016, 43, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Koohbor, B.; Kidane, A.; Lu, W.-Y.; Sutton, M.A. Investigation of the dynamic stress–strain response of compressible polymeric foam using a non-parametric analysis. Int. J. Impact Eng. 2016, 91, 170–182. [Google Scholar] [CrossRef]
- Bartelmo, S.; Rajan, S.; Li, N.; Sutton, M.; Rizos, D.C. Digital Image Correlation Techniques for Prestressed Concrete Tie Quality Control. In Proceedings of the 2016 Joint Rail Conference, Columbia, SC, USA, 12–15 April 2016. [Google Scholar]
- Sutton, M.; Turner, J.; Chao, Y.; Bruck, H.; Chae, T. Experimental investigations of three-dimensional effects near a crack tip using computer vision. Int. J. Fract. 1992, 53, 201–228. [Google Scholar]
- McNeill, S.; Sutton, M.; Miao, Z.; Ma, J. Measurement of surface profile using digital image correlation. Exp. Mech. 1997, 37, 13–20. [Google Scholar] [CrossRef]
- Ma, S.-P.; Jin, G.-C. New Correlation Coefficients Designed for Digital Speckle Correlation Method (DSCM). In Proceedings of the Optical Technology and Image Processing for Fluids and Solids Diagnostics, Bellingham, WA, USA, 3–6 Semptember 2002; pp. 25–33. [Google Scholar]
- Bruck, H.; McNeill, S.; Sutton, M.A.; Peters, W.H. Digital image correlation using newton-raphson method of partial differential correction. Exp. Mech. 1989, 29, 261–267. [Google Scholar] [CrossRef]
- Sutton, M.A.; McNeill, S.R.; Jang, J.; Babai, M. Effects of subpixel image restoration on digital correlation error estimates. Opt. Eng. 1988, 27, 870–877. [Google Scholar] [CrossRef]
- Schulson, E. The brittle compressive fracture of ice. Acta Metall. Mater. 1990, 38, 1963–1976. [Google Scholar] [CrossRef]
- Yu, T.-L.; Wang, J.-F.; Du, F.; Zhang, L.-Y. Experimental research on ice disaster in huma river. J. Nat. Dis. 2007, 16, 43–48. [Google Scholar]
- Timco, G.; Frederking, R. Compressive strength of sea ice sheets. Cold Reg. Sci. Technol. 1990, 17, 227–240. [Google Scholar] [CrossRef]
- Timco, G.; Frederking, R. Seasonal compressive strength of beaufort sea ice sheets. In Ice-Structure Interaction; Springer: Berlin, Germany, 1991; pp. 267–282. [Google Scholar]
- Manley, M.; Schulson, E. On the strain-rate sensitivity of columnar ice. J. Glaciol. 1997, 43, 408–410. [Google Scholar] [CrossRef]










| Loading Rate (m·s−1) | Serial Number | Uniaxial Compressive Strength (MPa) | |||
|---|---|---|---|---|---|
| −5 °C | −10 °C | ||||
| Horizontal Loading | Vertical Loading | Horizontal Loading | Vertical Loading | ||
| 0.1 | 1 | 2.224 | 3.159 | 6.391 | 5.520 |
| 2 | 5.187 | 3.271 | 5.462 | 7.143 | |
| 3 | 2.795 | 4.642 | 5.300 | 5.991 | |
| 4 | - | 3.702 | - | - | |
| 0.2 | 1 | 3.410 | 5.049 | 7.306 | 7.112 |
| 2 | 4.779 | 3.327 | 5.608 | 8.476 | |
| 3 | 3.370 | 2.974 | 8.380 | 7.459 | |
| 4 | 2.082 | 3.280 | - | - | |
| 0.5 | 1 | 3.726 | 5.372 | 6.196 | 6.438 |
| 2 | 3.277 | 3.970 | 6.627 | 6.869 | |
| 3 | 4.865 | 6.064 | 7.315 | 8.444 | |
| 4 | 5.288 | 8.294 | - | - | |
| 1.0 | 1 | 2.944 | 3.826 | 7.117 | 6.472 |
| 2 | 5.050 | 5.877 | 9.830 | 8.602 | |
| 3 | 4.007 | 7.391 | 6.001 | 6.126 | |
| 4 | - | 4.644 | - | - | |
| 2.0 | 1 | 4.567 | 6.539 | 8.181 | 8.341 |
| 2 | 7.413 | 9.553 | 7.020 | 12.949 | |
| 3 | 5.633 | 11.358 | 8.378 | 12.200 | |
| 4 | - | 6.242 | - | - | |
| Temperature (°C) | Sample Name | Nominal Strain-Rate (s−1) | Sustaining Time (ms) | Average True Strain-Rate (s−1) | Nominal Ultimate Strain (%) | True Ultimate Strain (‰) |
|---|---|---|---|---|---|---|
| −5 | HV01mps3 | 2 | 4.80 | 0.56 | 0.96 | 2.69 |
| HV02mps2 | 4 | 2.30 | 1.20 | 0.92 | 2.76 | |
| HV05mps3 | 10 | 1.05 | 2.20 | 1.05 | 2.31 | |
| HV1mps3 | 20 | 0.24 | 5.29 | 0.48 | 1.27 | |
| HV2mps2 | 40 | 0.11 | 10.26 | 0.44 | 1.13 | |
| HH01mps2 | 2 | 5.20 | 0.47 | 1.04 | 2.44 | |
| HH02mps2 | 4 | 2.45 | 1.02 | 0.98 | 2.50 | |
| HH05mps2 | 10 | 1.08 | 2.10 | 1.08 | 2.27 | |
| HH1mps2 | 20 | 0.45 | 4.65 | 0.90 | 2.09 | |
| HH2mps2 | 40 | 0.14 | 9.14 | 0.56 | 1.28 | |
| −10 | HV01mps3 | 2 | 4.84 | 0.43 | 0.97 | 2.08 |
| HV02mps2 | 4 | 2.36 | 0.97 | 0.94 | 2.29 | |
| HV05mps2 | 10 | 1.18 | 2.11 | 1.18 | 2.49 | |
| HV1mps3 | 20 | 0.20 | 4.93 | 0.40 | 0.99 | |
| HV2mps3 | 40 | 0.11 | 9.01 | 0.44 | 0.99 | |
| HH01mps2 | 2 | 5.20 | 0.49 | 1.04 | 2.55 | |
| HH02mps3 | 4 | 2.00 | 1.20 | 0.80 | 2.40 | |
| HH05mps2 | 10 | 0.85 | 2.49 | 0.85 | 2.12 | |
| HH1mps2 | 20 | 0.25 | 5.38 | 0.50 | 1.35 | |
| HH2mps2 | 40 | 0.13 | 9.65 | 0.52 | 1.25 |
| Loading Rate (m·s−1) | Serial Number | Compressive Strength (MPa) | |||
|---|---|---|---|---|---|
| −5 °C | −10 °C | ||||
| Horizontal Loading | Vertical Loading | Horizontal Loading | Vertical Loading | ||
| 0.1 | 1 | 2.912 | 4.859 | 2.989 | 4.862 |
| 2 | 2.548 | 3.001 | 4.130 | 6.423 | |
| 3 | 1.664 | 3.908 | 4.618 | 3.160 | |
| 4 | 1.170 | 4.119 | 3.426 | 7.300 | |
| 5 | 2.543 | - | 4.011 | - | |
| 6 | 3.228 | - | - | - | |
| 7 | 1.970 | - | - | - | |
| 0.2 | 1 | 1.809 | 4.743 | 3.680 | 7.171 |
| 2 | 2.012 | 3.107 | 4.200 | 8.402 | |
| 3 | 3.966 | 5.722 | 4.235 | 4.893 | |
| 4 | 2.646 | - | 4.499 | - | |
| 5 | 1.939 | - | - | - | |
| 0.5 | 1 | 1.541 | 2.975 | 4.512 | 5.814 |
| 2 | 1.905 | 5.782 | 4.911 | 4.823 | |
| 3 | 1.543 | 4.268 | 3.600 | 6.466 | |
| 4 | 2.863 | - | - | - | |
| 1.0 | 1 | 2.310 | 3.565 | 4.236 | 6.135 |
| 2 | 3.445 | 4.211 | 3.936 | 7.586 | |
| 3 | 3.100 | 5.522 | 5.130 | 6.550 | |
| 4 | 1.735 | - | - | - | |
| 2.0 | 1 | 3.183 | 5.651 | 6.226 | 6.982 |
| 2 | 4.157 | 4.790 | 4.866 | 8.861 | |
| 3 | 2.491 | 7.049 | 5.825 | 11.349 | |
| 4 | 1.966 | - | - | - | |
| Temperature (°C) | Sample Name | Nominal Strain-Rate (s−1) | Sustaining Time (ms) | Average True Strain-Rate (s−1) | Nominal Ultimate Strain (%) | True Ultimate Strain (‰) |
|---|---|---|---|---|---|---|
| −5 | SH01mps4 | 2 | 4.51 | 0.44 | 0.90 | 1.98 |
| SH02mps3 | 4 | 2.36 | 1.09 | 0.94 | 2.57 | |
| SH05mps3 | 10 | 0.84 | 2.79 | 0.84 | 2.34 | |
| SH1mps2 | 20 | 0.23 | 5.78 | 0.46 | 1.33 | |
| SH2mps3 | 40 | 0.16 | 9.16 | 0.64 | 1.47 | |
| SV01mps3 | 2 | 5.50 | 0.56 | 1.10 | 3.08 | |
| SV02mps3 | 4 | 2.35 | 0.89 | 0.94 | 2.09 | |
| SV05mps2 | 10 | 1.21 | 2.73 | 1.21 | 3.30 | |
| SV1mps2 | 20 | 0.20 | 4.31 | 0.40 | 0.86 | |
| SV2mps3 | 40 | 0.11 | 9.35 | 0.44 | 1.03 | |
| −10 | SH01mps5 | 2 | 6.19 | 0.41 | 1.24 | 2.54 |
| SH02mps3 | 4 | 2.80 | 0.88 | 1.12 | 2.46 | |
| SH05mps2 | 10 | 0.97 | 2.27 | 0.97 | 2.20 | |
| SH1mps3 | 20 | 0.41 | 5.46 | 0.82 | 2.24 | |
| SH2mps2 | 40 | 0.12 | 9.15 | 0.48 | 1.10 | |
| SV01mps2 | 2 | 6.03 | 0.48 | 1.21 | 2.89 | |
| SV02mps2 | 4 | 2.24 | 1.14 | 0.90 | 2.55 | |
| SV05mps3 | 10 | 1.26 | 2.01 | 1.26 | 2.53 | |
| SV1mps3 | 20 | 0.28 | 5.98 | 0.56 | 1.67 | |
| SV2mps3 | 40 | 0.15 | 9.53 | 0.60 | 1.43 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, J.; Ouyang, Q.; Zhao, X.; Liu, F.; Qi, C. Uniaxial Compressive Strength and Fracture Mode of Lake Ice at Moderate Strain Rates Based on a Digital Speckle Correlation Method for Deformation Measurement. Appl. Sci. 2017, 7, 495. https://doi.org/10.3390/app7050495
Lian J, Ouyang Q, Zhao X, Liu F, Qi C. Uniaxial Compressive Strength and Fracture Mode of Lake Ice at Moderate Strain Rates Based on a Digital Speckle Correlation Method for Deformation Measurement. Applied Sciences. 2017; 7(5):495. https://doi.org/10.3390/app7050495
Chicago/Turabian StyleLian, Jijian, Qunan Ouyang, Xin Zhao, Fang Liu, and Chunfeng Qi. 2017. "Uniaxial Compressive Strength and Fracture Mode of Lake Ice at Moderate Strain Rates Based on a Digital Speckle Correlation Method for Deformation Measurement" Applied Sciences 7, no. 5: 495. https://doi.org/10.3390/app7050495
APA StyleLian, J., Ouyang, Q., Zhao, X., Liu, F., & Qi, C. (2017). Uniaxial Compressive Strength and Fracture Mode of Lake Ice at Moderate Strain Rates Based on a Digital Speckle Correlation Method for Deformation Measurement. Applied Sciences, 7(5), 495. https://doi.org/10.3390/app7050495






