Inverse Identification of the Frequency-Dependent Mechanical Parameters of a Viscoelastic Core Layer Based on the Vibration Response

Abstract

The identification of the mechanical parameters of the viscoelastic core layer is of great significance for the modeling and damping design of the constrained layer damping (CLD) composite structure. In this study, based on the measured frequency vibration response of a CLD plate, an inverse approach was developed to identify the aforementioned parameters. Then, on the basis of considering both the viscoelastic material damping and the remaining equivalent viscous damping, the equation of motion of the CLD plate under base excitation was established and a method to obtain the vibration response was also presented. Further, a matching calculation based on sensitivity was proposed, to achieve the identification of the mechanical parameters. Finally, a CLD aluminum plate with a ZN_1 viscoelastic core layer was chosen to demonstrate the proposed method. In addition, the identification results were also introduced into the vibration response analysis and the rationality of the identified parameters were verified by comparing the vibration responses obtained by theoretical calculations and the experiment.

1. Introduction

Constrained layer damping (CLD) treatment uses a viscoelastic layer, laid onto the host structure surface covered by a stiff and thin constraining layer, and it can produce energy dissipation relying on the shear deformation of the viscoelastic layer [1]. It is well known that, compared with free-layer damping (FLD) treatment, the CLD generally produces a better damping effect. As an important method of vibration reduction, CLD treatment has been widely used in aeronautics, aerospace, and other engineering domains [2,3,4]. Modeling the dynamic behavior of the viscoelastic composite structure is very important for CLD design, and to achieve it, the mechanical parameters of the CLD structure (which are mainly the storage modulus and loss factor of each layer) have to be known in advance.

In a CLD structure, the constraining layer is mainly made of metal and its mechanical parameters can be easily found. Therefore, the identification mainly focuses on the mechanical properties of the viscoelastic core layer. It has been well understood that the mechanical properties of viscoelastic materials are influenced by temperature and frequency, and only frequency dependence is taken into account in most studies because of the temperature-frequency superposition principle [5,6]. Scholars have proposed a variety of constitutive models of viscoelastic material, and those which are commonly used include the complex modulus model [7], the Golla-Hughes-McTavish (GHM) model [8], the anelastic displacement fields (ADF) model [9], and the fractional derivative model [10]. Then, the identification of the parameters of viscoelastic material can be converted in order to obtain the characteristic parameters of the above models. Of the aforementioned models, the fractional derivative model is widely used for its effectiveness in characterizing the mechanical behavior of viscoelastic materials in the frequency and time domains [10,11,12]. The core of this paper is studies the method to identify the parameters of the fractional derivative model of the viscoelastic core layer.

The inverse method, combining numerical analysis and vibration tests, is an important method to identify the mechanical parameters of viscoelastic materials. The basic principle of the inverse method can be described as follows. The parameters which need to be identified are defined as design variables. To achieve the identification parameters, a matching algorithm (also known as an optimization process) is used to iteratively update the design variables in an analysis model, until the differences between the theoretical and the measured vibration parameters are minimal. Some typical researches were done, for example, based on the response surface optimization technique. Barkanov et al. [5] identified the mechanical properties of viscoelastic materials characterized using a complex modulus by testing the vibration attenuation response of composite beams. Shi et al. [13] used the numerical optimization method to identify the Young’s modulus and loss factor of viscoelastic materials by testing the resonant frequency and modal loss factor of a sandwich beam. The biggest problem of the above researches is that the parameter identifications only focus on the points at a resonant frequency. Thus, the insufficient number of points may lead to the difference between the identified parameters and their true value. For a cantilever beam attached with FLD, Kim and Lee [14] obtained its frequency response function by motivating it with a hammer and used two steps to identify the fractional derivative model parameters. Martinez-Agirre and Elejabarrieta [6] did a similar study on a cantilever beam with CLD treatment, and identified the mechanical parameters of viscoelastic materials with high damping properties, mainly through minimizing the experimental and theoretical frequency response functions at certain discrete frequency points. Kim’s and Martinez-Agirre’s methods are not limited to the identification focused on the resonant frequency points, and thus, this work represents great progress in the identification study.

However, the aforementioned researches still have some problems. First, most identifications are based on the cantilever beam specimen. Considering the variation in their polymeric composition and their mechanical states, viscoelastic materials will exhibit different mechanical characteristics. Therefore, the identification results of the beam specimen could not fully meet the requirements of other structures, such as the requirements of the dynamic analysis of a plate specimen. Moreover, most identification studies obtained the frequency response function of the composite beam by the hammer test and then inversely identified the mechanical parameters of viscoelastic material. While the hammer test involves the problem that the excitation position is difficult to accurately determine, the inaccurate excitation point may affect the identification accuracy of the parameters of the viscoelastic material. Finally, for all the aforementioned researches, only the viscoelastic material damping is contained in the analysis model, and the clamped damping of the specimen and the air damping (here both defined as the remaining equivalent viscous damping) are usually neglected. To the authors’ knowledge, such an analysis model will result in the measured damping always being greater than the calculated value, which may interfere with the identification accuracies of viscoelastic material parameters. In order to obtain the parameter values of viscoelastic materials accurately and efficiently, a new identification method needs to be developed.

Based on the aforementioned researches, this paper presents an inverse method to identify the mechanical parameters of a viscoelastic core layer based on the frequency vibration response. The features of the presented method are as follows: (1) the cantilever plate-shaped specimen attached with CLD was chosen to carry out the identification of the viscoelastic material parameters; (2) both the material damping and the remaining equivalent viscous damping were considered in the created analysis model; (3) the data at the resonance point and non-resonance point can both be used to identify the viscoelastic parameter; and (4) the frequency responses obtained by sweeping under base excitation were mainly used to identify the parameters. This study is organized as follows. In Section 2, the identification principle of the proposed method is given. In Section 3, both the viscoelastic material damping and the remaining equivalent viscous damping are considered in the analysis model. Meanwhile, an example is presented to illustrate the importance of introducing the two kinds of damping into the analysis model. In Section 4, the formula of the matching calculation between the theoretical analysis and experiment is derived, based on the sensitivity method. In Section 5, a CLD aluminum plate with a ZN_1 viscoelastic core layer is chosen to demonstrate the proposed method and the fractional derivative model is identified. The rationality of the obtained identification results is verified by comparing the calculated and measured frequency vibration response. Some conclusions are listed in Section 6.

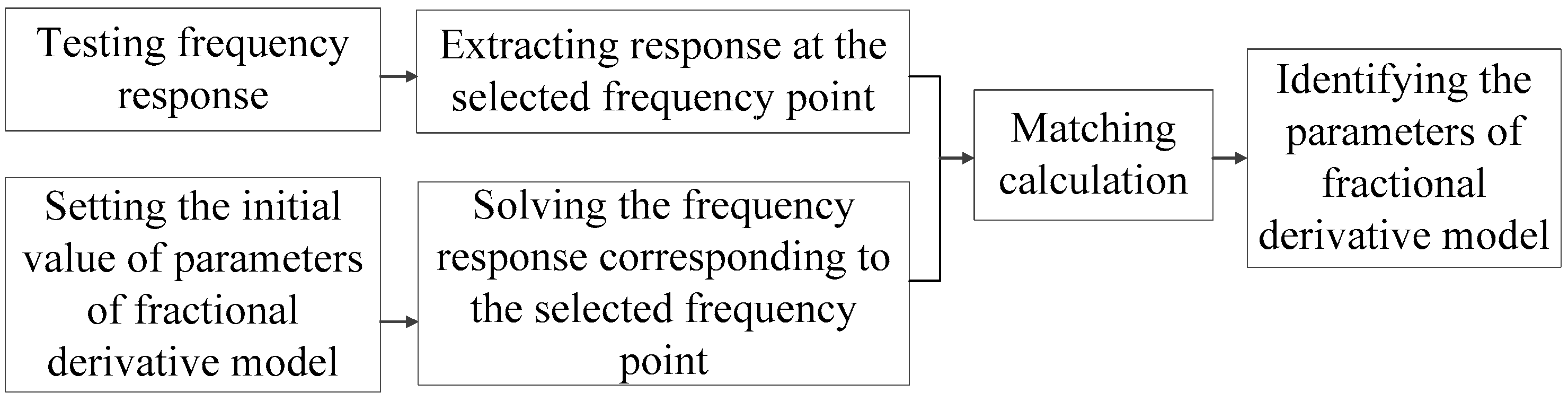
2. The Principle of Inverse Identification

The inverse method contains three basic contents: a vibration test, theoretical modeling, and a matching calculation. In view of the fact that the viscoelastic core layer is mainly subjected to shear stress, the fractional derivative model to be identified can be described as [15]:

$$G_{\mathrm{v}}^{*}(\omega )=\frac{G_0+G_{\infty }{(\mathrm{i}\omega \tau )}^{\alpha }}{1+{(\mathrm{i}\omega \tau )}^{\alpha }}$$

(1)

where, $G_v^{*}(\omega )$ is the complex shear modulus of the viscoelastic material (* is complex number). The matrix or vector containing $(\omega )$ means that it is influenced by the mechanical parameters of viscoelastic materials with frequency-dependent characteristics and is the function of the excitation frequency $\omega$. The model consists of four parameters, and $G_0$ and $G_{\infty }$ represent the shear modulus of the viscoelastic materials corresponding to the frequency of zero and an infinite figure, respectively. Symbol $\tau$ is the relaxation time and $\alpha$ is the fractional order parameter. The principle of inverse identification of the fractional derivative model of viscoelastic material is shown in Figure 1.

The vibration test involved in the identification principle consists of two parts. One is used to obtain the modal damping ratio of the cantilever plate without damping treatment, and the other is employed to obtain the frequency response of the CLD plate under base excitation. The identified modal damping ratios will be inputted into the analysis model of the viscoelastic composite plate as the remaining equivalent viscous damping, while the measured frequency response is mainly used to identify the viscoelastic material parameters. The theoretical analysis is mainly used to solve the vibration response of the CLD plate. In the established model, both the viscoelastic material damping and the remaining equivalent viscous damping were considered, which is described in detail in Section 3.

The matching calculation is applied to minimize the difference between the theoretical and experimental values of the vibration response, thus identifying the fractional derivative model parameters. Taking the vibration response as the objective function, the method of the matching calculation based on sensitivity is proposed and described in detail in Section 4. It should be noted here that the matching calculation can be used to identify the material parameters from the resonance and non-resonance frequency points, and the resonance point should be preferred for its relatively high signal-to-noise ratio. In addition, the total number of the selected resonance and non-resonance points should be larger than that of the parameters to be identified. Therefore, the number of frequency points selected for this case should be greater than four.

3. Frequency Response Calculation of the CLD Plate Considering Two Kinds of Damping

The finite element method will be used to derive the frequency response of the CLD plate under base excitation. In the analysis of the frequency vibration response, the complex modulus model of viscoelastic materials is usually easier to solve. So, the fractional derivative model shown in Equation (1) is decomposed according to the real part and imaginary part. It can be expressed as:

$$G_{\mathrm{v}}^{*}(\omega )=G_{\mathrm{v}}(\omega )+\mathrm{i}{G}_{\mathrm{v}}^{″}(\omega )=G_{\mathrm{v}}(\omega )[1+\mathrm{i}{\eta }_{\mathrm{v}}(\omega )]$$

(2)

where, $G_{\mathrm{v}}(\omega )$ and ${\eta }_{\mathrm{v}}(\omega )$ are the shear storage modulus and the loss factor of viscoelastic materials, respectively. Symbol $G_{\mathrm{v}}^{″}(\omega )=G_{\mathrm{v}}(\omega ){\eta }_{\mathrm{v}}(\omega )$ denotes the shear loss modulus. In the following analysis, the complex modulus model is used to obtain the stiffness matrix of the CLD plate in order to introduce the parameters of viscoelastic materials with a frequency dependence into the dynamic analysis equation.

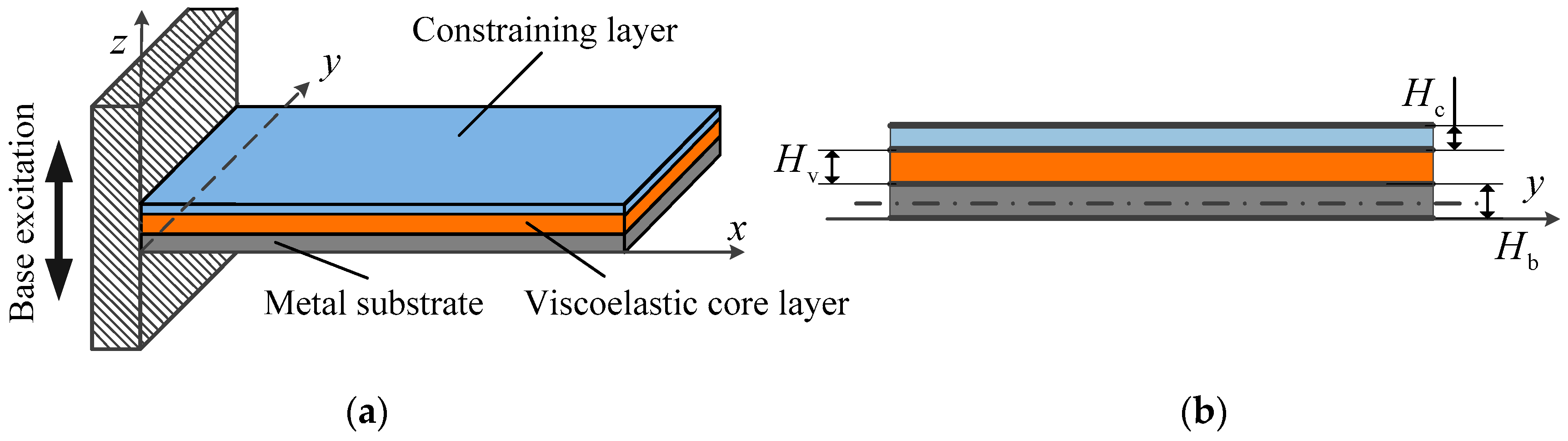
3.1. Derivation of Dynamic Equation of the CLD Plate Under Base Excitation

Figure 2a shows the cantilever thin plate attached with CLD on one side, and the partial cross section of the composite plate is shown in Figure 2b. Symbols $H_{\mathrm{v}}$, $H_{\mathrm{b}}$, and $H_{\mathrm{c}}$ represent the thickness of the viscoelastic core layer, metal substrate, and constraining layer, respectively. Subscript v, b, and c denote the viscoelastic core layer, metal substrate, and constraining layer, respectively.

For the viscoelastic composite structure, the equation of the motion in the frequency domain can be written as:

$$\left(-{\omega }^{2}M+\mathrm{i}\omega C_1+\mathrm{i}{C}_2(\omega )+K(\omega )\right)X=F$$

(3)

where, $M$ is the mass matrix of the composite structure, $C_1$ is the remaining equivalent viscous damping matrix, $C_2(\omega )$ is the material damping matrix, $K(\omega )$ is the stiffness matrix, $X$ is the response vector, and $F$ is the excitation force vector. Two kinds of damping are contained in Equation (3), while, for most researches about the modeling of the viscoelastic composite structure, only the material damping was considered.

Traditionally, the stiffness matrix $K(\omega )$ and the material damping matrix $C_2(\omega )$ can form the complex stiffness matrix, that is:

$$K^{*}(\omega )=K(\omega )+\mathrm{i}{C}_2(\omega )$$

(4)

The base excitation vector can be further expressed as:

$$F=-MG\ddot{U}$$

(5)

where, $\ddot{U}$ is the acceleration of base excitation, $G$ is the influence coefficient vector, and the dimension of the influence coefficient vector is consistent with the degree of freedom of the vibration system. For the degree of freedom which is in the direction of base excitation, the corresponding element in the influence coefficient vector is 1, and the other elements are 0. Equation (5) indicates that the vibration of the viscoelastic composite structure is produced by the inertia force of the base excitation, and the level of the force is related to the mass of the composite structure and the level of the base excitation.

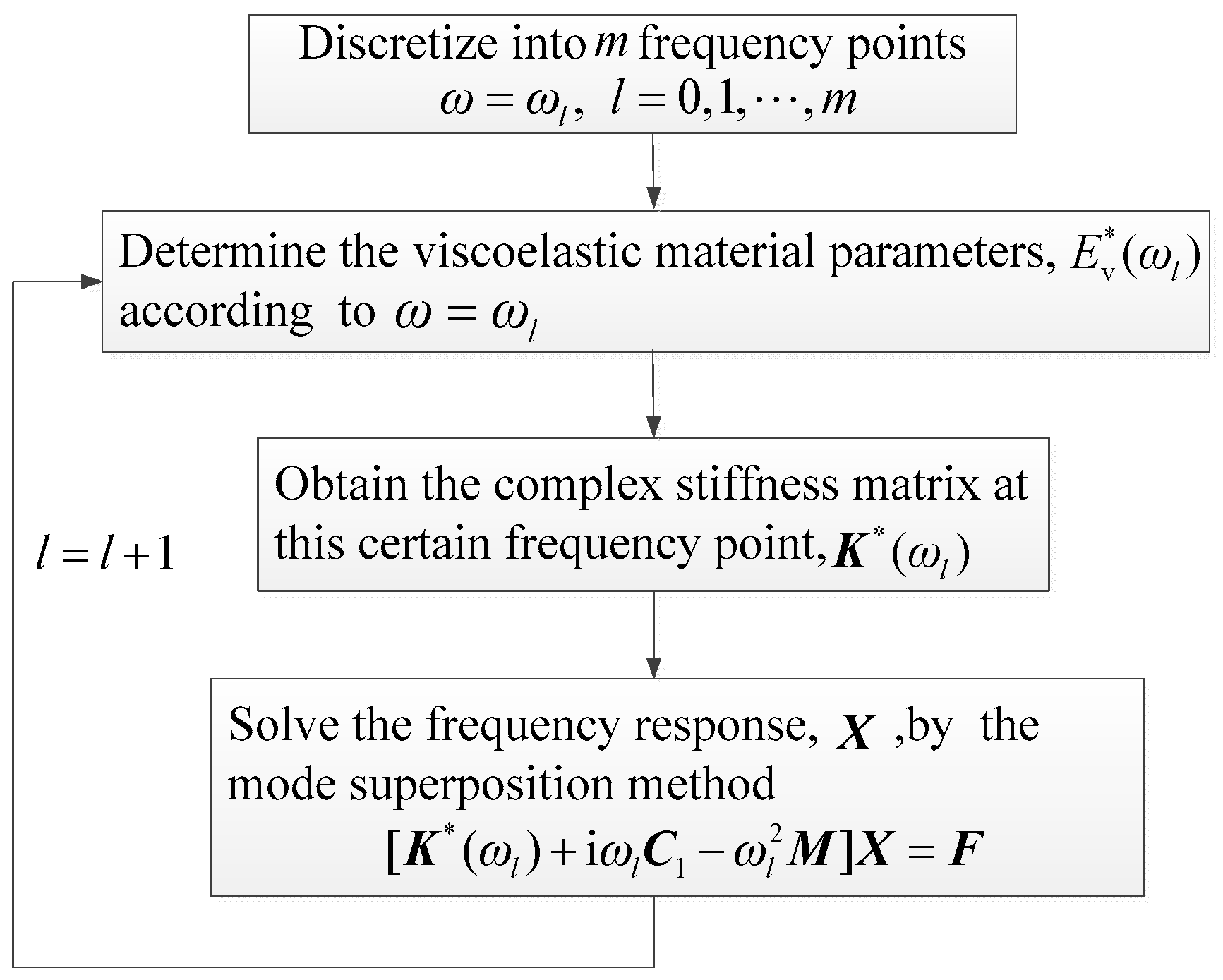
3.2. Derivation of the Frequency Response

The modal superposition method is applied to solve the frequency response of the CLD plate under base excitation. For most viscoelastic composite structures, the equivalent viscous modal damping ratio of system is usually less than 0.2, and thus, they can be thought of as a small damping system. In this system, the damping is believed to have no influence on the eigenvector of the system, so the real modal theory can be used to characterize the vibration behavior of the composite structure. In fact, the real modal theory has been used by many researchers [16,17] to analyze the dynamic behavior of the viscoelastic composite structure. The characteristic equation of solving the real mode can be expressed as:

$$\left[-{\omega }_r^{2}M+K(\omega )\right]{\phi }_r=0r=1,2,\cdots ,n$$

(6)

where ${\omega }_r^2$ and ${\phi }_r$ are the r-th order eigenvalue and eigenvector (or modal shape vector), respectively; and $n$ is the total dimension of the whole system. Here, the eigenvector ${\phi }_r$ is normal and satisfies ${\phi }_r^{T}M{\phi }_r=1$. In fact, ${\omega }_r^2$ and ${\phi }_r$ are also the function of excitation frequency $\omega$, but $(\omega )$ is not contained in the expression for the sake of convenience in writing.

The obtained modal shape vector can form the modal shape matrix $\phi$. Premultiply Equation (3) by the transpose matrix of the modal shape matrix ${\phi }^T$ and substitute $X=\phi X_N$ into Equation (3), and this yields:

$${\phi }^T[K^{*}(\omega )+\mathrm{i}\omega C_1-{\omega }^{2}M]\phi X_N=F_N$$

(7)

where, $F_N$ is the amplitude vector of base excitation expressed by modal coordinates and expressed as:

$$F_N={\phi }^{T}F$$

(8)

From Equation (7), a set of independent equations of motion expressed in modal coordinates $x_{Nr}(r=1,2,\dots ,n)$ can be obtained and expressed as:

$$\left({\phi }_r^T{K}^{*}(\omega ){\phi }_r+\mathrm{i}{\phi }_r^T{C}_1{\phi }_r\omega +{\phi }_r^{T}M{\phi }_r\right)x_{Nr}={\phi }_r^{T}F=f_{Nr}$$

(9)

The first and third items in the above equation can be expressed as:

$${\phi }_r^T{K}^{*}(\omega ){\phi }_r={\omega }_r^2[1+\mathrm{i}{\eta }_r],{\phi }_r^{T}M{\phi }_r=1$$

(10)

where, ${\eta }_r$ is the r-th order modal loss factor that is produced by viscoelastic materials.

According to the modal damping assumption, the second item in the brackets of Equation (9) can be written as:

$${\phi }_r^T{C}_1{\phi }_r=2{\xi }_r{\omega }_r$$

(11)

where, ${\xi }_r$ is the r-th order modal damping ratio produced by the remaining equivalent viscous damping, which is called the remaining equivalent modal damping ratio. It is important to note that obtaining Equation (11) is based on ${\phi }_r^T{C}_1{\phi }_r$, which is a diagonal matrix in the derivation. The remaining damping can be introduced by the measured modal damping ratio of the system before damping treatment.

Equation (9) can be transformed into the modal coordinates by substituting Equations (10) and (11) into it, which then yields:

$$x_{Nr}^{*}=\frac{f_{Nr}}{{\omega }_r^2\left[1+\mathrm{i}{\eta }_r\right]+\mathrm{i}2\omega {\xi }_r{\omega }_r-{\omega }^2}$$

(12)

The contribution of each mode $X_r^{*}$ is:

$$X_r^{*}=x_{Nr}^{*}{\phi }_r$$

(13)

Finally, the vibration response of the composite structure under base excitation is obtained:

$$X=\left|{\displaystyle \sum _{r=1}^n{X}_r^{*}}\right|$$

(14)

where, $|.|$ refers to the solution of the modular. In practice, it is not necessary to consider all the n order modes and the used order m only needs to be larger than that of the highest order of the structure in the frequency range of interest, that is, modal truncation is used in the actual analysis.

Because of the frequency dependence of viscoelastic materials, the above solution only obtained the response corresponding to a certain frequency point. In order to obtain the responses in the whole frequency range, the iterative calculation needs to be carried out, referring to Figure 3.

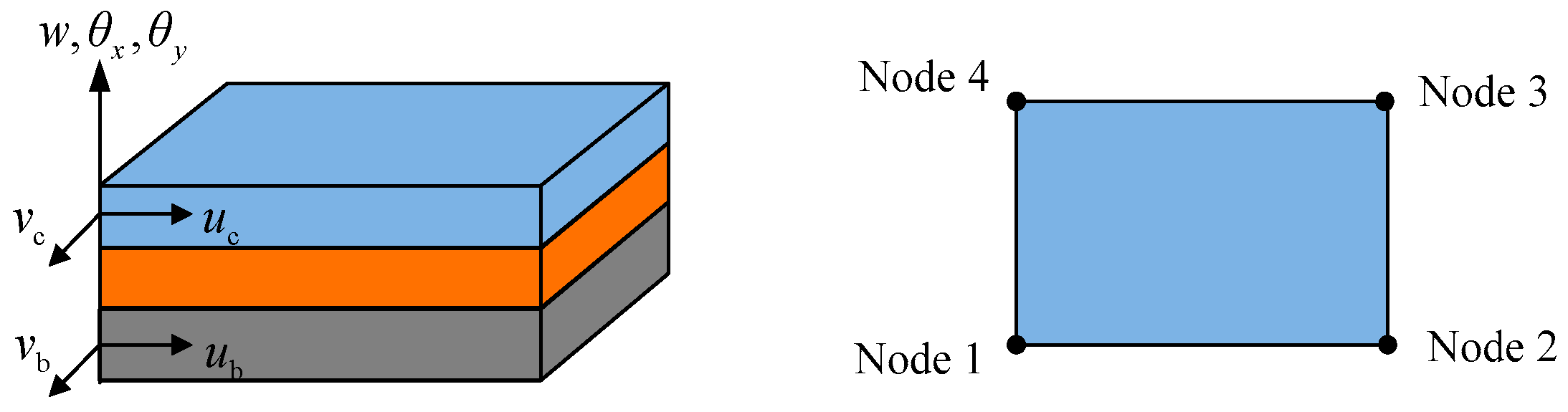
3.3. Derivation of the Mass Matrix and Stiffness Matrix

In this section, layer-wise theory was applied to derive the stiffness and mass matrices in Equation (3). As shown in Figure 4, the plane CLD plate element with four nodes and seven degrees of freedom of each node is selected to simulate the CLD plate [18]. The seven degrees of freedom are $u_{\mathrm{c}},v_{\mathrm{c}},u_{\mathrm{b}},v_{\mathrm{b}},w,{\theta }_x,{\theta }_y$, respectively, where, $u_{\mathrm{c}},v_{\mathrm{c}}$ are the x and y direction displacements in the neutral plane of the constraining layer and $u_{\mathrm{b}},v_{\mathrm{b}}$ are the x and y direction displacements in the neutral plane of the metal substrate, respectively. Symbols $w,{\theta }_x,{\theta }_y$ are the deflection of the composite plate and the rotation angle of the neutral plane of the composite plate around the x axis and y axis, respectively. The stiffness and mass matrix of the CLD plate can be derived according to the following procedure.

(1)

Dividing the composite thin plate into several elements.

(2)

Solving the contribution of each layer to the stiffness and mass matrices of the whole CLD element. The contribution of each layer to the element stiffness matrix can be expressed as:

$$K_i^{\mathrm{e}}=H_i{\displaystyle \underset{A}{\iint }{B}_i^{\mathrm{T}}{D}_i{B}_i}\mathrm{d}A+\frac{H_i^3}{12}{\displaystyle \underset{A}{\iint }{B}^{\mathrm{T}}{D}_{i}B}\mathrm{d}A,i=\mathrm{b},\mathrm{c}$$

(15a)

$$K_{\mathrm{v}}^{*\mathrm{e}}(\omega )=H_{\mathrm{v}}{\displaystyle \underset{A}{\iint }{B}_{\mathrm{v}}^{\mathrm{T}}{D}_{\mathrm{v}}{B}_{\mathrm{v}}}\mathrm{d}A+\frac{H_{\mathrm{v}}^3}{12}{\displaystyle \underset{A}{\iint }{B}^{\mathrm{T}}{D}_{\mathrm{v}}B}\mathrm{d}A+G_{\mathrm{v}}^{*}(\omega )H_{\mathrm{v}}{\displaystyle \underset{A}{\iint }{N}_{10}^{\mathrm{T}}{N}_{10}+N_{11}^{\mathrm{T}}{N}_{11}}\mathrm{d}A$$

(15b)

The contribution of each layer to the element mass matrix can be expressed as:

$$M_{\mathrm{c}}^{\mathrm{e}}={\displaystyle \underset{A}{\int }{\rho }_{\mathrm{c}}\left(N_1^{\mathrm{T}}{N}_1+N_2^{\mathrm{T}}{N}_2+N_5^{\mathrm{T}}{N}_5\right)}\mathrm{d}A$$

(16a)

$$M_{\mathrm{v}}^{\mathrm{e}}={\displaystyle \underset{A}{\int }{\rho }_{\mathrm{v}}\left(N_8^{\mathrm{T}}{N}_8+N_9^{\mathrm{T}}{N}_9+N_5^{\mathrm{T}}{N}_5\right)}\mathrm{d}A$$

(16b)

$$M_{\mathrm{b}}^{\mathrm{e}}={\displaystyle \underset{A}{\int }{\rho }_{\mathrm{b}}\left(N_3^{\mathrm{T}}{N}_3+N_4^{\mathrm{T}}{N}_4+N_5^{\mathrm{T}}{N}_5\right)}\mathrm{d}A$$

(16c)

where, $B$, $B_{\mathrm{b}}$, $B_{\mathrm{c}}$, and $B_{\mathrm{v}}$ are the strain matrices; $N_1$, $N_2$, $N_3$, $N_4$, $N_5$, $N_8$, $N_9$, $N_{10}$, and $N_{11}$ are the shape function vectors of the element; and ${\rho }_{\mathrm{c}}$, ${\rho }_{\mathrm{v}}$, and ${\rho }_{\mathrm{b}}$ refer to the densities of the constraining layer, viscoelastic core layer, and metal substrate, respectively. Symbols $D_{\mathrm{c}}$, $D_{\mathrm{b}}$, and $D_{\mathrm{v}}^{*}$ represent the elastic matrices of the constraining layer, metal substrate, and viscoelastic core layer, respectively, which are given by:

$$D_i=\frac{E_i}{(1-{\mu }_i^2)}\left[\begin{array}{ccc}1& {\mu }_i& 0\\ {\mu }_i& 1& 0\\ 0& 0& \frac{1}{2}(1-{\mu }_i)\end{array}\right]i=\mathrm{b},\mathrm{c}$$

(17a)

$$D_{\mathrm{v}}=\frac{2G_{\mathrm{v}}^{*}(\omega )}{1+{\mu }_{\mathrm{v}}}\left[\begin{array}{ccc}1& {\mu }_{\mathrm{v}}& 0\\ {\mu }_{\mathrm{v}}& 1& 0\\ 0& 0& \frac{1}{2}(1-{\mu }_{\mathrm{v}})\end{array}\right]$$

(17b)

where $E_{\mathrm{b}}$ and $E_{\mathrm{c}}$ are the Young’s modulus of the metal substrate and the constraining layer, respectively; and ${\mu }_{\mathrm{c}}$, ${\mu }_{\mathrm{b}}$, and ${\mu }_{\mathrm{v}}$ are the Poisson's ratio of the constraining layer, metal substrate, and viscoelastic core layer, respectively. Here, they are set as invariables.

(3)

Determining the mass and stiffness matrices of the whole element. The contribution of each layer to the element stiffness and mass matrices is added, thus forming the stiffness and mass matrices of the CLD element:

$$K^{*\mathrm{e}}(\omega )=K_{\mathrm{c}}^{\mathrm{e}}+K_{\mathrm{v}}^{*\mathrm{e}}(\omega )+K_{\mathrm{b}}^{\mathrm{e}}$$

(18a)

$$M^{\mathrm{e}}=M_{\mathrm{c}}^{\mathrm{e}}+M_{\mathrm{v}}^{\mathrm{e}}+M_{\mathrm{b}}^{\mathrm{e}}$$

(18b)

(4)

Assembling the element stiffness and mass matrices, and forming the total complex stiffness matrix $K^{*}(\omega )$ and the total mass matrix M on the basis of the consideration of the cantilever constraints.

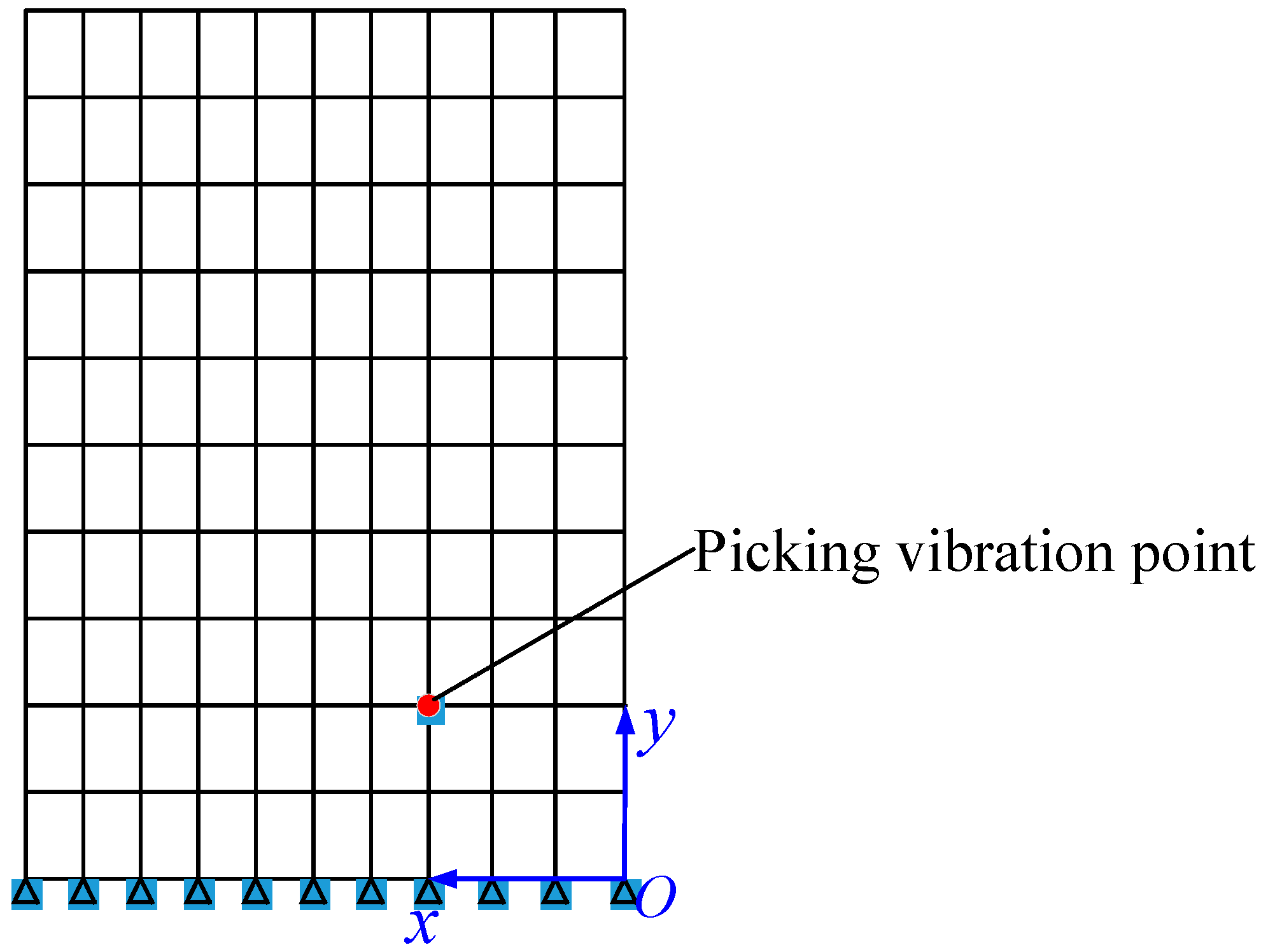
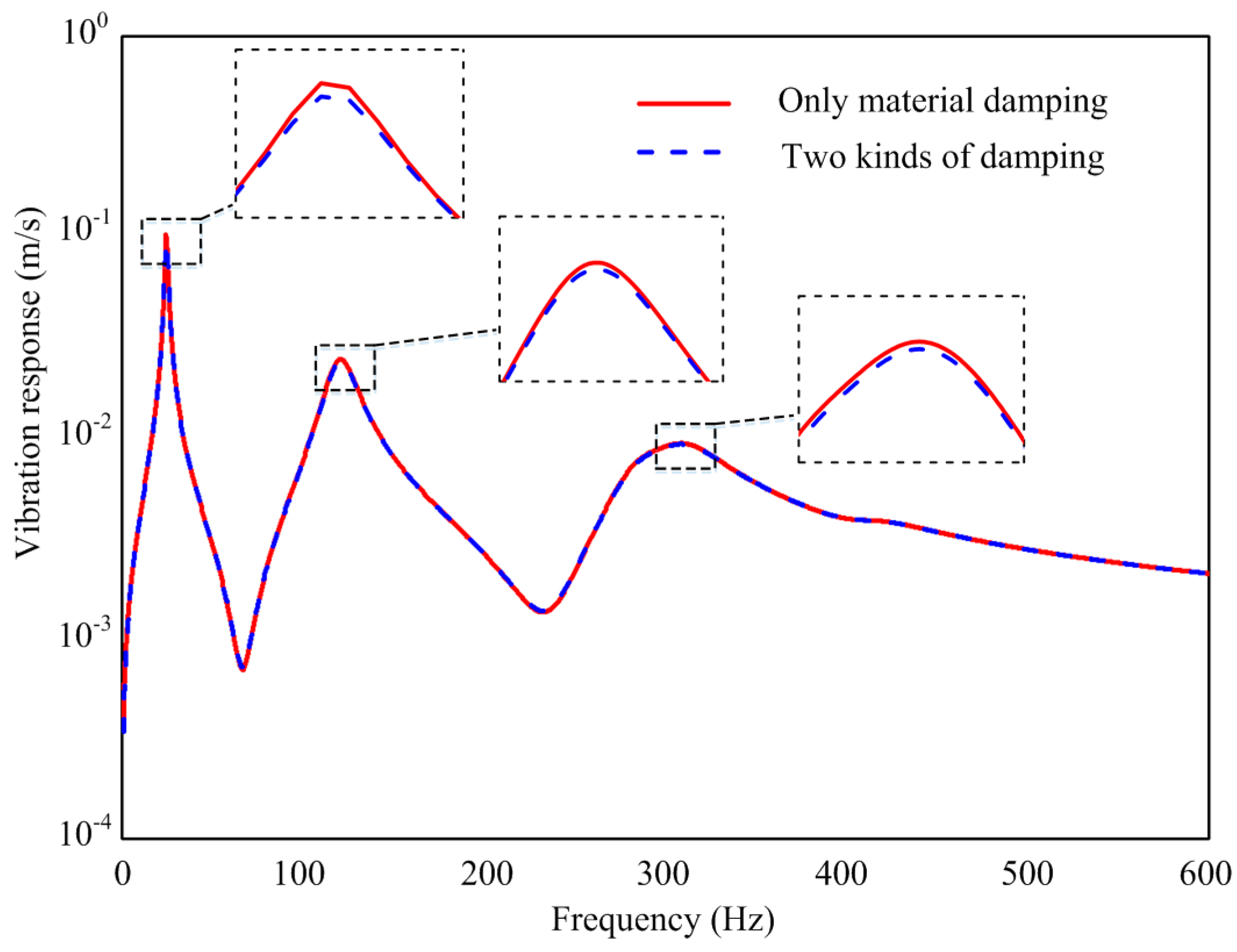
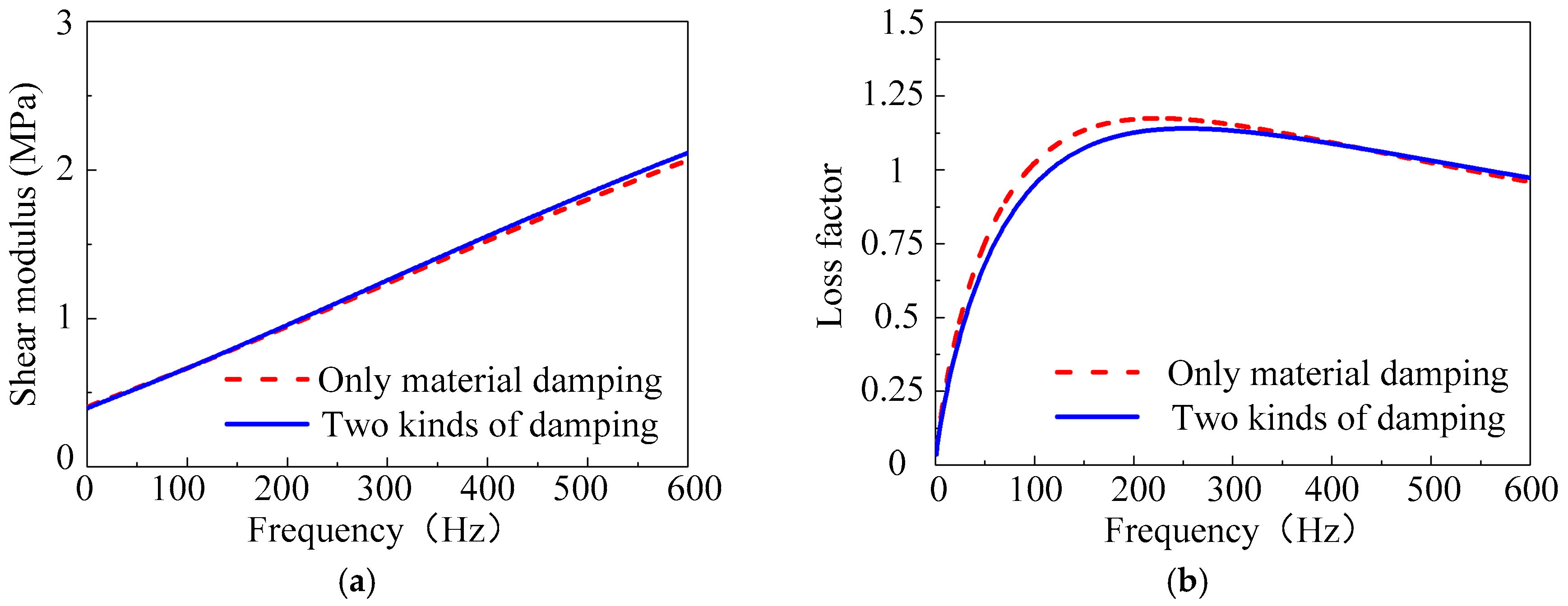
3.4. Analysis Examples

A case study was carried out to verify the developed method for solving the frequency response of the CLD plate. In addition, the comparison of the frequency responses obtained by considering only one damping and two kinds of damping was conducted.

Referring to the literature [5], the shear modulus and loss factor of 3M ISD-112 viscoelastic material with a frequency-dependent characteristic are:

$$G_{\mathrm{v}}(f)=2.783-1.023/(0.394+0.0003736f)$$

(19a)

$${\eta }_{\mathrm{v}}(f)=1.683+0.001468/(0.005+0.0006134f)-0.5274/{(0.005+0.0006134f)}^{0.25}$$

(19b)

where, $G_{\mathrm{v}}(f)$ is the shear modulus and f is the excitation frequency with unit Hz. Furthermore, the density and Poisson's ratio of this material are ${\rho }_{\mathrm{v}}=789.5\mathrm{kg}/{\mathrm{m}}^3$ and ${\mu }_{\mathrm{v}}=0.49$, respectively.

It is assumed that the geometric parameters of the composite plate, and the material parameters of the metal substrate and the constraining layer, are the same as those described in Section 5. To introduce two kinds of damping, it is assumed that the first eight modal damping ratios of the plate without damping treatment are known and the specific damping values can be found in Section 5. The composite plate element described in Section 3.3 is adopted to create the finite element model of the CLD plate. The created model consists of 121 nodes and 100 elements, and the picking vibration point is located at x = 60 mm, y = 60 mm, as shown in Figure 5. The frequency responses of the CLD plate were calculated using the modal superposition method within the range of 600 Hz, by considering only one damping and two kinds of damping, and the calculated results are shown in Figure 6.

Figure 6 reveals that the frequency response obtained by considering only material damping is different from that obtained by simultaneously considering two kinds of damping in the resonant region. In the authors’ opinions, the results of considering two kinds of damping should be closer to the actual values. The resonance point is generally used as a reference point for the identification of viscoelastic parameters, and thus, the accuracy of the identification results may be influenced when only material damping is considered.

4. Matching Calculation Based on the Sensitivity Method

The formula of the matching calculation is derived based on the sensitivity method in this section. Referring to Equation (1), the four parameters, $G_0$, $G_{\infty }$, $\tau$, and $\alpha$, to be identified in the fractional derivative model are taken as design variables and the differential method is used to obtain the sensitivity. Take $G_0$ as an example, where the sensitivity $S_{G_0,i}$ of the frequency response to design variable $G_0$ at the i-th frequency point can be described as:

$$S_{G_0,i}=\frac{△x_{G_0,i}}{△G_0}$$

(20)

where $△G_0$ refers to the variation of the design variable (also named as step), which is set to ${10}^{-4}\times G_0$ here. Symbol $△x_{G_0,i}$ is the variation of the vibration response when the change of the design variable is $△G_0$ and it is also named as residual. Similarly, the sensitivity $S_{G_{\infty },i}$, $S_{\tau ,i}$, and $S_{\alpha ,i}$ of the vibration response to $G_{\infty }$, $\tau$, and $\alpha$ can also be calculated, respectively. If the number of frequency points is P in the whole process of identification, then the calculated sensitivity of the design variables forms the sensitivity matrix $S$ and can be described as:

$$S=\left[\begin{array}{cccc}{S}_{G_0,1}& S_{G_{\infty },1}& S_{\tau ,1}& S_{\alpha ,1}\\ S_{G_0,2}& S_{G_{\infty },2}& S_{\tau ,2}& S_{\alpha ,2}\\ ⋮& ⋮& ⋮& ⋮\\ S_{G_0,P}& S_{G_{\infty },P}& S_{\tau ,P}& S_{\alpha ,P}\end{array}\right]$$

(21)

The objective function can be defined according to the principle of linear least square and is expressed as:

$$\mathrm{Min}\Vert W_{\mathrm{x}}(S△b-△x)\Vert$$

(22)

where $\Vert \cdot \Vert$ denotes the solution of 2-norm, $W_{\mathrm{x}}$ is the weight matrix of the vibration response, $△b$ is the vector consisting of the variation of design variables, and $△x$ is the vector consisting of the residuals of the vibration response at each frequency point. The above vectors can be described in detail as:

$$△b={\left[\begin{array}{cccc}△G_0& △G_{\infty }& △\tau & △\alpha \end{array}\right]}^{\mathrm{T}}$$

(23a)

$$△x={\left[\Delta x_1,\Delta x_2,\cdots ,\Delta x_{\mathrm{p}}\right]}^{\mathrm{T}}$$

(23b)

It should be noted that the residuals in Equation (23b) correspond to the variation of response when all the design variables change and Equation (22) denotes that the 2-norm of the difference between the response values obtained from the experiment and theoretical calculations at the considered frequency points is minimal.

Furthermore, if the design variable with a minimum change is also requested, then Equation (22) becomes:

$$\mathrm{Min}\left({\Vert W_{\mathrm{x}}(S△b-△x)\Vert }^2+|W_{\mathrm{b}}△b{|}^2\right)$$

(24)

where $W_{\mathrm{b}}$ is the weight matrix of the design variables.

In Equation (24), if the derivative about $△b$ is solved and the obtained derivative value is set to be zero, then the following iteration formula for the design variable can be yielded:

$$b_j=b_{j-1}-{(S^{\mathrm{T}}{W}_{\mathrm{x}}^{\mathrm{T}}{W}_{\mathrm{x}}S+W_{\mathrm{b}}^{\mathrm{T}}{W}_{\mathrm{b}})}^{-1}{S}^{\mathrm{T}}{W}_{\mathrm{x}}^{\mathrm{T}}△x$$

(25)

After several iterative calculations, until the convergence conditions are satisfied, the four parameters to be identified in the fractional derivative model can be obtained. In addition, it should be noted that considering the high signal-to-noise ratio of the corresponding response value at the resonance point, the weight at the resonance point should be set to a large value, while that at the non-resonance point should be set to a small one.

5. Case Study

In this section, a CLD plate with a ZN_1 viscoelastic core layer was chosen to demonstrate the proposed method. Then, the mechanical parameters of the viscoelastic core layer were identified inversely, based on the measured frequency response.

5.1. Specimens and Frequency Response Test of the CLD Plate

Figure 7 shows the aluminum plate specimens before and after damping treatment. The geometry and material parameters of the substrate, constraining layer, and viscoelastic core layer are listed in

Table 1. Geometry and material parameters of each layer of the CLD plate.

Type of Materials	Length (mm)	Width (mm)	Thickness (mm)	Storage Modulus (GPa)	Densith (kg/m3)	Poisson‘s Ratio	Loss Factor
Aluminum plate substrate	300.2	199.9	1.9	6.89	2700	0.3	0
Steel constraining layer	300.2	199.9	0.3	209	7890	0.3	0
Viscoelastic core layer ZN_1	300.2	199.9	0.5	-	789.5	0.49	-

. It should be noted that the lengths listed in Table 1 are the effective length used in dynamic analysis and the total length of this aluminum plate is 331.2 mm, so the clamping length of the cantilever constraint is 31 mm. All the geometry parameters are measured by a vernier caliper. The density, storage modulus, and Poisson’s ratio of the substrate, and constraining layer and the Poisson’s ratio of the viscoelastic core layer, are known, and the density of the ZN_1 viscoelastic material can be obtained according to the definition of density. However, the storage modulus and loss factor should be identified by the method developed in this study.

In the actual test, the aluminum plate was fixed on the vibration shaker in cantilever status and the tightening torque of bolts was 39 N⋅m. The testing instruments used in this test are all shown in

Table 2. The instruments used in this test.

Number	Name
1	KINGDESIGN EM-1000F vibration shaker
2	LMS SCADAS mobile front-end
3	PCB 8206-001 54627 modal hammer
4	Polytec PDV-100 laser vibrometer
5	LMS.Testlab workstation

, and the corresponding photograph is shown in Figure 8. The laser vibrometer was used to pick up the vibration signal in the process of the experiment and the coordinate of the pick vibration point was (60 mm, 60 mm), which is in accordance with the theoretical analysis in Section 3. According to the requirement of the parameter identification of viscoelastic material, a hammer test was carried out for the aluminum plate without damping treatment. The half-power bandwidth method was adopted to obtain the modal damping ratio of the plate without damping treatment, and the relevant results are listed in

Table 3. Modal damping ratios of the aluminum plate without damping treatment /%.

Order	1	2	3	4	5	6	7	8
Modal damping ratio	0.29	0.13	0.18	0.21	0.11	0.07	0.09	0.04

. Subsequently, using a vibration shaker, a segmented frequency sweeping test was carried out for the aluminum plate with damping treatment, according to the determined frequency sweeping interval which contains the resonance frequency. The frequency responses in the first, third, and fifth order resonance region were chosen to identify the parameters of the viscoelastic core layer. The corresponding level of excitation was 1 g and the relevant results are shown in Figure 9.

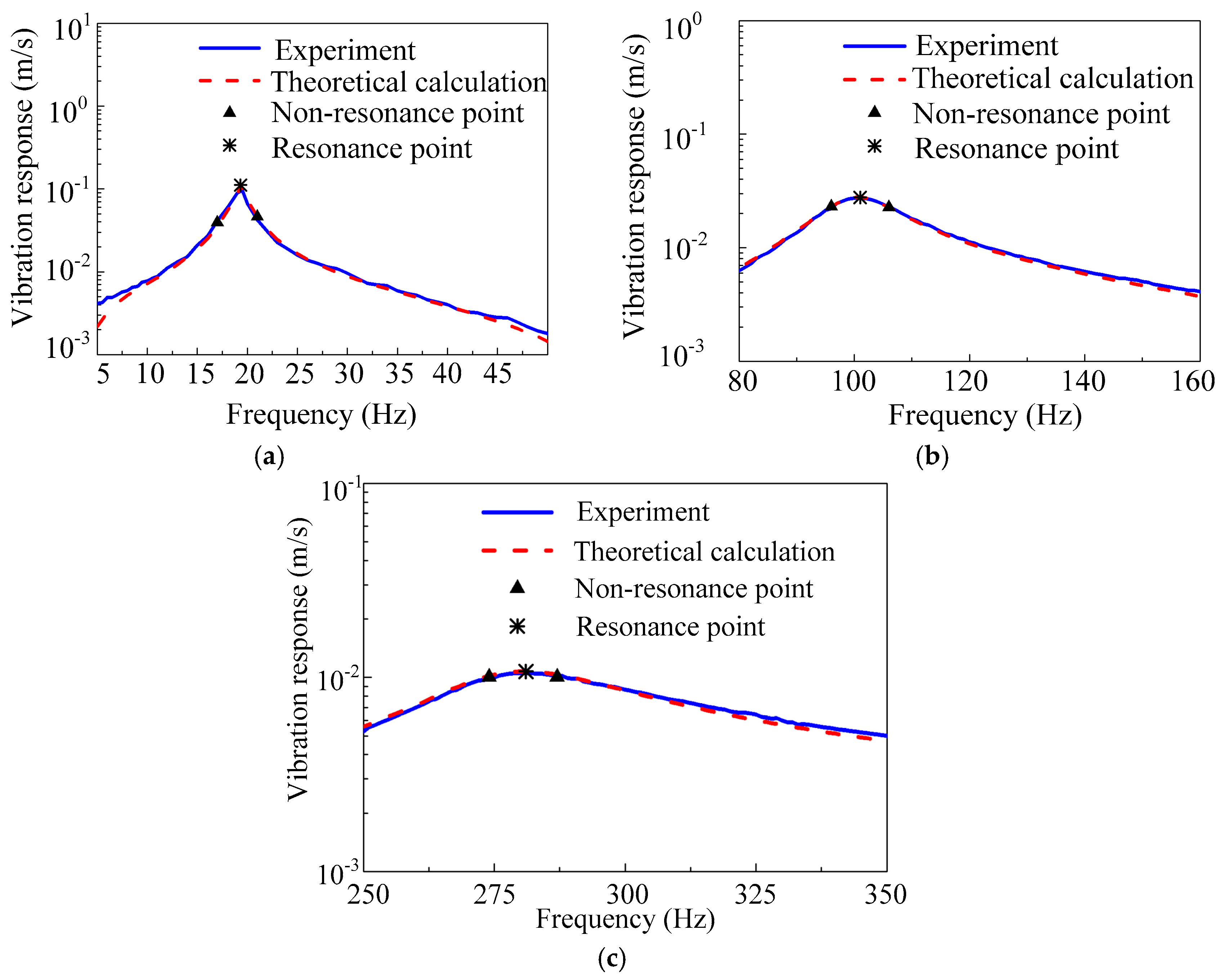
5.2. Parameter Identification of the Viscoelastic Core Layer

Referring to the frequency sweeping response shown in Figure 8, here, three resonant frequency points and six non-resonant frequency points were chosen to conduct the parameter identification using the developed method. The initial values of the fractional derivative model of the ZN_1 viscoelastic material were set as: $E_0=$ 1.2 Mpa, $E_{\infty }=$ 12.5 Mpa, $\tau =$ 1.42 × 10⁻⁴, and $\alpha =$ 0.89. Next, the sensitivity of the vibration response to the parameters of the fractional derivative model at each frequency point and the residual vector of the vibration response were calculated. Further, the weight value of each parameter in the fractional-derivative model was taken as 0.25 and the weight value at the resonance point was 0.2 in the weight matrix of the vibration response, while that of the non-resonant points was 0.06. Finally, the obtained sensitivity matrix, vibration response residual vector, and weight matrix were inputted into Equation (25) and an iterative calculation was performed. The convergence condition was set as follows: the difference between the calculated and measured vibration response was less than 5%. After five iterative calculations, the fractional derivative model parameters of the ZN_1 viscoelastic material were inversely identified and the final identification values are shown in

Table 4. Parameters of the fractional derivative model of ZN_1.

Parameters	${\mathit{G}}_0$	${\mathit{G}}_{\mathbf{\infty }}$	$\mathit{\tau }$	$\mathit{\alpha }$
Identified value	0.27 MPa	4.1 MPa	1.21 × ${10}^{-4}$	0.83

. One can set the excitation frequency as the horizontal axis and the storage modulus or loss factor of the viscoelastic material as the vertical axis. Then, the mechanical properties of the ZN_1 viscoelastic material can be characterized by plotting these curves, shown in Figure 10. In order to demonstrate the influence of the remaining equivalent viscous damping on the identification results, the identification results obtained by the analysis model only considering the material damping were given, and are also shown in Figure 10. It can be seen that there are some differences between the two identified results.

In order to demonstrate the rationality of the identification results, the fractional derivative model of viscoelastic materials was written in the form of the complex modulus and substituted into the analysis model. The frequency response of the CLD plate needs to be calculated at each frequency point (the calculation step is 1 Hz). Firstly, the storage modulus and loss factor of the viscoelastic material were determined according to each frequency value. Then, the total complex stiffness matrix $K^{*}$ and the total mass matrix M were determined using the method described in Section 3.3 and modal analysis was carried out for the composite structure. Subsequently, the remaining equivalent viscous damping in Table 3 was inputted into the analysis model and the corresponding response values at each frequency point were calculated using the mode superposition method (the first eight order modes were considered here). Finally, the frequency response curve was drawn in the considered frequency range and the relevant results are shown in Figure 9. The values obtained through theoretical calculations and the experimental test at each specified frequency point are compared and shown in

Table 5. Vibration responses obtained by theoretical calculations and the experiment/(m/s).

Frequency Point (Hz)	Experiment (${\mathit{R}}_{\mathbf{e}}$)	Theoretical Calculation (${\mathit{R}}_{\mathbf{t}}$)	Difference $\left|{\mathit{R}}_{\mathbf{t}}-{\mathit{R}}_{\mathbf{e}}\right|/{\mathit{R}}_{\mathbf{e}}$
18.4	0.0726	0.0708	2.48
19.3 *	0.1112	0.1128	1.44
20.2	0.0705	0.0729	3.40
94.3	0.0197	0.0206	4.57
100.5 *	0.0279	0.0276	1.08
105.0	0.0240	0.0229	4.58
264.8	0.0082	0.0086	4.87
281.1 *	0.0107	0.0109	1.58
295.2	0.0092	0.0088	4.99

Notation: symbol * refers to resonance point.

. It can be seen from Figure 8 and Table 5 that the frequency response of the CLD plate obtained by the theoretical calculation is almost identical with the measured value. Therefore, it demonstrates that the identification results of the mechanical parameters of the ZN_1 viscoelastic material are reasonable.

6. Conclusions

The identification of the mechanical parameters of the viscoelastic core layer is of great significance for the modeling of a viscoelasticlly damped structure and vibration reduction design. An identification method based on the obtained frequency sweeping response of a composite structure was proposed in this study and the relevant conclusions are listed as follows.

(1)

In the created vibration response analysis model of the CLD plate, both the material damping and the remaining equivalent viscous damping were considered. This kind of damping model is consistent with the real environment of the CLD plate, which is helpful to improve the identification accuracy of the material parameters of the viscoelastic core layer.

(2)

The method in which the sweeping frequency response under base excitation is mainly used to identify the mechanical parameters of the viscoelastic core layer was proposed. This identification method avoids the difference caused by the inaccurate location of the exciting point in the hammer test. On the other hand, it can also reduce the interference of noise seen in the identification results to the maximum extent.

(3)

Taking the minimum differences between the theoretical and experimental values of the vibration response as the objective function, a matching calculation based on sensitivity was proposed. On the premise of obtaining a reasonable initial value, the parameters of the viscoelastic core layer to be identified can quickly converge.

(4)

The CLD plate with ZN_1 viscoelastic material as the core layer was chosen to demonstrate the developed method. The identified viscoelastic mechanical parameters were substituted into the analysis model and the predicted vibration response was compared with the experimental values. The rationality of the identification results was verified.