A Short-Term Photovoltaic Power Prediction Model Based on an FOS-ELM Algorithm
Abstract
:1. Introduction
- (1)
- The computation complexion of ELM is much lower than many other machine learning algorithms.
- (2)
- The learning speed of ELM is much faster than most feed forward network learning algorithms.
- (3)
- The generalization performance of ELM is better than many others.
- (4)
- The amount of hidden layer nodes is small and they do not need to be tuned [16].
- We introduced an online learning model with a Forgetting Mechanism to the area of photovoltaic prediction, which can update the data in real time.
- We compared the ELM, OS-ELM and FOS-ELM prediction models in predicting PV power in different seasons.
- The simulation results showed that the FOS-ELM model can not only improve the accuracy but also reduce the training time.
2. Prediction Algorithm
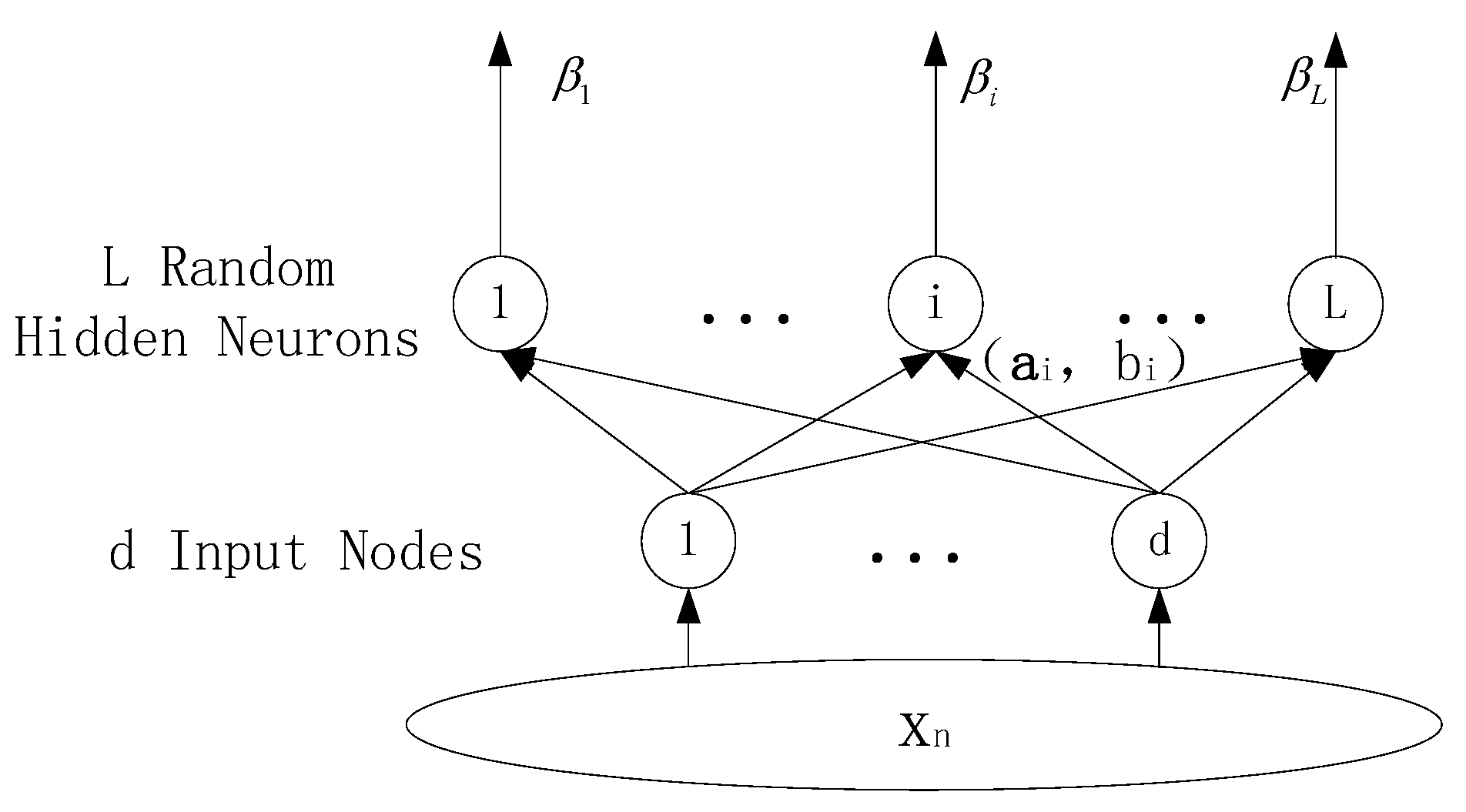
2.1. Classical Extreme Learning Machine (ELM)
2.2. Online Sequential ELM (OS-ELM)
- (a)
- Randomly generate and where .
- (b)
- Calculate the initial hidden layer output matrix .
- (c)
- Estimate the initial output weight vector:where
- (d)
- Set .
- (a)
- When the chunk of new data is ready,
- (b)
- Calculate the partial hidden layer output matrix based on the latest data.
- (c)
- Estimate the new and based on (7) and (8).
- (d)
- Set , and then go back to Step 2.
2.3. OS-ELM with Forgetting Mechanism (FOS-ELM)
- (a)
- Calculate the partial hidden layer output matrix , which corresponds to the latest data.
- (b)
- Estimate the new and based on (9) and (10).
- (c)
- Set , and then go back to Step 2.
3. Model Architecture
3.1. Physical Model
3.2. Input Vector
3.3. Data Pre-Processing
3.4. Error Evaluation
3.5. Flowchart of the Model
4. Examples and Simulation
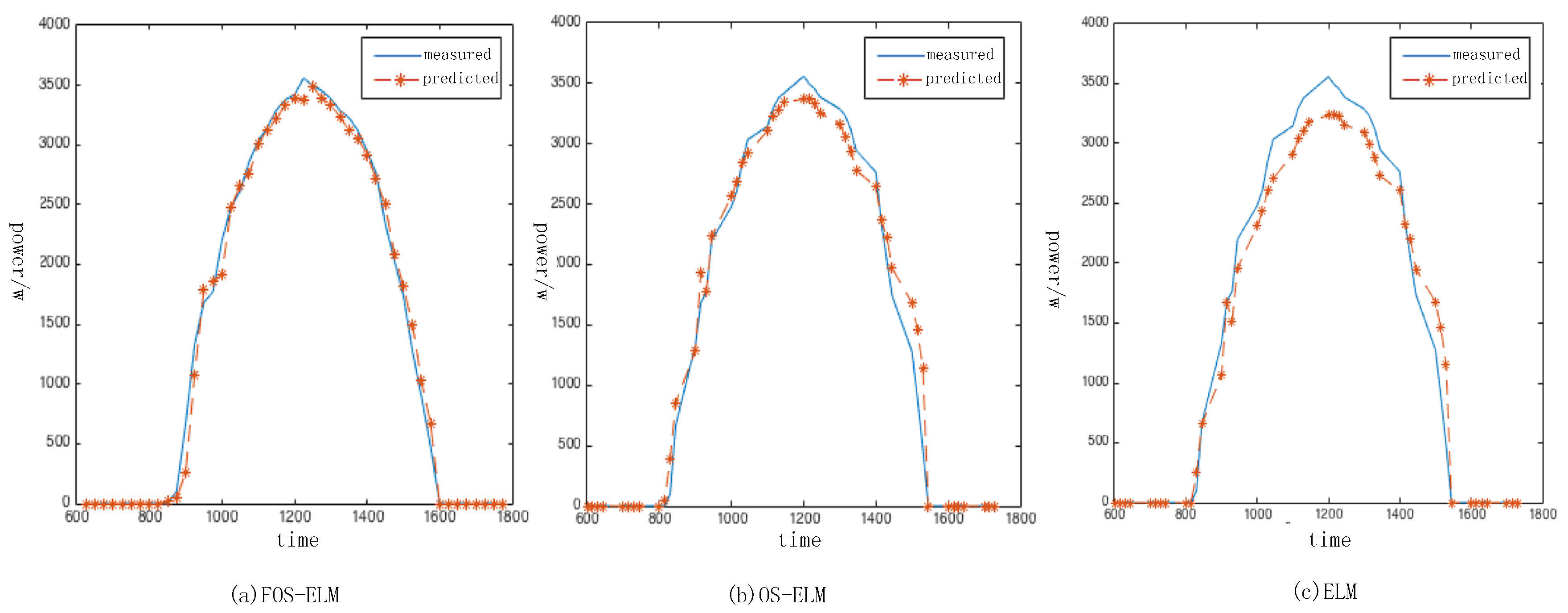
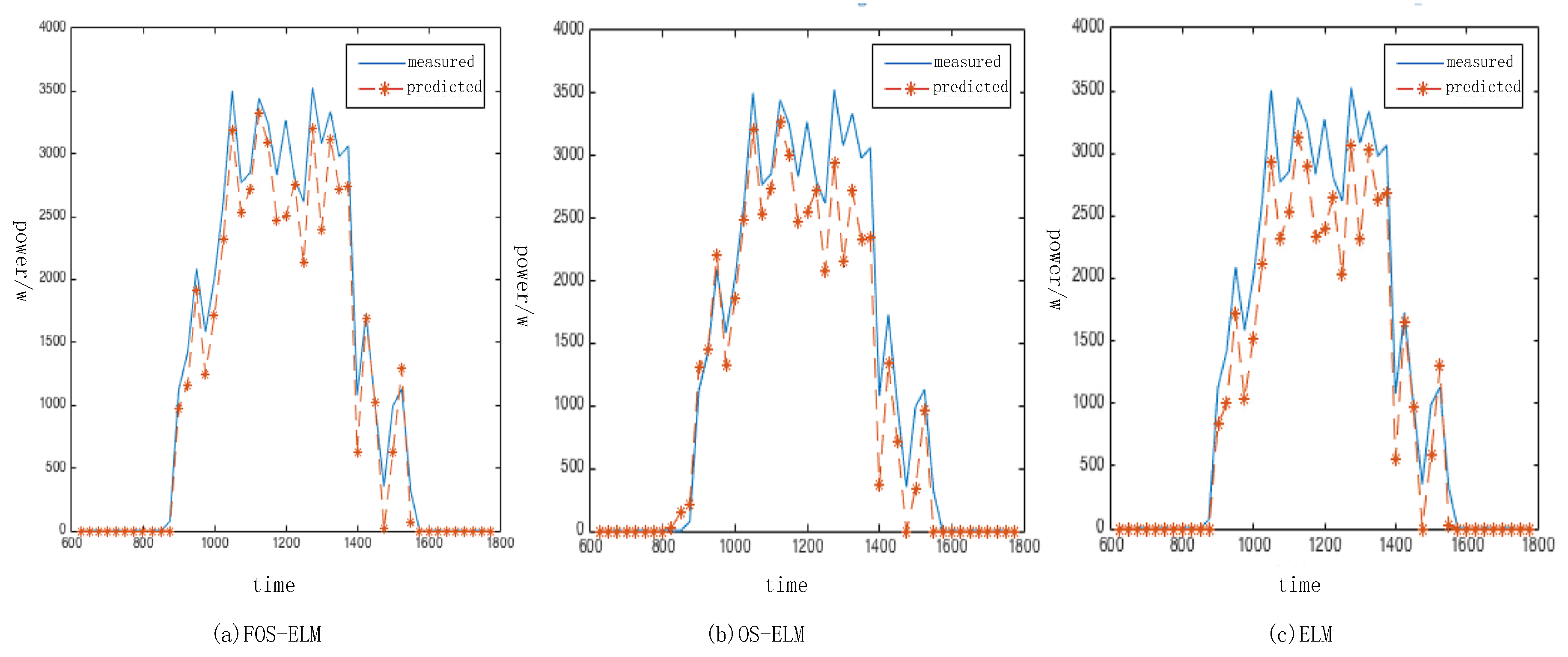
4.1. Accuracy Comparison in a Single Day
4.2. Monthly Average Accuracy Comparison
4.3. Comparison of Training Time
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Paravalos, C.; Koutroulis, E.; Samoladas, V.; Kerekes, T.; Sera, D.; Teodorescu, R. Optimal Design of Photovoltaic Systems Using High Time-Resolution Meteorological Data. IEEE Trans. Ind. Inform. 2014, 10, 2270–2279. [Google Scholar] [CrossRef]
- IEA. Technology Roadmap, Solar Photovoltaic Energy. Available online: http://www.iea.org/ (accessed on 10 July 2016).
- Paatero, J.V.; Lund, P.D. Effects of large-Scale photovoltaic power integration on electricity distribution networks. Renew. Energy 2007, 32, 216–234. [Google Scholar] [CrossRef]
- Bortolini, M.; Gamberi, M.; Graziani, A. Technical and economic design of photovoltaic and battery energy storage system. Energy Convers. Manag. 2014, 86, 81–92. [Google Scholar] [CrossRef]
- Mohamed, A.; Eltawil, M.A.; Zhengming, Z. Grid-Connected photovoltaic power systems: Technical and potential problems—A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar]
- Graditi, G.S.; Ferlito, S.; Adinolfi, G. Comparison of Photovoltaic plant power production prediction methods using a large measured dataset. Renew. Energy 2016, 90, 513–519. [Google Scholar] [CrossRef]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production. Part II: Probabilistic forecast of daily production. Sol. Energy 2014, 105, 792–803. [Google Scholar] [CrossRef]
- Baharin, K.A.; Abd Rahman, H.; Hassan, M.Y.; Gan, C.K. Hourly Photovoltaics Power Output Prediction for Malaysia Using Support Vector Regression. Appl. Mech. Mater. 2015, 785, 591–595. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Xiao, J.; Tan, Y. Short-Term prediction of the output power of PV system based on improved gray prediction model. In Proceedings of the IEEE International Conference on Advanced Mechatronic Systems, Kumamoto, Japan, 10–12 August 2014; pp. 547–551. [Google Scholar]
- Al-Amoudi, A.; Zhang, L. Application of radial basis function networks for solar-Array modelling and maximum power-Point prediction. IEE Gener. Transm. Distrib. 2000, 147, 310–316. [Google Scholar] [CrossRef]
- Shang, X.X.; Chen, Q.J.; Han, Z.F.; Qian, X.D. Photovoltaic super-Short term power prediction based on bp-Ann generalization neural network technology research. Adv. Mater. Res. 2013, 791, 1925–1928. [Google Scholar] [CrossRef]
- Mandal, P.; Madhira, S.T.S.; Haque, A.U.; Meng, J.; Pineda, R.L. Forecasting Power Output of Solar Photovoltaic System Using Wavelet Transform and Artificial Intelligence Techniques. Procedia Comput. Sci. 2012, 12, 332–337. [Google Scholar] [CrossRef]
- Bouzerdoum, M.A.; Mellit, A.; Pavan, A.M. A hybrid model (SARIMA–SVM) for short-Term power forecasting of a small-Scale grid-Connected photovoltaic plant. Sol. Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H.; Nielsen, H.A. Online short-Term solar power forecasting. Sol. Energy 2009, 83, 1772–1783. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feed forward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Chen, L.; Siew, C.K. Universal approximation using incremental constructive feedforward networks with random hidden. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [PubMed]
- Liang, N.Y.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. A fast and accurate online sequential learning algorithm for feed forward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.W.; Wang, Z.; Dong, S.P. Online sequential extreme learning machine with forgetting mechanism. Neurocomputing 2012, 87, 79–89. [Google Scholar] [CrossRef]
- Riffonneau, Y.; Bacha, S.; Barruel, F.; Ploix, S. Optimal Power Flow Management for Grid Connected PV Systems With Batteries. IEEE Trans. Sustain. Energy 2011, 2, 309–320. [Google Scholar] [CrossRef]
- Lynch, P. The origins of computer weather prediction and climate modeling. Comput. Phys. 2008, 227, 3431–3444. [Google Scholar] [CrossRef]
- University of Oregon Solar Radiation Monitoring Laboratory. Available online: http://solardat.uoregon.edu/SelectDailyTotal.html (accessed on 9 May 2016).
- Li, Z.; Zang, C.; Zeng, P.; Yu, H. Day-Ahead hourly photovoltaic generation forecasting using extreme learning machine. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems IEEE, Shenyang, China, 8–12 June 2015; pp. 779–783. [Google Scholar]
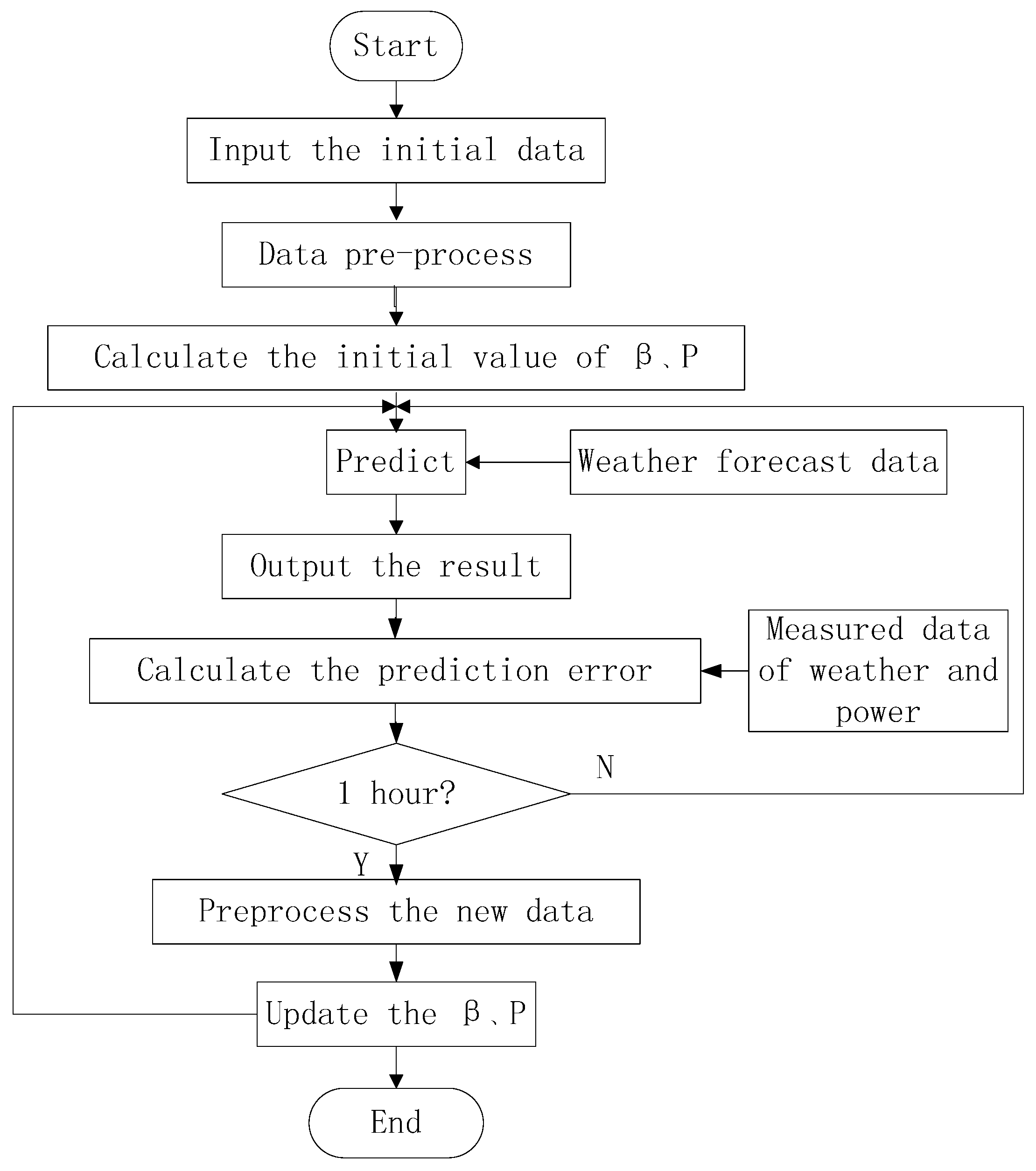

| Season | Model | /% | |
|---|---|---|---|
| Spring (Apri–June) | FOS-ELM | 0.0953 | 15.492 |
| OS-ELM | 0.1041 | 16.730 | |
| ELM | 0.1126 | 18.483 | |
| Summer (July–September) | FOS-ELM | 0.0892 | 14.329 |
| OS-ELM | 0.0933 | 15.883 | |
| ELM | 0.1083 | 16.032 | |
| Autumn (October–December) | FOS-ELM | 0.0974 | 15.289 |
| OS-ELM | 0.1018 | 16.325 | |
| ELM | 0.1219 | 17.933 | |
| Winter (January–March) | FOS-ELM | 0.0876 | 15.245 |
| OS-ELM | 0.0945 | 16.319 | |
| ELM | 0.0983 | 17.703 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ran, R.; Zhou, Y. A Short-Term Photovoltaic Power Prediction Model Based on an FOS-ELM Algorithm. Appl. Sci. 2017, 7, 423. https://doi.org/10.3390/app7040423
Wang J, Ran R, Zhou Y. A Short-Term Photovoltaic Power Prediction Model Based on an FOS-ELM Algorithm. Applied Sciences. 2017; 7(4):423. https://doi.org/10.3390/app7040423
Chicago/Turabian StyleWang, Jidong, Ran Ran, and Yue Zhou. 2017. "A Short-Term Photovoltaic Power Prediction Model Based on an FOS-ELM Algorithm" Applied Sciences 7, no. 4: 423. https://doi.org/10.3390/app7040423
APA StyleWang, J., Ran, R., & Zhou, Y. (2017). A Short-Term Photovoltaic Power Prediction Model Based on an FOS-ELM Algorithm. Applied Sciences, 7(4), 423. https://doi.org/10.3390/app7040423






