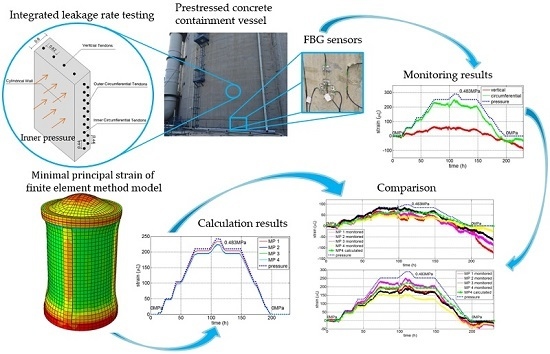
Nuclear Power Plant Prestressed Concrete Containment Vessel Structure Monitoring during Integrated Leakage Rate Testing Using Fiber Bragg Grating Sensors
Abstract
:1. Introduction
2. The Experimental Process and the FEM Model
2.1. Basic Principle of FBG
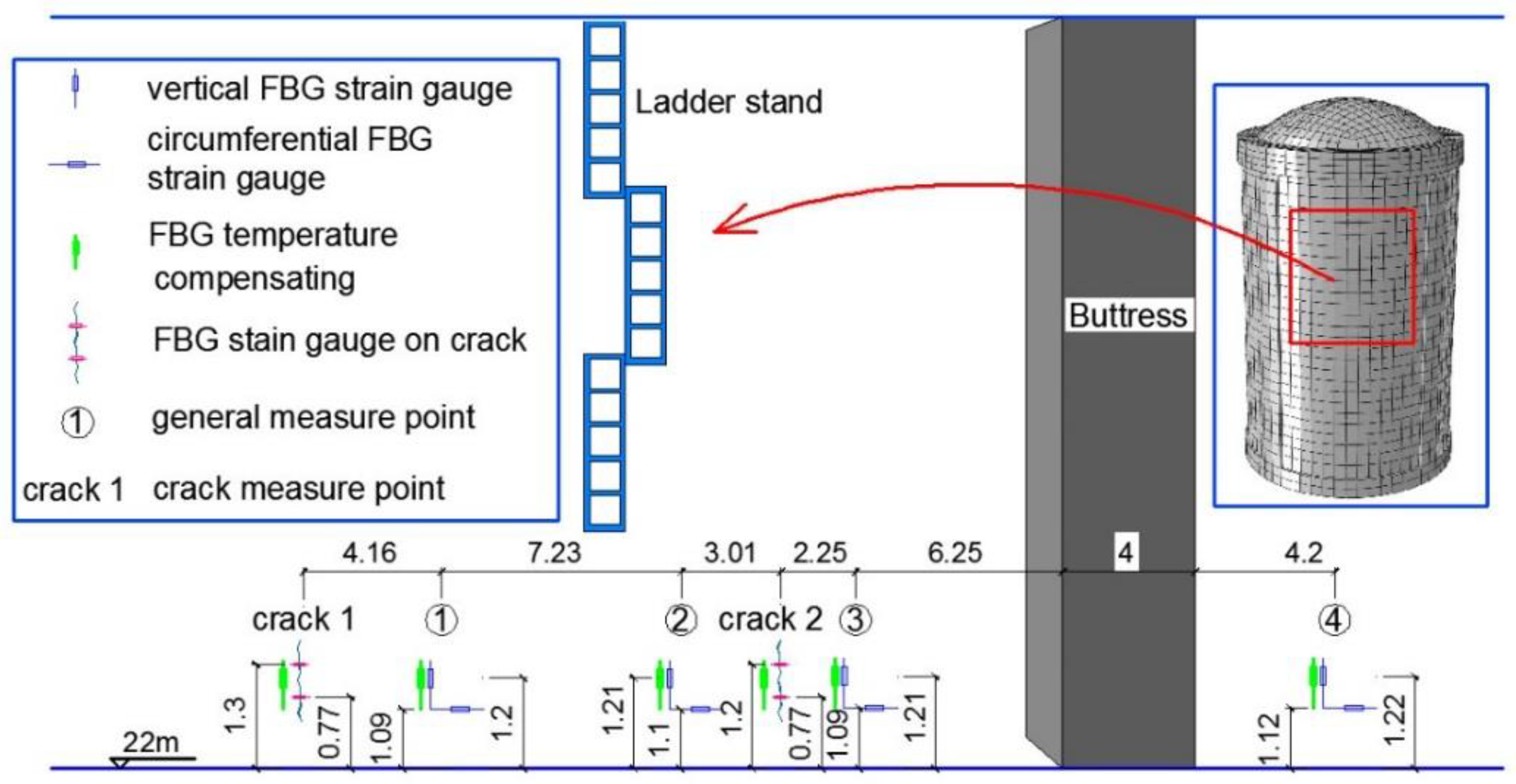
2.2. FBG Sensors Deployment
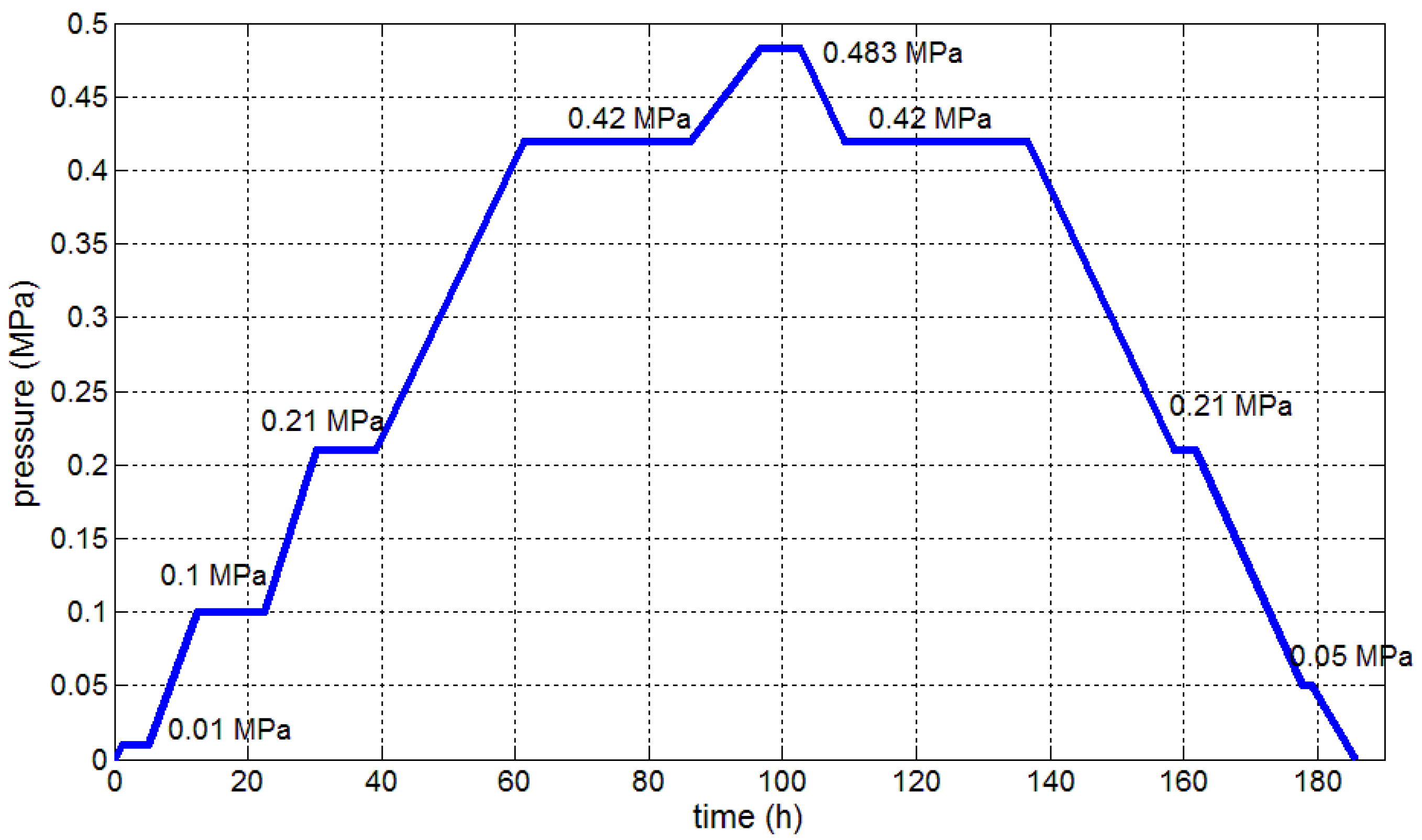
2.3. The Pressure Time Table
2.4. The FEM Model
2.4.1. Hypothesis
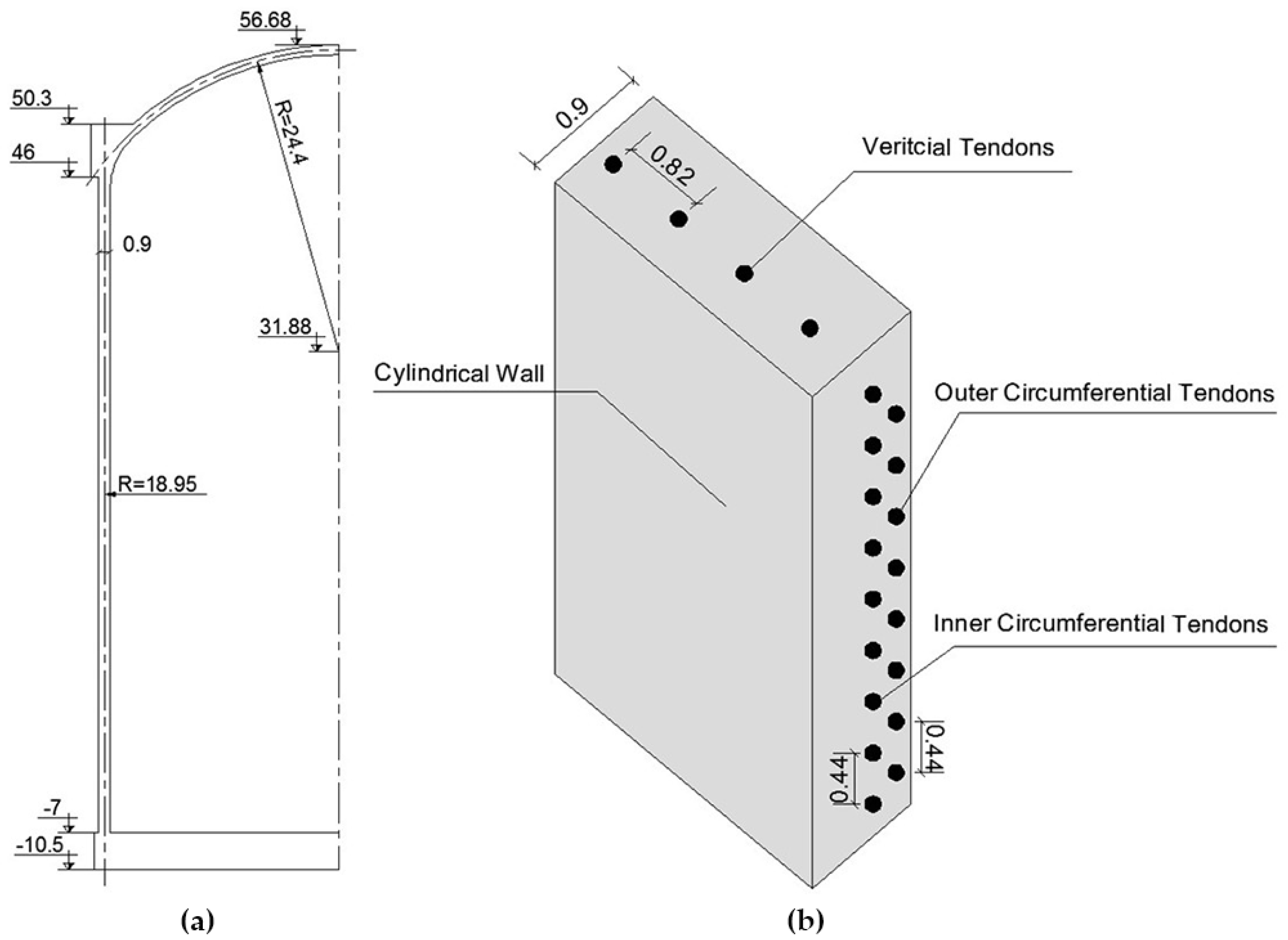
2.4.2. Geometry
2.4.3. Material
2.4.4. Mesh
2.4.5. Load
3. Results
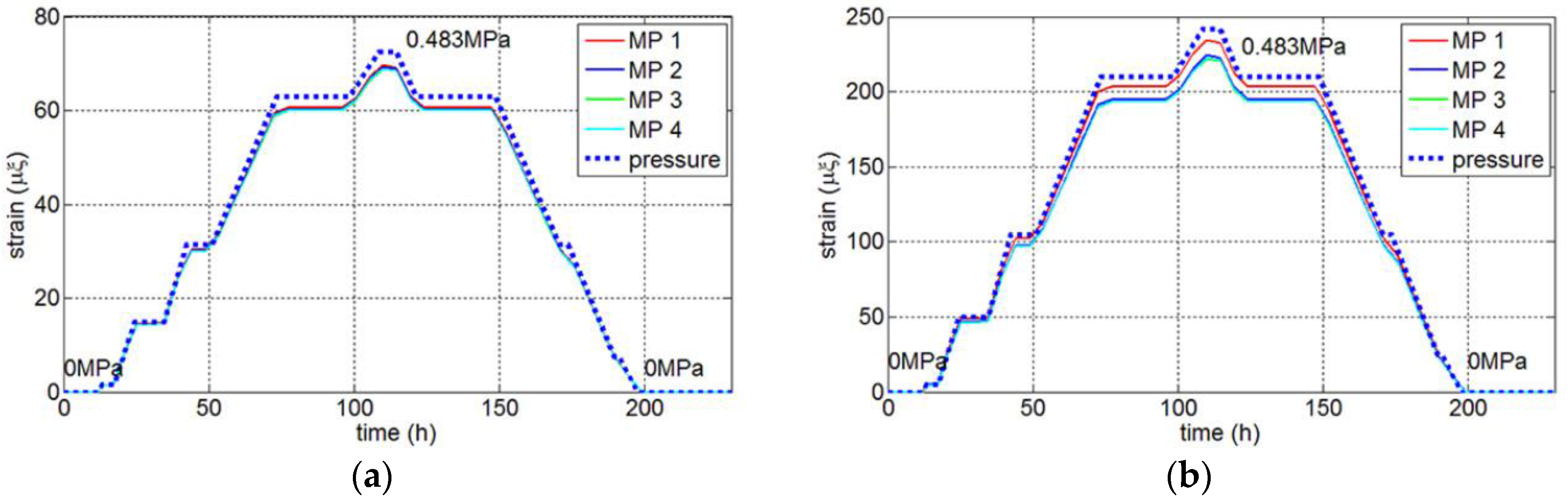
3.1. Monitoring Results
3.1.1. General Measure Points
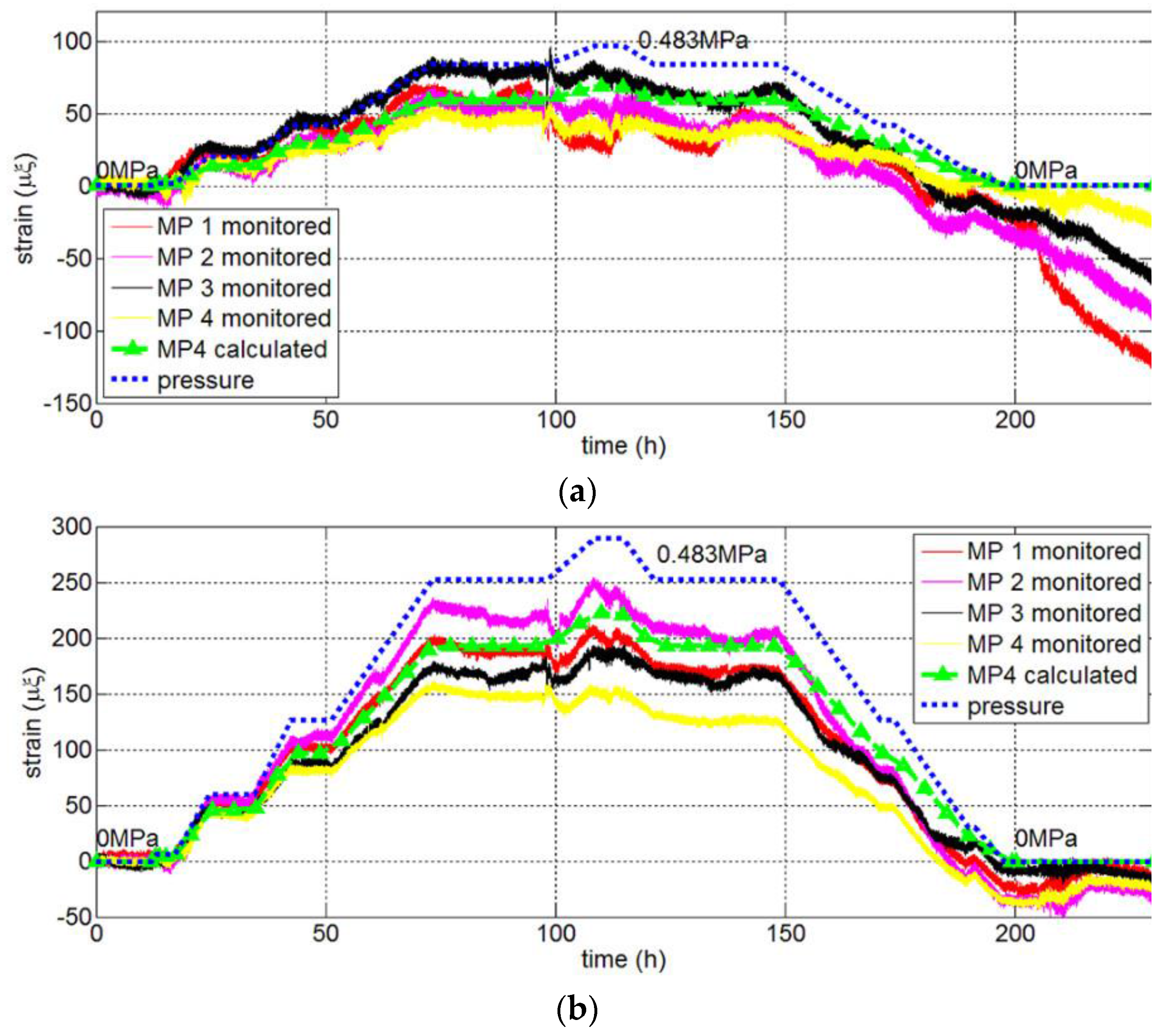
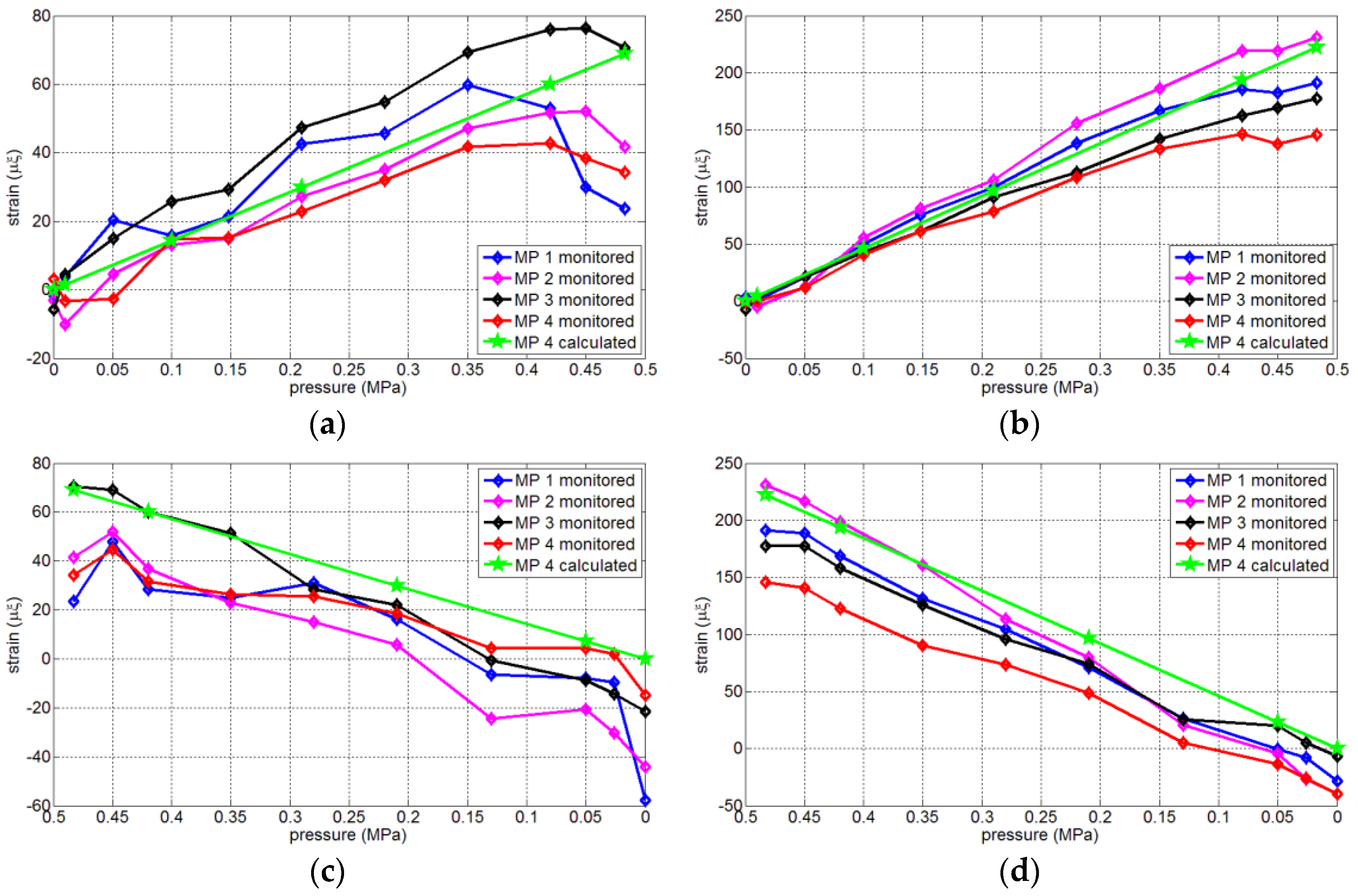
3.1.2. Crack Measure Points
3.2. The FEM Model Results
3.2.1. The Load Step History
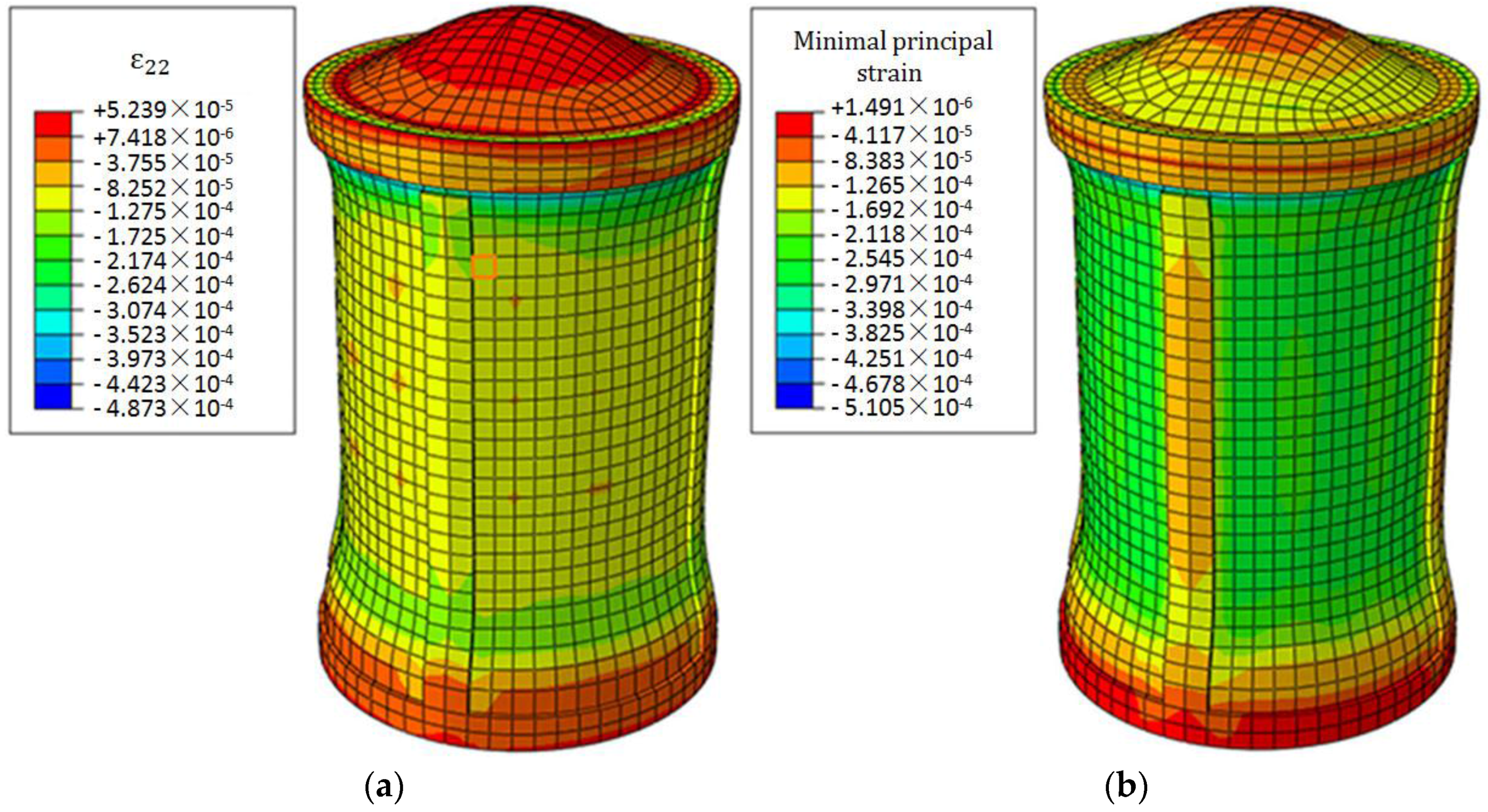
3.2.2. The Strain Distribution
3.2.3. Comparison between Monitoring Results and Calculation Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Glišić, B.; Simon, N. Monitoring of concrete at very early age using stiff SOFO sensor. Cem. Concr. Compos. 2000, 22, 115–119. [Google Scholar] [CrossRef]
- Hessheimer, M.F.; Shibata, S.; Costello, J.F. Functional and Structural Failure Mode Overpressurization Tests of 1: 4-Scale Prestressed Concrete Containment Vessel Model. In Proceedings of the 17th International Conference on Structural Mechanics in Reactor Technology (SMiRT 17), Prague, Czech Republic, 17–22 August 2003. H02-3. [Google Scholar]
- Zhao, X.; Cui, Y.; Wei, H.; Kong, X.; Zhang, P.; Sun, C. Research on corrosion detection for steel reinforced concrete structures using the fiber optical white light interferometer sensing technique. Smart Mater. Struct. 2013, 22, 1693. [Google Scholar] [CrossRef]
- Inaudi, D.; Glisic, B. Long-Range Pipeline Monitoring by Distributed Fiber Optic Sensing. J. Press. Vessel Technol. 2010, 132, 763–772. [Google Scholar] [CrossRef]
- Ferdinand, P.; Magne, S.; Marty, V.; Georges, T. Optical fibre Bragg grating sensors for structure monitoring within the nuclear power plants. Proc SPIE 1994, 2425, 11–20. [Google Scholar]
- Jang, J.B.; Hwang, K.M.; Lee, H.P.; Kim, B.H. An assessment of the prestress force on the bonded tendon by SI and impact signal analysis techniques. Nucl. Eng. Des. 2013, 255, 9–15. [Google Scholar] [CrossRef]
- Leng, J.; Asundi, A. Structural health monitoring of smart composite materials by using EFPI and FBG sensors. Sens. Actuators A Phys. 2003, 103, 330–340. [Google Scholar] [CrossRef]
- Wan, C.; Hong, W.; Liu, J.; Wu, Z.; Xu, Z.; Li, S. Bridge Assessment and Health Monitoring with Distributed Long-Gauge FBG Sensors. Int. J. Distrib. Sens. Netw. 2013, 2013, 494260. [Google Scholar] [CrossRef]
- Perry, M.; Yan, Z.; Sun, Z.; Zhang, L.; Niewczas, P.; Johnston, M. High stress monitoring of prestressing tendons in nuclear concrete vessels using fibre-optic sensors. Nucl. Eng. Des. 2014, 268, 35–40. [Google Scholar] [CrossRef]
- Li, W.; Ho, S.; Song, G. Corrosion Detection of Steel Reinforced Concrete Using Combined Carbon Fiber and Fiber Bragg Grating Active Thermal Probe. Smart Mater. Struct. 2016, 25. Available online: http://iopscience.iop.org/article/10.1088/0964-1726/25/4/045017/meta (accessed on 14 March 2016).
- Hu, H.; Lin, Y. Ultimate analysis of PWR prestressed concrete containment subjected to internal pressure. Int. J. Press. Vessel. Pip. 2006, 83, 161–167. [Google Scholar] [CrossRef]
- Sang, H.N.; Moon, I.H.; Lee, J.B.; Kim, J.H. Analysis of Prestressed Concrete Containment Vessel (PCCV) under Severe Accident Loading. Nucl. Eng. Technol. 2008, 40, 77–86. [Google Scholar]
- Lee, H.P. Shell finite element of reinforced concrete for internal pressure analysis of nuclear containment building. Nucl. Eng. Des. 2011, 241, 515–525. [Google Scholar] [CrossRef]
- Bílý, P.; Kohoutková, A. Sensitivity analysis of numerical model of prestressed concrete containment. Nucl. Eng. Des. 2015, 295, 204–214. [Google Scholar] [CrossRef]
- Jones, C.A.; Dameron, R.; Sircar, M. Improving the state of the art in FEM analysis of PCCVs with bonded and unbonded prestress tendons. Nucl. Eng. Des. 2015, 295, 782–788. [Google Scholar] [CrossRef]
- Shokoohfar, A.; Rahai, A. Nonlinear analysis of pre-stressed concrete containment vessel (PCCV) using the damage plasticity model. Nucl. Eng. Des. 2016, 298, 41–50. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Pereira, G.; McGugan, M.; Mikkelsen, L.P. Method for independent strain and temperature measurement in polymeric tensile test specimen using embedded FBG sensors. Polym. Test. 2016, 50, 125–134. [Google Scholar] [CrossRef]
- Jung, D.W.; Kwon, I.B.; Choi, N.S. Application of a Temperature-Compensating FBG Sensor to Strain Measurement. Adv. Mater. Res. 2007, 26–28, 1089–1092. [Google Scholar] [CrossRef]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 35–36. [Google Scholar]



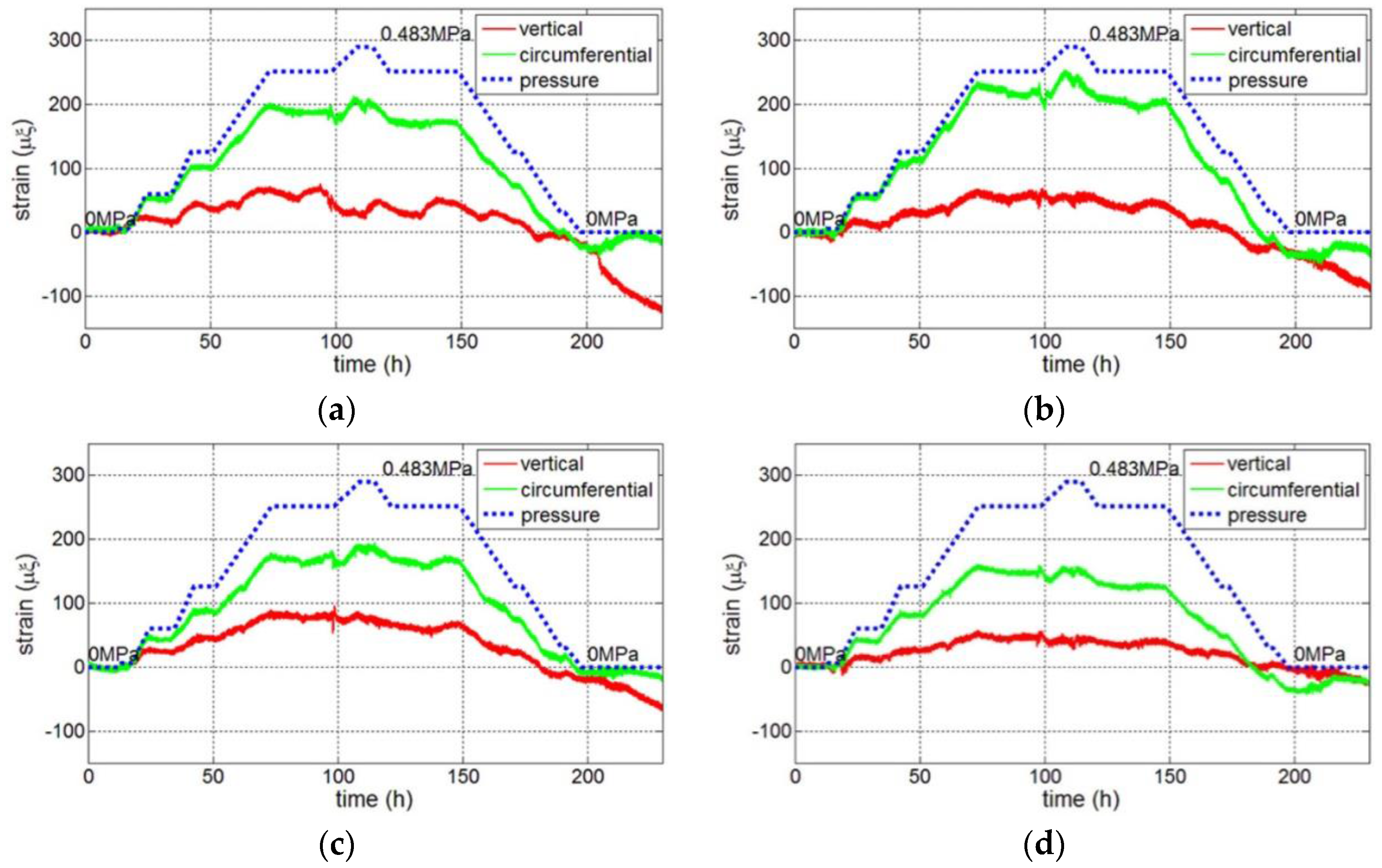
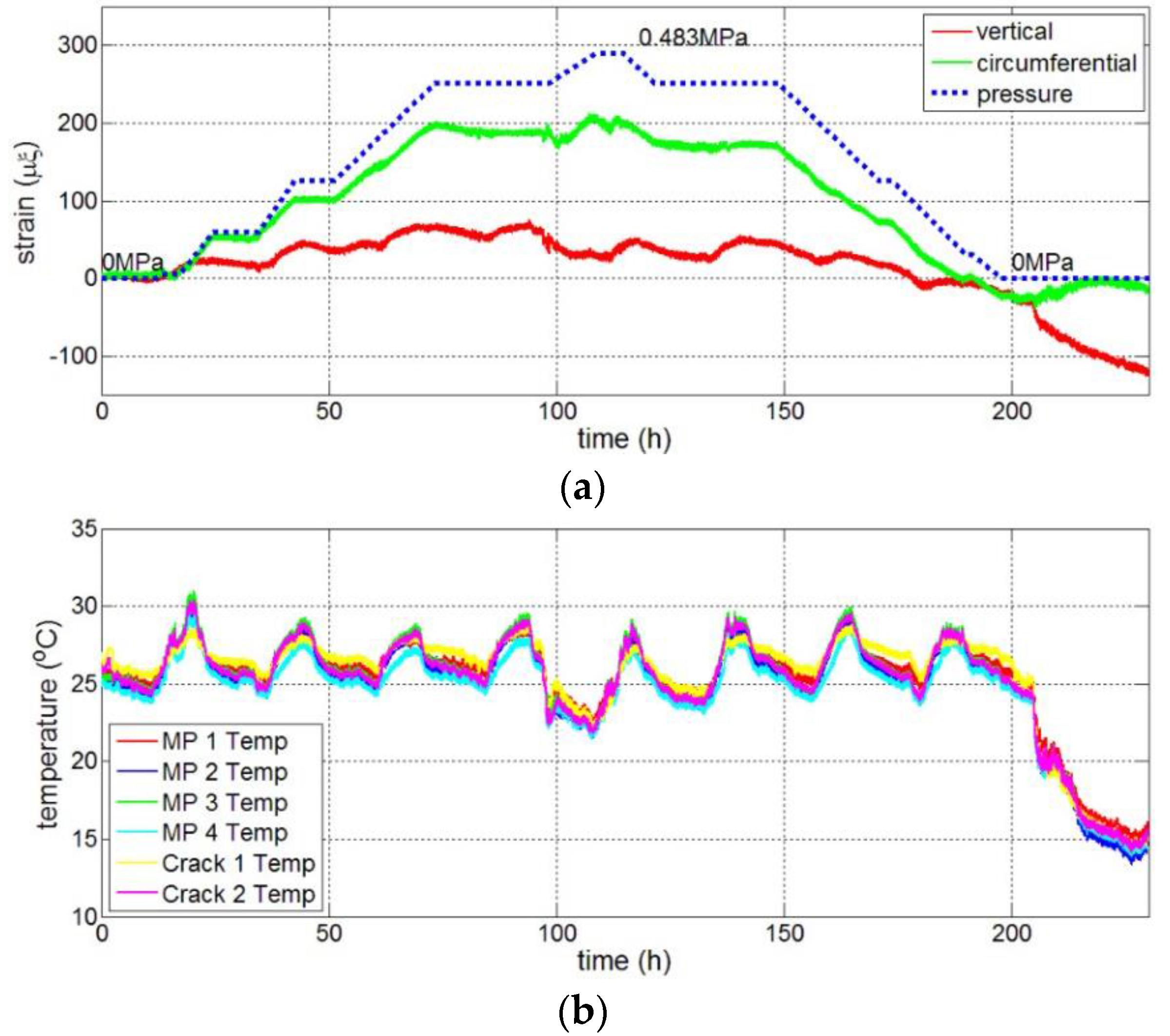
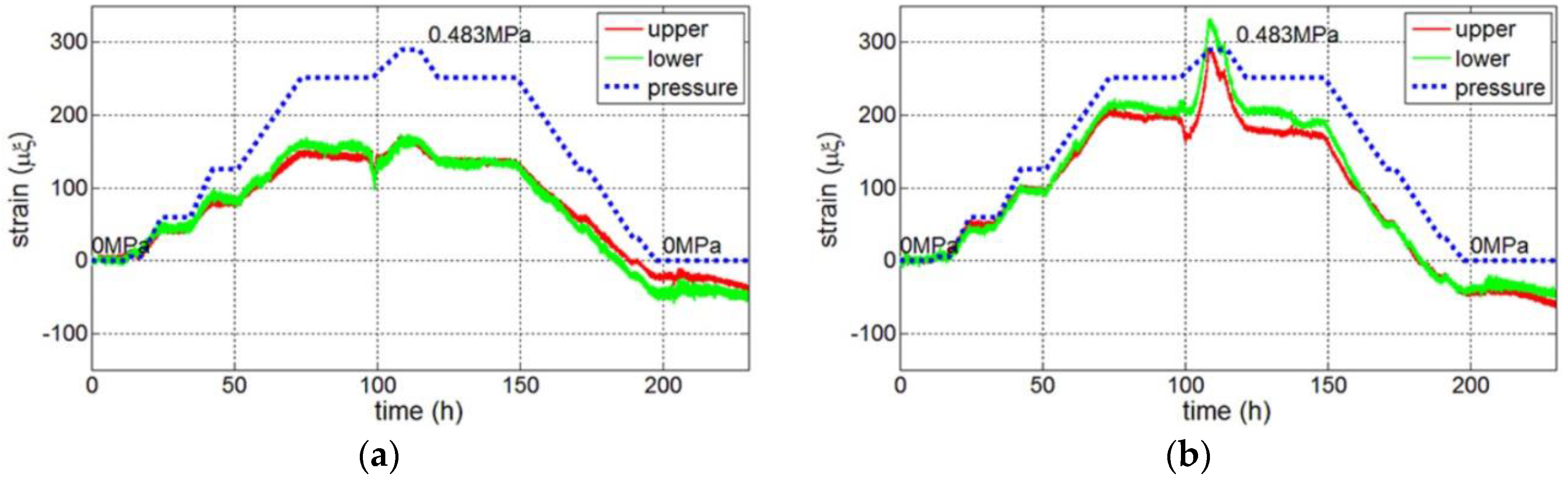
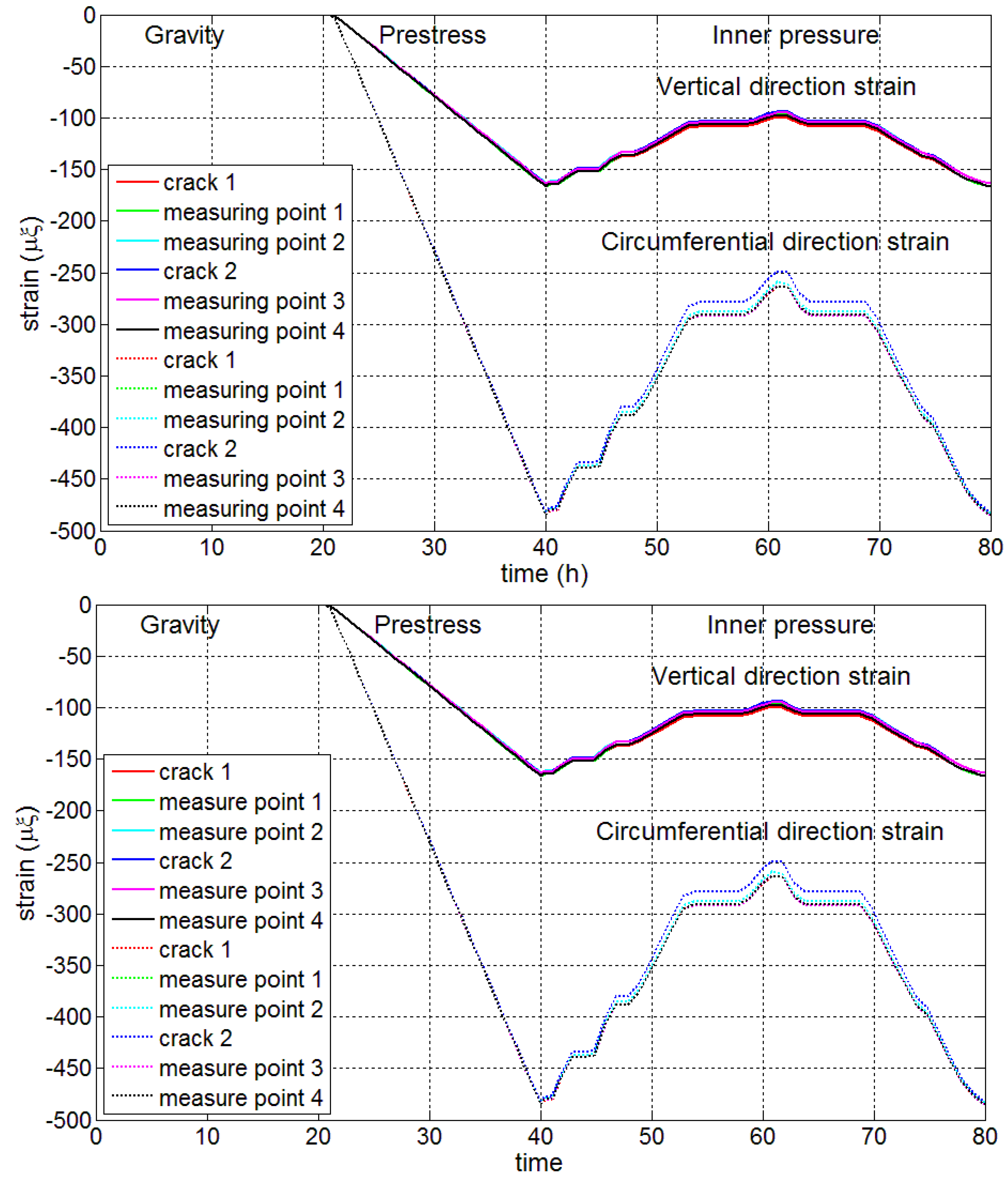
| Material | Elasticity Modulus (MPa) | Poisson Ratio | Density (kg/m3) | Thermal Expansion Coefficient |
|---|---|---|---|---|
| Concrete | 0.2 | 2500 | - | |
| Steel liner | 0.28 | 7850 | - | |
| Prestress tendon | - | 7850 | ||
| Rebar | - | 7850 | - |
| Load Step | Time (unit: h) |
|---|---|
| Gravity | 20 |
| Prestress | 20 |
| Inner pressure | 40 |
| Phase | Measure Point | Vertical | Circumferential |
|---|---|---|---|
| pressurization | MP 1 | 0.5372 | 0.0193 |
| pressurization | MP 2 | 0.0785 | 0.0106 |
| pressurization | MP 3 | 0.0516 | 0.0071 |
| pressurization | MP 4 | 0.1244 | 0.0324 |
| depressurization | MP 1 | 0.2718 | 0.0033 |
| depressurization | MP 2 | 0.0388 | 0.0026 |
| depressurization | MP 3 | 0.0083 | 0.011 |
| depressurization | MP 4 | 0.0954 | 0.0046 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liao, K.; Kong, X.; Li, S.; Zhang, X.; Zhao, X.; Sun, C. Nuclear Power Plant Prestressed Concrete Containment Vessel Structure Monitoring during Integrated Leakage Rate Testing Using Fiber Bragg Grating Sensors. Appl. Sci. 2017, 7, 419. https://doi.org/10.3390/app7040419
Li J, Liao K, Kong X, Li S, Zhang X, Zhao X, Sun C. Nuclear Power Plant Prestressed Concrete Containment Vessel Structure Monitoring during Integrated Leakage Rate Testing Using Fiber Bragg Grating Sensors. Applied Sciences. 2017; 7(4):419. https://doi.org/10.3390/app7040419
Chicago/Turabian StyleLi, Jinke, Kaixing Liao, Xianglong Kong, Shengyuan Li, Xinwang Zhang, Xuefeng Zhao, and Changsen Sun. 2017. "Nuclear Power Plant Prestressed Concrete Containment Vessel Structure Monitoring during Integrated Leakage Rate Testing Using Fiber Bragg Grating Sensors" Applied Sciences 7, no. 4: 419. https://doi.org/10.3390/app7040419
APA StyleLi, J., Liao, K., Kong, X., Li, S., Zhang, X., Zhao, X., & Sun, C. (2017). Nuclear Power Plant Prestressed Concrete Containment Vessel Structure Monitoring during Integrated Leakage Rate Testing Using Fiber Bragg Grating Sensors. Applied Sciences, 7(4), 419. https://doi.org/10.3390/app7040419