The Effect of Temperature Field on Low Amplitude Oscillatory Flow within a Parallel-Plate Heat Exchanger in a Standing Wave Thermoacoustic System

Abstract

Thermoacoustic technologies rely on a direct power conversion between acoustic and thermal energies using well known thermoacoustic effects. The presence of the acoustic field leads to oscillatory heat transfer and fluid flow processes within the components of thermoacoustic devices, notably heat exchangers. This paper outlines a two-dimensional ANSYS FLUENT CFD (computational fluid dynamics) model of flow across a pair of hot and cold heat exchangers that aims to explain the physics of phenomena observed in earlier experimental work. Firstly, the governing equations, boundary conditions and preliminary model validation are explained in detail. The numerical results show that the velocity profiles within heat exchanger plates become distorted in the presence of temperature gradients, which indicates interesting changes in the flow structure. The fluid temperature profiles from the computational model have a similar trend with the experimental results, but with differences in magnitude particularly noticeable in the hot region. Possible reasons for the differences are discussed. Accordingly, the space averaged wall heat flux is discussed for different phases and locations across both the cold and hot heat exchangers. In addition, the effects of gravity and device orientation on the flow and heat transfer are also presented. Viscous dissipation was found to be the highest when the device was set at a horizontal position; its magnitude increases with the increase of temperature differentials. These indicate that possible losses of energy may depend on the device orientation and applied temperature field.

1. Introduction and Literature Review

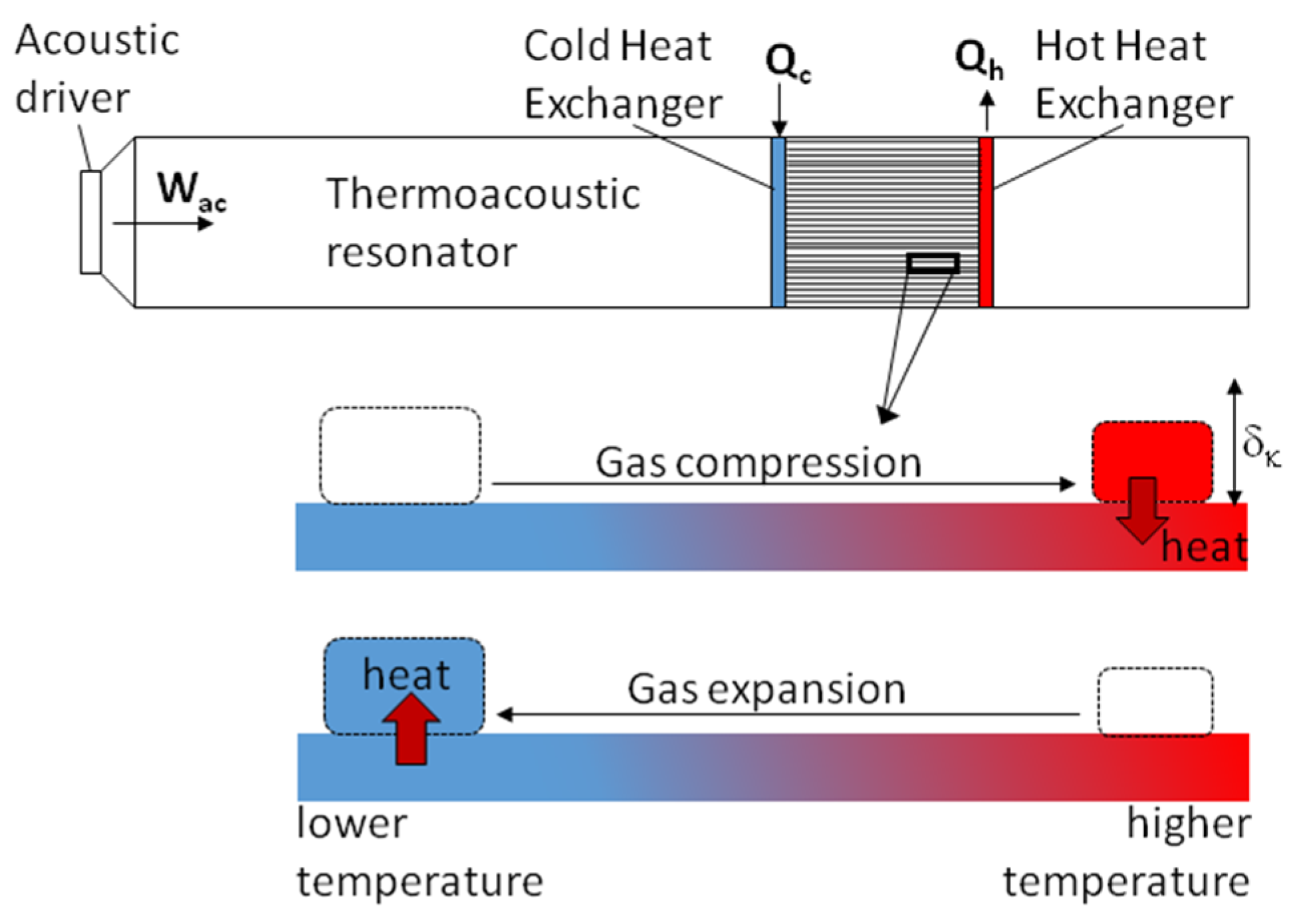
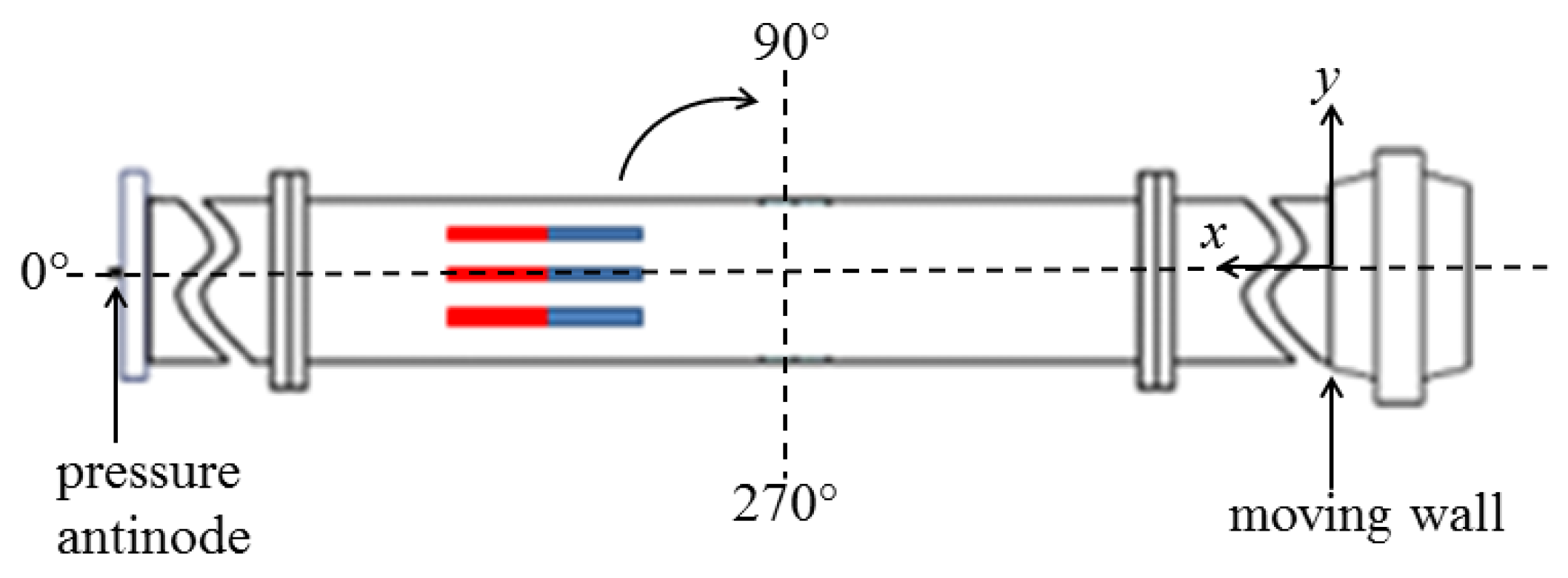
Thermoacoustic systems are usually divided into engines and refrigerators depending on the direction of energy conversion between the acoustic and thermal energy. The working principle of the thermoacoustic refrigerator is illustrated in Figure 1. The acoustic driver at the end of the resonator supplies acoustic power, $W_{ac}$, to the working gas inside the resonator. The standing wave acoustic field induces oscillatory motion of “gas parcels” coupled with their cyclic compression and expansion. Internal structures such as heat exchangers and stacks are placed at a location where the oscillating pressure and velocity are non-zero. A fragment of a single stack plate has been magnified at the bottom of Figure 1 together with a gas parcel undergoing an acoustic oscillation. The gas parcel is compressed as it moves to the right and the parcel temperature increases to be slightly higher than the plate temperature. Consequently, heat is being transferred from the parcel to the plate. As the flow reverses, the gas parcel expands and the temperature drops slightly lower than that of the plate. As a result, heat is being absorbed from the plate and the parcel returns to its original thermodynamic state. This completes the thermodynamic cycle. In essence, the acoustic wave provides power that allows the heat to be pumped up the temperature gradient. Conversely, if a high enough temperature gradient is imposed across the stack/regenerator, an acoustic power will be self-excited and useful energy will be produced [1]. This in turn could be extracted by a linear alternator to produce electricity, or used to drive a coupled thermoacoustic cooler.

The challenges in achieving efficient thermoacoustic devices were discussed comprehensively by Swift [1]. The difficulties with complex flows across the porous structures (stack, regenerator, and heat exchangers) that form the core of the thermoacoustic device have been raised as important research issues. Understanding phenomena such as vortex flow at the end of stacks [2], entrance effects [3], joining conditions [1], and streaming [4], is important as these could hold the key to an efficient device operation.

The structure of the vortex pattern, as observed for example by Mao et al. [5], is expected to influence the flow and possibly induce losses that may affect the efficiency of thermoacoustic systems. This has been illustrated through the observations of streamlines and viscous dissipation presented in the numerical investigation of Worlikar and Knio [6]. The viscous dissipation represents mechanical energy losses within the model. The choice of location for the stack/heat exchanger and blockage ratio (gap between plates) were reported as factors that influence mechanical energy losses.

The same group has made several improvements to their model [7,8,9]. These involve adiabatic stacks and heat exchangers, all working in a thermoacoustic standing wave environment. In all models, a simplified periodic configuration was used covering the area between the plates and some open area next to the plates to include the possible contribution from the vortex shedding phenomenon. The natural convection was assumed to be very small compared to the oscillatory flow magnitude, and was hence neglected. The effect of natural convection in an oscillatory flow has been previously tested in an experiment involving a heated wire located in an empty resonator [10]. The natural convection was found to dominate the flow under a small velocity regime. This result, however, is not very conclusive because the temperature difference investigated was not widely varied. Furthermore, it is speculated that the presence of additional structures such as the stack and heat exchanger may alter the influence of the natural convection effect on the flow even when the velocity is relatively small [11].

It is important to highlight that most numerical modelling work presented in this review applies a simplified model whereby a thin plate or a pair of adjacent plates with an implementation of periodic boundary conditions to replicate the array of plates is considered. In modelling, a periodic boundary condition means that the flows at the matching periodic boundary are linked so that flow conditions are shared at this boundary. As a result the flow will be duplicated for all other channels in a periodic manner [12]. While this has advantages in terms of computational cost, it must be carefully applied as it might give misleading information pertaining to the flow structure. This has been demonstrated experimentally by Guillaume and LaRue [13]. Their experimental results were later compared to a numerical model developed using commercial software, Fluent [14], using the same number of plates as in the experiment. Their works show that, for a structure with an array of plates, the flow structures at the end and in the middle of the plates are influenced by the adjacent plates. The Strouhal number (the ratio of a product of a characteristic length and the frequency of the vortex shedding to a reference velocity) is reported to have changed in magnitude when a comparison was made between the two arrangements. It is important to highlight here that the investigations reported in [13,14] were carried out in steady flow and might not be directly applicable to the oscillatory condition, but they do give an idea of possible sources of discrepancy if investigations of an array of plates are carried out using single plate approximation. The observation of asymmetry and non-periodic development of vortex structures at the end of a plate array was also reported by Mao et al. [5]. This suggests that a physical periodic structure (array of plates) does not guarantee that the flow structures are periodic. Hence modelling a single plate may not be adequate to describe the physics of flow around a structure with an array of plates.

Similarly, considering a single plate, the flow structures at two ends may not be identical in practice for reciprocating flows. Most investigations (cf., [7,9,12]) assumed that flows at the two ends are actually symmetrical and therefore the analysis was mainly focused on just one end. This seems reasonable for investigations that do not involve a temperature gradient (adiabatic stack). However, the presence of a temperature gradient on solid boundaries is necessary for the thermoacoustic effect to take place. Temperature effects must be considered to account for additional phenomena such as temperature-driven buoyancy [11,15,16,17,18] and non-linear effects [4] that could affect the flow symmetry. Experimental studies often reveal signs of nonlinearities that are insufficiently addressed by the linear model [1,11]. In most numerical studies (cf. [7,9,18]) the natural convection effect was neglected. This effect however was observed in many experimental works [1,11,17].

Current computational fluid dynamics (CFD) study aims to improve the understanding of physical processes involved in the phenomena reported in the earlier experimental work of Shi et al. [17]. However, bearing in mind more complex operating conditions (e.g., tilted-angle solar powered systems [19,20] or space applications), the scope of CFD is somewhat wider and extends to include gravity effects and effects of the device orientation on the physics of thermo-fluid processes across the heat exchanger plates. The novelty of this study stems from the fact that the model used attempts to take into account a far wider range of physical effects which are commonly neglected in numerical works related to thermoacoustics (i.e., natural convection or the use of a full array of plates to handle asymmetrical flow features). This is undertaken to explain the phenomena reported in [11,17]. In addition, the study of device orientation provides a new perspective of the importance of considering such seemingly minor details in modelling heat transfer phenomena in thermoacoustics.

2. Computational Model

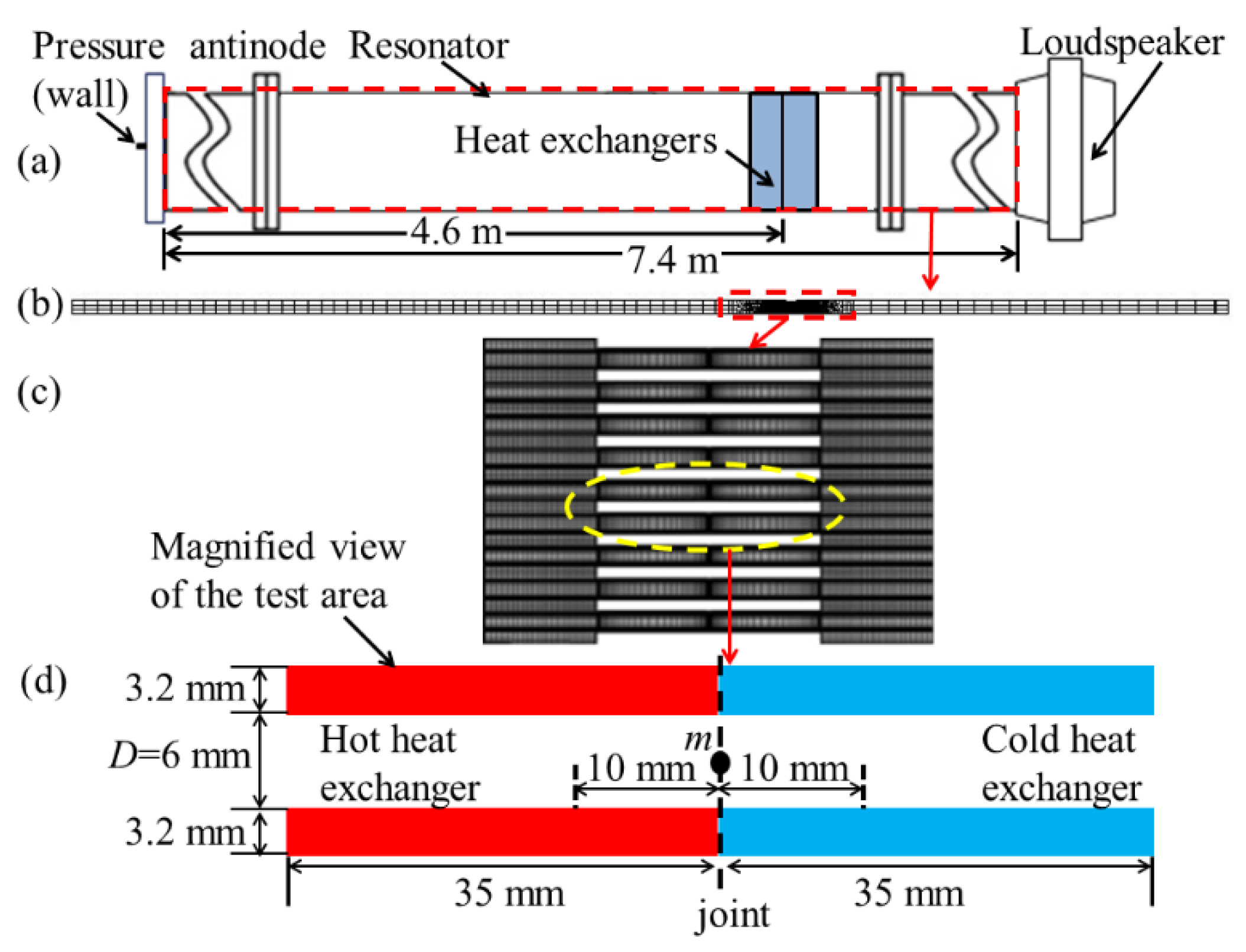
A two-dimensional computational domain based on the experimental setup of [11,17] is shown by the red-dashed box in Figure 2a. It covers a rectangular area of 0.132 m × 7.4 m of the quarter-wavelength resonator. The mesh is designed to be denser within the vicinity of the heat exchanger (300 mm to the left and right from the heat exchangers) to resolve vortex structures issuing from and returning into the heat exchanger assembly. Elsewhere, a much coarser mesh is adopted as the problem consists of solving the governing equations for an empty resonator. The coarse mesh is illustrated in Figure 2b and the fine mesh in Figure 2c. This approach was validated against the theoretical predictions of linear thermoacoustic theory [1]: 300 mm away from the heat exchanger, the pressure and velocity simply follow the linear model. A structured mesh of quadrilateral type was used for this model; the long computational domain is divided into several parts so that the distribution of mesh sizes could be made with acceptable quality. The minimum orthogonal quality was recorded to be 0.74 with maximum skewness of 0.31 (i.e., close to 1 for minimum orthogonality and close to 0 for maximum skewness [15]). The minimum mesh spacing in the x- and y-directions is 0.08 mm and 0.25 mm, respectively.

The plates of the hot and cold heat exchangers (subsequently denoted as HHX for “hot heat exchanger” and CHX for “cold heat exchanger” throughout the paper) have thickness, $d$, of 3 mm and are arranged in a parallel configuration with the spacing, $D$, of 6 mm between them. This is shown in Figure 2d as a magnified view of a single channel between a pair of hot and cold plates; point ‘m’ is the location of the joint where the hot and cold plates meet. The HHX and CHX are located next to each other with a joint positioned at $0.17\lambda$ from the pressure antinode. The wavelength, $\lambda$, is defined as $\lambda =a/f$, where $a$ is the speed of sound and $f$ is the frequency of the flow (13.1 Hz). Location of the pressure antinode for this 1/4-wavelength rig is at the end wall—cf. Figure 2a. The arrangement of the heat exchanger plates (10 pairs) follows the physical setup with five pairs of heated/cooled fins and five pairs of unheated ones, treated as adiabatic plates. The unheated plates provide consistent porosities for the flow (cf., [17]).

The model extends over the whole height of the resonator to resolve the flow asymmetries observed experimentally [17]. The use of symmetry or periodic boundary conditions is inappropriate due to the presence of temperature-driven buoyancy effects. In addition, the experimental data are based on phases determined by comparing the phase of the velocity between the plates to the phase of the pressure at the pressure antinode. As the intention was to replicate as closely as possible the phenomena taking place in the physical apparatus, a full two-dimensional model was chosen.

The boundary condition at the right end of the resonator is defined as a moving wall to replicate the acoustic displacement induced by the loudspeaker. The displacement, $\delta$, is simply modelled as:

$$\delta =\left[\frac{p_a}{\omega {\rho }_{m}a}\sin \left(k_w{x}_s\right)\right]\cos \left(\omega t\right).$$

(1)

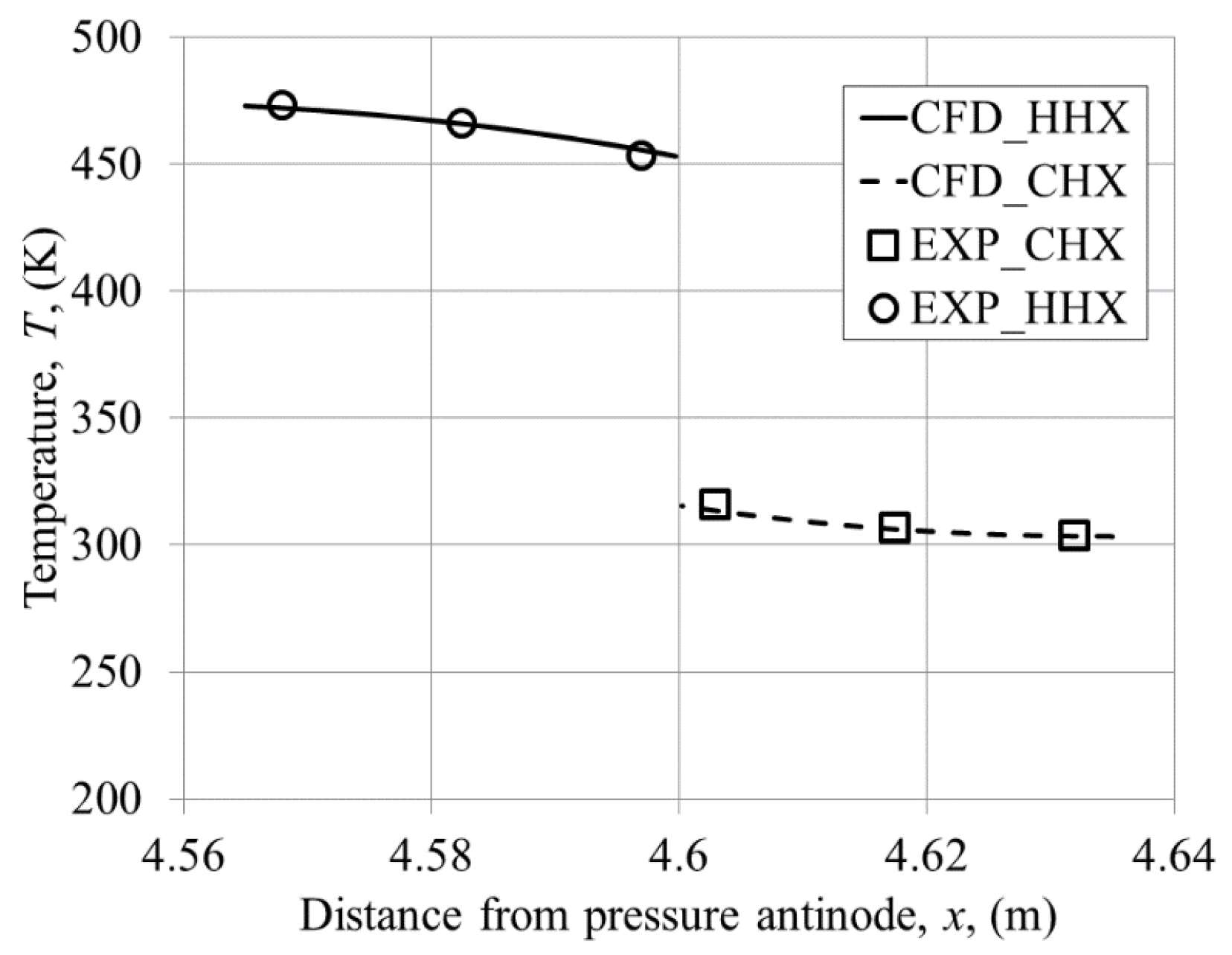
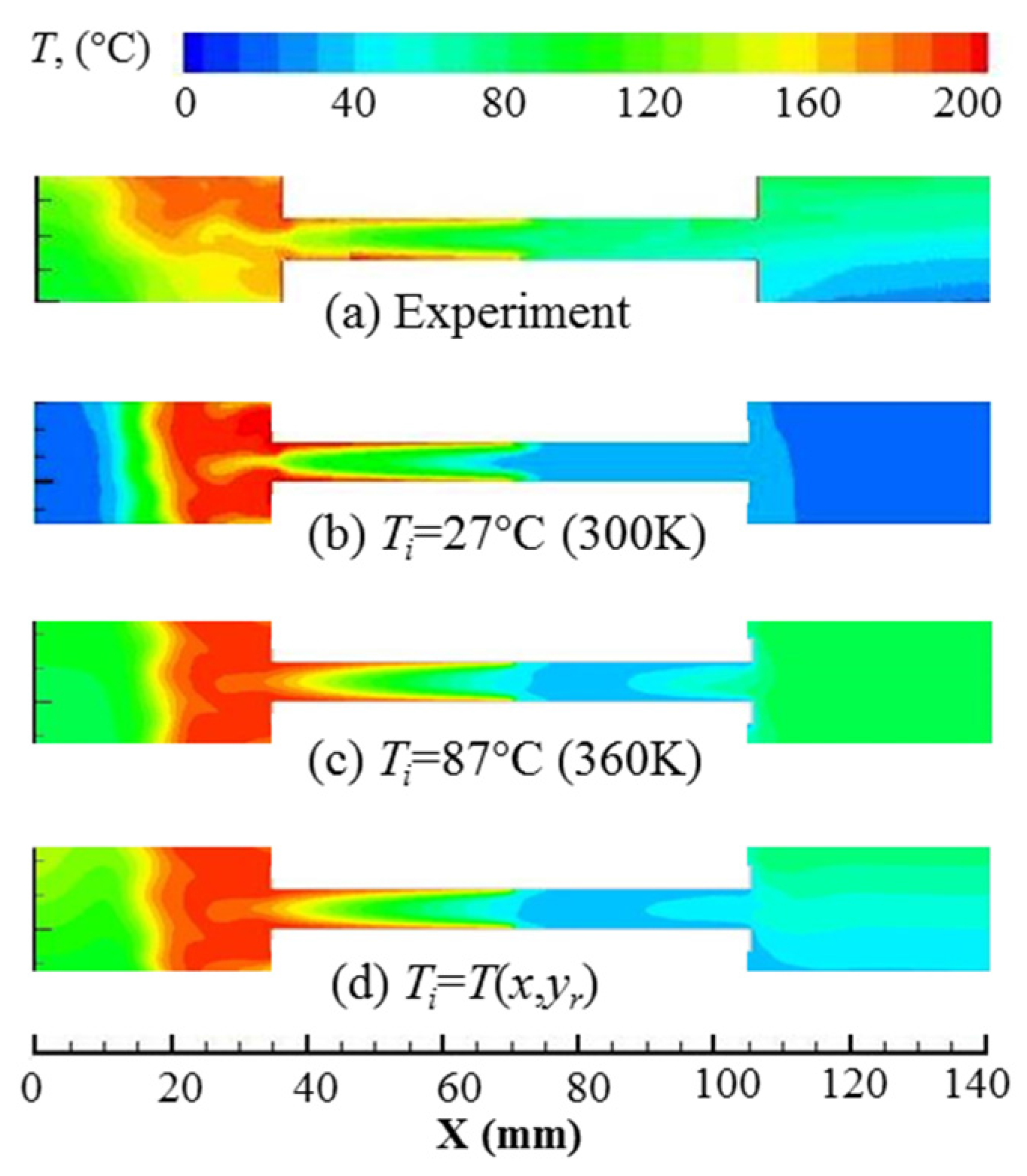
Here, $\omega$, ${\rho }_m$, $a$, $k_w$, and $t$ are the angular velocity, mean density, speed of sound, wave number, and time, respectively. The term $p_a$ is the oscillating pressure at the location of the pressure antinode and $x_s$ is the distance from the joint to the pressure antinode (shown as 4.6 m in Figure 2a). The mean pressure, $p_m$, is 0.1 MPa. The drive ratio, $p_a/p_m$, of the low amplitude flow investigated throughout this paper is 0.3%. The resonator wall was treated as adiabatic. The model was solved for two thermal conditions. In the first, the walls of heat exchangers are treated as adiabatic to replicate the experiments with no temperature gradient imposed on the heat exchangers (essentially ambient laboratory conditions), mainly to make comparisons between the experimental and numerical results for vortex structures. In the second, the temperature distributions were based on experiments using a linear interpolation of experimental data reported by Shi et al. [17], as shown in Figure 3, mainly for validation of the CFD model itself. Further extended studies into the system behaviour under arbitrary conditions assumed “flat” temperature profiles (as explained later).

The flow is modelled in ANSYS FLUENT [12] using two-dimensional Navier–Stokes equations as described by:

$$\frac{\partial \rho }{\delta t}+\nabla ·\left(\rho v\right)=0,$$

(2)

$$\frac{\partial }{\partial t}\left(\rho v\right)+\nabla ·\left(\rho vv\right)=-\nabla p+\nabla ·\left(\tau \right)+\rho g,$$

(3)

$$\frac{\partial }{\partial t}\left(\rho E\right)+\nabla ·\left(v\left(\rho E+p\right)\right)=\nabla ·\left(k\nabla T+\left(\tau ·v\right)\right).$$

(4)

The fluid used in this study is nitrogen modelled as an ideal gas with temperature-dependent properties. A power law model suggested by Swift [1] is used for the temperature-dependent viscosity while a seventh order polynomial model suggested by Abramenko et al. [21] is selected to model the temperature-dependent thermal conductivity:

$$\begin{gathered} p=\rho RT;\mu =1.82\times {10}^{-5}{\left(\frac{T}{T_0}\right)}^{0.69}; \\ k=-8.147\times {10}^{-4}+1.161\times {10}^{-4}T-1.136\times {10}^{-7}{T}^2+1.062\times {10}^{-10}{T}^3-5.406\times {10}^{-14}{T}^4+1.454\times {10}^{-17}{T}^5-1.942\times {10}^{-21}{T}^6+1.011\times {10}^{-25}{T}^7. \end{gathered}$$

(5)

In Equations (2) to (5), $\rho$, $v$, $t$, $p$, $g$, $E$, $k$, $T$, $T_0$, $\tau$, $R$ and $\mu$ are density, velocity vector, time, pressure, gravity, energy, thermal conductivity, temperature, reference temperature (300 K), stress tensor, gas constant and viscosity, respectively [12].

Viscous heating (the second term on the right-hand-side of Equation (4)) is taken into account in this model because of the presence of heat exchangers with large surface areas. The flow is assumed to be laminar due to the small Reynolds number involved in the case investigated. The Pressure-Implicit with Splitting Operators (PISO) algorithm is selected for pressure-velocity coupling as the algorithm provides better solutions for transient cases [12,22,23,24,25].

A first order implicit scheme is used for the discretisation of time due to the presence of the moving wall [12]. The momentum and energy equations are discretised using a second order upwind scheme with the convergence set to the absolute values of 1 × 10⁻⁴ for the continuity and momentum equation, and 1 × 10⁻⁷ for energy equation. The density is calculated using the second order upwind numerical scheme. Density is related to pressure and temperature by using the equation of state as shown in Equation (5). 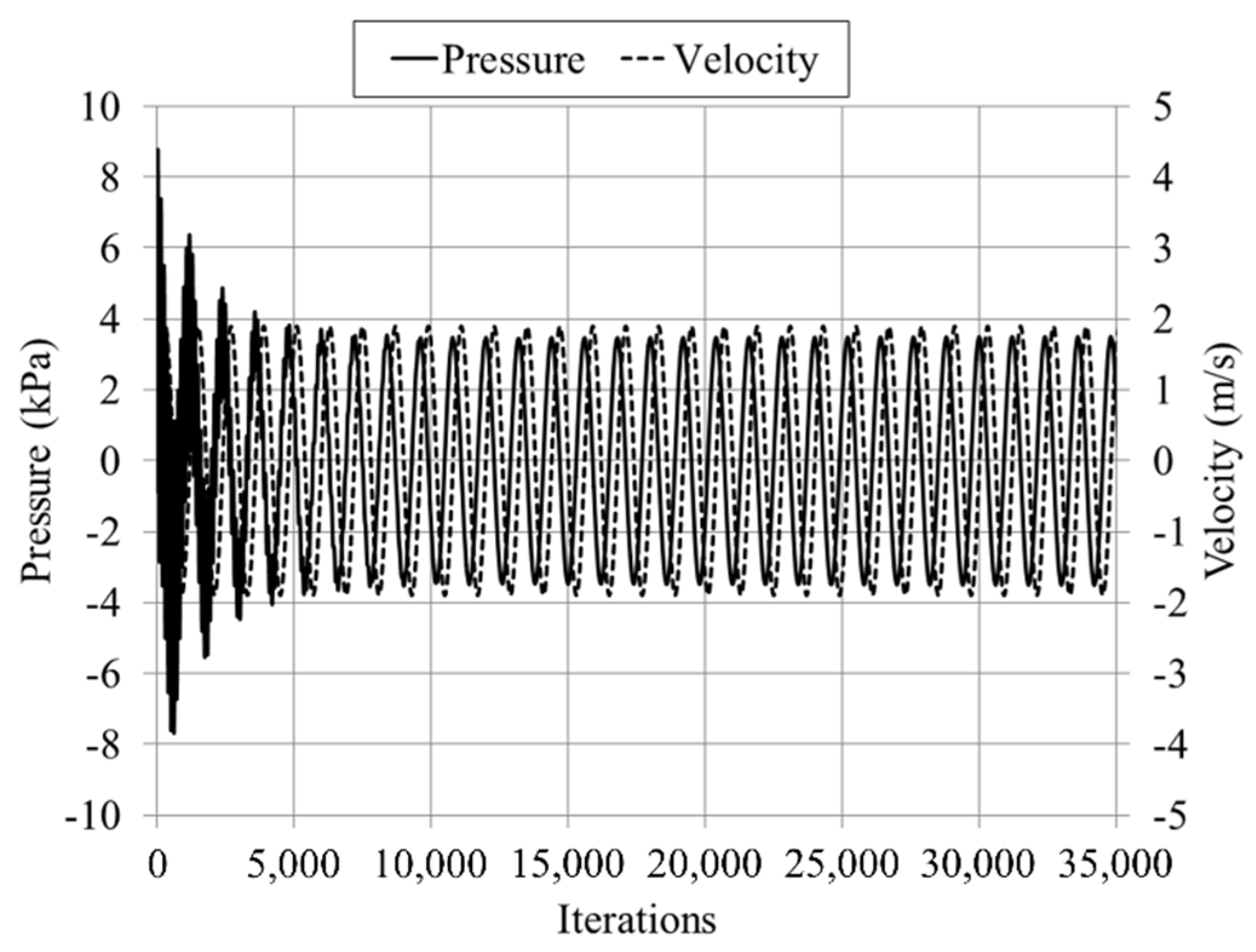The transient solution of the flow problem is solved in a segregated way using the pressure-based solver [12,25]. The time step size was chosen so that solution converged within 15 to 18 iterations in every time step. If the time step size was too large, the solution was found not to converge in every time step. If the size was too small, convergence occurred too fast within a certain time step (sometimes only requiring one iteration in one time step). The best time step for convergence was determined and set at 1200 steps per acoustic cycle. The area-weighted-average of pressure at the end wall, known as the pressure antinode, was monitored until a steady state oscillatory flow was obtained. This is defined as a state when pressure, velocity, and temperature do not change much from cycle to cycle. By way of example, Figure 4 shows the history of oscillating pressure and velocity monitored for location “m” as defined in Figure 2. A steady oscillatory flow condition is achieved after six flow cycles. However, as will be discussed later, results presented in this paper are obtained after 70 flow cycles, when both the flow and thermal oscillatory flow conditions have reached a steady oscillatory state. The solutions are also monitored so that they converge in every time step at every flow cycle (through the selection of the time step size).

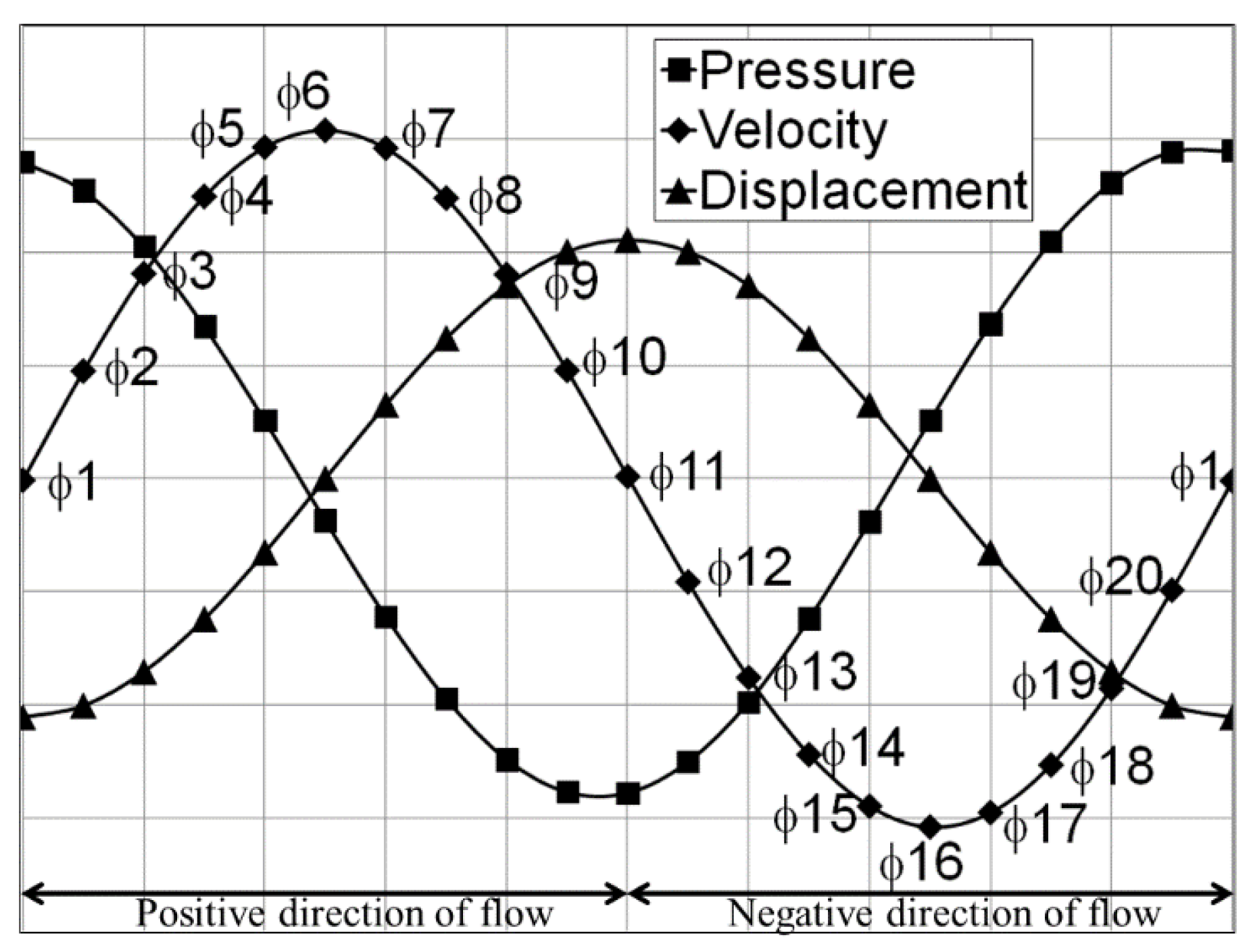
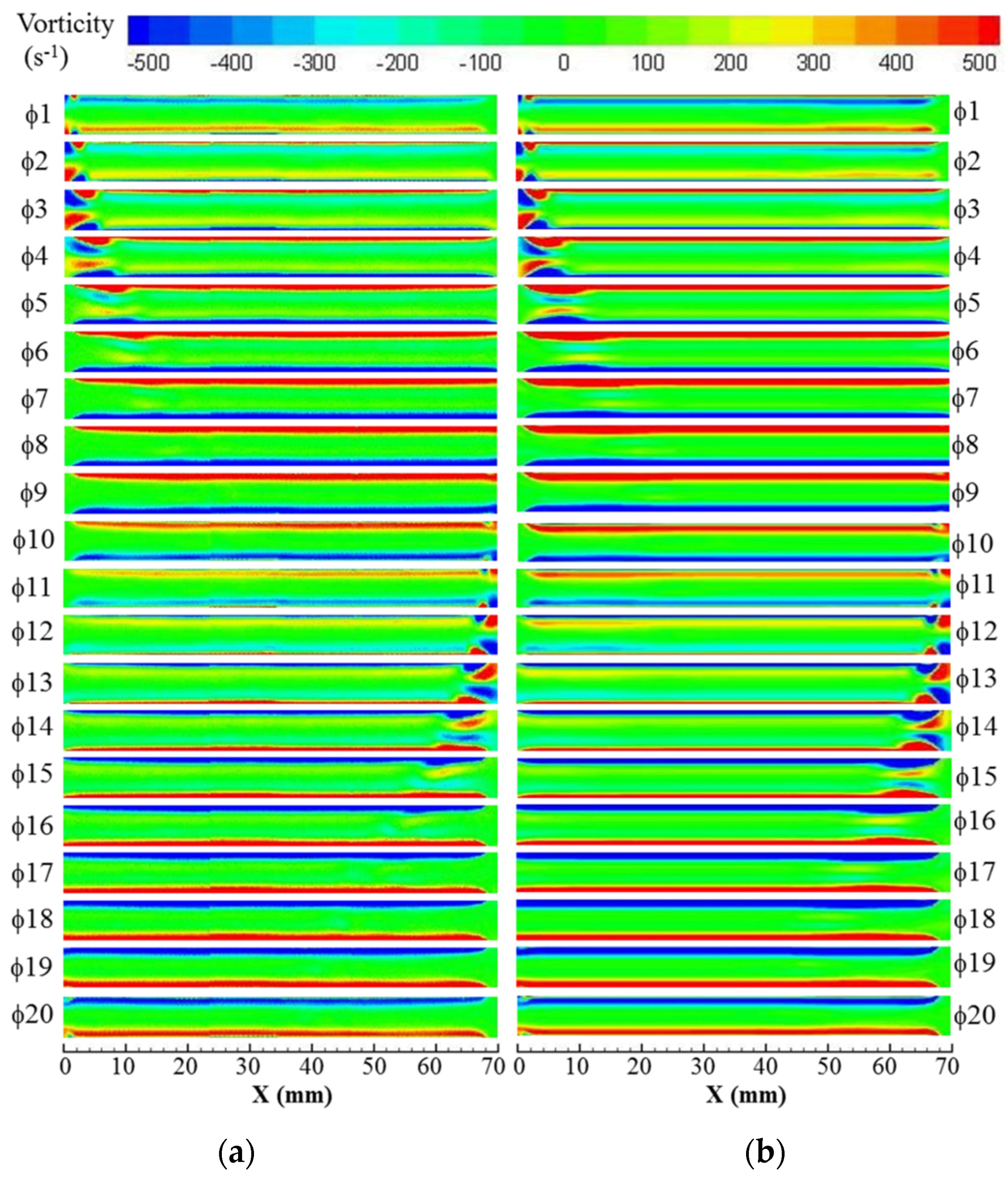
When the steady oscillatory state condition is reached, the model is validated and used for analysis. In this study, the development of flow within one oscillatory cycle is investigated according to the time frame defined in Figure 5. The cycle is subdivided into twenty phases starting from the first phase, $\mathsf{\varphi }$1. The relationship between pressure, velocity, and gas displacement, for the 20 phases of a flow cycle is illustrated. Phase $\mathsf{\varphi }$1 is set for the maximum value of the oscillating pressure at the location of the pressure antinode (rigid wall of the resonator). The period of one cycle is the inverse of the operating frequency—13.1 Hz.

The model was solved using the SPECTRE High Performance Computing facility at the University of Leicester (4 login nodes for solving one model, with 28 cores of 56 threads and 256 GB memory per one login node). With this computing facility, the 2D unsteady calculation for one cycle takes about 30 min. Therefore the solution for 490 cycles (as discussed later) takes about 9.5 days.

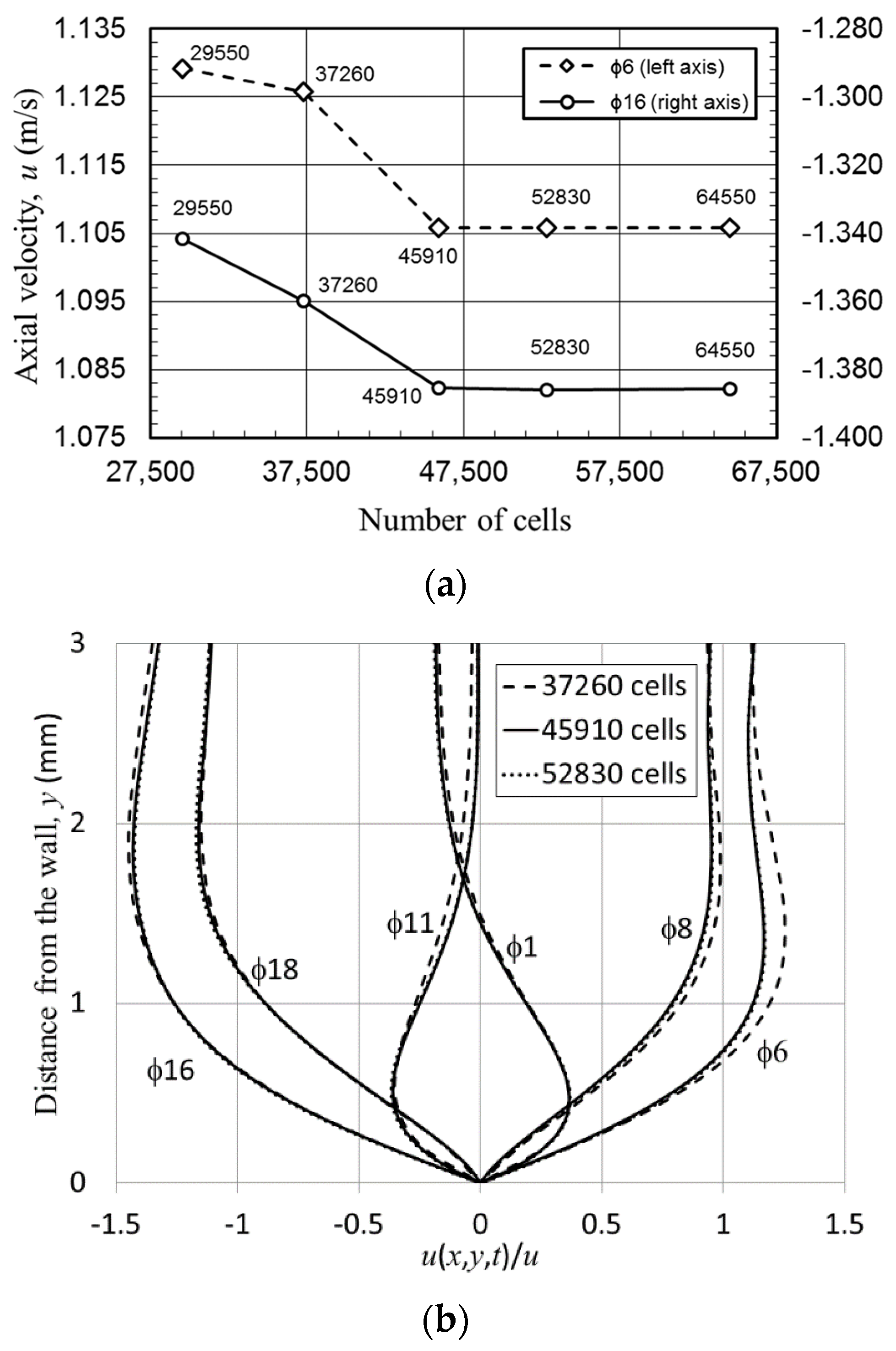
2.1. Grid Independency

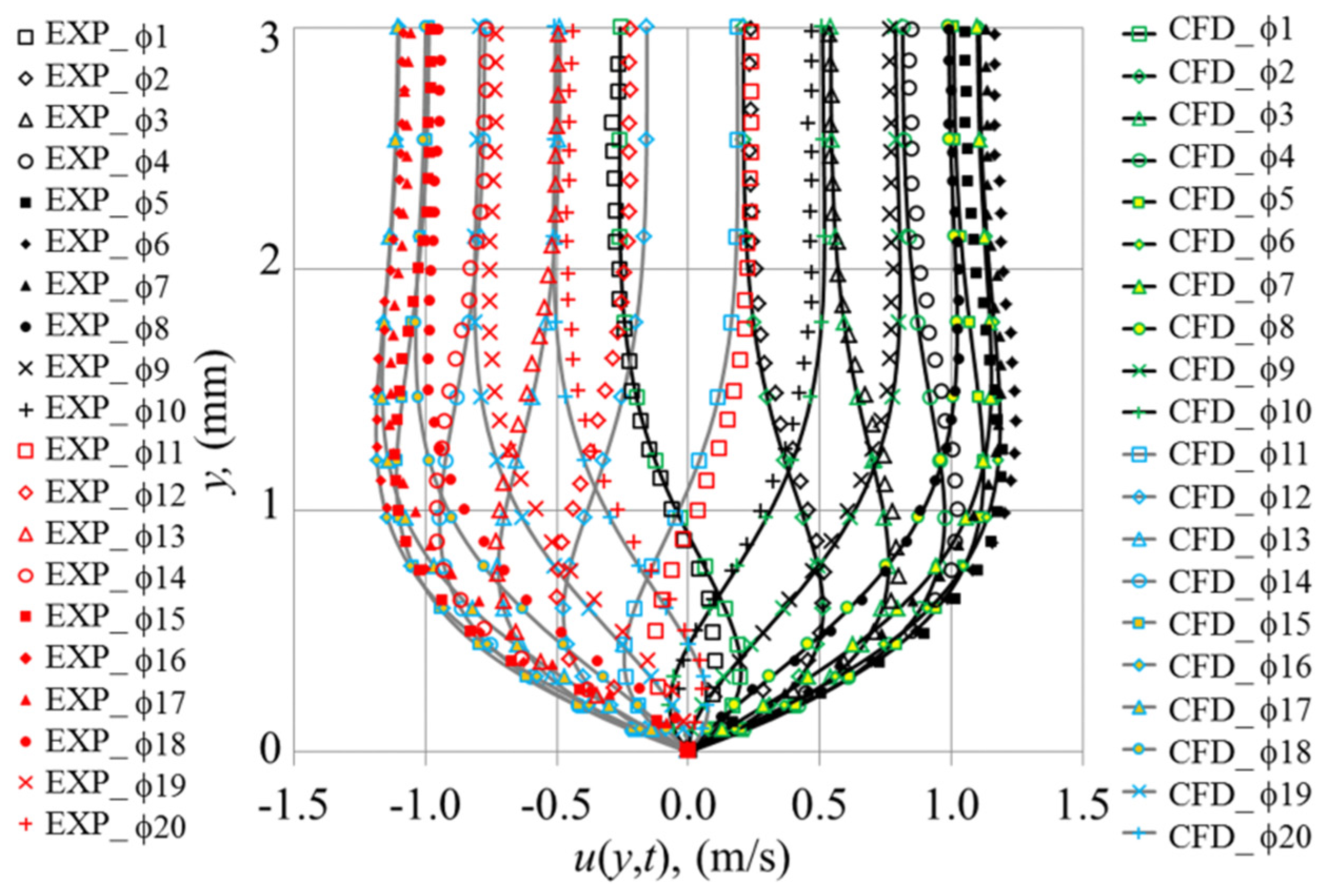
The grid independency tests are illustrated in Figure 6. In essence, the mesh was progressively refined in the part of the domain surrounding the heat exchangers (there was practically no need to do this in an empty resonator). The description of mesh density is given as cell counts in Figure 6a for five cases. Here, the velocity values at point “m” for phases 6 and 16 are taken as test variables (+ve and −ve values due to the change of direction). Similarly, the resulting axial velocity profiles (from the wall to channel centre), for selected phases in the cycle are further illustrated in Figure 6b. For clarity, velocity profiles are shown only for three cell counts. At low mesh density, the velocity profile is slightly over-predicted at all 6 phases shown. The velocity within the boundary layer appears to be the same for all cases because the mesh is always designed to be denser in that area. It is found that the model with a total of 45,910 cells is sufficient to provide a grid-independent solution.

2.2. CFD Model Validation

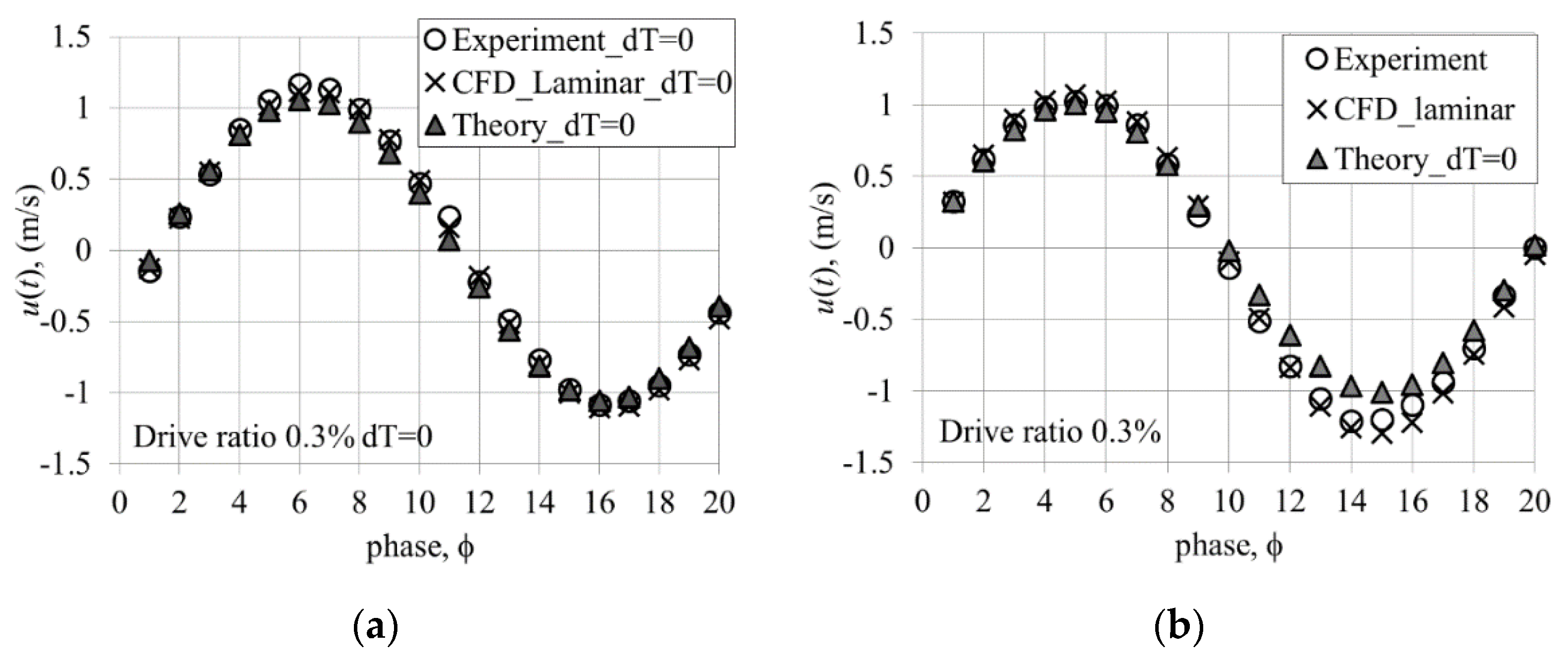
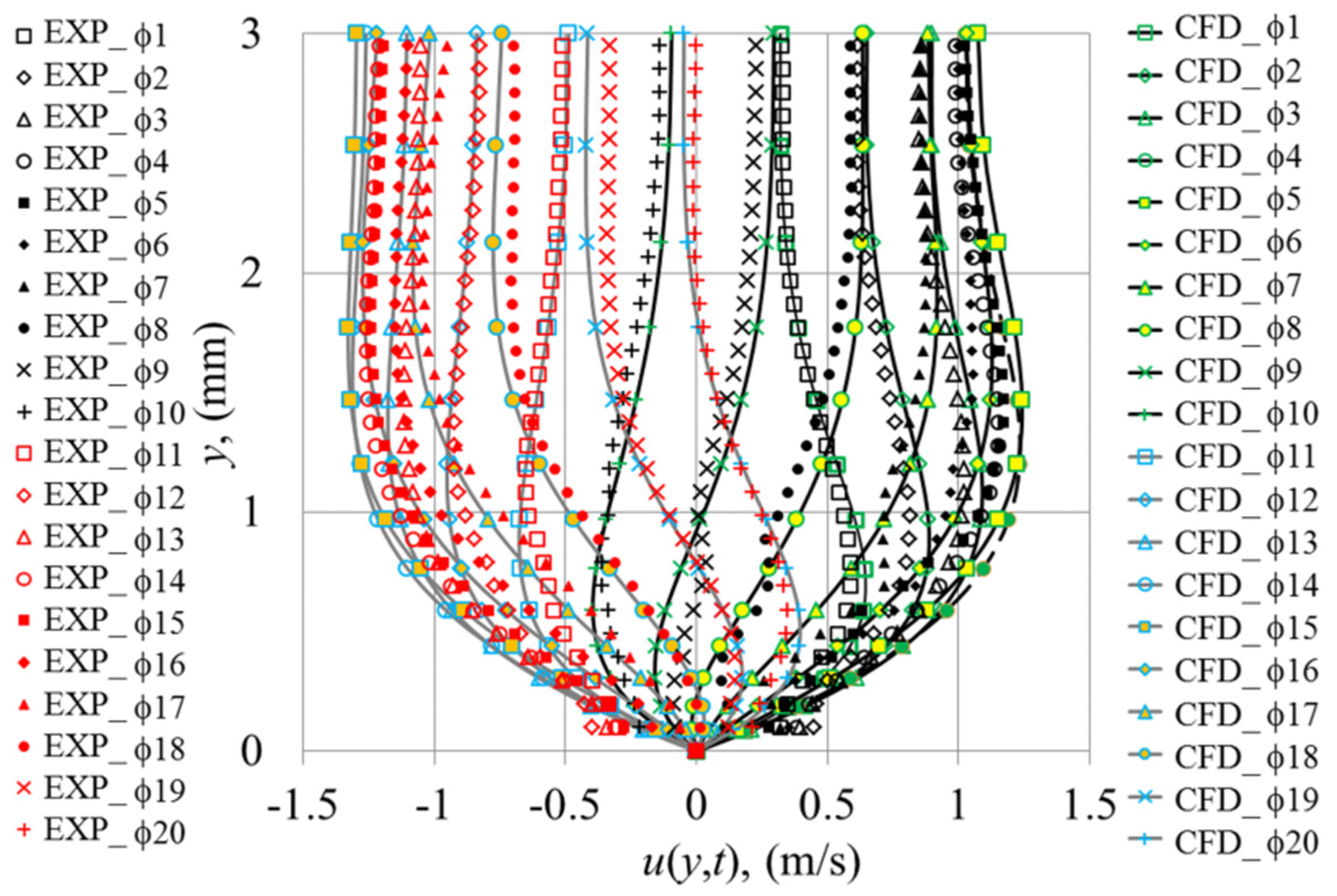
The velocity amplitude obtained from the converged model that reaches a steady oscillatory state is compared to the experimental result to validate the model. The velocity amplitudes shown in Figure 7a,b are for the location at the centre of the gap between the plates of the heat exchanger, 1 mm away from the joint—cf., Figure 2c—for all 20 phases in a cycle. In both graphs, the line denoted as “Theory_dT = 0” represents the theoretical/analytical solution for oscillatory velocity calculated from the general thermoacoustic theory as given by [1]:

$$u_1=\frac{i}{\omega {\rho }_m}\left[1-h_{\upsilon }\left(y,z\right)\right]\frac{\partial p_1}{\partial x},$$

(6)

where $\omega$, ${\rho }_m$, and $\partial p_1/\partial x$ are the angular velocity, mean density, and the pressure gradient of the oscillatory flow, respectively. The term $h_{\nu }$ is a viscous shape factor which varies according to the geometry of the internal structure involved in the system. The shape factor for parallel plate geometry is given as [1]:

$$h_{\kappa ,\nu }=\frac{\cosh \left[\left(1+i\right)y/{\delta }_{\kappa ,\nu }\right]}{\cosh \left[\left(1+i\right)y_0/{\delta }_{\kappa ,\nu }\right]}.$$

(7)

The shape factor defines the viscous, $\nu$, or thermal, $\kappa$, effects depending on the definition of the penetration depths used. The terms: $y$, $y_o$, and ${\delta }_{\kappa ,\nu }$ are the distance from the centre of the gap to the wall of the plate, the centre of the gap, and the thermal (${\delta }_{\kappa }=\sqrt{2\kappa /\omega }$) or viscous (${\delta }_{\upsilon }=\sqrt{2\upsilon /\omega }$) penetration depth.

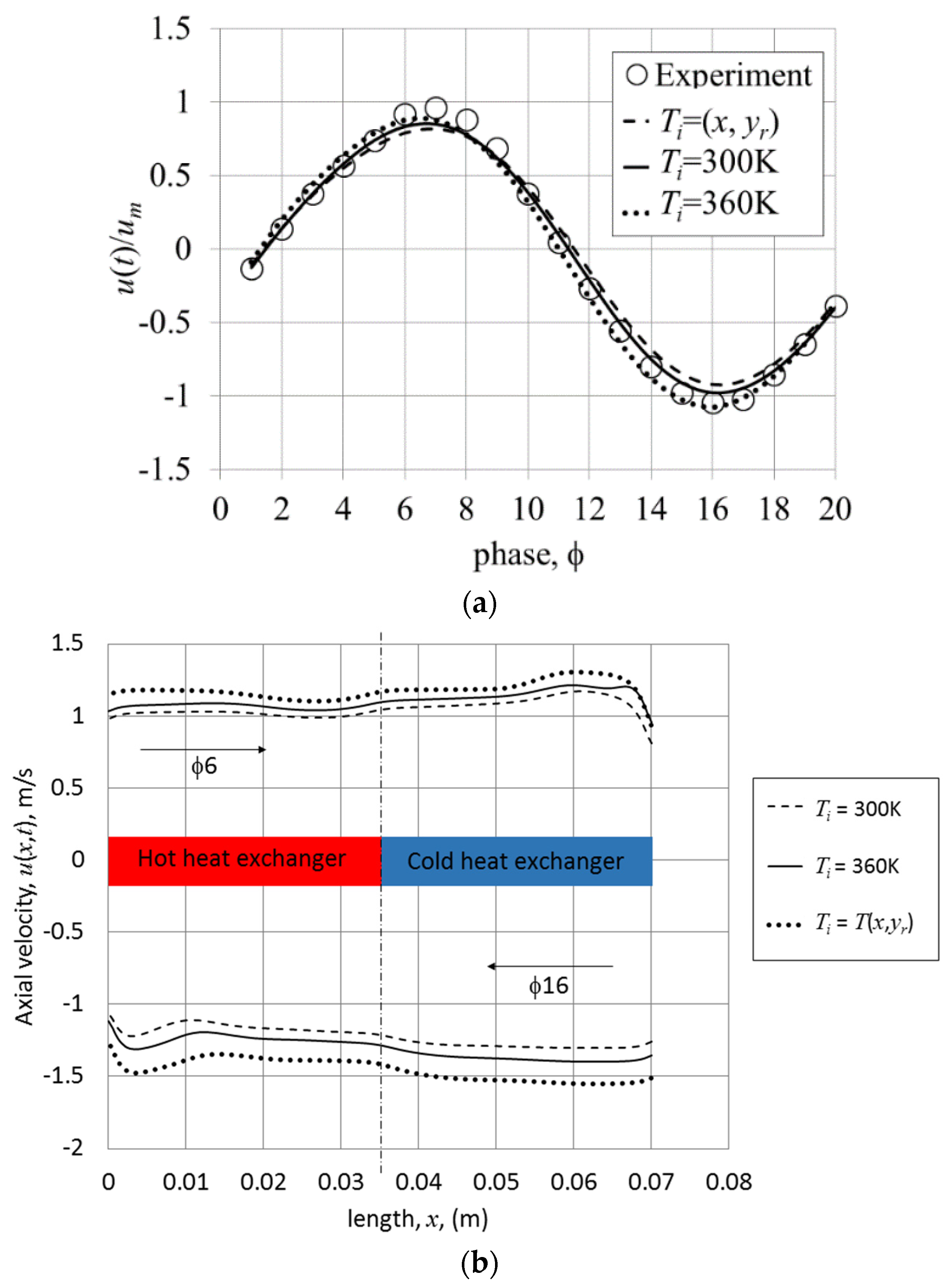
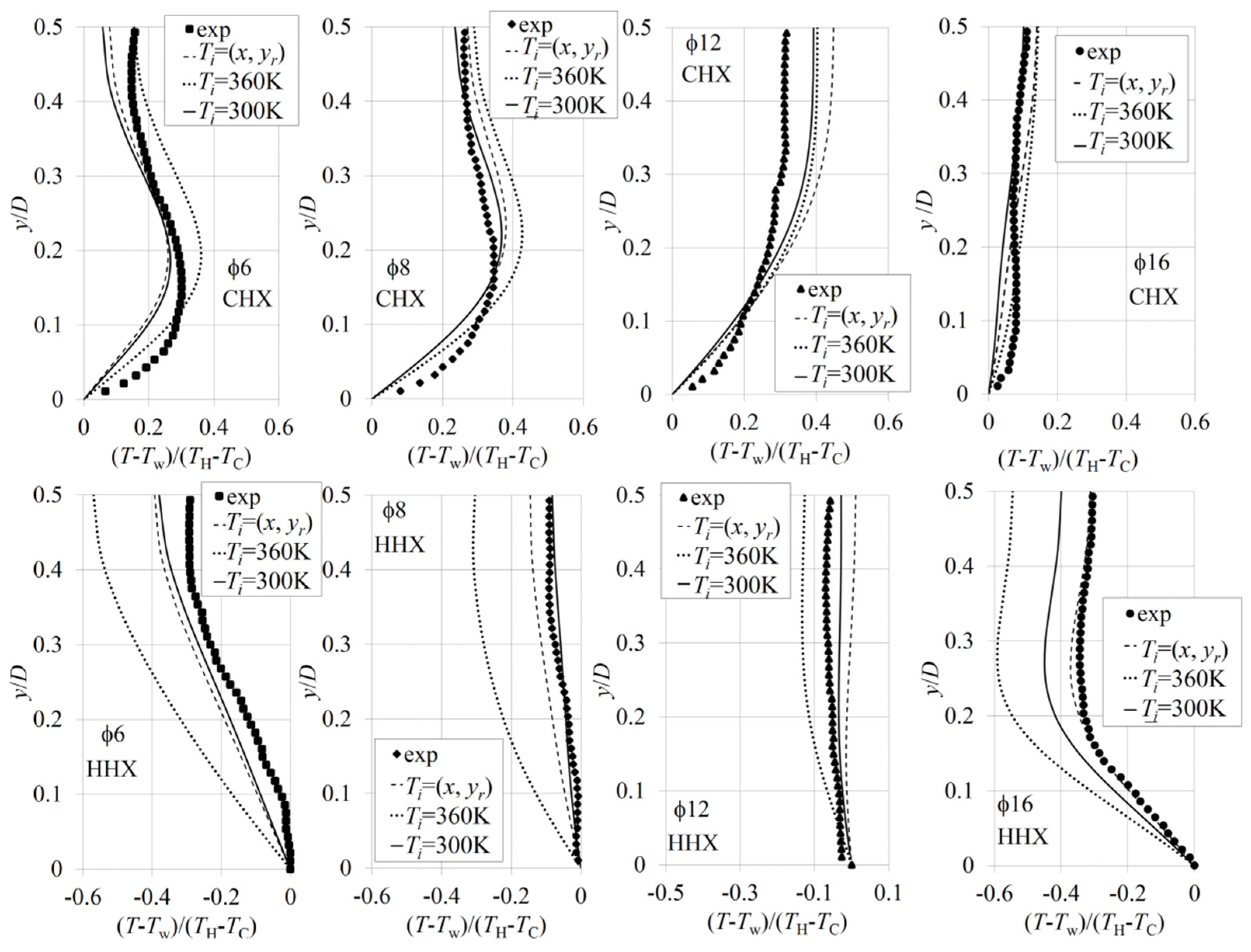
Figure 7a, for the adiabatic case, compares the experimental results of Shi et al. [11] (“Experiment_dT = 0”) with the current numerical results (“CFD_Laminar_dT = 0”). The theoretical solution is calculated for the mean density taken at 300 K. A good match between the experiment, CFD, and analytical solution can be seen. Maximum discrepancies between the three methods appear at phases $\mathsf{\varphi }$6 and $\mathsf{\varphi }$16 representing the highest velocity values for the two parts of the flow cycle. Comparison between the theory and experiment shows that the theoretical value is 9.3% lower than the experimental value at $\mathsf{\varphi }$6, and 2.6% lower at $\mathsf{\varphi }$16. However, CFD results differ from the experimental results only by 0.3% and 1.8% for $\mathsf{\varphi }$6 and $\mathsf{\varphi }$16, respectively.

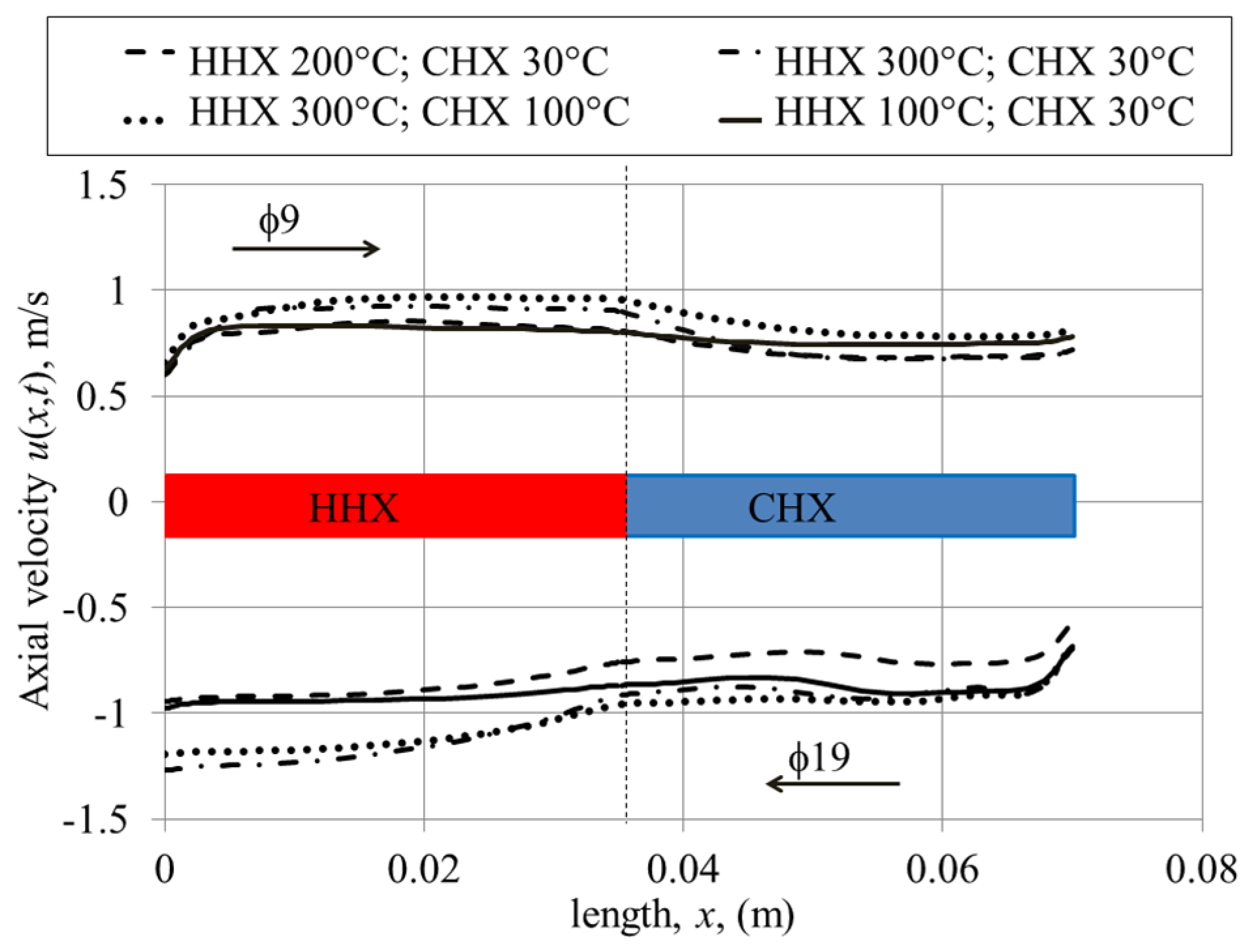
Figure 7b shows the velocity oscillations obtained from the experiment and CFD for the case with imposed temperature difference (the theoretical adiabatic solution is only plotted for reference). Experimental and CFD results show that, with the imposed wall temperature condition, the flow in the second half of the cycle exhibits a larger amplitude of velocity compared to the first half of the cycle. This is counterintuitive since one would expect that a hotter fluid would travel with higher velocity in the first half of the cycle, while cold fluid would flow with a lower velocity in the second half of the cycle. However it is possible that there is a mean flow along the channels (streaming effect) due to the convective currents as discussed later in Section 3.2.2.

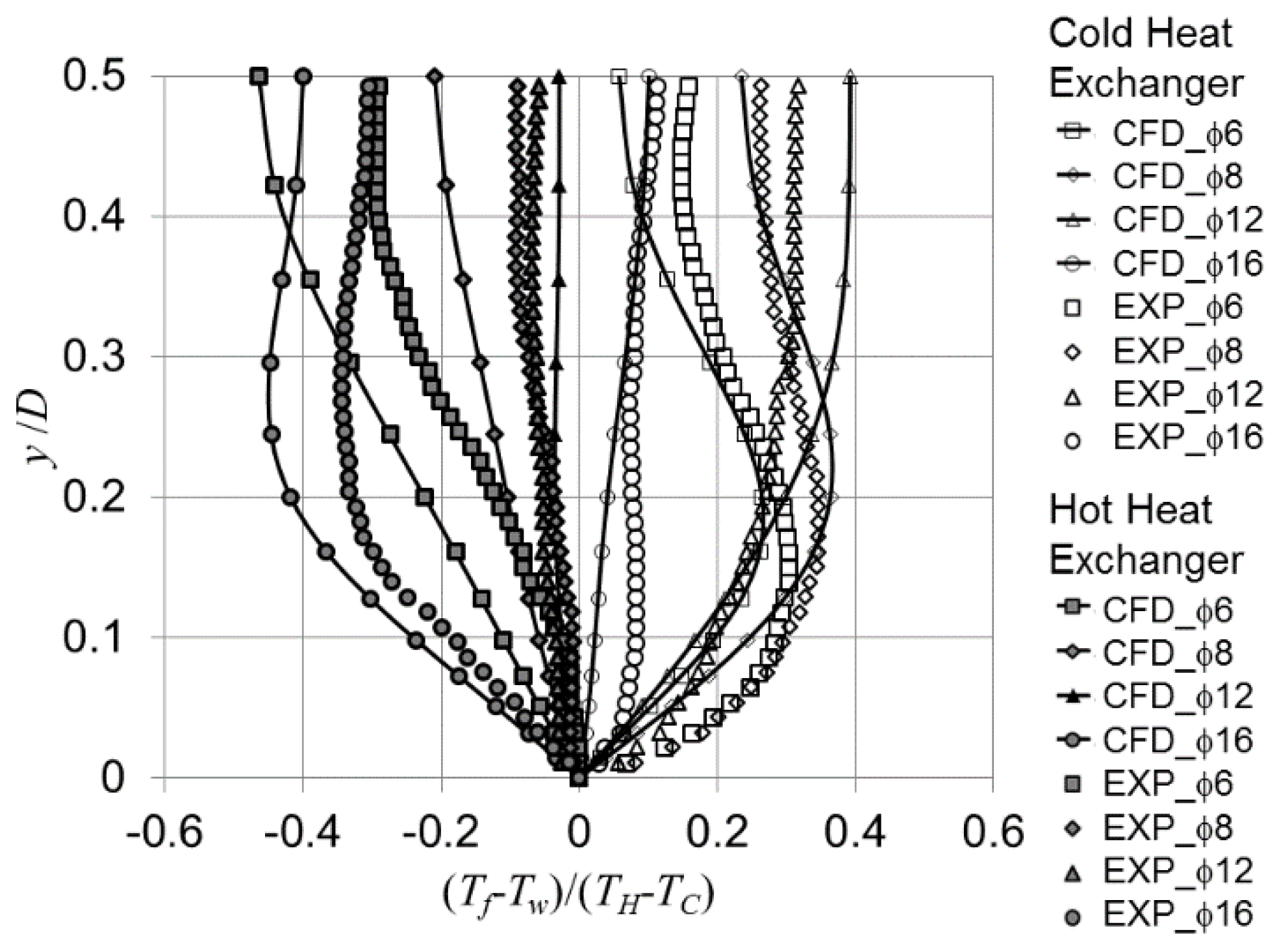
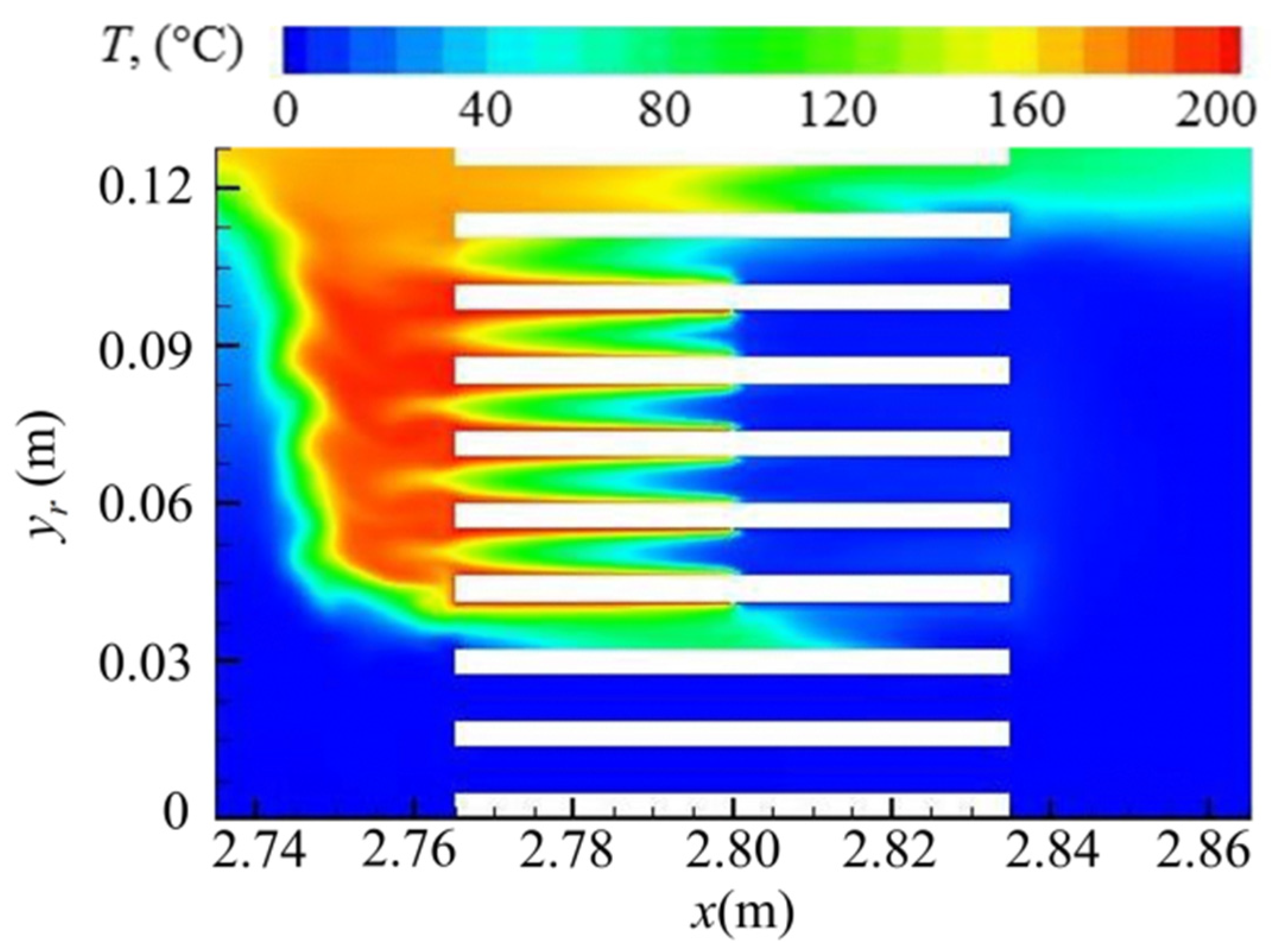
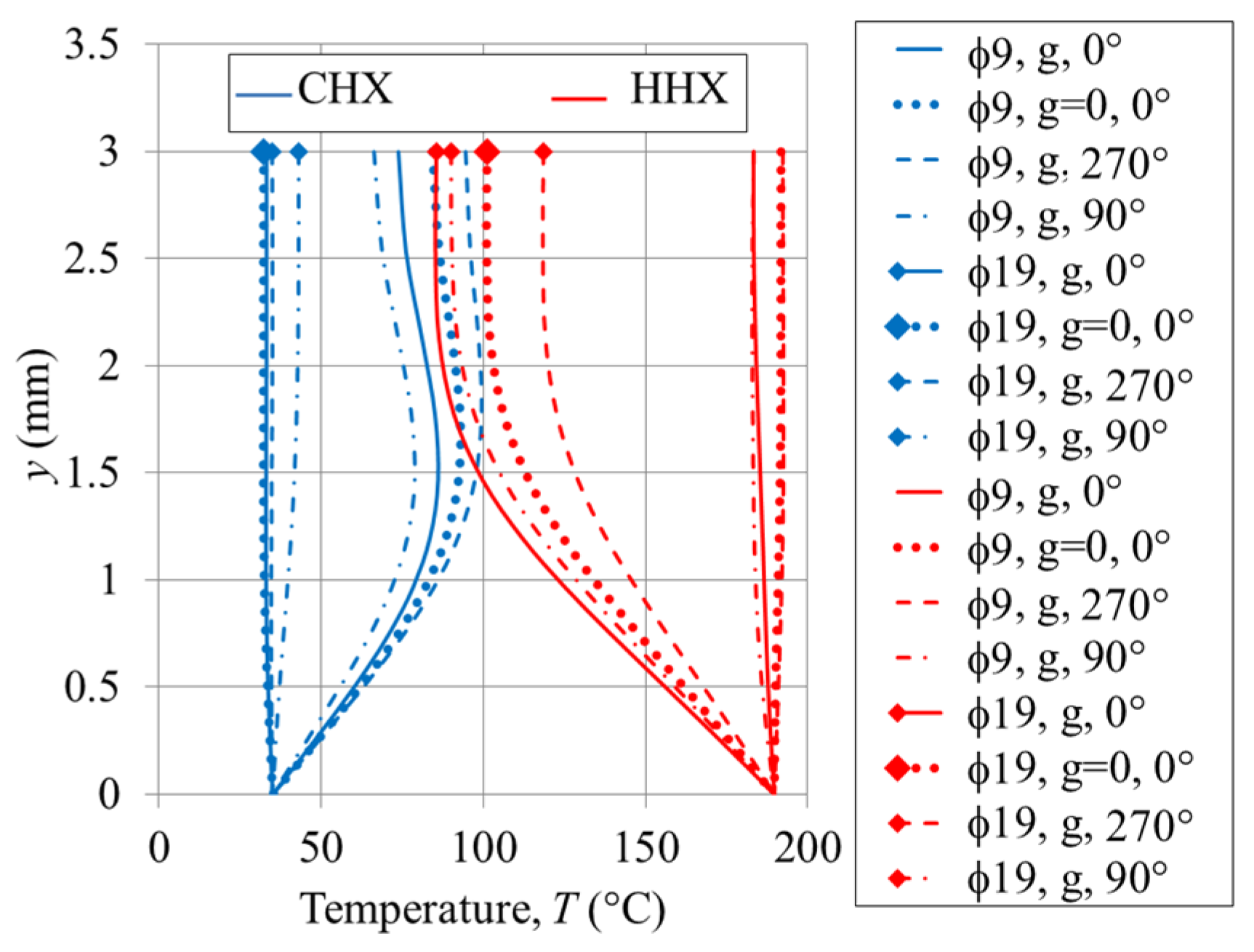
Figure 8 shows the validation of temperature profiles for a location 15 mm from the joint—cf., Figure 2c—above both the cold and hot plates. The maximum relative discrepancies of 6% were found between the numerical and experimental values when using the absolute temperature scale (17 K on the HHX and 18 K on CHX). However these discrepancies need to be seen in the context of high experimental uncertainty of the temperature field when using acetone based planar laser induced fluorescence (PLIF) method (16 K reported in [17]) as well as a large temperature span between the heated and cooled plates—cf. 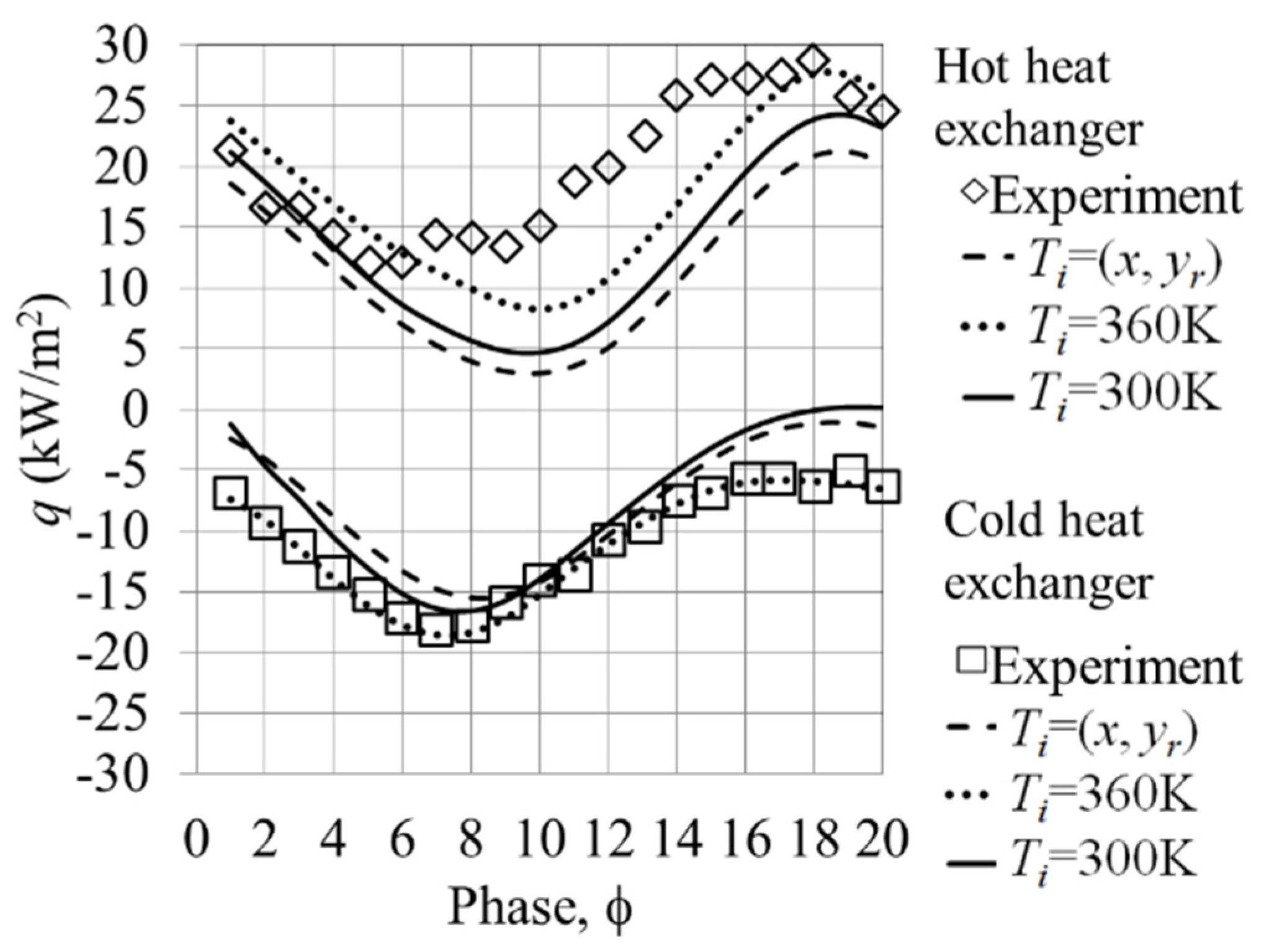Figure 3. Clearly, the trend of the temperature profiles agrees very well qualitatively with the experimental values. Indeed, the original PLIF experiments were more concerned with temperature gradients than absolute temperature values in order to calculate surface heat fluxes.

Of course, even if the temperature measurement had zero error, there would still inevitably be discrepancies in CFD arising from the inability to model all aspects of the physical process. For example, in reality the walls of the rig are not adiabatic, and in addition they do accumulate heat and tend to induce thermal inertia processes with the scale of hours. The role of the three-dimensional flow effects within the system is also unclear—unfortunately, the experiment could only provide “planar” results close to the resonator centreline.

3. Results and Discussions

Results presented in this paper look at four aspects of CFD modelling: the choice of temperature field initialisation, the effects of wall temperature on the flow field, device orientation relative to gravity force and viscous dissipation.

3.1. Investigation of the Effect of the Initial Fluid Temperature on Flow and Heat Transfer

The current CFD study deals with flow fields with relatively high imposed temperature gradients which results in difficulties to achieve numerically a temperature field similar to that obtained from the experiment. A possible way of bringing these close to each other, within a reasonable computational time, was through setting an appropriate initial fluid temperature in the model. Three approaches were investigated and these are discussed below. Their outcomes are illustrated for phase $\mathsf{\varphi }$1 in Figure 9; the experimental data shown in Figure 9a are compared against CFD data in Figure 9b–d.

First, the model was initialised with a uniform fluid temperature, $T_i=300\mathrm{K}$. The model was iterated until it reached 70 flow cycles which is equivalent to 5 s of real time. Figure 9b shows that the resulting temperature field is still dominated by the low temperature of the initial 300 K. On the other hand, the experimental data in Figure 9a show that the average fluid temperature is considerably higher due to the fact that the experimental data was collected after the flow has conveniently settled in the steady oscillatory state. At that stage, the heat has been accumulated in the system giving rise to the mean temperature of the flow. For the computational model with initial temperature of 300 K, a significant amount of computational time and effort would be required if a similar heat accumulation as in the experiment were to be achieved.

Second, the model was initialised with a uniform fluid temperature close to the mean temperature from the experiments, $T_i=360\mathrm{K}$ and was similarly iterated for 70 cycles. Although the resulting temperature field in Figure 9c is closer to the experimental results, the effect of natural convection in the open area next to the CHX is not visible in the computational result. In addition, the temperature of the fluid within the channel of the CHX reduces from the initial high temperature to a lower temperature due to the cooling effect at that location. The reason for the mismatch is not clear, especially as the wall of the heat exchanger is already modelled following the temperature measured by the thermocouples as reported in the experimental work [17]. However, it is possible that additional features need to be introduced into the model such as heat losses (the modelled resonator is adiabatic, in reality there are considerable heat losses), heat accumulation, or heat leakages. The known issues of experimental temperature uncertainties need to be borne in mind too.

The third approach tried to improve the predictions of natural convection observed experimentally at the plate ends by initialising the model with an approximate temperature field estimated from the experimental results ($T_i\approx T\left(x,y_r\right)$). The resulting temperature contour after 70 cycles is shown in Figure 9d. The effect of the initialisation temperature seems to dominate the temperature field especially at the open area next to the plates. In the area between the plates of the heat exchanger, the wall temperature seems to control the temperature within the area.

Figure 10 shows the effect of initial temperatures on the velocity amplitudes at a location 1 mm away from the joint above the cold plate. Evidently, a higher mean temperature of 360 K results in a slightly higher amplitude of the velocity, especially during the second half of the cycle. This may suggest that the experimental temperature field is affected by the accumulation of heat within the investigated area since raising the initial temperature from 300 to 360 K brings the solution closer to the experimental results. The same observation can be made for all locations along the heat exchanger plate as illustrated in Figure 10b. The velocity amplitudes at $\mathsf{\varphi }$6 and $\mathsf{\varphi }$16 shown in Figure 10b represent the highest velocity amplitude during the first and second parts of the flow cycle. The velocity amplitude for the model initialised at 360 K is always higher than the other two models for all the locations along the heat exchanger plate.

Finally, the effect of initial temperature on the heat flux is shown in Figure 11. Here, the heat flux is spatially averaged over the length of the heat exchanger (the same way as in [8]), and is presented as a function of time (phase in the cycle):

$$q_{h,c}=\frac{1}{l}{{{\displaystyle \int }}_0^l-k\frac{dT}{dy}|}_{wall}dx.$$

(8)

Subscripts $h$ and $c$ refer to HHX and CHX, respectively. The results were taken at cycle 70 after the model reached a steady oscillatory condition.

Overall, the space-averaged wall heat fluxes from CFD are in-phase with the experimental values at both heat exchangers. However the magnitude differs at the HHX, especially when the flow starts slowing down at $\mathsf{\varphi }$6 and changes direction. The numerical space-time-averaged wall heat flux is calculated to be 30% lower than the experimental values. However, the difference is within the range reported in other numerical investigations [26]. The wall heat flux predicted by the model initialised at 360 K seems closest to the experiment. Also, the predictions for CHX seem to follow the experiment better. The above discussion shows that the choice of initial temperature field is an important factor in the model, and it may lead to difficulties with convergence and accuracy.

Figure 12 shows the temperature profiles plotted along the vertical direction $y_r$, between the bottom and top wall of the resonator, at locations in the open areas: 40 mm from the cold end and 38 mm from the hot end of the heat exchangers, that is where most of natural convection effects are identified experimentally. Clearly, initialising the temperature at 360 K (dotted lines) gives the wrong values of temperature especially at the lower area of the domain compared to the experiments. Initialising the temperature field as $T\left(x,y_r\right)$ (dashed lines), seems to give a closer match in this area.

Finally, it is interesting to look at the development of the temperature field as a function of the number of cycles taken in the solution. Here the model initialised at 300 K is taken as an example; the temperature profiles are plotted in Figure 12 for increasing the total number of cycles as coloured lines between the dash-dotted black line (45 cycles) and solid black line (490 cycles). The temperature profiles seem to tend towards the experimental values. However, the changes become smaller and smaller (especially after about 70 cycles) and it is unlikely that the profiles would ever reach the experimental data. Following this observation, all the models used in the analysis reported in this paper were run for at least 70 cycles so that the steady oscillatory thermal condition is reached from a practical point of view, in addition to the steady oscillatory flow condition reported in Figure 4.

Figure 13 shows the temperature field within and around the heat exchanger assembly for the initial temperature of 300 K after 490 cycles. This illustrates the convective currents at both the hot and cold ends to supplement Figure 12. The heat accumulation phenomena shown in Figure 13 were also seen in [8]. The results illustrate a potential source of streaming in thermoacoustic systems [1] caused by buoyancy driven flows, which may interfere with the main thermoacoustic processes.

Figure 14 shows the temperature profiles plotted from the heat exchanger wall to $y=D/2$ (centre of the channel between the plates) at a location 10 mm from the joint above both the hot and cold plates. These are plotted for selected phases in the cycle ($\mathsf{\varphi }$6, $\mathsf{\varphi }$8, $\mathsf{\varphi }$12, and $\mathsf{\varphi }$16) for the experiment and three temperature initialisation cases, after 70 cycles. The top four plots are for the cold plate; the bottom four plots are for the hot plate. An initial temperature of 360 K leads to profiles with magnitudes larger than the experiment and it was already shown that it models the natural convection in the open areas poorly. The use of temperature distribution $T\left(x,y_r\right)$ provides solutions almost similar to a model initialised at 300 K. Both offer temperature profiles closer to the experiment. However, from the practical perspective of experimental accuracies, it would be hard to obtain the actual experimental temperature distributions for the sake of CFD, and therefore all subsequent models developed in this study are initialised at 300 K and iterated for 70 cycles.

Figure 15a shows the experimental temperature contours for all twenty phases of the cycle inside the channel formed by the HHX and CHX walls, while Figure 15b shows the CFD solutions for the same “viewing area” as used in the experiment. Qualitatively, there seems to be a fairly good agreement between the two in terms of flow physics. The differences in magnitude, particularly at the right side of the viewing area, are mainly due to the difficulty of achieving numerically the experimentally recorded mean temperature of the flow. However the trends of the temperature distributions are the same for all phases in the cycle. Hot fluid starts flowing into the channel from the left during the first part of the cycle ($\mathsf{\varphi }$1–$\mathsf{\varphi }$10). As the flow reverses ($\mathsf{\varphi }$11–$\mathsf{\varphi }$20), the cold fluid starts flowing from the right. The temperature within the channel is bounded by the experimental temperature profile set at the cold plate (cf. Figure 3). Therefore achieving higher mean temperature within the cold channel, as observed in the experiment, cannot be obtained under the current numerical time integration and modelling. Of course the discrepancies between CFD and the experiments may come from a variety of sources including the already discussed experimental errors as well as incorrect assumptions behind the numerical model compared to reality, e.g., the already discussed adiabatic boundary conditions, heat accumulation (vs. leakage) problems, or unknown (and experimentally unverifiable) three-dimensional effects.

3.2. The Effect of the Heat Exchanger Wall Temperature on the Flow Field

The presence of the temperature field introduces new elements to the flow physics including natural convection, stronger forced convection due to gas thermal expansion, or thermo-viscous interplay in the boundary layers. A few different sets of thermal boundary conditions were applied to heat exchangers, as summarised in

Table 1. Wall temperature condition of the heat exchanger.

Drive Ratio (%)	Working Medium	Frequency (Hz)	Mean Pressure (bar)	Heat Exchanger Wall Temperature (°C)
				Hot, ${\mathit{T}}_{\mathit{H}}$	Cold, ${\mathit{T}}_{\mathit{C}}$
0.3	Nitrogen	13.1	1	Adiabatic	Adiabatic
				200	30
				100	30
				300	30
				300	100

. Here, the temperature profile was assumed to be “flat” as only one case had experimental data available. However, this particular case ($T_H$ = 200 °C, $T_C$ = 30 °C) was solved in two ways: first, with the wall temperature from Figure 3, for code validation, and second, with the “flat” temperature profiles to compare between different numerical cases. The drive ratio (defined as the ratio of pressure at the antinode to the mean pressure) of the flow is maintained at 0.3%.

3.2.1. Study of Flow Using the Adiabatic Model

The investigation of flow across the parallel plate structure starts with a model where the walls of the heat exchangers are treated as adiabatic. The resulting velocity profiles plotted at a location of 1 mm from the joint above the cold plate are shown in Figure 16 for comparison to the experimental results of Shi et al. [11]. The agreement with the experimental data is very good. Figure 17 shows the contours of vorticity, ${\omega }_z$, plotted for selected phases of the oscillatory flow, obtained as:

$${\omega }_z=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y},$$

(9)

where $u$ and $v$ are the velocity components in the $x$ and $y$ directions of the flow. The contours are plotted within the same “viewing area” as in the experiment [11]—cf. also Figure 2d. For phases $\mathsf{\varphi }$1 to $\mathsf{\varphi }$10, the fluid is flowing into the channel from the left; for phases $\mathsf{\varphi }$11 to $\mathsf{\varphi }$20 from the right. At the beginning of the cycle, a pair of small vortices appear at the entry to the channel followed by a pair of stronger counter-rotating vortices, which appear to “leap-frog” the original pair around phase $\mathsf{\varphi }$4. However, both vortex structures dissipate by about phase $\mathsf{\varphi }$8. A similar feature is present at the other end of the channel when the flow changes direction. The laminar model captures the features of the oscillatory flow at 0.3% drive ratio very well.

3.2.2. The Effect of Wall Temperature on the Flow and Heat Transfer

The effect of temperature on the flow and heat transfer is investigated by setting the heat exchanger wall temperatures to the values shown in Table 1. It should be noted that all comparisons to experiments were made using the model that applies the experimental temperature profiles of Figure 3 on the hot and cold plates (of course, except cases marked as “adiabatic” or “dT = 0”). However, for the sake of comparisons between numerical cases, “flat” temperature profiles were set up, as already mentioned in the introduction to Section 3.2. Figure 18 shows the comparison between the experimental and numerical velocity profiles for the flow at the location of 10 mm from the joint above the cold plate for comparable temperature gradients set up along the plates. The slight differences in the magnitude between the experimental and CFD data can be accounted for by the typical errors of particle image velocimetry (PIV), although it is worth mentioning that thermophoresis which affects seeding particles in the presence of temperature gradients [27] can also have an additional impact on the experimental data.

As shown in Figure 9a, buoyancy effects are observed in the experimental results. The heat supplied by the HHX causes reduced density of the fluid, which results in a buoyancy driven flow in the open area next to the HHX superimposed on the forced convection due to the flow being ejected from the channel by acoustic excitation as well as thermal expansion of the fluid travelling in the hot part of the channel. These temperature effects are likely contributors to the flow asymmetries observed in Figure 7b. These effects are also seen through a comparison of velocity profiles between the models with and without the temperature gradient imposed on the heat exchanger walls (cf., Figure 16 vs. Figure 18).

The above asymmetry can be observed in two ways: Firstly, the whole structure of the velocity profile plotted in Figure 18 seems to be “leaning” to the left in comparison to Figure 16. This is clearly illustrated in Figure 19, where the presence of temperature makes the velocity profile of $\mathsf{\varphi }$9 and its counterpart in reversed flow, $\mathsf{\varphi }$19, “lean” to the left.

Secondly, the maximum magnitude of velocity fluctuation extends further to the centreline when temperature effects are included in the model as seen in Figure 20a. In the absence of temperature effects (adiabatic wall condition shown in Figure 20 as dT = 0), the velocity profile is similar at both CHX and HHX. When the temperature effect is considered, the velocity profile at the HHX seems shifted up towards the centreline ($y$ = 3 mm) and the magnitude of the velocity is larger compared to an equidistant location at the CHX. On the other hand, focusing on one location, Figure 20b shows that the velocity profiles at the selected point of the CHX in analogous phases of the two flow directions (i.e., $\mathsf{\varphi }$9 vs. $\mathsf{\varphi }$19 here), are also affected by the presence of temperature effects. For ease of comparison, the axial velocity of $\mathsf{\varphi }$19 in Figure 20b is presented as a negative (−ve) value. The presence of temperature effects results in a lower centreline velocity at $\mathsf{\varphi }$9 but bigger magnitudes in the reversed flow direction at $\mathsf{\varphi }$19. The results indicate the changes in the viscous boundary layer due to the presence of temperature.

The asymmetry of the flow structure can be further illustrated through the vorticity contours at the open area next to the heat exchanger for three different wall temperature conditions (Figure 21, Figure 22 and Figure 23). The vorticity is plotted for two phases corresponding to the opposite flow direction ($\mathsf{\varphi }$1 and $\mathsf{\varphi }$11). For each phase, the contour is shown with two views of the two ends of the heat exchanger assembly.

Figure 21 illustrates the case of adiabatic conditions and it is clear that the flow around two ends of the heat exchanger assembly is symmetrical, without any noticeable buoyancy driven convective patterns. Figure 22 shows the structure of the vortices when there is a temperature difference imposed: 200 °C at the hot plate, and 30 °C at the cold plate. The symmetry of the flow is broken: as the viscosity of the gas increases with temperature, the thicknesses of the viscous penetration depth increases, as seen, for example, in different separations of the vorticity contours on the right and left ends of the channel, which is also congruent with the velocity profiles in Figure 19a. Consequently, the vortex structures rolling up on the two sides of the plate assembly differ in size and strength. However, in addition, the temperature-driven flow at the open area at the left introduces some differences in the vortex patterns between the top and bottom side of the plate—note the hot plume observed in Figure 9 and Figure 13 which adds a “cross-flow” (vertically upward) component relative to the hot fluid ejected from the channels. Interestingly Figure 22a, for phase $\mathsf{\varphi }$11, shows the artefacts of a vortex structure on the top of the hot plate, but not on the bottom. These flow features are strengthened in Figure 23, for temperature conditions of 300 °C at the hot, and 30 °C at the cold plates.

There are two more effects that could be speculated on: First, that the large vortex structures created on the left side of hot plates may provide additional resistance to the flow when it reverses and starts to move from left to right by “bottlenecking” the channel. The same effect may be at play on the right side of the CHX when the flow reverses and starts moving to the left, but such flow would only need to handle much smaller vortices. Second, the temperature driven flow in the open area to the left of the hot plates may lead to setting up a variety of convective “cells” (loops), which could be contained on one side of the plate assembly, but equally induce a local streaming current between the plates (some of these being also adiabatic plates above and below the heated/cooled channels). Both of these effects could be further contributors to breaking the flow symmetry in the acoustic cycle.

Figure 24 summarizes all studies with the varied temperature difference between the hot and cold plates (cf., Table 1) in terms of the centreline velocity amplitude along the length of the heat exchanger channel. Two selected phases, $\mathsf{\varphi }$9 and $\mathsf{\varphi }$19, representing the first half (flow to the right) and the second half of the cycle (flow to the left) are chosen, respectively; the legend with thermal conditions is shown at the top. The variation of the plots with varying thermal conditions is indicative of a very complex physics with a number of effects at play. Clearly, the variation of the channel wall temperature and corresponding gas expansion (or contraction) causes gas particles to travel to a different distance back and forth during its reciprocating movement, causing asymmetrical velocity amplitudes on the centreline. However, the exact shape of the velocity profile depends on thermal (and thus viscous) conditions across the oscillatory boundary layers causing velocity “overshoots” and “deficits”. These may correspond to the counterintuitive reduction in the centreline velocity for the cold channel in phase $\mathsf{\varphi }$9 when the case ($T_H$ = 100 °C, $T_C$ = 30 °C) is replaced by cases ($T_H$ = 200 °C, $T_C$ = 30 °C) and ($T_H$ = 300 °C, $T_H$ = 30 °C) and an increase for case ($T_H$ = 300 °C, $T_C$ = 100 °C). Similar counterintuitive phenomena can be seen in other places of Figure 24 for both selected phases. The already mentioned convection “cells” appearing across the overall domain and the varying size and structure of vortices rolling up on the plate ends (and subsequently sucked back into the channels) may also need to be considered as contributors to the appearance of plots in Figure 24.

3.3. The Effect of Gravity and Device Orientation on Flow and Heat Transfer

The orientations of the resonator, relative to the gravity field, investigated in this study are schematically illustrated in Figure 25 (the three pairs of plates are for illustration only—all ten pairs are included in the model as before). The direction of the gravity field is modelled accordingly following the orientation. 0° corresponds to the horizontal layout in the figure, 90° indicates the hot plates above the cold plates, and 270° indicates the hot plates below the cold plates. The case with gravity switched off (g = 0) is also considered for reference. Experimental temperature profiles shown in Figure 3 are applied at the cold and hot plates in the models.

Figure 26 shows the effect of gravity and device orientation (tilt angle 0°, 90°, and 270°) on the velocity profile plotted 15 mm from the joint above the cold and hot plates for selected phases $\mathsf{\varphi }$9 and $\mathsf{\varphi }$19. In order to differentiate between the data for the cold and hot channels, the lines for the velocity profiles at the hot channel are assigned a “diamond” symbol at the top end of the lines. The effect of gravity can be seen by comparing cases assigned as “g, 0°” (presented by solid-lines) and “g = 0” (presented by dashed-lines). For phase $\mathsf{\varphi }$9 (Figure 26b), the comparison shows that gravity has little effect on the flow structure in the horizontal orientation. However, the effect of gravity is seen to be larger at $\mathsf{\varphi }$19. Comparison between the magnitude of the velocity between $\mathsf{\varphi }$9 and $\mathsf{\varphi }$19 for both “g, 0°” and “g = 0” shows that the temperature-driven buoyancy flow seems to cause a stronger asymmetry between the first and second parts of the flow cycle. The temperature-driven flow due to gravity seems to significantly assist the flow at $\mathsf{\varphi }$19 and slightly resist the flow at $\mathsf{\varphi }$9.

For an orientation other than horizontal, the gravity field affects the flow depending on the direction of flow and the relative locations of the HHX and CHX. At an orientation of 90° (presented by the dashed-dotted lines), the cold plate is located below the hot plate resulting in a reduced velocity magnitude during $\mathsf{\varphi }$9 of the flow cycle, because the buoyancy effects are resisting the flow. As the flow reverses (shown as $\mathsf{\varphi }$19), the buoyancy effect is helping the flow. As a result, the velocity magnitude becomes bigger than that at the first half of the cycle.

Conversely, when the device is at an orientation of 270° (presented by the dotted-lines), the temperature-driven buoyancy effect assists the flow at $\mathsf{\varphi }$9 (Figure 26b), resulting in a higher velocity amplitude and hence a greater fluid displacement between the plates. At $\mathsf{\varphi }$19 (Figure 26a), the flow reverses and the temperature-driven buoyancy effect is resisting the flow. Consequently, the velocity amplitude within the channel is lower than that in the first part of the cycle. For all device orientations, the velocity amplitude within the hot channel is always bigger than that at the cold channel. This is a logical consequence of the temperature-dependent density as previously discussed.

The effect of gravity and device orientation on the wall heat transfer is shown in Figure 27. The heat flux is averaged over the length of the heat exchanger and is calculated using Equation (8). The effect of gravity is less pronounced in the CHX compared to the HHX. This is in accordance with the effect of buoyancy driven flow, which is more pronounced at the HHX compared to the CHX. These effects can be looked at from the point of view of temperature profiles shown in Figure 28. It can be seen that the orientation changes the temperature field depending on the location of the HHX, the direction of flow, and the resulting temperature-driven buoyancy effect. When the flow is moving in the positive direction ($\mathsf{\varphi }$9), the effect of device orientation on the temperature profiles is more pronounced at the CHX. When the flow reverses ($\mathsf{\varphi }$19), the effect appears to be more obvious at the location of the HHX. Natural convection effect at $\mathsf{\varphi }$19 for HHX is stronger than that at $\mathsf{\varphi }$9 for CHX because the ‘hot plume’ appears next to the HHX (as seen in Figure 13). This is congruent with the weak gravity effects on the heat flux at the CHX compared to the HHX as seen in Figure 27. Of course, at an orientation of 270° (dashed line), when the HHX is located below the CHX, the temperature between both the HHX and CHX increases due to the temperature-driven buoyancy effect. At an orientation of 90°, presented by a dashed-dotted line, the temperature between the plates and hence the wall heat flux is lower because heat is driven away from the plates of the heat exchanger by the buoyancy effect.

3.4. Viscous Dissipation

Typically, it is assumed that viscous dissipation effects play a small role for low speed flows. However, in the flow situations presented in this paper, the contribution of viscous dissipation due to the existence of internal structures within the investigated domain may be significant and hence it is considered here. Dimensional analysis presented in Appendix A reveals the dimensionless parameters that need to be considered. In particular, it is found that comparison between viscous dissipation in areas of empty resonator and heat exchanger plates should take into consideration porosity, $\sigma$, and Eckert number, Ec—cf., Equation (A7).

In a viscous flow, the energy of the fluid motion (kinetic energy) is transformed into the internal energy of the fluid through the existence of viscous dissipation. Viscous dissipation for a two-dimensional model is defined as [28]:

$$\mathsf{\Phi }=2\left\{{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2\right\}+{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}^2-\frac{2}{3}{\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)}^2.$$

(10)

The computational domain is divided into four regions defined in Figure 29. The normalised viscous dissipation is averaged over the cycle and space, $A$, corresponding to each region and calculated as:

$$\langle {\mathsf{\Phi }}^{*}\rangle =\frac{1}{2\pi A}{{\displaystyle \int }}_0^A{{\displaystyle \int }}_0^{2\pi }\left({\mu }^{*}{\mathsf{\Phi }}^{*}\right)d\varphi dA.$$

(11)

The term in the bracket on the right-hand-side of Equation (11) is calculated as follows:

$${\mu }^{*}{\mathsf{\Phi }}^{*}=\frac{1}{{\mu }_c}{\left(\frac{d_c}{u_c\sigma }\right)}^2\mu \left[2\left\{{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2\right\}+{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}^2-\frac{2}{3}{\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)}^2\right].$$

(12)

Following the dimensional analysis, the weighted-average value is further multiplied by the dimensionless parameters identified as porosity, $\sigma$, and Eckert number, $Ec$:

$$\langle \mathsf{\Phi }\rangle ={\sigma }^{2}Ec\langle {\mathsf{\Phi }}^{*}\rangle .$$

(13)

The reference velocity is taken at 300 mm from the joint of the heat exchangers (labelled as m in Figure 2 and Figure 29) towards the right end of the figure within the region called the “cold end”. The reference location is selected to avoid the influence of temperature on the open area next to the HHX, where a hot plume is observed. A value of porosity, $\sigma$, is appropriately used when calculating dissipation for the open area and the area of the heat exchanger following the earlier discussion. For the open area, the porosity is set to one while an appropriate value of porosity (0.65 for the geometry investigated) is used for the heat exchangers.

Figure 30 shows the effect of the heat exchanger wall temperature on the dimensionless viscous dissipation. The viscous dissipation at the open areas at both ends of the heat exchangers are one order of magnitude lower than the dissipation in the area containing the plates. This is consistent with the fact that the working medium interacts with more wall surfaces within the area of the heat exchanger where viscous resistance is significant, hence causing more energy dissipation. When the HHX becomes hotter, the dissipation becomes bigger. This is a consequence of gas viscosity that becomes bigger as the temperature increases. Figure 30b has an expanded y-axis to show dissipation levels at the ends of the heat exchanger assembly. It shows that the dissipation of energy at the open area next to the hot end is bigger than that next to the cold end and that it increases with an increase of temperature of the HHX. This is likely the combined effect of the larger gas viscosity at higher temperature and the more pronounced gravity-driven flow as seen by the development of the hot plume at that end.

Figure 31 shows that viscous dissipation is lower in all areas when the device is set at a vertical orientation. Gravity determines the flow direction of the hot plume. For vertical arrangements (90° and 270°), the temperature-driven flow is in line with the direction of the flow. The temperature-driven flow can either assist or obstruct the flow depending on the device orientation and the direction of flow within a flow cycle. This may affect the magnitude of the velocity as the fluid flows back and forth within the heat exchanger, but the gradients of velocity near the wall are approximately the same, as seen in Figure 26. However, the low dissipation of the device arranged at vertical orientation indicates that the combined effect of temperature-driven flow and the mean flow may help reduce the viscous dissipation that may relate to the re-circulation of the fluid. The horizontal arrangement (0°) results in a temperature-driven flow perpendicular to the direction of the flow. Hence, re-circulation tends to be bigger in comparison to the vertical arrangement.

4. Conclusions

The two-dimensional ANSYS FLUENT CFD model has been set up to investigate the oscillatory flow across the parallel-plate heat exchanger at the low drive ratio of 0.3%. The flow, as represented by the velocity profiles, is well predicted by the model. For example, the velocity amplitudes at the centre of the heat exchanger channel have a maximum discrepancy of 1.8% compared to the experimental data. On the other hand, the numerically calculated temperatures have the maximum discrepancies of 6% compared to the experimental values. The differences noted in the temperature profiles and the resulting heat fluxes are likely to be the result of the combination of factors related to experimental uncertainties and the inability of the model to capture all the complexities of the real experimental setup. Overall, the current model under-predicts the space-time-averaged wall heat transfer by up to 30% in comparison to the experimental values.

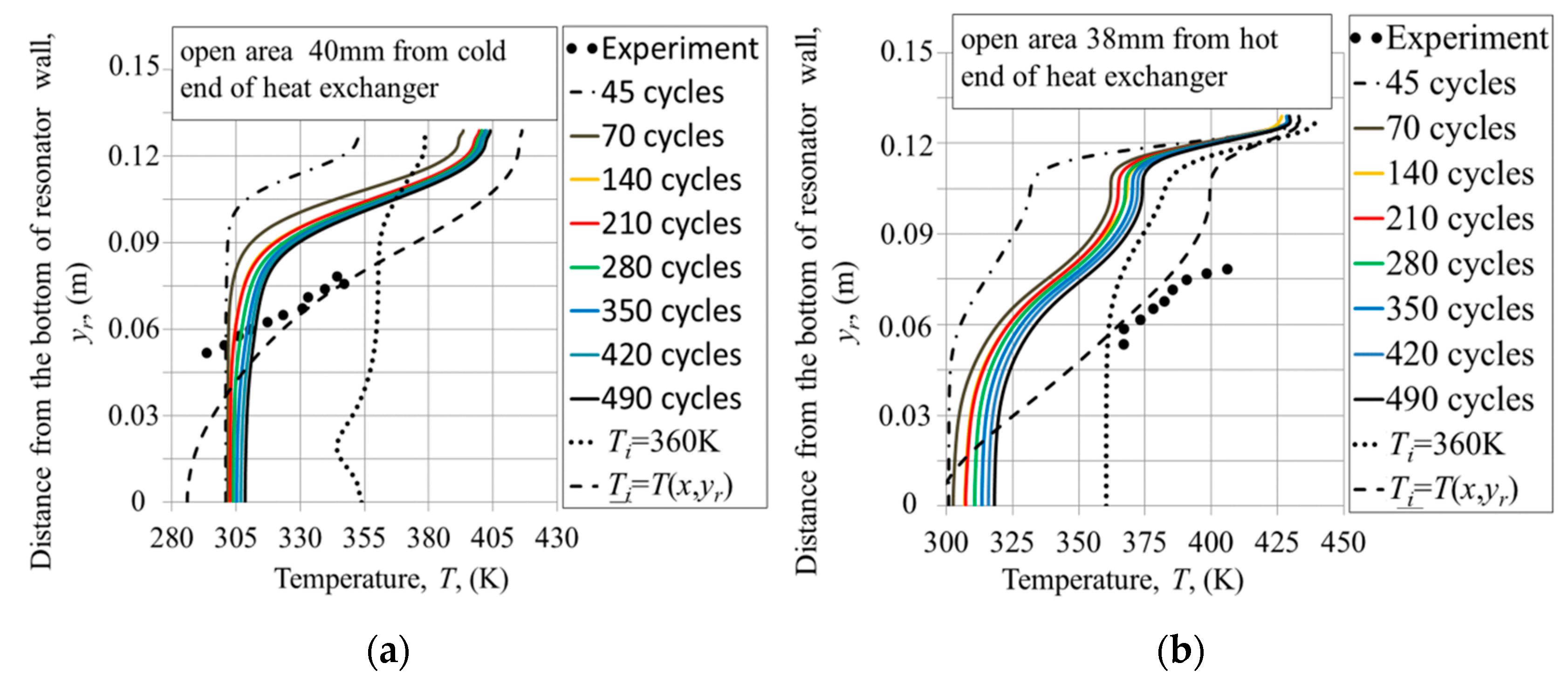
The investigation of the effect of initial temperature on the flow and heat transfer helps explain the selection of an appropriate initial temperature that best suits the model. The current approaches of prescribing the initial temperature fields showed that the initialisation procedure influences both the magnitude of heat flux and velocity profiles within the structures. The investigation suggests that the current model is best initialised at 300 K. The model initialised with a temperature field defined more closely to the experimental conditions resulted in a change of the flow character, incongruent with the real flow behaviour. It can be speculated that the reason for this is the type of boundary conditions imposed on the model, which may not fully represent the reality of the experiment with its long time-history (hours), far beyond the capabilities of the current CFD model.

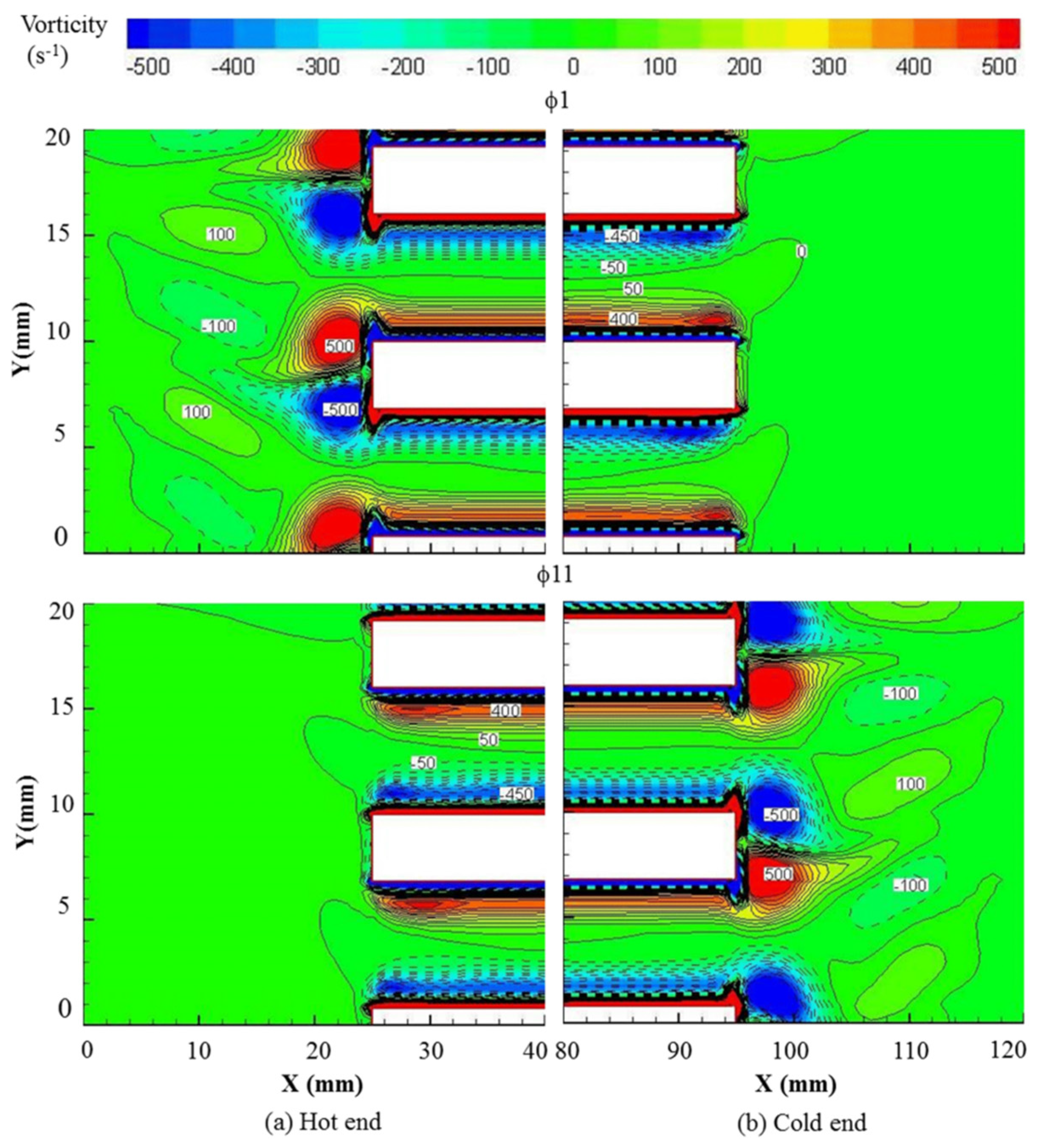
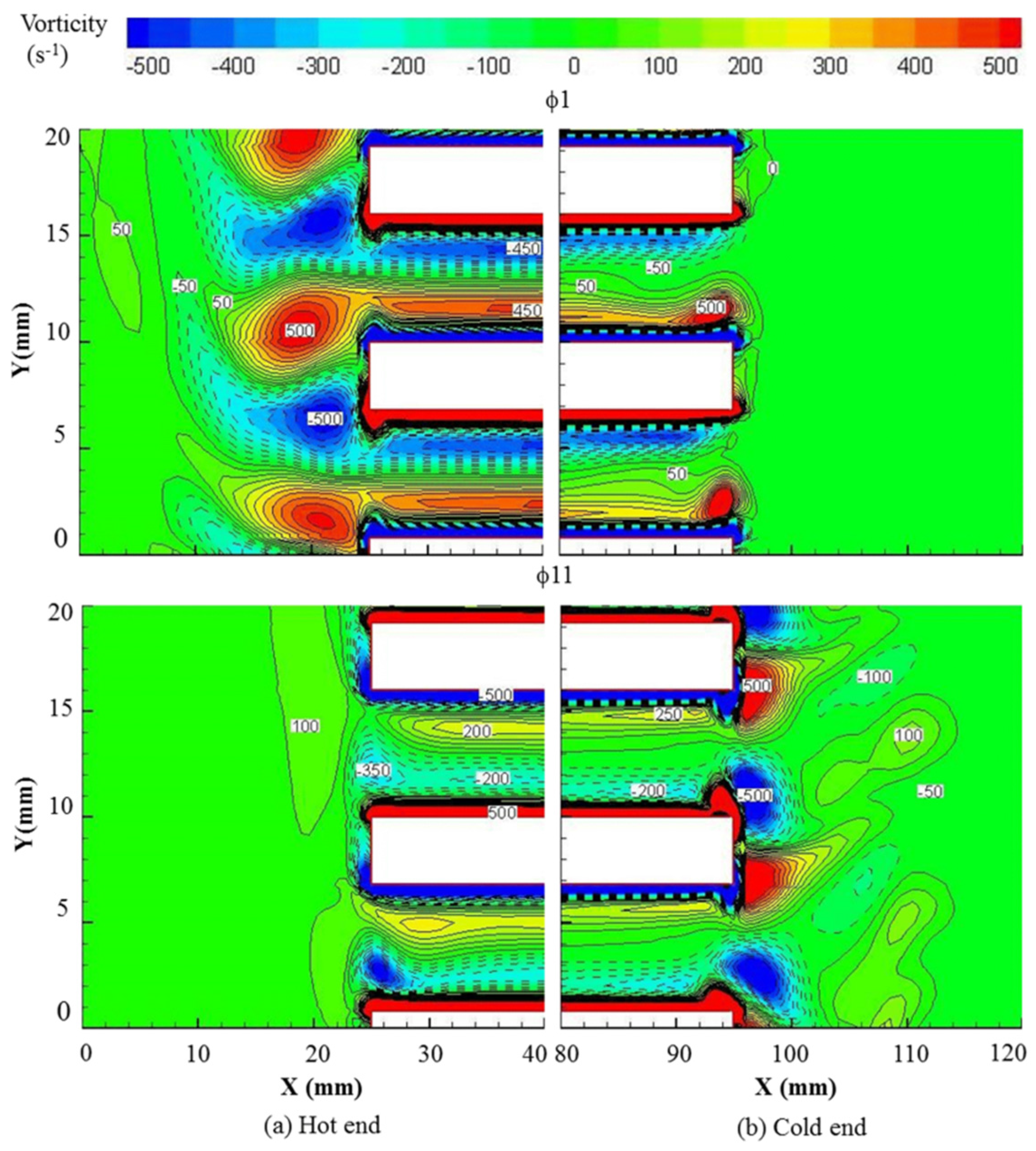
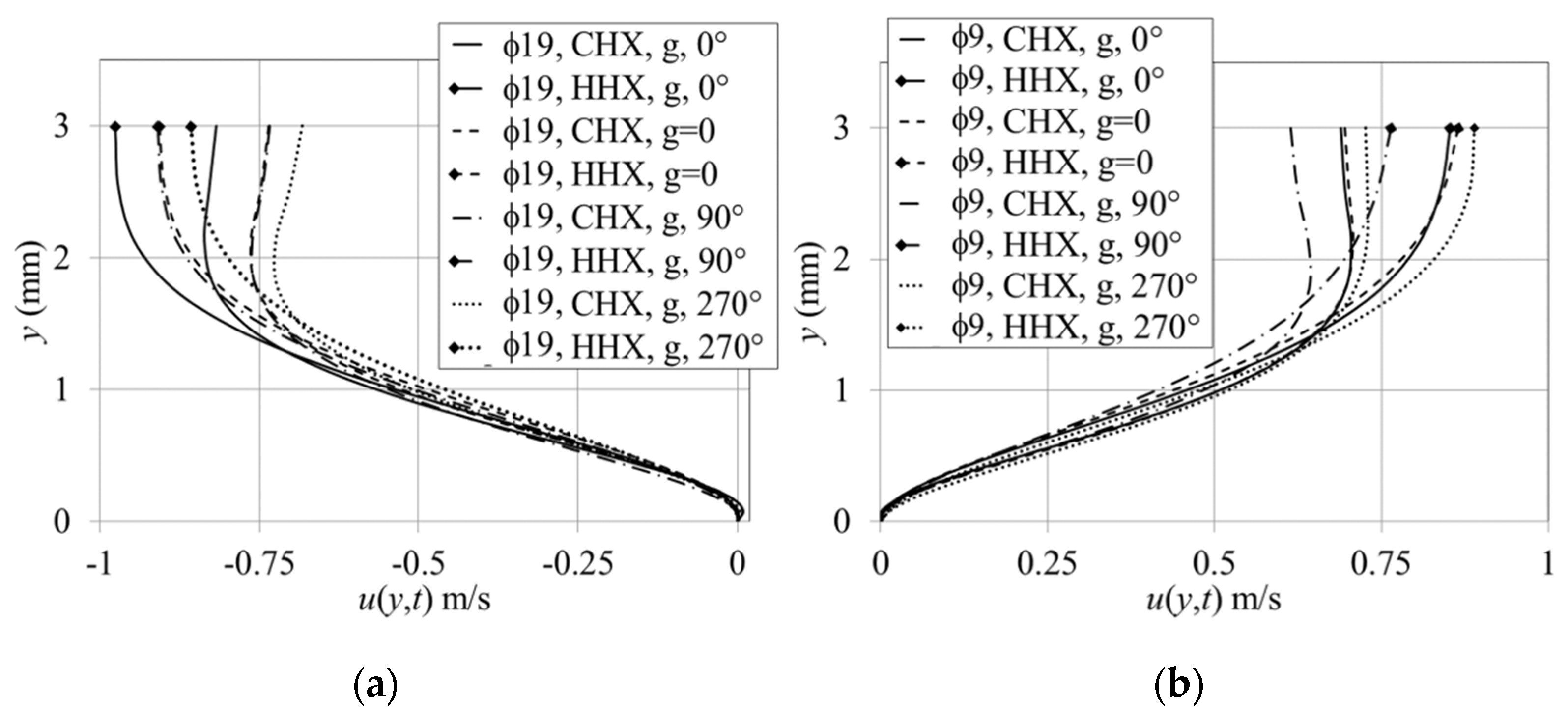
The imposed temperature boundary conditions (on the heat exchanger plates) is shown to cause asymmetry to the flow seemingly related to the nonlinearity caused by the combined effects of the temperature-dependent density and viscosity and the temperature-driven flow (buoyancy). The change in fluid density with respect to the temperature results in lower velocity amplitudes during the first part of the cycle and relatively higher magnitudes of velocity for the second part of the cycle. Here, an “asymmetrical boundary” creates asymmetries in the temperature and velocity fields. In addition, the temperature-driven buoyancy flow creates further “distortions” to the already asymmetrical features of the velocity and temperature fields. The results indicate that there are “net flows” through channels (or in other words “streaming”). These effects are well illustrated through changing the orientation of the device relative to the gravity field.

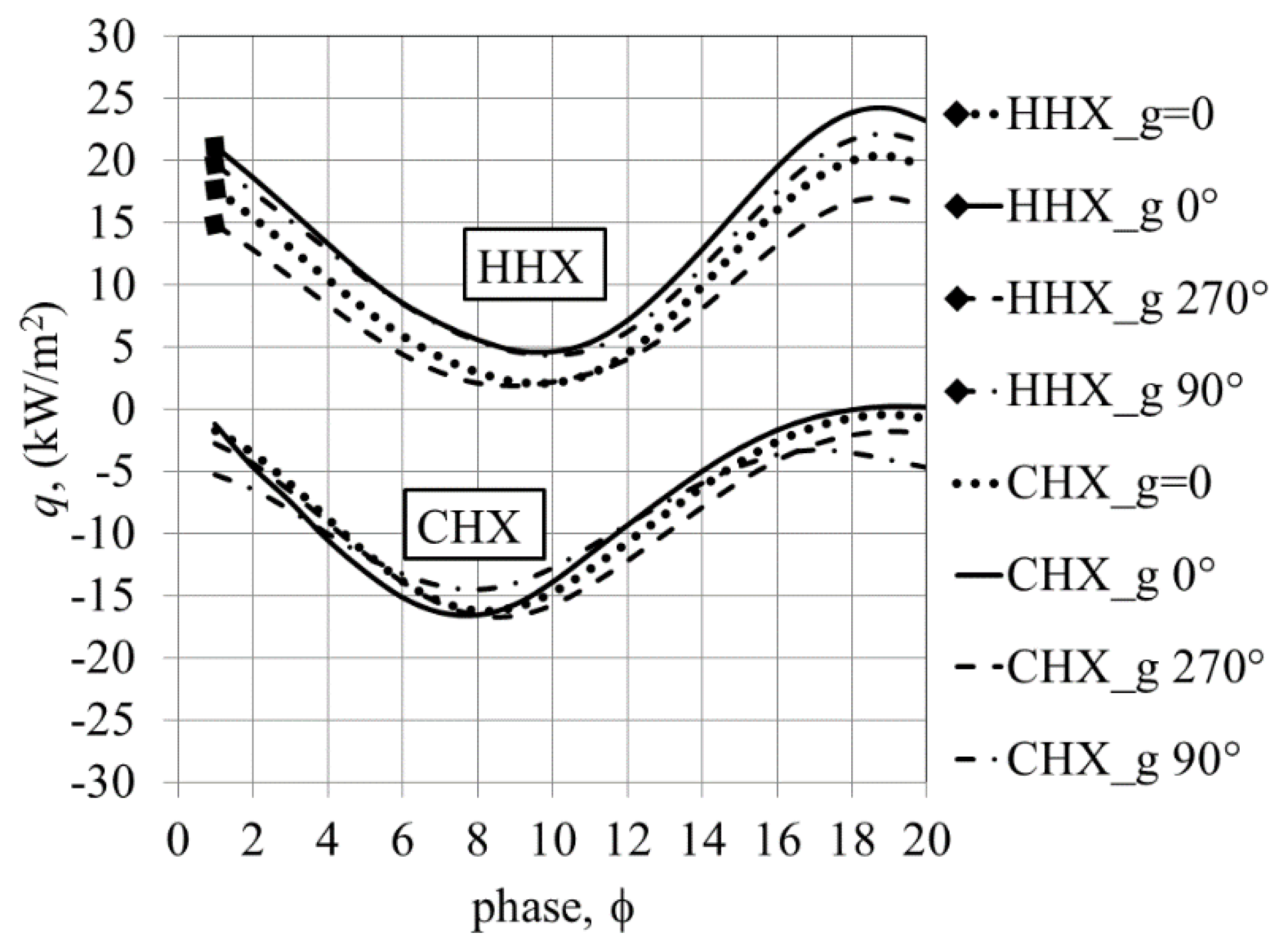
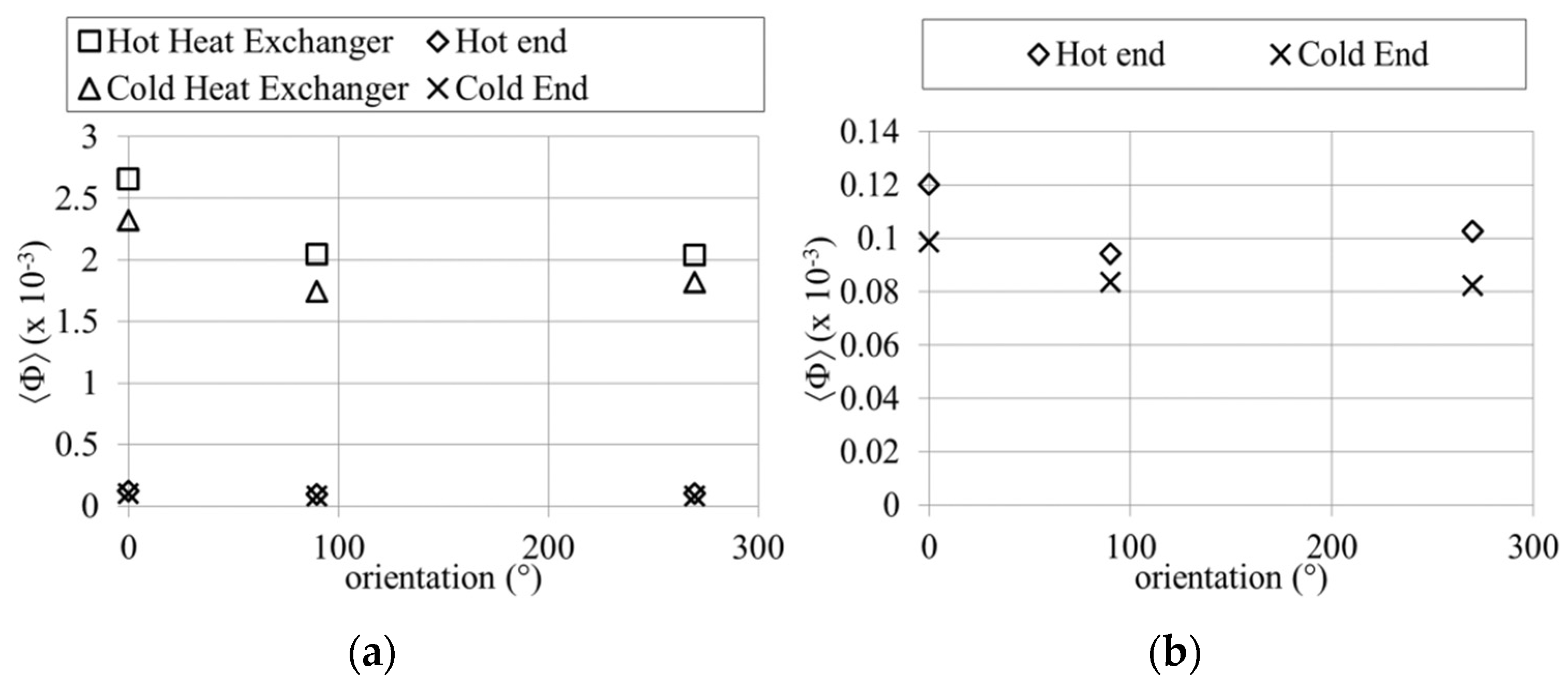
Temperature-dependent gravity effects influence the magnitudes of velocity profiles and temperature profiles between the plates depending on the direction of the flow and the locations of the CHX/HHX. Consequently, the heat fluxes also change. The presence of the imposed temperature field is shown to influence the velocity profile and gas displacement across the plates, hence breaking the symmetry of the flow. The vortex structures at the end of the plates, and the shear layer within the area bounded by the plates, change with temperature. Device orientation influences the flow and heat transfer due to temperature-driven buoyancy effects.

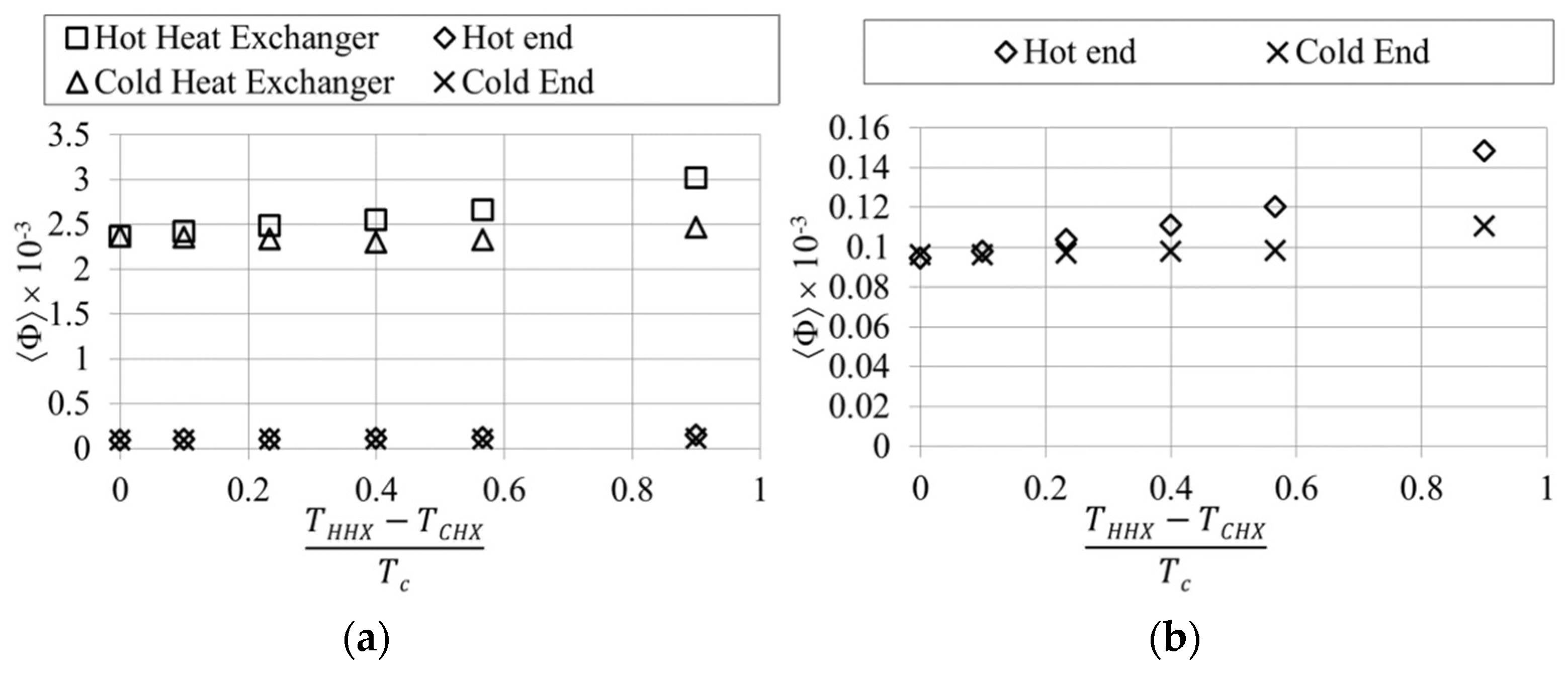
The viscous dissipation is also affected. The vertical arrangement is shown to provide a lower viscous dissipation but care should also be taken when dealing with this kind of arrangement because the temperature-driven flow changes the temperature and velocity field within the channel.