Viscosity Prediction of Different Ethylene Glycol/Water Based Nanofluids Using a RBF Neural Network

Abstract

In this study, a radial basis function (RBF) neural network with three-layer feed forward architecture was developed to effectively predict the viscosity ratio of different ethylene glycol/water based nanofluids. A total of 216 experimental data involving CuO, TiO₂, SiO₂, and SiC nanoparticles were collected from the published literature to train and test the RBF neural network. The parameters including temperature, nanoparticle properties (size, volume fraction, and density), and viscosity of the base fluid were selected as the input variables of the RBF neural network. The investigations demonstrated that the viscosity ratio predicted by the RBF neural network agreed well with the experimental data. The root mean squared error (RMSE), mean absolute percentage error (MAPE), sum of squared error (SSE), and statistical coefficient of multiple determination (R²) were respectively 0.04615, 2.12738%, 0.46007, and 0.99925 for the total samples when the Spread was 0.3. In addition, the RBF neural network had a better ability for predicting the viscosity ratio of nanofluids than the typical Batchelor model and Chen model, and the prediction performance of RBF neural networks were affected by the size of the data set.

1. Introduction

As a very important heat transfer medium, ethylene glycol/water mixtures are widely used in many different kinds of industrial equipment including car radiators, air conditioning systems, and liquid cooled computers [1]. In the past few decades, with the rapid development of various compact heat exchange components, the conventional ethylene glycol/water mixtures have been unable to effectively meet the ever-increasing demand for cooling due to their lower thermal conductivity. Therefore, how to develop enhanced heat transfer technology has become a very important problem in the fields of thermal engineering [2].

Nanofluids, a special liquid-solid mixture containing a base fluid and nanoparticles (usually less than 100 nm), have drawn increasing attention recently because of their advantages in thermal conductivity and stability [3]. Many investigations indicated that nanofluids could be an effective technology to improve the heat transfer performance of systems using ethylene glycol/water mixtures as coolant [4]. For example, the experimental results of Vajjha and Das [5] showed that at the temperature of 299 K, the thermal conductivities of the 60:40 (by weight ratio) ethylene glycol/water mixture could be increased by about 12.3% by adding ZnO nanoparticles (29 nm) with a volume fraction of 2%. Sundar et al. [6] experimentally investigated the effects of Fe₃O₄ nanoparticles (13 nm) on three different kinds of ethylene glycol/water mixtures with weight ratios of 20:80, 40:60, and 60:40. They found that at the temperature of 60 °C and the nanoparticle volume fraction of 2%, the thermal conductivity enhancements of the above three ethylene glycol/water mixtures were 46%, 42%, and 33%, respectively.

Thermo-physical parameters are very important factors that affect the heat and mass transfer performance of nanofluids [7,8,9]. Due to the fact that viscosity can significantly affect the flow internal resistance, inlet Reynolds number, and pressure drop, many experimental investigations have been carried out regarding the viscosity of different nanofluids. As reported by Azmi et al. [10], the viscosity of the 40:60 (by volume ratio) ethylene glycol/water mixture could be increased obviously by dispersing TiO₂ nanoparticles. For example, the viscosity enhancement was about 12% when the nanoparticle volume fraction changed from 0.5% to 1.5%. Sundar et al. [11] investigated the viscosity variations of Fe₃O₄-ethylene glycol/water nanofluids with different nanoparticle fractions and working temperatures. Their experimental results indicated that the viscosity of ethylene glycol/water based nanofluids could be increased by increasing the nanoparticle volume fraction and decreasing temperature. At a nanoparticle volume fraction of 1%, the viscosity of the base fluid could be enhanced by 2.9 times. Chen et al. [12], Jamshidi et al. [13], Kulkarni et al. [14], Rudyak et al. [15], Namburu et al. [16], Lim et al. [17], Chiam et al. [18], and Li et al. [19] respectively measured the viscosity of various ethylene glycol/water mixture based nanofluids with the effects of different factors. According to their experimental results, it was found that a suspension of nanoparticles could enhance the viscosity of the base fluid in different degrees. Additionally, temperature, base fluid, and nanoparticle properties including volume fraction, size, type, and shape were the important factors affecting the enhancement of nanofluids’ viscosity.

For the basis of the experimental research, the modeling and prediction of viscosity is also very important for understanding the rheological behavior of nanofluids. Murshed and Estellé [20] reviewed the latest developments of viscosity models for nanofluids. Their analysis indicated that although many theoretical models and empirical correlations have been developed for nanofluid viscosity, only a few of them were used for ethylene glycol/water based nanofluids. Additionally, since the effects of different factors on nanofluid viscosity were usually coupled and uncertain, it was still very difficult to accurately describe the viscosity characteristics of different nanofluids in a wide range of nanoparticle volume fractions, sizes, temperatures, etc. Therefore, how to develop an effective solution for the viscosity prediction of nanofluids is a hot topic in the field of nanofluids.

Artificial neural networks (ANN), a black box data analysis approach, has a strong nonlinear mapping ability to establish the relationship between input and output variables without considering the detailed physical process. Due to the advantages of ANNs such as high speed, simplicity, and large capacity, various ANNs were put forward to solve the modeling and prediction problems of nanofluid viscosity [21]. Selecting five variables (temperature, nanoparticle volume fraction, nanoparticle size, viscosity of the base fluid, and relative density of the base fluid) and nanoparticles as the input, Yousefi et al. [22] developed a diffusional neural network (DNN) to predict the viscosity of six different types of nanofluids. As reported in their analysis, DNN could be used for predicting the viscosity of nanofluids with satisfactory accuracy. On this basic, Mehrabi et al. [23] analyzed the application of a Fuzzy C-Means-based Adaptive neuro-fuzzy inference system (FCM-ANFIS) for the viscosity prediction of various water based nanofluids. They found that the FCM-ANFIS predicted values agreed well with the experimental data. Attracted by the better nonlinear mapping and recognition abilities of ANN, Zhao et al. [24,25] investigated the feasibility of RBF neural networks for predicting the viscosity of two water based nanofluids containing Al₂O₃ and CuO nanoparticles. Their results demonstrated that ANN was an effective tool in comparison with the traditional model-based approach for describing the enhancement behavior of nanofluid viscosity. They indicated that the addition of temperature as an input variable could improve the prediction performance of the RBF neural network.

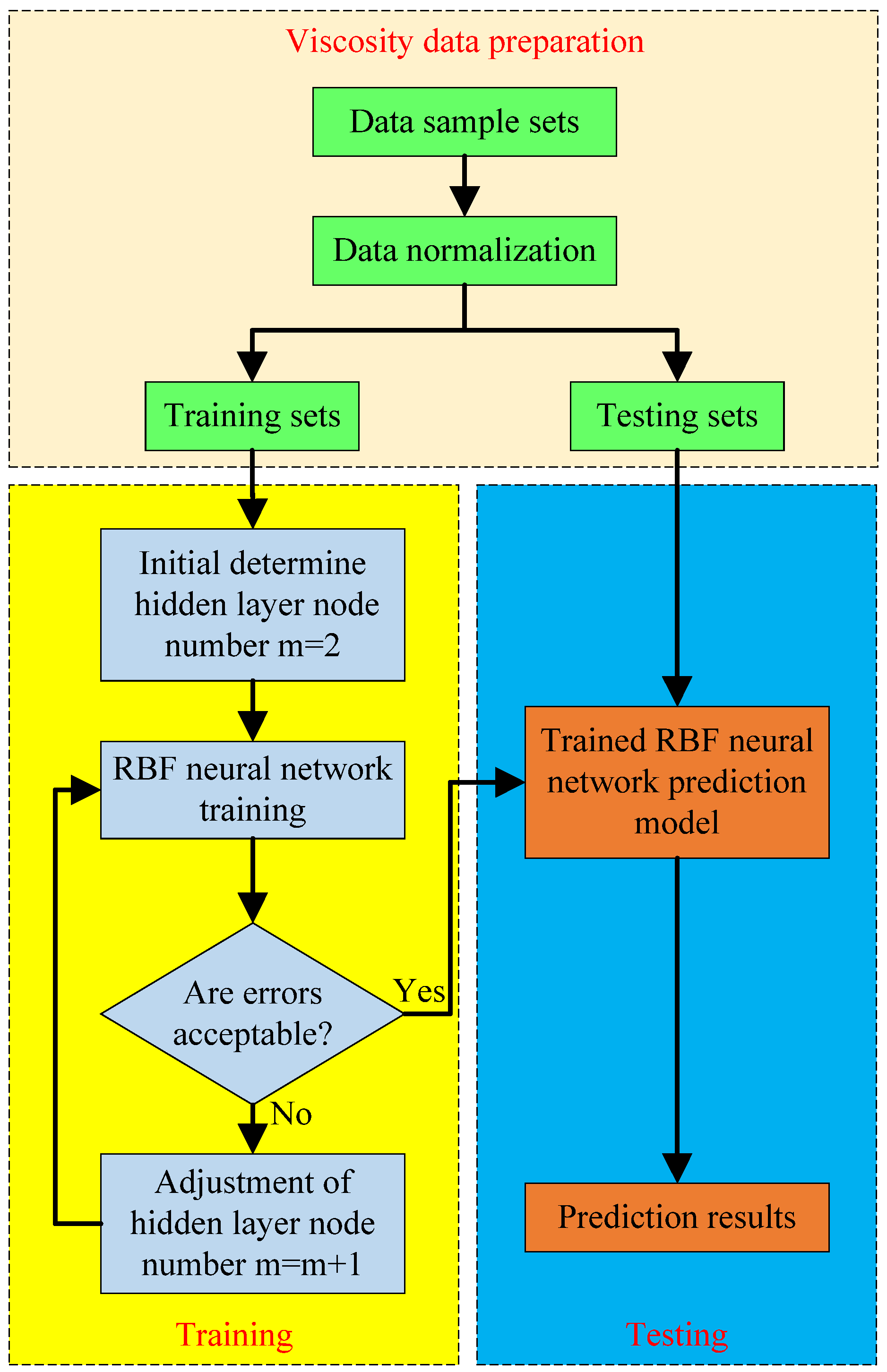
To the best of the authors’ knowledge, there are few publications that study the modeling and prediction of different ethylene glycol/water based nanofluids using ANN. Considering the advantages of RBF neural networks that are easier to design, and have faster training speed, higher training accuracy, stronger generalization ability, and stronger tolerance for input noise [26], this paper selects a RBF neural network as a competitive method for predicting the viscosity characteristics of different ethylene glycol/water based nanofluids with different influence factors. Firstly, the basis theory and modeling process of the RBF neural network are introduced briefly. On this basis, the available measurements from various published studies are obtained to establish the data sample sets and train the RBF neural network for determining the network configuration. Finally, the RBF neural networks’ predicted results are compared with the experimental data to evaluate the prediction performance of the proposed model.

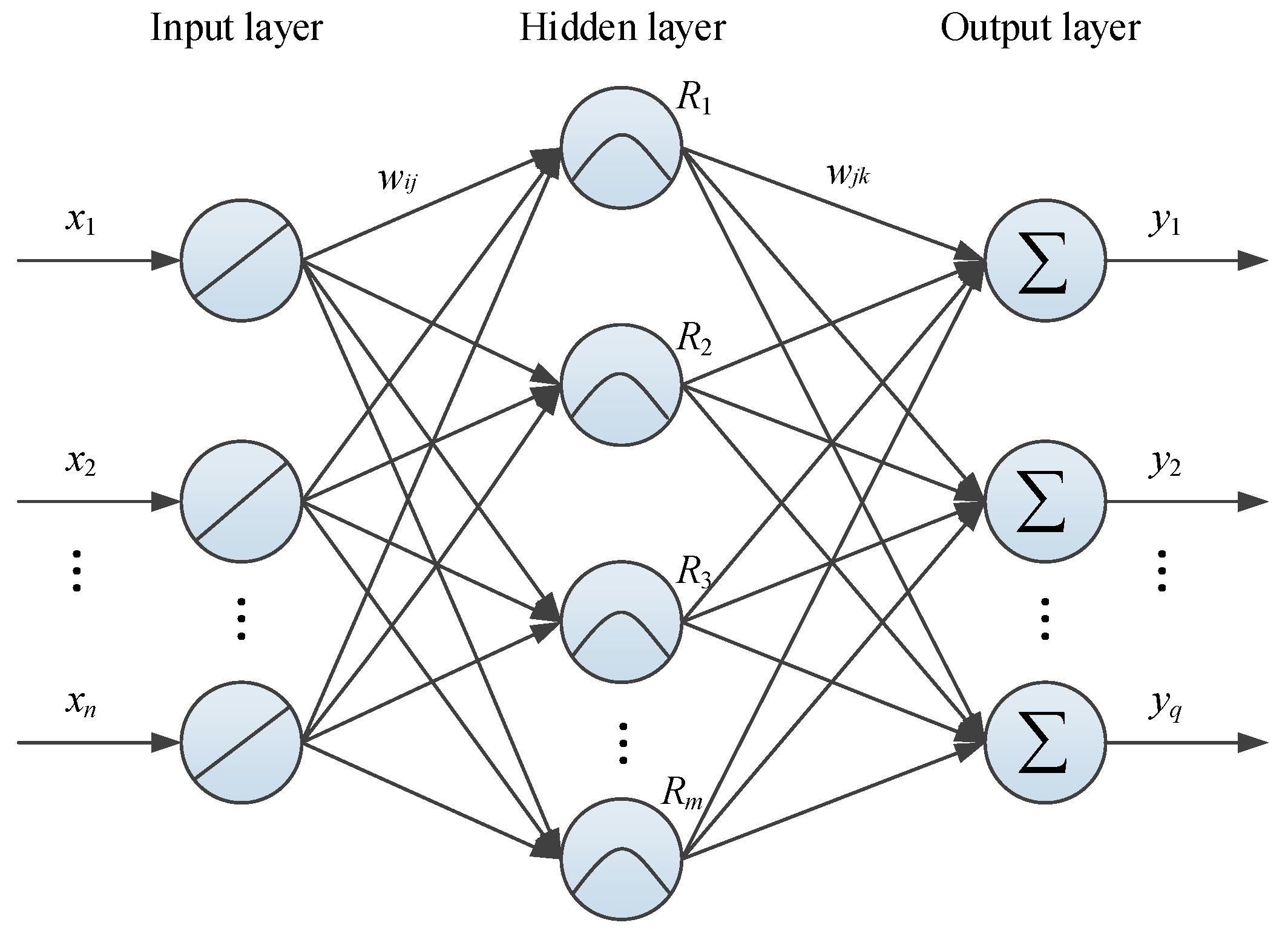
2. Basic Theory of a RBF Neural Network

Benefiting from the inspiration of the human brain’s structure and activity mechanism, many different artificial neural networks have been developed for different purposes including classification and regression. In the fields of curve-fitting and nonlinear predictive modeling, the RBF neural network proposed by Broomhead and Lowe [27] can exhibit a good ability because of its high accuracy and stability [28].

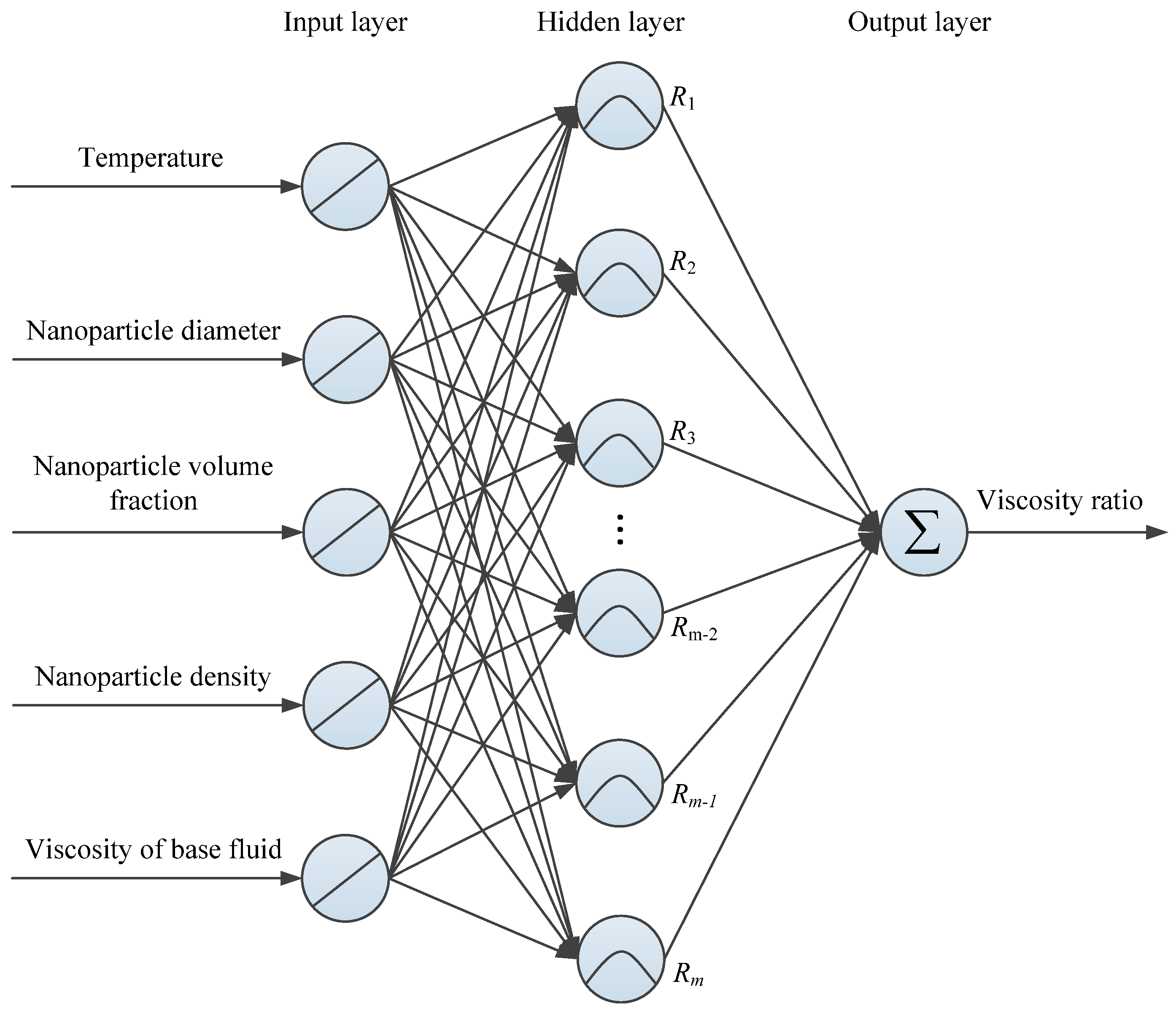
Figure 1 presents the basic structure of a typical three-layer RBF neural network. The input and output layers respectively correspond to the dendrite and synapse of biological neurons, which are used to mathematically describe the modeling object. The hidden layer, similar to the function of the cyton, plays a role of intermediation to process the input-output information and deliver it to the output layer. The connections between different layers are established through a series of artificial neurons and weights.

Figure 1. A typical three-layer RBF neural network.

Theoretically, the modeling process of the RBF neural network is to solve the mapping from $X^n$ to $Y^q$ ($n,q\ge 1$) in Euclidean space. Assuming that the input vector of the RBF neural network is $X$, the response of the $k$th neuron in the output layer ($y_k\in Y^q$) can be obtained by using the following linear weighting function [29].

$$\begin{array}{cc}{y}_k={\displaystyle \sum _{j=1}^m{\omega }_{jk}{R}_j(X)},& (k=1,2,\cdots ,q)\end{array}$$

(1)

where ${\omega }_{jk}$ is the connection weight between the $j$th hidden layer neuron and the $k$th output layer neuron. $m$ and q are the numbers of neurons in the corresponding layer, respectively.

Different from many other ANNs, the response of the RBF neural network’s $j$th hidden layer neuron is usually determined by the RBF. When it selects a Gaussian function, the corresponding $R_j(X)$ can be defined as,

$$\begin{array}{cc}{R}_j(X)=\exp (-\frac{{\Vert X-c_j\Vert }^2}{2{\sigma }_j^2}),& (j=1,2,\cdots ,m)\end{array}$$

(2)

where $\Vert \Vert$ is the Euclidean distance between the input vector $X$ and the $j$th neuron center $c_j$. ${\sigma }_j$ is the width of the $j$th neuron.

Analyzing Equations (1) and (2), it can be easily found that the key of RBF neural network training is how to determine ${\omega }_{jk}$, $c_j$, and ${\sigma }_j$. In the past few decades, different unsupervised and supervised algorithms have been developed to solve this problem [30]. In this study, the network parameters are updated by using an orthogonal least squares (OLS) approach, of which the minimizing function is shown in Equation (3). More detailed information about OLS can be found in [31].

$$\min J={\displaystyle \sum _{k=1}^q({\left|y_{nk}-y_{dk}\right|}^2)}$$

(3)

where $y_{nk}$ and $y_{dk}$ are the network output and desired output of the $k$th output layer node, respectively.

3. Modeling Implementation of a RBF Neural Network

According to the above theory, the modeling process of the RBF neural network involves three main parts which are data preparation, training, and testing. Figure 2 depicts the basic applied flow chart of the RBF neural network for predicting the relative viscosity of ethylene glycol/water based nanofluids. The specific implementations are discussed in the following.

Figure 2. Implementation process of a RBF neural network for viscosity prediction.

3.1. Preparation of Viscosity Data

As previously mentioned, many experimental investigations have been published to discuss the effects of different factors including temperature and nanoparticle properties (such as type, size, concentration, and shape) on the viscosity of ethylene glycol/water based nanofluids. Considering the integrity of the measuring information, a total of 216 viscosity data involving TiO₂, CuO, SiO₂, and SiC are obtained to establish the sample sets. The detailed information of the nanofluids regarding nanoparticle diameter ($d_p$), nanoparticle volume fraction (φ_p), nanoparticle density (${\rho }_p$), temperature ($T$), and viscosity of the base fluid (${\mu }_f$) and nanofluids (${\mu }_{nf}$) are listed in Table 1. According to the modeling principle, 198 data (about 90%) are selected to train the RBF neural network, and the remaining 18 data (about 10%) are used to test the performance of the trained RBF neural network.

Table 1. Viscosity information of ethylene glycol/water based nanofluids.

Nanofluids	TiO2-EG [12]	SiO2-EG/W a [13]	SiO2-EG/W b [13]	CuO-EG/W c [14]	SiO2-EG [15]	CuO-EG/W c [16]	SiC-EG/W d [19]
dp (nm)	25	10	10	30/45/50	18.1/28.3/45.6	29	30
φp (%)	0.1–1.8	0.1	0.1	1–6	0.6–8.4	1–4	0.1–0.5
ρp (kg/m3)	4230	2650	2650	6310	2650	6310	110
T (°C)	20.1–60.2	28.45–59	28–59	−35–50	25–59	0–40	10–50
μf (mPa.s)	3.87–23	0.98–1.68	1.6–3.11	2.33–99.5	4.08–18.5	4.35–11.5	9.2–11.34
μnf/μf	0.81–1	1–1.15	1.05–1.13	1.1–4.65	1.04–2.02	1.14–2.09	1.13–1.29
No. of data	27	11	10	80	31	12	45

^a EG/W: 25:75 by volume ratio; ^b EG/W: 50:50 by volume ratio; ^c EG/W: 60:40 by weight ratio; ^d EG/W: 40:60 by weight ratio.

To improve the learning and training performances of the RBF neural network, the following equation is used to normalize the input and output variables.

$$x\text{'}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$$

(4)

where x is the original value, x’ is the normalized value, and $x_{\max }$ and $x_{\min }$ are the corresponding maximum and minimum of x.

3.2. Configuration of a RBF Neural Network

Considering the nonlinear characteristics of the ethylene glycol/water based nanofluid viscosity ratio with different factors, a three layer RBF neural network is developed in the present investigation. Temperature, nanoparticle diameter, nanoparticle volume fraction, nanoparticle density, and viscosity of the base fluid are selected as the input variables. The objective output of the RBF neural network is the viscosity ratio between the nanofluids and the base fluid. Therefore, the basic structure of the developed RBF neural network for predicting the viscosity ratio of ethylene glycol/water based nanofluids is 5-m-1, as illustrated in Figure 3. For the neurons, the numbers in the hidden layer (m) and other parameters are determined in the training process.

Figure 3. RBF neural network developed in this study.

3.3. Evaluation Criteria

To effectively evaluate the training and prediction performance of the RBF neural network, the following four important parameters are used.

Root mean squared error (RMSE),

$$RMSE={(\frac{1}{t}{\displaystyle \sum _{l=1}^t{\left|P_l-Q_l\right|}^2})}^{1/2}$$

(5)

Mean absolute percentage error (MAPE),

$$MAPE=\frac{100\%}{t}{\displaystyle \sum _{l=1}^t\left|\frac{P_l-Q_l}{P_l}\right|}$$

(6)

Sum of squared error (SSE),

$$SSE={\displaystyle \sum _{l=1}^t{(P_l-Q_l)}^2}$$

(7)

Statistical coefficient of multiple determination (R²),

$$R^2=1-\frac{{\displaystyle \sum _{l=1}^t{(P_l-Q_l)}^2}}{{\displaystyle \sum _{l=1}^t{(P_l)}^2}}$$

(8)

where P is the desired value, Q is the network output value, and t is the number of samples.

4. Results and Discussion

For the RBF neural network, the Spread is usually a very important factor influencing the training process. Figure 4 shows the relationships of the mean square error (MSE) and the number of hidden layer neurons with different Spreads. Analyzing the results reported in Figure 4, it is found that for the same converged target, the neuron numbers in the hidden layer need to be increased obviously with the decrease of the Spread. When the Spread varies from 1 to 0.1, the corresponding neuron configuration of the RBF neural network are 5-38-1, 5-40-1, 5-56-1, 5-67-1, and 5-105-1, respectively. With the decrease of the Spread, the CPU time for computing the RBF neural network will also increase. At a Spread of 1, 0.5, 0.3, 0.2, and 0.1, the corresponding CPU times are 6.318, 6.396, 8.798, 10.827, and 15.772 s, respectively. In addition, Table 2 lists the values of four evaluation criteria for predicting the viscosity ratio of ethylene glycol/water based nanofluids by using the RBF neural network with different Spreads. It can be seen from Table 2 that although all $R^2$ are within the acceptable level of 0.99, the prediction performance of the RBF neural network is still affected by the value of the Spread, especially for the testing samples. Based on the comprehensive considerations of modeling complexity, prediction accuracy, and CPU time, the RBF neural network with the neuron configuration of 5-56-1 and Spread of 0.3 is used in this study. The related weights and biases of the 5-56-1 RBF neural network can be found in Table 3.

Figure 4. The relationships of mean square error (MSE) and the number of hidden layer neurons with different Spreads.

Table 2. Performance evaluation of RBF neural networks with different Spreads.

Object	Evaluation Criteria	Spread
		1	0.5	0.3	0.2	0.1
Training samples	RMSE	0.04651	0.04460	0.04630	0.04502	0.04400
	MAPE (%)	2.3335	2.27321	2.09967	1.93784	2.00530
	SSE	0.42829	0.39383	0.42454	0.40125	0.38337
	R2	0.99925	0.99932	0.99927	0.99930	0.99934
Testing samples	RMSE	0.09190	0.07035	0.04443	0.05124	0.10061
	MAPE (%)	4.65795	3.90042	2.43228	2.67720	4.27471
	SSE	0.15201	0.08908	0.03553	0.04727	0.18221
	R2	0.99590	0.99760	0.99904	0.99872	0.99508
Total samples	RMSE	0.05183	0.04728	0.04615	0.04557	0.05117
	MAPE (%)	2.52721	2.40881	2.12738	1.99945	2.19442
	SSE	0.58030	0.48291	0.46007	0.44852	0.56558
	R2	0.99906	0.99921	0.99925	0.99927	0.99908

Table 3. Weight and bias coefficients of the developed RBF neural network.

Neuron	Hidden Layer						Output Layer
	Weights (wij) a and Biases						Weights (wij) b and Biases
	T	dp	φp	ρp	μf	Biases	μnf/μf	Biases
1	0.1616	0.6000	0.5952	1.0000	0.0817	2.7752	1.5072	0.0163
2	−0.4874	0.6000	0.7143	1.0000	0.6859	2.7752	2.5903
3	0.6452	0.5660	0.3214	0.4200	0.0973	2.7752	0.0601
4	0.8200	0.6000	0.7143	1.0000	0.0233	2.7752	3.4089
5	0.4080	0.6000	0.0119	0.0174	0.1053	2.7752	−0.4782
6	−0.1629	0.6000	0.7143	1.0000	0.2041	2.7752	24.6321
7	0.4080	0.5660	0.9881	0.4200	0.1861	2.7752	−0.1055
8	0.7818	0.2000	0.0119	0.4200	0.0211	2.7752	−0.0298
9	−0.5716	0.6000	0.5952	1.0000	1.0000	2.7752	−2.4385
10	0.4892	0.6000	0.1190	1.0000	0.0403	2.7752	0.0877
11	0.3270	0.6000	0.7143	1.0000	0.0559	2.7752	2.0103
12	−0.1629	0.6000	0.1190	1.0000	0.2041	2.7752	−16.7539
13	0.8159	0.6000	0.0595	0.0174	0.0925	2.7752	0.2123
14	0.3264	0.6000	0.0595	0.0174	0.1075	2.7752	1.5469
15	0.4080	0.9120	0.4762	0.4200	0.1861	2.7752	0.1479
16	0.9620	0.5660	0.5714	0.4200	0.0410	2.7752	0.2334
17	0.4080	0.3620	0.1548	0.4200	0.1861	2.7752	−0.0212
18	−0.1629	0.6000	0.5952	1.0000	0.2041	2.7752	−75.1746
19	−0.4905	0.6000	0.1190	1.0000	0.6952	2.7752	−0.0522
20	−0.4874	0.6000	0.5952	1.0000	0.6859	2.7752	−3.3888
21	0.9819	0.5000	0.0476	0.6704	0.0389	2.7752	0.0377
22	−0.1629	0.6000	0.4762	1.0000	0.2041	2.7752	115.2566
23	0.6540	1.0000	0.7143	1.0000	0.0301	2.7752	1.0610
24	0.6540	0.9000	0.7143	1.0000	0.0301	2.7752	−1.1272
25	−0.3251	0.6000	0.5952	1.0000	0.3582	2.7752	0.2584
25	−0.5685	0.6000	0.7143	1.0000	0.9855	2.7752	2.1391
26	−0.5716	0.6000	0.4762	1.0000	1.0000	2.7752	1.2104
27	0.4080	0.3620	1.0000	0.4200	0.1861	2.7752	0.4979
28	0.4080	0.9120	1.0000	0.4200	0.1861	2.7752	0.2536
29	0.6562	0.5000	0.2143	0.6704	0.0945	2.7752	−0.0974
30	0.3270	0.6000	0.5952	1.0000	0.0559	2.7752	−3.6703
31	0.4080	0.9120	0.0714	0.4200	0.1861	2.7752	0.1275
32	0.4080	0.3620	0.4762	0.4200	0.1861	2.7752	0.2454
33	0.4553	0.2000	0.0119	0.4200	0.0172	2.7752	0.1747
34	1.0000	0.2000	0.0119	0.4200	0.0161	2.7752	0.1852
35	0.1616	0.6000	0.4762	1.0000	0.0817	2.7752	−0.5112
36	0.8169	0.6000	0.1190	1.0000	0.0234	2.7752	0.4325
37	−0.4874	0.6000	0.4762	1.0000	0.6859	2.7752	1.6740
38	−0.1629	0.6000	0.3571	1.0000	0.2041	2.7752	−107.8889
39	0.3270	0.6000	0.4762	1.0000	0.0559	2.7752	1.4652
40	0.1632	0.6000	0.0595	0.0174	0.1139	2.7752	0.9067
41	0.8169	0.6000	0.5952	1.0000	0.0234	2.7752	−6.2589
42	0.8169	0.6000	0.4762	1.0000	0.0234	2.7752	5.5200
43	0.5739	0.5000	0.0119	0.6704	0.1182	2.7752	0.0349
44	0.4080	0.3620	0.8095	0.4200	0.1861	2.7752	−0.1272
45	0.4892	0.6000	0.5952	1.0000	0.0403	2.7752	0.6498
46	−0.1629	0.6000	0.2381	1.0000	0.2041	2.7752	61.3817
47	0.3283	0.5000	0.0119	0.6704	0.2312	2.7752	0.0577
48	0.4080	0.5660	0.3095	0.4200	0.1861	2.7752	−0.1083
49	0.2448	0.6000	0.0595	0.0174	0.1096	2.7752	−1.7397
50	−0.4855	0.9000	0.7143	1.0000	0.6804	2.7752	−0.7083
51	−0.4886	1.0000	0.7143	1.0000	0.6896	2.7752	0.6218
52	−0.0007	0.6000	0.7143	1.0000	0.1252	2.7752	−0.7176
53	−0.5692	0.9000	0.7143	1.0000	0.9885	2.7752	−0.0385
54	0.6514	0.6000	0.2381	1.0000	0.0302	2.7752	−0.1993
55	0.8169	0.6000	0.3571	1.0000	0.0234	2.7752	−2.0841
56	0.1616	0.6000	0.5952	1.0000	0.0817	2.7752	1.5072

^a Weight connection from the input layer to the hidden layer; ^b Weight connection from the hidden layer to the output layer.

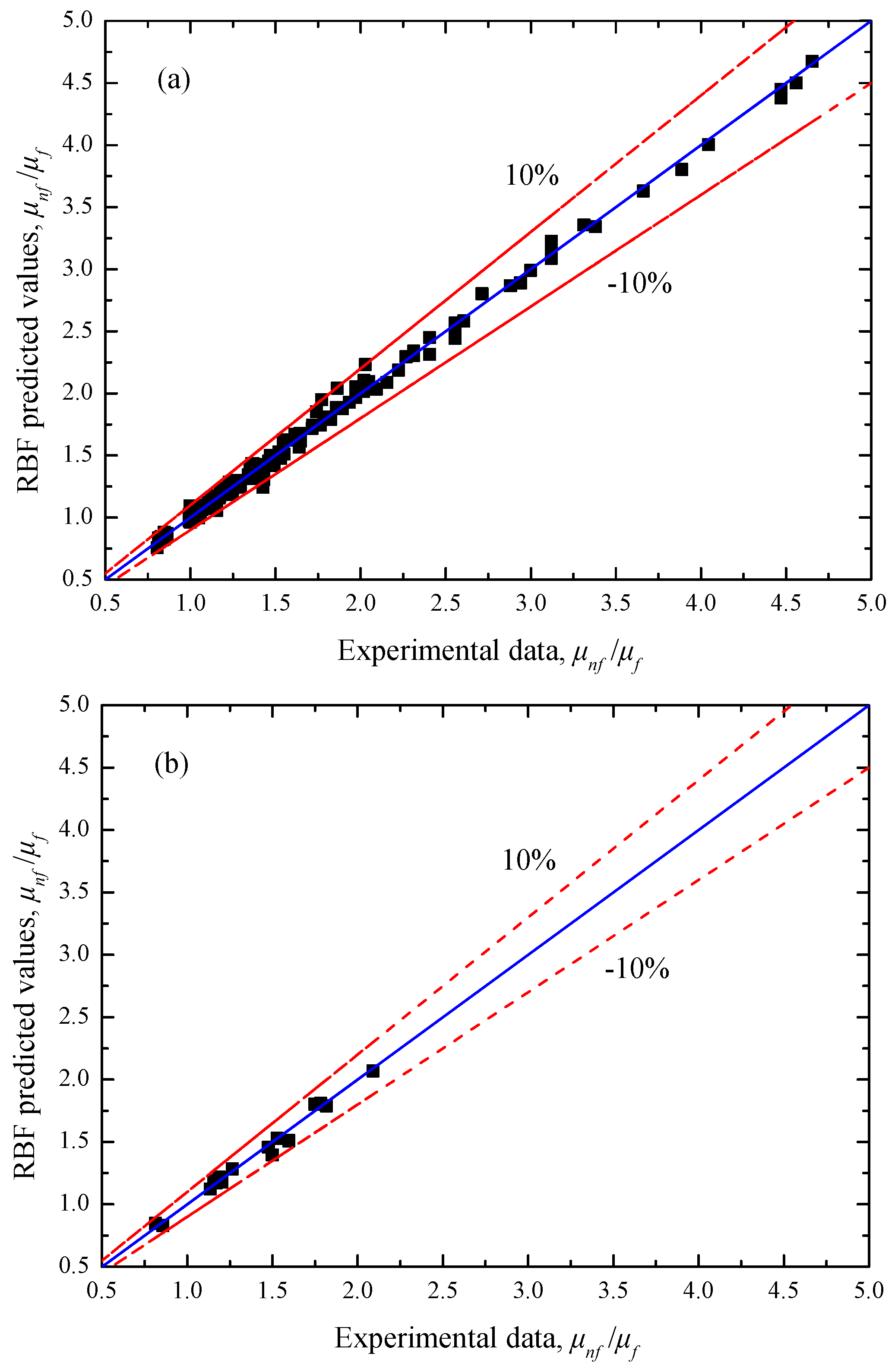
Figure 5 compares the predicted viscosity ratio of the RBF neural network and the experimental data involving the training and testing samples. It can be seen that all the prediction errors of the RBF neural network are within the ±10% error bands. As shown in Table 2, the values of the four evaluation criteria are RMSE = 0.04630, MAPE = 2.09967%, SSE = 0.42454, and R² = 0.99927 for the training samples, and RMSE = 0.04443, MAPE = 2.43228%, SSE = 0.03553, and R² = 0.99904 for the testing samples, which preliminarily indicates that the RBF neural network has a good ability to predict the viscosity ratio of ethylene glycol/water based nanofluids.

Figure 5. Scatter plots of (a) training and (b) testing μ_nf/μ_f for the RBF predicted results and experimental data.

To further evaluate the prediction performance of the RBF neural network for nanofluid viscosity, the following typical viscosity models which consider the effects of nanoparticle Brownian motion and aggregation are selected for analysis.

Batchelor model [32]:

$${\mu }_{nf}=(1+2.5{\varphi }_p+6.25{\varphi }_p^2){\mu }_f$$

(9)

Chen model [33]:

$${\mu }_{nf}={[1-\frac{{\varphi }_p}{0.605}{(\frac{r_a}{r_p})}^{1.2}]}^{-1.5125}{\mu }_f$$

(10)

where r_p and r_a are the radius of nanoparticle and nanoparticle aggregation, respectively.

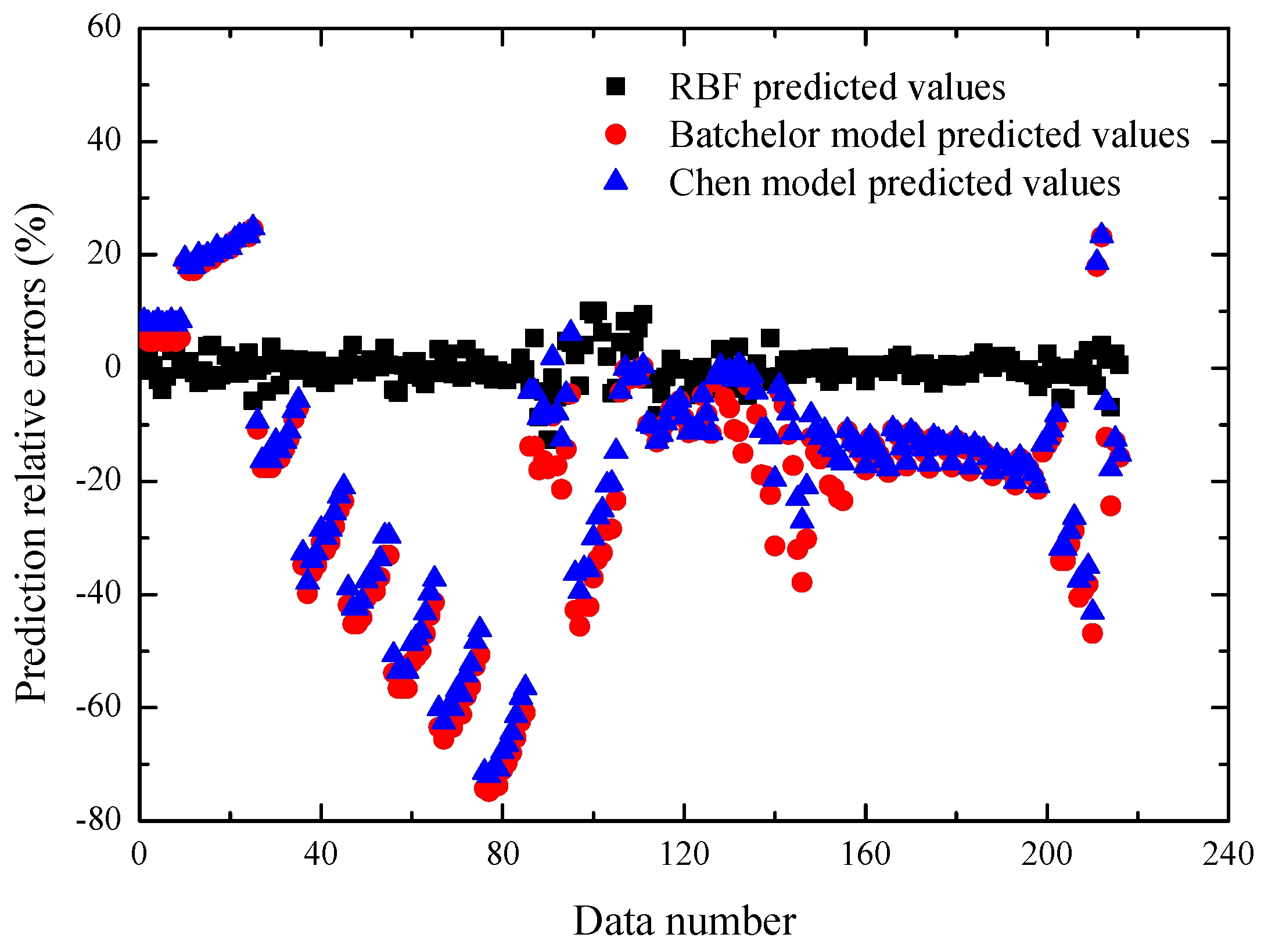
Figure 6 and Table 4 respectively compare the prediction performances of the different models for the total viscosity data. It is easily seen that the RBF neural network has a better prediction accuracy than the above two typical models. The main reason is that the Batchelor model and Chen model cannot fully quantitatively describe the relationship between the nanofluid viscosity ratio and the various factors including the nanoparticle properties, temperature, and base fluid.

Figure 6. Prediction relative errors of different models for the total viscosity data.

Table 4. Performance evaluation of different modes for the total viscosity data.

Evaluation Criteria	RBF Neural Network	Batchelor Model	Chen Model
RMSE	0.04615	0.82200	0.77129
MAPE (%)	2.12738	24.2349	21.79539
SSE	0.46007	145.94871	128.49640
R2	0.99925	0.76244	0.79085

Moreover, Table 5, Table 6 and Table 7 respectively present the comparisons between the predicted viscosity ratio of the RBF neural network and the corresponding experimental data of Chen et al. [12], Jamshidi et al. [13], and Namburu et al. [16]. It can be seen that there is good agreement between the RBF predicted and the experimental viscosity ratio of the different ethylene glycol/water based nanofluids. At the temperature range of 20–40 °C, the maximum and minimum prediction errors of the RBF neural network are respectively 5.788% and 0.434% for the experimental data of Chen et al. [12]. For the viscosity ratio of the SiO₂-ethylene glycol/water (50:50 by volume ratio) nanofluid provided by Jamshidi et al. [13], the RBF neural network can accurately predict the viscosity ratio with an average error of 1.772% at the nanoparticle volume fraction of 0.1%. Moreover, the comparisons shown in Table 7 further illustrate that the developed RBF neural network has high accuracy (average error: 2.097%) for predicting the viscosity ratio of CuO-ethylene glycol/water (60:40 by weight ratio) nanofluids.

Table 5. Comparisons of the RBF predicted viscosity ratio of TiO₂-ethylene glycol nanofluids with the experimental data of Chen et al. [12].

T (°C)	φp (%)	Experiment (P)	RBF Prediction (Q)	$\frac{\mathbf{\left|}\mathit{P}\mathbf{-}\mathit{Q}\mathbf{\right|}}{\mathit{P}}\mathbf{\times }\mathbf{100}\mathbf{\%}$
60.17	1.8	0.994	0.990	0.434
55.26	1.8	1.000	1.023	2.330
50.03	1.8	1.000	1.005	0.488
45.27	1.8	0.994	0.974	2.090
40.21	1.8	1.000	0.961	3.875
35.17	1.8	1.000	0.985	1.529
30.16	1.8	0.994	1.025	3.055
25.19	1.8	1.000	1.041	4.068
20.12	1.8	0.994	0.995	0.082
60.17	0.4	0.852	0.850	0.270
55.10	0.4	0.862	0.872	1.217
50.03	0.4	0.862	0.855	0.829
45.12	0.4	0.857	0.830	3.173
40.07	0.4	0.847	0.825	2.603
35.17	0.4	0.852	0.848	0.424
30.16	0.4	0.847	0.880	3.868
25.19	0.4	0.847	0.881	4.038
20.12	0.4	0.837	0.819	2.193
60.17	0.1	0.833	0.822	1.268
55.10	0.1	0.828	0.846	2.220
50.19	0.1	0.828	0.833	0.609
45.12	0.1	0.819	0.810	1.011
40.07	0.1	0.814	0.806	1.020
35.17	0.1	0.814	0.824	1.284
30.16	0.1	0.814	0.847	4.039
25.19	0.1	0.814	0.836	2.675
20.12	0.1	0.805	0.758	5.788

Table 6. Comparisons of the RBF predicted viscosity ratio of SiO₂-ethylene glycol/water (50:50 by volume ratio) nanofluids with the experimental data of Jamshidi et al. [13].

T (°C)	φp (%)	Experiment (P)	RBF Prediction (Q)	$\frac{\mathbf{\left|}\mathit{P}\mathbf{-}\mathit{Q}\mathbf{\right|}}{\mathit{P}}\mathbf{\times }\mathbf{100}\mathbf{\%}$
28.65	0.1	1.082	1.099	1.549
38.18	0.1	1.076	1.073	0.258
47.91	0.1	1.064	1.063	0.067
55.81	0.1	1.100	1.098	0.202
61.28	0.1	1.132	1.078	4.746
28.45	0.1	1.128	1.098	2.703
36.55	0.1	1.119	1.082	3.323
45.07	0.1	1.054	1.056	0.196
50.95	0.1	1.091	1.078	1.243
58.85	0.1	1.134	1.095	3.432

Table 7. Comparisons of the RBF predicted viscosity ratio of CuO-ethylene glycol/water (60:40 by weight ratio) nanofluids with the experimental data of Namburu et al. [16].

T (°C)	φp (%)	Experiment (P)	RBF Prediction (Q)	$\frac{\mathbf{\left|}\mathit{P}\mathbf{-}\mathit{Q}\mathbf{\right|}}{\mathit{P}}\mathbf{\times }\mathbf{100}\mathbf{\%}$
9.970	1.000	1.204	1.181	1.940
20.305	1.000	1.187	1.217	2.547
29.860	1.000	1.170	1.174	0.308
40.196	1.000	1.136	1.123	1.195
0.006	2.000	1.596	1.511	5.307
10.146	2.000	1.596	1.508	5.504
20.288	2.000	1.528	1.528	0.019
30.040	2.000	1.477	1.459	1.216
−0.199	3.000	1.817	1.789	1.566
10.137	3.000	1.783	1.809	1.451
20.082	3.000	1.749	1.803	3.085
29.620	4.000	2.089	2.068	1.028

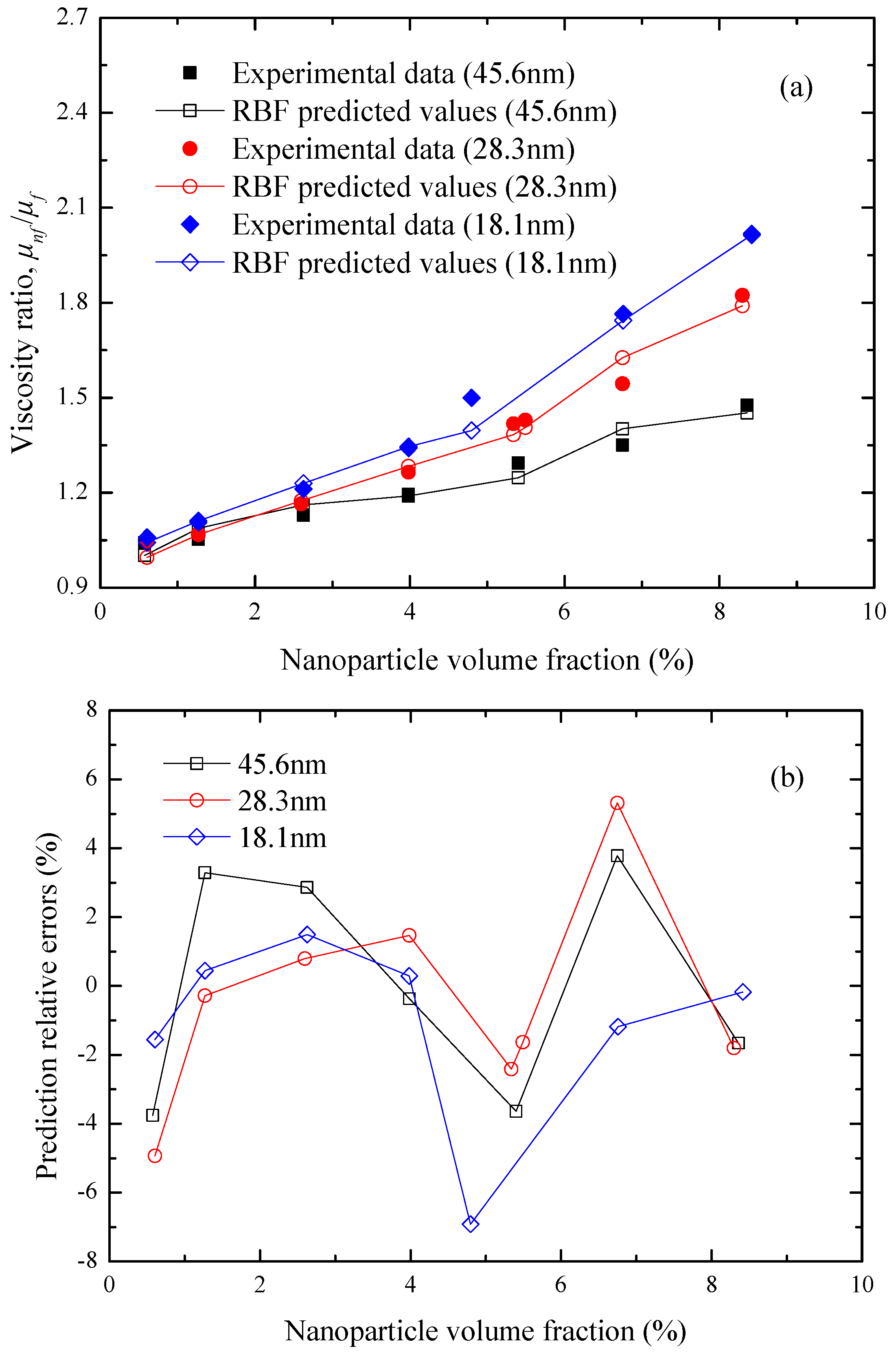
Figure 7 compares the experimental viscosity ratio of Rudyak et al. [15] with the predicted values of the RBF neural network for the SiO₂-ethylene glycol nanofluids at T = 25 °C as a function of the nanoparticle volume fraction and diameter. It can be found from Figure 7a that the RBF predicted viscosity ratio of nanofluids are obviously enhanced with the increase of the SiO₂ nanoparticle volume fraction and the decrease of the nanoparticle size, which are consistent with the experimental results. All the prediction relative errors are within ±8%, as shown in Figure 7b. 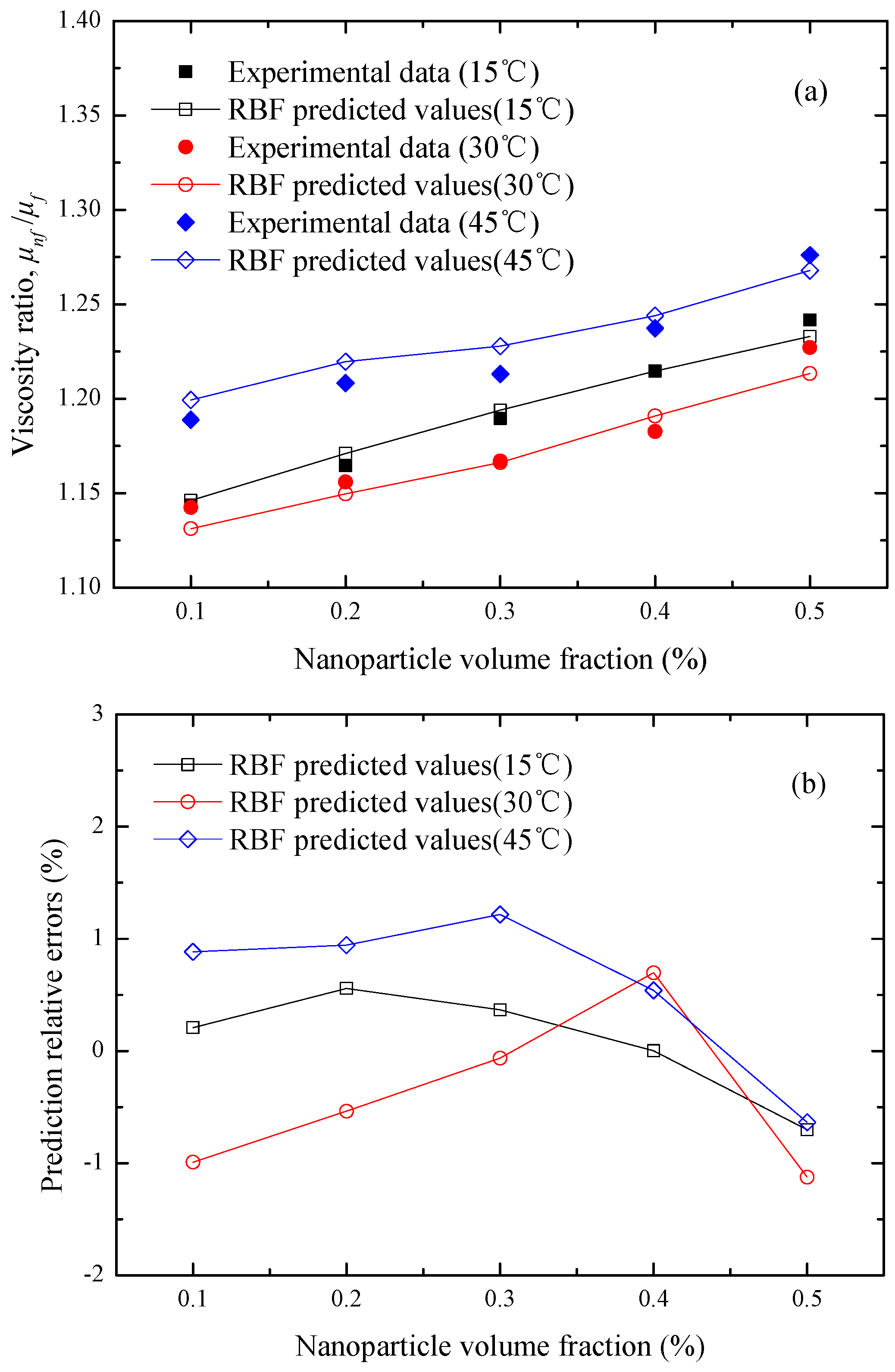On this basis, Figure 8 illustrates the comparisons between the RBF predicted values and the corresponding experimental data of Li et al. [19]. The results indicate that the RBF neural network developed in this study can be applied successfully for predicting the effects of the nanoparticle volume fraction and temperature on the viscosity ratio of SiC-ethylene glycol/water (40:60 by weight ratio) nanofluids with a satisfactory accuracy. 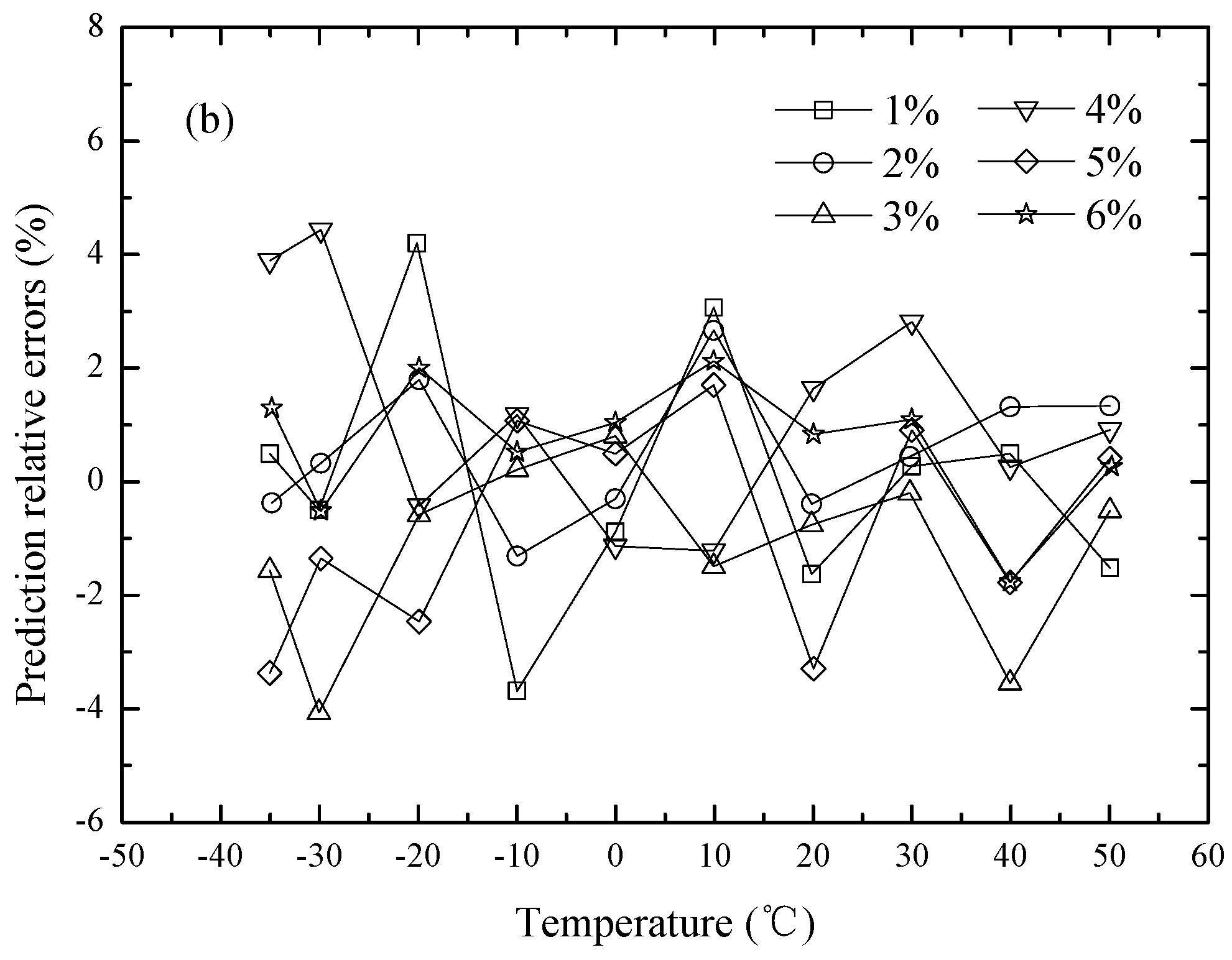In addition, a similar analysis is performed for the CuO-ethylene glycol/water (60:40 by weight ratio) nanofluids as a function of temperature, which is presented in Figure 9. It is demonstrated that the viscosity ratio characteristics of the above nanofluids are effectively predicted by the RBF neural network in a wide range of nanoparticle volume fractions (from 1% to 6%) and temperatures (from −35 to 50 °C). The maximum prediction relative errors are only 4.2%. All the above analyses further demonstrate that the RBF neural network is one of the potential tools to quantitatively establish nonlinear relationships between inputs and outputs.

Figure 7. (a) Predicted comparisons and (b) relative errors of the RBF predicted μ_nf/μ_f and the experimental data [15] for SiO₂-ethylene glycol nanofluids at T = 25 °C.

Figure 8. (a) Predicted comparisons and (b) relative errors of the RBF predicted μ_nf/μ_f and the experimental data [19] for SiC-ethylene glycol/water (40:60 by weight ratio) nanofluids at d_p = 30 nm.

Figure 9. (a) Predicted comparisons and (b) relative errors of the RBF predicted μ_nf/μ_f and the experimental data [14] for CuO-ethylene glycol/water (60:40 by weight ratio) nanofluids at d_p = 30 nm.

Table 8 shows the prediction performance of the RBF neural network using different viscosity data sets. It is worth noting that the data sets are selected randomly. From Table 8, we found that the size of the data set can affect the modeling and prediction of the RBF neural network significantly. With the decrease of the data set size, the prediction accuracy will decrease. This may mean that to accurately predict the viscosity of ethylene glycol/water based nanofluids using the RBF neural network, a large enough data set is necessary.

Table 8. Performance evaluation of the RBF neural network with different viscosity data.

Evaluation Criteria	216 Data	200 Data	160 Data	120 Data
RMSE	0.04615	0.07017	0.09547	0.37982
MAPE (%)	2.12738	2.88920	3.64470	8.75159
SSE	0.46007	0.98468	1.45844	17.31116
R2	0.99925	0.99832	0.99505	0.90323

5. Conclusions

To accurately predict the viscosity ratio between ethylene glycol/water nanofluids and a base fluid, a RBF neural network based model was developed and evaluated in the present study. Based on the comparative analysis, the following conclusions were obtained.

(1)

Considering the complex effects of different factors including temperature, nanoparticle properties (such as volume fraction, density, diameter), and viscosity of the base fluid on the viscosity ratio and the effect of Spread on modeling performance of the RBF neural network, the final network structure was determined to be 5-56-1 neurons.

(2)

By comparing the RBF predictive values and the experimental data published in various studies, it was demonstrated that the RBF neural network not only exhibited good modeling accuracy (RMSE = 0.04615, MAPE = 2.12738%, SSE = 0.46007, R² = 0.99925), but also could effectively predict the influences of temperature, nanoparticle volume fraction, and diameter on the viscosity ratio of different ethylene glycol/water based nanofluids.

(3)

Compared to the typical viscosity models, namely the Batchelor model and Chen model, the RBF neural network has a good ability to predict the viscosity ratio of different ethylene glycol/water based nanofluids. However, the prediction performance can be affected by the size of the data set.

(4)

The present investigation may play an active role for developing the modeling of nanofluid viscosity. However, how to extend the application of ANN to predict other thermo-physical properties of nanofluids is still worthy of study in the future.