Modeling and Dynamics of a MDOF Isolation System

Abstract

This study analyzes the modeling and dynamics of a novel passive multi-degree-of-freedom (MDOF) vibration isolation platform which can achieve a significant isolation effect. Symmetrical scissor-like structures (SLSs) are utilized in the proposed MDOF isolation platform as the supporting and isolation elastic components. Based on the mathematical modeling and theoretical analysis of the MDOF vibration isolation system with SLSs, the effects of structural parameters and joint friction on the stiffness and damping properties are investigated. It is shown that due to geometric relations within the SLSs, the natural frequencies can be reduced via adjusting structural parameters of the SLS for different direction vibration isolation. Theoretical and experimental results show that the SLS isolation platform can achieve much better loading capacity and vibration isolation performance simultaneously by only using linear passive components because of the MDOF adjustable stiffness property. Therefore, with low cost and energy consumption, the proposed novel isolation platform can improve the vibration suppression in various engineering practices.

1. Introduction

High stability and significant isolation performance are required for isolation systems because they isolate vibration to protect instruments and equipment from many vibrational environments. For different applications, different structures and control methods are carried out for different vibration suppression mechanisms; for example, energy transferring between different vibration modes [1,2,3,4,5,6], vibration suppression with absorbers [7,8,9], or utilizing semi-active/active vibration control methods, etc. [10,11,12]. In most cases in vibration isolation, better isolation effectiveness can be obtained by using elements with smaller restoring forces which results in a lower natural frequency of the system, especially for microgravity environments in aerospace engineering [13,14,15].

For various vibration isolation purposes, quasi-zero-stiffness (QZS) vibration isolation systems for one direction vibration have been extensively studied to improve working environments and provide a better background for aerospace devices and precision instruments [16,17,18,19,20,21,22,23,24]. In order to induce the adjustable stiffness property with sufficient loading capacity, a structure with springs, called scissor-like structure (SLS), is proposed. The most obvious advantage of the vibration isolation system with SLSs is that the natural frequency and nonlinear stiffness coefficients are dependent on the structural parameters, which could realize high static and low dynamic properties. Considering the advantages of the structure with SLSs, the SLSs are utilized to construct a novel MDOF vibration isolation system. The proposed isolation system has nonlinear stiffness and damping characteristics in six directions, which are all adjustable and can achieve superior vibration isolation using only pure linear and passive elements in the system with a simple and flexible installation structure.

In the literature, the techniques of vibration isolation for multi-direction excitation with excellent isolation performance over a larger frequency region have always been an attractive and difficult research topic. For the MDOF vibration isolation platform, active controllers are the chief method [13,14,15,25,26,27,28,29,30,31]. The key point of the mechanism of active control in a MDOF isolator is to generate anti-vibration forces in different directions by actuators and sensors in the designed system. The studies of MDOF isolation systems are focused on the controllers and control strategies. Different designs and the analysis of the dynamics of parallel mechanisms are studied [25,26,27,28,29,30,31], for example, a hybrid magnet consisting of an electromagnet and permanent magnets is used as the active actuators in [25,26]. Although active controllers can actively isolate vibration and control vibration in a timely manner, considering the energy required by active actuators, passive isolation techniques provide higher stability without any external power [32].

This paper proposed a MDOF isolation platform using SLSs as the elastic components. Then the natural frequencies and vibration responses are studied to show the isolation effectiveness of the proposed system. The multiple-degrees of freedom vibration isolation system can be achieved using only pure linear and passive elements in the system with a simple and flexible installation structure because of the adjustable stiffness. This system could provide an effective solution to many engineering problems for excellent MDOF vibration suppression and sustainable development for microgravity environments due to the multi-direction zero-stiffness property. The paper is organized as follows: The prototype of the isolation platform with SLSs is carried out and its mathematical modeling is obtained in Section 2. In Section 3, the responses of the isolation system obtained by the harmonic balance method (HBM) [33] and experiments are conducted, and the isolation effectiveness of the proposed isolation system is compared to the one using linear springs as isolators. A conclusion is drawn at the last section.

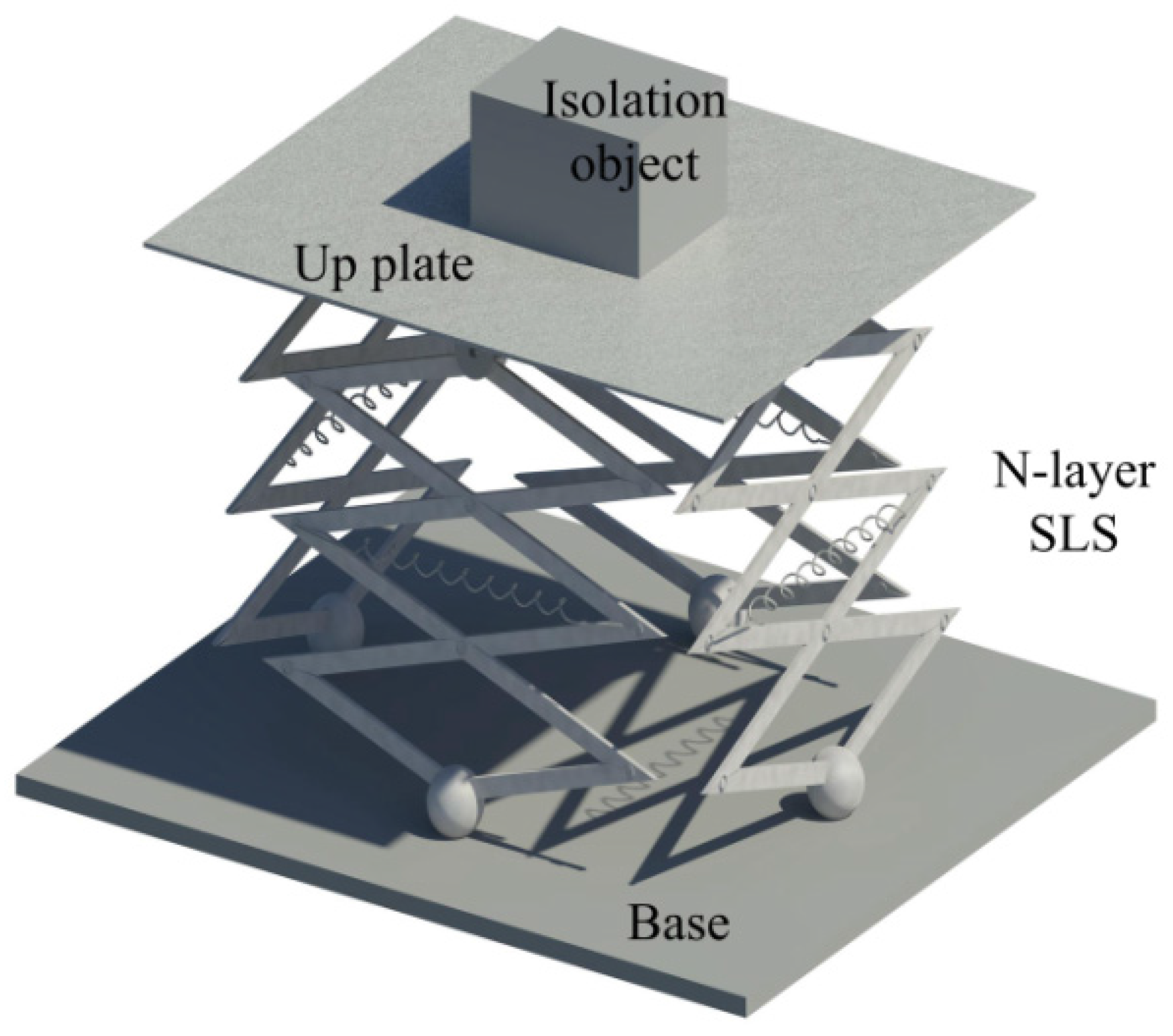
2. The Prototype and Modeling of the Proposed Isolation Platform

2.1. Experimental Prototype

Figure 1 is the experimental prototype of the proposed MDOF isolation system with SLSs. As shown in Figure 1, the up plate of the isolation platform is connected with the base by four scissor-like structures (SLSs). The SLS consists of several connecting rods and a linear spring is assembled in one layer in each SLS.

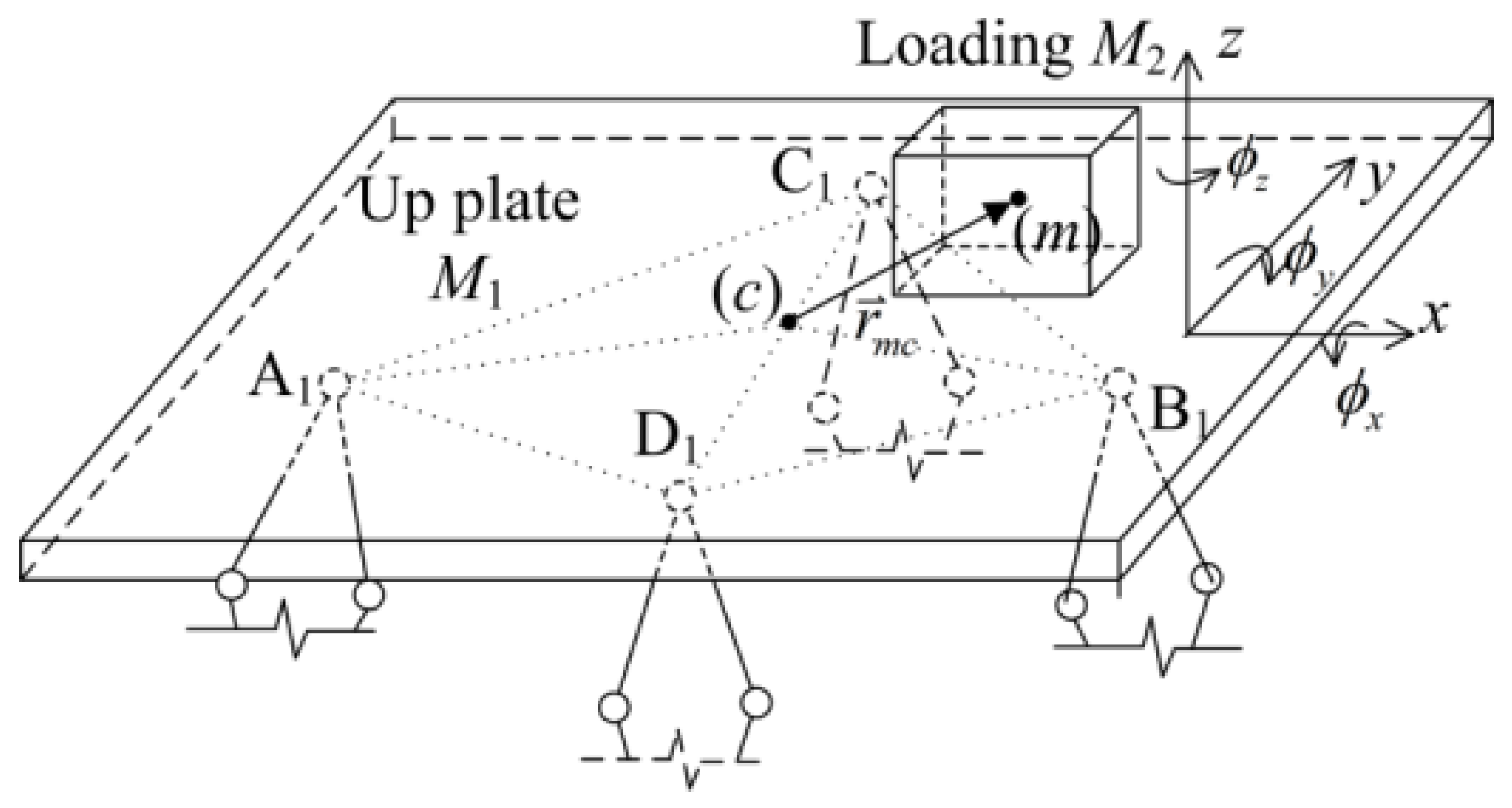
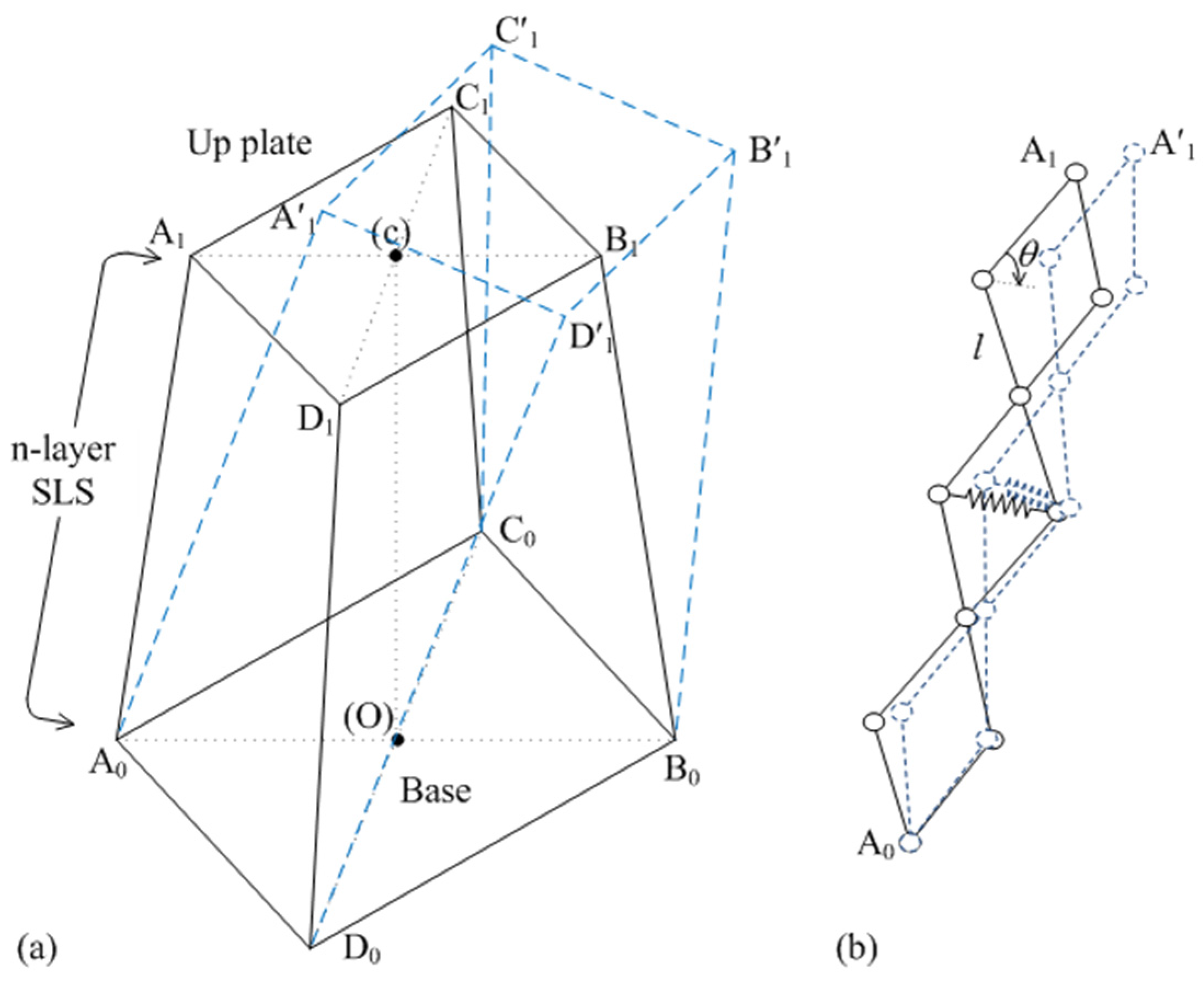
2.2. Structural Diagram

Figure 2 is the structural diagram of the isolation system. Considering the isolation platform is proposed for protecting an instrument (the isolation object) which is put in an arbitrary position on the up plate, the location of the isolation object and the connecting point of the SLS are shown in Figure 3.

In Figure 3, point (c) is the geometrical and mass center of the up plate M₁ and point (m) is the center of isolation object with mass M₂. The vector the origin of the up plate (c) and the isolation object (m) is as ${\mathit{r}}_{mc}$ = {L₁, L₂, L₃}. The absolute motions of the platform x = {x, y, z, φ_x, φ_y, φ_z} are chosen as generalized coordinates.

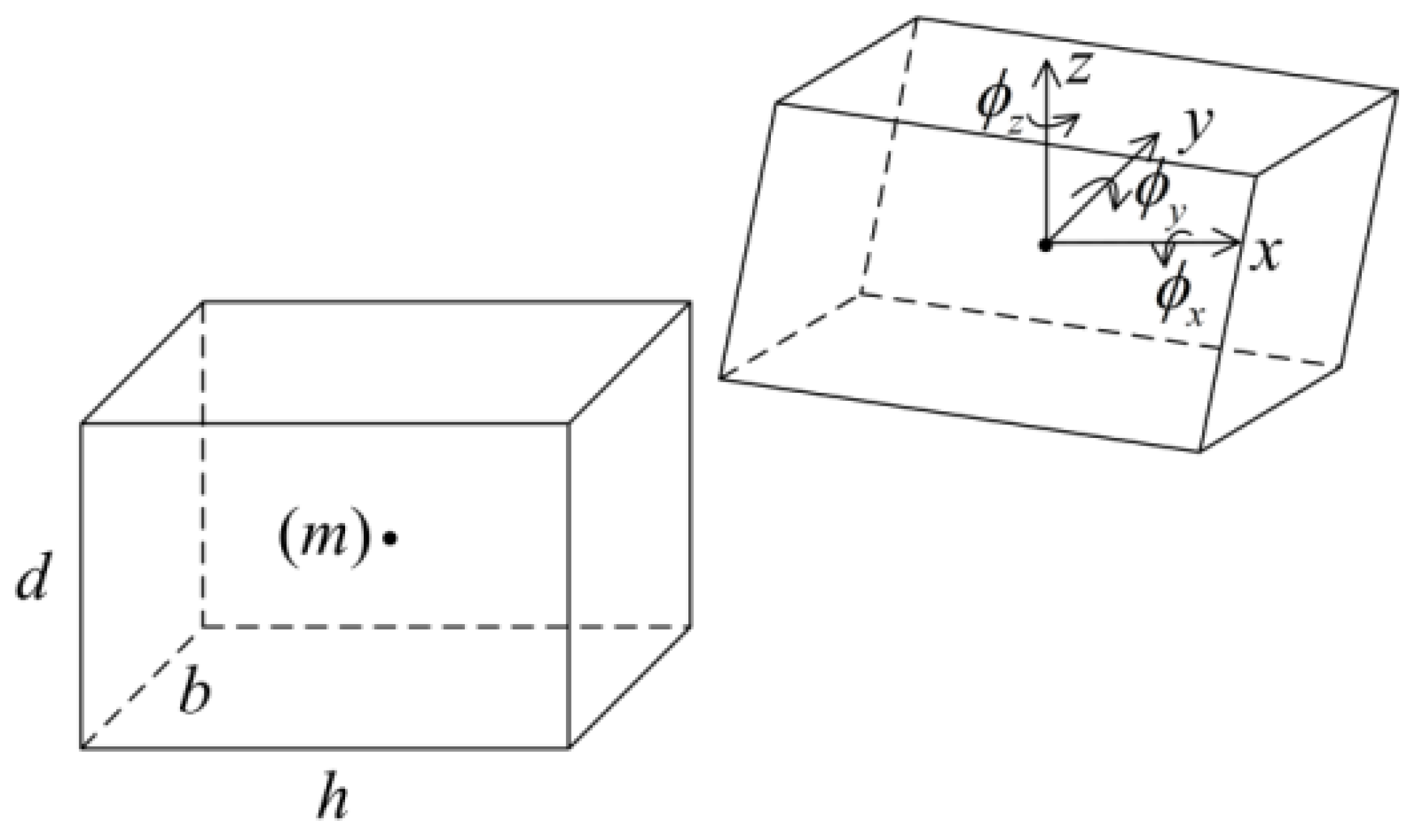
2.3. Modeling

Lagrange principle is used to obtain the model of the isolation platform. The mass of the connecting rods and joints in SLSs are neglected because their weights are much smaller compared to the up plate, base, and isolation object. The kinetic energy consists of the up plate and the isolation object M₂, which are set as T₁ and T₂. The velocity of the up plate is the velocity at the center (c); thus, the kinetic energy T₁ is:

$$T_1=\frac{1}{2}{M}_1({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)+\frac{1}{2}{J}_{xx}{\dot{\varphi }}_x^2+\frac{1}{2}{J}_{yy}{\dot{\varphi }}_y^2+\frac{1}{2}{J}_{zz}{\dot{\varphi }}_z^2$$

(1)

For the isolation object M₂ whose center has a distance from the center of the up plate, its velocity contains the translational velocity around point (c) and the rotational velocity around the center point (m). Figure 4 is the motions of the isolation object M₂ which represents the isolation object (e.g., precise instruments etc.).

Figure 4 is the motion of the isolation object M₂ on the up plate whose moments of inertia in different rotational directions are defined as J_xxm, J_yym, and J_zzm. Figure 5 is the deflection of one of the SLSs in the isolator. From Figure 4, the kinetic energy T₂ of the isolation object is:

$$T_2=\frac{1}{2}{M}_2\left[{\left(\dot{x}+{\dot{\varphi }}_y{L}_3-{\dot{\varphi }}_z{L}_2\right)}^2+{\left(\dot{y}-{\dot{\varphi }}_x{L}_3+{\dot{\varphi }}_z{L}_1\right)}^2+{\left(\dot{z}+{\dot{\varphi }}_x{L}_2-{\dot{\varphi }}_y{L}_1\right)}^2\right]+\frac{1}{2}{J}_{xxm}{\dot{\varphi }}_x^2+\frac{1}{2}{J}_{yym}{\dot{\varphi }}_y^2+\frac{1}{2}{J}_{zzm}{\dot{\varphi }}_z^2$$

(2)

Therefore, the kinetic energy T of the system is:

$$\begin{array}{cc}\hfill T=T_1+T_2& =\frac{1}{2}{M}_1({\dot{x}}^2+{\dot{y}}^2+{\dot{z}}^2)+\frac{1}{2}{J}_{xx}{\dot{\varphi }}_x^2+\frac{1}{2}{J}_{yy}{\dot{\varphi }}_y^2+\frac{1}{2}{J}_{zz}{\dot{\varphi }}_z^2\hfill \\ & +\frac{1}{2}{M}_2[{\left(\dot{x}+{\dot{\varphi }}_y{L}_3-{\dot{\varphi }}_z{L}_2\right)}^2+ {\left(\dot{y}-{\dot{\varphi }}_x{L}_3+{\dot{\varphi }}_z{L}_1\right)}^2\hfill \\ & +{\left(\dot{z}+{\dot{\varphi }}_x{L}_2-{\dot{\varphi }}_y{L}_1\right)}^2]+\frac{1}{2}{J}_{xxm}{\dot{\varphi }}_x^2+ \frac{1}{2}{J}_{yym}{\dot{\varphi }}_y^2+\frac{1}{2}{J}_{zzm}{\dot{\varphi }}_z^2\hfill \end{array}$$

(3)

The potential energy V of the system is from the deformation of the springs in the SLSs. The deflections of the SLSs in the system are shown in Figure 5. The points connected by the SLSs in the base are defined as A₀, B₀, and C₀; the points in the up plate are defined as A₁, B₁, and C₁; and the points in the up plate for deflections are defined as A′₁, B′₁, and C′₁.

Figure 5 shows the deflections of the MDOF vibration isolation system and each SLS. From Figure 5a, it can be seen that the points A₀, B₀, C₀, and D₀ make a quadrilateral, and A₁, B₁, C₁, and D₁ also make a quadrilateral. From Figure 5b, which is the deflection of the SLS, the original length of the springs in a SLS is 2lcosθ, and the length of the springs can be obtained by $\Vert A_0{A}_1\Vert$. Since the absolute motions of the up plate at the center x = {x, y, z, φ_x, φ_y, φ_z} are chosen as generalized coordinate where x, y, and z are the absolute translational motions and φ_x, φ_y, and φ_z are absolute rotational motions, the location of point A′₁, B′₁, and C′₁ can be obtained by a coordinate transformation matrix. Due to the six-excitation excitations from the base, which are x_e = {x_e, y_e, z_e, φ_xe, φ_ye, φ_ze}, the relative motions of the up plate at the center are $\widehat{\mathit{x}}$ = {$\widehat{x}$, $\widehat{y}$, $\widehat{z}$, ${\widehat{\varphi }}_x$, ${\widehat{\varphi }}_y$, ${\widehat{\varphi }}_z$}. The transformation matrices in the three rotational directions are R_x, R_y, and R_z; thus, the rotational transformation matrix is defined as R, which is the dot product of the three transformation matrices.

$$\begin{array}{cc}\hfill R& =R_x\cdot R_y\cdot R_z=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos {\widehat{\varphi }}_x& \sin {\widehat{\varphi }}_x\\ 0& -\sin {\widehat{\varphi }}_x& \cos {\widehat{\varphi }}_x\end{array}\right]\cdot \left[\begin{array}{ccc}\cos {\widehat{\varphi }}_y& 0& -\sin {\widehat{\varphi }}_y\\ 0& 1& 0\\ \sin {\widehat{\varphi }}_y& 0& \cos {\widehat{\varphi }}_y\end{array}\right]\cdot \left[\begin{array}{ccc}\cos {\widehat{\varphi }}_z& \sin {\widehat{\varphi }}_z& 0\\ -\sin {\widehat{\varphi }}_z& \cos {\widehat{\varphi }}_z& 0\\ 0& 0& 1\end{array}\right]\hfill \\ & =\left[\begin{array}{ccc}\cos {\widehat{\varphi }}_y\cos {\widehat{\varphi }}_z& \cos {\widehat{\varphi }}_y\sin {\widehat{\varphi }}_z& -\sin {\widehat{\varphi }}_y\\ \sin {\widehat{\varphi }}_x\sin {\widehat{\varphi }}_y\cos {\widehat{\varphi }}_z-\cos {\widehat{\varphi }}_x\sin {\widehat{\varphi }}_z& \cos {\widehat{\varphi }}_x\cos {\widehat{\varphi }}_z+\sin {\widehat{\varphi }}_x\sin {\widehat{\varphi }}_y\sin {\widehat{\varphi }}_z& \sin {\widehat{\varphi }}_x\cos {\widehat{\varphi }}_y\\ \cos {\widehat{\varphi }}_x\sin {\widehat{\varphi }}_y\cos {\widehat{\varphi }}_z+\sin {\widehat{\varphi }}_x\sin {\widehat{\varphi }}_z& -\sin {\widehat{\varphi }}_x\cos {\widehat{\varphi }}_z+\cos {\widehat{\varphi }}_x\sin {\widehat{\varphi }}_y\sin {\widehat{\varphi }}_z& \cos {\widehat{\varphi }}_x\cos {\widehat{\varphi }}_y\end{array}\right]\hfill \end{array}$$

(4)

where R_x, R_y, and R_z are rotational transformation matrices in the φ_x, φ_y, and φ_z directions.

From Figure 5, assuming the coordinate of point (c) is {0, 0, 0}, for the generalization of the results, the vector cA₀, cB₀, cC₀, and cD₀ are assumed as cA₀ = {x_a0, y_a0, z_a0}, cB₀ = {x_b0, y_b0, z_b0}, cC₀ = {x_c0, y_c0, z_c0}, and cD₀ = {x_d0, y_d0, z_d0}, and the vector cA₁, cB₁, cC₁, and cD₁ are assumed as cA₁ = {x_a1, y_a1, z_a1}, cB₁ = {x_b1, y_b1, z_b1}, cC₁ = {x_c1, y_c1, z_c1}, and cD₁ = {x_d1, y_d1, z_d1}. Therefore, the vector A₀A′₁, B₀B′₁, C₀C′₁, and D₀D′₁ can be obtained by the translational motion matrix and rotational transformation matrix as:

$$\{\begin{array}{l}{A}_0{A^{\prime }}_1=c{A^{\prime }}_0-c{A}_0=\left\{\widehat{x},\widehat{y},\widehat{z}\right\}+R\cdot c{A}_1-c{A}_0\\ B_0{B^{\prime }}_1=c{B^{\prime }}_0-c{B}_0=\left\{\widehat{x},\widehat{y},\widehat{z}\right\}+R\cdot c{B}_1-c{B}_0\\ C_0{C^{\prime }}_1=c{C^{\prime }}_0-c{C}_0=\left\{\widehat{x},\widehat{y},\widehat{z}\right\}+R\cdot c{C}_1-c{C}_0\\ D_0{D^{\prime }}_1=c{D^{\prime }}_0-c{D}_0=\left\{\widehat{x},\widehat{y},\widehat{z}\right\}+R\cdot c{D}_1-c{D}_0\end{array}$$

(5)

From Equation (5), the deflection of the axis of an SLS is obtained, and then the deformations of springs in an SLS can be obtained by the analysis of the shape of the SLS. Figure 6 shows the deflection of one layer of the SLS.

From Figure 6a, it can be seen that the original length of springs in the SLS is 2lcosθ. For deflection, the lengths of the springs in the three SLS are defined as l_a, l_b, l_c, and l_d, which can be obtained by the triangular relationship shown in Figure 6b which is:

$$\{\begin{array}{l}{l}_a^2+{\left(\Vert A_0{A^{\prime }}_1\Vert /n\right)}^2=4l^2\\ l_b^2+{\left(\Vert B_0{B^{\prime }}_1\Vert /n\right)}^2=4l^2\\ l_c^2+{\left(\Vert C_0{C^{\prime }}_1\Vert /n\right)}^2=4l^2\\ l_d^2+{\left(\Vert D_0{D^{\prime }}_1\Vert /n\right)}^2=4l^2\end{array}$$

(6)

The potential energy V of the system is consisted of the elastic energy of the four springs in SLSs, which can be expressed as:

$$\begin{array}{cc}\hfill V& =\frac{1}{2}k{\left(l_a-2l\cos \theta \right)}^2+\frac{1}{2}k{\left(l_b-2l\cos \theta \right)}^2+\frac{1}{2}k{\left(l_c-2l\cos \theta \right)}^2+\frac{1}{2}k{\left(l_d-2l\cos \theta \right)}^2\hfill \\ & =\frac{1}{2}k{\left(\sqrt{4l^2-\frac{{\Vert A_0{A^{\prime }}_1\Vert }^2}{n^2}}-2l\cos \theta \right)}^2+\frac{1}{2}k{\left(\sqrt{4l^2-\frac{{\Vert B_0{B^{\prime }}_1\Vert }^2}{n^2}}-2l\cos \theta \right)}^2\hfill \\ & +\frac{1}{2}k{\left(\sqrt{4l^2-\frac{{\Vert C_0{C^{\prime }}_1\Vert }^2}{n^2}}-2l\cos \theta \right)}^2+\frac{1}{2}k{\left(\sqrt{4l^2-\frac{{\Vert D_0{D^{\prime }}_1\Vert }^2}{n^2}}-2l\cos \theta \right)}^2\hfill \end{array}$$

(7)

Considering the air damping of the system, the dynamic equation can be obtained by the Lagrange principle as:

$$\frac{d}{dt}\left[\frac{\partial \left(T-V\right)}{\partial \dot{\mathit{x}}}\right]-\frac{\partial \left(T-V\right)}{\partial \mathit{x}}=-\mathit{C}\cdot \left(\dot{\mathit{x}}-{\dot{\mathit{x}}}_e\right)$$

(8)

where T is the kinetic energy and V is the potential energy shown as Equations (3) and (7), the mass matrix M of the system is:

$$\begin{array}{cc}\hfill \mathit{M}=& [\begin{array}{ccc}{M}_1+M_2& 0& 0\\ 0& M_1+M_2& 0\\ 0& 0& M_1+M_2\\ 0& -M_2{L}_3& M_2{L}_2\\ M_2{L}_3& 0& -M_2{L}_1\\ -M_2{L}_2& M_2{L}_1& 0\end{array}\hfill \\ & \begin{array}{ccc}0& M_2{L}_3& -M_2{L}_2\\ -M_2{L}_3& 0& M_2{L}_1\\ M_2{L}_2& -M_2{L}_1& 0\\ J_{xc}+J_{xm}+M_2\left(L_2^2+L_3^2\right)& -M_2{L}_1{L}_2& -M_2{L}_1{L}_3\\ -M_2{L}_1{L}_2& J_{yc}+J_{ym}+M_2\left(L_1^2+L_3^2\right)& -M_2{L}_2{L}_3\\ -M_2{L}_1{L}_3& -M_2{L}_2{L}_3& J_{zc}+J_{zm}+M_2\left(L_1^2+L_2^2\right)\end{array}]\hfill \end{array}$$

(9)

After first-order Taylor series expansion, the stiffness matrix K is:

$$\mathit{K}=\left[\begin{array}{cccccc}\frac{k{\left(l_2-l_1\right)}^2}{2l^2{n}^4{\cos }^2\theta }& 0& 0& 0& \frac{k{l}_1\left(l_1-l_2\right)H}{2l^2{n}^4{\cos }^2\theta }& 0\\ 0& \frac{k{\left(l_2-l_1\right)}^2}{2l^2{n}^4{\cos }^2\theta }& 0& \frac{k{l}_1\left(l_2-l_1\right)H}{2l^2{n}^4{\cos }^2\theta }& 0& 0\\ 0& 0& \frac{k{H}^2}{l^2{n}^4{\cos }^2\theta }& 0& 0& 0\\ 0& \frac{k{l}_1\left(l_2-l_1\right)H}{2l^2{n}^4{\cos }^2\theta }& 0& \frac{k{l}_1^2{H}^2}{2l^2{n}^4{\cos }^2\theta }& 0& 0\\ \frac{k{l}_1\left(l_1-l_2\right)H}{2l^2{n}^4{\cos }^2\theta }& 0& 0& 0& \frac{k{l}_1^2{H}^2}{2l^2{n}^4{\cos }^2\theta }& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

(10)

where $H=\sqrt{4n^2{l}^2{\sin }^2\theta -{\left(l_2-l_1\right)}^2}$, and matrix C is the damping matrix of the system:

$$\mathit{C}=\left[\begin{array}{cccccc}{c}_1& & & \cdots & & 0\\ & c_2& & & & \\ & & c_3& & & ⋮\\ ⋮& & & c_4& & \\ & & & & c_5& \\ 0& & \cdots & & & c_6\end{array}\right]$$

(11)

where c_i (i = 1, …, 6) are damping coefficients in the six coordinates.

Due to the assumptions that the amplitudes of motions are sufficiently small, each term in the dynamic equation can be expanded by a Taylor series and higher-order terms can be neglected. Therefore, the dynamic equation of the system is:

$$M\ddot{x}+Kx+C\dot{x}=K{x}_e+C{\dot{x}}_e$$

(12)

where M is the mass matrix, K is the stiffness matrix, and C is the damping matrix, respectively, and x is the motion vector and x_e is the base excitation vector. It can be seen that the stiffness coefficients in the stiffness matrix K are dependent on the structural parameters. The parameters θ and n are considered as adjustable parameters for the requirements of different applications.

According to the stiffness matrix K, the linear stiffness equals zero in the φ_z direction; thus, the minimum natural frequency of the system is zero. Therefore, it defined the value of the frequency where the first resonant peak occurs as the fundamental natural frequency of the proposed system. In this six-direction isolation system, the structural parameters’ stiffness and damping coefficients k and c_i are difficult to be changed because the springs and dampers are fixed components, while the structural parameters of SLSs n, θ, and l are easily adjusted. For M₁ = 2.75 (kg), M₂ = 0.34375 (kg), k = 10,000 (N·m⁻¹), L₁ = 0.05 (m), L₂ = 0.05 (m), L₃ = 0.025 (m), J_xc = J_yc = 0.0573, J_zc = 0.11458, J_xm = J_ym = J_zm = 0.0001432, l₁ = 0.2 (m), l₂ = 0.5 (m), and c_i = 2 (N·s·m⁻¹), the values of the natural frequencies of the system for different values of n, θ, and l are shown in Figure 7.

From Figure 7, the fundamental natural frequency of the isolation platform with SLSs can be adjusted by different structural parameters n, θ, and l. It can be seen that the fundamental natural frequency is reduced for increasing n or decreasing θ and l of the SLSs in the isolation platform. As the layer of SLSs increases from one layer to five layers, the fundamental natural frequency reduces from about 70 rad/s to 20 rad/s, as raising the assembly angle of the connecting rods in SLSs from 0.4 to 1.2 rad, the natural frequency increases to about 110 rad/s, and for increasing the length of the rods to 0.4 m, the natural frequency increases to 50 rad/s. Therefore, adjusting the structural parameters of the SLSs in the isolation platform system is effective in reducing the natural frequency, which could improve the isolation effectiveness of the system.

3. Isolation Effect

3.1. Solutions of the System

The isolation effect of the proposed MDOF isolation platform with SLSs reflected by displacement transmissibility is based on the dynamic equation (Equation (12)) and the responses for different structural parameters can be obtained by solving the linearized dynamic equations. When vibration only exits in one direction, the natural frequency in this direction follows $\sqrt{\raisebox{1ex}{$linear stiffness coeffcient$}\!\left/ \!\raisebox{-1ex}{$equvalient mass$}\right.}$, e.g., ${\omega }_x=\sqrt{\frac{2k_l{\cos }^2\varphi {\tan }^2\theta }{M{n}^2}}$ for $z_y=z_{\phi }=\widehat{y}=\widehat{\phi }=0$; ${\omega }_y=\sqrt{\frac{2k_l{\sin }^2\varphi {\tan }^2\theta }{M{n}^2}}$ for $z_x=z_{\phi }=\widehat{x}=\widehat{\phi }=0$; ${\omega }_{\phi }=\sqrt{\frac{2k_l{L}^2{\sin }^2\varphi {\tan }^2}{J{n}^2\theta }}$ for $z_x=z_y=\widehat{x}=\widehat{y}=0$. While there are vibrations in all the three directions, the stiffness matrix in Equation (13) reveals that the three-direction vibrations are coupled in linear parts; thus, the anti-frequency band, where the amplitude of response is very small because of the anti-frequency point, occurs and the bandwidth of the bandgap is dependent on the adjustable structural parameters n, θ, and φ. When the excitation is harmonic excitation, such as x_ei = e_icosωt, the responses could be set as x_i = a_icos(ωt + ϕ). Then, the displacement transmissibility T_i (dB) could be defined as the ratio between the amplitude of the response and the excitation in respective directions as:

$$T_i=10{\log }_{10}\left(\frac{\left|a_i\right|}{\left|e_i\right|}\right)\left(i=x,y,z,{\varphi }_x,{\varphi }_y,{\varphi }_z\right)$$

(13)

where a_i is the amplitude of response and e_i is the amplitude of the harmonic excitation in different directions. The dynamic equation (Equation (12)) and mass, stiffness, and damping matrices, reveal that the values of the components of the dynamic equations of each degree of freedom can be adjusted by changing the values of the structural parameters n, θ, and l. The isolation effects for different structural parameters are shown in Figure 8.

From Figure 8, it can be seen that, firstly, the natural frequency where has largest peak is reduced by increasing n, or decreasing θ and l, which verifies the analysis of natural frequencies in the previous section. Secondly, the value of the peak is reduced by increasing n and l, while changing θ has no obvious effect on the value of the peak and, thirdly, the response of the amplitudes are lower for larger n and l, or smaller θ. Additionally, it demonstrates that the value of the displacement transmissibility (dB) in the frequency range from zero to the first resonant peak could be controlled to less than zero and the displacement transmissibility is always below zero after the first resonant peak for larger n or l and smaller θ. Therefore, it can be concluded that the isolation effectiveness in a broad frequency band of the proposed isolation platform with SLSs can be improved by adjusting the structural parameters n, θ, and l easily.

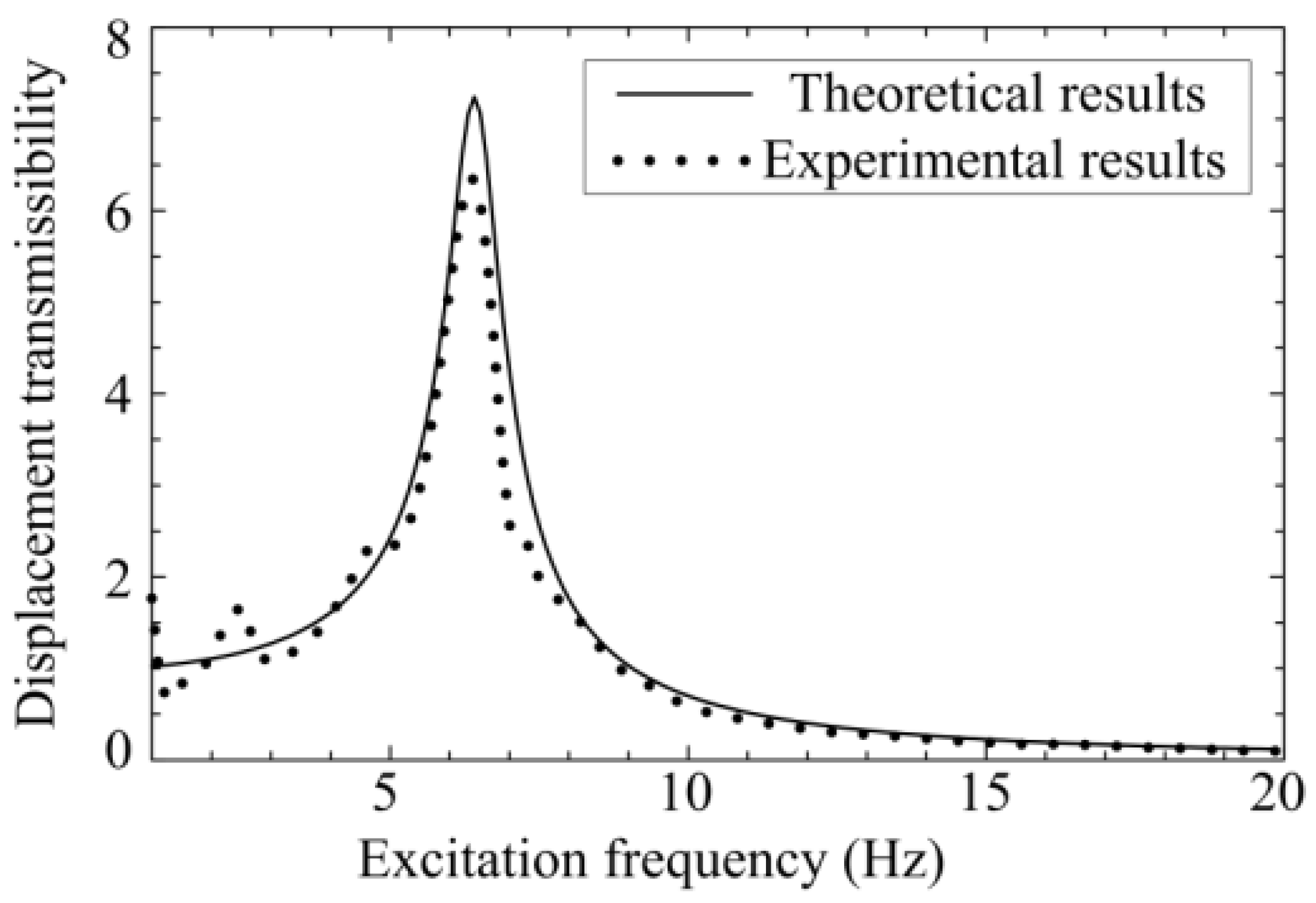
3.2. Comparison with a Normal Spring-Mass Isolation Platform

The isolation effectiveness of the isolation platform with SLSs and springs are compared, which is shown in Figure 9. For two cases, n = 2, θ = π/4, l = 0.2 (case 1) and n = 3, θ = π/6, l = 0.2 (case 2), the performances of isolation platform with springs and SLSs are obtained and shown in Figure 9.

From Figure 9, it can be seen that the isolation platform with springs has two obvious resonant peaks are about 100 and 110 rad·s⁻¹ expect zero. While for the two cases of the isolation platform using SLSs, the fundamental natural frequency is much smaller than the one using springs. For case 1 as n = 2, θ = π/4 and l = 0.2, the first resonant peak is at about 50 rad·s⁻¹, and for case 2 as n = 3, θ = π/6 and l = 0.2, the first resonant peak is at 25 rad·s⁻¹. Additionally, the values of displacement transmissibility for the two cases of the platform with SLSs are much smaller than the case with springs in a broad frequency domain.

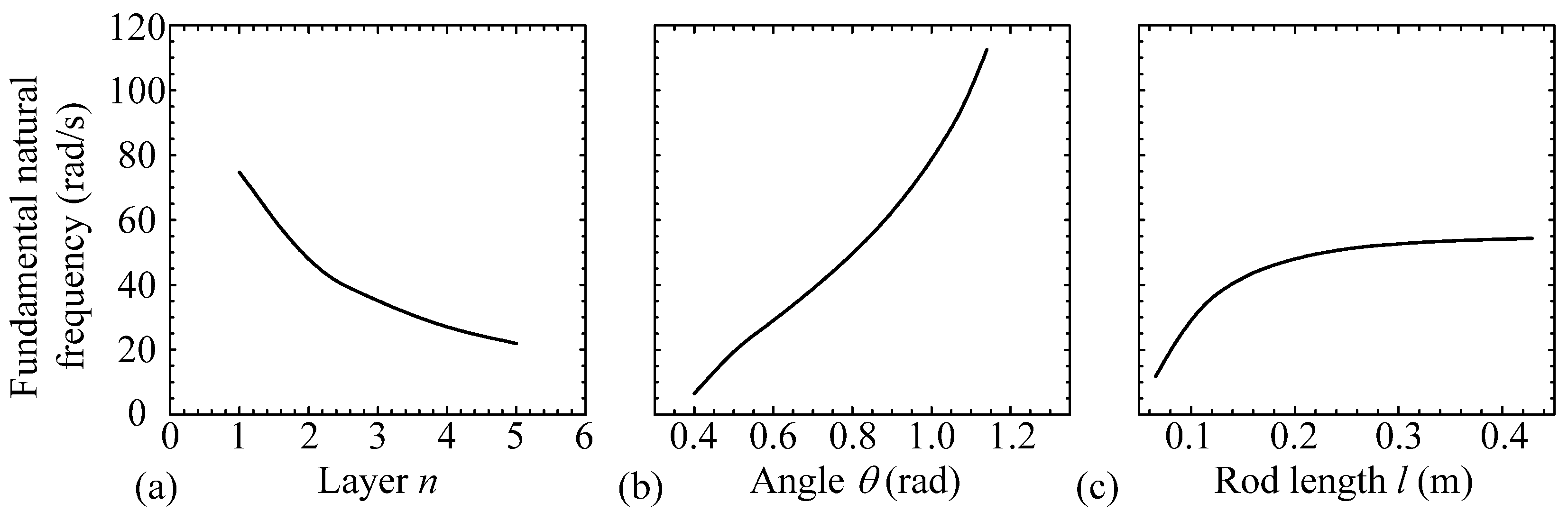
3.3. Isolation Effectiveness

In order to obtain the natural frequency of the proposed MDOF isolation platform and its isolation effectiveness, random excitation is proposed on the base and the response of the experimental prototype. The frequency domain of the random excitation is from 0 to 100 Hz. The structural parameters of the experimental prototype are n = 2, l = 0.1, l₂ = 0.285, l₁ = 0.105, M₂ = 0.22, M₁ = 0, L₁ = L₂ = L₃ = 0, and other structural parameters θ and k_l could be adjusted easily for different isolation requirements. In Figure 10, two cases of isolation effectiveness are shown with θ = π/3 and k_l = 900.

Figure 11 shows the comparison between the theoretical results and experimental results for the periodic excitation with z_e = 0.03, x_e = y_e = φ_xe = φ_ye = φ_ze = 0, θ = π/3, and k_l = 900. The signals of the measured base and the up plate are acceleration signals and the acceleration signals are converted to displacement signals by dividing the square of the frequency since the vibrations are periodic motions.

From Figure 11, the natural frequency of the proposed isolation platform could be reduced by adjusting the structural parameters of the SLSs for different structural parameters. When utilizing four springs with k_l = 900 in a normal spring-damping isolator, the vertical-direction natural frequency is as $\sqrt{\frac{4\times 900}{0.22}}=128\mathrm{rad}/\mathrm{s}$ ≈ 20.38 Hz, while for utilizing the SLSs the natural frequency could be reduced to about 6.4, Hz as shown in Figure 11 for θ = π/3, k_l = 900. Therefore, using SLSs instead of springs could improve the isolation effectiveness, based on the fact that the natural frequency is reduced and the effective isolation range is increased.

4. Conclusions

This study proposed a MDOF vibration isolation platform with four symmetrical scissor-like structures (SLSs), which is designed for multi-direction isolation applications, especially in microgravity environments, such as protecting instruments and isolation devices in aerospace applications. Theoretical modeling, analysis, and comparison studies demonstrated its advantages and versatility in vibration isolation/control. The advantages of this isolation platform are listed as follows:

(a)

By designing the structural parameters of SLSs, the proposed MDOF isolation platform can achieve a lower natural frequency and a much larger effective isolation frequency range compared with normal spring-mass isolators;

(b)

Due to the stiffness property with small linear coefficients in different directions of the proposed isolation platform, the system becomes an improved MDOF adjustable isolation platform; and

(c)

The adjustable stiffness coefficients in different directions and isolation effectiveness of the isolation platform with SLSs are verified by an experimental prototype and experimental results.

Further studies will focus on the effect of active control for a MDOF vibration isolation system using the scissor-like structures (SLSs) and the combined effect of control parameters and nonlinear coefficients on isolation performance.