The Experimental Study of the Temperature Effect on the Interfacial Properties of Fully Grouted Rock Bolt
Abstract
:1. Introduction
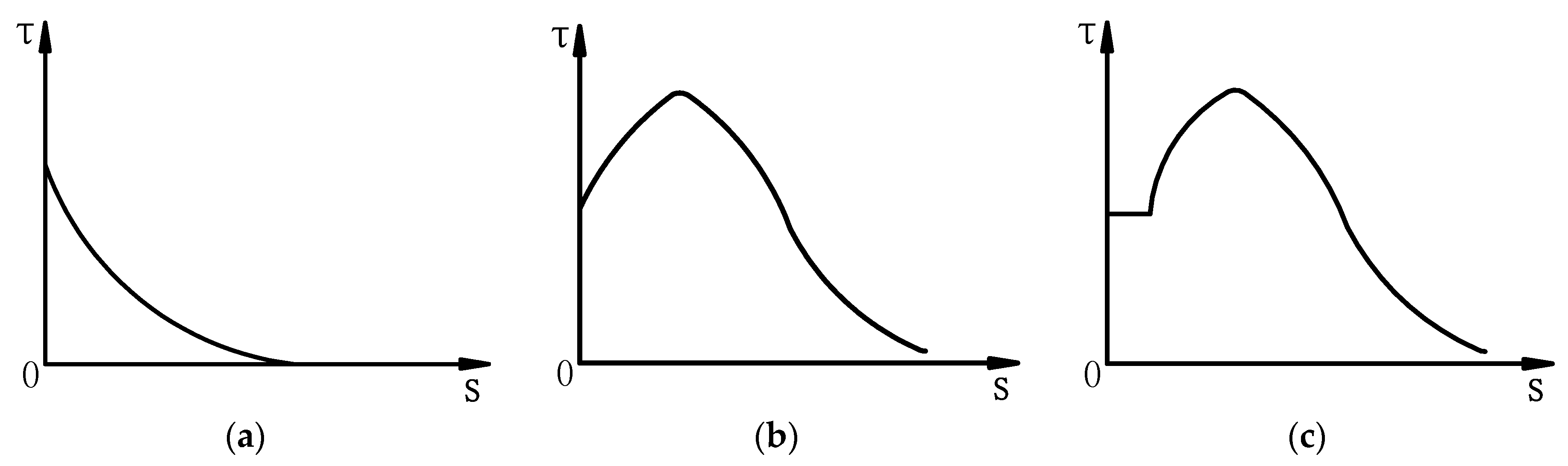
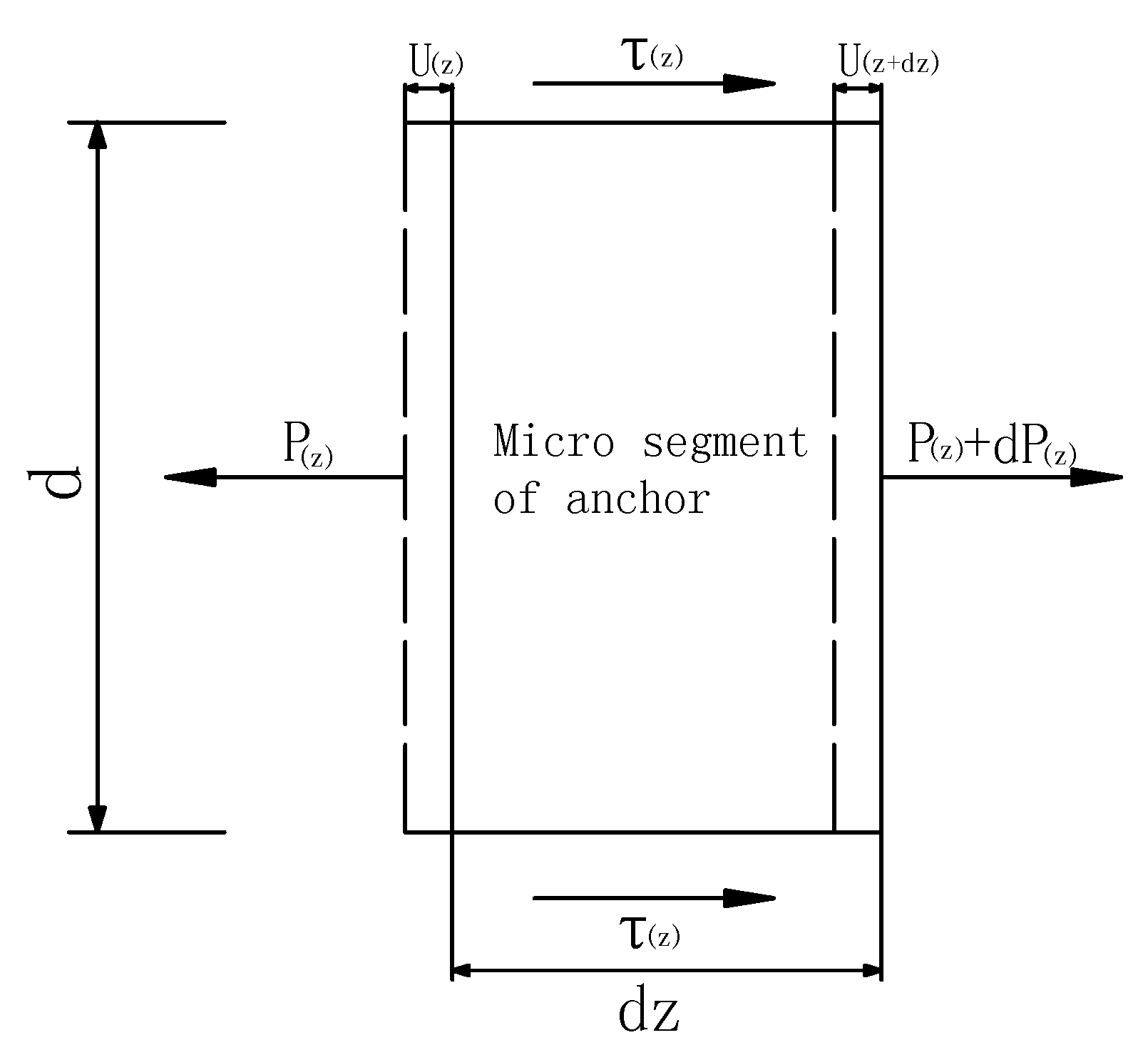
2. The Mechanical Principle of the Interfacial Bond between the Rock Bolt and the Grouting Body
3. Test Schemes
3.1. Test Introduction
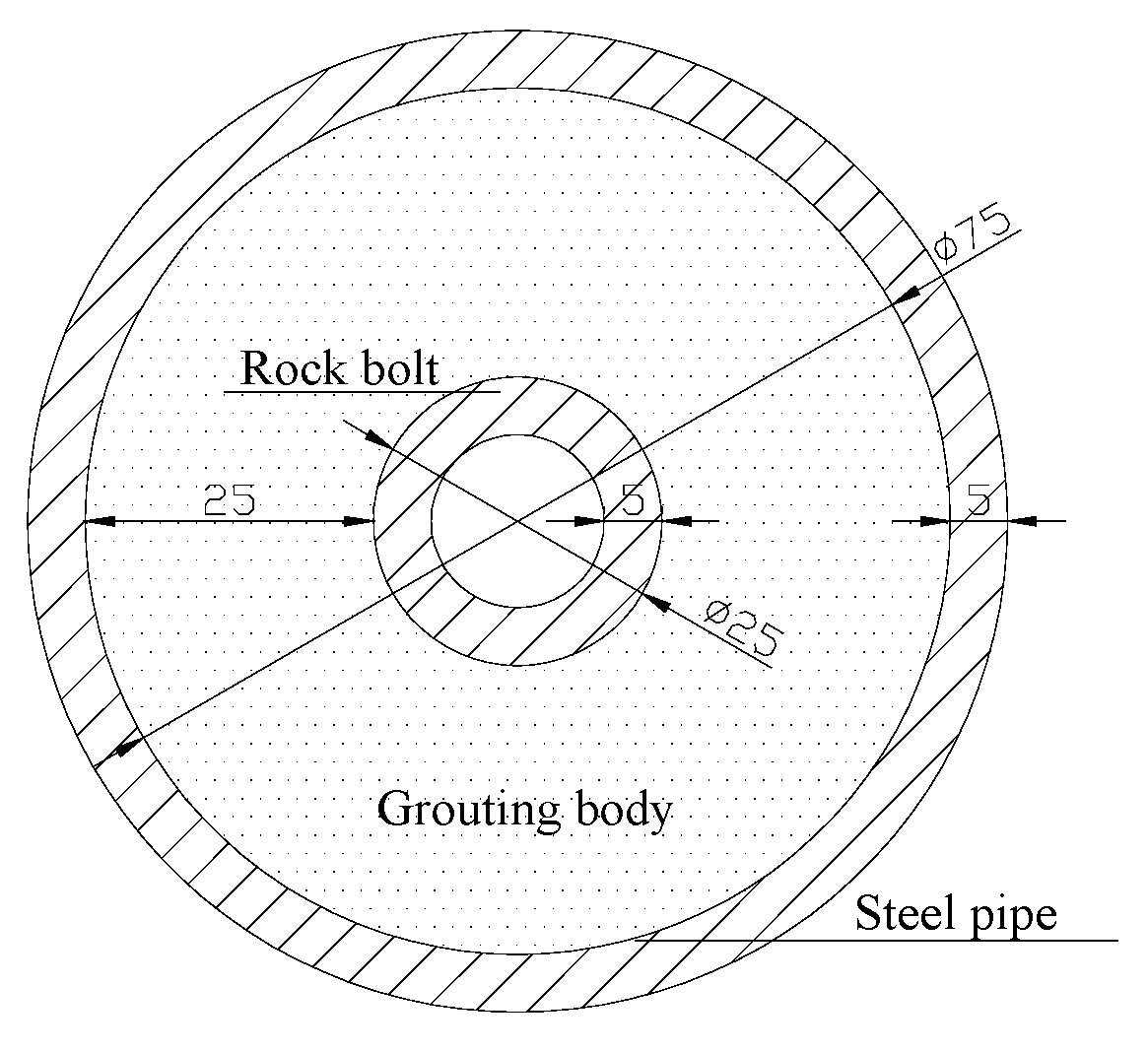
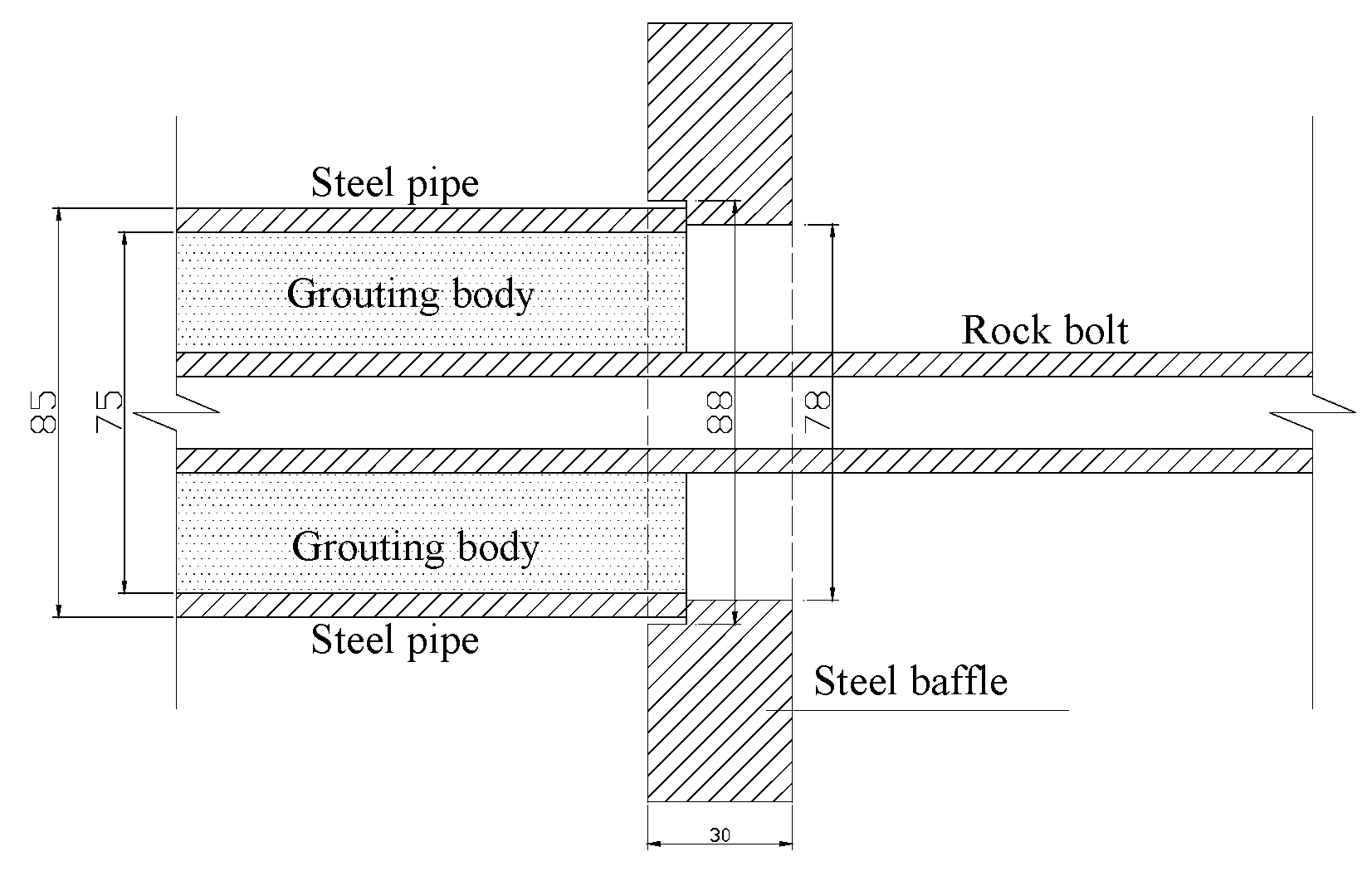
3.2. Test Materials and Device
3.3. Strain Gauge Layout and Test Procedure
4. Results and Discussion
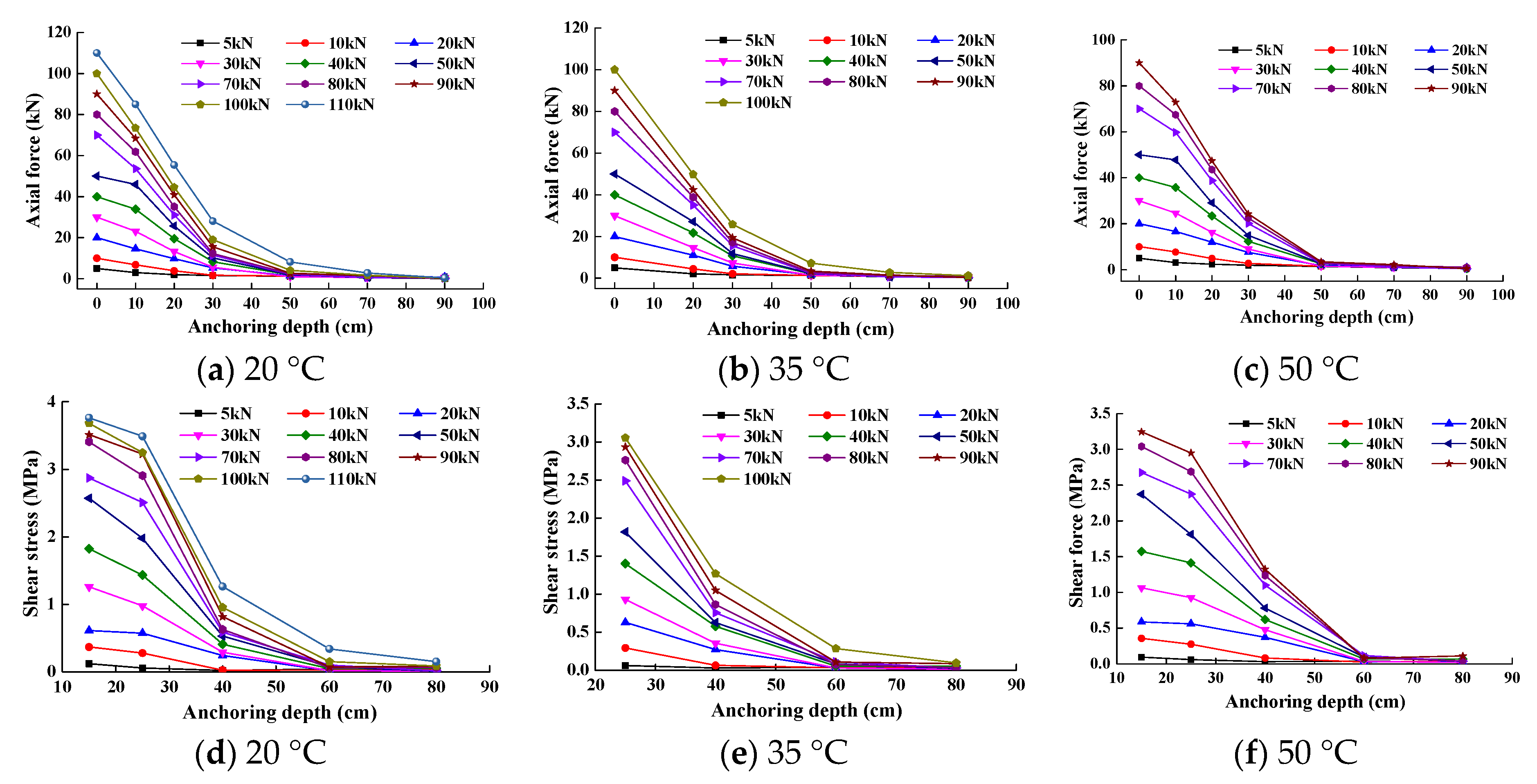
4.1. Distribution of Internal Force under Different Loads
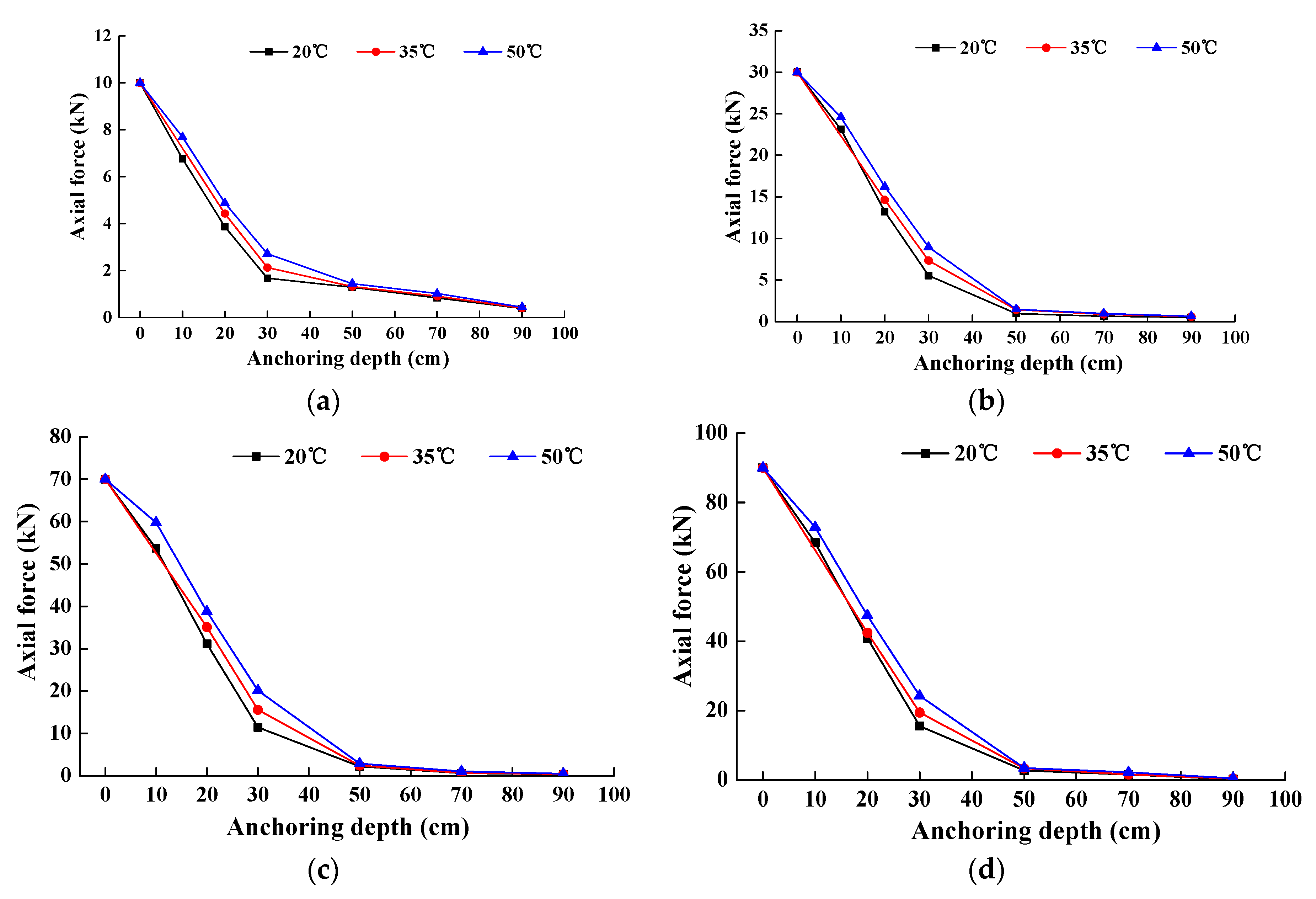
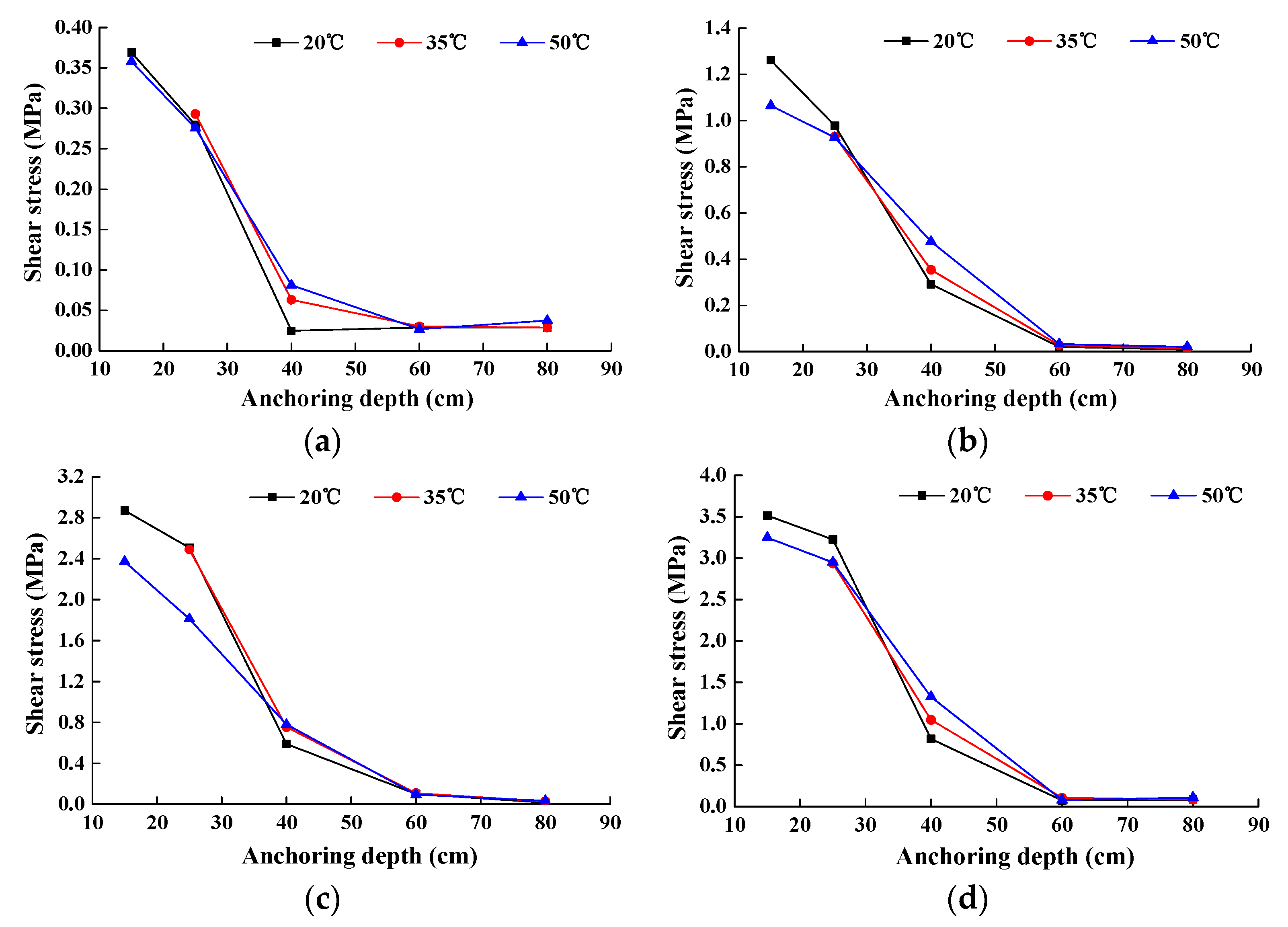
4.2. Effect of Temperature on the Axial Force and Shear Stress on the Interface of Specimens
5. Conclusions
- (1)
- With an increase in environmental temperature, the maximum shear stress on the interface between rock bolt and grouting body becomes smaller, while the distribution of shear stress along the length of the anchorage section becomes relatively uniform. A high temperature has little influence on the fully grouted rock bolt used in tunnel support construction with high geothermal activities. It is very important to avoid the evaporation of water during the strength growth process in future anchor construction.
- (2)
- With an increase in tensile force, the axial force and maximum shear stress on the interface between the rock bolt and the grouting body along the anchorage section increase correspondingly. Axial force and shear stress all gradually decreased from the pull end to the non-pull end until they became zero. The design length of the rock bolt should be longer than the critical length.
- (3)
- The performance of the anchorage system is also related to other factors except high geothermal The deformation of the surrounding rock will produce a large tensile force on the rock bolt. The coupling of high temperature and load will lead to further deterioration of the anchorage system. In addition, the roughness of the surrounding rock will affect the ultimate pull-out force of rock bolts. These are very important research areas for the future.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, T.; Zhu, B.; Zheng, J.; Liang, L. Numerical analysis of load transfer mechanism of recursive control rock bolt. J. Railw. Eng. Soc. 2013, 7, 11–15. [Google Scholar]
- Phillips, S. Factors Affecting the Design of Anchorages in Rock; Cementation Research Ltd.: London, UK, 1970. [Google Scholar]
- You, C. Theory and application study on stress-transfer mechanism of anchoring system. Shandong Univ. Sci. Technol. 2005, 24, 1272–1272. [Google Scholar]
- Zhang, J.; Tang, B. Hyperbolic function model to analyze load transfer mechanism on bolts. Chin. J. Geotech. Eng. 2002, 24, 188–192. [Google Scholar]
- Zhong, Z.; Lv, L.; Deng, R. Mechanicalanalysis of wholly grouted bolt considering axial distribution along the bars. J. Disaster Prev. Mitig. Eng. 2013, 33, 311–315. [Google Scholar]
- Zhang, P.; Yin, K. An analysis method of the whole working course for the force transferring mechanism in fixed segment of tensile-type anchor bar. Chin. J. Undergr. Space Eng. 2009, 5, 716–723. [Google Scholar]
- Huang, M. Analysis on Pullout Load Transfer Mechanism of Geotechnical Anchor and Its Validating Monitor with Smart FRP Anchor. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, July 2014. [Google Scholar]
- Delhomme, F.; Debicki, G.; Chaib, Z. Experimental behaviour of anchor bolts under pullout and relaxation tests. Constr. Build. Mater. 2010, 24, 266–274. [Google Scholar] [CrossRef]
- Deb, D.; Das, K.C. Modelling of fully grouted rock bolt based on enriched finite element method. Int. J. Rock Mech. Min. Sci. 2011, 48, 283–293. [Google Scholar] [CrossRef]
- Xu, H.; Wang, W.; Jiang, M.; Dong, Q. Theoretical analysis of pullout deformation and stiffness of grouted rock bolts. Chin. J. Geotech. Eng. 2011, 33, 1511–1516. [Google Scholar]
- Zhang, W.; Liu, Q. Synthetical deformation analysis of anchor bolt in jointed rock mass. Rock Soil Mech. 2012, 33, 1067–1074. [Google Scholar]
- Yao, X.; Li, N.; Chen, Y. Theoretical solution for shear stresses on interface of fully grouted bolt in tunnels. Chin. J. Rock Mech. Eng. 2005, 24, 2272–2276. [Google Scholar]
- Zou, J.; Li, L.; Yang, X.; Wang, Z.; Zhao, H. Study on load transfer mechanism for span-type anchor based on the damage theory. J. China Railw. Soc. 2007, 29, 84–88. [Google Scholar]
- Abdelmoneim Elamin Mohamad, A.-B.; Chen, Z. Experimental and numerical analysis of the compressive and shear behavior for a new type of self-insulating concrete masonry system. Appl. Sci. 2016, 245, 1–14. [Google Scholar] [CrossRef]
- Zhang, A.; Gao, X. The feasibility of modified magnesia-phosphate cement as a heat resiatant adhesive for strengthening concrete with carbon sheets. Appl. Sci. 2016, 178, 1–13. [Google Scholar]
- Jia, X.; Yuan, Y.; Li, C.-F. Experimental study on bond behavior of new type cement grouted GFRP bolts. Chin. J. Rock Mech. Eng. 2006, 25, 2108–2114. [Google Scholar]
- Cheng, L.; Li, C.; Zheng, Y. Technical Code for Engineering of Ground Anchorage and Shotcrete Support; China Planning Press: Beijing, China, 2016. [Google Scholar]
- Xu, B. Analytical and Experimental Study on Adhesive Anchors. Ph.D. Thesis, Dalian University of Technology, Dalian, China, October 2006. [Google Scholar]
- Fang, Y.; He, C. Study on the interaction of whole bonded rock bolt and tunnel surrounding rock. Eng. Mech. 2007, 24, 111–116. [Google Scholar]



| Parameters | Maximum Tensile Force (kN) | Cross Sectional Area (mm2) | Ultimate Tensile Strength (MPa) | Elongation (%) |
|---|---|---|---|---|
| Test values | 161.5 | 314.2 | 514 | 19.47 |
| Project | Fineness | Initial Setting Time (s) | Final Setting Time (s) | Stability | Compressive Strength (MPa) | |
|---|---|---|---|---|---|---|
| 3 d | 28 d | |||||
| Test results | 3.9 | 171 | 259 | Qualified | 30 | 49 |
| National standards | ≤10 | >45 | <600 | / | ≥17 | ≥42.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Quan, X.; Jia, Y.; Wang, B.; Zhang, G.; Chen, S. The Experimental Study of the Temperature Effect on the Interfacial Properties of Fully Grouted Rock Bolt. Appl. Sci. 2017, 7, 327. https://doi.org/10.3390/app7040327
Li F, Quan X, Jia Y, Wang B, Zhang G, Chen S. The Experimental Study of the Temperature Effect on the Interfacial Properties of Fully Grouted Rock Bolt. Applied Sciences. 2017; 7(4):327. https://doi.org/10.3390/app7040327
Chicago/Turabian StyleLi, Fuhai, Xiaojuan Quan, Yi Jia, Bo Wang, Guibin Zhang, and Siyin Chen. 2017. "The Experimental Study of the Temperature Effect on the Interfacial Properties of Fully Grouted Rock Bolt" Applied Sciences 7, no. 4: 327. https://doi.org/10.3390/app7040327
APA StyleLi, F., Quan, X., Jia, Y., Wang, B., Zhang, G., & Chen, S. (2017). The Experimental Study of the Temperature Effect on the Interfacial Properties of Fully Grouted Rock Bolt. Applied Sciences, 7(4), 327. https://doi.org/10.3390/app7040327




