Abstract
Axial compressors in aero engines are prone to suffering a breakdown of orderly flow when operating at the peak of the pressure rise characteristic. The damaging potential of separated flows is why a safe distance has to be left between every possible operating point and an operating point at which stall occurs. During earlier investigations of stall inception mechanisms, a new type of prestall instability has been found. In this study, it could be demonstrated that the prestall instability characterised by discrete flow disturbances can be clearly assigned to the subject of “Rotating Instabilities”. Propagating disturbances are responsible for the rise in blade passing irregularity. If the mass flow is reduced successively, the level of irregularity increases until the prestall condition devolves into rotating stall. The primary objective of the current work is to highlight the basic physics behind these prestall disturbances by complementary experimental and numerical investigations. Before reaching the peak of the pressure rise characteristic flow, disturbances appear as small vortex tubes with one end attached to the casing and the other attached to the suction surface of the rotor blade. These vortex structures arise when the entire tip region is affected by blockage and at the same time the critical rotor incidence is not exceeded in this flow regime. Furthermore, a new stall indicator was developed by applying statistical methods to the unsteady pressure signal measured over the rotor blade tips, thus granting a better control of the safety margin.
1. Introduction
The operating range of an axial compressor is strictly limited by instabilities such as rotating stall. A huge effort has been made to gain detailed information about the flow topology of rotating stall cells, the stall inception process and a wide range of prestall phenomena representing various routes to stalled flows. The most common stall inception pattern, the spike stall inception, is linked to short length-scale disturbances of large amplitudes. Many proposed mechanisms of spike formation are associated with blockage growth, critical incidence, forward spillage and radial vorticity. Common to all investigated mechanisms for stall onset is the extremely transient character of the inception process. Small disturbances pass over into fully developed stall cells within a few rotor revolutions. This property has been a great challenge for all researchers who concentrate on stall warning. Regarding this topic, useful prestall activity was mainly taken into account when it could be identified at least hundreds of revolutions before stall. One of the earliest studies of stall warning signatures was made by Garnier et al. (1990) [1] by identifying prestall modal disturbances. Different correlations and stall warning devices emerged during the following 20 years [2,3,4]. In this context, Young et al. (2011) [5] paid attention to discrete disturbances which appear well before the onset of stall. The footprint of “discrete prestall propagating disturbances” was identified by areas of low pressure on the casing wall. Also referred to as “blue holes”, the low pressure spots have been ascribed to one of the fundamental reasons for the rise in blade passing irregularity. In addition, Young et al. (2011) [5] focused on the level of irregularity being affected by the tip clearance height and eccentricity. The results demonstrate the future relevance of this particular type of prestall pattern, especially in the light of smaller engine cores and larger relative tip gaps [6].
Moreover, the identified prestall disturbances were linked to a broad peak in frequency spectra. This characteristic hump arising at approximately 40% of the blade passing frequency is an identification feature in one of the most controversially discussed areas of compressor research known as “Rotating Instability” (RI). Even the term “Rotating Instability” which was first introduced by Kameier and Neise in 1997 [7] was considered inappropriate by parts of the community. However, Mathioudakis and Breugelmann (1985) [8] observed “the simultaneous existence of disturbances of different wavelength” 12 years earlier. Inoue et al. (1991) [2] noted “propagating coherent disturbances” which neither fit to the modal nor the spike stall model and which appear in a broad operating range before the compressor drops into stall. All findings suggest that the knowledge about this special type of prestall phenomenon is older than the term “Rotating Instability”.
Over the years, many features of RI have transpired. The general findings in this subject can be summarised as follows:
- Rotating Instability occurs when the compressor is operating at off-design conditions. If the mass flow is reduced at a constant rotational speed, the nominally uniform still unstalled flow becomes unstable and transitions into a “prestall condition” which is significantly non-uniform. Meanwhile, the compressor is nominally unstalled.
- The RI phenomenon can be located in the vicinity of the rotor tips, where the occurrence of RI is more likely with larger tip gaps [9].
- The inception of RI can be identified by a broad chain of peaks in the frequency spectrum taken by time-resolved pressure measurements near the rotor blade tips.
All statements are indisputable in the class where RI is discussed. Early explanations on related physics focused on the unsteadiness due to the tip clearance vortex breakdown [10,11,12]. Later, it was found that these models do not provide a sufficient explanation on the formation mechanism of RI because Beselt et al. (2013) [13] were able to prove RI without a tip gap. This finding led to the following conclusion. It is true that over-tip leakage has an influence on the severity of RI, however the clearance vortex is not essential. Hence, existing models need to be reconsidered.
The primary purpose of the current work is to place RI within the established theory of rotating stall in axial compressors. Experimental results demonstrate that RI is initiated far before stall onset and is therefore representing a prestall instability. In this context, the link between RI and well known prestall flow disturbances is highlighted. Whereas prestall disturbances are investigated experimentally with regard to their potential as a stall indicator, numerical work contributes to a better physical understanding of the underlying flow mechanism.
2. Experimental Setup
The experiments were conducted in a single-stage, low speed axial compressor at the Department of Aeronautics and Astronautics of the Technische Universität Berlin. Key details of the test rig are provided in Table 1. A schematic of the measurement domain and its instrumentation is shown in Figure 1. The test rig is an open flow wind tunnel with a bellmouth and flow straighteners at the inlet and a throttle at the outlet. The compressor rotor is driven by an electrical motor being installed inside the hub. An active control system ensures a constant rotational speed when the mass flow is reduced. Comparable to an engine core in bypass engines, a small amount of mass flow is guided into the hub in order to cool down the motor.

Table 1.
Compressor design.
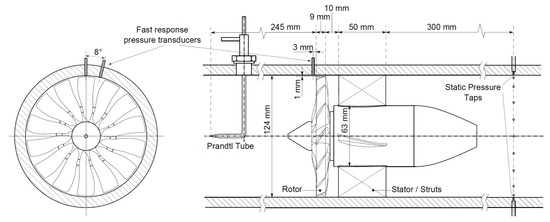
Figure 1.
Measurement setup.
The rotor is designed for constant exit swirl using radial equilibrium with a 80% reaction at midspan. The 124-mm-dia rotor with a hub-to-tip ratio of 0.4 comprises 14 blades. The stator consists of four blades and is therefore rather representative of a strut. Blade profiles of the rotor and the stator are chosen from NACA 65 series. Considering the slip factor, the required geometrical deflection of the blades is adjusted via the lift coefficient .
Instrumentation
To measure the irregularity in the blade passing pressure signature, two fast response pressure transducers (MEGGITT 8507C-1, Meggitt PLC, Christchurch, UK) were flush mounted in the casing wall near the rotor tips. Those two pressure sensors were fitted 3 mm upstream of the rotor leading edge plane. The circumferential displacement of the sensors is shown in Figure 1. The total-to-static pressure rise characteristic was determined using a Prandtl-tube upstream of the rotor and 20 circumferentially distributed static pressure taps downstream of the compressor stage. Measurement data was sampled at 24 kHz and a hardware low-pass filter at 10 kHz was used in order to avoid aliasing.
3. Computational Setup
Computational Fluid Dynamics (CFD) simulations using ANSYS CFX (ANSYS R17.0, Academic, ANSYS, Inc., Canonsburg, PA, USA) have been carried out to provide detailed flow field data to gain an even deeper understanding of the flow phenomena. ANSYS Turbogrid was used to mesh a full annulus model with 14 passages. The Low-Reynolds-Mesh features about 2.7 million hexahedral elements and is divided into the stationary inlet and outlet section and a rotating mid-section. According to the experiments, tip clearance was set to 2.4% of the blade height and is meshed using six layers to capture the tip flow. An exemplary section mesh is displayed in Figure 2. Early attempts modelling only one half of the rotor stage showed disturbances within the frequency spectrum due to the periodic interfaces used therein. Thus, the approach has been changed and the rotor stage was modelled as a whole annulus. Due to computation, all resource limitations Y+ values of 2.5 at the blade‘s surfaces and 4.9/6.9 at the hub/shroud respectively have been set which sufficiently resolve the sub-layer. Flow is propagated in time-space, resolving each passage period with 13 time steps, resulting in a mean Courant-Friedrichs-Lewy (CFL) condition of 17 results in data, capturing all identification features of RI which could be proved in the experiments. A total pressure and normal flow direction inlet boundary condition and a mass flow rate outlet condition were determined in the experiments and are prescribed at the domain‘s inlet and outlet respectively. Turbulence is modelled using the SST-SAS model, regularly available in Ansys CFX. The model utilises the Unsteady Reynolds-averaged Navier-Stokes (URANS) approach in stable regions whereas LES-like behaviour is enforced in detached regions. That encourages the resolution of a turbulent spectrum by adjusting the URANS large-scale unsteadiness. The authors thereby suspected vortex decay to be an important flow mechanism regarding RI.
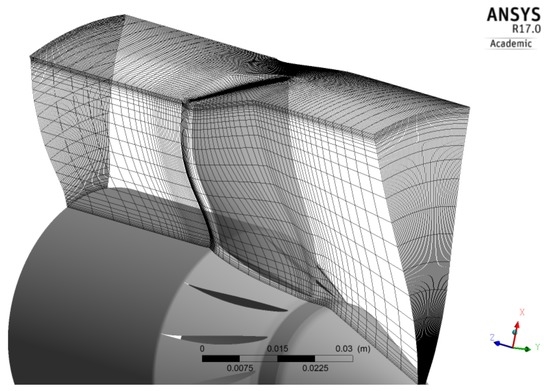
Figure 2.
Rotor mesh.
4. Model Validation
The model has been validated for an operating point, found during measurements, at which RI occurs. The boundary conditions, inlet total pressure and outlet mass flow, have therefore been set according to the measured data. Two main objectives have been pursued when setting up the CFD analysis. At first, a long-term run has been performed, modelling about 20 revolutions and only monitoring the static pressure at selected shroud locations near the blades’ leading edges and omitting any field data. The run produced time series of more than 4000 points at 200 circumferential positions, on each of which a Fourier transformation has been applied. The computed spectra have been compared to the measured spectra to validate the capabilities of the simulation.That being validated, more data has been extracted at a given time at which the unsteady flow pattern of RI did not change anymore. In total, more than 400 time steps, equalling about two revolutions have been solved, extracting full data fields from every time step.
5. Performance Characteristics
For all measurements, the clearance height has been kept constant at a value of 1 mm which corresponds to 2.4% of the blade height. Total-to-static pressure rise characteristic curves were captured at selected rotational speeds (5500 rpm (A) and 9000 rpm (B)) for 20 operating points, see Figure 3a. For both characteristics the stalling flow coefficient is at , the maximum pressure rise coefficient is about . A further reduction of the mass flow leads to a sudden decrease of the pressure rise coefficient. Low-pass filtered pressure traces being measured by the pressure transducers upstream of the leading edge plane comprise harmonic fluctuations covering approximately one rotor revolution (Figure 3b; B20). Thus, stall is initiated by long length-scale stall cells (LLSC). They become visible in the pressure traces when the flow coefficient is below the stalling flow coefficient (Figure 3a between A18–A19 and B19–B20 respectively).
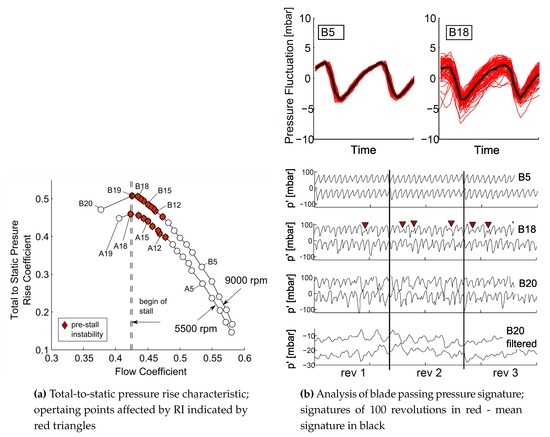
Figure 3.
Compressor performance (Experiment).
At stable operation (B5) the pressure trace is dominated by the blade passing pressure signature (see Figure 3b). The mean blade passing of an entire rotor revolution has been calculated by the phase average of 100 revolutions. The resulting sequence contains pressure fluctuations from 14 blades, whereby two of them are depicted in Figure 3b (top/left) as a black thick line. Additionally, the data from all revolutions are plotted in red. This analysis procedure was then repeated for an operating point at near stall conditions (B18). It is clearly visible that the variation in blade passing pressure signature increases when the compressor stage approaches stall. The question now arises whether any kind of coherent flow structure is responsible for this variation. To answer this question, the difference between the average blade passing signal and the signal for one individual revolution has been evaluated (see Figure 4). The resulting sequence shows significant pressure drops which are known as prestall propagating disturbances. The pressure spikes, highlighted by red triangles (cf. Figure 3b and Figure 4), appear stochastically distributed and with varying intensities. The following chapters concentrate on the flow non-uniformity which does not appear briefly but in a wide operating range before stall.
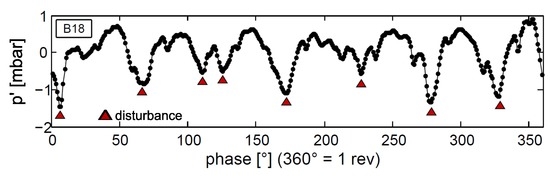
Figure 4.
Filtered pressure fluctuations at B18; Difference between mean blade passing (black line in Figure 3b) and the first revolution (one exemplary red line).
6. Prestall Disturbances
In the next step, different analysis methods are presented in order to quantify the development and intensity of prestall disturbances. The primary objective is to obtain a representative scalar value that gives a clear indication of the beginning of prestall disturbances as the flow coefficient is reduced. Data processing was performed at specific operating points which have been already shown in the total-to-static pressure rise characteristic.
The preceding analysis of the blade passing signature by phase averaging has been carried out at a constant flow coefficient. In the following, the root mean square (RMS) calculation was applied on the difference between the average trace and the signal of the first revolution. After repeating this process for 100 revolutions, the mean of all RMS was nondimensionalised by the dynamic pressure at the rotor inlet. A detailed description of the presented analysis procedure is given by Young et al. (2011) [5]. It is now possible to determine the variance of pressure fluctuations caused by the disturbances themselves. In order to be consistent with the well established nomenclature of prestall instabilites, this special evaluation of RMS is called irregularity. The level of irregularity is computed for the same operating points as shown in Figure 3 and plotted against the flow coefficient.
For both speeds, a clear ramp-up in irregularity can be observed when going from open throttle position to stall (see Figure 5a). Especially at near stall, the intensity of prestall disturbances increases disproportionately. At the last stable operating point, the amplitude of fluctuations induced by the disturbances is nearly 0.5% of the dynamic pressure at the rotor inlet. Regarding the fact that the disturbances are characterised by a sharp pressure drop, the third statistical momentum (skewness) seems to be suitable for analysing the inception process of prestall instabilities. If the majority of pressure fluctuations is higher than the average or the signal contains drops of very low pressure respectively, the skewness is negative [14]. Hence, evidence of prestall disturbances is indicated by negative values of the skewness. Equal to the RMS calculation, the skewness is applied to the difference between the average trace of the blade passing signature and every individual rotor revolution.
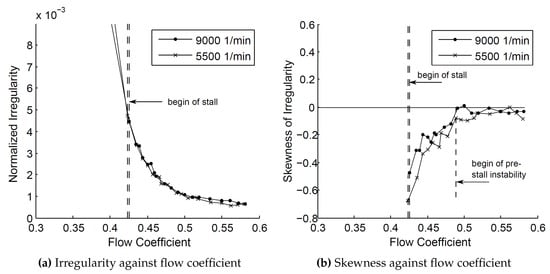
Figure 5.
Identification criteria for the detection of prestall disturbances (Experiment).
In an operating range where the flow coefficient is higher than , the skewness is almost zero—no prestall disturbances are detectable (see Figure 5b). The inception of prestall instability is indicated by a significant drop of the skewness at . The flow becomes non-uniform. The intensity of negative pressure spikes increases as the compressor approaches stall. Nevertheless, it should be noted that the skewness just gives a rough idea of when the inception process of flow disturbances is initiated.
Young pointed out that the level of irregularity depicted in Figure 5a does not allow a reliable stall warning because the ramping up trend changes due to compressor degradation over life time. As a result, it is not appropriate to define a constant alarm level in the distribution of irregularity. In contrast, a new stall indicator now represents an unmistakable parameter which can be used to announce the stalling limit even at transient operation (not shown here). For this purpose, the third statistical momentum has been applied on the unsteady pressure data without excluding the blade passing signal. The skewness is evaluated at several steady operating points between open throttle and stall. In the following text, the skewness of the unprocessed pressure signal measured 3 mm upstream of the leading edge plane is called “stall indicator”. It is displayed in Figure 6 as an averaged value from both fast response pressure transducers and plotted against the flow coefficient (circles). In addition, the stall indicator is computed for every individual pressure transducer (red lines). Reading the diagram from right to left, inception of prestall instability is indicated by a local minimum. However, the most important characteristic within the distribution of the stall indicator can be found just before reaching the stalling limit. At the penultimate stable operating point, the slope changes from negative to positive. The local maximum occurs even if the signal of just one pressure sensor is analysed. Based on a gradient determination, an accurate estimation of the stalling limit can be performed without the risk of exceeding the limit itself.
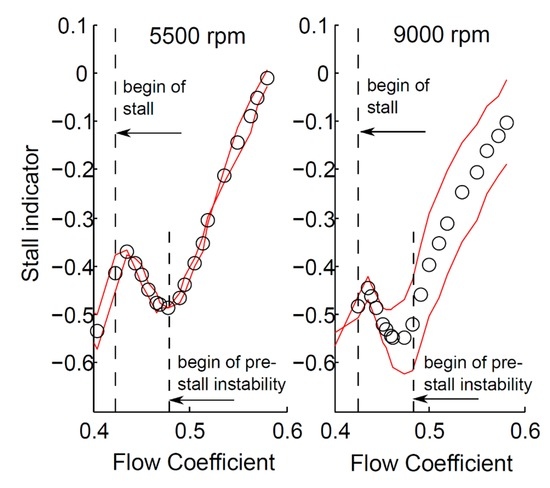
Figure 6.
Stall indicator; distribution for each pressure transducer in red—average distribution marked with circles (Experiment).
6.1. Nature of Prestall Disturbances
An analysis of the frequency spectra allows a more precise estimation of the onset of prestall activity. Figure 7 shows the power spectral density (PSD [mbar/Hz]) for selected operating points. The nominal uniform flow at A5 is dominated by the blade passing frequency (BPF). Starting in A12, a broad banded chain of peaks arises that is centered at approximately 45% of the BPF. In detail, the broad band peak is composed of several side-by-side peaks with a constant frequency spacing in-between. The characteristic signature is a typical identification feature of so-called “Rotating Instabilities” and will be discussed in more detail in Section 6.2. As the mass flow is reduced, the peak chain grows in amplitude and is being shifted towards smaller frequencies. The rise in flow irregularity happens exactly at the same flow coefficient at which the characteristic peak signature arises, thus answering the question whether there is a link between finite prestall disturbances and Rotating Instabilities positively. The amplitude of the broad peak grows until the compressor becomes unstable. At A19 (and B20), where the stage is operating above the stall point, a peak at 47% of the first engine order (3.4% BPF) indicates the existence of rotating stall cells. Thus, the stall cells propagate at approximately half of the rotational speed. Please note that the peaks in the signature of RI do not represent higher harmonics of the RS peak. Furthermore, the frequency analysis demonstrates that rotating stall and prestall disturbances can indeed coexist. In general, the behaviour of prestall instabilities is very similar for both investigated speeds but at 9000 rpm the amplitudes of the prestall fluctuations are about ten times higher than the amplitudes measured at 5500 rpm. A complementary evaluation of frequency spectra and the skewness allows to clearly identify operating points where prestall activity exists. Within the pressure rise characteristic, the affected operating range is highlighted in red (cf. Figure 3a).
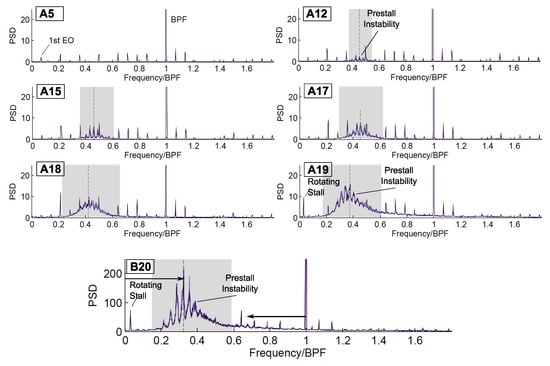
Figure 7.
Analysis of the Power Spectral Density (PSD); Development of prestall instability at various operating points for different speeds (BPF: blade passing frequency) (Experiment).
6.2. Prestall Propagating Disturbances
The propagation of the identified disturbances was analysed by applying coherence and phase spectra on the data of the pressure transducers over the rotor blade tips. Corresponding analysis methods are described precisely by Beselt and Peitsch (2012) [15]. Results are shown for an operating point with intense prestall activity but without stall. At a constant speed of 5500 rpm, the pressure rise coefficient and the flow coefficient have been set to and . The same operating point was chosen for CFD calculations (see Figure 8).
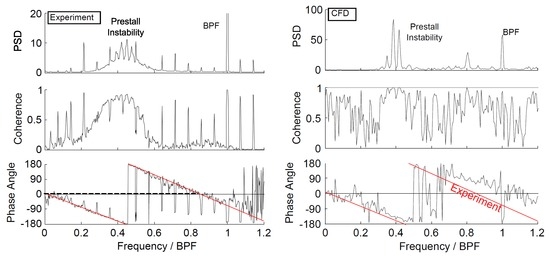
Figure 8.
Frequency analysis - comparison between experiment and simulation.
Again, the mean power spectrum comprises the typical spectral signature with side-by-side peaks centered on approximately 45% of the BPF. In the same frequency range, increased values of the coherence show that disturbances propagate around the circumference of the rotor. Generally, the coherence function allows to verify if the signals of two pressure sensors are correlated. The phase angle provides additional information about the relationship between the relative phase of frequency components of two correlated signals. The linear phase response (re-drawn with a red solid line at ) covers nearly 85% of the BPF corresponding to 1090 Hz. Using the circumferential distance b between the sensors, it is now possible to calculate the propagation velocity. The latter is
and thus 49% of the blade tip speed. Using the spectral characteristics as an unmistakable identification feature, the well-known discrete propagating prestall disturbances can now clearly be attributed to RI.
6.3. Prestall Propagating Disturbances; Numerical Results
The frequency analysis was then applied to the numerically acquired pressure fluctuations sampled at 200 monitor points evenly distributed around the circumference. The axial positions of the pressure transducers in the experiment and the monitor points in the CFD model were the same. The simulated period of time was 0.26 s covering nearly 24 rotor revolutions with a resolution of 16,683 steps per second. The main purpose of this analysis procedure is to prove that the computational setup is suitable for modelling RI.
The average Fourier transform of all 200 series demonstrates that the short sequence of pressure data is sufficient to verify the existence of RI based on its characteristic signature in the frequency spectrum. In comparison to the experimental results, the side-by-side peaks arise in the same frequency range—they have approximately the same frequency spacing in-between (see Figure 8). Furthermore, the peaks within the signature do not represent lower harmonics of the BPF. In order to enable an explicit comparison between the experimental and numerical data, coherence and phase spectra have been evaluated for two selected monitor points with a circumferential offset of 8 deg. In general, increased coherence values higher than 0.5 can be found in the entire frequency range, but two global maxima standing out at 0.4% BPF and 0.8% BPF coincide with RI (RI and first higher harmonic). The decreased slope of the phase response indicates that in the numerical simulations the propagation velocity of prestall disturbances is slightly higher. Even if there are minor differences between the experimental and numerical results regarding the amplitudes of pressure fluctuations, the computational setup is able to capture the predominating characteristics of RI. The primary achievement of the computation was to simulate the propagation of modal flow disturbances as they could be proved in the experiments.
By applying a mode decomposition technique to the pressure signal of all monitor points, it is possible to assign a circumferential mode to each peak in the frequency spectrum. The analysis procedure has been precisely described by [16,17]. Using 200 monitor points, an azimuthal mode analysis is feasible up to mode orders . Generally, the circumferential mode is equal to the number of flow disturbances being evenly distributed around the casing. Figure 9 shows that the peaks are of subsequent numbered modes with a dominant mode order of . Corresponding to the number of blades, the BPF is linked to the mode order . The interaction between rotor blades and propagating disturbances is responsible for the modal pattern symmetrically arranged around the BPF at about 800 Hz and 1800 Hz (BPF − RI; BPF + RI, circled in red). It is assumed that associated modes are cut-on. Correspondingly, in the experiments at this very operating point, a distinct sound with a certain howling quality was noted. The special modal signature in Figure 9, also shown in the experimental results of Pardowitz et al. (2015) [18], represents the most important indication that the computational setup used in this work is able to capture the main properties of RI.
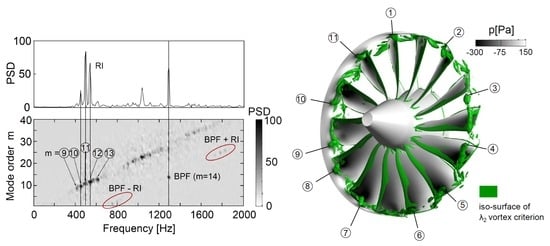
Figure 9.
Mode analysis and visualisation of flow disturbances (CFD).
To understand which particular flow mechanism can be assigned to the disturbances, an isosurface of the vortex criterion has been evaluated at a specific time (see Figure 9, right). Eleven discrete disturbances are represented by vortex tubes being concentrated at the blade tips. The vortices appear as tornado-like tubes with a highly deflected trajectory where the casing ends of the tubes propagate circumferentially along a path which is located upstream of the leading edges. Meanwhile, the number of vortices varies slightly in time (Video S1).
In the context of RI, existence of radial vortex structures has been already suggested in the past [19]. Considering the dynamic process of the mode number, it is obvious that there is a link between the vortices and the spectral signature in the frequency domain. Grey-scaled static pressures on all surfaces reveal that each vortex filament induces a low pressure spot on the casing wall. This finding is in good agreement with the experimental results presented in Figure 4. The pressure signal also contained spikes of low static pressure.
A detailed picture of the vortex topology is shown in Figure 10. The streakline pattern on the casing contains several features which can be ascribed to the subject of stall inception mechanisms. Also known as “forward spilling”, the clearance flow is being redirected and is spilling around the leading edge of the neighbouring blade. This particular flow pattern arises when the clearance vortex trajectory is aligned in parallel with the rotor leading edge plane. As each passage is affected by spilling forward, the result is a continuous separation line upstream of the rotor.
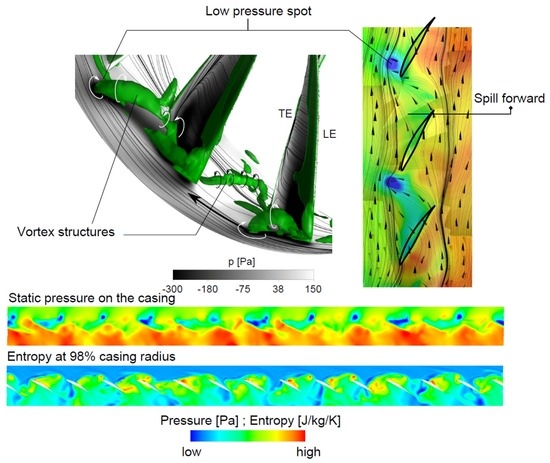
Figure 10.
Flow mechanism of Rotating Instability (CFD).
Furthermore, the discrete vortex filament spans between the casing and the suction side of the rotor blade, thus shielding the clearance flow from the main flow. Rotation of the vortex tube is indicated by white and black arrows. In general, the coherent flow topology strongly resembles a classical spike formation known from spike stall inception mechanisms [20]. A similar flow topology was also addressed by Inoue et al. (2001) [21] who described the occurrence of short length-scale stall cells when the compressor is operating in a mild stall condition. Intense areas of low pressure on the casing gave rise to the assumption that a “separation vortex” with one end attached to the casing and the other attached to the suction surface appears as a “mini-cell”.
However, in contrast to the findings of Pullan et al (2015) [20], the localised disturbance does not evolve into a stall cell after a few rotor revolutions. In the presented case, discrete vortex structures remain unchanged when the through-flow is constant—they represent indeed a kind of flow non-uniformity but they are not responsible for flow separation or part span stall. The vortex dynamics is depicted in Figure 11. Again, the vortices are visualised by the -isosurfaces. The motion of the vortex tubes is characterised as follows.
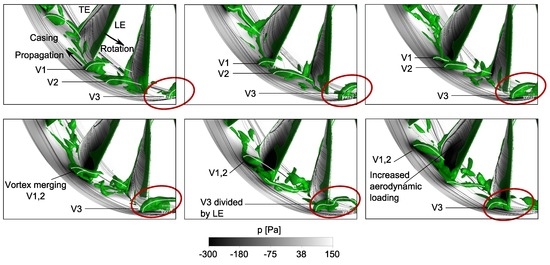
Figure 11.
Vortex dynamics (CFD).
While the end of the vortex tube at the casing moves circumferentially, the end on the suction-surface convects downstream. During this process, each vortex trajectory is periodically divided by the leading edges (vortex V3; circled in red). The grey-scaled static pressures show that the aerodynamic loading increases at the blade tip when the casing end of the vortex has just passed the leading edge. This finding confirms the potential impact of RI on aeroelasticity. Additionally, vortices are affected by a decay mechanism or they pass into one another. The vortex merging is exemplarily demonstrated by the vortices V1 and V2. The most important finding is that shedding of vorticity being known from spike formation in its embryonic stage is not involved in the general flow topology of prestall vortices. The authors believe that this illustration allows the formation and the interaction mechanism of prestall disturbances to be shown for the first time.
7. Discussion
The high level of agreement between the Fourier transforms derived from the experimental and numerical data provides an indication that the spectral signature of RI is caused by discrete vortices. Regarding the fact that the signature can be measured in a certain operating range before stall and not only in a brief moment during transient maneuvers, the special vortices rather belong to a whole prestall phenomenon than just being a feature of an inception process of rotating stall. The authors assume that the reversed clearance flow and associated blockage enables the formation of a Kelvin–Helmholtz-Instability (KHI). A corresponding flow model is shown in Figure 12. Once the interface between the reversed clearance flow (red) and the inflow (blue) extends circumferentially as a continuous shear layer, small disturbances appear as vortices. Even the entropy distribution upstream of the rotor in Figure 10 (bottom) resembles a typical wave-like pattern of a KHI. The basic physics behind the vortices is illustrated by the sketch in Figure 12 (mid/left). Accordingly, the vortex structures shown in green can be interpreted as a roller bearing, allowing the main flow to roll-off on the blockage region (dark grey). If a small perturbation emerges in the interface between the blockage and the inflow, it is being amplified and interacts with other perturbations while moving around the circumference. The resulting flow instability can therefore be regarded as an infinite 3D-KHI. At higher flow rates, when the trajectory of the clearance vortex is mainly deflected downstream, there is no continuous shear layer in which any small perturbation could grow to a prestall vortex (cf. Figure 12; mid/right). However, why is a compressor setup prone to such a remarkable prestall condition as RI? It is supposed that the reason can be found in a specific combination of blockage and critical rotor incidence (see Figure 12; top). As the mass flow is reduced, the trajectory of the clearance vortex moves in the upstream direction until a blockage of the entire tip region is excited. From then on, RI begins to develop in operating range “B”, if the critical rotor incidence has not yet been reached in this flow regime. This assumption implies that forward spillage of the clearance flow and associated blockage does not necessarily lead to an inception process of rotating stall.
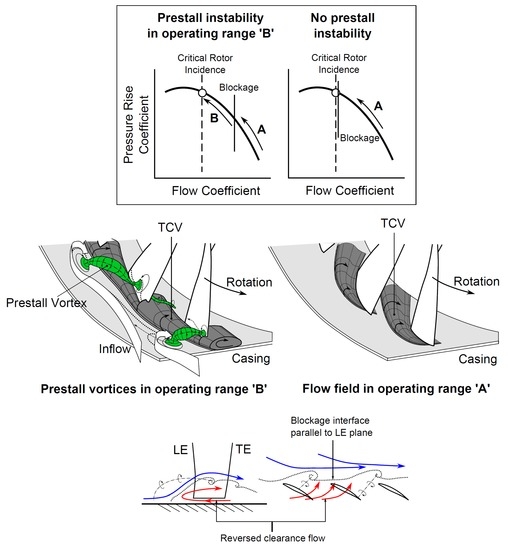
Figure 12.
Model of prestall instability.
If the stalling incidence is reached before the entire rotor inlet is blocked by any secondary flow, compressor instabilities such as rotating stall can be triggered immediately by modes or spikes depending on the slope of the pressure rise characteristic: in this particular case, blockage and critical incidence coincide in one operating point. Weichert and Day (2014) [22] could even demonstrate that forward spillage of the clearance flow and associated blockage is rather a consequence of the spike initiation process and not the cause of it.
8. Conclusions
A new miniature single-stage low speed axial compressor was built to investigate a special type of prestall instability and its potential for a stall warning algorithm. In addition, numerical simulations contribute to better understand the physics behind discrete flow disturbances representing a special feature of the prestall phenomenon. The following conclusions can be drawn:
- Discrete propagating prestall disturbances can be measured over the tips of the rotor blades. They represent a kind of flow non-uniformity and appear in a broad operating range before the compressor reaches its stalling limit.
- The disturbances can be clearly identified and quantified by analysing the blade passing signature irregularity. As the mass flow is reduced, the intensity of flow disturbances increases. Furthermore, they become amplified disproportionately with increasing rotor speed.
- Based on a spectral analysis, it could be proven that these particular disturbances can be assigned to the subject of Rotating Instabilities. The number of disturbances coincides with the mode order in the spectral signature of RI.
- It could be demonstrated that RI and rotating stall cells can indeed coexist in an operating range where the flow coefficient is below the stalling flow coefficient.
- A new stall indicator has been found which indicates the last stable operating point before stall. For this purpose, the third statistical momentum was applied to the unsteady pressure data measured upstream of the leading edge plane.
- Numerical simulations revealed that the flow disturbances appear as small vortex tubes where the casing ends of the tubes induce low pressure spots while propagating around the circumference. The highly deflected vortices behave like a characteristic feature of a Kelvin–Helmholtz-Instability which is triggered when the entire tip region of the rotor is affected by blockage. It is assumed that the prestall vortices arise if the critical rotor incidence is not exceeded in this flow regime.
Supplementary Materials
The following are available online at www.mdpi.com/2076-3417/7/3/285/s1, Video S1: Rotating Instability.
Acknowledgments
Grateful thanks are extended to all our collegues who supported us in the preparation of this paper. The authors would also like to thank the German Research Foundation (DFG) for funding parts of the investigations. In particular, the extremely fruitful discussions with Benjamin Pardowitz and Mehdi Vahdati are also gratefully acknowledged.
Author Contributions
Mario Eck is the leading author of this paper, performed the measurements and the data reduction of experimentally and numerically acquired data. Silvio Geist performed to the simulations and the post processing. Dieter Peitsch contributed to the measurements and the simulations. All three authors contributed to writing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| BPF | Blade passing frequency |
| KHI | Kelvin–Helmholtz-Instability |
| LE | Leading edge |
| LLSC | Long length-scale stall cell |
| PSD | Power spectral density |
| RI | Rotating Instability |
| RMS | Root mean square |
| RS | Rotating stall |
| SST-SAS | Shear-stress transport scale-adaptive simulation |
| TCV | Tip clearance vortex |
| TE | Trailing edge |
References
- Garnier, V.H.; Epstein, A.H.; Greitzer, E.M. Rotating waves as a stall inception indicator in axial compressors. ASME J. Turbomach. 1991, 113, 290–301. [Google Scholar] [CrossRef]
- Inoue, M.; Kuroumaru, M.; Iwamoto, T.; Ando, Y. Detection of a rotating stall precursor in isolated axial flow compressor rotors. ASME J. Turbomach. 1991, 113, 281–287. [Google Scholar] [CrossRef]
- Dhringa, M.; Neumeier, Y.; Prasad, J. Stall and surge precursor in axial compressors. In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, AL, USA, 20–23 July 2003.
- Christensen, D.; Cantin, P.; Gutz, D.; Szucz, P.; Waida, A.; Armor, J.; Dhringa, M.; Neumeier, Y.; Prasad, J. Development and demonstration of a stability management system for gas turbine engines. ASME J. Turbomach. 2008, 130, 031011. [Google Scholar] [CrossRef]
- Young, A.; Day, I.; Pullan, G. Stall warning by blade passing signature analysis. ASME J. Turbomach. 2012, 135, 1589–1599. [Google Scholar] [CrossRef]
- Day, I. Stall, surge, and 75 years of research. ASME J. Turbomach. 2015, 138. [Google Scholar] [CrossRef]
- Kameier, F.; Neise, W. Experimental study of tip clearance losses and noise in axial turbomachines and their reduction. ASME J. Turbomach. 1997, 119, 461–467. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Breugelmans, F. Development of small rotating stall in a single stage axial compressor. In ASME 1985 International Gas Turbine Conference and Exhibit, Volume 1: Aircraft Engine; Marine; Turbomachinery; Microturbines and Small Turbomachinery; Paper No. 85-GT-227; ASME: New York, NY, USA, 1985; p. V001T03A064. [Google Scholar]
- Beselt, C.; van Rennings, R.; Peitsch, D.; Thiele, F. Impact of hub clearance on endwall flow in a highly loaded axial compressor stator. In ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, Volume 6C: Turbomachinery; Paper No. GT2013-95463; ASME: New York, NY, USA, 2013; p. V06CT42A034. [Google Scholar]
- Mailach, R.; Lehmann, I.; Vogeler, K. Rotating instabilites in an axial compressor originating from the fluctuating blade tip vortex. ASME J. Turbomach. 2001, 123, 453–460. [Google Scholar] [CrossRef]
- Schrapp, H.; Stark, U.; Saathoff, H. Breakdown of the tip clearance vortex in a rotor equivalent cascade amd in a single-stage low-speed compressor. In ASME Turbo Expo 2008: Power for Land, Sea, and Air, Volume 6: Turbomachinery, Parts A, B, and C; Paper No. GT2008-50195; ASME: New York, NY, USA, 2008; pp. 115–129. [Google Scholar]
- Schrapp, H. Experimentelle Untersuchungen zum Aufplatzen des Spaltwirbels in Axialverdichtern; Shaker: Braunschweig, Germany, 2008; ISBN-10: 3832278427. [Google Scholar]
- Beselt, C.; Pardowitz, B.; van Rennings, R.; Sorge, R.; Peitsch, D.; Enghardt, L.; Thiele, F.; Ehrenfried, K.; Thamsen, P.U. Influence of clearance size on rotating instability in an axial compressor stator. In Proceedings of the 10th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics ETC 10, Lappeenranta, Finnland, 15–19 April 2013.
- Beselt, C.; Eck, M.; Peitsch, D. Three-dimensional flow field in highly loaded compressor cascade. ASME J. Turbomach. 2014, 136, 101007. [Google Scholar] [CrossRef]
- Beselt, C.; Peitsch, D. Influence of Mach number and aerodynamic loading on Rotating Instability in an annular compressor cascade. In ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Volume 8: Turbomachinery, Parts A, B, and C; Paper No. GT2012-69393; ASME: New York, NY, USA, 2012; pp. 2711–2720. [Google Scholar]
- Liu, J.M.; Holste, F.; Neise, W. On the azimuthal mode structure of rotating blade flow instabilities in axial turbomachines. In Proceedings of the Aeroacoustics Conference, State College, PA, USA, 6–8 May 1996. AIAA Paper No. 96-1741.
- Jürgens, W.; Tapken, U.; Pardowitz, B.; Kausche, P.; Bennett, G.J.; Enghardt, L. Technique to analyse characteristics of turbomachinery broadband noise sources. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010. AIAA Paper No. 2010-3979.
- Pardowitz, B.; Moreau, A.; Tapken, U.; Enghardt, L. Experimental identification of rotating instability in an axial fan with shrouded rotor. Proc. Inst. Mech Eng. A J. Power Energy 2015, 229, 520–528. [Google Scholar]
- Pardowitz, B.; Peter, J.; Tapken, U.; Thamsen, P.U.; Enghardt, L. Visualization of secondary flow structures caused by Rotating Instabilities: Synchronized stereo high-speed PIV and unsteady pressure measurements. In Proceedings of the 45th AIAA Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. AIAA Paper No. 2015-2930.
- Pullan, G.; Young, A.; Day, I.J.; Greitzer, E.M.; Spakovszky, S.Z. Origins and structure of spike-type rotating stall. ASME J. Turbomach. 2015, 137. [Google Scholar] [CrossRef]
- Inoue, M.; Koroumaru, M.; Tanino, T.; Yoshida, S.; Furukawa, M. Comparative studies on short and long length-scale stall cell propagating in an axial compressor rotor. ASME J. Turbomach. 2001, 123, 24–30. [Google Scholar] [CrossRef]
- Weichert, S.; Day, I. Detailed measurements of spike formation in an axial compressor. ASME J. Turbomach. 2014, 136. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).