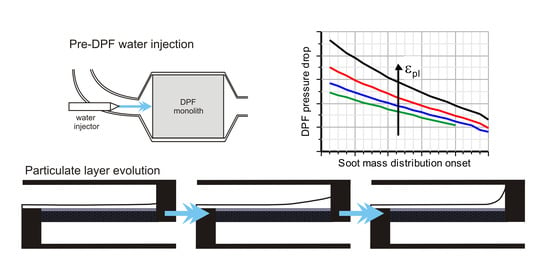
On the Impact of Particulate Matter Distribution on Pressure Drop of Wall-Flow Particulate Filters
Abstract
:1. Introduction
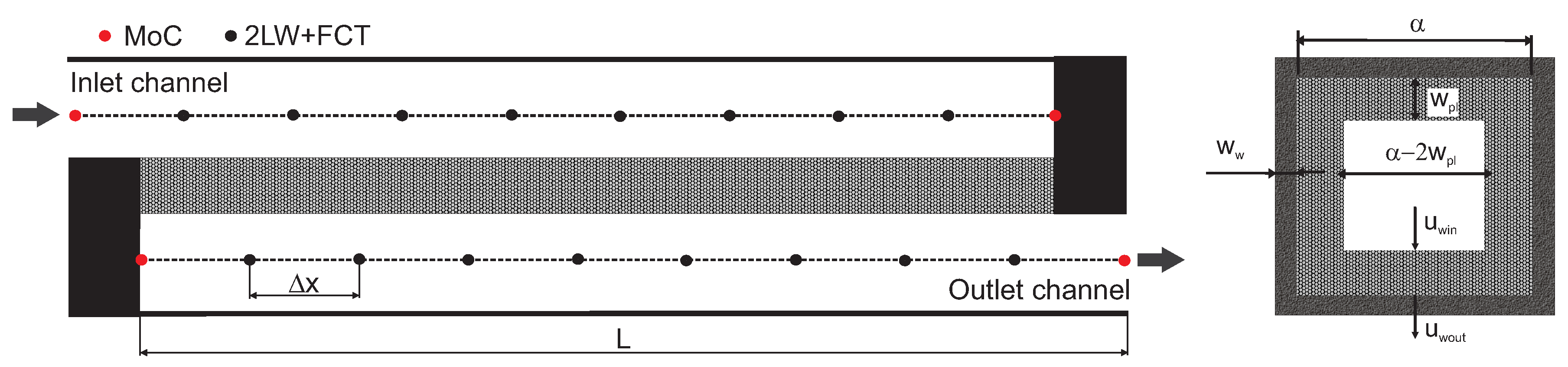
2. Wall-Flow DPF Model
- Mass conservation:
- Momentum conservation:
- Energy conservation:
- Chemical species conservation:
3. Experimental Setup
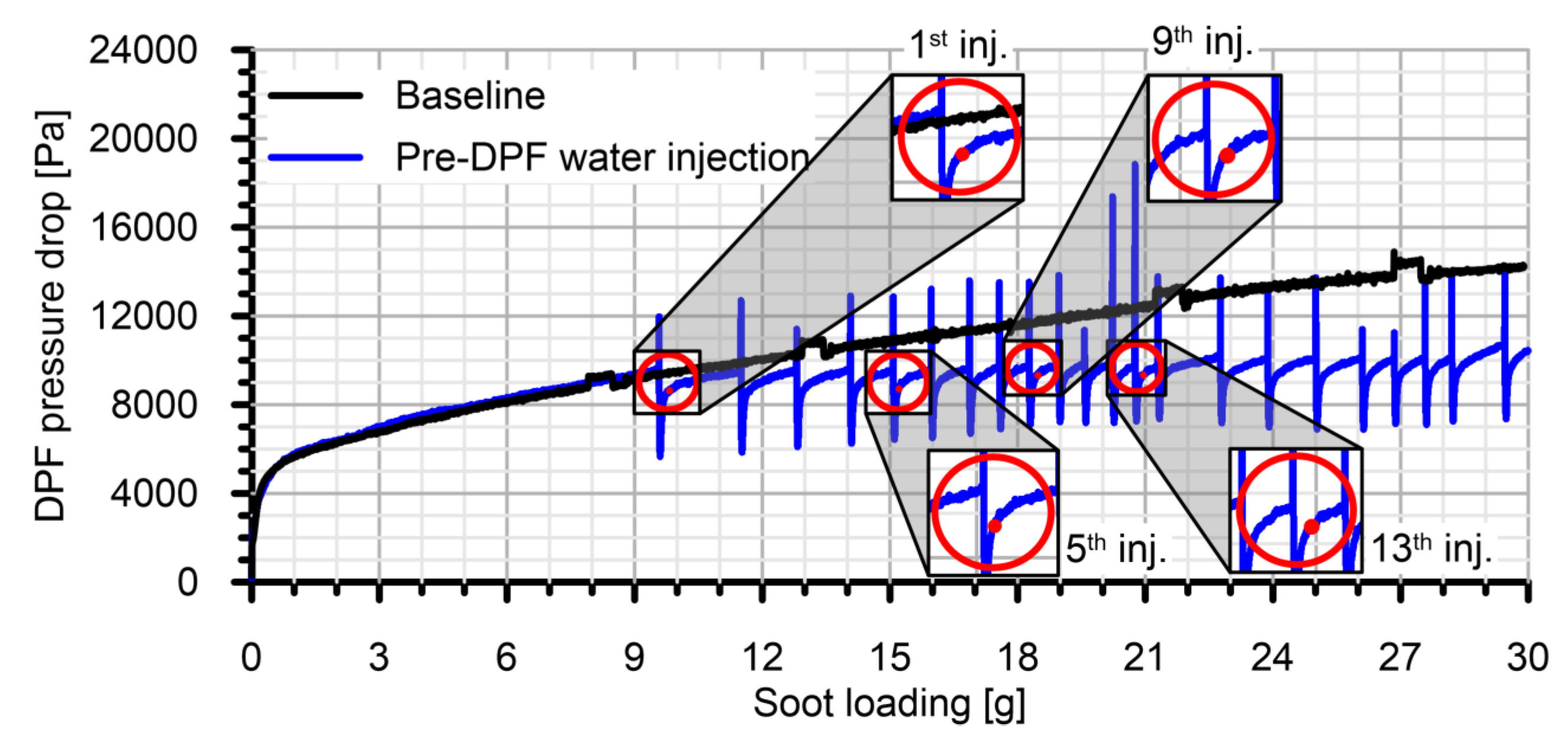
3.1. Tests
4. Discussion of the Results
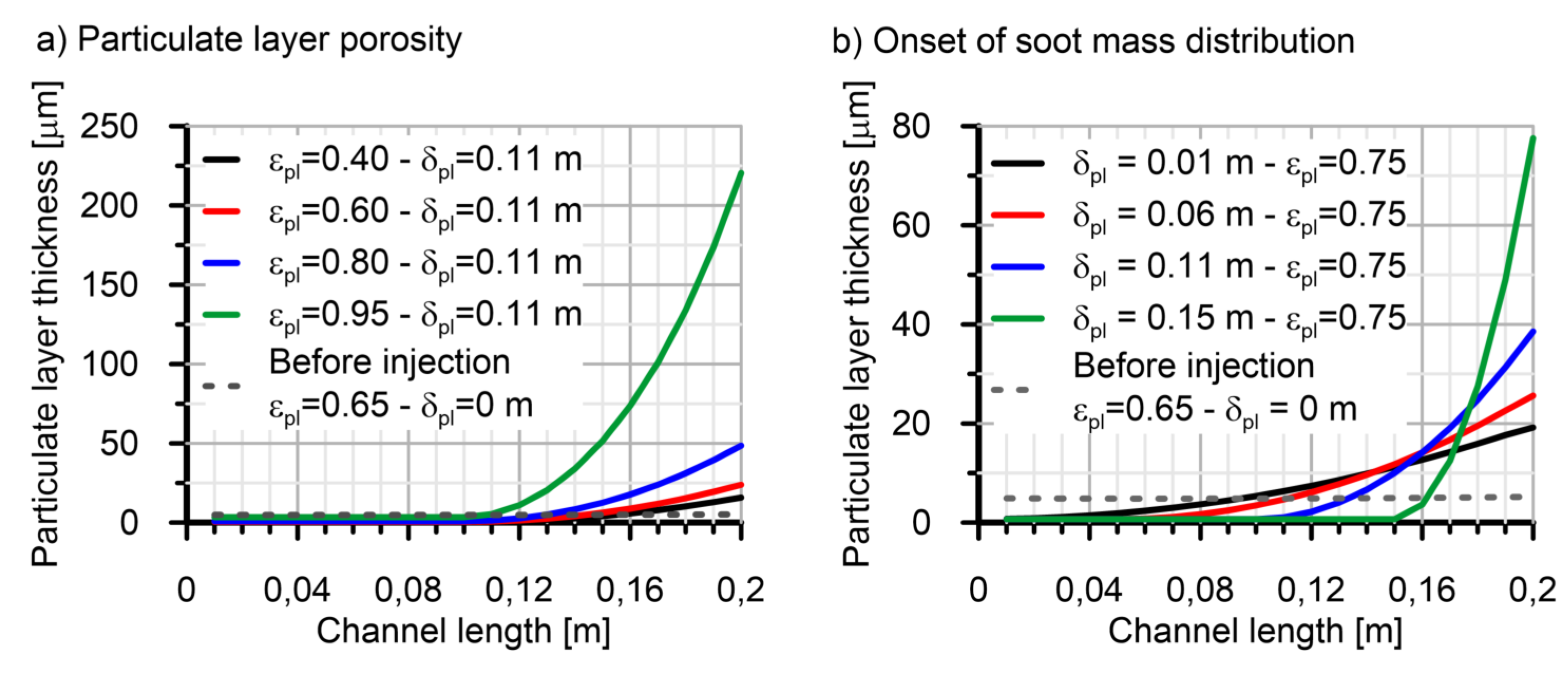
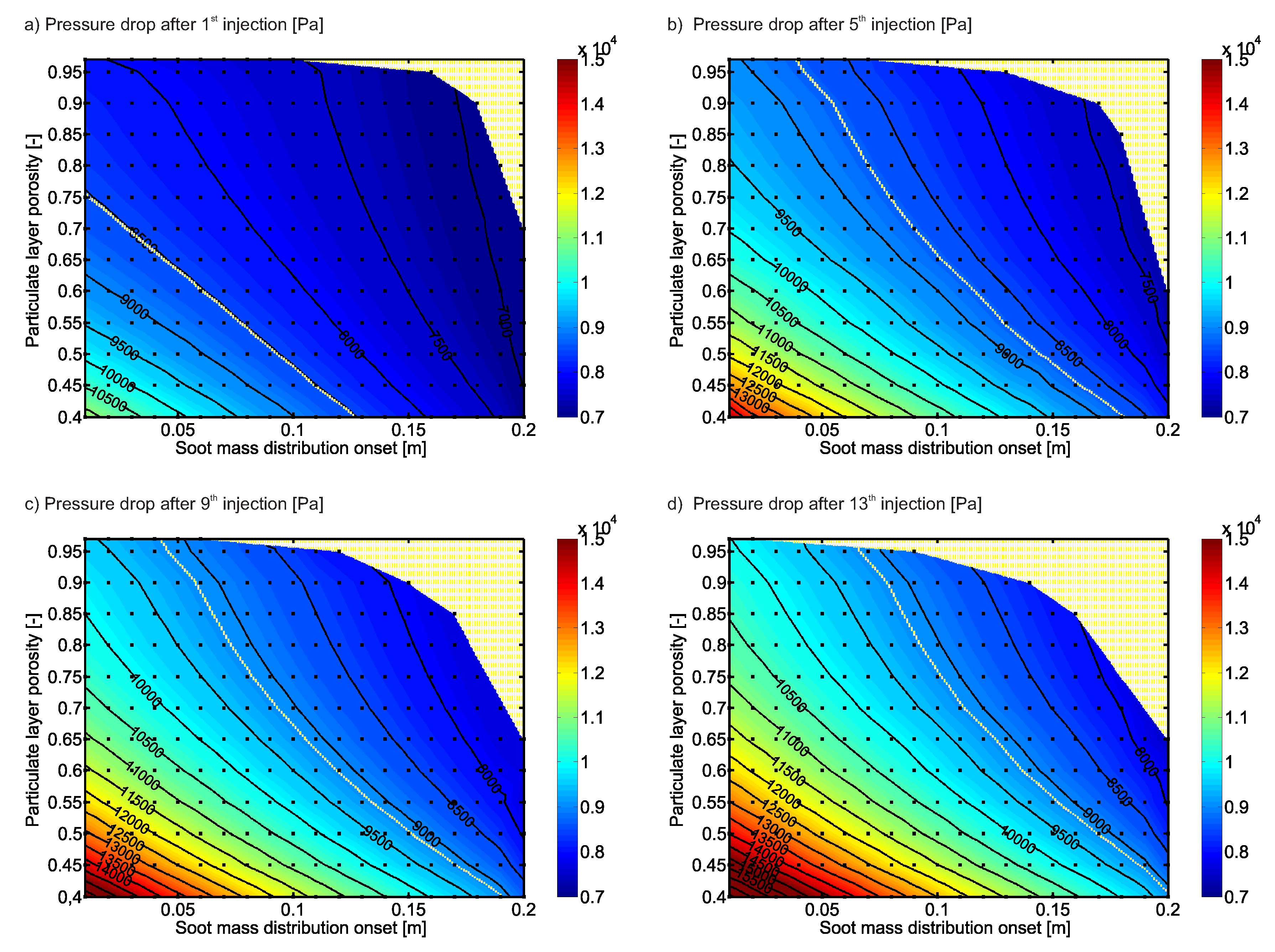
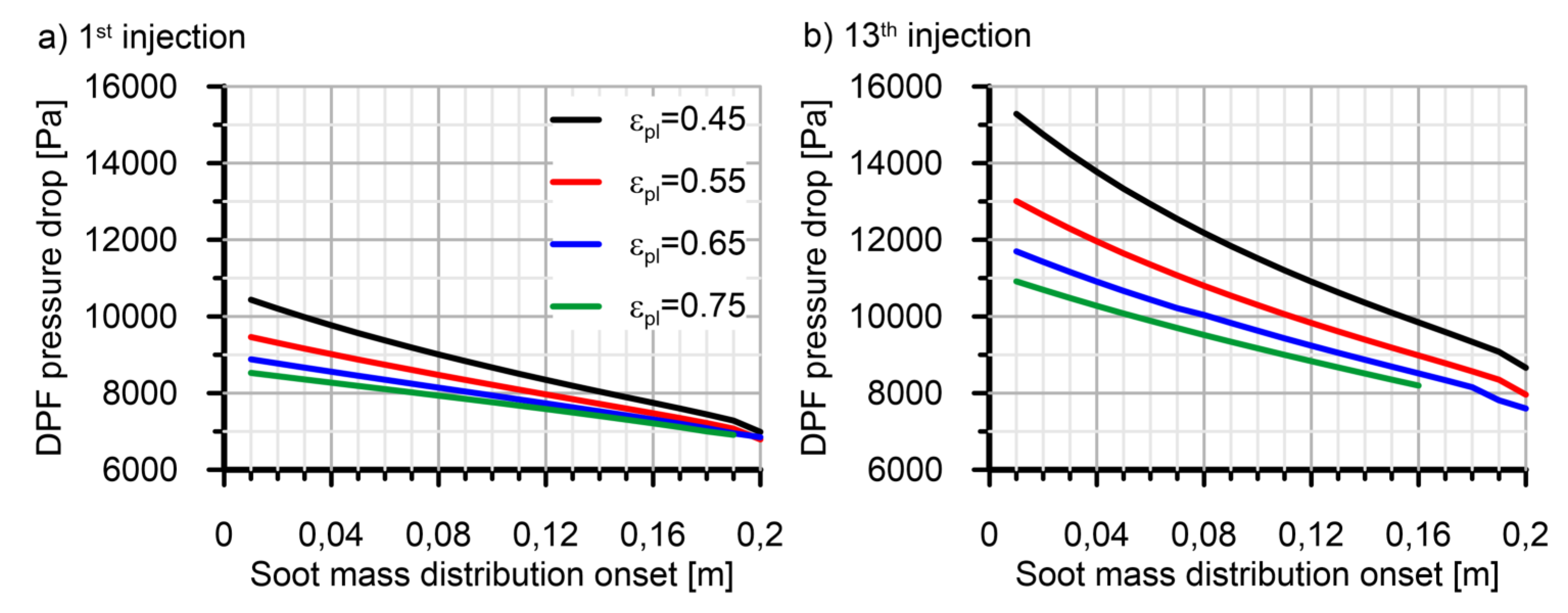
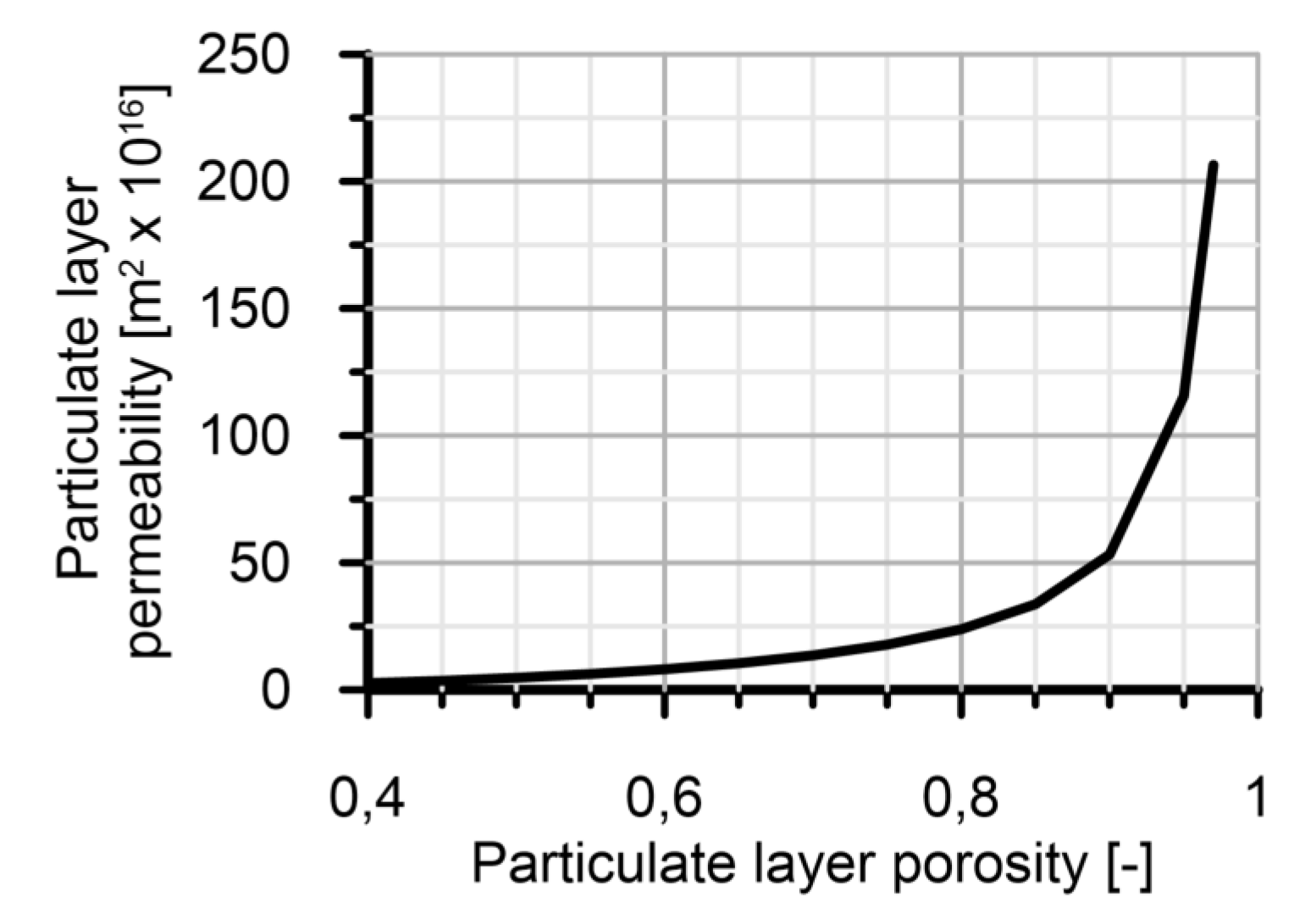
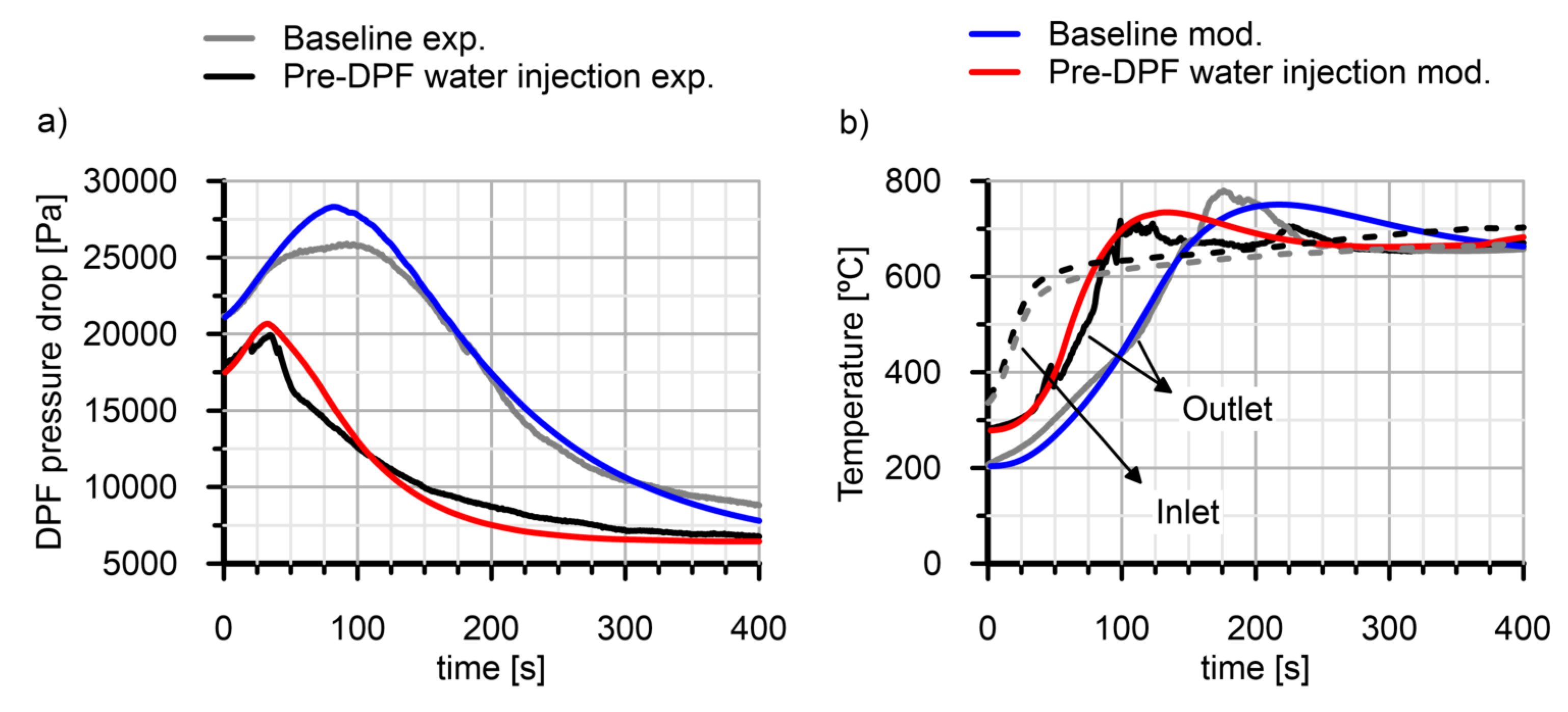
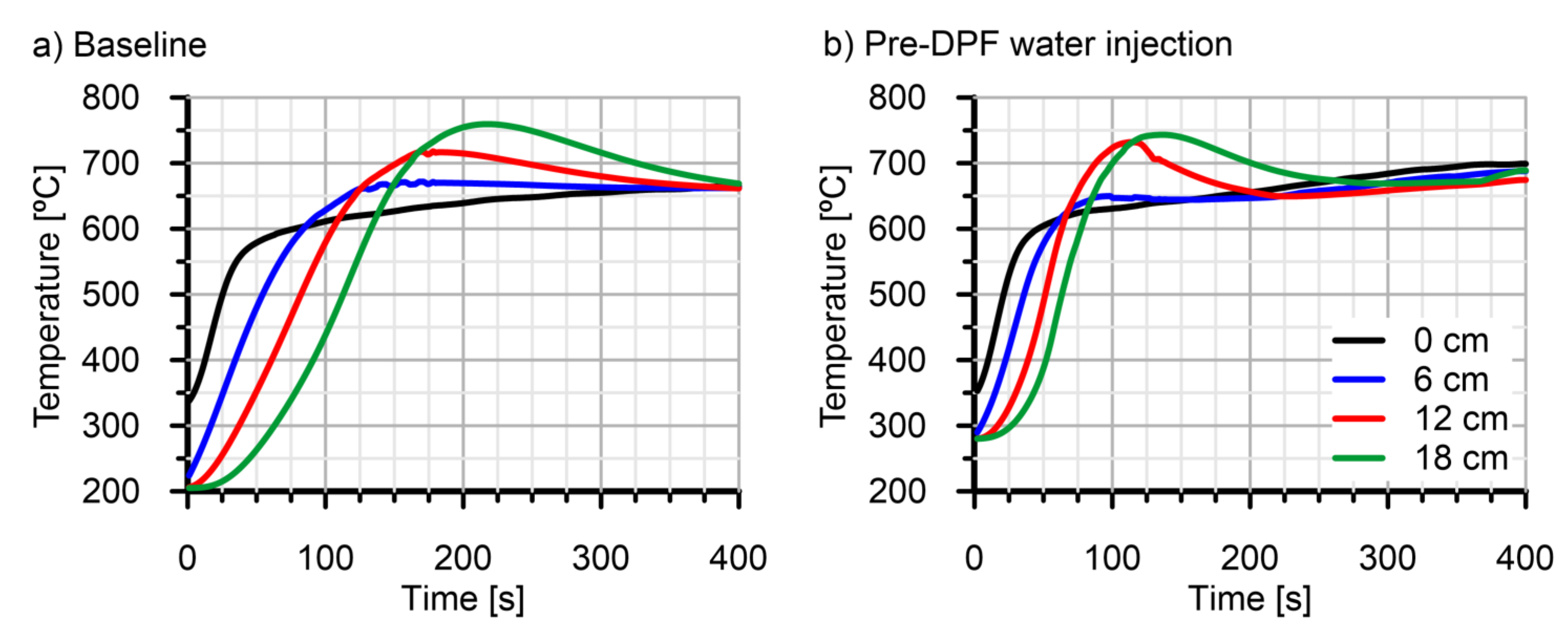
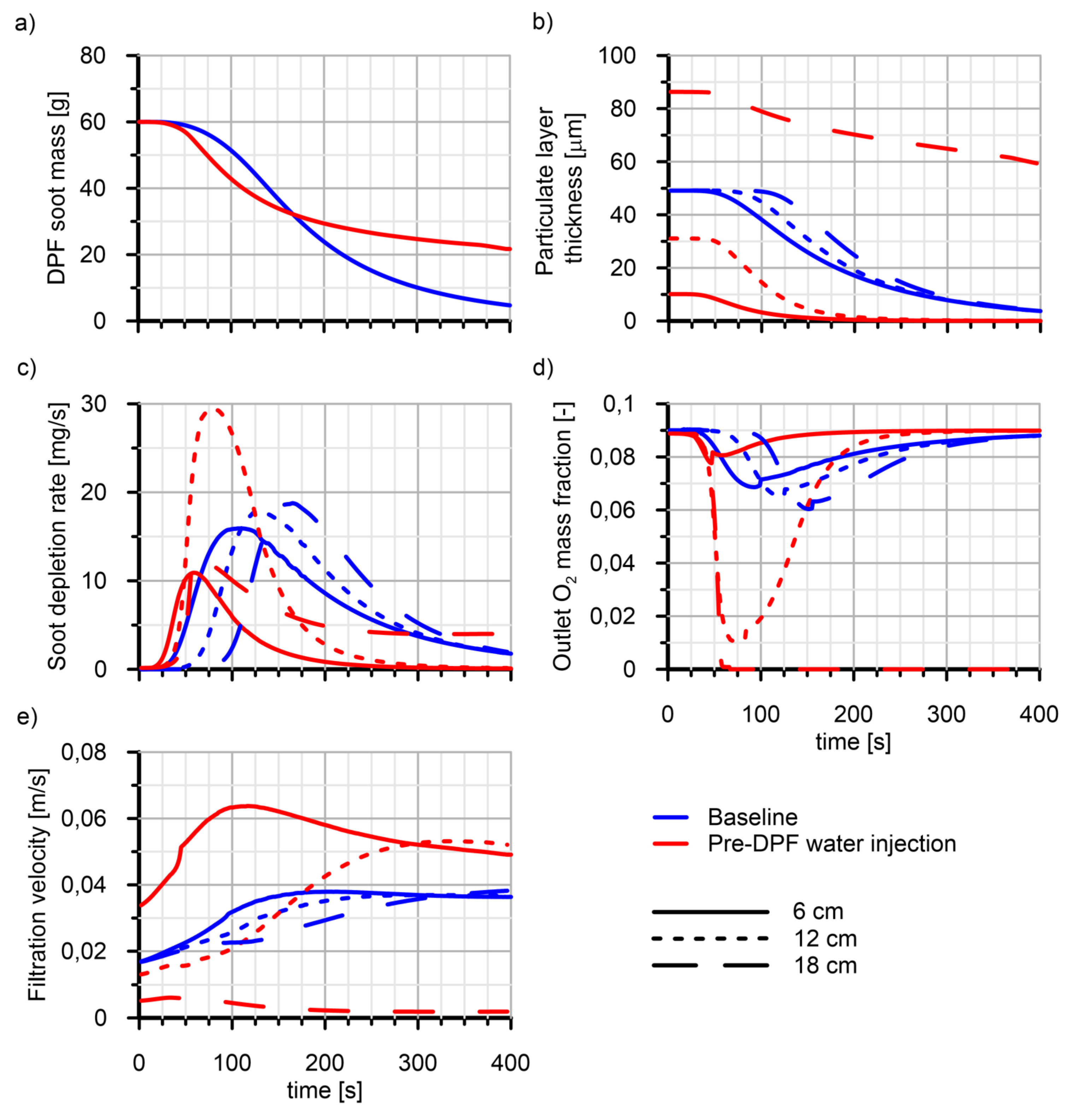
4.1. Pressure Drop
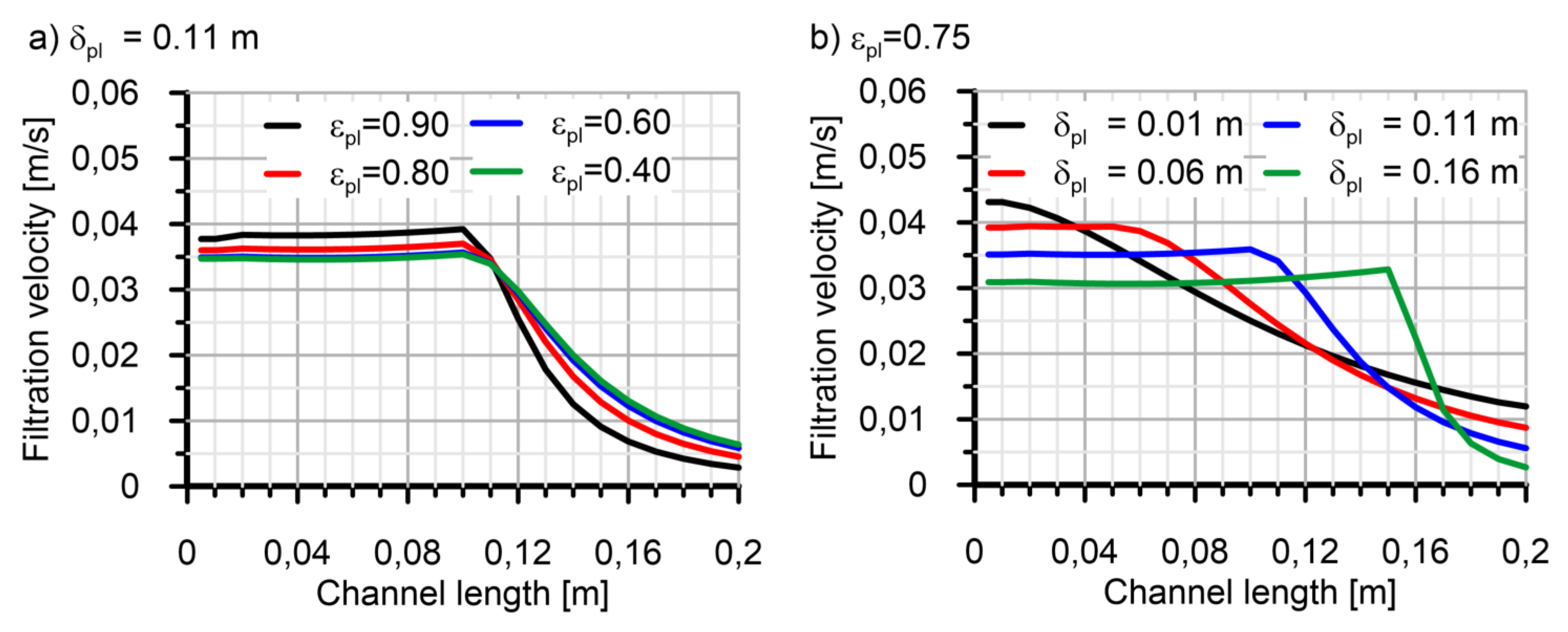
4.2. Filtration Efficiency and Regeneration
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| filtration area | |
| gas concentration | |
| collector unit diameter | |
| cell unit diameter | |
| mean pore diameter | |
| D | diameter |
| specific stagnation internal energy | |
| porous wall filtration efficiency | |
| saturated fraction of porous wall thickness | |
| F | area |
| momentum transfer coefficient for square channels | |
| specific stagnation enthalpy | |
| k | permeability |
| kinetic constant of reagent n | |
| L | channel length |
| soot mass | |
| carbon molecular weight | |
| p | pressure |
| q | heat per unit of time and mass |
| specific surface | |
| t | time |
| u | velocity |
| filtration velocity | |
| particulate layer thickness | |
| porous wall thickness | |
| x | axial dimension |
| X | molar fraction |
| Y | mass fraction |
| z | tangential dimension |
| Greek letters | |
| α | honeycomb cell size |
| stoichiometric coefficient of reagent n | |
| soot mass distribution onset | |
| Δ | variation |
| ε | porosity |
| single sphere filtration efficiency | |
| μ | dynamic viscosity |
| ρ | gas density |
| carbon density | |
| soot packing density inside the porous wall | |
| σ | cell density |
| χ | shape factor |
| Subscripts | |
| cell | referred to the cell unit |
| e | effective |
| in | referred to the inlet channel |
| j | channel type |
| n | reagent (O2, NO2) |
| out | referred to the outlet channel |
| pl | referred to the particulate layer |
| reg | referred to the regeneration |
| w | referred to the porous wall |
| w0 | referred to the clean porous wall |
| Abbreviations | |
| 2LW | Two-step Lax and Wendroff method |
| DOC | Diesel Oxidation Catalyst |
| DPF | Diesel Particulate Filter |
| EEPS | Engine Exhaust Particle Sizer |
| FCT | Flux-Corrected Transport |
| HSDI | High-Speed Direct Injection |
| MoC | Method of Characteristics |
| NEDC | New European Driving Cycle |
| SCF | Stokes–Cunningham Factor |
| SCR | Selective Catalytic Reduction |
| SCRF | Selective Catalytic Reduction Filter |
| SEM | Scanning Electron Microscope |
References
- Johnson, T.V. Review of vehicular emissions trends. SAE Int. J. Engines 2015, 8, 1152–1167. [Google Scholar] [CrossRef]
- Bermúdez, V.; Serrano, J.R.; Piqueras, P.; García-Afonso, O. Assessment by means of gas dynamic modeling of a pre-turbo diesel particulate filter configuration in a turbocharged HSDI diesel engine under full-load transient operation. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2011, 225, 1134–1155. [Google Scholar] [CrossRef]
- Subramaniam, M.N.; Joergl, V.; Keller, P.; Weber, O.; Toyoshima, T.; Vogt, C.D. Feasibility Assessment of a pre-turbo after-treatment system with a 1D modeling approach. SAE Tech. Pap. 2009. [Google Scholar] [CrossRef]
- Luján, J.M.; Bermúdez, V.; Piqueras, P.; García-Afonso, O. Experimental assessment of pre-turbo aftertreatment configurations in a single stage turbocharged Diesel engine. Part 1: Steady-state operation. Energy 2015, 80, 599–613. [Google Scholar] [CrossRef]
- Luján, J.M.; Serrano, J.R.; Piqueras, P.; García-Afonso, O. Experimental assessment of a pre-turbo aftertreatment configuration in a single stage turbocharged Diesel engine. Part 2: Transient operation. Energy 2015, 80, 614–627. [Google Scholar] [CrossRef]
- Lee, J.H.; Michael, J.; Brown, D.B. Evaluation of Cu-based SCR/DPF technology for diesel exhaust emission control. SAE Int. J. Fuels Lubr. 2009, 1, 96–101. [Google Scholar] [CrossRef]
- Watling, T.C.; Ravenscroft, M.R.; Avery, G. Development, validation and application of a model for an SCR catalyst coated diesel particulate filter. Catal. Today 2012, 188, 32–41. [Google Scholar] [CrossRef]
- Marchitti, F.; Nova, I.; Tronconi, E. Experimental study of the interaction between soot combustion and NH3–SCR exhaust reactivity over a Cu–Zeolite SDPF catalyst. Catal. Today 2016, 217, 110–118. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Kostoglou, M. Analysis of asymmetric and variable cell geometry wall-flow particulate filters. SAE Int. J. Fuels Lubr. 2014, 7, 489–495. [Google Scholar] [CrossRef]
- Bollerhoff, T.; Markomanolakis, I.; Koltsakis, G. Filtration and regeneration modeling for particulate filters with inhomogeneous wall structure. Catal. Today 2012, 188, 24–31. [Google Scholar] [CrossRef]
- Iwata, H.; Konstandopoulos, A.G.; Nakamura, K.; Ogiso, A.; Ogyu, K.; Shibata, T.; Ohno, K. Further experimental study of asymmetric plugging layout on DPFs: Effect of Wall thickness on pressure drop and soot oxidation. SAE Tech. Pap. 2015. [Google Scholar] [CrossRef]
- Serrano, J.R.; Bermúdez, V.; Piqueras, P.; García-Afonso, O. Pre-DPF water injection technique for loaded DPF pressure drop reduction and control. Appl. Energy 2015, 140, 234–245. [Google Scholar]
- Serrano, J.R.; Bermúdez, V.; Piqueras, P.; Angiolini, E. Application of pre-DPF water injection technique for pressure drop limitation. SAE Tech. Pap. 2015. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, V.; Sappok, A.; Munnis, S. The sensitivity of DPF performance to the spatial distribution of ash inside DPF inlet channels. SAE Tech. Pap. 2013. [Google Scholar] [CrossRef]
- Sappok, A.; Govani, I.; Kamp, C.; Wang, Y.; Wong, V. In-situ optical analysis of ash formation and transport in diesel particulate filters during active and passive regeneration processes. SAE Int. J. Fuels Lubr. 2013, 6, 336–349. [Google Scholar] [CrossRef]
- Torregrosa, A.J.; Serrano, J.R.; Arnau, F.J.; Piqueras, P. A fluid dynamic model for unsteady compressible flow in wall-flow Diesel particulate filters. Energy 2011, 36, 671–684. [Google Scholar] [CrossRef]
- OpenWAM Website. CMT-Motores Tèrmicos (Universitat Politècnica de València). 2017. Available online: www.openwam.org (accessed on 15 January 2017).
- Galindo, J.; Serrano, J.R.; Arnau, F.J.; Piqueras, P. Description and analysis of a one-dimensional gas-dynamic model with Independent Time Discretization. In Proceedings of the ASME Internal Combustion Engine Division 2008 Spring Technical Conference ICES 2008, Chicago, IL, USA, 27–30 April 2008.
- Lax, P.; Wendroff, B. Systems of conservation laws. Commun. Pure Appl. Math. 1964, 17, 381–398. [Google Scholar] [CrossRef]
- Serrano, J.R.; Arnau, F.J.; Piqueras, P.; García-Afonso, O. Application of the two-step Lax&Wendroff-FCT and the CE-SE method to flow transport in wall-flow monoliths. Int. J. Comput. Math. 2014, 91, 71–84. [Google Scholar]
- Benson, R.S. The Thermodynamics and Gas Dynamics of Internal-Combustion Engines; Clarendon Press: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Desantes, J.M.; Serrano, J.R.; Arnau, F.J.; Piqueras, P. Derivation of the method of characteristics for the fluid dynamic solution of flow advection along porous wall channels. Appl. Math. Model. 2012, 36, 3144–3152. [Google Scholar] [CrossRef]
- Serrano, J.R.; Arnau, F.J.; Piqueras, P.; Garcia-Afonso, O. Packed bed of spherical particles approach for pressure drop prediction in wall-flow DPFs (diesel particulate filters) under soot loading conditions. Energy 2013, 58, 644–654. [Google Scholar] [CrossRef]
- Murtagh, M.; Sherwood, D.; Socha, L. Development of a diesel particulate filter composition and its effect on thermal durability and filtration performance. SAE Tech. Pap. 1994. [Google Scholar] [CrossRef]
- Fino, D.; Russo, N.; Millo, F.; Vezza, D.; Ferrero, F.; Chianale, A. New tool for experimental analysis of diesel particulate filter loading. Top Catal. 2009, 52, 13–20. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Johnson, J.H. Wall-flow diesel particulate filters—Their pressure drop and collection efficiency. SAE Tech. Pap. 1989. [Google Scholar] [CrossRef]
- Lapuerta, M.; Ballesteros, R.; Martos, F. A method to determine the fractal dimension of diesel soot agglomerates. J. Coll. Interface Sci. 2006, 303, 149–158. [Google Scholar] [CrossRef] [PubMed]
- Serrano, J.R.; Climent, H.; Piqueras, P.; Angiolini, E. Filtration modeling in wall-flow particulate filters of low soot penetration thickness. Energy 2016, 112, 883–888. [Google Scholar] [CrossRef]
- Logan, B.E.; Jewett, D.G.; Arnold, R.G.; Bouwer, E.J.; O’Melia, C.R. Clarification of clean-bed filtration models. J. Environ. Eng. 1995, 121, 869–873. [Google Scholar] [CrossRef]
- Koltsakis, G.C.; Stamatelos, A.M. Modes of catalytic regeneration in Diesel particulate filters. Ind. Eng. Chem. 1997, 36, 4155–5165. [Google Scholar] [CrossRef]
- Bisset, E.J. Mathematical model of the thermal regeneration of a wall-flow monolith diesel particulate filter. Chem. Eng. Sci. 1984, 39, 1233–1244. [Google Scholar] [CrossRef]
- Galindo, J.; Serrano, J.R.; Piqueras, P.; García-Afonso, O. Heat transfer modeling in honeycomb wall-flow diesel particulate filters. Energy 2012, 43, 201–213. [Google Scholar] [CrossRef]
- Payri, F.; Broatch, A.; Serrano, J.R.; Piqueras, P. Experimental-theoretical methodology for determination of inertial pressure drop distribution and pore structure properties in wall-flow diesel particulate filters (DPFs). Energy 2011, 36, 6731–6744. [Google Scholar] [CrossRef]
- Angiolini, E. Contribution to the Understanding of Filtration and Pressure Drop Phenomena in Wall-Flow DPFs. Ph.D. Thesis, Universitat Politècnica de València, València, Spain, 2017. [Google Scholar]
- Konstandopoulos, A.G.; Skaperdas, E.; Masoudi, M. Microstuctural properties of soot deposits in diesel particulate traps. SAE Tech. Pap. 2002. [Google Scholar] [CrossRef]
- Bermúdez, V.; Serrano, J.R.; Piqueras, P.; Campos, D. Analysis of the influence of pre-DPF water injection technique on pollutants emission. Energy 2015, 89, 778–792. [Google Scholar] [CrossRef]


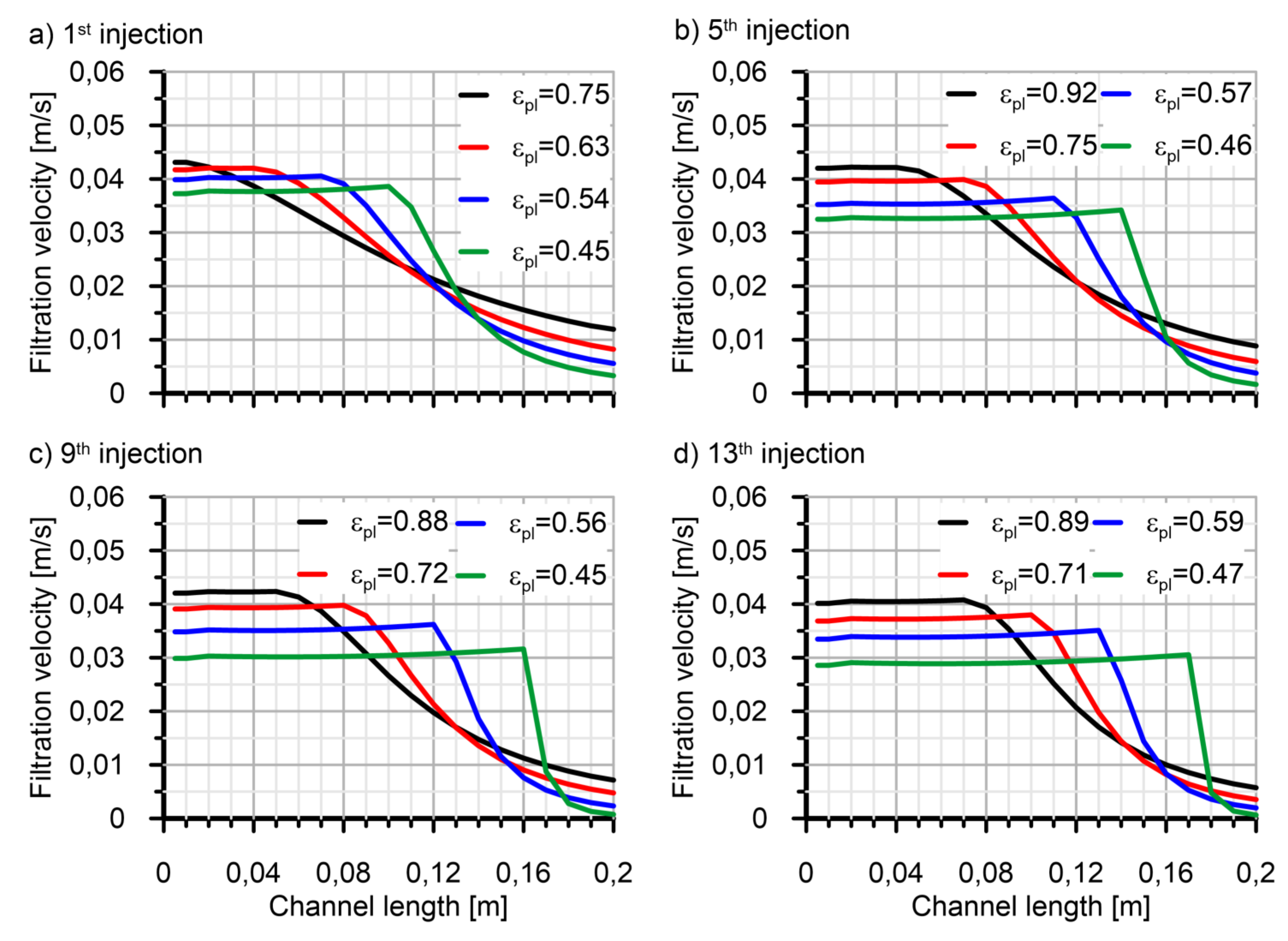
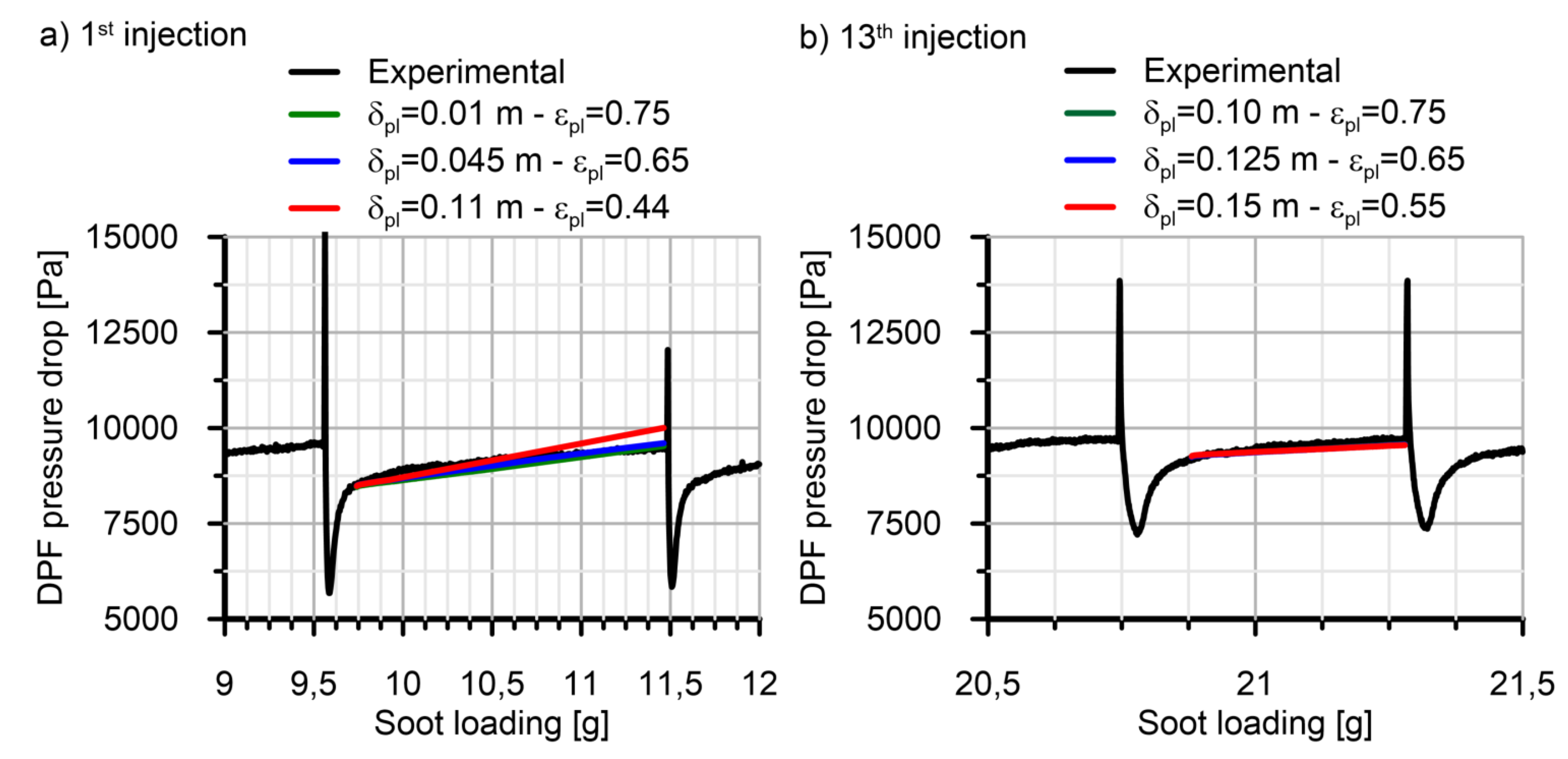
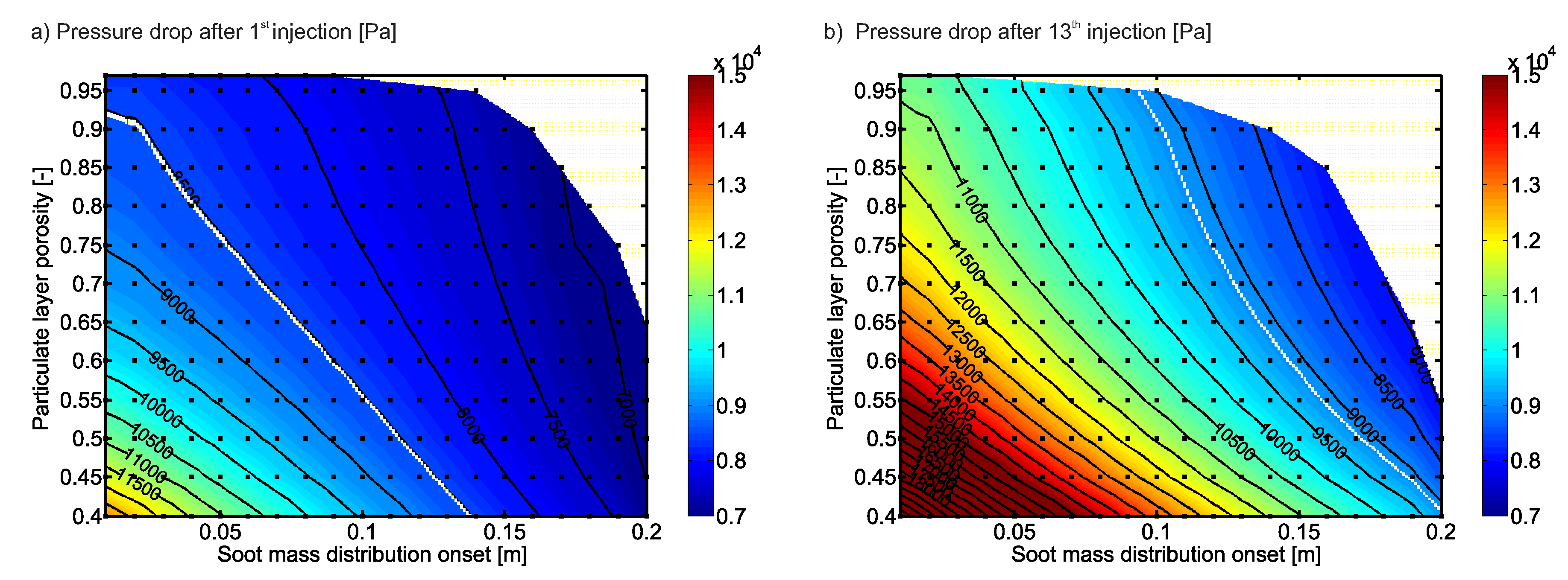
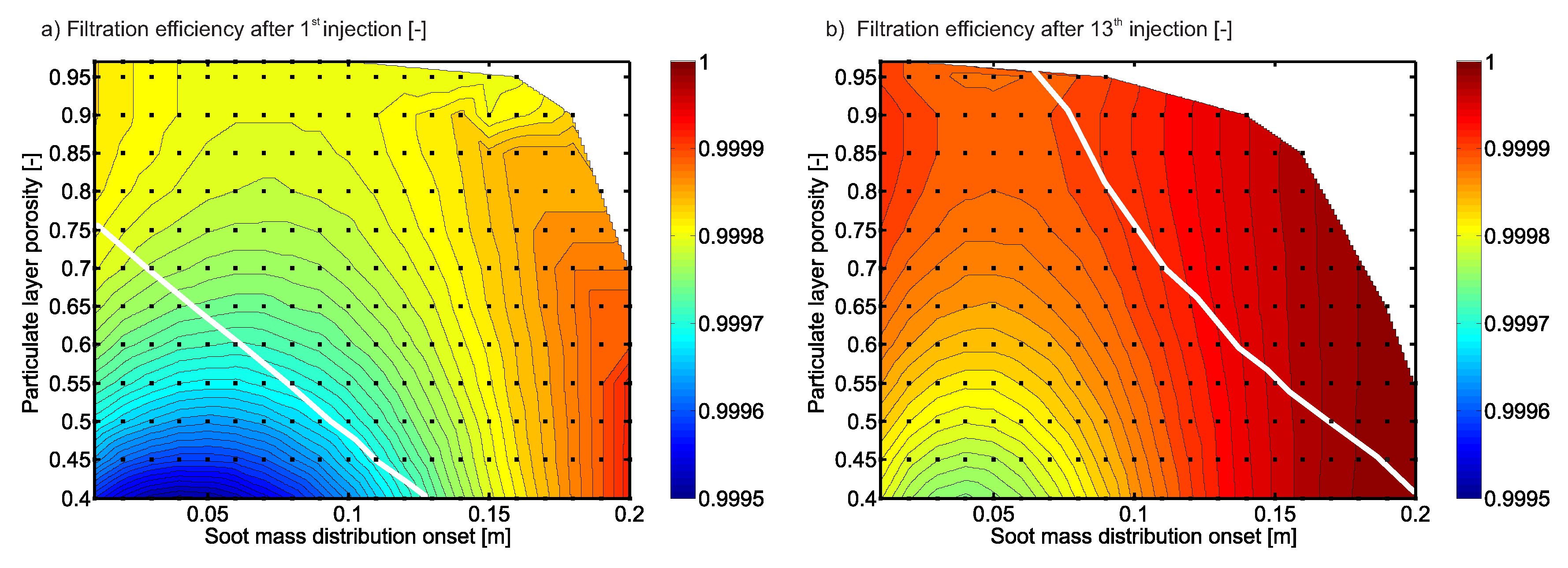
| #A [33] | #B [34] | ||
|---|---|---|---|
| Diameter (D) | (mm) | 132 | 140 |
| Channel length (L) | (mm) | 200 | 230 |
| Honeycomb cell size (α) | (mm) | 1.48 | 1.42 |
| Porous wall thickness () | (mm) | 0.31 | 0.46 |
| Cell density (σ) | (cpsi) | 200 | 180 |
| Porosity () | (-) | 0.41 | 0.41 |
| Mean pore diameter () | (μm) | 12.1 | 18.55 |
| Permeability () | (×10−13 m2) | 2.49 | 5.85 |
| Type | HSDI Diesel Passenger Car |
|---|---|
| Emission standards | Euro 4 |
| Displacement | 1997 cm3 |
| Bore | 85 mm |
| Stroke | 88 mm |
| Number of cylinders | 4 in line |
| Number of valves | 4 per cylinder |
| Compression ratio | 18:1 |
| Maximum power @ speed | 100 kW @4000 rpm |
| Maximum torque @ speed | 320 Nm @ 1750 rpm |
| Aftertreatment | Close-coupled DOC + Underfloor DOC-DPF |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bermúdez, V.; Serrano, J.R.; Piqueras, P.; Sanchis, E.J. On the Impact of Particulate Matter Distribution on Pressure Drop of Wall-Flow Particulate Filters. Appl. Sci. 2017, 7, 234. https://doi.org/10.3390/app7030234
Bermúdez V, Serrano JR, Piqueras P, Sanchis EJ. On the Impact of Particulate Matter Distribution on Pressure Drop of Wall-Flow Particulate Filters. Applied Sciences. 2017; 7(3):234. https://doi.org/10.3390/app7030234
Chicago/Turabian StyleBermúdez, Vicente, José Ramón Serrano, Pedro Piqueras, and Enrique José Sanchis. 2017. "On the Impact of Particulate Matter Distribution on Pressure Drop of Wall-Flow Particulate Filters" Applied Sciences 7, no. 3: 234. https://doi.org/10.3390/app7030234
APA StyleBermúdez, V., Serrano, J. R., Piqueras, P., & Sanchis, E. J. (2017). On the Impact of Particulate Matter Distribution on Pressure Drop of Wall-Flow Particulate Filters. Applied Sciences, 7(3), 234. https://doi.org/10.3390/app7030234