Abstract
Microwave-based all-analogue (orthogonal) subcarrier multiplexing (SCM) permits a direct processing of baseband data at Gbit/s while achieving low power consumption, low latency, low cost, and tolerance to dispersion. A key figure of merit in any SCM link is the sensitivity in the receiver, which depends on the transmitter, the link and the receiver. By analysing the impact of the nonlinearities of an optical IQ modulator in the presence of optical noise, sensitivities are mathematically estimated as a function of the optical modulation index (OMI) at the transmitter. The results are verified with simulations achieving a good agreement with the mathematical model. The theoretical model provided can be employed as a tool to predict the best achievable sensitivities and the optimum OMI in broadband SCM and orthogonal SCM links.
1. Introduction
Digital subcarrier multiplexing (SCM) consists of the generation of a multicarrier electrical signal that is then modulated onto an optical carrier and transmitted over fiber [1,2]. The (de)modulation of the electrical digital subchannels can be accomplished by digital signal processing (DSP) [1] and analogue signal processing (ASP) [2]. Broadband DSP-based SCM schemes can potentially achieve high modulation orders with a high spectral efficiency, but they require expensive analogue-to-digital and digital-to-analogue converters (ADC and DAC) and are also penalised by a high power consumption and latency [3]. In contrast, ASP-based SCM systems rely on the maturity of microwave components, leveraging the excellent stability and frequency selectivity of microwave devices and the low phase noise of microwave oscillators, to potentially achieve broadband communications systems with low power consumption and low latency. Furthermore, all electrical ASP can be implemented with inexpensive monolithic microwave integrated circuit (MMIC) technology [4], benefiting from integration but with a reduced transistor count with respect to DSP. The main weakness of traditional broadband ASP-based SCM systems has been the spectral efficiency. Recently, it has been proven that this disadvantage can be overcome by transmitting orthogonally overlapping electrical subchannels according to filter bank multicarrier (FBMC) theory [5]. For the remainder of the paper, this technique will be referred to as orthogonal subcarrier multiplexing (OSCM). Note that the feasibility of OSCM has been demonstrated in real-time schemes relying largely on off-the-shelf components [5], employing realistic synchronization [6] and in combination with wavelength division multiplexing (WDM) [7].
The main advantage of SCM with respect to a single channel implementation is the higher tolerance to dispersion [2]. However, standard modulation of an optical carrier produces a double sideband (DSB) spectrum. Due to dispersion, associated subcarriers suffer a different delay in the upper and the lower sidebands, which translates into dispersive fading after photo-detection [8]. Consequently, optical single side band (SSB) modulation is preferred as it eliminates dispersive fading [9] and achieves the higher tolerance to dispersion expected from SCM. SCM/SSB can be directly obtained without employing optical filters with dual-drive Mach Zehnder modulators (DD-MZM) [2] and with optical IQ modulators [10]. The optical modulators exhibit a nonlinear behaviour that produces intermodulation distortion (IMD) between the electrical subchannels. This IMD has been thoroughly analysed in a number of theoretical studies [11,12], where results are often provided in terms of signal to noise ratio per subchannel in the receiver. However, from a practical perspective, the performance of digital electro-optical transceivers is typically specified in terms of receiver sensitivity, which is the minimum received power at which data can be successfully recovered. Calculations to obtain the best achievable sensitivities in digital broadband SCM links in the presence of optical noise were presented in [2], but did not include the IMD. In contrast, a model that includes IMD was developed in [10] for the case of optical IQ modulators.
This paper employs the model presented in [10] to estimate the best achievable sensitivities in broadband SCM/SSB and OSCM/SSB links consisting of an optical IQ modulator and a pre-amplified optical receiver as a function of the optical modulation index (OMI). While previous works showed how the mathematical model predicted differential variations in performance [10], this manuscript investigates the accuracy of the model to predict the receiver sensitivity as a function of OMI, which are the key parameters in the design of such an optical link. The model is implemented in MATLAB and compared to simulations performed with the “VPI Transmission Maker” simulation platform. A good agreement, especially for the optimum OMI, is obtained.
2. Electro-Optical System
The system that was analysed and simulated is illustrated in Figure 1a. Data was generated in the form of delta trains that were shaped with low pass square root raised cosine (SRRC) filters. The roll-off factor β was equal to 1 as a full-bandwidth is more realistic to emulate an ASP-based system. The shaped digital streams were then used to modulate carriers from microwave local oscillators (LO) with ideal IQ mixers, performing a quadrature phase shift keying (QPSK) modulation on each subchannel. Once the subchannels were combined, the resultant signal and its Hilbert transform, required for the optical SSB generation [10], were fed to an optical IQ modulator. The laser at the input of the optical modulator was ideal (a noise free optical carrier). The parallel MZMs inside the optical modulator were biased at quadrature. The amplitude of the obtained optical SSB signal was modified with a variable optical attenuator (VOA) that simulated fibre losses. The Erbium doped fibre amplifier (EDFA) in the pre-amplified receiver presented a noise figure of 5 dB and produced a constant output average optical power that was fed to an ideal noise-free photo-receiver that performed the direct detection (DD) of the received signal. The resultant electrical signal was demodulated with ideal IQ mixers and the matched low pass SRRC filters. The obtained digital binary streams were analysed by measuring bit error rate (BER). Note that the use of SRRC filters and the particular phase alignment imposed in the local oscillators and the baseband signals are required to make the scheme compatible with orthogonal transmission in accordance with FBMC theory [5,13,14]. From the previous description of the simulated electro-optical scheme, it can be derived that the only sources of impairments were the IMD coming from the optical modulator and the amplified spontaneous emission (ASE) generated in the EDFA. These conditions were considered because the signal-ASE beat noise is the main source of optical noise in practical SCM systems implementing pre-amplified receivers [2], especially when working close to the sensitivity level.
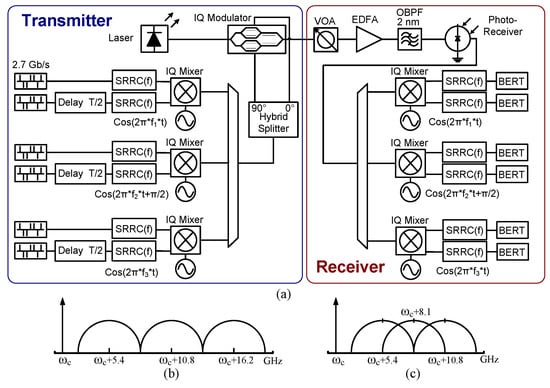
Figure 1.
(a) Direct Detection (DD) electro-optical scheme compatible with subcarrier multiplexing (SCM)/single side band (SSB) and orthogonal subcarrier multiplexing (OSCM)/SSB transmission based on optical IQ modulator and pre-amplified optical receiver; (b) example of transmitted optical spectrum for the case of SCM/SSB consisting of three 2.7 Gbaud quadrature phase shift keying (QPSK) subchannels; (c) example of transmitted optical spectrum for the case of OSCM/SSB consisting of three orthogonally overlapping 2.7 Gbaud QPSK subchannels.
Two different microwave frequency plans were analysed. The first case corresponds to a SCM/SSB signal consisting of three 2.7 Gbaud QPSK subchannels with LOs located at 5.4, 10.8, and 16.2 GHz, as depicted in Figure 1b. The electrical signal presents a data rate of 16.2 Gbit/s with a spectral efficiency of 1 bit/s/Hz. The second case halves the LO separation and achieves the OSCM/SSB spectrum shown in Figure 1c, increasing the spectral efficiency to 1.5 bit/s/Hz. Note that both spectra are only illustrative and the real optical carrier to signal power ratio (CSPR) depends on OMI.
3. Mathematical Model
The sensitivity in the presented DD SCM/SSB scheme is the result of the following trade-off. OMI needs to be high to obtain a low CSPR, which reduces the relative power wasted in the optical carrier, thereby achieving a better sensitivity. However, higher values of OMI translate into higher IMD due to the nonlinear response of the optical modulator, which can translate into a penalty in the sensitivity if the IMD is higher than the noise floor originating from the ASE and obtained in the photocurrent. Therefore, a mathematical model that considers only the main source of optical noise, namely the ASE, obtains the best sensitivity that is potentially achievable as a function of OMI. Such a model was presented in [10] for the case of optical IQ modulators, and is employed in this work. As IMD at a given subchannel is the result of summing the interfering intermodulation products (IMP), a perfect model would require considering all the individual electrical phases in the system. However, for simplicity, IMD is modelled as random noise with Gaussian distribution, and, accordingly, discrepancies with the model are expected for higher OMIs. In the conditions stated in Section 2, the best achievable optical sensitivity is [10]:
where F represents the noise figure of the EDFA, h is Planck’s constant, ν is the optical frequency, B is the electrical baseband bandwidth of the subchannels, QF represents the quality factor of the digital communication, N states the number of electrical subchannels, Jn(x) stands for the nth order Bessel function of the first kind, m represents the rms OMI per subchannel (m = πVAC/2Vπ where Vπ is the half-wave voltage of the MZMs and VAC is the peak voltage of a tone in theory but represents the rms voltage per subchannel at the electrical input of the MZMs in practice [10]), and, finally, DIMD represents the distortion associated with IMD.
Typically, the main sources of IMD are second order intermodulation (Ω = Ωi − Ωj), third order intermodulation (Ω = Ωi ± 2Ωj), and a different case of third order intermodulation that is called triple beat (Ω = Ωi ± Ωj ± Ωk), where Ωi, Ωj, and Ωk are any three arbitrary frequencies [15]. For systems consisting of many subchannels, triple beat is the dominant third order intermodulation [15], but for the presented case which consists of a low number of subchannels, the described subdivision of the third order IMD is necessary. For each subchannel in a given frequency plan, there can be a different number of interfering intermodulation products of each kind. These values are denoted as NCSO for the second order intermodulation, NIM3 for the third order intermodulation, and NCTB for the triple beat. In the case under analysis, with the MZMs biased at quadrature, the received photocurrent is free of second order intermodulation [10]. For that reason, only NIM3 and NCTB are analysed, and are reported in Table 1 for the two frequency plans under analysis. Finally, from [10], DIMD is expressed as

Table 1.
IMP (intermodulation products) count for each subchannel in the photocurrent.
Note that DIMD can be different for every subchannel, which translates into different optical sensitivities for each subchannel.
4. Results
The system shown in Figure 1 was simulated for the depicted SCM/SSB and OSCM/SSB frequency plans. Pseudo random binary sequences (PRBS) of 210 − 1 bits were generated in each baseband source. Each PRBS was delayed by a random integer number of bits to ensure a degree of decorrelation between subchannels. In the baseband receivers, the digital signals were sampled in the middle of the bit period before performing a binary decision. It is important to note that the BER was calculated emulating a real system, in contrast with other approaches that estimate BER according to statistical distributions of noise. For different values of OMI, the attenuation of the VOA in the receiver was increased until a BER of 3.8 × 10−3 was achieved, which is the typical BER threshold for hard-decision forward error correction (HD-FEC) codes with a 7% overhead. With this procedure, the optical receiver sensitivities were obtained as a function of OMI. The simulated results, obtained with the VPI software, are illustrated in Figure 2, where they are also compared with the theoretical calculations obtained with the mathematical model presented in Section 3. Note that the results are shown as a function of overall rms OMI with respect to Vπ:
where vrms is the rms voltage per subchannel and VRMS is the overall rms voltage.
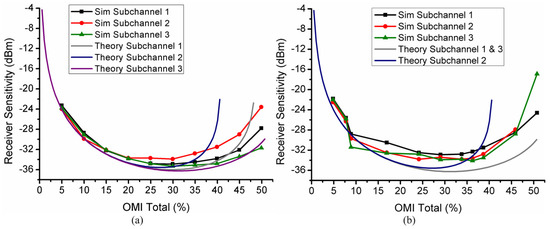
Figure 2.
Simulated and theoretical best achievable optical receiver sensitivities for (a) the SCM/SSB frequency plan consisting of three 2.7 Gbaud QPSK subchannels and (b) the OSCM/SSB frequency plan consisting of three orthogonally overlapping 2.7 Gbaud QPSK subchannels. The values employed in the simulation and the theoretical calculations are: N = 3, F = 5 dB, v = 193.4 THz (1550 nm), QF = 2.67 (BER = 3.8 × 10−3), B = 2.7 GHz, and intermodulation product count according to Table 1.
Focusing on the SCM/SSB case, from Figure 2a, it can be deduced that the mathematical model estimates the sensitivities with an error ≤2 dB when the optical noise is dominant over nonlinearities (M% ≤ 35%). When nonlinearities are dominant, especially triple-beat for Subchannel 2, the error can be higher. This effect occurs because the Gaussian approximation is more accurate to model the ASE noise than the IMD. In reality, the effect of IMD is also related to the phase alignment of subchannels and can vary for different sampling points. Apart from that, the IMD count in this particular case is small, and Gaussian approximations tend to be more accurate when a higher number of intermodulation products take place. However, and despite the inaccuracies of the model, it can be observed that the optimum OMI that gives rise to the best achievable optical sensitivity for each subchannel is accurately predicted by the mathematical model (M% ≈ 30%).
The mathematical model was developed for the non-overlapping SCM case. However, as the OSCM eye diagrams also present an ideal sampling point in the middle of the bit period [13], which is impaired only by noise and distortion, the mathematical model can also be applied to OSCM. A perfect compatibility of the model with OSCM is expected when the optical noise is completely dominant over IMD and determines the final sensitivity. In other cases, as any intermodulation product also distorts the adjacent subchannels, higher deviations between the VPI simulation and theory are expected. This effect can be observed in Figure 2b. In this case, even for low values of OMI (M% ≤ 35%), the error is higher than in the previous case, ≤4 dB. However, similarly to the previous case, the optimum OMI for each subchannel is predicted with a negligible error (M% ≈ 25% for Subchannel 2 and M% ≈ 35% for Subchannels 1 and 3).
5. Conclusions
The key figure of merit of any digital electro-optical transceiver is the sensitivity for a given BER. However, traditional mathematical models calculate the signal-to-noise ratio per subchannel without investigating the accuracy of the associated BER and, consequently, the sensitivity. In contrast, the mathematical model presented in [10] attempts to predict the best achievable receiver sensitivities for DD SCM/SSB links based on optical IQ modulators and pre-amplified receivers. Previous works have shown the accuracy of the model in terms of performance difference as a function of parameters like OMI [10]. This paper further extends the accuracy of the model to estimate the best achievable sensitivities as a function of OMI.
The model has been compared with simulations for a case where the BER threshold is high, in line with modern high-performance transceivers. A good agreement with theory has been obtained and the optimum OMI can be predicted with small errors in sensitivity. The inaccuracies are the result of modelling IMPs and IMD, a deterministic phenomenon, as Gaussian noise. The mathematical model can also be applied to the case of OSCM/SSB, obtaining slightly higher errors. The additional errors occur because the model does not include the impact of IMP on adjacent overlapping subchannels.
Acknowledgments
This work was supported by EI CFTD CF/2011/1627 and SFI grants CTVR (10/CE/I1853), IPIC (12/RC/2276), and US-Ireland (15/US-C2C/I3132).
Author Contributions
Fernando. A. Gutiérrez, Andrew D. Ellis, and Philip Perry developed the mathematical model. Eamonn P. Martin performed the VPI simulations. Fernando A. Gutiérrez, Eamonn P. Martin, and Liam P. Barry analysed the results. Fernando A. Gutiérrez wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Flood, F.A. A 20 Gb/s per wavelength subcarrier multiplexed optical transmission system. In Proceedings of the Optical Fiber Communication Conference and Exhibit, Anaheim, CA, USA, 17–22 March 2002.
- Rongqing, H.; Benyuan, Z.; Renxiang, H.; Allen, C.T.; Demarest, K.R.; Richards, D. Subcarrier multiplexing for high-speed optical transmission. J. Lightwave Technol. 2002, 20, 417–427. [Google Scholar] [CrossRef]
- Morea, A.; Spadaro, S.; Rival, O.; Perelló, J.; Agraz, F.; Verchere, D. Power management of optoelectronic interfaces for dynamic optical networks. In Proceedings of the 2011 37th European Conference and Exhibition on Optical Communication, Geneva, Switzerland, 18–22 September 2011.
- Salter, M.; Platt, D.; Pettersson, L.; Aspemyr, L.; Bao, M. Circuits and system simulations for 100 Gb/s optical SCM transmission. In Proceedings of the IEEE International Conference on electronics, Circuits, and Systems (ICECS), Yasmine Hammamet, Tunisia, 13–16 December 2009; pp. 960–963.
- Gutiérrez, F.A.; Perry, P.; Martin, E.P.; Ellis, A.D.; Smyth, F.; Barry, L.P. All-Analogue Real-Time Broadband Filter Bank Multicarrier Optical Communications System. J. Lightwave Technol. 2015, 33, 5073–5083. [Google Scholar] [CrossRef]
- Gutiérrez, F.A.; Martin, E.P.; Perry, P.; Ellis, A.D.; Barry, L. All-Analogue Real-Time Filter Bank OFDM over 50 Km of SSMF using a Novel Synchronization Technique. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–24 March 2016.
- Gutiérrez, F.A.; Martin, E.P.; Perry, P.; Ellis, A.D.; Anandarajah, P.M.; Barry, L.P. WDM Orthogonal Subcarrier Multiplexing. J. Lightwave Technol. 2016, 34, 1815–1823. [Google Scholar] [CrossRef]
- Schmuck, H. Comparison of optical millimetre-wave system concepts with regard to chromatic dispersion. Electron. Lett. 1995, 31, 1848–1849. [Google Scholar] [CrossRef]
- Smith, G.H.; Novak, D.; Ahmed, Z. Overcoming chromatic-dispersion effects in fiber-wireless systems incorporating external modulators. IEEE Trans. Microw. Theory Tech. 1997, 45, 1410–1415. [Google Scholar] [CrossRef]
- Gutiérrez, F.A.; Perry, P.; Smyth, F.; Ellis, A.D.; Barry, L.P. Optimum Bias Point in Broadband Subcarrier Multiplexing With Optical IQ Modulators. J. Lightwave Technol. 2015, 33, 258–266. [Google Scholar] [CrossRef]
- Chen, W.H.; Way, W.I. Multichannel single-sideband SCM/DWDM transmission systems. J. Lightwave Technol. 2004, 22, 1679–1693. [Google Scholar] [CrossRef]
- Laurencio, P.; Simoes, S.O.; Medeiros, M.C.R. Impact of the Combined Effect of RIN and Intermodulation Distortion on OSSB/SCM Systems. J. Lightwave Technol. 2006, 24, 4250–4262. [Google Scholar] [CrossRef]
- Saltzberg, B. Performance of an Efficient Parallel Data Transmission System. IEEE Trans. Commun. Technol. 1967, 15, 805–811. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B. OFDM Versus Filter Bank Multicarrier. IEEE Signal Process. Mag. 2011, 28, 92–112. [Google Scholar] [CrossRef]
- Way, W.I. Broadband Hybrid Fiber Coax Access System Technologies; Academic Press, Inc.: Orlando, FL, USA, 1998. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).