Design of a Tubular Permanent Magnet Actuator for Active Lateral Secondary Suspension of a Railway Vehicle
Abstract
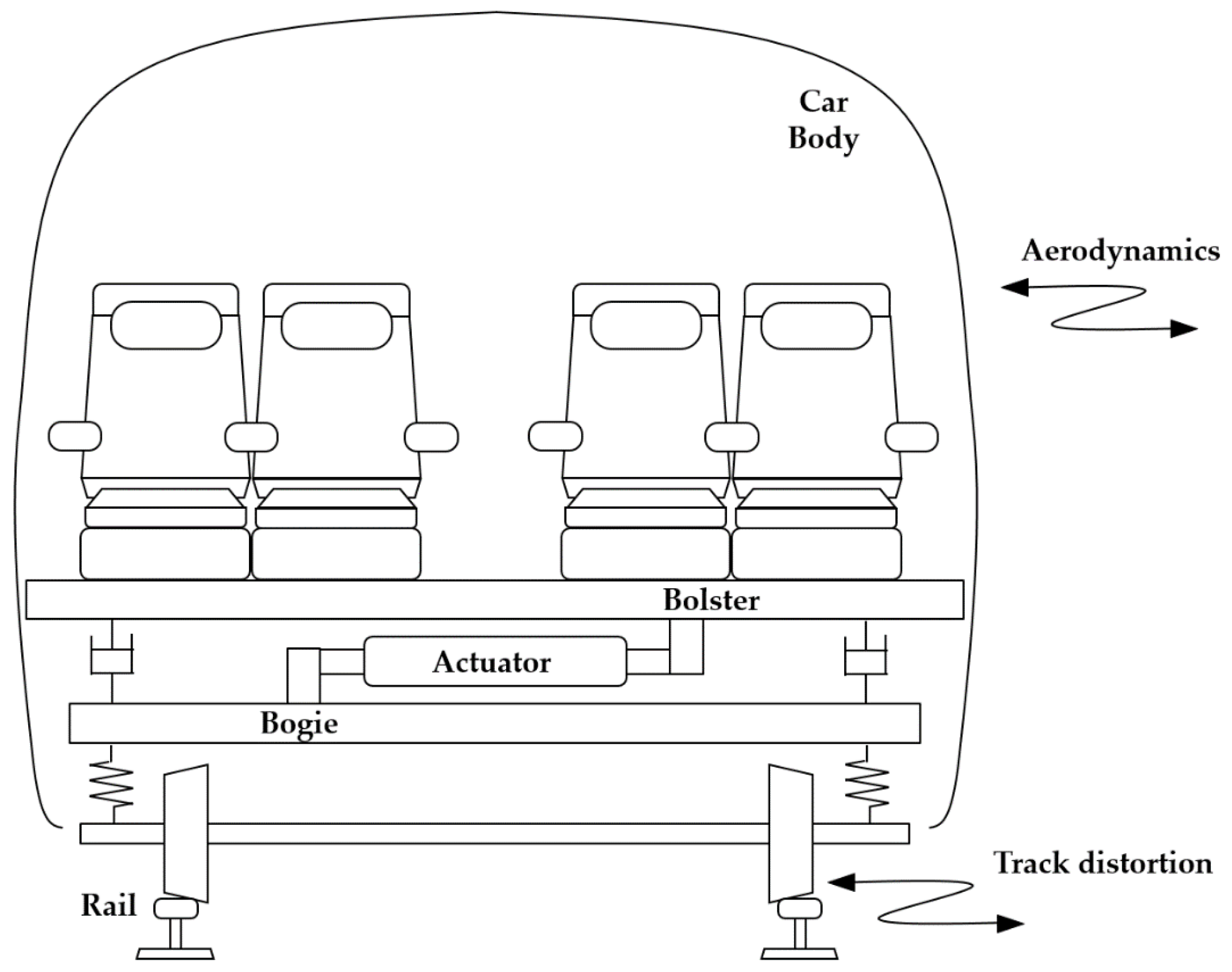
:1. Introduction
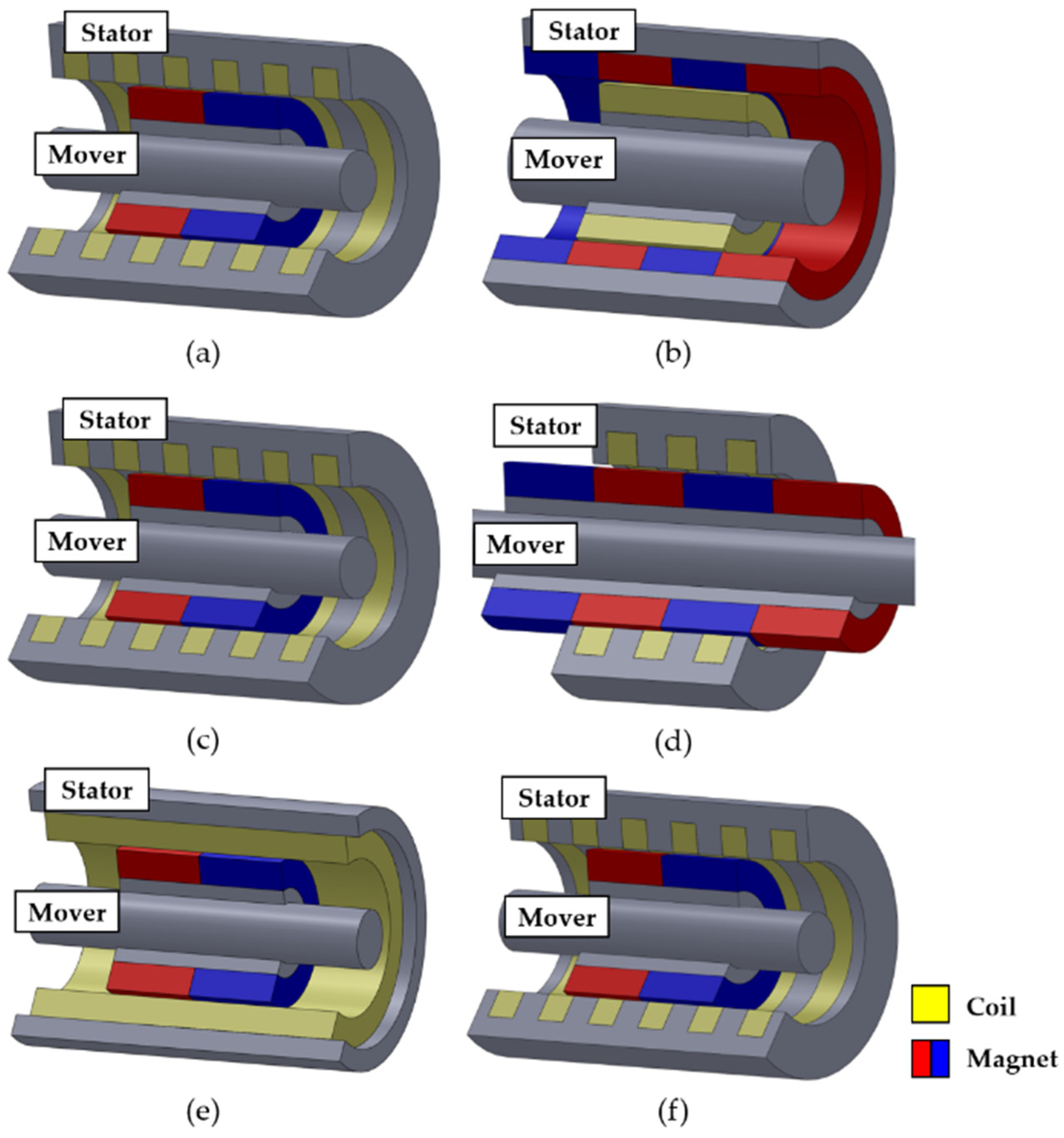
2. Tubular Permanent Magnet Actuator (TPMA) Specifications
3. Electromagnetic and Thermal Finite Element (FE) Model
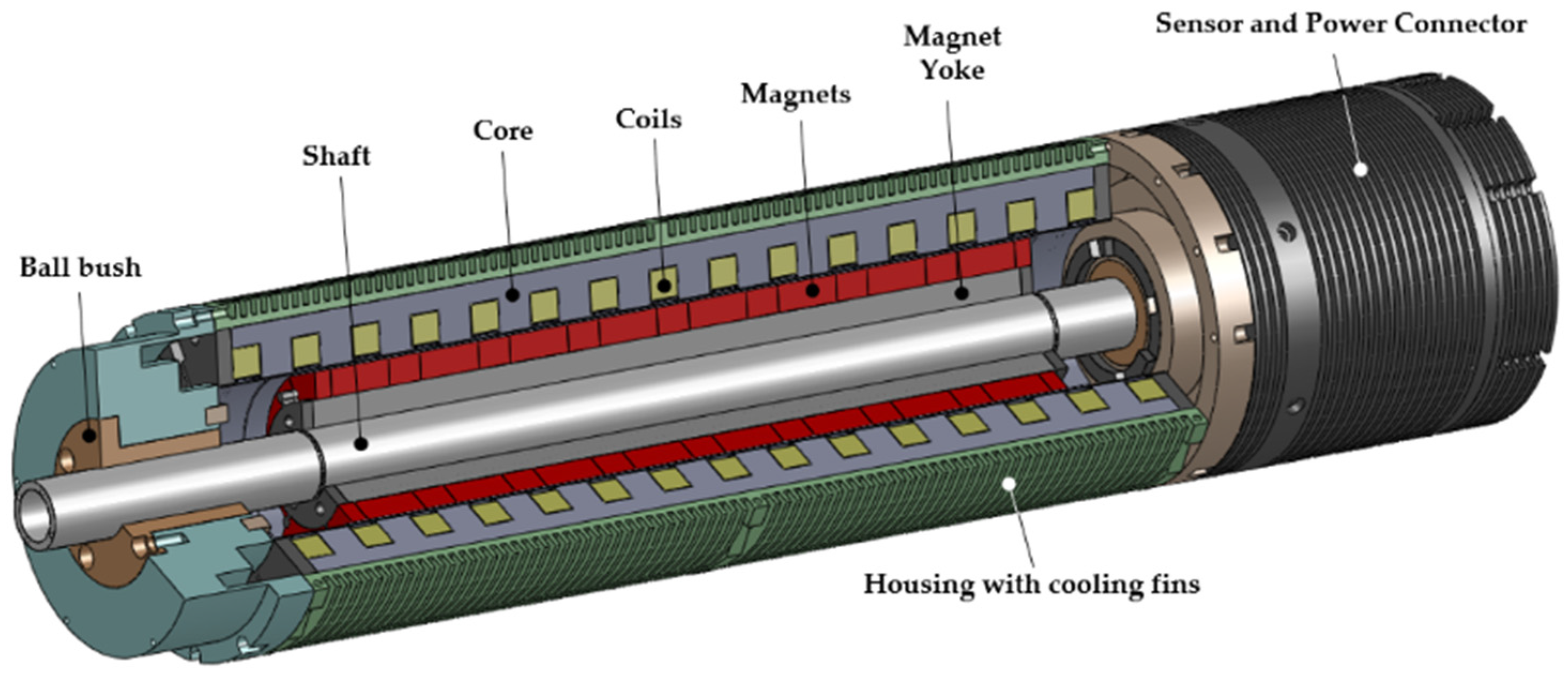
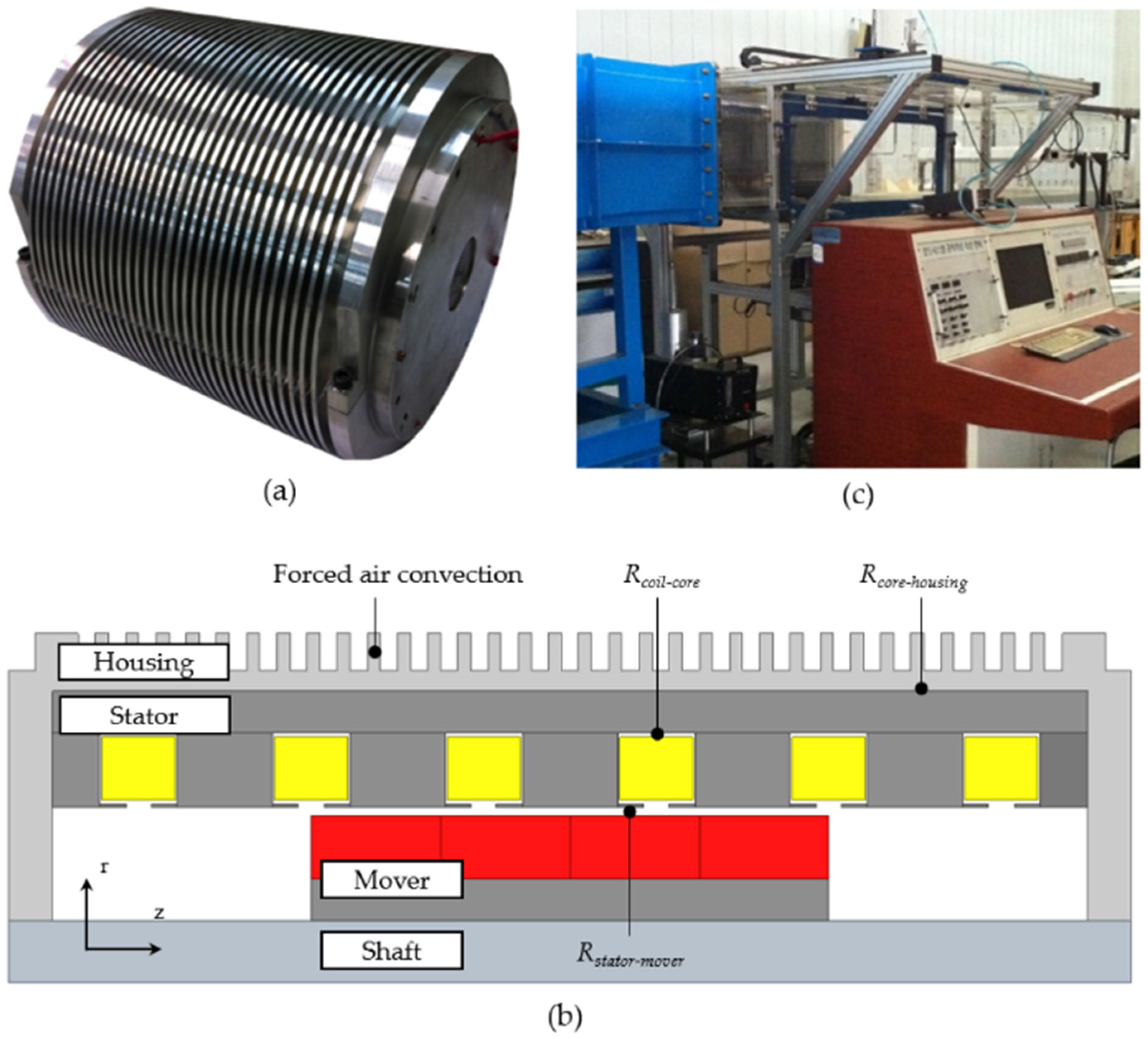
3.1. Overall Structure
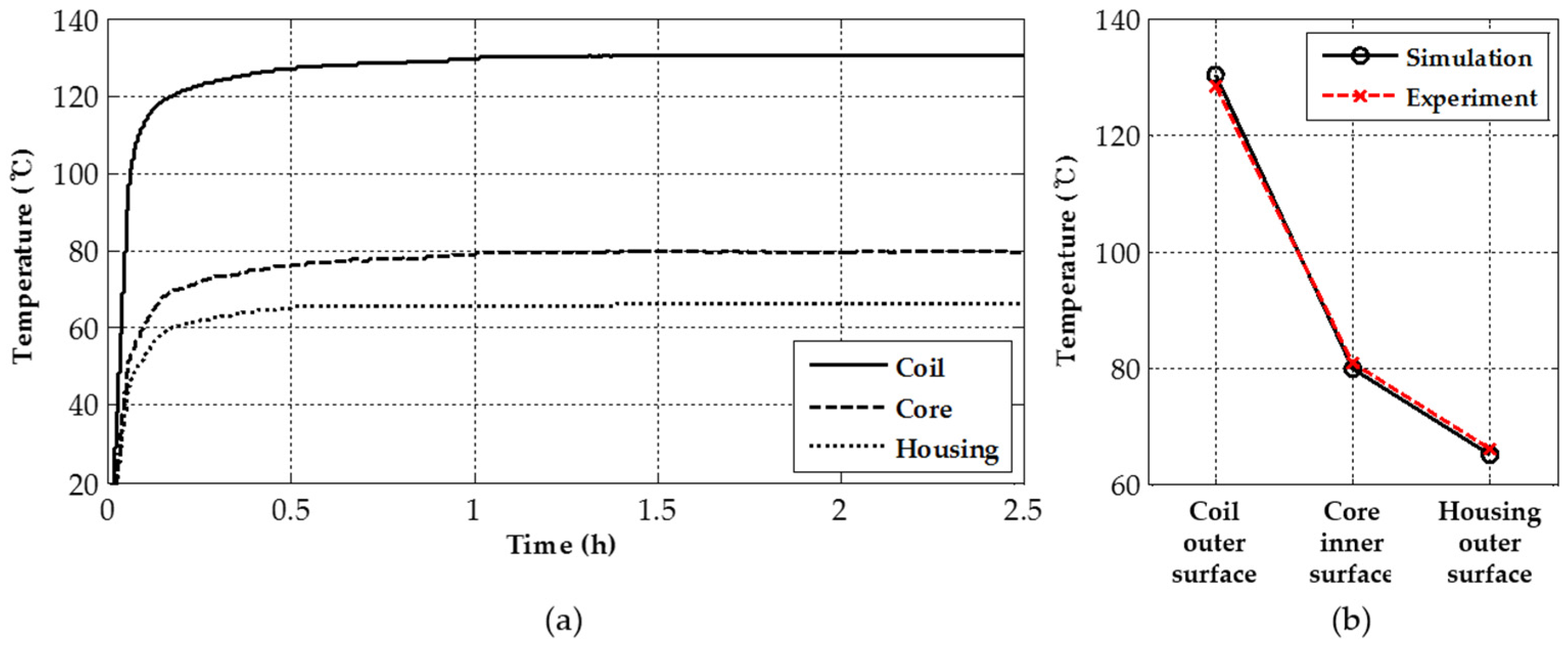
3.2. Thermal Model Parameters
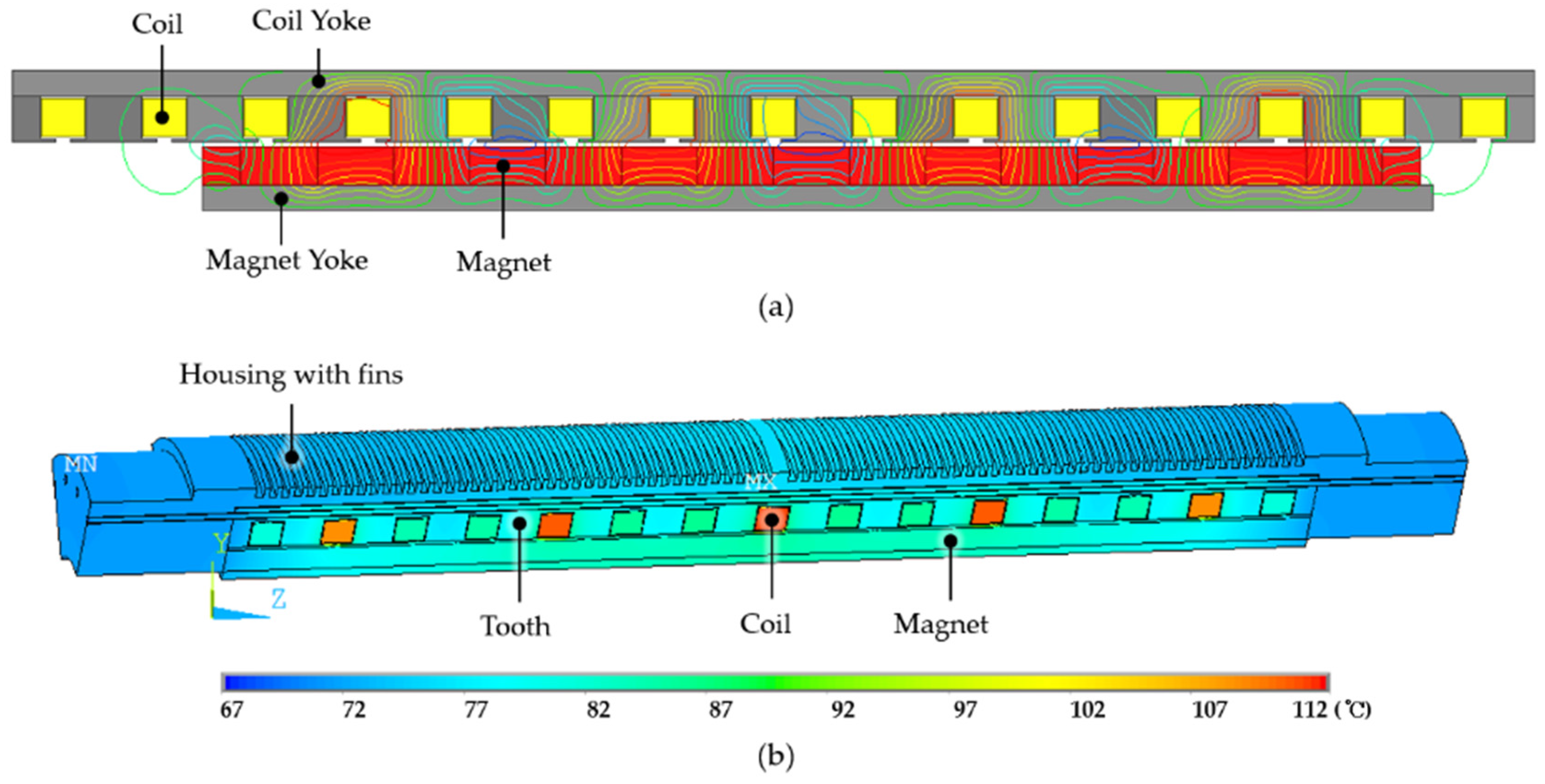
3.3. Electromagnetic and Thermal Modelling of TPMA
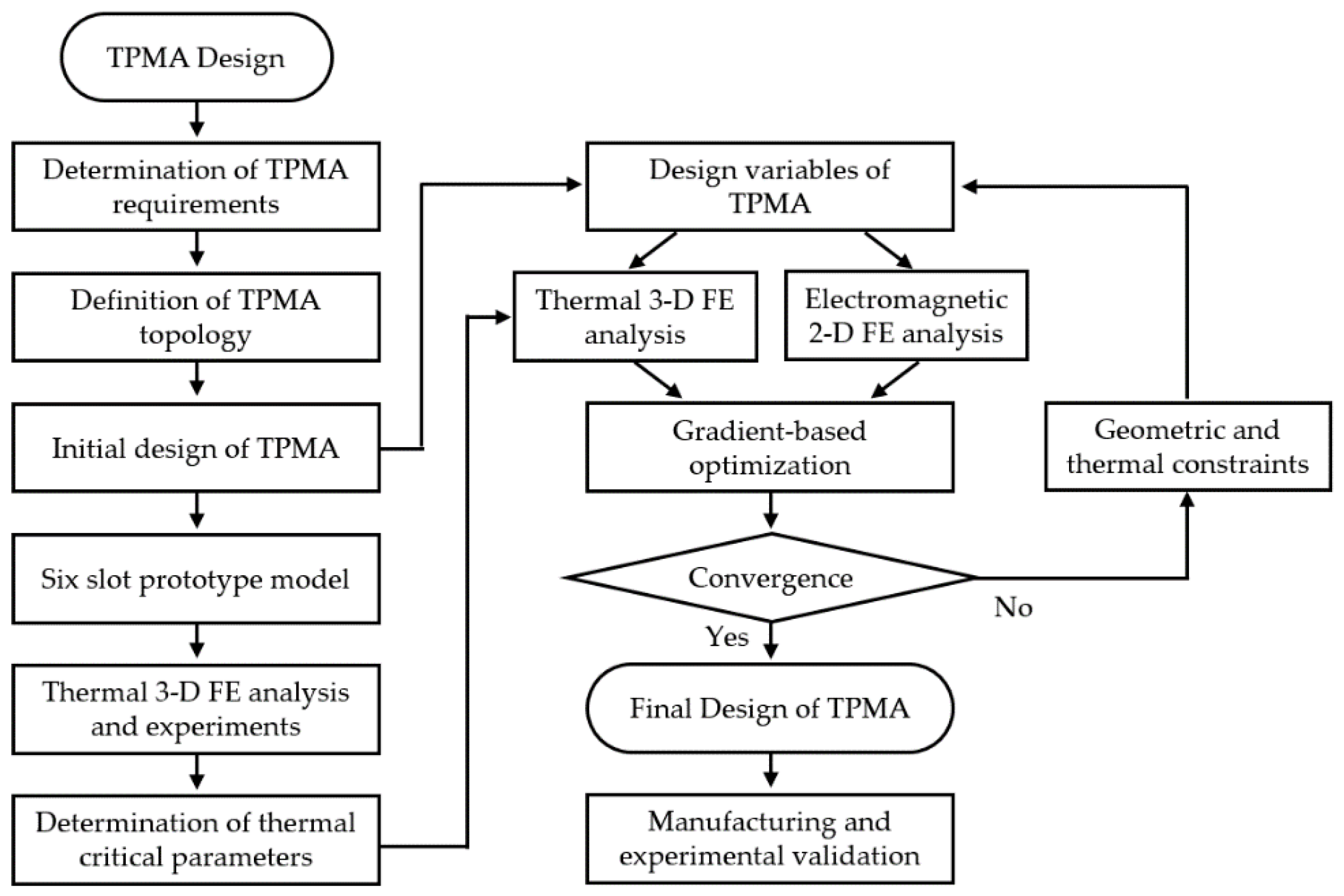
4. Performance Analysis and Design of the TPMA
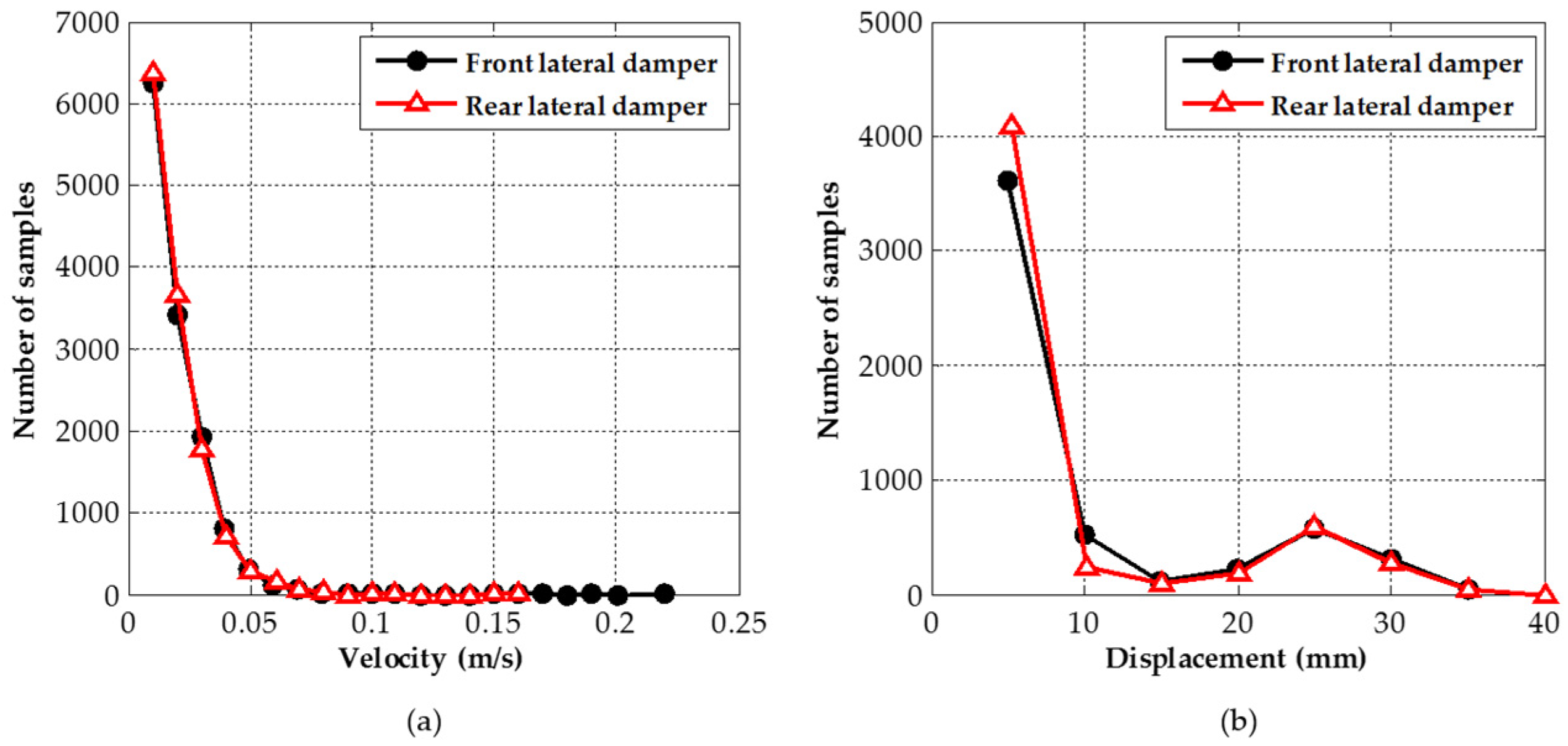
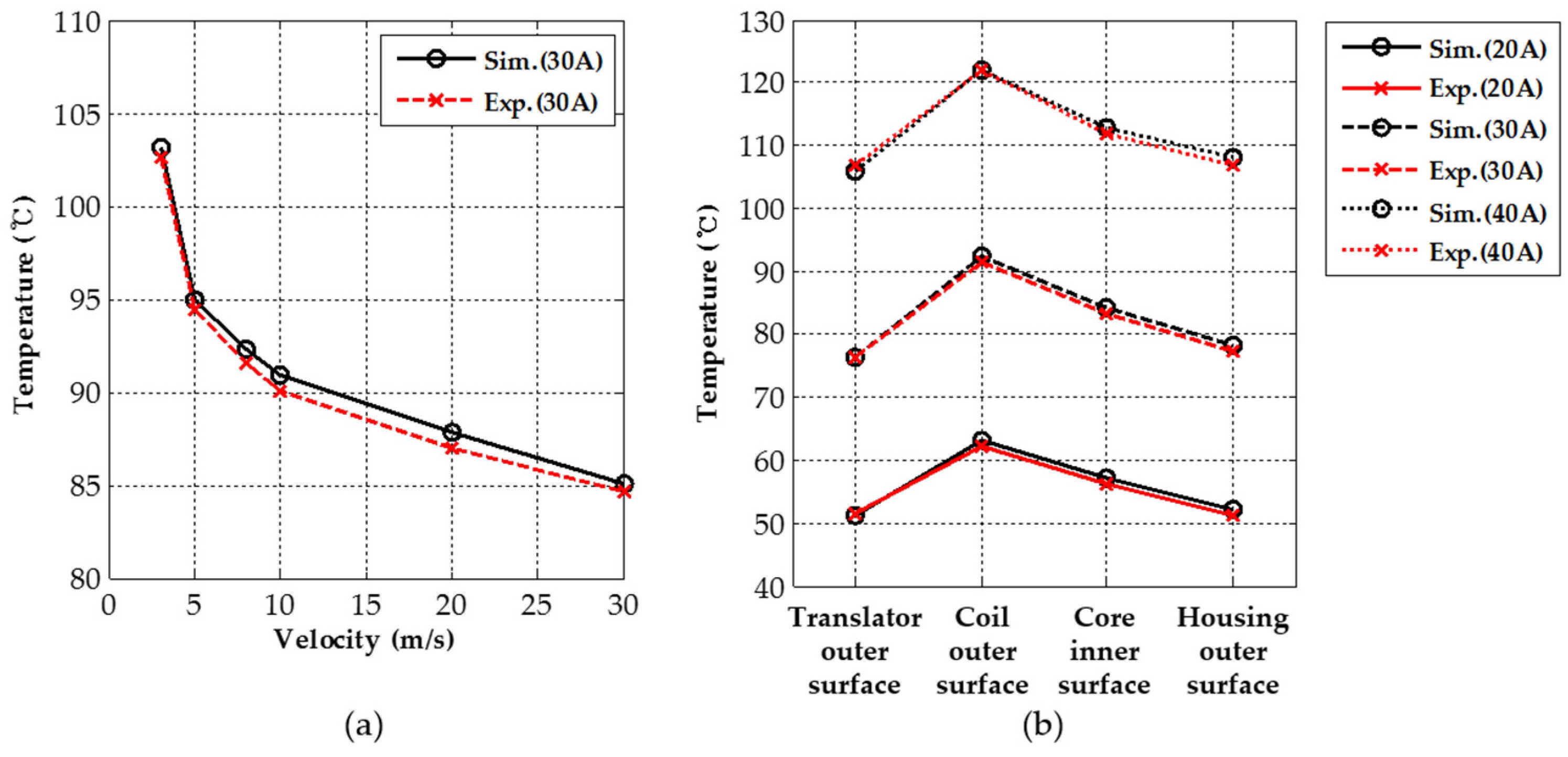
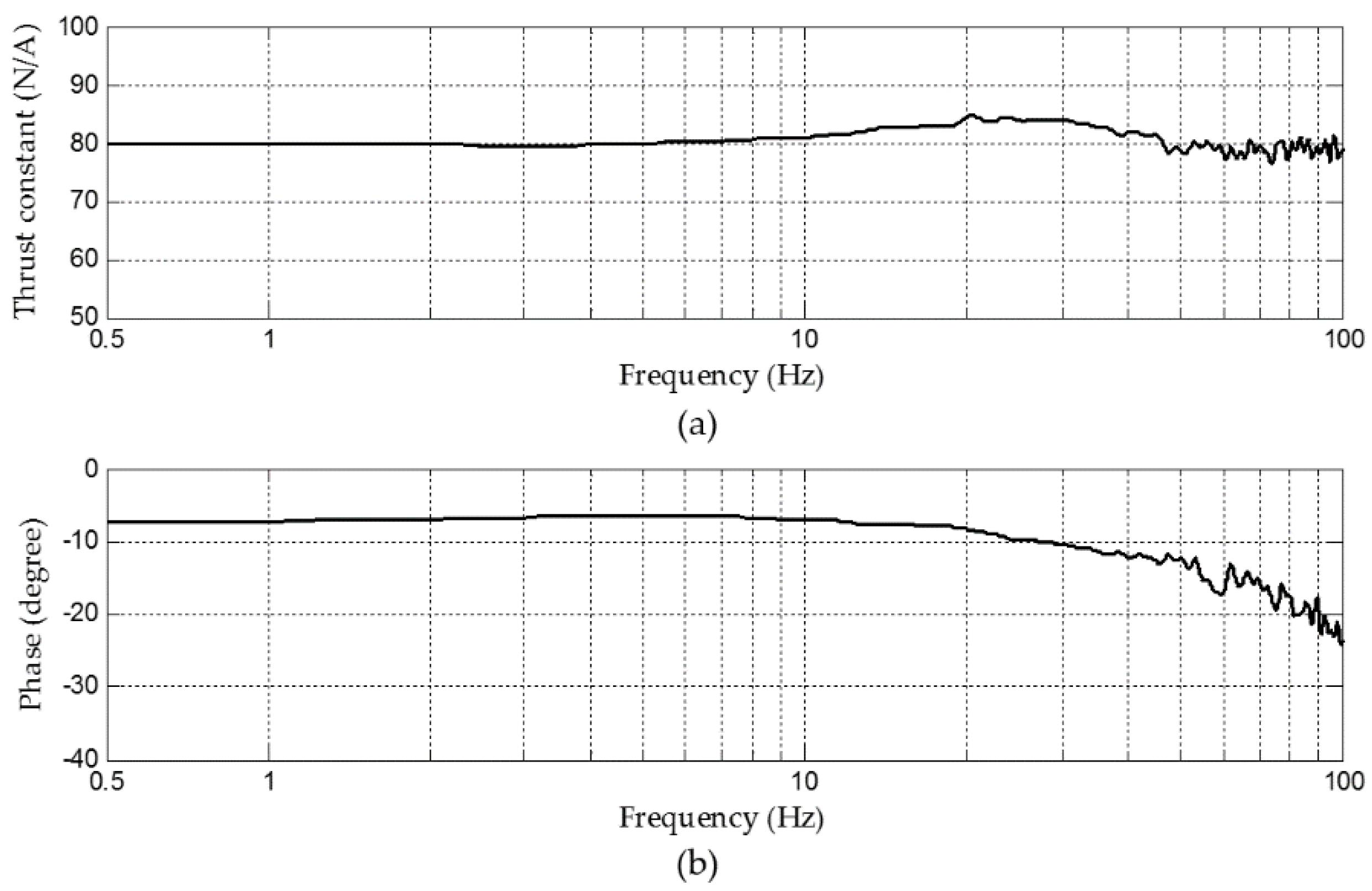
5. Experimental Verification
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kaloop, M.R.; Hu, J.W.; Elbeltagi, E. Evaluation of high-speed railway bridges based on a nondestructive monitoring system. Appl. Sci. 2016, 6, 24. [Google Scholar] [CrossRef]
- Lee, C.-M.; Goverdovskiy, V.; Sim, C.-S.; Lee, J.-H. Ride comfort of a high-speed train through the structural upgrade of a bogie suspension. J. Sound Vib. 2016, 361, 99–107. [Google Scholar] [CrossRef]
- Orvnäs, A.; Stichel, S.; Persson, R. Ride comfort improvements in a high-speed train with active secondary suspension. J. Mech. Syst. Transp. Logist. 2010, 3, 206–215. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Zhang, J.; Mei, T. An analytical design approach for self-powered active lateral secondary suspensions for railway vehicles. Veh. Syst. Dyn. 2015, 53, 1439–1454. [Google Scholar] [CrossRef]
- Foo, E.; Goodall, R. Active suspension control of flexible-bodied railway vehicles using electro-hydraulic and electro-magnetic actuators. Control Eng. Pract. 2000, 8, 507–518. [Google Scholar] [CrossRef]
- Goodall, R.; Freudenthaler, G.; Dixon, R. Hydraulic actuation technology for full-and semi-active railway suspensions. Veh. Syst. Dyn. 2014, 52, 1642–1657. [Google Scholar] [CrossRef]
- Goodall, R.; Pearson, J.; Pratt, I. Actuator Technologies for Secondary Active Suspension on Railway Vehicles. In Proceedings of the International Conference on Speedup Technology for Railway and Maglev Vehicles, Yokohama, Japan, 22–26 November 1993; 1993. [Google Scholar]
- Karimi, H.R. Optimal vibration control of vehicle engine-body system using haar functions. Int. J. Control Autom. Syst. 2006, 4, 714. [Google Scholar]
- Martins, I.; Esteves, J.; Marques, G.D.; da Silva, F.P. Permanent-magnets linear actuators applicability in automobile active suspensions. IEEE Trans. Veh. Technol. 2006, 55, 86–94. [Google Scholar] [CrossRef]
- Li, H.; Jing, X.; Karimi, H.R. Output-feedback-based h∞ control for vehicle suspension systems with control delay. IEEE Trans. Ind. Electron. 2014, 61, 436–446. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Karimi, H.R. A robust predictive control design for nonlinear active suspension systems. Asian J. Control 2016, 18, 122–132. [Google Scholar] [CrossRef]
- Rath, J.J.; Defoort, M.; Karimi, H.R.; Veluvolu, K.C. Output feedback active suspension control with higher order terminal sliding mode. IEEE Trans. Ind. Electron. 2016, 64, 1392–1403. [Google Scholar] [CrossRef]
- Norinao, H. Active and semi-active suspensions smooth 300 km/h ride. Railw. Gaz. Int. 1997, 241–242. [Google Scholar]
- Mellado, A.C.; Casanueva, C.; Vinolas, J.; Giménez, J.G. A lateral active suspension for conventional railway bogies. Veh. Syst. Dyn. 2009, 47, 1–14. [Google Scholar] [CrossRef]
- Zapateiro, M.; Luo, N.; Karimi, H.; Vehi, J. Vibration control of a class of semiactive suspension system using neural network and backstepping techniques. Mech. Syst. Signal Process. 2009, 23, 1946–1953. [Google Scholar] [CrossRef]
- Zapateiro, M.; Pozo, F.; Karimi, H.R.; Luo, N. Semiactive control methodologies for suspension control with magnetorheological dampers. IEEE/ASME Trans. Mechatron. 2012, 17, 370–380. [Google Scholar] [CrossRef]
- Pollard, M.; Simons, N. Passenger comfort—the role of active suspensions. Proc. Inst. Mech. Eng. D J. Automob. Eng. 1984, 198, 161–175. [Google Scholar] [CrossRef]
- Ribeiro, R.; Asadi, E.; Khamesee, M.B.; Khajepour, A. Hybrid variable damping control: Design, simulation, and optimization. Microsyst. Technol. 2014, 20, 1723–1732. [Google Scholar] [CrossRef]
- Asadi, E.; Ribeiro, R.; Khamesee, M.B.; Khajepour, A. Analysis, prototyping and experimental characterization of an adaptive hybrid-electromagnetic damper for automotive suspension systems. IEEE Trans. Veh. Technol. 2016. [Google Scholar] [CrossRef]
- Gysen, B.L.; Paulides, J.J.; Janssen, J.L.; Lomonova, E.A. Active electromagnetic suspension system for improved vehicle dynamics. IEEE Trans. Veh. Technol. 2010, 59, 1156–1163. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Atallah, K. A linear permanent-magnet motor for active vehicle suspension. IEEE Trans. Veh. Technol. 2011, 60, 55–63. [Google Scholar] [CrossRef]
- Gysen, B.L.; van der Sande, T.P.; Paulides, J.J.; Lomonova, E.A. Efficiency of a regenerative direct-drive electromagnetic active suspension. IEEE Trans. Veh. Technol. 2011, 60, 1384–1393. [Google Scholar] [CrossRef]
- Asadi, E.; Ribeiro, R.; Khamesee, M.B.; Khajepour, A. A new adaptive hybrid electromagnetic damper: Modelling, optimization, and experiment. Smart Mater. Struct. 2015, 24, 075003. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and modern approaches for thermal analysis of electrical machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef]
- Gysen, B.L.; Janssen, J.L.; Paulides, J.J.; Lomonova, E.A. Design aspects of an active electromagnetic suspension system for automotive applications. IEEE Trans. Ind. Appl. 2009, 45, 1589–1597. [Google Scholar] [CrossRef]
- Wang, J.; Jewell, G.W.; Howe, D. A general framework for the analysis and design of tubular linear permanent magnet machines. IEEE Trans. Magn. 1999, 35, 1986–2000. [Google Scholar] [CrossRef]
- ISO 2631-1. Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration-Part 1: General Requirements; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Kim, Y.; Kwon, H.; Kim, S.; Kim, C.; Kim, T. Correlation of ride comfort evaluation methods for railway vehicles. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit 2003, 217, 73–88. [Google Scholar] [CrossRef]
- Han, C. Lifetime evaluation of class e electrical insulation for small induction motors. IEEE Electr. Insul. Mag. 2011, 3, 14–19. [Google Scholar]
- Vese, I.-C.; Marignetti, F.; Radulescu, M.M. Multiphysics approach to numerical modeling of a permanent-magnet tubular linear motor. IEEE Trans. Ind. Electron. 2010, 57, 320–326. [Google Scholar] [CrossRef]
- Bracikowski, N.; Hecquet, M.; Brochet, P.; Shirinskii, S.V. Multiphysics modeling of a permanent magnet synchronous machine by using lumped models. IEEE Trans. Ind. Electron. 2012, 59, 2426–2437. [Google Scholar] [CrossRef]
- Encica, L.; Paulides, J.J.; Lomonova, E.A.; Vandenput, A.J. Electromagnetic and thermal design of a linear actuator using output polynomial space mapping. IEEE Trans. Ind. Appl. 2008, 44, 534–542. [Google Scholar] [CrossRef]
- Oh, S.Y.; Cho, S.-Y.; Han, J.-H.; Lee, H.J.; Ryu, G.-H.; Kang, D.; Lee, J. Design of IPMSM rotor shape for magnet eddy-current loss reduction. IEEE Trans. Magn. 2014, 50, 841–844. [Google Scholar] [CrossRef]
- Grauers, A.; Kasinathan, P. Force density limits in low-speed PM machines due to temperature and reactance. IEEE Trans. Energy Convers. 2004, 19, 518–525. [Google Scholar] [CrossRef]
- Wang, J.; Howe, D. Tubular modular permanent-magnet machines equipped with quasi-halbach magnetized magnets-part I: Magnetic field distribution, EMF, and thrust force. IEEE Trans. Magn. 2005, 41, 2470–2478. [Google Scholar] [CrossRef]
- Eckert, P.R.; Flores Filho, A.F.; Perondi, E.; Ferri, J.; Goltz, E. Design methodology of a dual-halbach array linear actuator with thermal-electromagnetic coupling. Sensors 2016, 16, 360. [Google Scholar] [CrossRef] [PubMed]
- González-Palomino, G.; Rivas-Conde, J.; Laniado, E. Optimization of permanent magnet skew in permanent magnet linear synchronous motors using finite element and statistical method. Engineering 2011, 3, 577. [Google Scholar] [CrossRef]
- Ashabani, M.; Mohamed, Y.A.-R.I.; Milimonfared, J. Optimum design of tubular permanent-magnet motors for thrust characteristics improvement by combined taguchi–neural network approach. IEEE Trans. Magn. 2010, 46, 4092–4100. [Google Scholar] [CrossRef]
- Xuzhen, H.; Jiaxi, L.; Chengming, Z.; Liyi, L. Calculation and experimental study on temperature rise of a high overload tubular permanent magnet linear motor. IEEE Trans. Plasma Sci. 2013, 41, 1182–1187. [Google Scholar] [CrossRef]

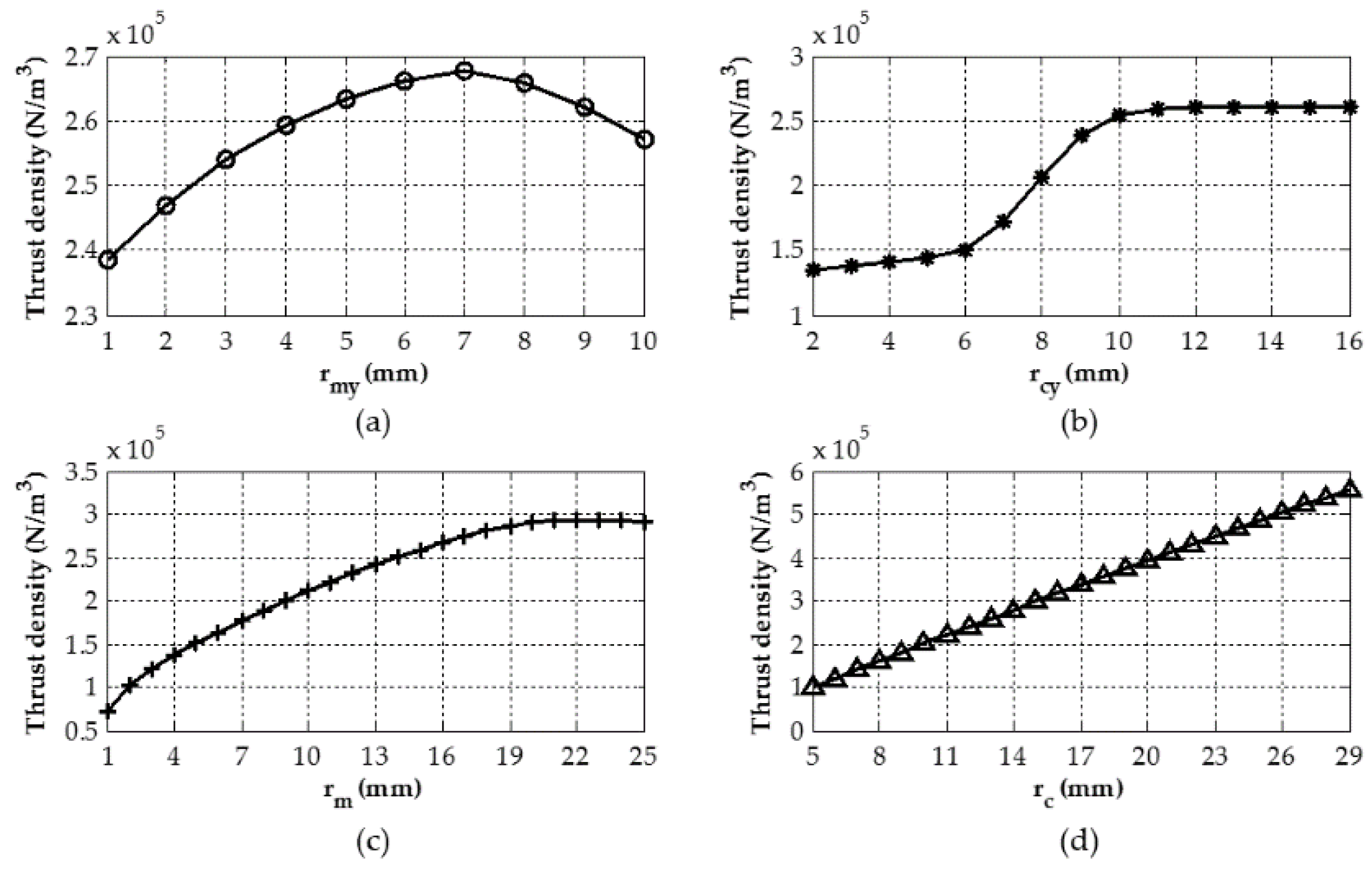
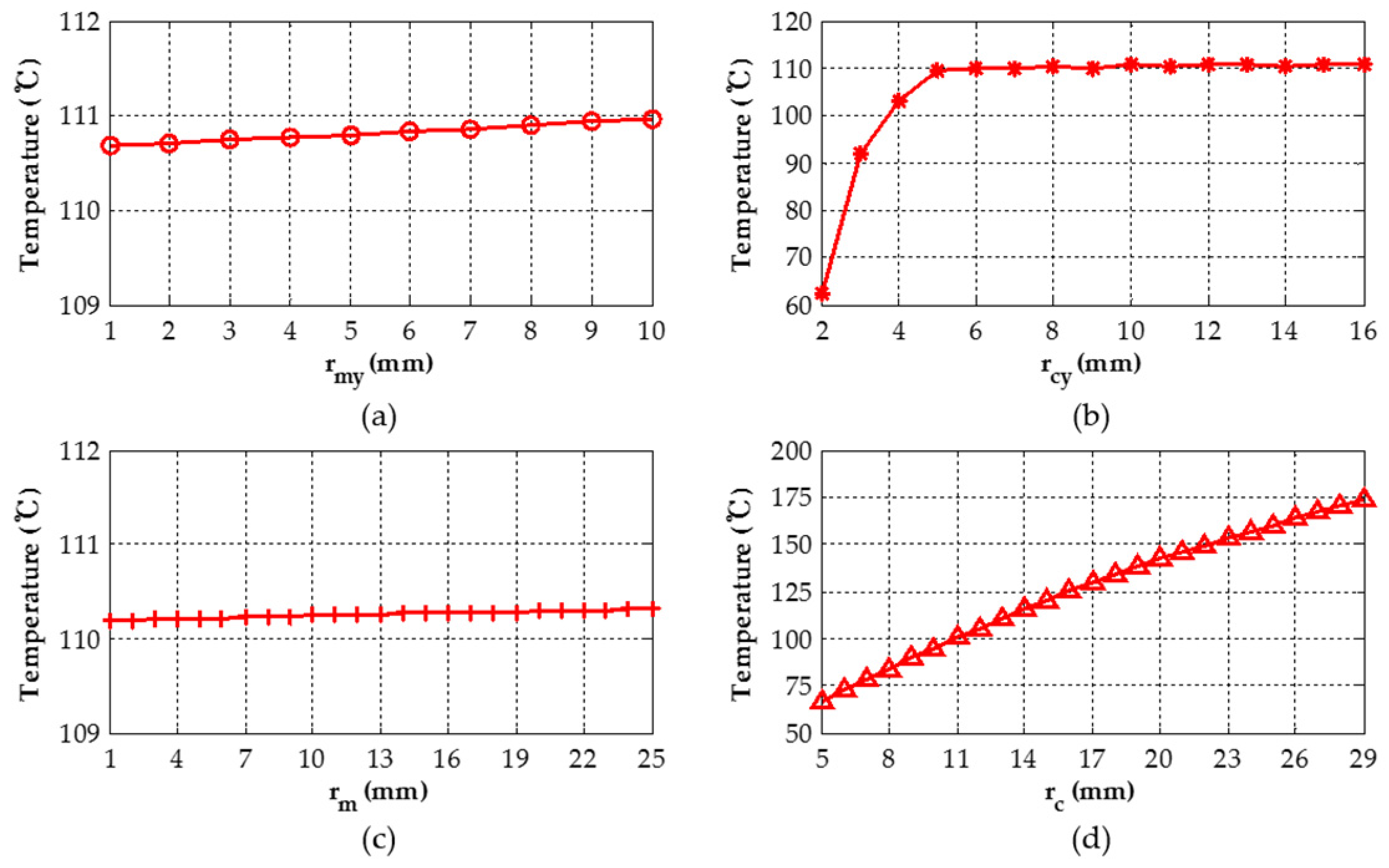
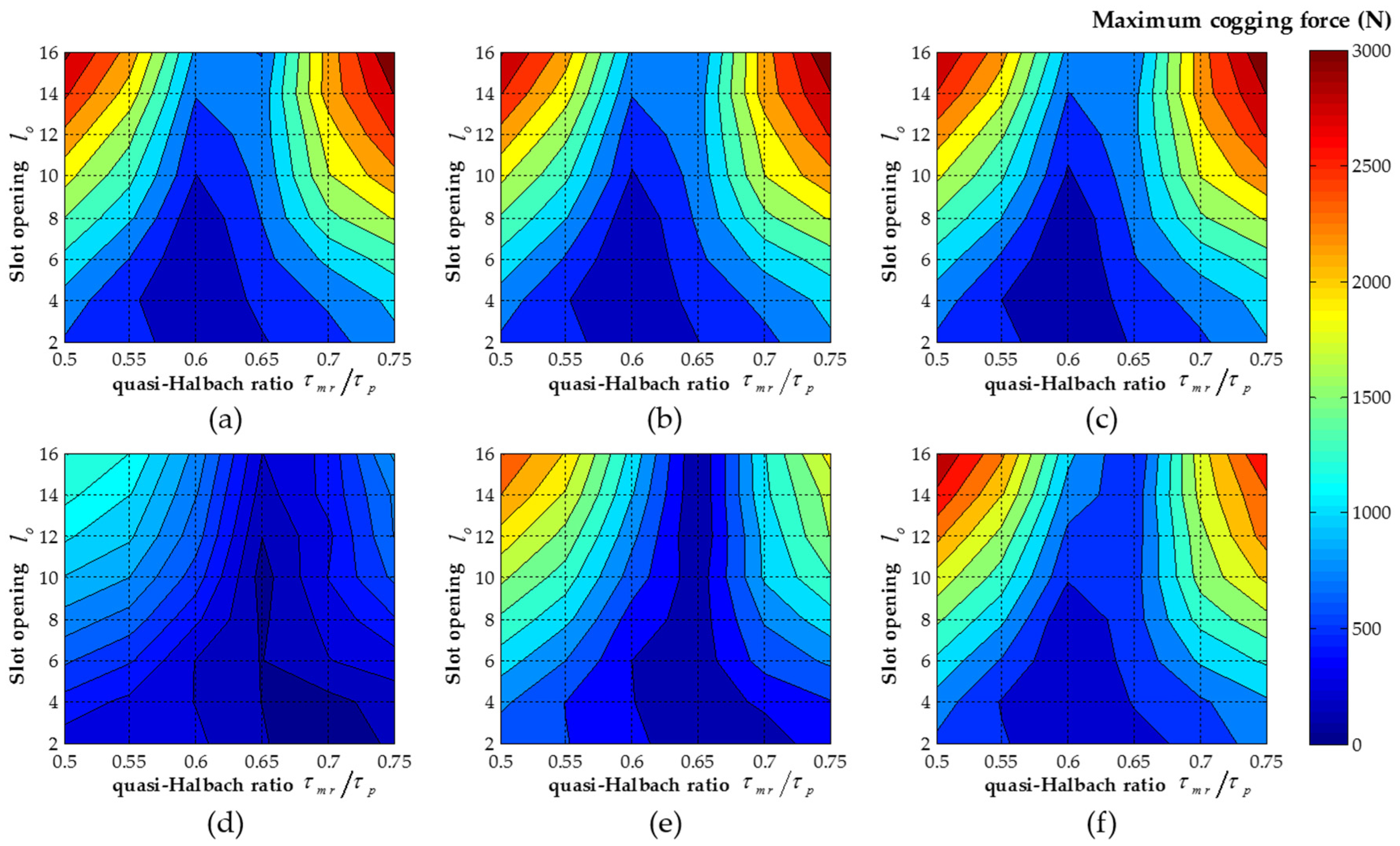

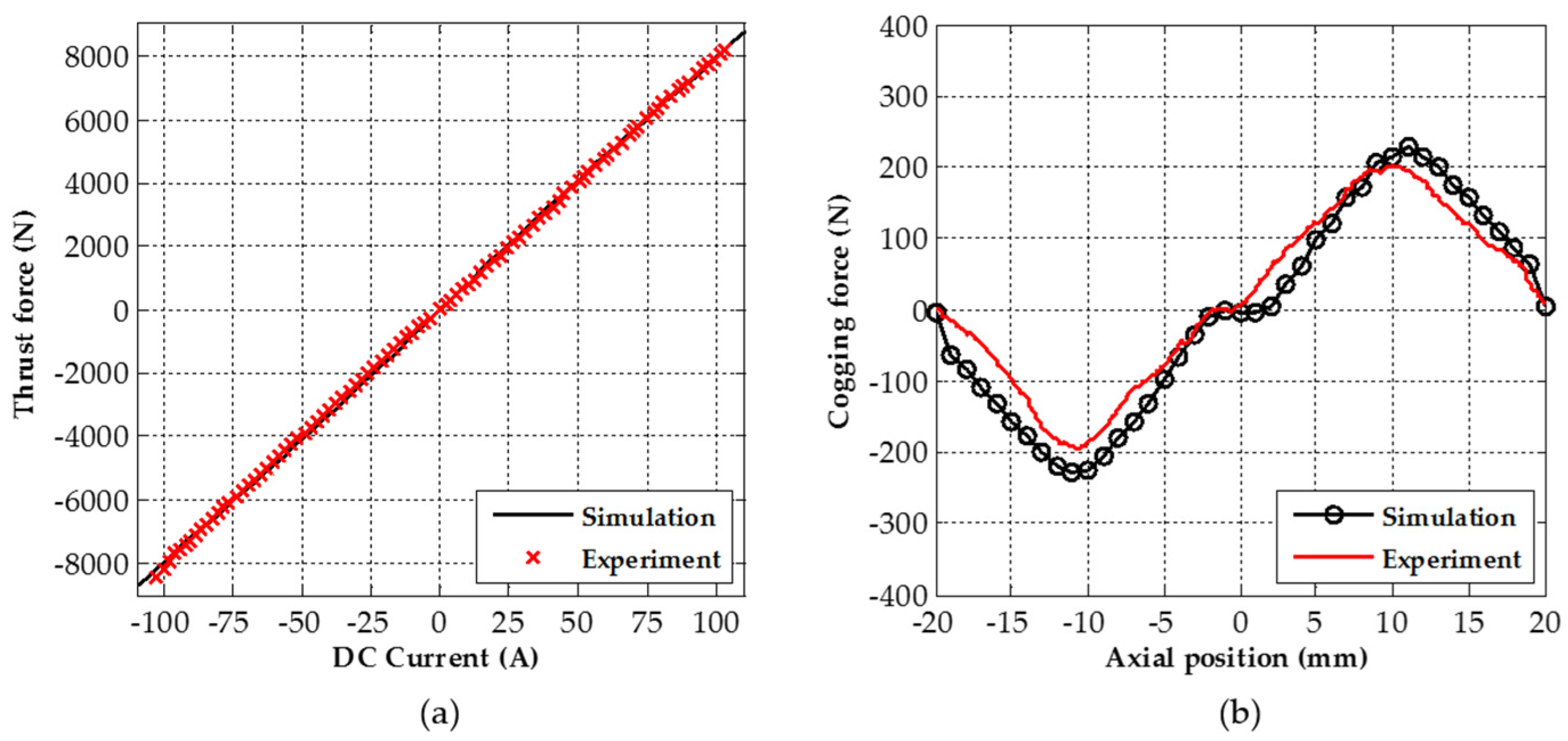
| Specification | Value |
|---|---|
| Stator outer diameter | 0.200 m |
| Axial length | 1.000 m |
| Bandwidth | 10 Hz |
| Stroke | ±0.050 m |
| Maximum thrust force | 7700 N |
| Allowable maximum temperature | 130 °C |
| Maximum current limit | 100 A |
| Initial Design Variables | Value | Fixed Variables | Value |
|---|---|---|---|
| Height of coil yoke | 10 mm | Height of housing | 14 mm |
| Height of coil | 15 mm | Radius of shaft | 15 mm |
| Height of magnet | 15 mm | Pole-pitch | 60 mm |
| Height of magnet yoke | 10 mm | Air gap | 2 mm |
| to ratio | 0.5 | Thickness of insulating paper | 0.5 mm |
| Slot opening | 6 mm | Number of pole-pairs | 4 |
| - | - | Number of slots | 15 |
| Material | Conductivity (W/m-k) | Specific Heat (J/kg-k) | Density (kg/m3) |
|---|---|---|---|
| Air | 0.0263 | 1007 | 1.1614 |
| Copper | 400.0 | 385.0 | 8933 |
| Silicon Steel | 24.2 (r direction) | 446.0 | 7650 |
| 5.0 (z direction) | |||
| Aluminum | 210.0 | 900.0 | 2700 |
| NdFeB | 6.5 | 460.0 | 7600 |
| 0.1 | - | - | |
| 0.15 | - | - | |
| 0.3 | - | - |
| Type | Values |
|---|---|
| Thermal constraints | Maximum temperature |
| Geometric constraints | Stator outer radius |
| Design domain | |
| Other data | Current density |
| Forced convection coefficient 1 |
| Variables | Initial | Optimized |
|---|---|---|
| Stator outer radius | 100 mm | 100 mm |
| Height of housing | 14 mm | 14 mm |
| Height of coil yoke | 10 mm | 12 mm |
| Height of coil | 15 mm | 17 mm |
| Air gap | 2 mm | 2 mm |
| Height of magnet | 15 mm | 16 mm |
| Height of magnet yoke | 10 mm | 6 mm |
| to ratio | 0.5 | 0.64 |
| Slot opening | 6 mm | 13.4 mm |
| Radius of shaft | 15 mm | 15 mm |
| Pole-pitch | 60 mm | 60 mm |
| Thickness of insulating paper | 0.5 mm | 0.5 mm |
| Number of pole-pairs | 4 | 4 |
| Number of slots | 15 | 15 |
| Current density | 7.36 A/mm2 | 7.36 A/mm2 |
| Winding turns | 117 | 133 |
| Saturation temperature | 93 °C | 130 °C |
| Thrust density | 2.252 × 105 N/m3 | 3.120 × 105 N/m3 |
| Maximum cogging force | 2216 N | 220 N |
| Thrust ripple | 28.8% | 2.86% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.-H.; Kim, D.; Park, N.-C.; Park, Y.-P. Design of a Tubular Permanent Magnet Actuator for Active Lateral Secondary Suspension of a Railway Vehicle. Appl. Sci. 2017, 7, 152. https://doi.org/10.3390/app7020152
Yoon J-H, Kim D, Park N-C, Park Y-P. Design of a Tubular Permanent Magnet Actuator for Active Lateral Secondary Suspension of a Railway Vehicle. Applied Sciences. 2017; 7(2):152. https://doi.org/10.3390/app7020152
Chicago/Turabian StyleYoon, Jun-Ho, Dongwook Kim, No-Cheol Park, and Young-Pil Park. 2017. "Design of a Tubular Permanent Magnet Actuator for Active Lateral Secondary Suspension of a Railway Vehicle" Applied Sciences 7, no. 2: 152. https://doi.org/10.3390/app7020152
APA StyleYoon, J.-H., Kim, D., Park, N.-C., & Park, Y.-P. (2017). Design of a Tubular Permanent Magnet Actuator for Active Lateral Secondary Suspension of a Railway Vehicle. Applied Sciences, 7(2), 152. https://doi.org/10.3390/app7020152






