A Two-Step Strategy for System Identification of Civil Structures for Structural Health Monitoring Using Wavelet Transform and Genetic Algorithms
Abstract
:1. Introduction
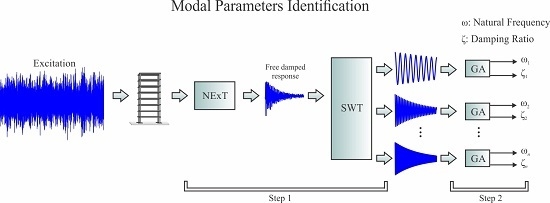
2. Methodology
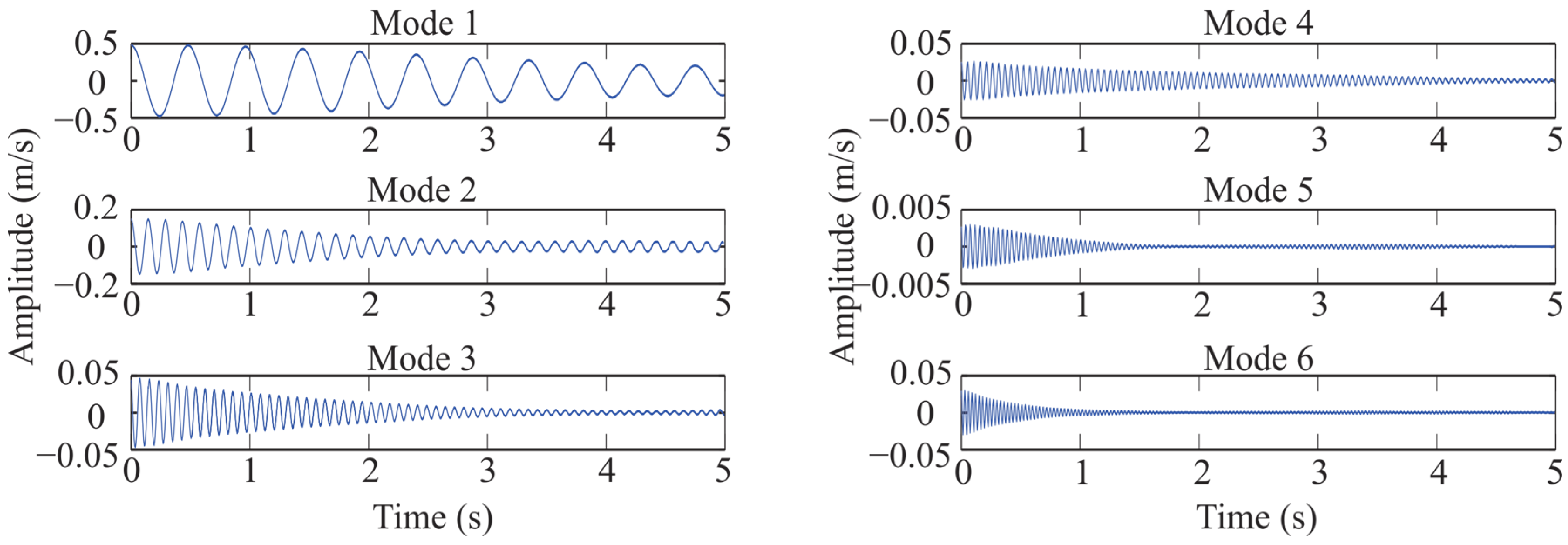
2.1. Step 1: Estimation of the Individual Modes
2.1.1. Free-Decay Form Estimation
2.1.2. Mode Extraction
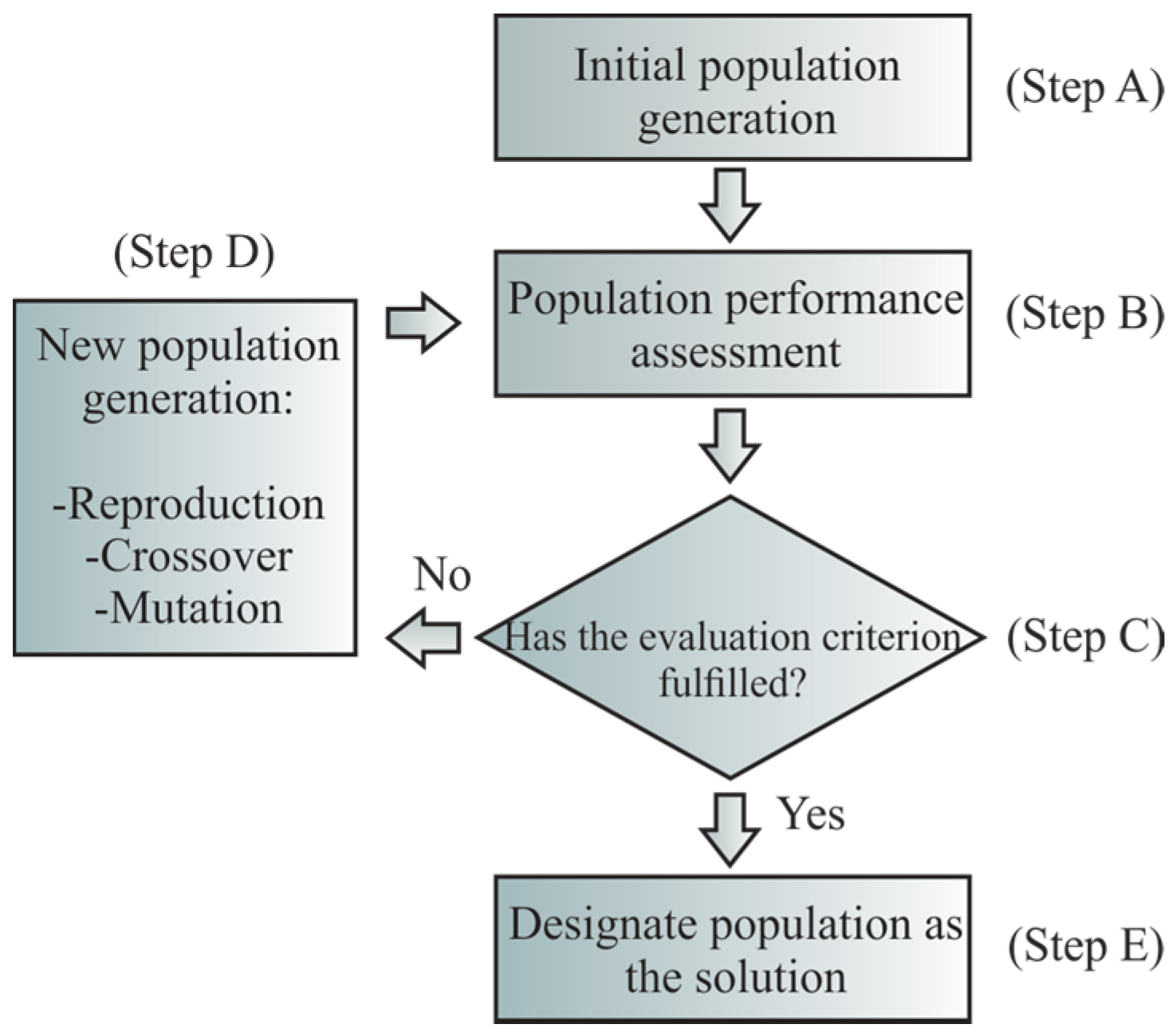
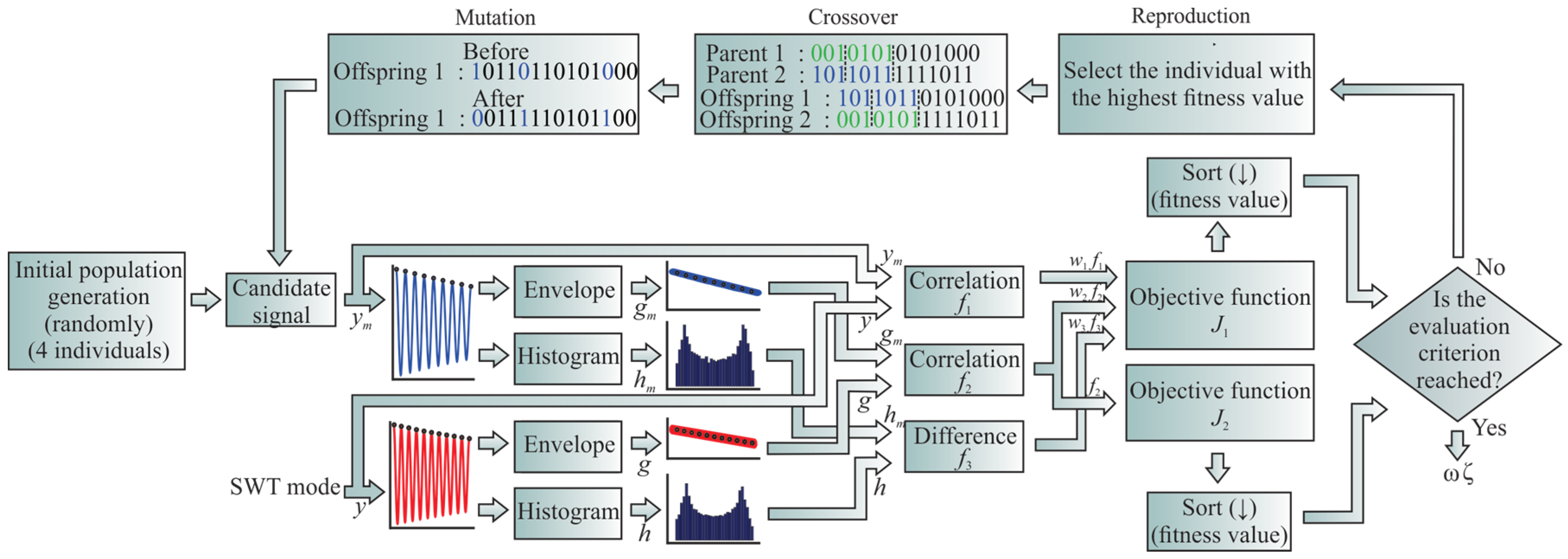
2.2. Step 2: Modal Parameters Identification
3. Numerical Assessment of the New Methodology Performance
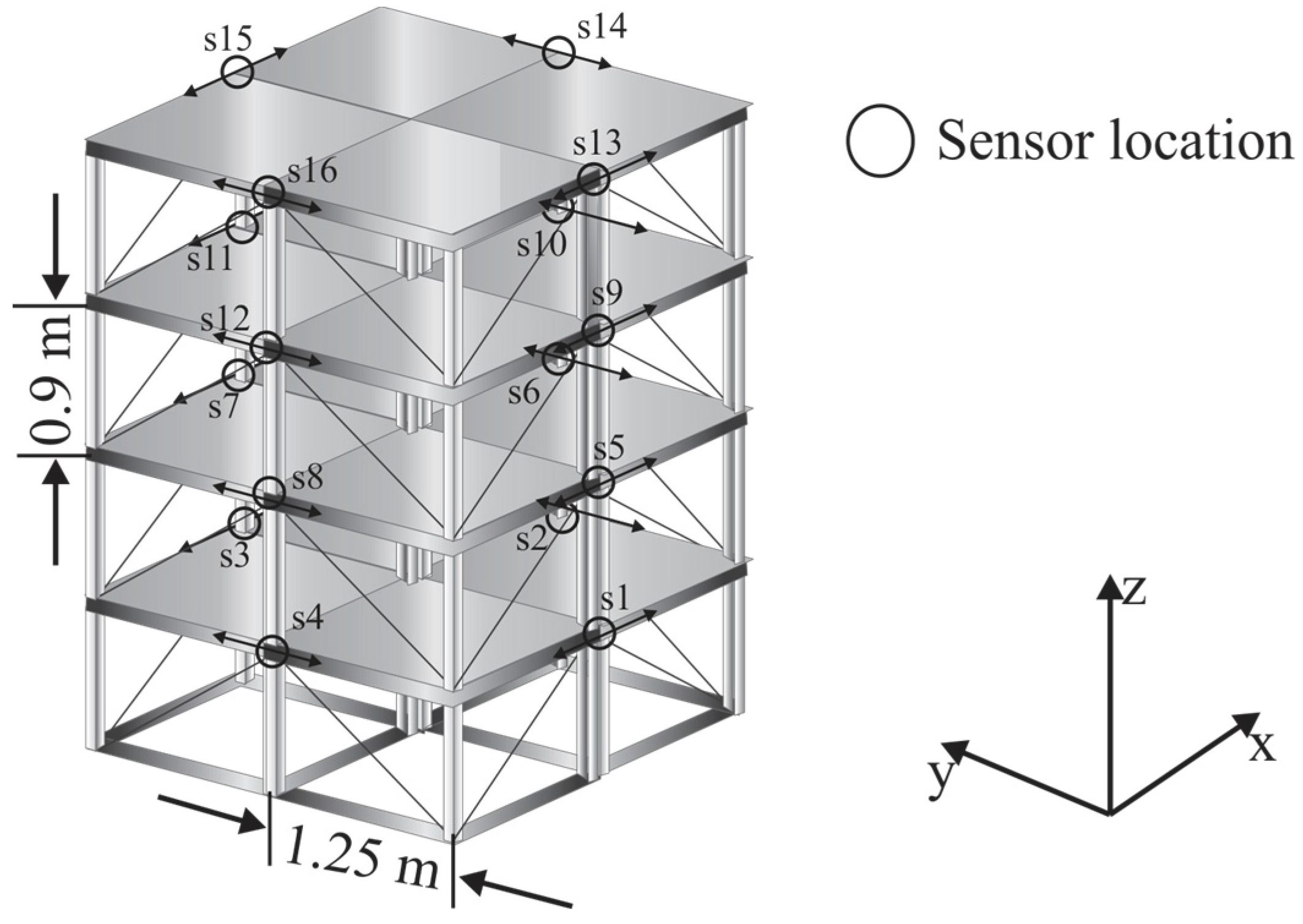
4. Application to an Eight-Story Building
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pei, Q.; Li, L. Modal parameter identification of civil engineering structures under seismic excitations. Adv. Mater. Res. 2014, 859, 163–166. [Google Scholar] [CrossRef]
- Çelebi, M.; Kashima, T.; Ghahari, S.F.; Abazarsa, F.; Taciroglu, E. Responses of a tall building with US code-type instrumentation in Tokyo, Japan—To events before, during and after the Tohoku earthquake of March 11, 2011. Earthq. Spectra 2015, 32, 497–522. [Google Scholar] [CrossRef]
- Coffield, A.; Adeli, H. Irregular steel building structures subjected to blast loading. J. Civ. Eng. Manag. 2016, 22, 17–25. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Boduroğlu, M.H. Active tendon control of torsionally irregular structures under near-fault ground motion excitation. Comput. Aided Civ. Infrastruct. Eng. 2013, 28, 718–736. [Google Scholar] [CrossRef]
- Jiang, X.; Adeli, H. Pseudospectra, MUSIC, and dynamic wavelet neural network for damage detection of highrise buildings. Int. J. Numer. Methods Eng. 2007, 71, 606–629. [Google Scholar] [CrossRef]
- Gangone, M.V.; Whelan, M.J.; Janoyan, K.D. Wireless monitoring of a multi-span bridge superstructure for diagnostic load testing and system identification. Comput. Aided Civ. Infrastruct. Eng. 2011, 26, 560–579. [Google Scholar] [CrossRef]
- Osornio-Rios, R.A.; Amezquita-Sanchez, J.P.; Romero-Troncoso, R.J.; Garcia-Perez, A. MUSIC-ANN analysis for locating structural damages in a truss-type structure by means of vibrations. Comput. Aided Civ. Infrastruct. Eng. 2012, 27, 687–698. [Google Scholar] [CrossRef]
- Foti, D.; Gattulli, V.; Potenza, F. Output-only identification and model updating by dynamic testing in unfavorable conditions of a seismically damaged building. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 659–675. [Google Scholar] [CrossRef]
- Skafte, A.; Aenlle, M.L.; Brincker, R. A general procedure for estimating dynamic displacements using strain measurements and operational modal analysis. Smart Mater. Struct. 2016, 25, 025020. [Google Scholar] [CrossRef]
- Peeters, B.; Maeck, J.; De Roeck, G. Vibration-based damage detection in civil engineering: excitation sources and temperature effects. Smart Mater. Struct. 2001, 10, 518–527. [Google Scholar] [CrossRef]
- Perez-Ramirez, C.A.; Amezquita-Sanchez, J.P.; Adeli, H.; Valtierra-Rodriguez, M.; Camarena-Martinez, D.; Romero-Troncoso, R.J. New methodology for modal parameters identification of smart civil structures using ambient vibrations and synchrosqueezed wavelet transform. Eng. Appl. Artif. Intell. 2016, 48, 1–12. [Google Scholar] [CrossRef]
- García-Palencia, A.J.; Santini-Bell, E. A two-step model updating algorithm for parameter identification of linear elastic damped structures. Comput. Aided Civ. Infrastruct. Eng. 2013, 28, 509–521. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, Y.L.; Xiao, X. Multiscale modeling and model updating of a cable-stayed bridge. I: Modeling and influence line analysis. J. Bridge Eng. 2015, 20, 04014112. [Google Scholar] [CrossRef]
- Li, J.; Ruiz-Sandoval, M.; Spencer, B.F., Jr.; Elnashai, A.S. Parametric time-domain identification of multiple-input systems using decoupled output signals. Earthq. Eng. Struct. Dyn. 2014, 43, 1307–1324. [Google Scholar] [CrossRef]
- Niu, Y.; Fritzen, C.-P.; Jung, H.; Buethe, I.; Ni, Y.-Q.; Wang, Y.-W. Online simultaneous reconstruction of wind load and structural responses—Theory and application to Canton Tower. Comput. Aided Civ. Infrastruct. Eng. 2015, 30, 666–681. [Google Scholar] [CrossRef]
- Górski, P. Investigation of dynamic characteristics of tall industrial chimney based on GPS measurements using Random Decrement Method. Eng. Struct. 2014, 83, 30–49. [Google Scholar] [CrossRef]
- Wethyavivorn, B.; Surit, S.; Apichatyakul, C.; Lerdsivanon, N. Model verification of Thai historic masonry monuments. J. Perform. Construct. Facil. 2016, 30, 04014188. [Google Scholar] [CrossRef]
- Marulanda, J.; Caicedo, J.M.; Thomson, P. Modal identification using mobile sensors under ambient excitation. J. Comput. Civ. Eng. 2017. [Google Scholar] [CrossRef]
- Bursi, O.S.; Kumar, A.; Abbiati, G.; Ceravolo, R. Identification, model updating, and validation of a steel twin deck curved cable-stayed footbridge. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 703–722. [Google Scholar] [CrossRef]
- Nohutcu, H.; Demir, A.; Ercan, E.; Hokelekli, E.; Altintas, G. Investigation of a historic masonry structure by numerical and operational modal analyses. Struct. Des. Tall Spec. Build. 2015, 24, 821–834. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal processing techniques for vibration-based health monitoring of smart structures. Arch. Comput. Meth. Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Ceravolo, R.; Abbiati, G. Time domain identification of structures: Comparative analysis of Output-Only Methods. J. Eng. Mech. 2013, 139, 537–544. [Google Scholar] [CrossRef]
- Dorvash, S.; Pakzad, S.N. Effects of measurement noise on modal parameter identification. Smart Mater. Struct. 2012, 21, 065008. [Google Scholar] [CrossRef]
- Zhang, G.; Tang, B.; Tang, G. An improved stochastic subspace identification for operational modal analysis. Measurement 2012, 45, 1246–1256. [Google Scholar] [CrossRef]
- Adeli, H.; Kim, H. Wavelet-Based Vibration Control of Smart Buildings and Bridges; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, Z.-C.; Chen, G.-D. Analytical mode decomposition of time series with decaying amplitudes and overlapping instantaneous frequencies. Smart Mater. Struct. 2013, 22, 095003. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Perez-Ramirez, C.A.; Amezquita-Sanchez, J.P.; Romero-Troncoso, R.J.; Garcia-Perez, A. Novel down-sampling empirical mode decomposition approach for power quality analysis. IEEE Trans. Ind. Electr. 2016, 63, 2369–2378. [Google Scholar] [CrossRef]
- Bao, C.; Hao, H.; Li, Z.-X. Multi-stage identification scheme for detecting damage in structures under ambient excitations. Smart Mater. Struct. 2013, 22, 045006. [Google Scholar] [CrossRef]
- Qarib, H.; Adeli, H. A new adaptive algorithm for automated feature extraction in exponentially damped signals for health monitoring of smart structures. Smart Mater. Struct. 2015, 24, 125040. [Google Scholar] [CrossRef]
- Musafere, F.; Sadhu, A.; Liu, K. Towards damage detection using blind source separation integrated with time-varying auto-regressive modeling. Smart Mater. Struct. 2016, 25, 015013. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. A new music-empirical wavelet transform methodology for time–frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Proc. 2015, 45, 55–68. [Google Scholar] [CrossRef]
- Jaen-Cuellar, A.Y.; Romero-Troncoso, R.J.; Morales-Velazquez, L.; Osornio-Rios, R.A. PID-controller tuning optimization with genetic algorithms in servo systems. Int. J. Adv. Robot. Syst. 2013, 10, 324. [Google Scholar] [CrossRef]
- Li, P.J.; Xu, D.W.; Zhang, J. Probability-based structural health monitoring through Markov chain Monte Carlo sampling. Int. J. Struct. Stab. Dyn. 2016, 16, 1550039. [Google Scholar] [CrossRef]
- Amini, F.; Hedayati, Y. Underdetermined blind modal identification of structures by earthquake and ambient vibration measurements via sparse component analysis. J. Sound Vib. 2016, 366, 117–132. [Google Scholar] [CrossRef]
- The Natural Excitation Technique (NExT) for Modal Parameter Extraction from Operating Wind Turbines. Available online: http://prod.sandia.gov/techlib/access-control.cgi/1992/921666.pdf (accessed on 15 November 2016).
- Giraldo, D.; Caicedo, J.M.; Song, W.; Mogan, B.; Dyke, S.J. Modal identification through ambient vibration: A comparative study. In Proceedings of the 2006 IMAC-XXIV: Conference & Exposition on Structural Dynamics Conference, San Louis, MO, USA, 30 January–2 February 2009.
- Moser, P.; Moaveni, B. Design and deployment of a continuous monitoring system for the dowling hall footbridge. Exp. Tech. 2011, 37, 15–26. [Google Scholar] [CrossRef]
- Zhang, G.; Ma, J.; Chen, Z.; Wang, R. Automated eigensystem realization algorithm for operational modal analysis. J. Sound Vib. 2014, 333, 3550–3563. [Google Scholar] [CrossRef]
- Dammika, A.J.; Kawarai, K.; Yamaguchi, H.; Matsumoto, Y.; Yoshioka, T. Analytical damping evaluation complementary to experimental structural health monitoring of bridges. J. Bridge Eng. 2015, 20, 04014095. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Synchrosqueezed wavelet transform-fractality model for locating, detecting, and quantifying damage in smart highrise building structures. Smart Mater. Struct. 2015, 24, 065034. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. App. Comput. Harm. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Chakravarty, S.; Mittra, R.; Williams, N.R. Application of a microgenetic algorithm (MGA) to the design of broad-band microwave absorbers using multiple frequency selective surface screens buried in dielectrics. IEEE Tran. Antennas Propag. 2002, 50, 284–296. [Google Scholar] [CrossRef]
- Krishnakumar, K. Micro-genetic algorithms for stationary and non-stationary function optimization function. In Proceedings of the SPIE Intelligent Control and Adaptive Systems, Philadelphia, PA, USA, 1 November 1989; Volume 1196.
- Dennis, B.H.; Dulikravich, G.S. Optimization of magneto-hydrodynamic control of diffuser flows using micro-genetic algorithms and least-squares finite elements. Finite Elem. Anal. Des. 2001, 37, 349–363. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Pearson Education: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Hilbert, D. Begrundung der kinetischen Gastheorie. Math. Ann. 1912, 72, 562–577. [Google Scholar] [CrossRef]
- Adeli, H.; Cheng, N.-T. Integrated genetic algorithm for optimization of space structures. J. Aerosp. Eng. 1993, 6, 315–328. [Google Scholar] [CrossRef]
- Greenwell, R.N.; Angus, J.E.; Finck, M. Optimal mutation probability for genetic algorithms. Math. Comput. Model. 1995, 21, 1–11. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. Syst. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. Phase I IASC-ASCE structural health monitoring benchmark problem using simulated data. J. Eng. Mech. 2004, 130, 3–15. [Google Scholar] [CrossRef]
- Caicedo, J.M. Practical guidelines for the Natural Excitation Technique (NExT) and the Eigensystem Realization Algorithm (ERA) for modal identification using ambient vibration. Exp. Tech. 2011, 35, 52–58. [Google Scholar] [CrossRef]
- Su, W.C.; Huang, C.S.; Chen, C.H.; Liu, C.Y.; Huang, H.C.; Le, Q.T. Identifying the modal parameters of a structure from ambient vibration data via the stationary wavelet packet. Comput. Aided Civ. Infrastruct. Eng. 2014, 29, 738–757. [Google Scholar] [CrossRef]

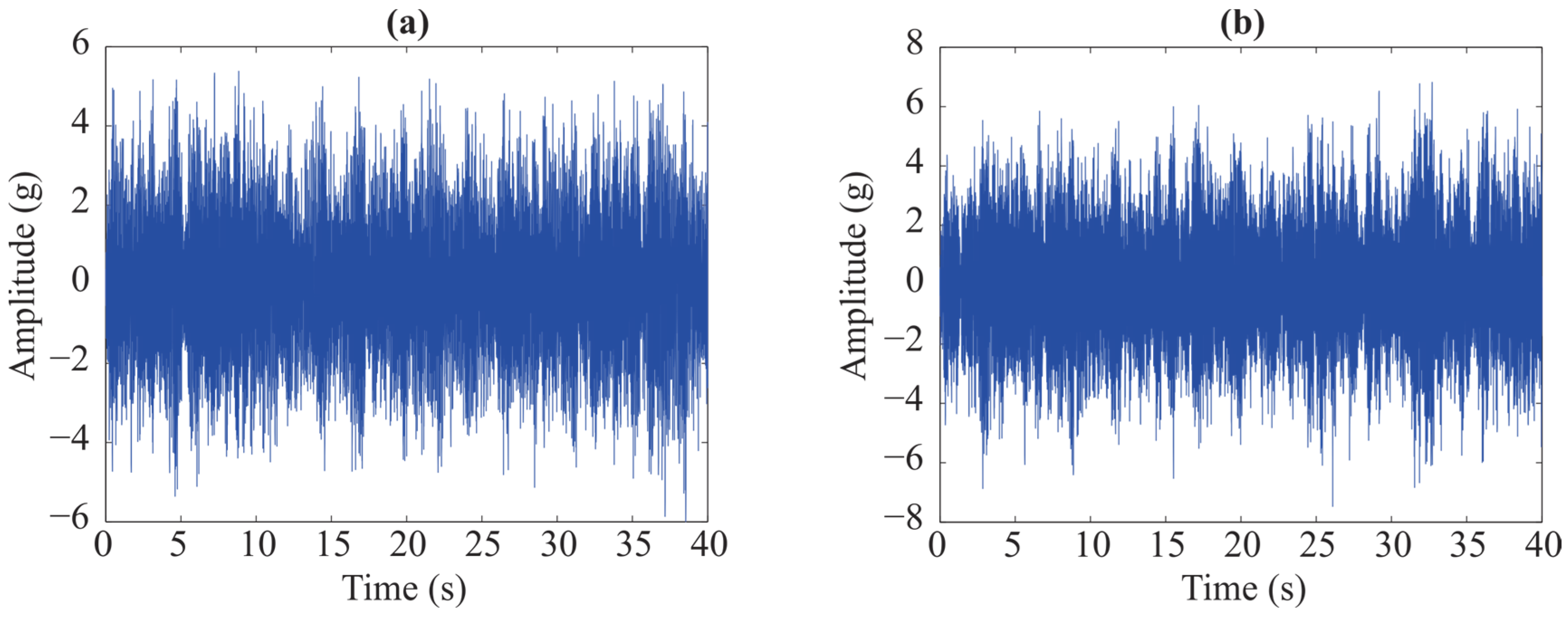
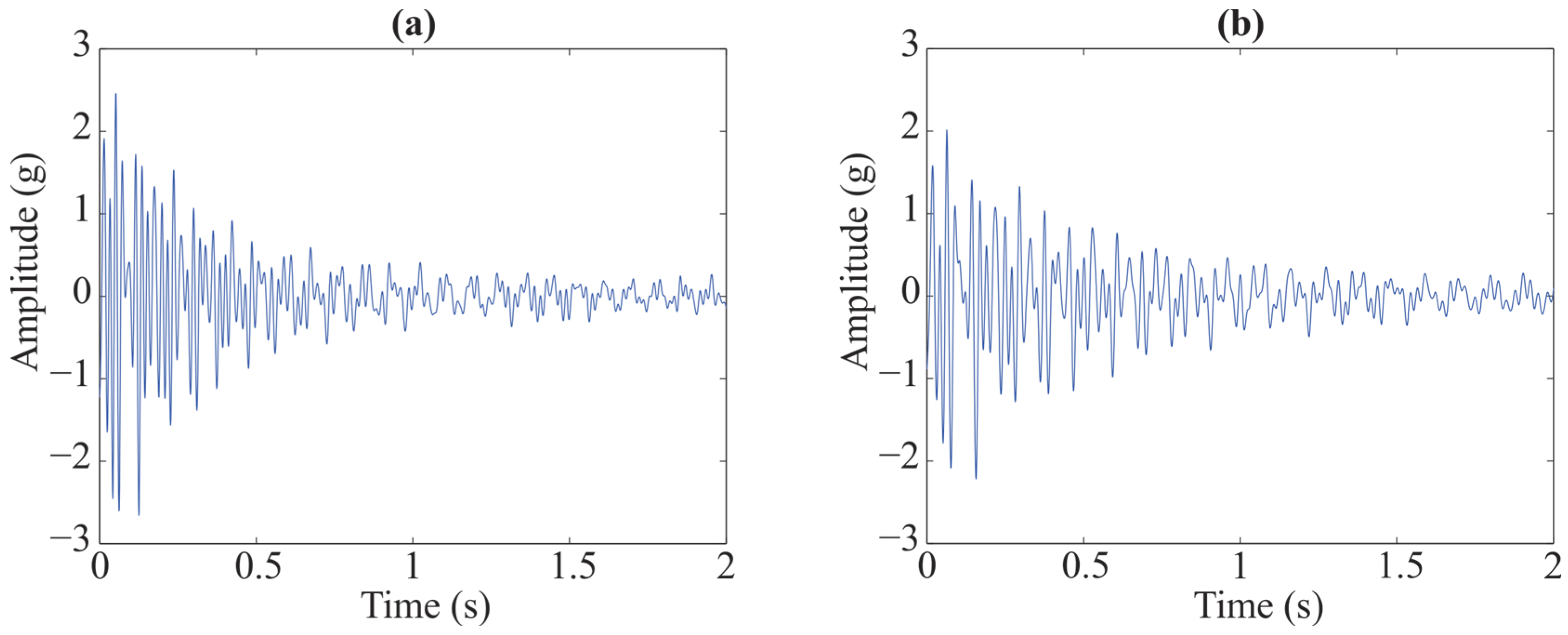
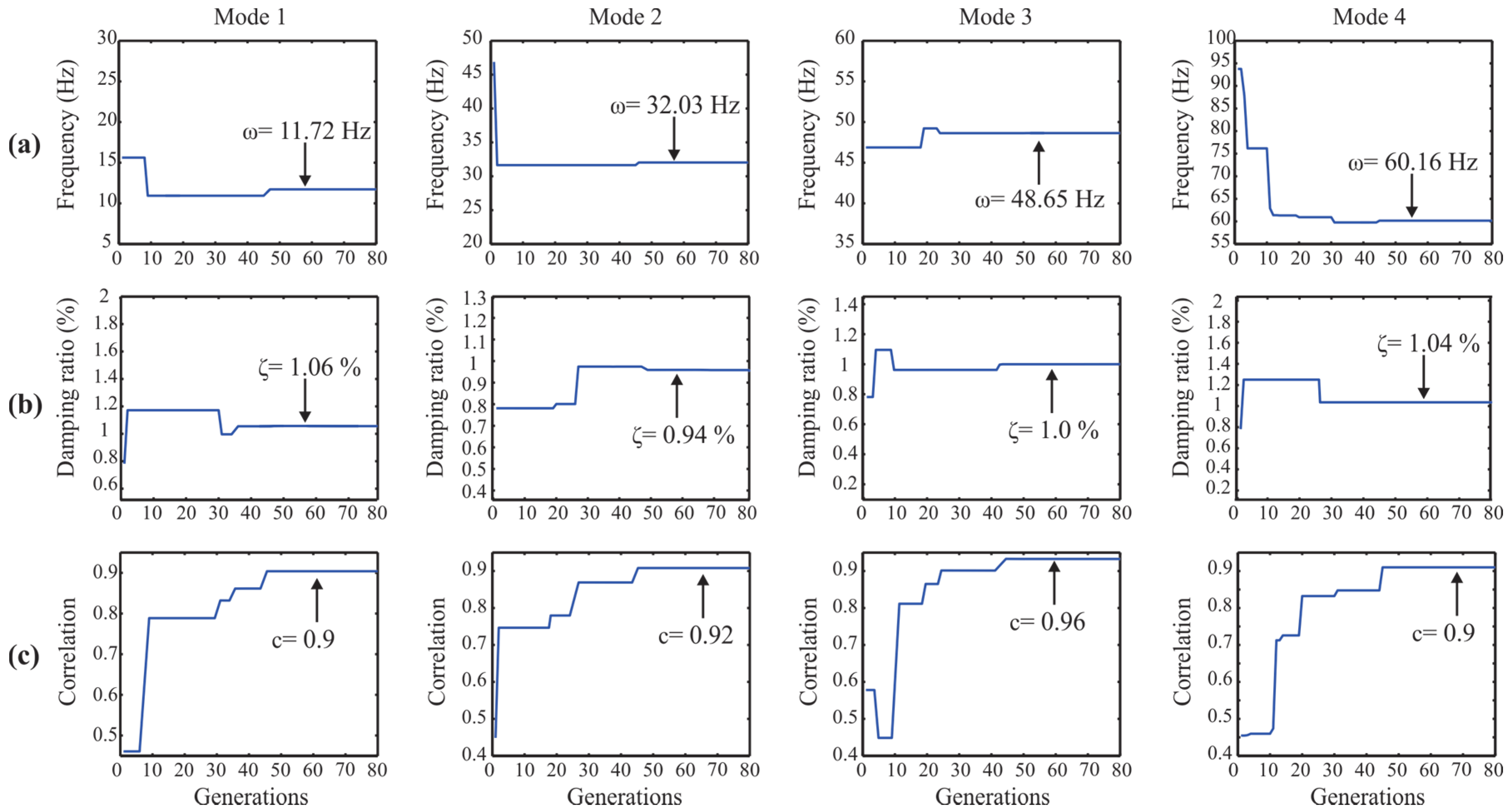
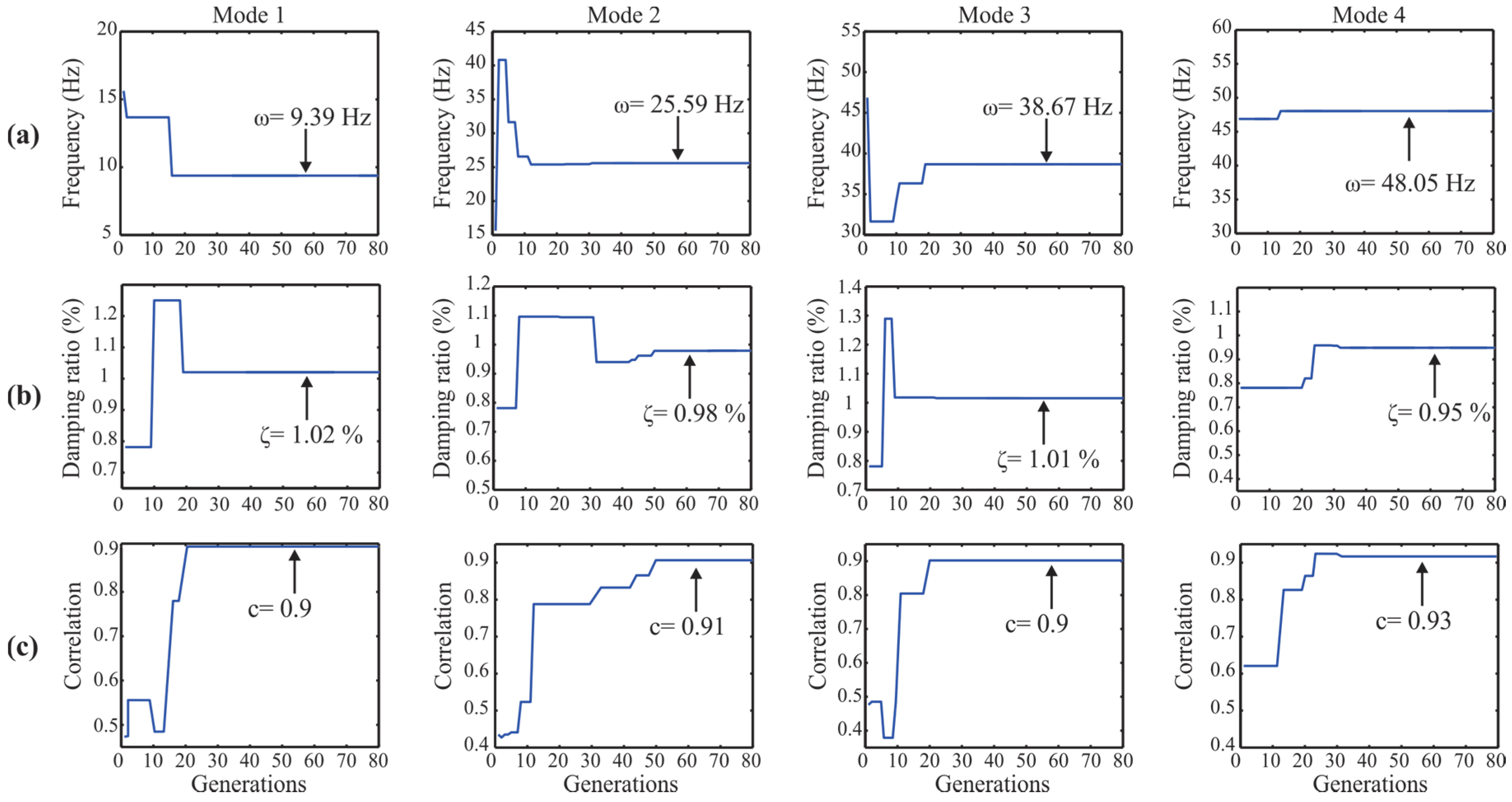
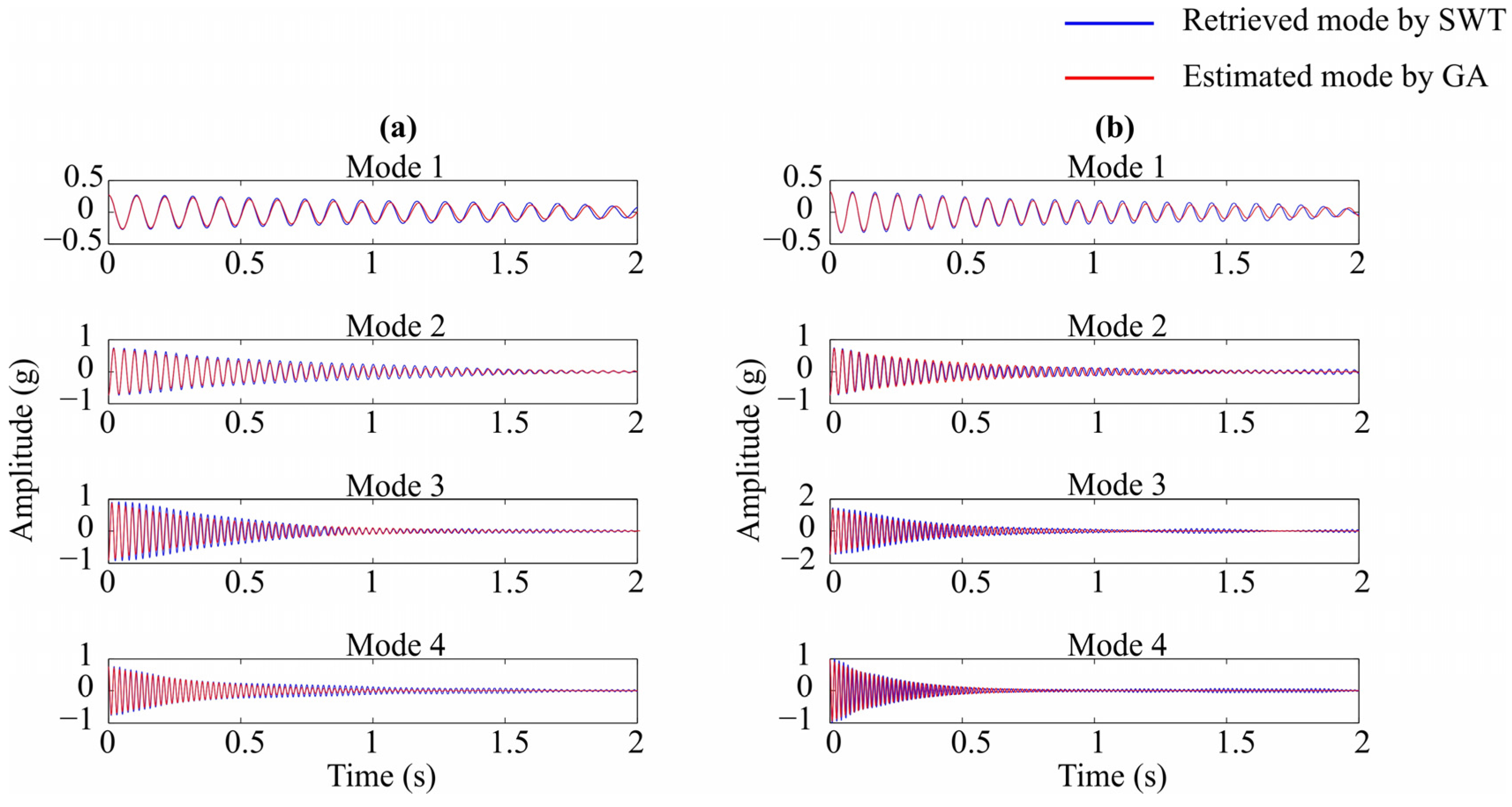
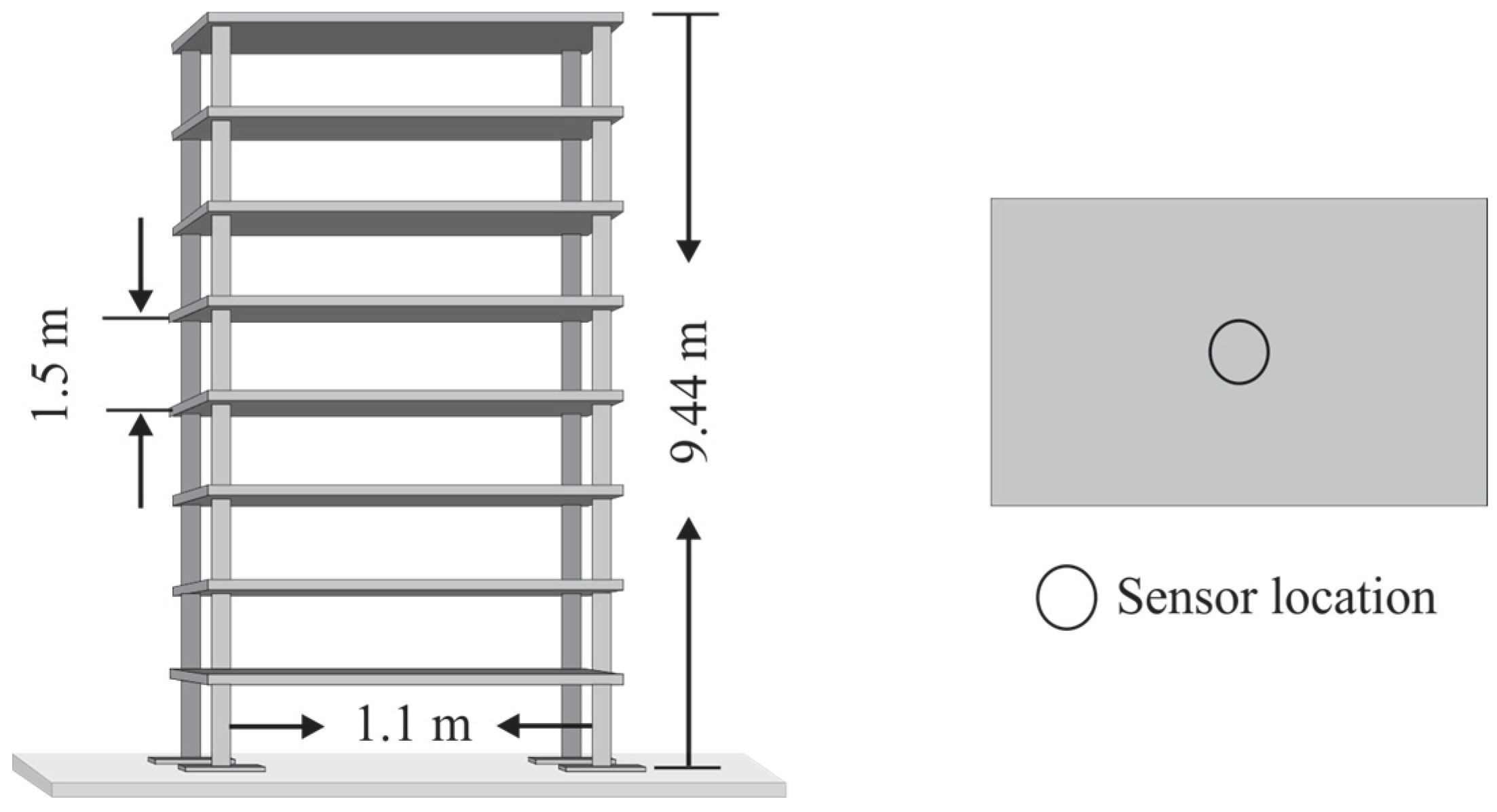
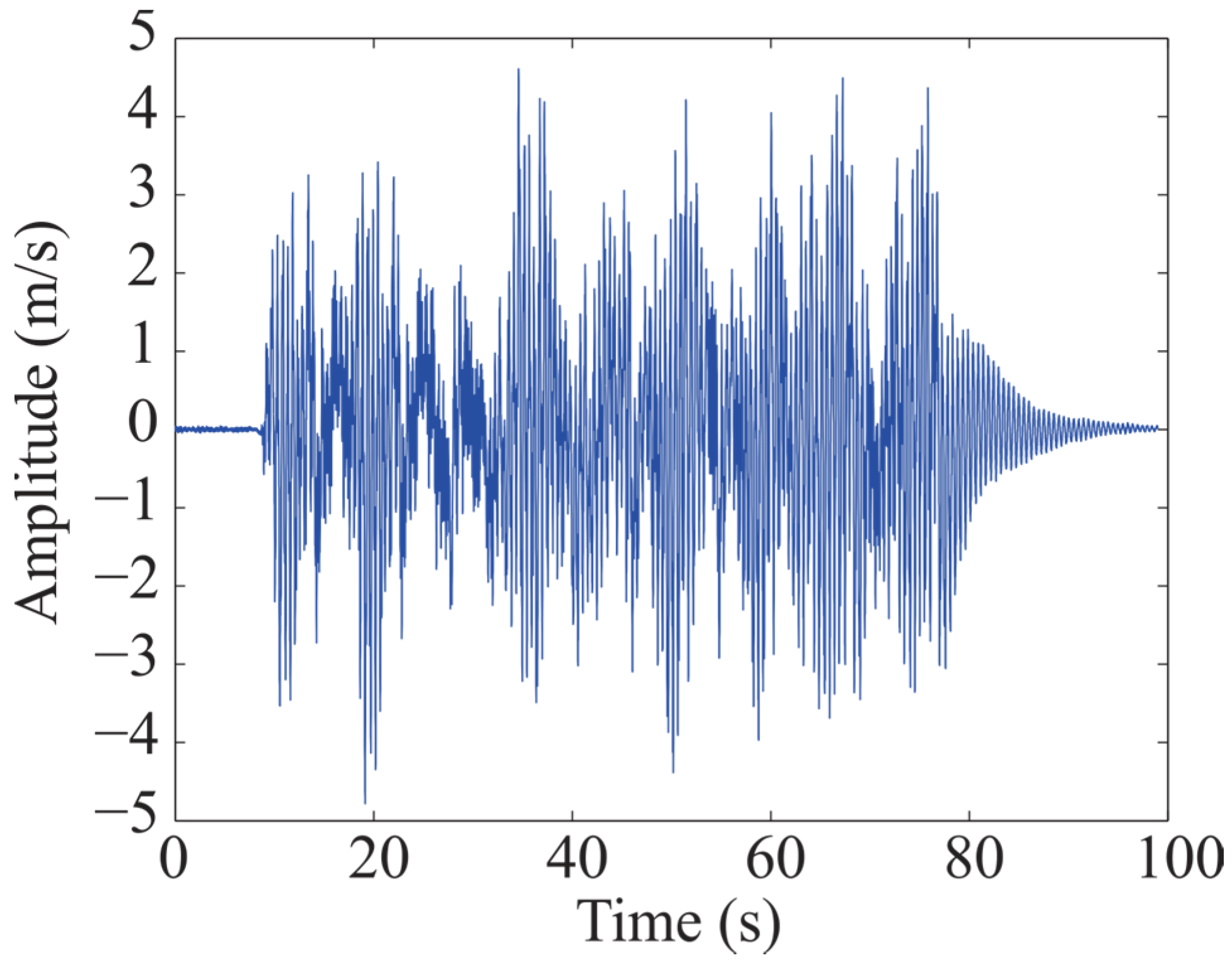
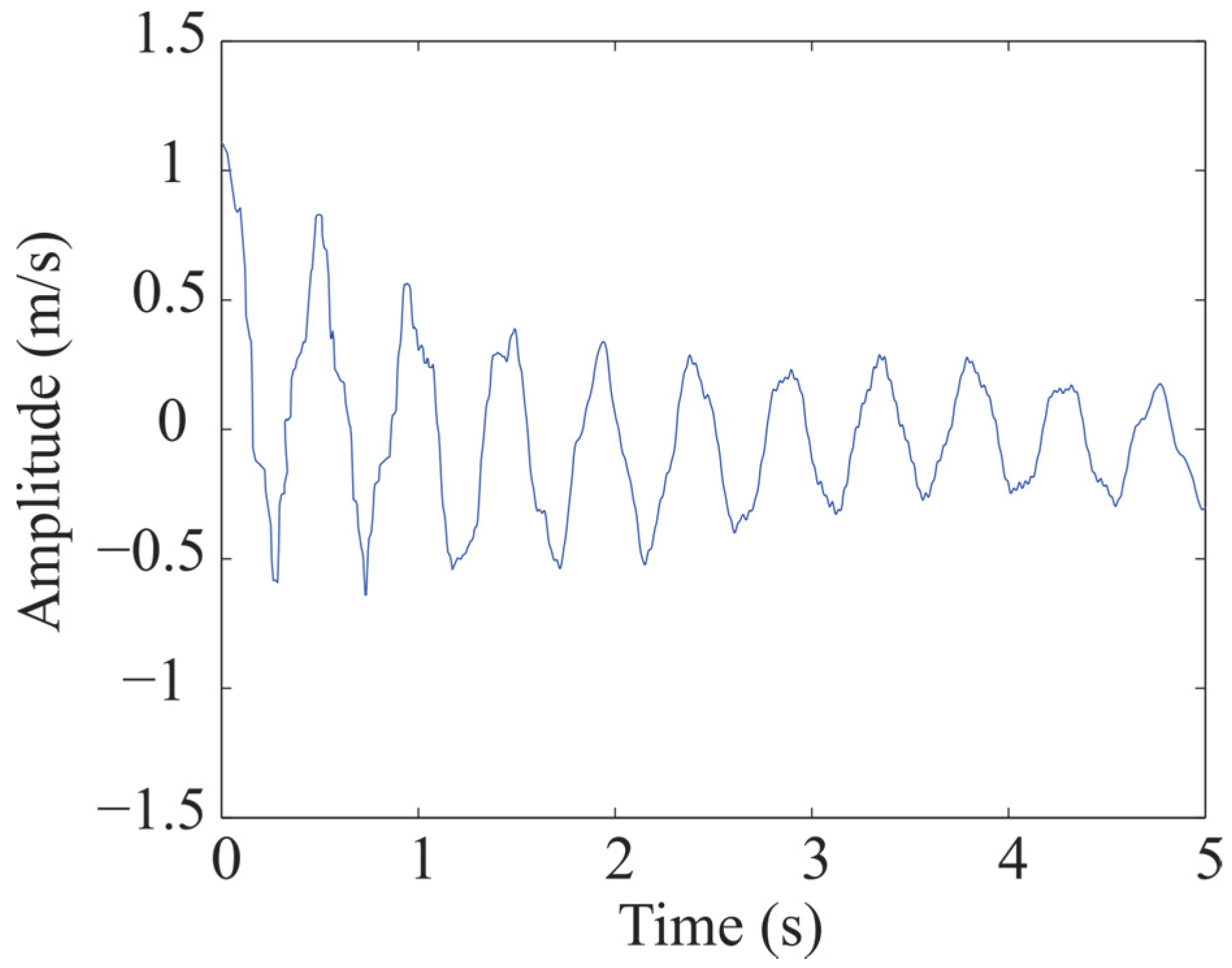
| Modal Parameter | Minimum Value | Maximum Value |
|---|---|---|
| Natural Frequency (Hz) | 0.01 | 100 |
| Damping Ratio (%) | 0.01 | 20 |
| Mode (Direction) | Natural Frequency (Hz) (Error %) | ||||
| FEA | Li et al. [34] | Amini and Hedayati [35] | Perez-Ramirez et al. [11] | New Methodology | |
| 1 (y) | 9.410 | 8.48 (9.88) | 10.62 (12.86) | 9.407 (0.03) | 9.39 (0.21) |
| 2 (x) | 11.79 | 9.03 (23.41) | - | 11.82 (0.20) | 11.72 (0.59) |
| 3 (y) | 25.54 | 23.07 (9.67) | 25.39 (0.59) | 25.55 (0.03) | 25.59 (0.20) |
| 4 (x) | 32.01 | 25.45 (20.49) | - | 31.95 (0.20) | 32.03 (0.06) |
| 5 (y) | 38.66 | 36.32 (6.05) | - | 38.61 (0.13) | 38.67 (0.03) |
| 6 (y) | 48.01 | 41.81 (12.91) | 47.97 (0.08) | 47.97 (0.08) | 48.05 (0.08) |
| 7 (x) | 48.44 | 46.57 (3.86) | - | 48.50 (0.10) | 48.65 (0.44) |
| 8 (x) | 60.15 | 56.09 (6.75) | - | 60.35 (0.33) | 60.16 (0.02) |
| Mode (Direction) | Damping Ratios (%) (Error %) | ||||
| FEA | Li et al. [34] | Amini and Hedayati [35] | Perez-Ramirez et al. [11] | New Methodology | |
| 1 (y) | 1.0 | - | 1.03 (3) | 0.90 (10) | 1.02 (2) |
| 2 (x) | 1.0 | - | - | 0.96 (4) | 1.06 (6) |
| 3 (y) | 1.0 | - | 0.88 (12) | 0.88 (12) | 0.98 (2) |
| 4 (x) | 1.0 | - | - | 0.85 (15) | 0.94 (6) |
| 5 (y) | 1.0 | - | - | 0.86 (14) | 1.01 (1) |
| 6 (y) | 1.0 | - | 0.90 (10) | 1.04 (4) | 0.95 (5) |
| 7 (x) | 1.0 | - | - | 1.0 (0) | 1.0 (0) |
| 8 (x) | 1.0 | - | - | 1.10 (10) | 1.04 (4) |
| Mode (Direction) | Natural Frequency (Hz) | |||
| FEA | Su et al. [53] | Methodology Proposed by Perez-Ramirez et al. [11] | New Methodology | |
| 1 | 2.01 | 2.11 | 2.10 | 2.15 |
| 2 | 6.49 | 7.00 | 6.98 | 7.03 |
| 3 | 12.38 | 12.86 | 12.84 | 12.95 |
| 4 | 19.80 | 19.15 | 19.14 | 19.53 |
| 5 | 26.46 | 25.89 | 25.90 | 26.17 |
| 6 | 34.36 | 33.42 | 33.39 | 34.16 |
| Mode (Direction) | Damping Ratio (%) | |||
| FEA | Su et al. [53] | Methodology Proposed by Perez-Ramirez et al. [11] | New Methodology | |
| 1 | 2.01 | 1.40 | 1.69 | 1.57 |
| 2 | 6.49 | 0.90 | 1.28 | 0.95 |
| 3 | 12.38 | 0.70 | 0.75 | 0.65 |
| 4 | 19.80 | 0.40 | 0.41 | 0.33 |
| 5 | 26.46 | 0.90 | 0.95 | 0.98 |
| 6 | 34.36 | 1.0 | 0.89 | 1.11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez-Ramirez, C.A.; Jaen-Cuellar, A.Y.; Valtierra-Rodriguez, M.; Dominguez-Gonzalez, A.; Osornio-Rios, R.A.; Romero-Troncoso, R.D.J.; Amezquita-Sanchez, J.P. A Two-Step Strategy for System Identification of Civil Structures for Structural Health Monitoring Using Wavelet Transform and Genetic Algorithms. Appl. Sci. 2017, 7, 111. https://doi.org/10.3390/app7020111
Perez-Ramirez CA, Jaen-Cuellar AY, Valtierra-Rodriguez M, Dominguez-Gonzalez A, Osornio-Rios RA, Romero-Troncoso RDJ, Amezquita-Sanchez JP. A Two-Step Strategy for System Identification of Civil Structures for Structural Health Monitoring Using Wavelet Transform and Genetic Algorithms. Applied Sciences. 2017; 7(2):111. https://doi.org/10.3390/app7020111
Chicago/Turabian StylePerez-Ramirez, Carlos Andres, Arturo Yosimar Jaen-Cuellar, Martin Valtierra-Rodriguez, Aurelio Dominguez-Gonzalez, Roque Alfredo Osornio-Rios, Rene De Jesus Romero-Troncoso, and Juan Pablo Amezquita-Sanchez. 2017. "A Two-Step Strategy for System Identification of Civil Structures for Structural Health Monitoring Using Wavelet Transform and Genetic Algorithms" Applied Sciences 7, no. 2: 111. https://doi.org/10.3390/app7020111
APA StylePerez-Ramirez, C. A., Jaen-Cuellar, A. Y., Valtierra-Rodriguez, M., Dominguez-Gonzalez, A., Osornio-Rios, R. A., Romero-Troncoso, R. D. J., & Amezquita-Sanchez, J. P. (2017). A Two-Step Strategy for System Identification of Civil Structures for Structural Health Monitoring Using Wavelet Transform and Genetic Algorithms. Applied Sciences, 7(2), 111. https://doi.org/10.3390/app7020111