Adjustment of track level, pan position and equalisation are common in audio processing. While level and pan are fundamental operations in multichannel mixing, equalisation is one of the most commonly used processors. Together, these three operations form a basic channel strip. As such, the scope of this paper considers these three operations.
2.1. Track Gains
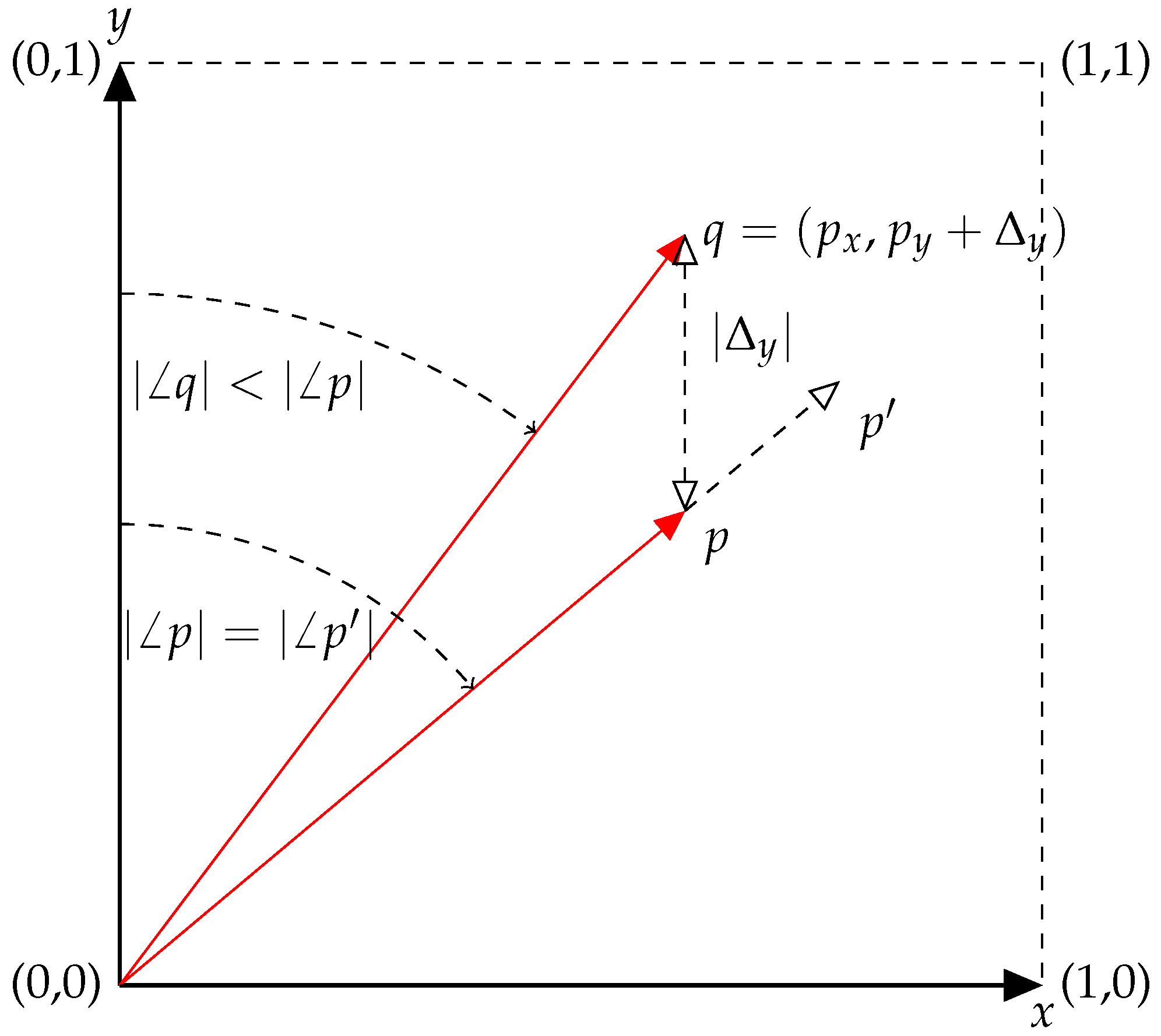
Consider the trivial case where two audio signals are to be mixed, where only the absolute levels of each signal can be adjusted. In
Figure 1, the gains of two signals are represented by
x and
y, where both are positive-bound. Consider the point
p as a configuration of the signal gains, i.e.,
. From this point, the values of
x and
y are both increased in equal proportion, arriving at the point
. The magnitude of
p is less than that of
(
) yet since the ratio of
x to
y is identical, the angles subtended by the vectors from the
y-axis are equal (
). In the context of a mix of two tracks, what this means is that the volume of
is greater than
p, yet the blend of input tracks is the same.
As an alternate to Equation (
1), a mix can be thought of as the relative balance of audio signals. From this definition, the points
p and
are the same mix, only
is being presented at a greater volume. If the listener has control over the master volume of the system, then any difference between
p and
becomes ambiguous.
Definition 1. Mix: an audio stream constructed by the superposition of others in accordance with a specific blend, balance or ratio.
From p, the level of fader y can be increased by , arriving at q. In this particular example, the value of was chosen such that . However, for any , . Therefore, q clearly represents a different mix to either p or . Consequently, the definition of a mix is clarified by what it is not: when two audio streams contain the same blend of input tracks but the result is at different overall amplitude levels, these two outputs can be considered the same mix. For this mixing example, where there are signals, represented by n gain values, the mix is dependant on variables; in this case, the angle to the vector. The norm of the vector is simply proportional to the overall loudness of the mix.
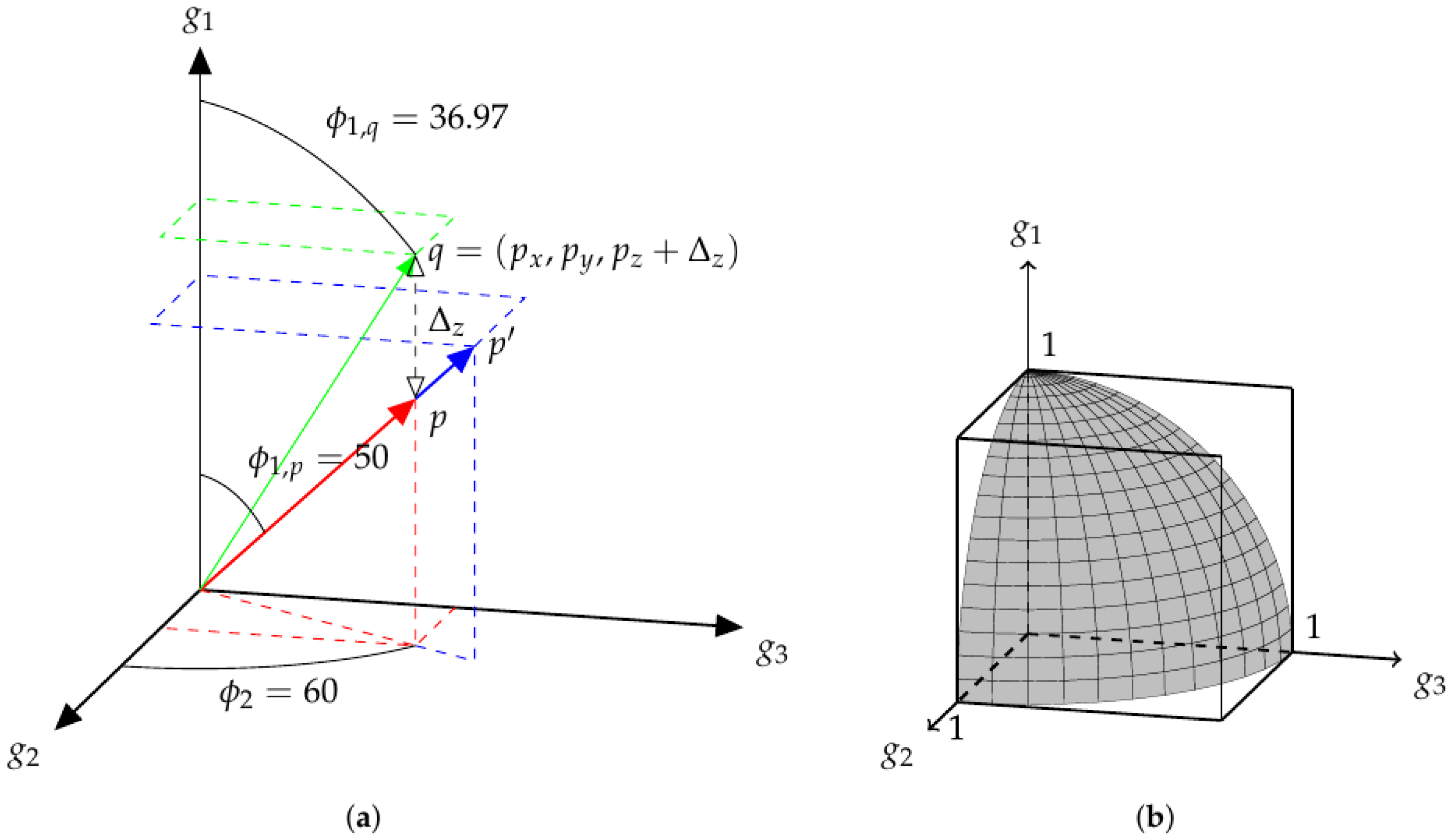
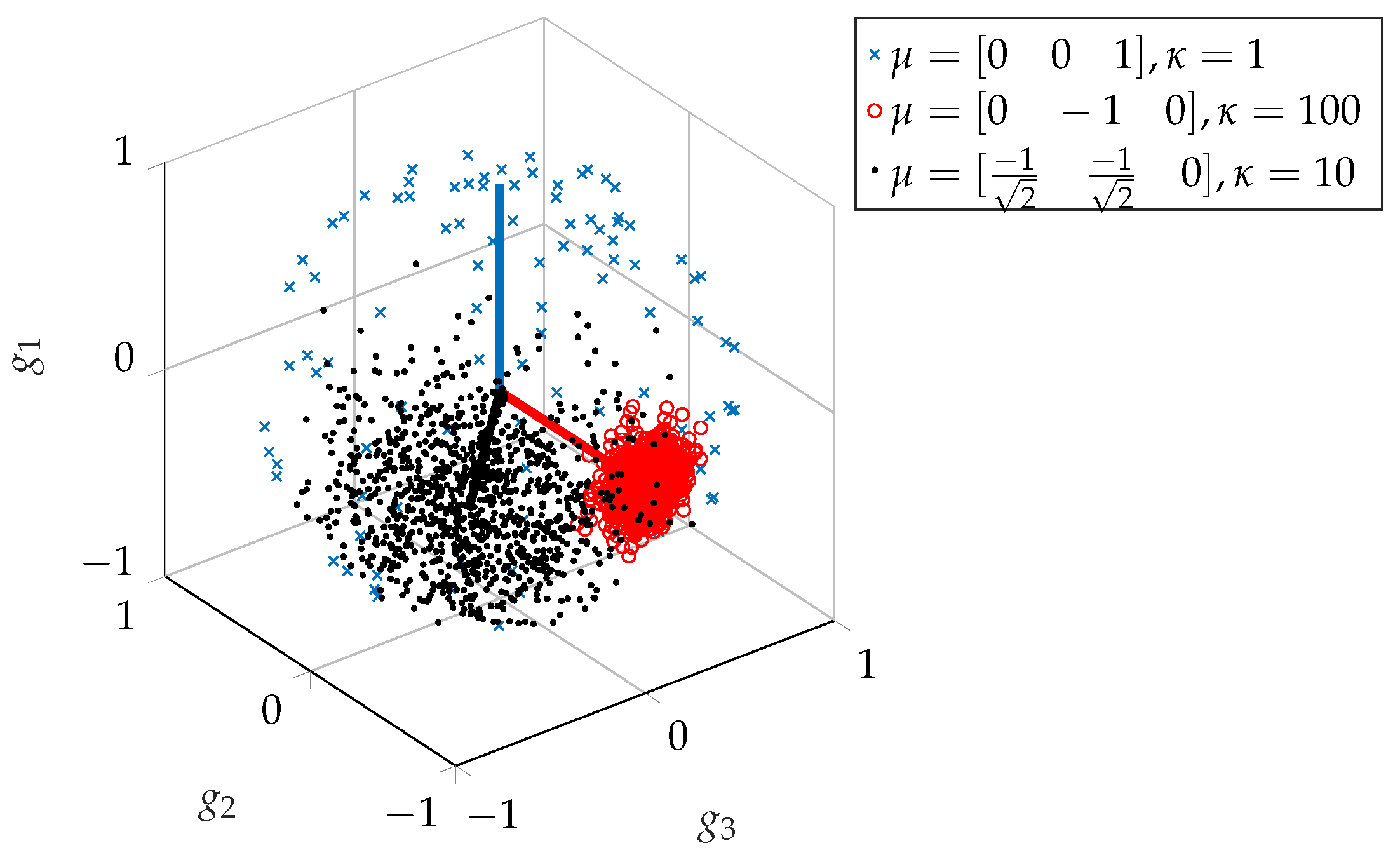
Figure 2a shows a similar structure, with
. Here, the point
is also an extension of
p. As in
Figure 1,
q is located by increasing the value of
y from the point
p and
. Here, the values of each angle are explicitly determined and displayed. All three vectors share the equatorial angle of 60. The polar angle of
p and
is 50, while the polar angle of
q is less than this, at ≈37. As in the two-dimensional case, it is the angles which determine the parameters of the mix and the norm of the vector is related to the overall loudness.
While
Figure 1 and
Figure 2a show a space of track gains, there is clearly a redundancy of mixes in this space. What is ultimately desired is a space of mixes.
Definition 2. Mix-space: a parameter space containing all the possible audio mixes that can be achieved using a defined set of processes.
It becomes apparent that a Euclidean space with track gains as basis vectors is not an efficient way to represent a space of mixes, according to Definition 2. This explains why Equation (
1) would not be appropriate when searching for mixes. If, in
Figure 2a, a set of
m points randomly selected on
were chosen, the number of mixes could be less than
m, as the same mix could be chosen multiple times at different overall volumes. A set of
m randomly selected points on a sphere of any radius (
) would result in a number of mixes equal to
m. This surface is represented in
Figure 2b, which shows the portion of a unit-sphere in positively-unbounded
, upon which exist all possible mixes of three tracks.
While both the 2-content of
(surface area) and the 3-content of the enclosing
, (volume) both, strictly, contain an infinite amount of points, the reduced dimensionality of
makes it a more attractive content to use in optimisation, as
is a subset of
(in this context,
content can be considered as “hypervolume”. See
http://mathworld.wolfram.com/Content.html). As a consequence, the
mix-space,
, is a more compact representation of audio mixes than the gain-space,
g.
While the examples so far have used polar and spherical coordinates, for
and
respectively, to extend the concept to any
n dimensions, hyperspherical coordinates are used. The conversion from Cartesian to hyperspherical coordinates is given below in Equation (
5). The inverse operation, from hyperspherical to Cartesian, is provided in Equation (
6), based on [
11]. Here,
is the gain of the
jth track out of a total of
n tracks. The angles are represented by
. By convention,
is the equatorial angle, over the range
radians, while all other angles range over
radians.
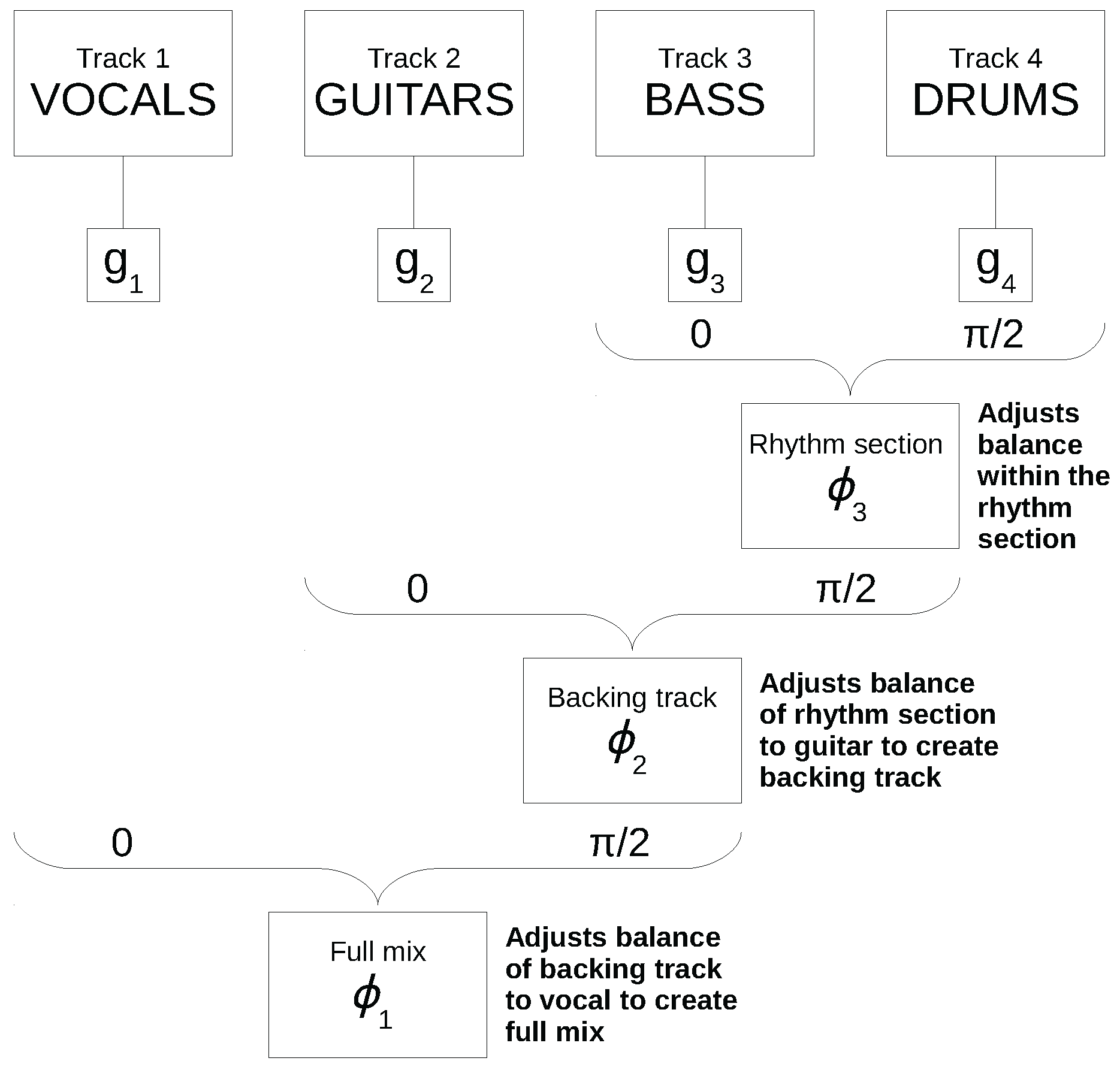
Figure 3 represents a comparable 4-track mixing exercise, as described in [
7]. The four audio sources were specifically chosen for this example (vocals, guitar, bass and drums) and assigned to
,
,
and
respectively. Consequently, the set of mixes is represented by a 3-sphere of radius
r. Due to the deliberate assignment of tracks in this example, the parameters
and
represent a set of inter-channel balances which, due to the specific relationships of instruments, have importance to musicians and audio engineers:
determines the balance of bass to drums, the rhythm section in this case;
describes the projection of this balance onto the
axis, i.e., the blend of guitar to rhythm section, and finally,
describes the balance of the vocal to this backing track.
From here, the parameter space comprising the angular components of the hyperspherical coordinates of a ()-sphere in a n-dimensional gain-space, is referred to as a ()-dimensional mix-space. More simply, this can be stated by saying the mix-space is the surface of a hypersphere in gain-space. In the case of music mixing, only the positive values of g are of interest. Subsequently, the interesting region of the mix-space is only a small proportion of the total hypersurface. This fraction is .
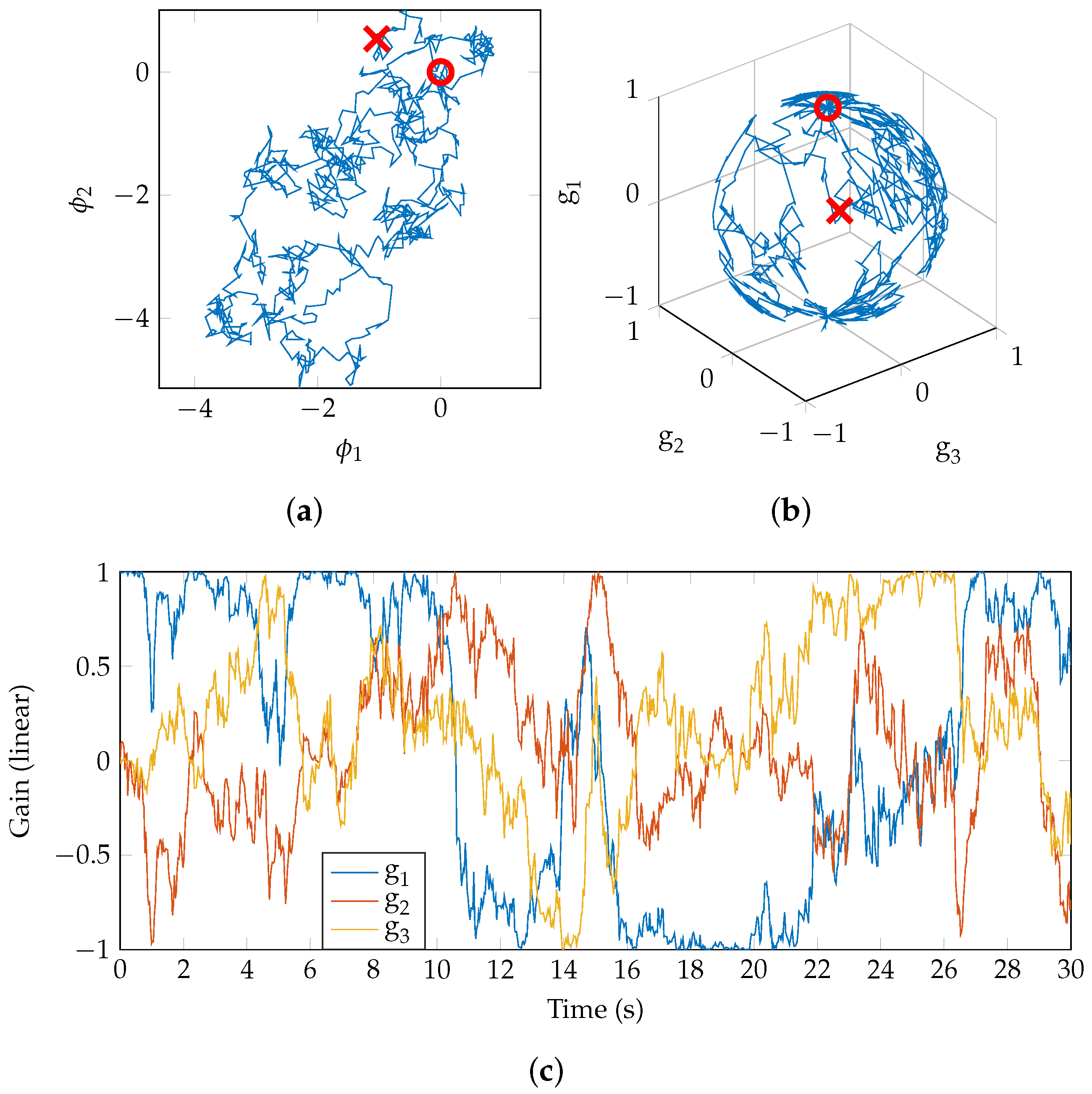
As each point in
represents a unique mix, the process of mixing can be represented as a path through the space. In
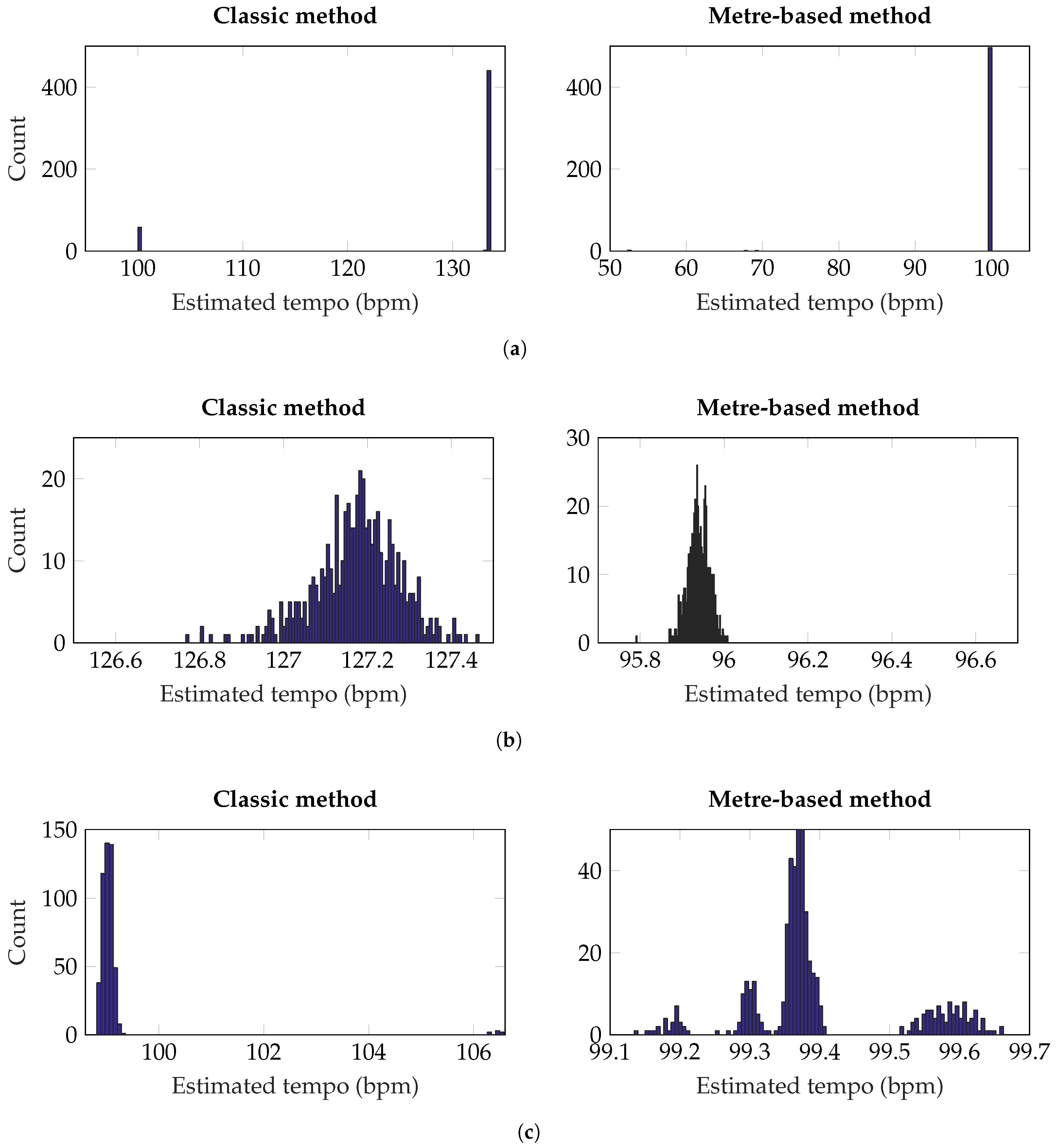
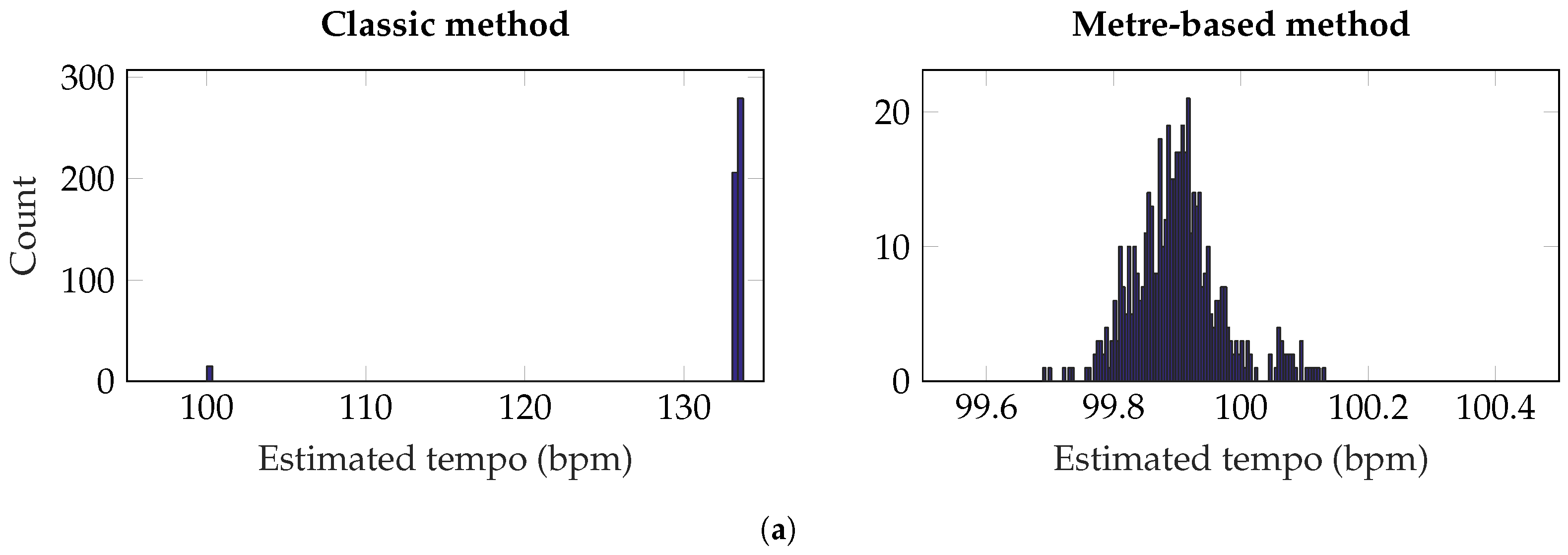
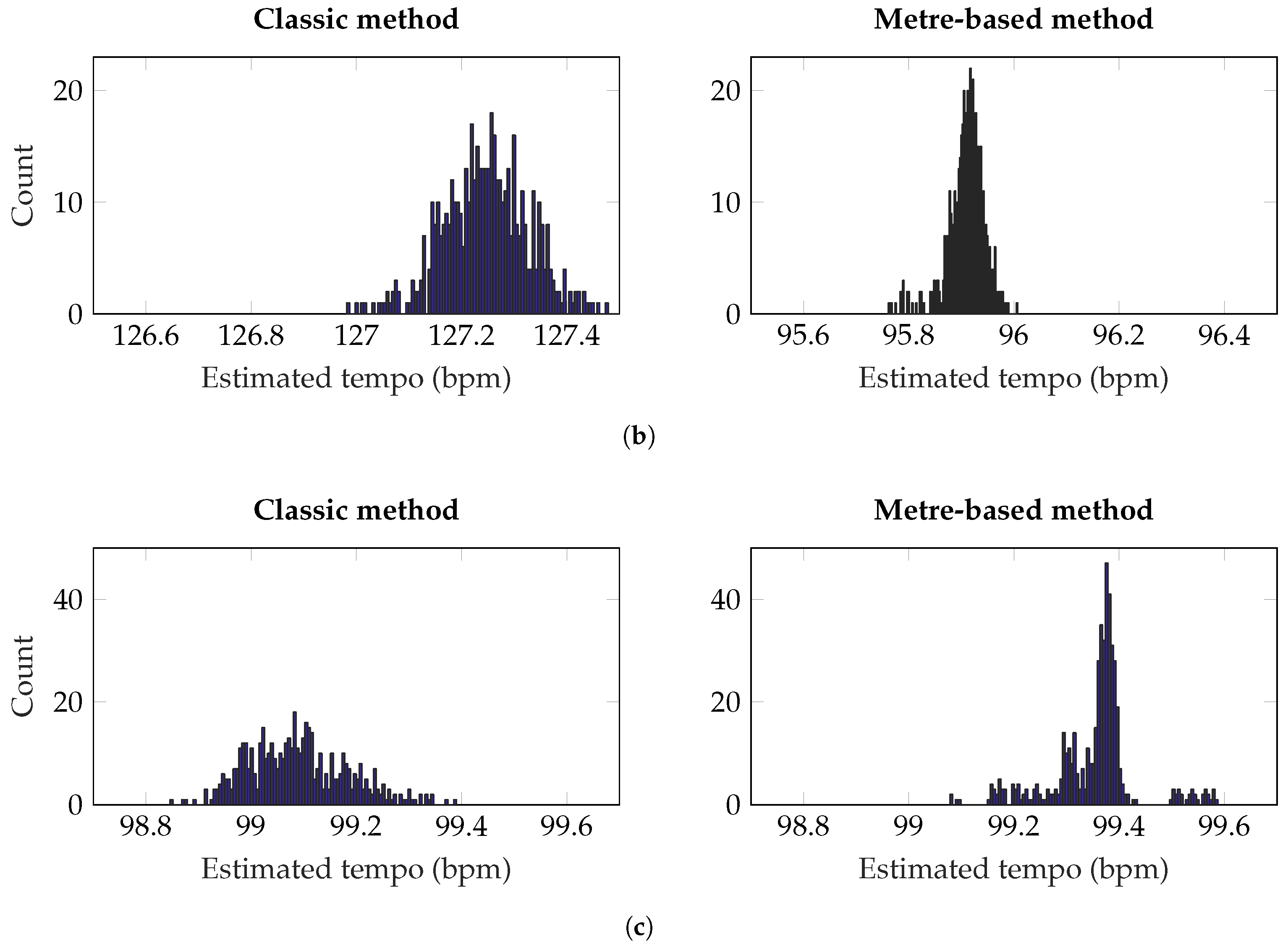
Figure 4a, a random walk begins at the point marked ‘∘’ in the 2D mix-space (the origin [0,0], which corresponds to a gain vector of [1,0,0]). The model for the walk is a simple Brownian motion (
http://people.sc.fsu.edu/~jburkardt/m_src/brownian_motion_simulation/brownian_motion_simulation.html). After 30 s, the walk is stopped and the final point reached is marked ‘×’. The gain values for each of the three tracks are shown in
Figure 4b and it is clear that the random walk is on a 2-sphere, as anticipated. The time-series of gain values is shown in
Figure 4c. Note that
, so for positive
g the region explored is as represented in
Figure 2b.
When presented in isolation, such a random mix, whether static or time-varying, may be unrealistic. It is hypothesised that real mix engineers do not carry out a random walk but a guided and informed walk, from some starting point (“source”) to their ideal final mix (“sink”). For further discussion of these terms, see [
7], which uses the mix-space as a framework for the analysis of a simple 4-track mixing experiment. The power in these methods comes from generating a large number of mixes, more so than realistically could be obtained from real-world examples, and estimating parameters using statistical methods. Further generation and statistical analysis of time-varying mixes is left to further work.
2.3. Track Panning
Thus far, only mono mixes have been considered, where all audio tracks are summed to one channel. In creative music production, it is rare that mono mixes are encountered. The same mathematical formulations of the mix-space can be used to represent panning. Consider
Figure 4, which shows track gains in the range
. Should these be replaced with track pan positions
(with
and 1 corresponding to extreme left and right pan positions, for example) then the mix-space (or “pan-space”) can be used to generate a position for each track in the stereo field. To avoid confusion with the earlier use of
, the pan-space is denoted by
, although the formalism is identical.
However, the mix-space for gains () takes advantage of the fact that a mix (in terms of track gains only) is comprised of a series of inter-channel gain ratios, meaning that the radius r is arbitrary and represents a master volume. In terms of track panning, one obtains a series of inter-channel panning ratios, the precise meaning of which is not intuitive. Additionally, the radius would still be required to determine the exact pan position of the individual tracks. Therefore, the pan-space describes the relative pan positions of audio tracks to one another.
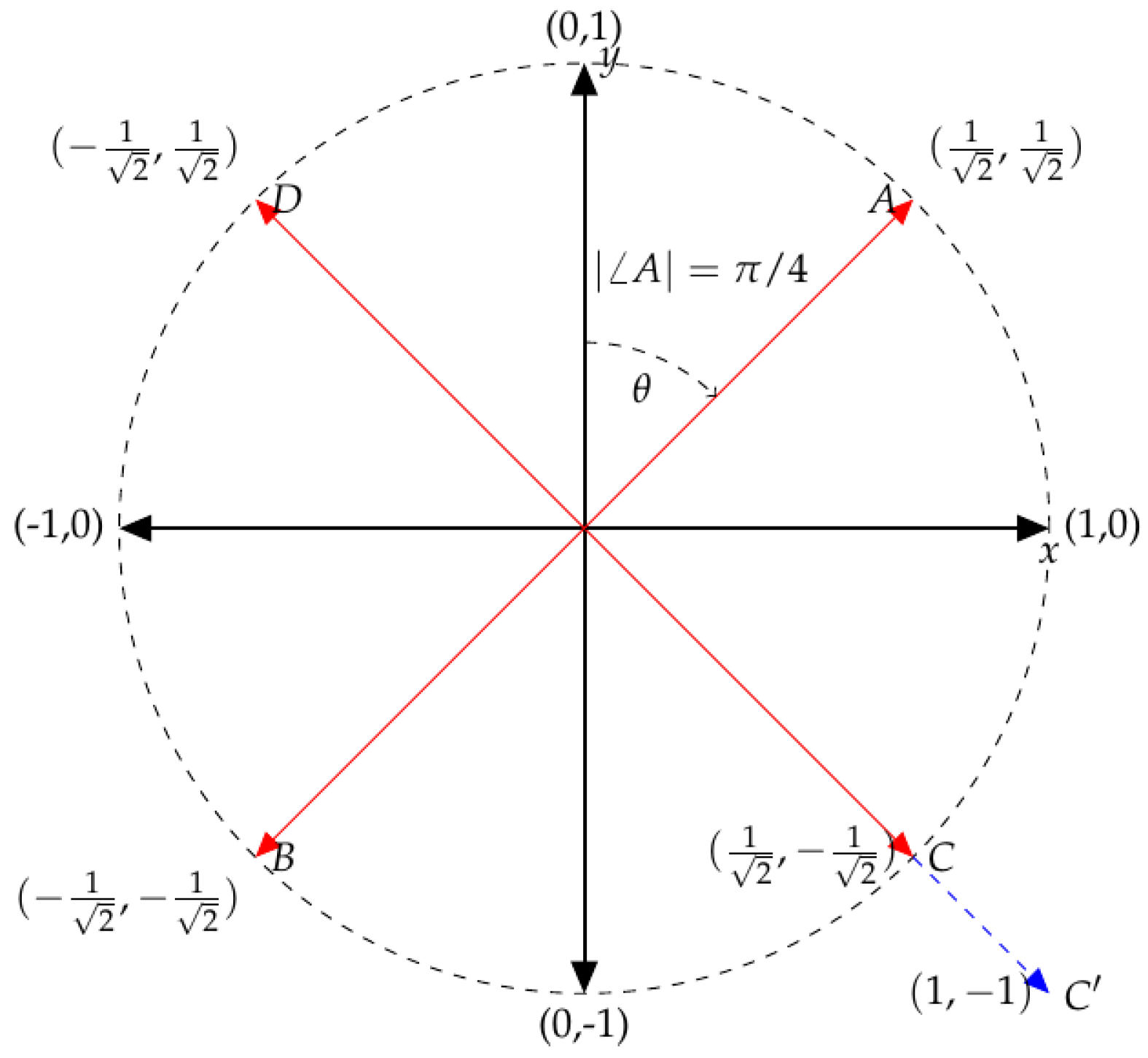
For a simple example with only two tracks, the meaning of
and
is relatively simple to understand. Consider the unit circle in a plane where the Cartesian coordinates
represent the pan positions of two tracks, as shown in
Figure 7. Mix
A is at the point
: both tracks are panned at the same position. As this is a circle with arbitrary radius,
, then the radius controls how far positive (right) the two tracks are panned, from 0 (centre) to
(far right). Mix
B does the same but towards the left channel. One may ask whether
A and
B are identical “panning-mixes”, as
p and
in
Figure 1 were identical “level-mixes”?
Now consider mix C, where one track is panned left and the other right. Mix D is simply the mirror image of this. Are these to be considered as the same mix, or as different mixes? Here, adjusts the distance between the two tracks, from both centre when , to when (as indicated by mix ). Does a change in change the mix, or is it simply the same mix only wider/narrower? Overall, the angle adjusts the panning mix and is used to obtain absolute positions in the stereo field, at a particular width-scale (i.e., to zoom in or zoom out).
2.3.1. Method 1—Separate Left and Right Gain Vectors
The method for random gains (see
Section 2.2) was used to create separate mixes for the left and right channels of a stereo mix. In absolute terms, hard-panning only exists when the gain in one channel is 0 (
perceptually, the impression of hard-panning can be achieved when the difference between one channel and the other is sufficiently large [
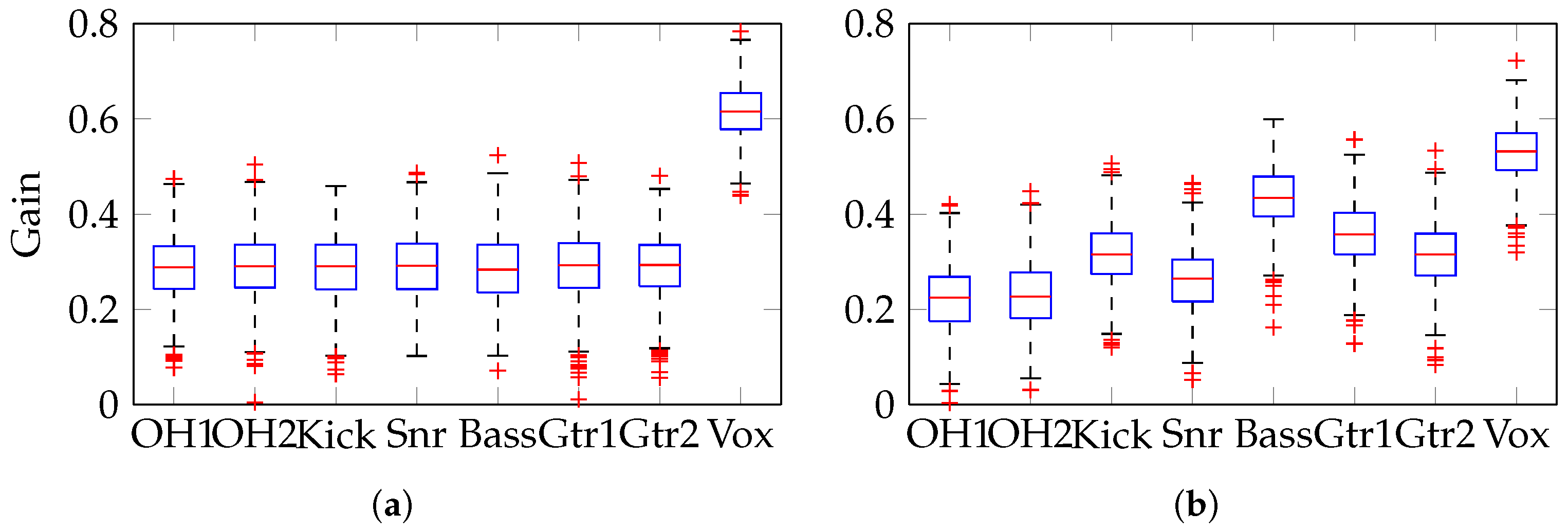
18]). Since the vocal boost prevents any vocal gain of zero, the panning of the vocals is much less wide than the other tracks. Additionally, since
was chosen to prevent any negative gains, there are few zero-gain instances; therefore, there is a lack of hard-panning.
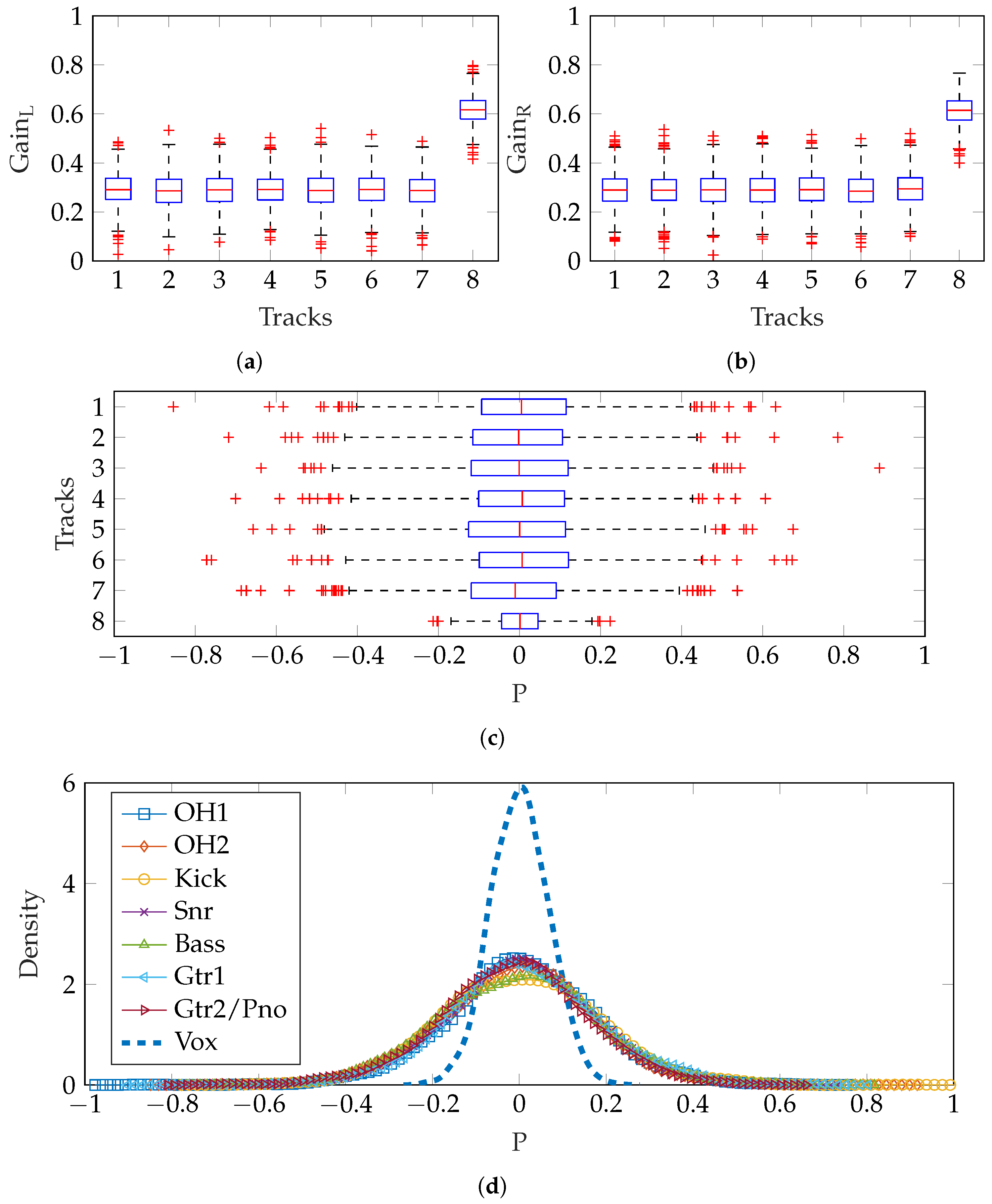
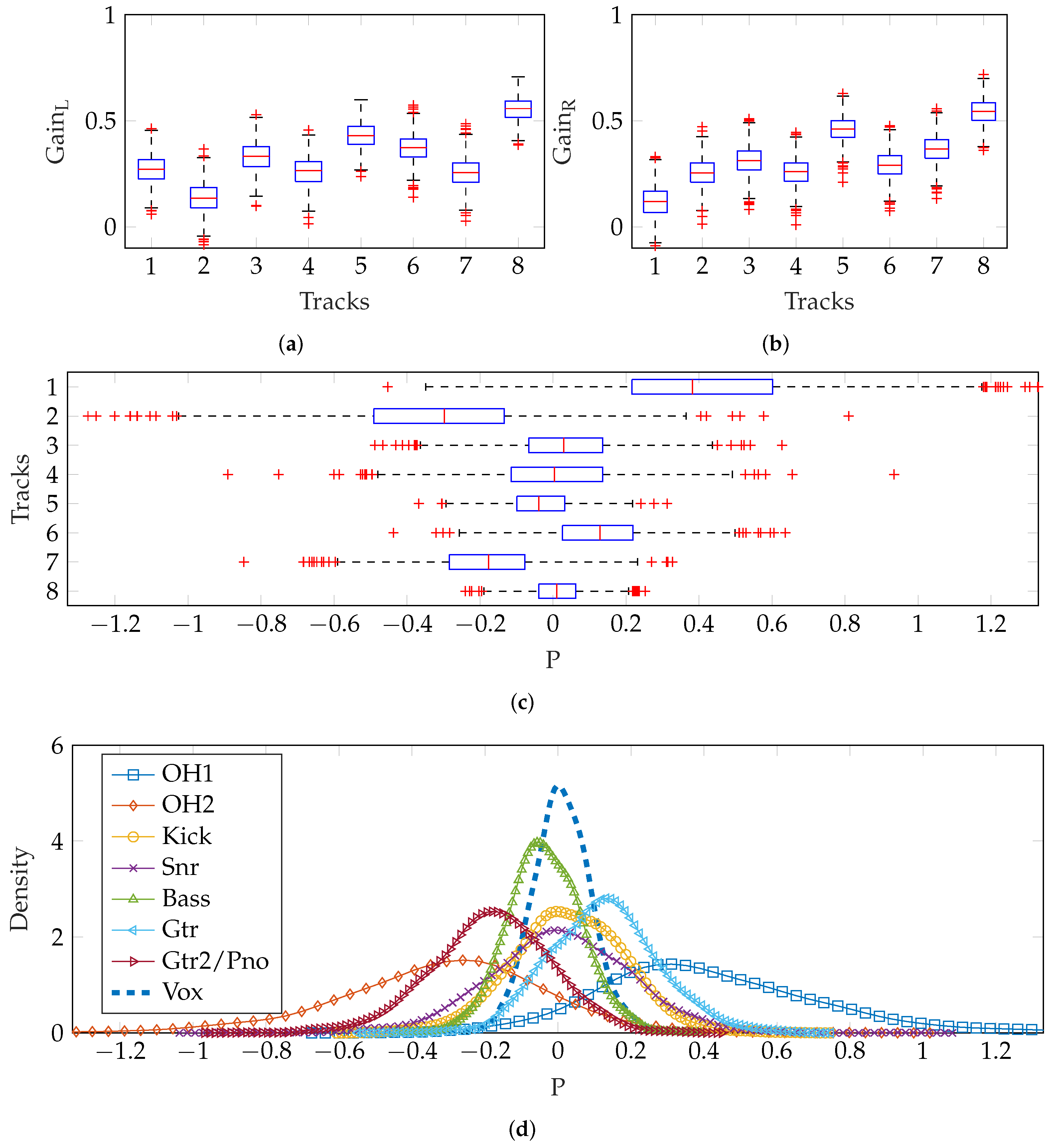
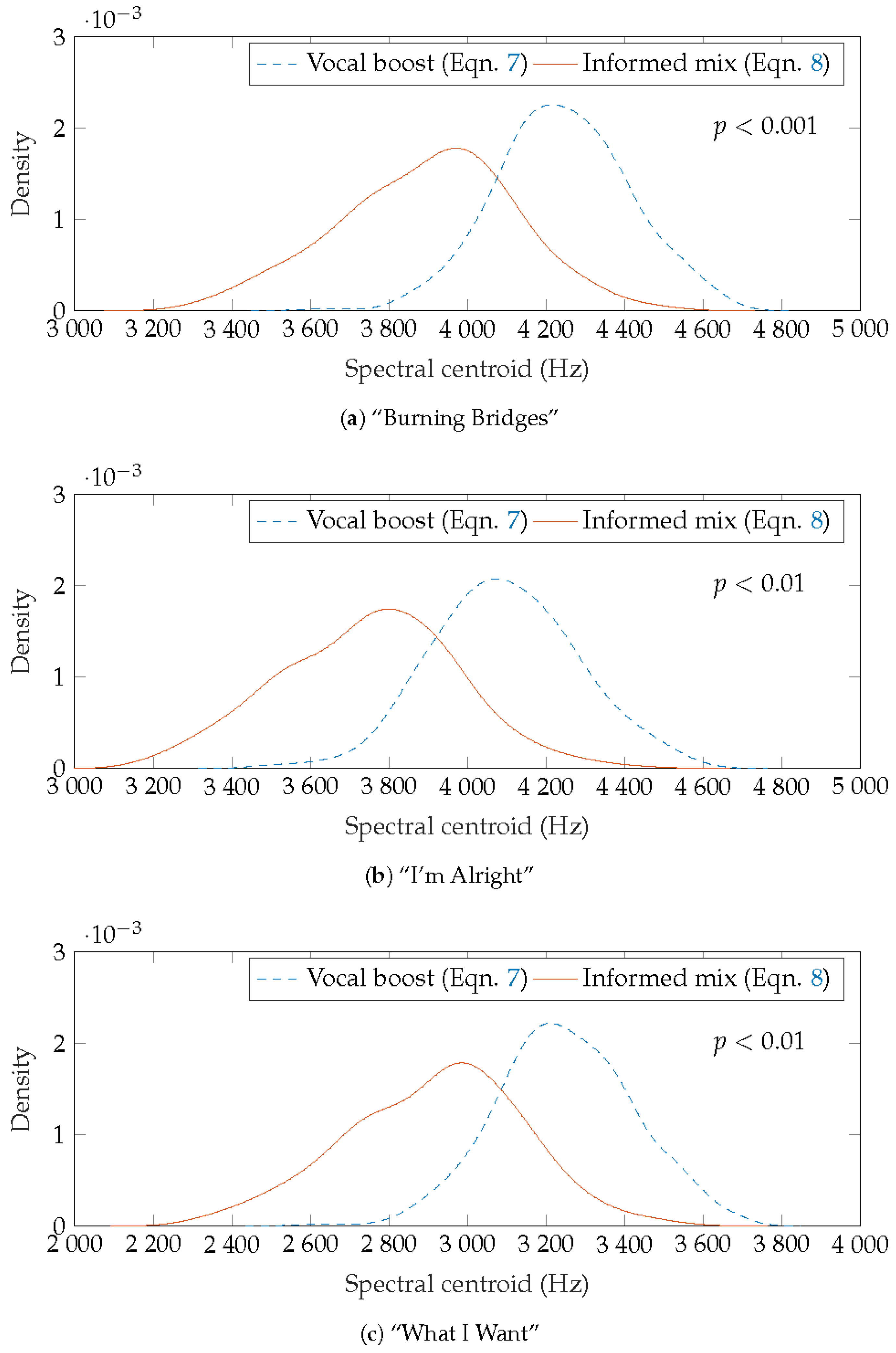
Figure 8a,b show the gain settings produced and a boxplot of the resulting pan positions is shown in
Figure 8c, where the inter-quartile range extends to ±0.4 for the seven instrument tracks and about ±0.2 for the vocals. The estimated density of pan positions for each track is shown, illustrating the relatively narrow vocal panning. As expected, these estimated density functions are Gaussian, to a good approximation.
Rather than using the same
for both left and right channels, a unique choice of
and
can be made, as described in
Section 2.2.2. The vectors used are shown in Equations (
10) and (
11). When summed to mono, this is equivalent to Equation (
8).
Figure 9 shows the difference in gains produced for left and right channels. There were some negative track gains produced: when generating audio mixes, the absolute magnitude of the gain was used to avoid phase inversions which would alter spatial perception of the stereo overhead pair. It is clear that the similarity of vocals gains in left and right channels produces a limited variety of pan positions close to the central position, as shown in
Figure 9c,d. Other instruments are panned with mean position and variance in accordance with the experimental results [
15].
2.3.2. Method 2—Separate Gain and Panning
This method involved generating random mono mixes as
Section 2.2 (using Equation (
7) and then generating pan positions separately. A
was created for a vMF distribution. This vector was based on experimental results reported in [
15], which showed that, generally, overheads and guitars were widely panned while kick, snare, bass and vocals were positioned centrally.
This then needs to be a unit vector for it to be used in creating vMF-distributed points. Consequently, the precise values are not critically important, as it is the relative pan positions that are reflected in the normalised vector and
which would be used to adjust the scaling of these relative positions.
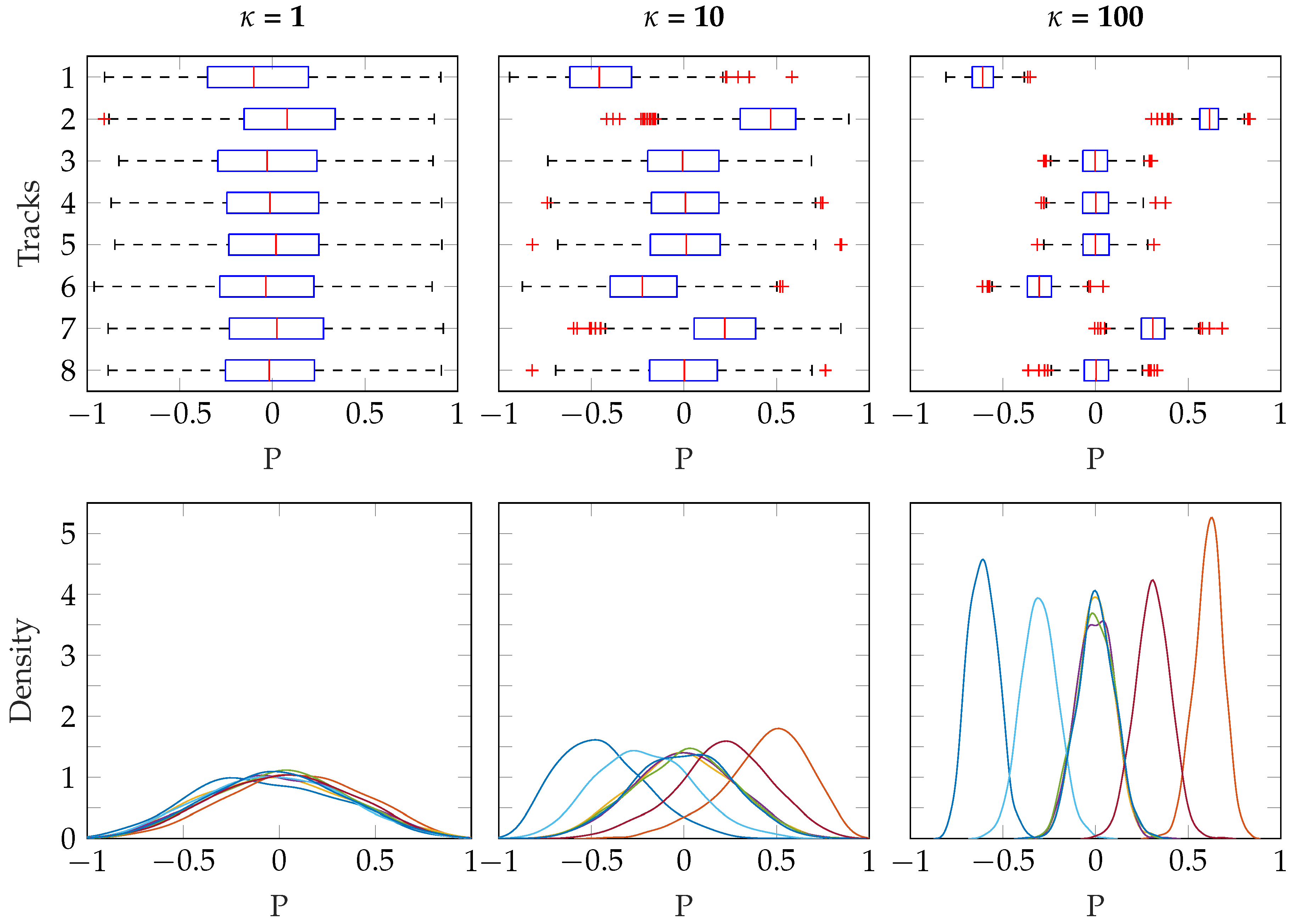
Three different values for
were used, which illustrates how this parameter controls the distribution of panning. The results are shown in
Figure 10, where the influence of
is clear. When
, the distribution of pan positions approaches uniform over the sphere, and so the median pan positions are close to 0 (central position in the stereo field) for all tracks, regardless of
. As
increases, the distribution of pan positions is narrower, more concentrated on the specific pan positions specified in
.
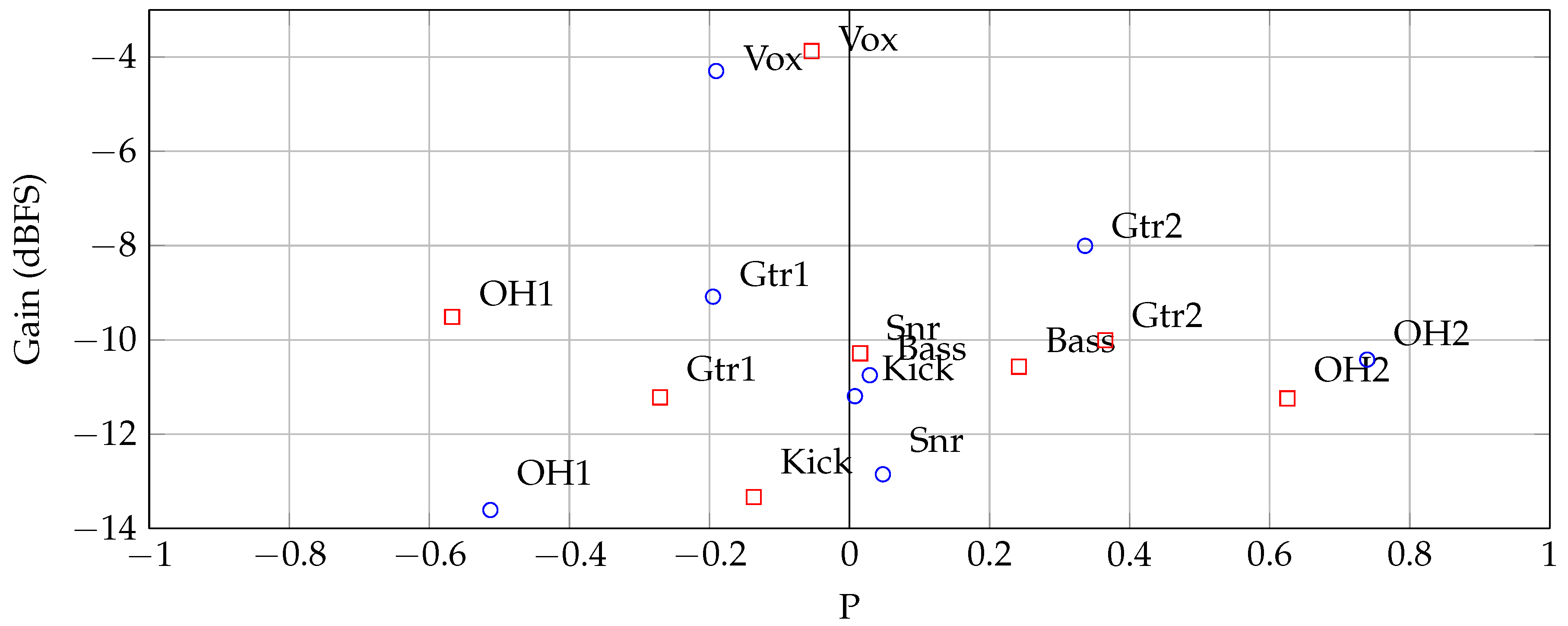
Figure 11 shows an example of two mixes created using this method. The gains and pan positions of each track are displayed. It is clear that the instruments are typically panned close to the positions specified in the pan vector (Equation (
13). In this example,
; increasing this parameter would produce wider mixes, while a decrease would produce a less wide mix.
2.4. Track Equalisation
Similarly to how the mix can be considered as a series of
inter-channel gain ratios, when the frequency-response of a single audio track is split into a fixed number of bands, the
inter-band gain ratios can be used to construct a
tone-space using the same formulae. For three bands, with gain of low, middle and high bands in the filter being
,
and
respectively, the problem is comparable to the 3-track mixing problem shown in
Figure 2a. Again, one can convert this to spherical coordinates (by EquationS (
5) and obtain
, yet, in this case, the values of
control the EQ filter applied, and
is the total amplitude change produced by equalisation (to avoid confusion,
is used in place of
when referring to equalisation). As before, if all three bands are increased or decreased by the same proportion, then the tone of the instrument does not change apart from an overall change in presented amplitude,
. Analogous to its use in track gains, the value of
adjusts the balance between
and
, while
adjusts the balance of
to the previous balance.
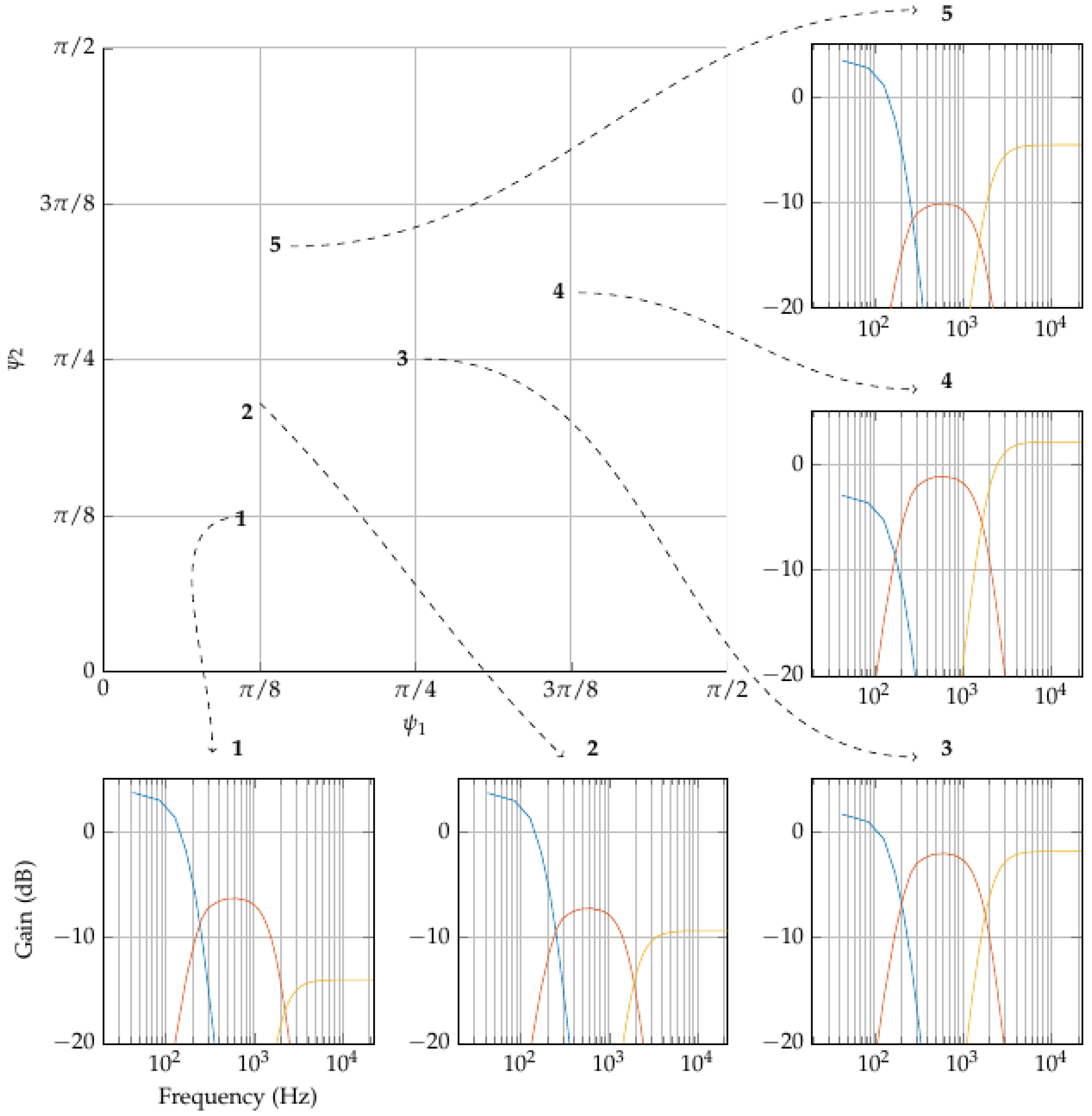
In
Figure 12, five points are randomly chosen in the
tone-space. These co-ordinates are converted to three band gains as before, except that, in order to centre on a gain vector of
,
, which is
in this example. Of course, this method can be used for any number of bands.
With this method, one must assume that an audio track has equal amplitude in each band, which is rarely the case. When is increased on a hi-hat track, there may be little effect, compared to a bass guitar. Therefore, the loudness change is a function of and the spectral envelope of the track, prior to equalisation. This is not considered here and is left to further work.