Imaging Flow Velocimetry with Laser Mie Scattering
Abstract
1. Introduction
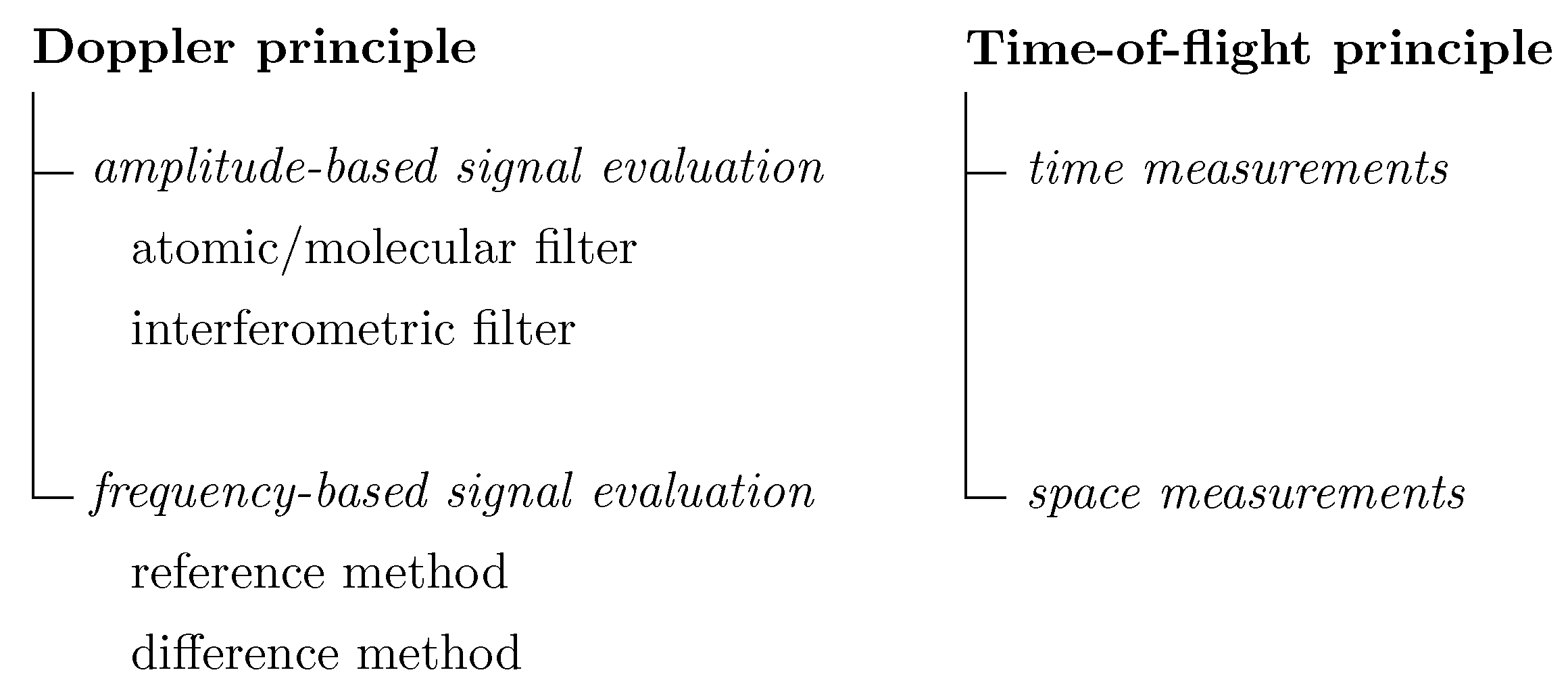
2. Measurement Approaches
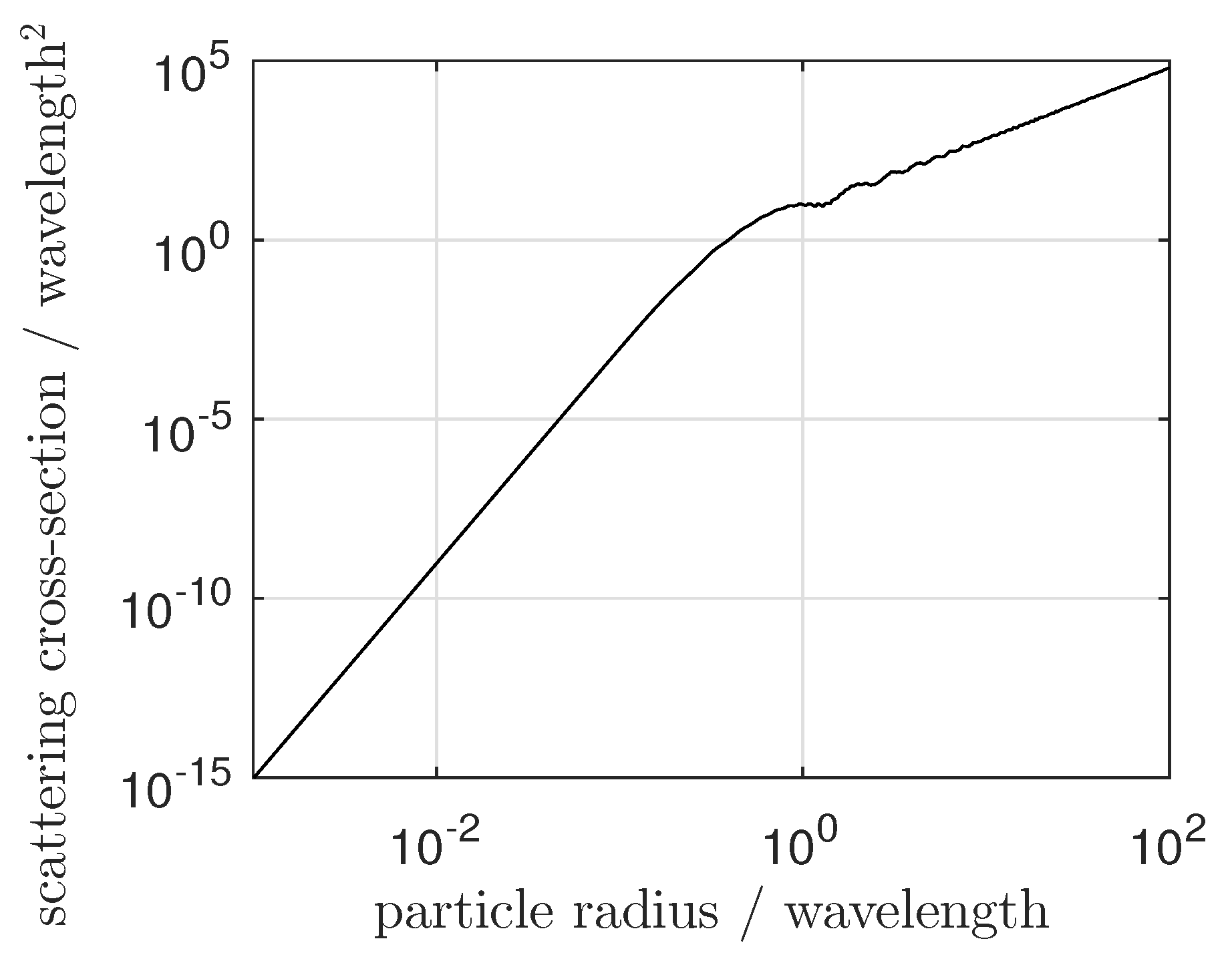
2.1. Application of Mie Scattering
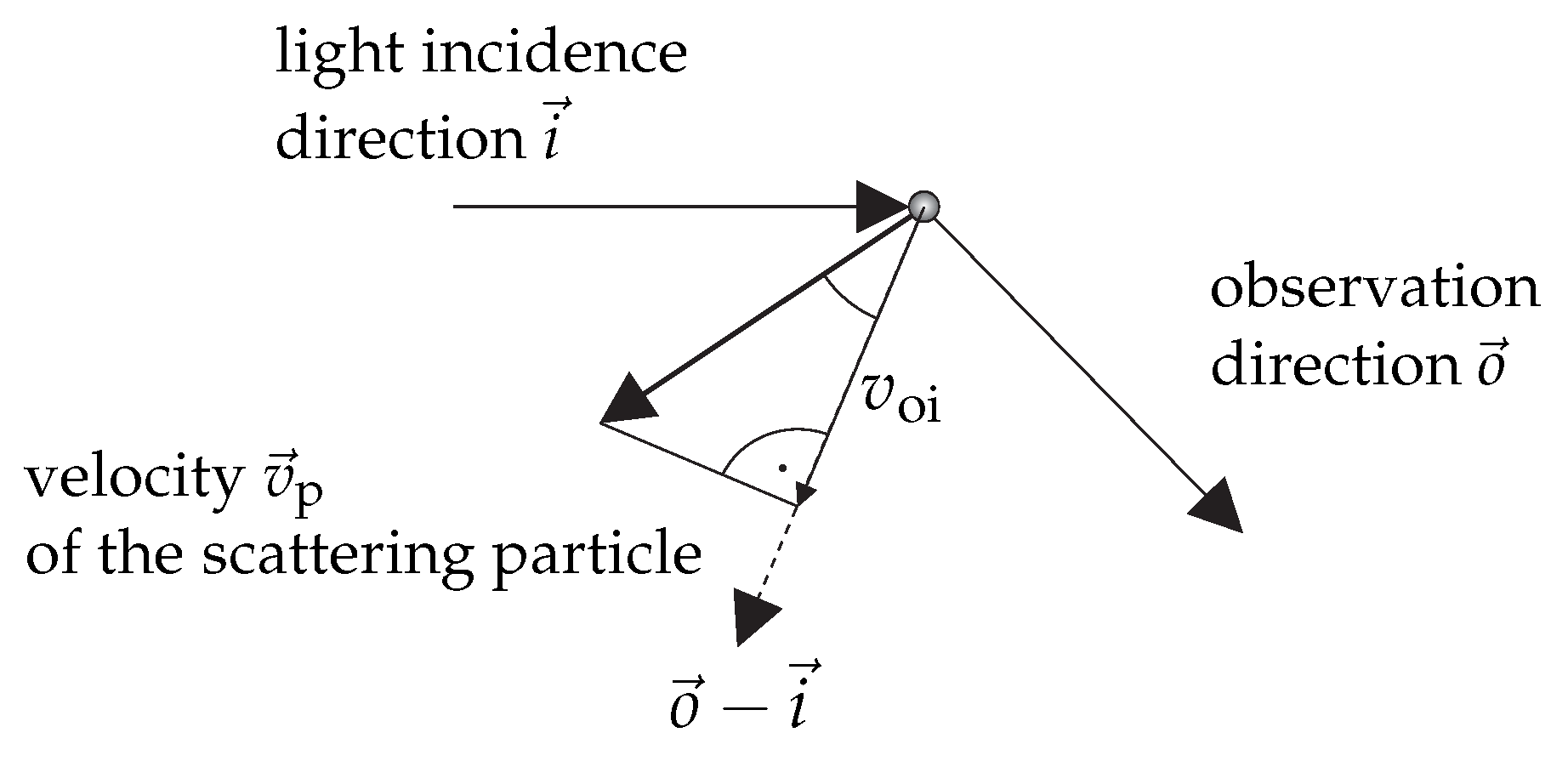
2.2. Scattered Light Evaluation
- Doppler principles,
- Time-of-flight principles.
3. Developed Measurement Techniques and Their Imaging Evolution
3.1. Fundamentals for the Evaluation of the Measurement Techniques
- The flow velocity is a vector quantity. Therefore, the number of measured velocity components is an important property. The abbreviated form 1c, 2c or 3c means that one, two or three components are measured, respectively.
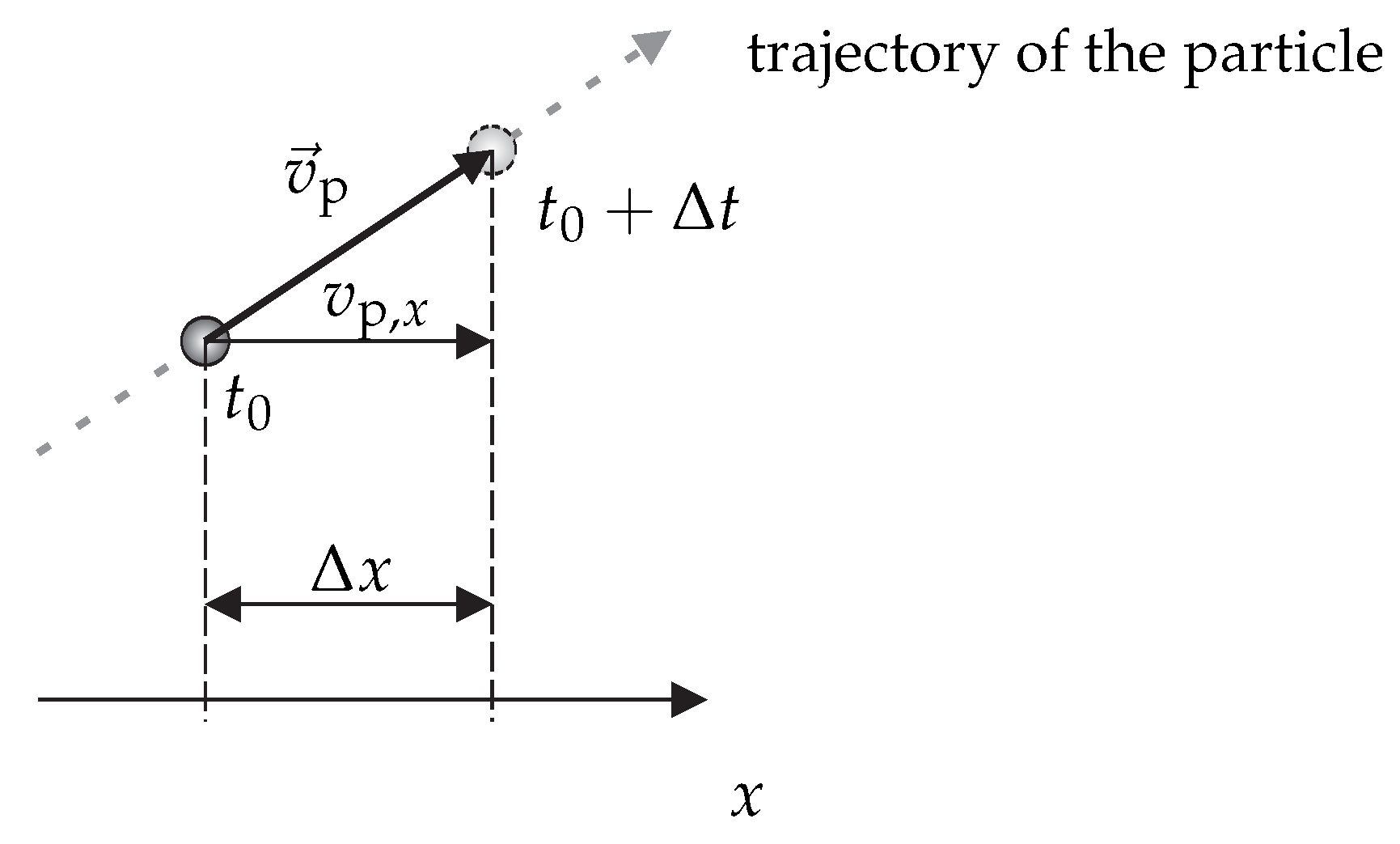
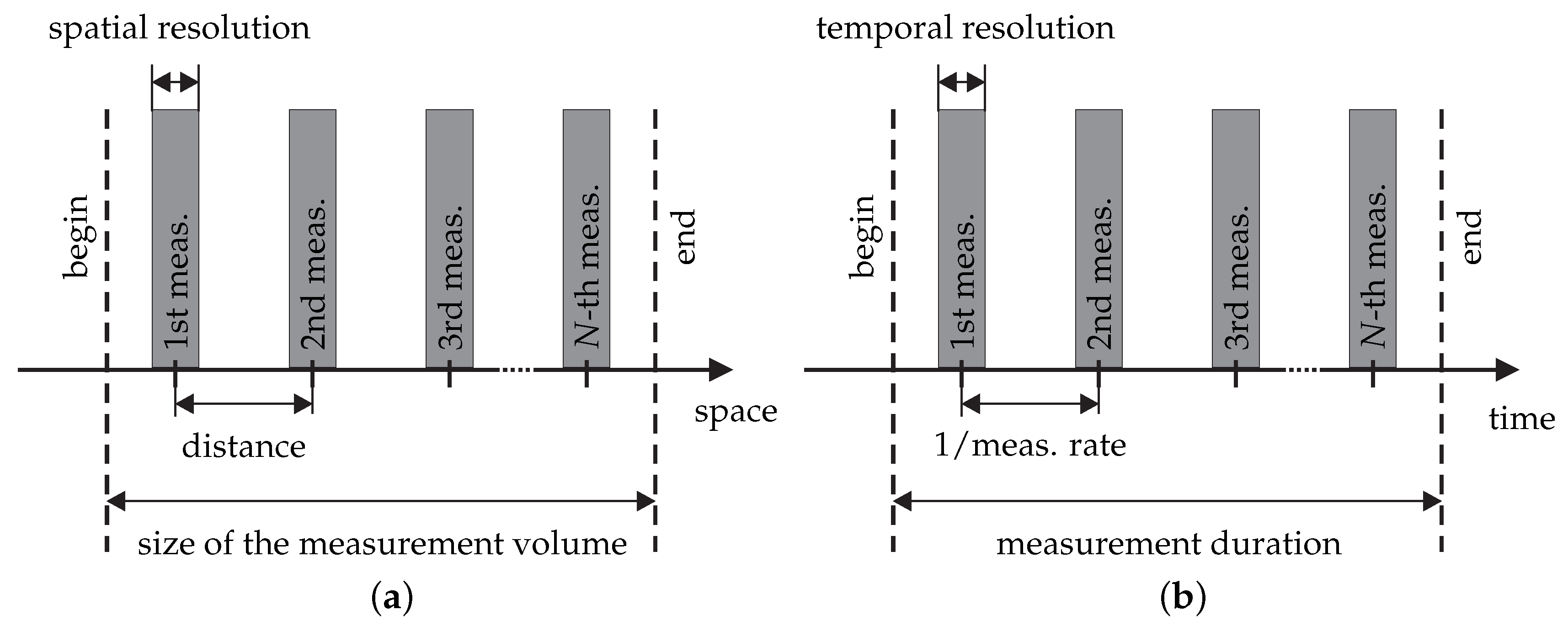
- In order to characterize the spatial behavior of the flow velocity, the number of resolved space dimensions is an important property. Measurements are for instance pointwise, along a line, planar or volumetric, which is indicated by the abbreviated forms 0d, 1d, 2d or 3d, respectively. Characterizing the measurement along each space dimension is possible with the following parameters (cf. Figure 5a):
- -
- spatial resolution,
- -
- spatial distance between the adjacent measurements,
- -
- number of measurements along the respective space dimension or size of the measurement volume in the respective space dimension.
- In addition, the temporal behavior of the measured flow velocity is characterized with the parameters
- -
- temporal resolution,
- -
- temporal distance between the sequent measurements or measurement rate,
- -
- number of measurements along the time dimension or measurement duration.
The term measurement rate requires temporally-equidistant measurements. Otherwise, a mean measurement rate can be specified. The introduced terms are explained in Figure 5b. Note that the temporal resolution does not necessarily equal (or is smaller than) the reciprocal value of the measurement rate. Both quantities are independent. - Each velocity value over space and time can finally be characterized with a measurement uncertainty by applying the international guide to the expression of uncertainty in measurements (GUM) [38,39]. According to the GUM, the measurement uncertainty is a parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurand.
- Due to possible cross-sensitivities (for instance with respect to the temperature, vibrations or electromagnetic fields) or other impairments of the measurements (for instance limited optical access), it is important if the measurements concern non-reactive or reactive flows (flames), if the measurements are performed in a laboratory or in an industrial environment, if the measurement object is a simplified model or the real measurement object. For this reason, the surrounding and boundary conditions have to be described.
3.2. Measurement Techniques Using the Doppler Principle
3.2.1. Amplitude-Based Signal Evaluation
3.2.2. Frequency-Based Signal Evaluation
3.3. Measurement Techniques Using the Time-Of-Flight Principle
3.3.1. Time Measurement
3.3.2. Space Measurement
4. Fundamental Measurement Limits
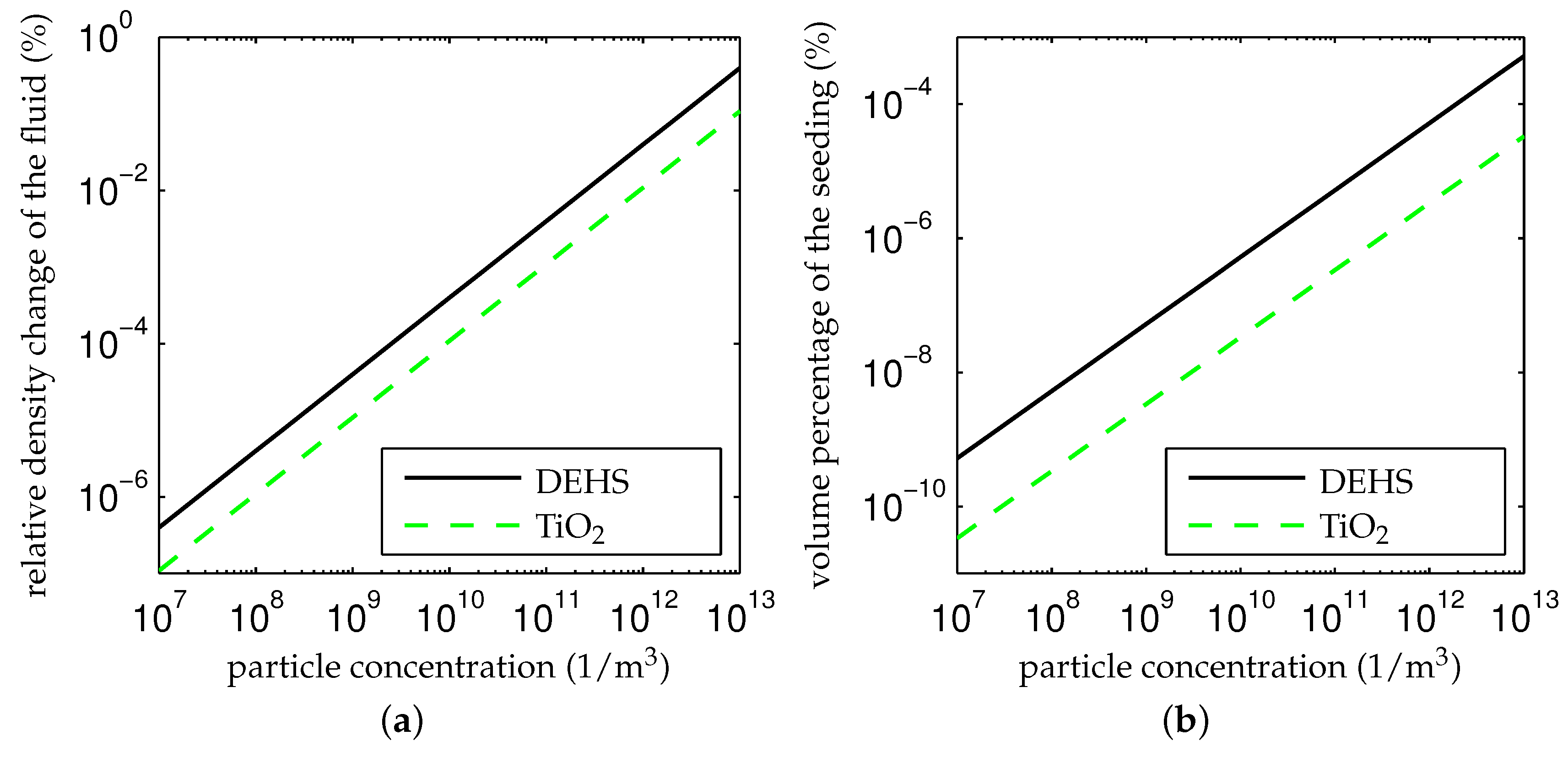
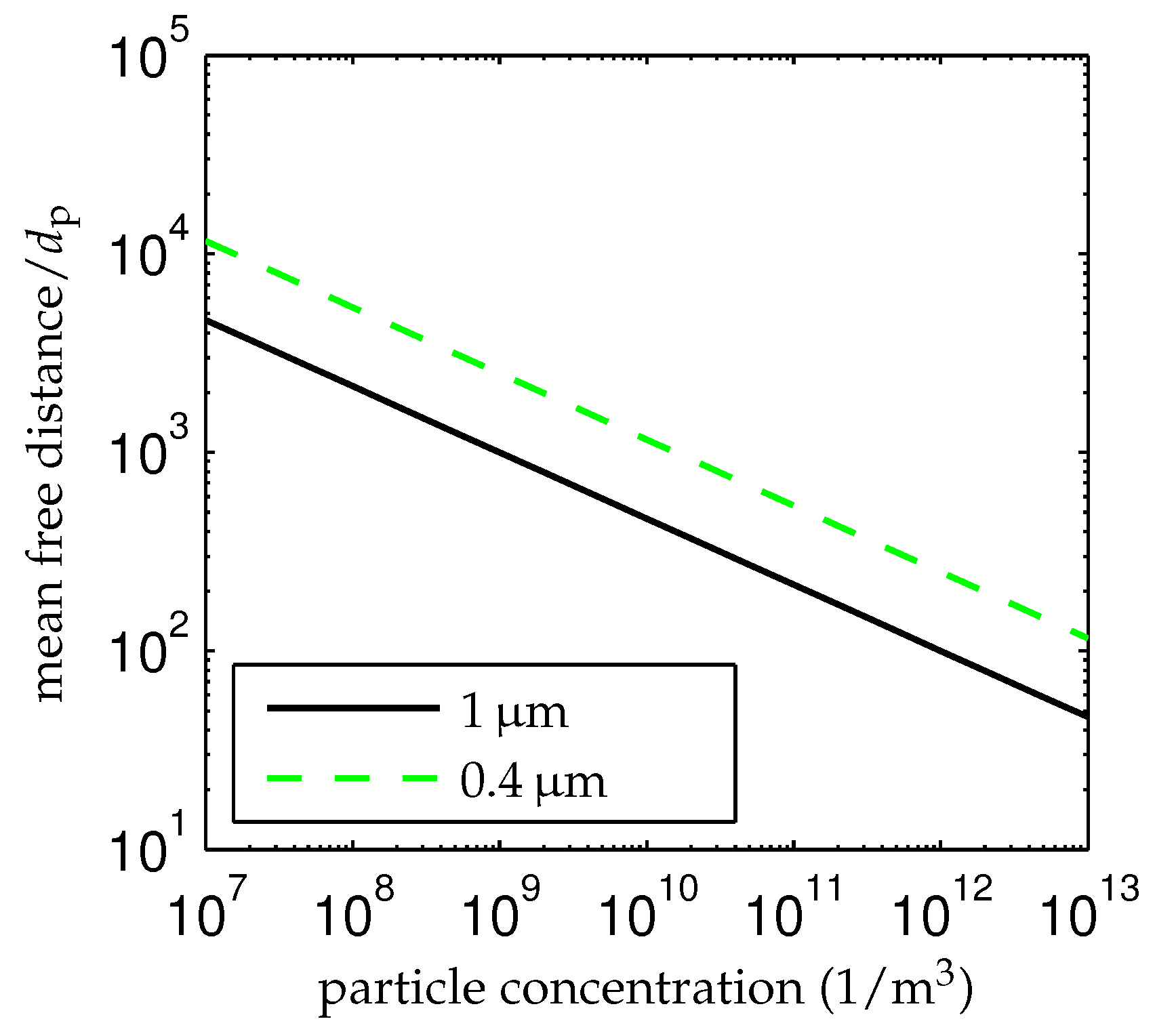
4.1. Seeding
4.1.1. Influence on the Flow
4.1.2. Flow Sampling Phenomenon
4.2. Particle Motion
4.2.1. Flow Following Behavior
4.2.2. Brownian Motion
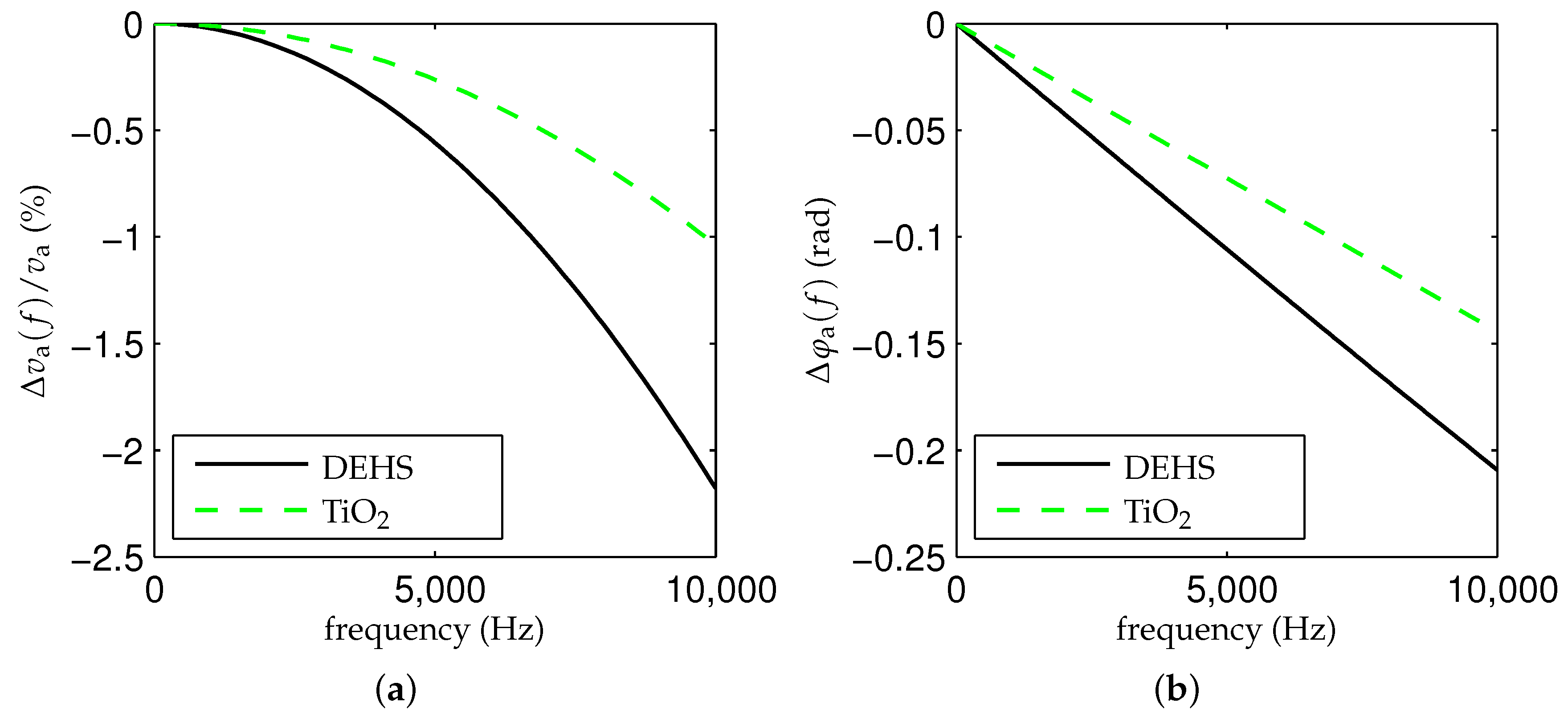
4.2.3. Illumination Effects
4.3. Photon Shot Noise
5. Application Examples, Challenges and Perspectives
6. Conclusions
Conflicts of Interest
References
- Fansler, T.D.; Parrish, S.E. Spray measurement technology: A review. Meas. Sci. Technol. 2015, 26, 012002. [Google Scholar] [CrossRef]
- Nathan, G.J.; Kalt, P.A.M.; Alwahabi, Z.T.; Dally, B.B.; Medwell, P.R.; Chan, Q.N. Recent advances in the measurement of strongly radiating, turbulent reacting flows. Progress Energy Combust. Sci. 2012, 38, 41–61. [Google Scholar] [CrossRef]
- Candel, S.; Durox, D.; Schuller, T.; Bourgouin, J.F.; Moeck, J.P. Dynamics of Swirling Flames. Ann. Rev. Fluid Mech. 2014, 46, 147–173. [Google Scholar] [CrossRef]
- Anderson, R.; Zhang, L.; Ding, Y.; Blanco, M.; Bi, X.P.; Wilkinson, D. A critical review of two-phase flow in gas flow channels of proton exchange membrane fuel cells. J. Power Sources 2010, 195, 4531–4553. [Google Scholar] [CrossRef]
- Barlas, T.K.; van Kuik, G.A.M. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Tucker, P.G. Computation of unsteady turbomachinery flows: Part 1—Progress and challenges. Prog. Aerosp. Sci. 2011, 47, 522–545. [Google Scholar] [CrossRef]
- Pollard, A.; Uddin, M.; Shinneeb, A.M.; Ball, C. Recent advances and key challenges in investigations of the flow inside human oro-pharyngeal-laryngeal airway. Int. J. Comput. Fluid Dyn. 2012, 26, 363–381. [Google Scholar] [CrossRef]
- Ford, M.D.; Nikolov, H.N.; Milner, J.S.; Lownie, S.P.; DeMont, E.M.; Kalata, W.; Loth, F.; Holdsworth, D.W.; Steinman, D.A. PIV-Measured Versus CFD-Predicted Flow Dynamics in Anatomically Realistic Cerebral Aneurysm Models. J. Biomech. Eng. 2008, 130, 021015. [Google Scholar] [CrossRef] [PubMed]
- Roy, C.J.; Blottner, F.G. Review and assessment of turbulence models for hypersonic flows. Prog. Aerosp. Sci. 2006, 42, 469–530. [Google Scholar] [CrossRef]
- Thurow, B.; Jiang, N.; Lempert, W. Review of ultra-high repetition rate laser diagnostics for fluid dynamic measurements. Meas. Sci. Technol. 2013, 24, 012002. [Google Scholar] [CrossRef]
- Forkey, J.N.; Finkelstein, N.D.; Lempert, W.R.; Miles, R.B. Demonstration and characterization of filtered Rayleigh scattering for planar velocity measurements. AIAA J. 1996, 34, 442–448. [Google Scholar] [CrossRef]
- Seasholtz, R.G.; Buggele, A.E.; Reeder, M.F. Flow Measurements Based on Rayleigh Scattering and Fabry-Perot Interferometer. Opt. Laser Eng. 1997, 27, 543–570. [Google Scholar] [CrossRef]
- Grinstead, J.H.; Finkelstein, N.D.; Lempert, W.R. Doppler velocimetry in a supersonic jet by use of frequency-modulated filtered light scattering. Opt. Lett. 1997, 22, 331–333. [Google Scholar] [CrossRef] [PubMed]
- Forkey, J.N.; Lempert, W.R.; Miles, R.B. Accuracy limits for planar measurements of flow field velocity, temperature and pressure using Filtered Rayleigh Scattering. Exp. Fluids 1998, 24, 151–162. [Google Scholar] [CrossRef]
- Mach, J.; Varghese, P.L. Velocity Measurements by Modulated Filtered Rayleigh Scattering Using Diode Lasers. AIAA J. 1999, 37, 695–699. [Google Scholar] [CrossRef]
- Elliott, G.S.; Glumac, N.; Carter, C.D. Molecular filtered Rayleigh scattering applied to combustion. Meas. Sci. Technol. 2001, 12, 452. [Google Scholar] [CrossRef]
- Schroll, M.; Doll, U.; Stockhausen, G.; Meier, U.; Willert, C.; Hassa, C.; Bagchi, I. Flow Field Characterization at the Outlet of a Lean Burn Single-Sector Combustor by Laser-Optical Methods. J. Eng. Gas Turbines Power 2016, 139, 011503. [Google Scholar] [CrossRef]
- Miles, R.B.; Lempert, W.R.; Forkey, J.N. Laser Rayleigh scattering. Meas. Sci. Technol. 2001, 12, R33–R51. [Google Scholar] [CrossRef]
- Doll, U.; Stockhausen, G.; Willert, C. Endoscopic filtered Rayleigh scattering for the analysis of ducted gas flows. Exp. Fluids 2014, 55, 1690. [Google Scholar] [CrossRef]
- Doll, U.; Burow, E.; Stockhausen, G.; Willert, C. Methods to improve pressure, temperature and velocity accuracies of filtered Rayleigh scattering measurements in gaseous flows. Meas. Sci. Technol. 2016, 27, 125204. [Google Scholar] [CrossRef]
- Mielke, A.F.; Elam, K.A.; Sung, S.J. Multiproperty Measurements at High Sampling Rates Using Rayleigh Scattering. AIAA J. 2009, 47, 850–862. [Google Scholar] [CrossRef]
- Chen, L.; Yang, F.R.; Su, T.; Bao, W.Y.; Yan, B.; Chen, S.; Li, R.B. High sampling-rate measurement of turbulence velocity fluctuations in Mach 1.8 Laval jet using interferometric Rayleigh scattering. Chin. Phys. B 2017, 26, 025205. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metalllösungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Dover Publications: New York, NY, USA, 1981. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-VCH Verlag: Weinheim, Germany, 2004. [Google Scholar]
- Albrecht, H.E.; Damaschke, N.; Borys, M.; Tropea, C. Laser Doppler and Phase Doppler Measurement Techniques; Springer: Berlin, Germany, 2003. [Google Scholar]
- Tu, C.; Yin, Z.; Lin, J.; Bao, F. A Review of Experimental Techniques for Measuring Micro- to Nano-Particle-Laden Gas Flows. Appl. Sci. 2017, 7, 120. [Google Scholar] [CrossRef]
- Charrett, T.O.H.; James, S.W.; Tatam, R.P. Optical fibre laser velocimetry: A review. Meas. Sci. Technol. 2012, 23, 032001. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Phys. Chem. 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Drain, L.E. The Laser Doppler Technique; John Wiley & Sons: Chichester, UK, 1980. [Google Scholar]
- Adrian, R.J. Particle-Imaging Techniques for Experimental Fluid Mechanics. Ann. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- Hain, R.; Kähler, C.J. Fundamentals of multiframe particle image velocimetry (PIV). Exp. Fluids 2007, 42, 575–587. [Google Scholar] [CrossRef]
- Cierpka, C.; Lütke, B.; Kähler, C.J. Higher order multi-frame particle tracking velocimetry. Exp. Fluids 2013, 54, 1533. [Google Scholar] [CrossRef]
- Förster, W.; Karpinsky, G.; Krain, H.; Röhle, I.; Schodl, R. 3-Component-Doppler-Laser-Two-Focus velocimetry applied to a transonic centrifugal compressor. In Proceedings of the 10th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 10–13 July 2000; Number 7.2. pp. 1–12. [Google Scholar]
- Wernet, M.P. Planar particle imaging Doppler velocimetry: A hybrid PIV/DGV technique for three-component velocity measurements. Meas. Sci. Technol. 2004, 15, 2011–2028. [Google Scholar] [CrossRef]
- Willert, C.; Hassa, C.; Stockhausen, G.; Jarius, M.; Voges, M.; Klinner, J. Combined PIV and DGV applied to a pressurized gas turbine combustion facility. Meas. Sci. Technol. 2006, 17, 1670–1679. [Google Scholar] [CrossRef]
- Grosjean, N.; Graftieaux, L.; Michard, M.; Hubner, W.; Tropea, C.; Volkert, J. Combining LDA and PIV for turbulence measurements in unsteady swirling flows. Meas. Sci. Technol. 1997, 8, 1523–1532. [Google Scholar] [CrossRef]
- Lira, I. Evaluating the Measurement Uncertainty: Fundamentals and Practical Guidance; Institute of Physics Publishing: Bristol, PA, USA, 2002. [Google Scholar]
- Joint Committee for Guides in Metrology (JCGM). Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. 2008. Available online: www.bipm.org/en/publications/guides/gum.html (accessed on 9 November 2017).
- Jackson, D.A.; Paul, D.M. Measurement of hypersonic velocities and turbulence by direct spectral analysis of Doppler shifted laser light. Phys. Lett. 1970, 32A, 77–78. [Google Scholar] [CrossRef]
- Kentischer, T.J.; Schmidt, W.; Sigwarth, M.; Uexkull, M.V. TESOS, a double Fabry-Perot instrument for solar spectroscopy. Astron. Astrophys. 1998, 340, 569–578. [Google Scholar]
- Büttner, L.; Schlüßler, R.; Fischer, A.; Czarske, J. Multipoint velocity measurements in flows using a Fabry-Pérot interferometer. Opt. Lasers Eng. 2013, 51, 325–333. [Google Scholar] [CrossRef]
- Chehura, E.; Ye, C.C.; Tatam, R.P. In-line laser Doppler velocimeter using fibre-optic Bragg grating interferometric filters. Meas. Sci. Technol. 2003, 14, 724–735. [Google Scholar] [CrossRef]
- Smeets, G.; George, A. Instantaneous laser Doppler velocimeter using a fast wavelength tracking Michelson interferometer. Rev. Sci. Instrum. 1978, 49, 1589. [Google Scholar] [CrossRef] [PubMed]
- Smeets, G.; George, A. Michelson spectrometer for instantaneous Doppler velocity measurements. J. Phys. E Sci. Instrum. 1981, 14, 838–845. [Google Scholar] [CrossRef]
- Oertel, H.; Seiler, F.; George, A. Visualisierung von Geschwindigkeitsfeldern mit Dopplerbildern; Visualization of Velocity Fields With Doppler Pictures; ISL-report R 115/82; Springer: Berlin, Germany, 1982. [Google Scholar]
- Seiler, F.; Oertel, H. Visualization of velocity fields with Doppler-pictures. In Proceedings of the 3rd International Symposium on Flow Visualization, Ann Arbor, MI, USA, 6–9 September 1983. [Google Scholar]
- Seiler, F.; George, A.; Srulijes, J.; Havermann, M. Progress in Doppler picture velocimetry (DPV). Exp. Fluids 2008, 44, 389–395. [Google Scholar] [CrossRef]
- Landolt, A.; Roesgen, T. Anomalous dispersion in atomic line filters applied for spatial frequency detection. Appl. Opt. 2009, 48, 5948–5955. [Google Scholar] [CrossRef] [PubMed]
- Landolt, A.; Rösgen, T. Global Doppler frequency shift detection with near-resonant interferometry. Exp. Fluids 2009, 47, 733–743. [Google Scholar] [CrossRef]
- Lu, Z.H.; Charett, T.O.H.; Ford, H.D.; Tatam, R.P. Mach-Zehnder interferometric filter based planar Doppler velocimetry (MZI-PDV). J. Opt. A Pure Appl. Opt. 2007, 9, 1002–1013. [Google Scholar] [CrossRef]
- Lu, Z.H.; Charett, T.O.H.; Tatam, R.P. Three-component planar velocity measurements using Mach-Zehnder interferometric filter-based planar Doppler velocimetry (MZI-PDV). Meas. Sci. Technol. 2009, 20, 034019. [Google Scholar] [CrossRef]
- Komine, H. System for Measuring Velocity Field of Fluid Flow Utilizing a Laser-Doppler Spectral Image Converter. U.S. Patent 4,919,536, 24 April 1990. [Google Scholar]
- Meyers, J.F. Development of Doppler global velocimetry as a flow diagnostic tool. Meas. Sci. Technol. 1995, 6, 769–783. [Google Scholar] [CrossRef]
- Ainsworth, R.W.; Thorpe, S.J.; Manners, R.J. A new approach to flow-field measurement—A view of Doppler global velocimetry techniques. Int. J. Heat Fluid Flow 1997, 18, 116–130. [Google Scholar] [CrossRef]
- Nobes, D.S.; Ford, H.D.; Tatam, R.P. Instantaneous, three-component planar Doppler velocimetry using imaging fibre bundles. Exp. Fluids 2004, 36, 3–10. [Google Scholar] [CrossRef]
- Röhle, I.; Willert, C.E. Extension of Doppler global velocimetry to periodic flows. Meas. Sci. Technol. 2001, 12, 420–431. [Google Scholar] [CrossRef]
- Charrett, T.O.H.; Bledowski, I.A.; James, S.W.; Tatam, R.P. Frequency division multiplexing for interferometric planar Doppler velocimetry. Appl. Opt. 2014, 53, 4363–4374. [Google Scholar] [CrossRef] [PubMed]
- Willert, C.; Stockhausen, G.; Klinner, J.; Lempereur, C.; Barricau, P.; Loiret, P.; Raynal, J.C. Performance and accuracy investigations of two Doppler global velocimetry systems applied in parallel. Meas. Sci. Technol. 2007, 18, 2504–2512. [Google Scholar] [CrossRef]
- Thurow, B.; Jiang, N.; Lempert, W.; Samimy, M. MHz rate planar Doppler velocimetry in supersonic jets. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2004. Number AIAA-2004-0023. [Google Scholar]
- Bloom, S.H.; Kremer, R.; Searcy, P.A.; Rivers, M.; Menders, J.; Korevaar, E. Long-range, noncoherent laser Doppler velocimeter. Opt. Lett. 1991, 16, 1794–1796. [Google Scholar] [CrossRef] [PubMed]
- Crafton, J.; Messersmith, N.M.; Sullivan, J.P. Filtered Doppler Velocimetry: Development of a Point System. In Proceedings of the 36th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 12–15 January 1998. Number AIAA-98-0509. [Google Scholar]
- Arnette, S.A.; Samimy, M.; Elliot, G.S. Two-component planar Doppler velocimetry in the compressible turbulent boundary layer. Exp. Fluids 1998, 24, 323–332. [Google Scholar] [CrossRef]
- Charrett, T.O.H.; Ford, H.D.; Nobes, D.S.; Tatam, R.P. Two-Frequency Planar Doppler Velocimetry (2-ν-PDV). Rev. Sci. Instrum. 2004, 75, 4487–4496. [Google Scholar] [CrossRef]
- Charrett, T.O.H.; Tatam, R.P. Single camera three component planar velocity measurements using two-frequency planar Doppler velocimetry (2ν-PDV). Meas. Sci. Technol. 2006, 17, 1194–1206. [Google Scholar] [CrossRef]
- Müller, H.; Eggert, M.; Pape, N.; Dopheide, D.; Czarske, J.; Büttner, L.; Razik, T. Time resolved DGV based on laser frequency modulation. Proceeding of the 12th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 12–15 July 2004; Number 25.2. 10p. [Google Scholar]
- Müller, H.; Eggert, M.; Czarske, J.; Büttner, L.; Fischer, A. Single-camera Doppler global velocimetry based on frequency modulation techniques. Exp. Fluids 2007, 43, 223–232. [Google Scholar] [CrossRef]
- Eggert, M.; Müller, H.; Czarske, J.; Büttner, L.; Fischer, A. Self-calibrating Single Camera Doppler Global Velocimetry based on Frequency Shift Keying. In Imaging Measurement Methods for Flow Analysis; Nitsche, W., Dobriloff, C., Eds.; Springer: Berlin, Germany, 2009; pp. 43–52. [Google Scholar]
- Eggert, M.; Müller, H.; Czarske, J.; Büttner, L.; Fischer, A. Self calibrating FSK-Doppler global velocimetry for three-componential time resolved and phase averaged flow field measurements. In Proceedings of the 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 7–10 July 2010; Number 1.11.1. 11p. [Google Scholar]
- Müller, H.; Lehmacher, H.; Grosche, G. Profile sensor based on Doppler Global Velocimetry. In Proceedings of the 8th International Conference Laser Anemometry Advances and Applications, Rome, Italy, 6–8 September 1999; pp. 475–482. [Google Scholar]
- Müller, H.; Pape, N.; Grosche, G.; Strunck, V.; Dopheide, D. Simplified DGV on-line profile sensor. In Proceedings of the 11th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 8–11 July 2002; Number 9.3. 8p. [Google Scholar]
- Fischer, A.; Büttner, L.; Czarske, J.; Eggert, M.; Grosche, G.; Müller, H. Investigation of time-resolved single detector Doppler global velocimetry using sinusoidal laser frequency modulation. Meas. Sci. Technol. 2007, 18, 2529–2545. [Google Scholar] [CrossRef]
- Fischer, A.; Büttner, L.; Czarske, J.; Eggert, M.; Müller, H. Measurement uncertainty and temporal resolution of Doppler global velocimetry using laser frequency modulation. Appl. Opt. 2008, 47, 3941–3953. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.; Büttner, L.; Czarske, J.; Eggert, M.; Müller, H. Array Doppler global velocimeter with laser frequency modulation for turbulent flow analysis—Sensor investigation and application. In Imaging Measurement Methods for Flow Analysis; Nitsche, W., Dobriloff, C., Eds.; Springer: Berlin, Germany, 2009; pp. 31–41. [Google Scholar]
- Cadel, D.R.; Lowe, K.T. Cross-correlation Doppler global velocimetry (CC-DGV). Opt. Lasers Eng. 2015, 71, 51–61. [Google Scholar] [CrossRef]
- Cadel, D.R.; Lowe, K.T. Investigation of measurement sensitivities in cross-correlation Doppler global velocimetry. Opt. Lasers Eng. 2016, 86, 44–52. [Google Scholar] [CrossRef]
- Fischer, A.; Büttner, L.; Czarske, J. Simultaneous measurements of multiple flow velocity components using frequency modulated lasers and a single molecular absorption cell. Opt. Commun. 2011, 284, 3060–3064. [Google Scholar] [CrossRef]
- Fischer, A.; Kupsch, C.; Gürtler, J.; Czarske, J. High-speed light field camera and frequency division multiplexing for fast multi-plane velocity measurements. Opt. Express 2015, 23, 24910. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A. Model-based review of Doppler global velocimetry techniques with laser frequency modulation. Opt. Lasers 2017, 93, 19–35. [Google Scholar] [CrossRef]
- Fischer, A.; Büttner, L.; Czarske, J.; Eggert, M.; Müller, H. Measurements of velocity spectra using time-resolving Doppler global velocimetry with laser frequency modulation and a detector array. Exp. Fluids 2009, 47, 599–611. [Google Scholar] [CrossRef]
- Fischer, A.; König, J.; Haufe, D.; Schlüßler, R.; Büttner, L.; Czarske, J. Optical multi-point measurements of the acoustic particle velocity with frequency modulated Doppler global velocimetry. J. Acoust. Soc. Am. 2013, 134, 1102–1111. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.; Wilke, U.; Schlüßler, R.; Haufe, D.; Sandner, T.; Czarske, J. Extension of frequency modulated Doppler global velocimetry for the investigation of unsteady spray flows. Opt. Lasers Eng. 2014, 63, 1–10. [Google Scholar] [CrossRef]
- Fischer, A.; Schlüßler, R.; Haufe, D.; Czarske, J. Lock-in spectroscopy employing a high-speed camera and a micro-scanner for volumetric investigations of unsteady flows. Opt. Lett. 2014, 39, 5082–5085. [Google Scholar] [CrossRef] [PubMed]
- Schlüßler, R.; Gürtler, J.; Czarske, J.; Fischer, A. Planar near-nozzle velocity measurements during a single high-pressure fuel injection. Exp. Fluids 2015, 56, 176. [Google Scholar] [CrossRef]
- Gürtler, J.; Haufe, D.; Schulz, A.; Bake, F.; Enghardt, L.; Czarske, J.; Fischer, A. High-speed camera-based measurement system for aeroacoustic investigations. J. Sens. Sens. Syst. 2016, 5, 125–136. [Google Scholar] [CrossRef]
- Gürtler, J.; Schlüßler, R.; Fischer, A.; Czarske, J. High-speed non-intrusive measurements of fuel velocity fields at high pressure injectors. Opt. Lasers Eng. 2017, 90, 91–100. [Google Scholar] [CrossRef]
- Yeh, Y.; Cummins, H.Z. Localized Fluid Flow Measurements with an He-Ne Laser Spectrometer. Appl. Phys. Lett. 1964, 4, 176–178. [Google Scholar] [CrossRef]
- Li, C.H.; Benedick, A.J.; Fendel, P.; Glenday, A.G.; Kartner, F.X.; Phillips, D.F.; Sasselov, D.; Szentgyorgyi, A.; Walsworth, R.L. A laser frequency comb that enables radial velocity measurements with a precision of 1 cm s−1. Nature 2008, 452, 610–612. [Google Scholar] [CrossRef] [PubMed]
- Coupland, J. Coherent detection in Doppler global velocimetry: a simplified method to measure subsonic fluid flow fields. Appl. Opt. 2000, 39, 1505–1510. [Google Scholar] [CrossRef] [PubMed]
- Meier, A.H.; Rösgen, T. Heterodyne Doppler global velocimetry. Exp. Fluids 2009, 47, 665–672. [Google Scholar] [CrossRef]
- Tropea, C. Laser Doppler anemometry: recent developments and future challenges. Meas. Sci. Technol. 1995, 6, 605–619. [Google Scholar] [CrossRef]
- Czarske, J.W. Laser Doppler velocimetry using powerful solid-state light sources. Meas. Sci. Technol. 2006, 17, R71–R91. [Google Scholar] [CrossRef]
- Czarske, J. Laser Doppler velocity profile sensor using a chromatic coding. Meas. Sci. Technol. 2001, 12, 52–57. [Google Scholar] [CrossRef]
- Czarske, J.; Büttner, L.; Razik, T.; Müller, H. Boundary layer velocity measurements by a laser Doppler profile sensor with micrometre spatial resolution. Meas. Sci. Technol. 2002, 13, 1979–1989. [Google Scholar] [CrossRef]
- Voigt, A.; Bayer, C.; Shirai, K.; Büttner, L.; Czarske, J. Laser Doppler field sensor for high resolution flow velocity imaging without camera. Appl. Opt. 2008, 47, 5028–5040. [Google Scholar] [CrossRef] [PubMed]
- Meier, A.H.; Rösgen, T. Imaging laser Doppler velocimetry. Exp. Fluids 2012, 52, 1017–1026. [Google Scholar] [CrossRef]
- Thompson, D.H. A tracer-particle fluid velocity meter incorporating a laser. J. Phys. E Sci. Instrum. 1968, 1, 929–932. [Google Scholar] [CrossRef]
- Tanner, L. A particle timing laser velocity meter. Opt. Laser Technol. 1973, 5, 108–110. [Google Scholar] [CrossRef]
- Schodl, R. A Laser-Two-Focus (L2F) Velocimeter for Automatic Flow Vector Measurements in the Rotating Components of Turbomachines. J. Fluids Eng. 1980, 102, 412–419. [Google Scholar] [CrossRef]
- Ator, J.T. Image-velocity sensing with parallel-slit reticles. J. Opt. Soc. Am. 1963, 53, 1416–1419. [Google Scholar] [CrossRef]
- Gaster, M. A new technique for the measurement of low fluid velocities. J. Fluid Mech. 1964, 20, 183–192. [Google Scholar] [CrossRef]
- Aizu, Y.; Asakura, T. Principles and development of spatial filtering velocimetry. Appl. Phys. B Lasers Opt. 1987, 43, 209–224. [Google Scholar] [CrossRef]
- Aizu, Y.; Asakura, T. Spatial Filtering Velocimetry: Fundamentals and Applications; Springer: Berlin, Germany, 2006. [Google Scholar]
- Christofori, K.; Michel, K. Velocimetry with spatial filters based on sensor arrays. Flow Meas. Instrum. 1996, 7, 265–272. [Google Scholar] [CrossRef]
- Michel, K.C.; Fiedler, O.F.; Richter, A.; Christofori, K.; Bergeler, S. A Novel Spatial Filtering Velocimeter Based on a Photodetector Array. IEEE Trans. Instrum. Meas. 1998, 47, 299–304. [Google Scholar] [CrossRef]
- Bergeler, S.; Krambeer, H. Novel optical spatial filtering methods based on two-dimensional photodetector arrays. Meas. Sci. Technol. 2004, 15, 1309–1315. [Google Scholar] [CrossRef]
- Schaeper, M.; Damaschke, N. Fourier-based layout for grating function structure in spatial filtering velocimetry. Meas. Sci. Technol. 2017, 28, 055008. [Google Scholar] [CrossRef]
- Pau, S.; Dallas, W.J. Generalized spatial filtering velocimetry and accelerometry for uniform and nonuniform objects. Appl. Opt. 2009, 48, 4713–4722. [Google Scholar] [CrossRef] [PubMed]
- Hosokawa, S.; Mastumoto, T.; Tomiyama, A. Tomographic spatial filter velocimetry for three-dimensional measurement of fluid velocity. Exp. Fluids 2013, 54, 1597. [Google Scholar] [CrossRef]
- Schaeper, M.; Damaschke, N. Velocity Measurement for Moving Surfaces by Using Spatial Filtering Technique Based on Array Detectors. In Proceedings of the AIS: International Conference on Autonomous and Intelligent Systems, Povoa de Varzim, Portugal, 21–23 June 2011; pp. 303–310. [Google Scholar]
- Adrian, R.J. Scattering particle characteristics and their effect on pulsed laser measurements of fluid flow: Speckle velocimetry vs. particle image velocimetry. Appl. Opt. 1984, 23, 1690–1691. [Google Scholar] [CrossRef] [PubMed]
- Adrian, R.J. Twenty years of particle image velocimetry. Exp. Fluids 2005, 39, 159–169. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry; Springer: Berlin, Germany, 2018. [Google Scholar]
- Willert, C.; Stasicki, B.; Klinner, J.; Moessner, S. Pulsed operation of high-power light emitting diodes for imaging flow velocimetry. Meas. Sci. Technol. 2010, 21, 075402. [Google Scholar] [CrossRef]
- Wernet, M.P. Temporally resolved PIV for space-time correlations in both cold and hot jet flows. Meas. Sci. Technol. 2007, 18, 1387–1403. [Google Scholar] [CrossRef]
- Arroyo, M.P.; Greated, C.A. Stereoscopic particle image velocimetry. Meas. Sci. Technol. 1991, 2, 1181–1186. [Google Scholar] [CrossRef]
- Boxx, I.; Stöhr, M.; Carter, C.; Meier, W. Sustained multi-kHz flamefront and 3-component velocity-field measurements for the study of turbulent flames. Appl. Phys. B 2009, 95, 23–29. [Google Scholar] [CrossRef]
- Boxx, I.; Arndt, C.M.; Carter, C.D.; Meier, W. High-speed laser diagnostics for the study of flame dynamics in a lean premixed gas turbine model combustor. Exp. Fluids 2012, 52, 555–567. [Google Scholar] [CrossRef]
- Boxx, I.; Carter, C.D.; Stöhr, M.; Meier, W. Study of the mechanisms for flame stabilization in gas turbine model combustors using kHz laser diagnostics. Exp. Fluids 2013, 54, 1532. [Google Scholar] [CrossRef]
- Scarano, F. Tomographic PIV: Principles and practice. Meas. Sci. Technol. 2013, 24, 012001. [Google Scholar] [CrossRef]
- Hinsch, K.D. Holographic particle image velocimetry. Meas. Sci. Technol. 2002, 13, R61–R72. [Google Scholar] [CrossRef]
- Buchmann, N.A.; Atkinson, C.; Soria, J. Ultra-high-speed tomographic digital holographic velocimetry in supersonic particle-laden jet flows. Meas. Sci. Technol. 2013, 24, 024005. [Google Scholar] [CrossRef]
- Cenedese, A.; Cenedese, C.; Furia, F.; Marchetti, M.; Moroni, M.; Shindler, L. 3D particle reconstruction using light field imaging. In Proceedings of the 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 9–12 July 2012; Number 1.1.2. 9p. [Google Scholar]
- Belden, J.; Truscott, T.T.; Axiak, M.C.; Techet, A.H. Three-dimensional synthetic aperture particle image velocimetry. Meas. Sci. Technol. 2010, 21, 125403. [Google Scholar] [CrossRef]
- Fahringer, T.W.; Lynch, K.P.; Thurow, B.S. Volumetric particle image velocimetry with a single plenoptic camera. Meas. Sci. Technol. 2015, 26, 115201. [Google Scholar] [CrossRef]
- Deem, E.; Zhang, Y.; Cattafesta, L.; Fahringer, T.; Thurow, B. On the resolution of plenoptic PIV. Meas. Sci. Technol. 2016, 27, 084003. [Google Scholar] [CrossRef]
- Wernet, M.P. Two-dimensional particle displacement tracking in particle imaging velocimetry. Appl. Opt. 1991, 30, 1839–1846. [Google Scholar] [CrossRef] [PubMed]
- Maas, H.G.; Gruen, A.; Papantoniou, D. Particle tracking velocimetry in three-dimensional flows—Part 1: Photogrammetric determination of particle coordinates. Exp. Fluids 1993, 15, 133–146. [Google Scholar] [CrossRef]
- Malik, N.A.; Dracos, T.; Papantoniou, D.A. Particle tracking velocimetry in three-dimensional flows—Part II: Particle tracking. Exp. Fluids 1993, 15, 279–294. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Three-dimensional particle imaging with a single camera. Exp. Fluids 1992, 12, 353–358. [Google Scholar] [CrossRef]
- Stolz, W.; Köhler, J. In-plane determination of 3D-velocity vectors using particle tracking anemometry (PTA). Exp. Fluids 1994, 17, 105–109. [Google Scholar] [CrossRef]
- Cierpka, C.; Segura, R.; Hain, R.; Köhler, C.J. A simple single camera 3C3D velocity measurement technique without errors due to depth of correlation and spatial averaging for microfluidics. Meas. Sci. Technol. 2010, 21, 045401. [Google Scholar] [CrossRef]
- Kreizer, M.; Ratner, D.; Liberzon, A. Real-time image processing for particle tracking velocimetry. Exp. Fluids 2010, 48, 105–110. [Google Scholar] [CrossRef]
- Kreizer, M.; Liberzon, A. Three-dimensional particle tracking method using FPGA-based real-time image processing and four-view image splitter. Exp. Fluids 2011, 50, 613–620. [Google Scholar] [CrossRef]
- Buchmann, N.A.; Cierpka, C.; Köhler, C.J.; Soria, J. Ultra-high-speed 3D astigmatic particle tracking velocimetry: Application to particle-laden supersonic impinging jets. Exp. Fluids 2014, 55, 1842. [Google Scholar] [CrossRef]
- Willert, C.; Stockhausen, G.; Beversdorff, M.; Klinner, J.; Lempereur, C.; Barricau, P.; Quest, J.; Jansen, U. Application of Doppler global velocimetry in cryogenic wind tunnels. Exp. Fluids 2005, 39, 420–430. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- McKenzie, R.L. Measurement capabilities of planar Doppler velocimetry using pulsed lasers. Appl. Opt. 1996, 35, 948–964. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.; Haufe, D.; Büttner, L.; Czarske, J. Scattering effects at near-wall flow measurements using Doppler global velocimetry. Appl. Opt. 2011, 50, 4068–4082. [Google Scholar] [CrossRef] [PubMed]
- Shirai, K.; Pfister, T.; Büttner, L.; Czarske, J.; Müller, H.; Becker, S.; Lienhart, H.; Durst, F. Highly spatially resolved velocity measurements of a turbulent channel flow by a fiber-optic heterodyne laser-Doppler velocity-profile sensor. Exp. Fluids 2006, 40, 473–481. [Google Scholar] [CrossRef]
- Woisetschläger, J.; Göttlich, E. Recent Applications of Particle Image Velocimetry to Flow Research in Thermal Turbomachinery. In Particle Image Velocimetry; Topics in Applied Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 112, pp. 311–331. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Durst, F.; Martinuzzi, R.; Sender, J.; Thevenin, D. LDA-Measurements of Mean Velocity, RMS-Values and Higher Order Moments of Turbulence Intensity Fluctuations in Flow Fields with Strong Velocity Gradients. In Proceedings of the 6th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 20–23 July 1992; Number S5-1. 6p. [Google Scholar]
- Durst, F.; Jovanović, J.; Sender, J. LDA measurements in the near-wall region of a turbulent pipe flow. J. Fluid Mech. 1995, 295, 305–355. [Google Scholar] [CrossRef]
- Fischer, M.; Jovanović, J.; Durst, F. Near-wall behaviour of statistical properties in turbulent Fows. Int. J. Heat Fluid Flow 2000, 21, 471–479. [Google Scholar] [CrossRef]
- Nobach, H. Influence of individual variations of particle image intensities on high-resolution PIV. Exp. Fluids 2011, 50, 919–927. [Google Scholar] [CrossRef]
- Basset, A.B. Treatise on Hydrodynamics; Deighton Bell & Co.: Cambridge, UK, 1888; Volume 2. [Google Scholar]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Durst, F.; Melling, A.; Whitelaw, J.H. Principles and Practice of Laser-Doppler Anemometry; Academic Press: London, UK, 1981. [Google Scholar]
- Mei, R. Velocity fidelity of flow tracer particles. Exp. Fluids 1996, 22, 1–13. [Google Scholar] [CrossRef]
- Crowe, C.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Melling, A. Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1406–1416. [Google Scholar] [CrossRef]
- Hjelmfelt, A.T.; Mockros, L.F. Motion of discrete particles in a turbulent fluid. App. Sci. Res. 1966, 16, 149–161. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of Brownian motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Wang, M.C.; Uhlenbeck, G.E. On the theory of Brownian motion II. Rev. Mod. Phys. 1945, 17, 323–342. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation: With Applications in Physics, Chemistry, and Electrical Engineering; World Scientific Publishing: Singapore, 1996. [Google Scholar]
- Durst, F.; Ruck, B. Influence of laser radiation on particle properties, Part 1: Influence of radiation pressure on the particle motion. tm—Technisches Messen 1980, 47, 230–233. (In German) [Google Scholar]
- Durst, F.; Ruck, B. Influence of laser radiation on particle properties, Part 2: Particle heating by radiation absorption. tm—Technisches Messen 1980, 47, 267–272. (In German) [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Cramer, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Schervish, M.J. Theory of Statistics; Springer: Berlin, Germany, 1997. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury Press: Belmont, CA, USA, 1990. [Google Scholar]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Fischer, A. Fundamental uncertainty limit of optical flow velocimetry according to Heisenberg’s uncertainty principle. Appl. Opt. 2016, 55, 8787–8795. [Google Scholar] [CrossRef] [PubMed]
- Fischer, A.; Czarske, J. Signal processing efficiency of Doppler global velocimetry with laser frequency modulation. Opt. Int. J. Light Electron Opt. 2010, 121, 1891–1899. [Google Scholar] [CrossRef]
- Fischer, A.; Pfister, T.; Czarske, J. Derivation and comparison of fundamental uncertainty limits for laser-two-focus velocimetry, laser Doppler anemometry and Doppler global velocimetry. Measurement 2010, 43, 1556–1574. [Google Scholar] [CrossRef]
- Rife, D.C.; Boorstyn, R.R. Single-tone parameter estimation from discrete-time observations. IEEE Trans. Inf. Theory 1974, 20, 591–598. [Google Scholar] [CrossRef]
- Besson, O.; Galtier, F. Estimating Particles Velocity from Laser Measurements: Maximum Likelihood and Cramér-Rao Bounds. IEEE Trans. Signal Process. 1996, 12, 3056–3068. [Google Scholar] [CrossRef]
- Shu, W.Q. Cramér-Rao Bound of Laser Doppler Anemometer. IEEE Trans. Instrum. Meas. 2001, 50, 1770–1772. [Google Scholar]
- Sobolev, V.S.; Feshenko, A.A. Accurate Cramer-Rao Bounds for a Laser Doppler Anemometer. IEEE Trans. Instrum. Meas. 2006, 55, 659–665. [Google Scholar] [CrossRef]
- Oliver, C.J. Accuracy in laser anemometry. J. Phys. D Appl. Phys. 1980, 13, 1145–1159. [Google Scholar] [CrossRef]
- Lading, L. Estimating time and time-lag in time-of-flight velocimetry. Appl. Opt. 1983, 22, 3637–3643. [Google Scholar] [CrossRef] [PubMed]
- Lading, L.; Jørgensen, T.M. Maximizing the information transfer in a quantum-limited light-scattering system. J. Opt. Soc. Am. A 1990, 7, 1324–1331. [Google Scholar] [CrossRef]
- Wernet, M.P.; Pline, A. Particle displacement tracking technique and Cramer-Rao lower bound error in centroid estimates from CCD imagery. Exp. Fluids 1993, 15, 295–307. [Google Scholar] [CrossRef]
- Fischer, A. Messbarkeitsgrenzen Optischer Strömungsmessverfahren: Theorie und Anwendungen; Shaker: Aachen, Germany, 2013. (In German) [Google Scholar]
- Westerweel, J. Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1379–1392. [Google Scholar] [CrossRef]
- Westerweel, J. Theoretical analysis of the measurement precision in particle image velocimetry. Exp. Fluids 2000, 29 (Suppl. S1), S3–S12. [Google Scholar] [CrossRef]
- Schröder, A.; Willert, C.E. Particle Image Velocimetry: New Developments and Recent Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Meyers, J.F.; Lee, J.W.; Cavone, A.A. Boundary layer measurements in a supersonic wind tunnel using Doppler global velocimetry. In Proceedings of the 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 7–10 July 2010; Number 1.8.1. 11p. [Google Scholar]
- Kähler, C.J.; Scharnowski, S.; Cierpka, C. On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 2012, 52, 1641–1656. [Google Scholar] [CrossRef]
- Fischer, A.; König, J.; Czarske, J.; Rakenius, C.; Schmid, G.; Schiffer, H.P. Investigation of the tip leakage flow at turbine rotor blades with squealer. Exp. Fluids 2013, 54, 1462. [Google Scholar] [CrossRef]
- Voges, M.; Willert, C.; Mönig, R.; Müller, M.W.; Schiffer, H.P. The challenge of stereo PIV measurements in the tip gap of a transonic compressor rotor with casing treatment. Exp. Fluids 2010, 52, 581–590. [Google Scholar] [CrossRef]
- Voges, M.; Schnell, R.; Willert, C.; Mönig, R.; Müller, M.W.; Zscherp, C. Investigation of Blade Tip Interaction With Casing Treatment in a Transonic Compressor – Part I: Particle Image Velocimetry. J. Turbomach. 2011, 133, 011007. [Google Scholar] [CrossRef]
- Schlüßler, R.; Blechschmidt, C.; Czarske, J.; Fischer, A. Optimizations for optical velocity measurements in narrow gaps. Opt. Eng. 2013, 52, 094101. [Google Scholar] [CrossRef]
- Sciacchitano, A.; Scarano, F. Elimination of PIV light reflections via a temporal high pass filter. Meas. Sci. Technol. 2014, 25, 084009. [Google Scholar] [CrossRef]
- Schodl, R.; Röhle, I.; Willert, C.; Fischer, M.; Heinze, J.; Laible, C.; Schilling, T. Doppler global velocimetry for the analysis of combustor flows. Aerosp. Sci. Technol. 2002, 6, 481–493. [Google Scholar] [CrossRef]
- Fischer, A.; König, J.; Czarske, J.; Peterleithner, J.; Woisetschläger, J.; Leitgeb, T. Analysis of flow and density oscillations in a swirl-stabilized flame employing highly resolving optical measurement techniques. Exp. Fluids 2013, 54, 1622. [Google Scholar] [CrossRef]
- Schlüßler, R.; Bermuske, M.; Czarske, J.; Fischer, A. Simultaneous three-component velocity measurements in a swirl-stabilized flame. Exp. Fluids 2015, 56, 183. [Google Scholar] [CrossRef]
- Stöhr, M.; Boxx, I.; Carter, C.; Meier, W. Experimental study of vortex-flame interaction in a gas turbine model combustor. Combust. Flame 2012, 159, 2636–2649. [Google Scholar] [CrossRef]
- Tokarev, M.P.; Sharaborin, D.K.; Lobasov, A.S.; Chikishev, L.M.; Dulin, V.M.; Markovich, D.M. 3D velocity measurements in a premixed flame by tomographic PIV. Meas. Sci. Technol. 2015, 26, 064001. [Google Scholar] [CrossRef]
- Stella, A.; Guj, G.; Kompenhans, J.; Raffel, M.; Richard, H. Application of particle image velocimetry to combusting flows: Design considerations and uncertainty assessment. Exp. Fluids 2001, 30, 167–180. [Google Scholar] [CrossRef]
- Elsinga, G.E.; van Oudheusden, B.W.; Scarano, F. Evaluation of aero-optical distortion effects in PIV. Exp. Fluids 2005, 39, 246–256. [Google Scholar] [CrossRef]
- Schlüßler, R.; Czarske, J.; Fischer, A. Uncertainty of flow velocity measurements due to refractive index fluctuations. Opt. Lasers Eng. 2014, 54, 93–104. [Google Scholar] [CrossRef]
- Cao, Z.M.; Nishino, K.; Mizuno, S.; Torii, K. PIV measurement of internal structure of diesel fuel spray. Exp. Fluids 2000, 29, S211–S219. [Google Scholar] [CrossRef]
- Zhu, J.; Kuti, O.A.; Nishida, K. An investigation of the effects of fuel injection pressure, ambient gas density and nozzle hole diameter on surrounding gas flow of a single diesel spray by the laser-induced fluorescence-particle image velocimetry technique. Int. J. Engine Res. 2012, 14, 630–645. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, M.; Hung, D.L.S. Simultaneous two-phase flow measurement of spray mixing process by means of high-speed two-color PIV. Meas. Sci. Technol. 2014, 25, 095204. [Google Scholar] [CrossRef]
- Rulliere, C. (Ed.) Femtosecond Laser Pulses; Springer: Berlin, Germany, 2005. [Google Scholar]
| Material | (kg/m) | (m) |
|---|---|---|
| diethylhexyl sebacate (DEHS) | 912 | 1 |
| titanium dioxide (TiO) | 3900 | 0.4 |
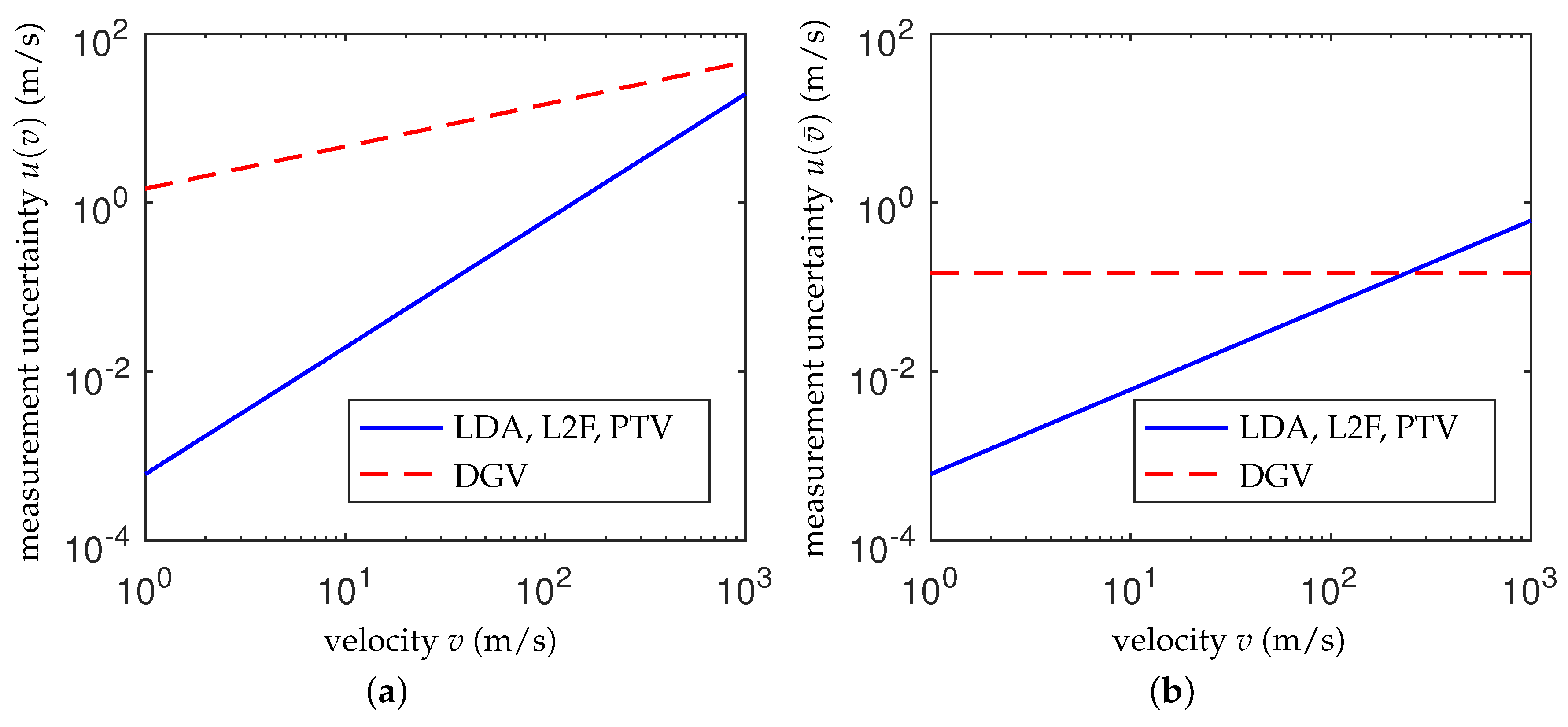
| for a Single Particle | for Multiple Particles | ||
|---|---|---|---|
| DGV | |||
| LDA | |||
| L2F | |||
| PTV |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, A. Imaging Flow Velocimetry with Laser Mie Scattering. Appl. Sci. 2017, 7, 1298. https://doi.org/10.3390/app7121298
Fischer A. Imaging Flow Velocimetry with Laser Mie Scattering. Applied Sciences. 2017; 7(12):1298. https://doi.org/10.3390/app7121298
Chicago/Turabian StyleFischer, Andreas. 2017. "Imaging Flow Velocimetry with Laser Mie Scattering" Applied Sciences 7, no. 12: 1298. https://doi.org/10.3390/app7121298
APA StyleFischer, A. (2017). Imaging Flow Velocimetry with Laser Mie Scattering. Applied Sciences, 7(12), 1298. https://doi.org/10.3390/app7121298





