Automatic Transcription of Polyphonic Vocal Music †
Abstract
1. Introduction
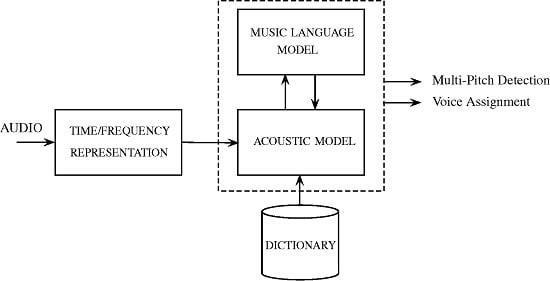
2. Proposed Method
2.1. Acoustic Model
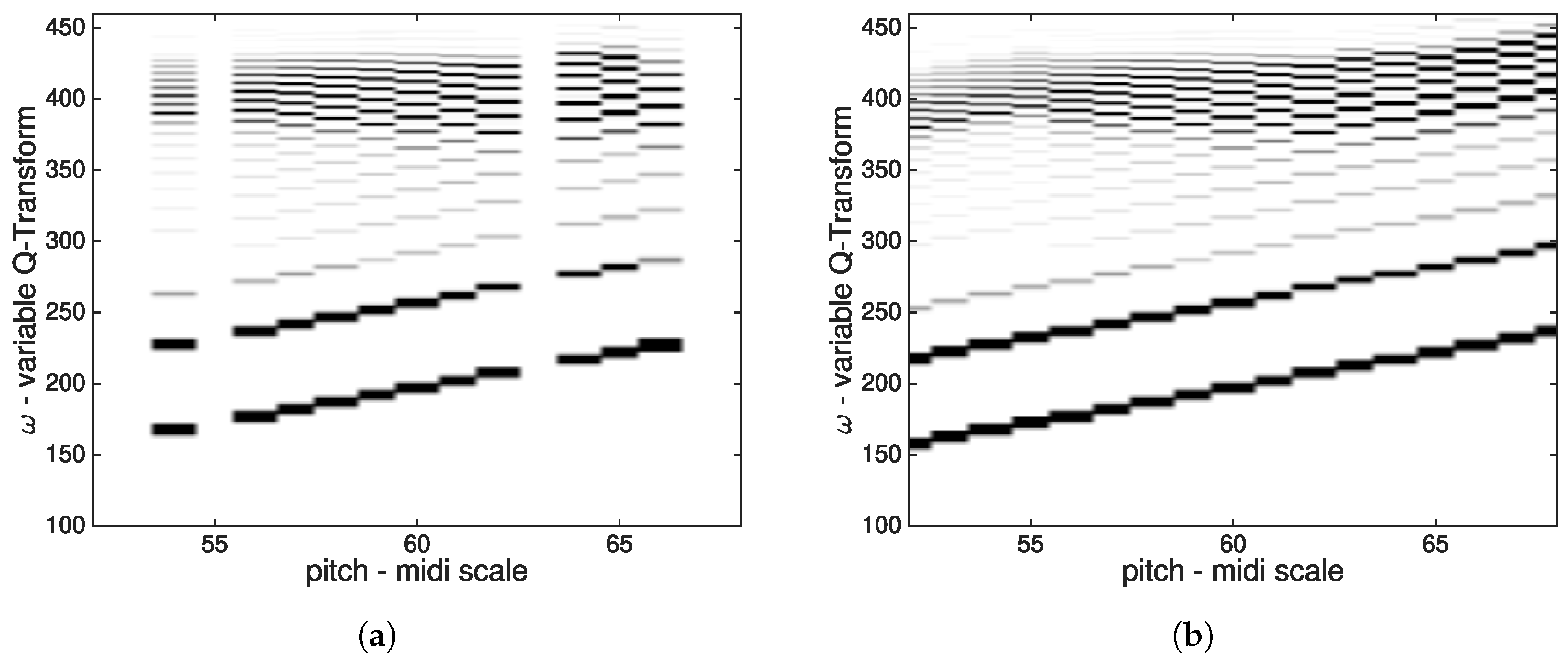
2.1.1. Acoustic Model Output
2.1.2. Dictionary Extraction
2.2. Music Language Model
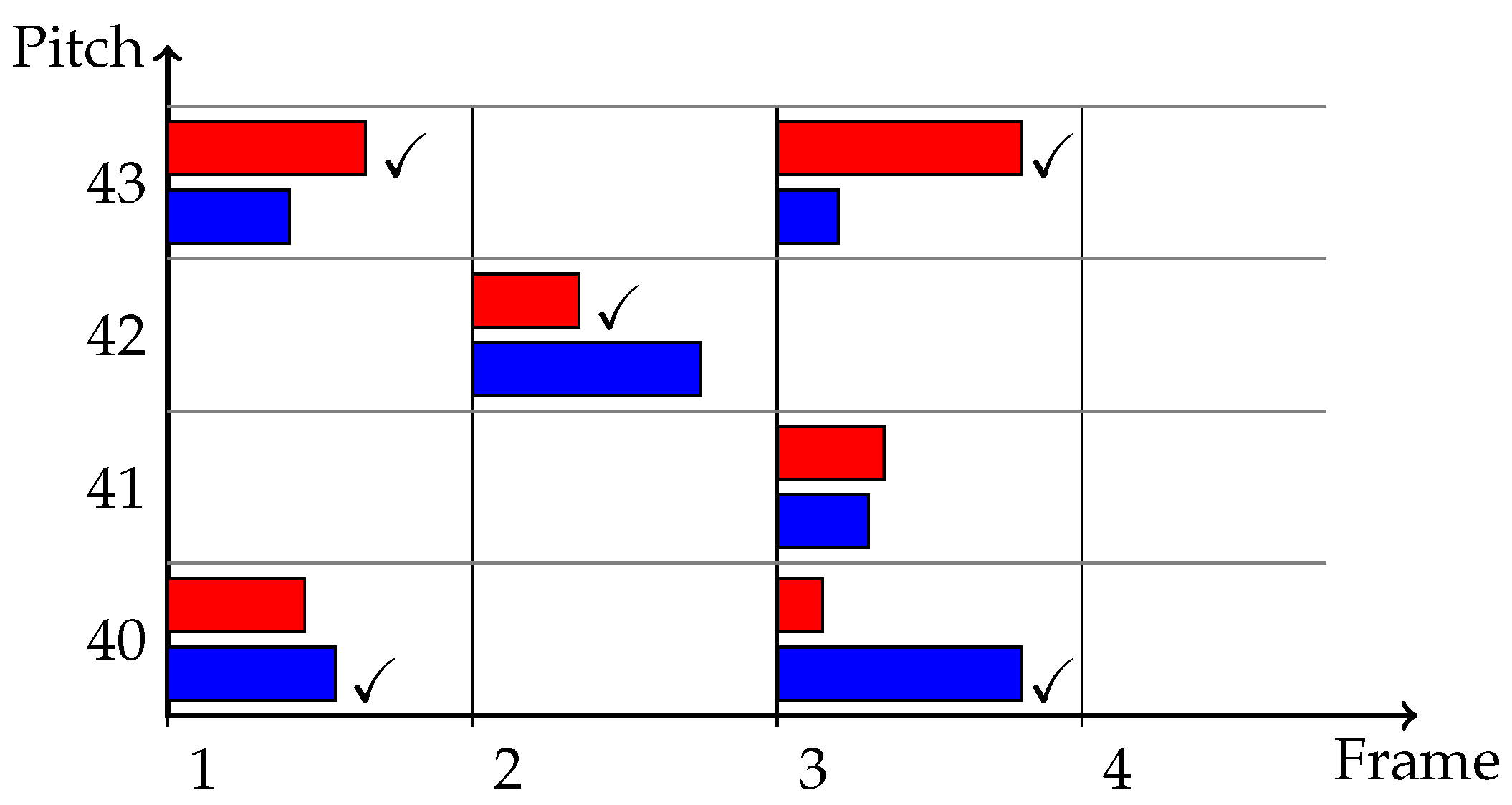
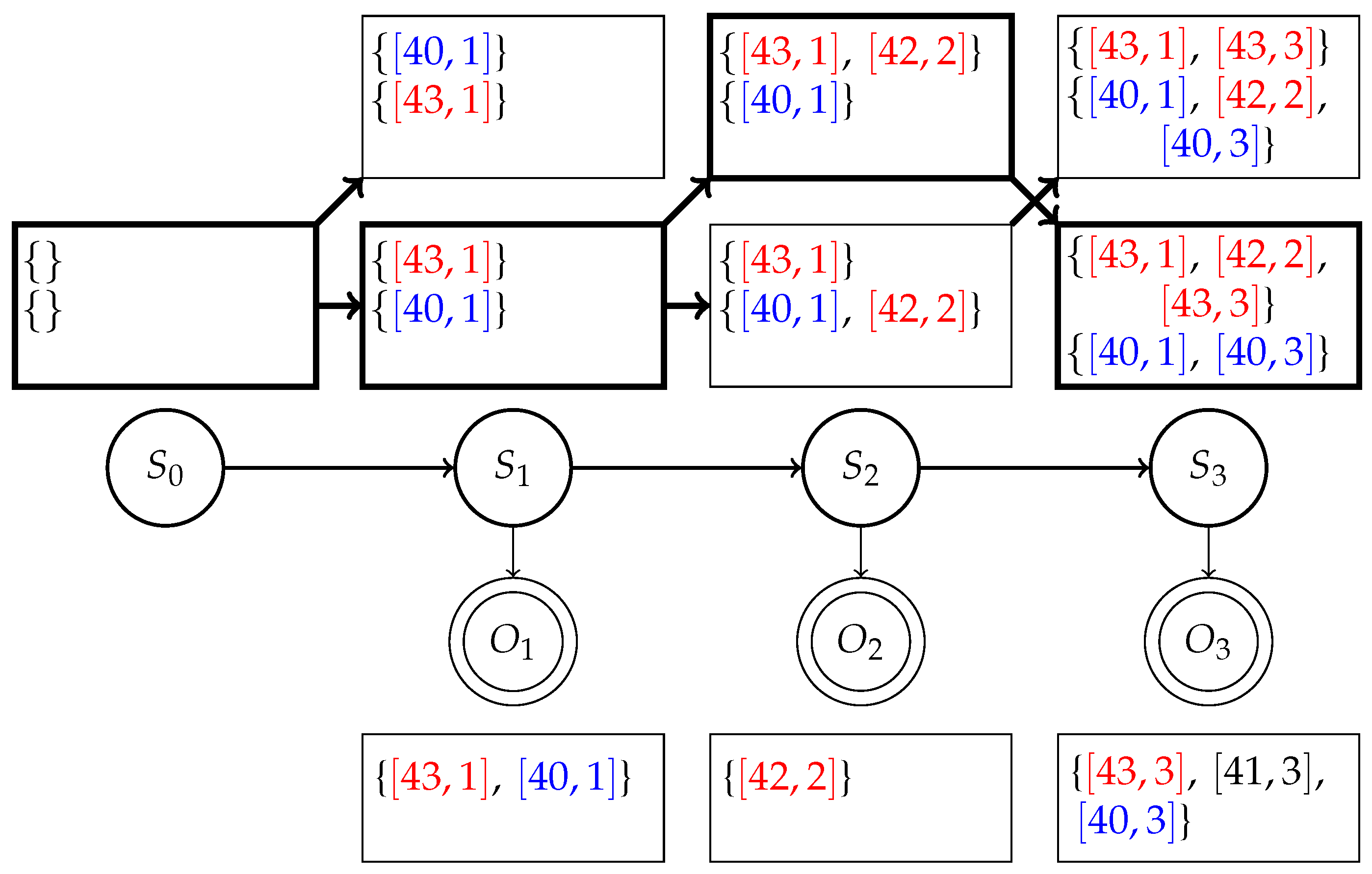
2.2.1. State Space
2.2.2. Transition Function
- and
- and
2.2.3. Emission Function
2.2.4. Inference
2.3. Model Integration
3. Evaluation
3.1. Datasets
3.2. Evaluation Metrics
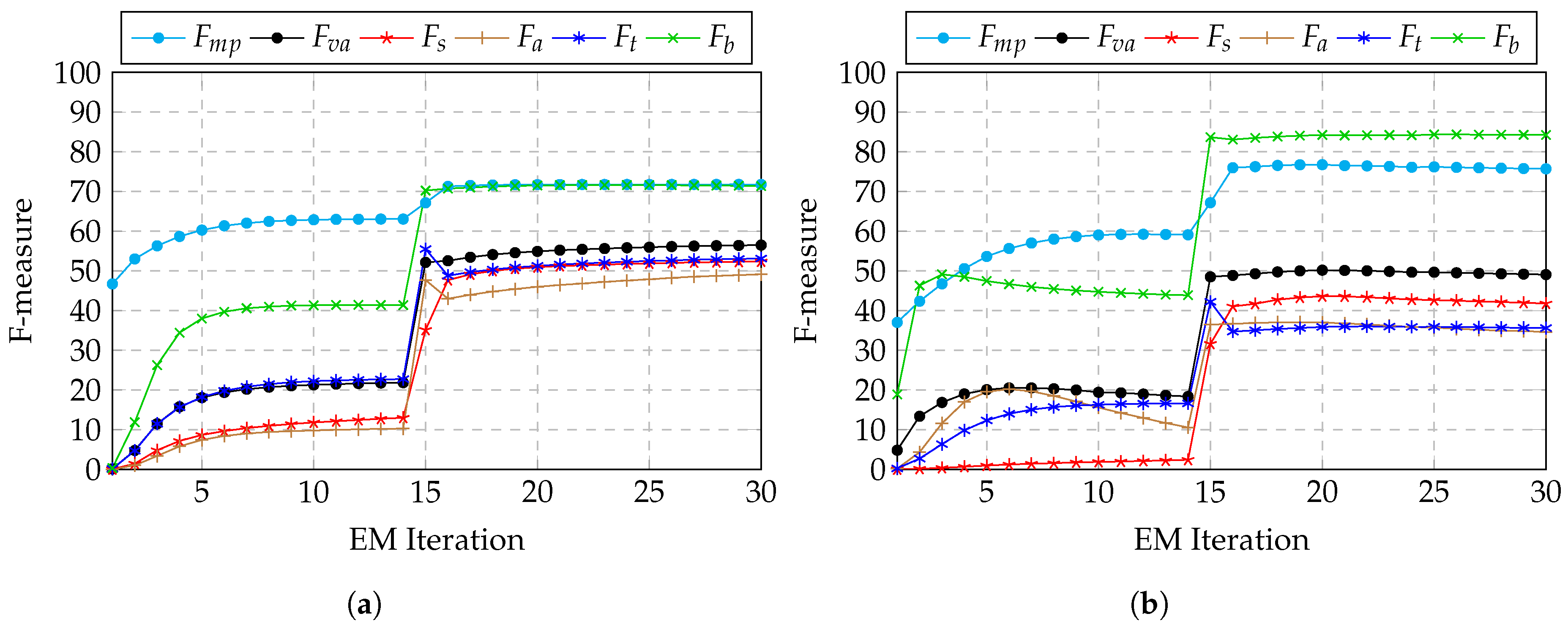
3.3. Training
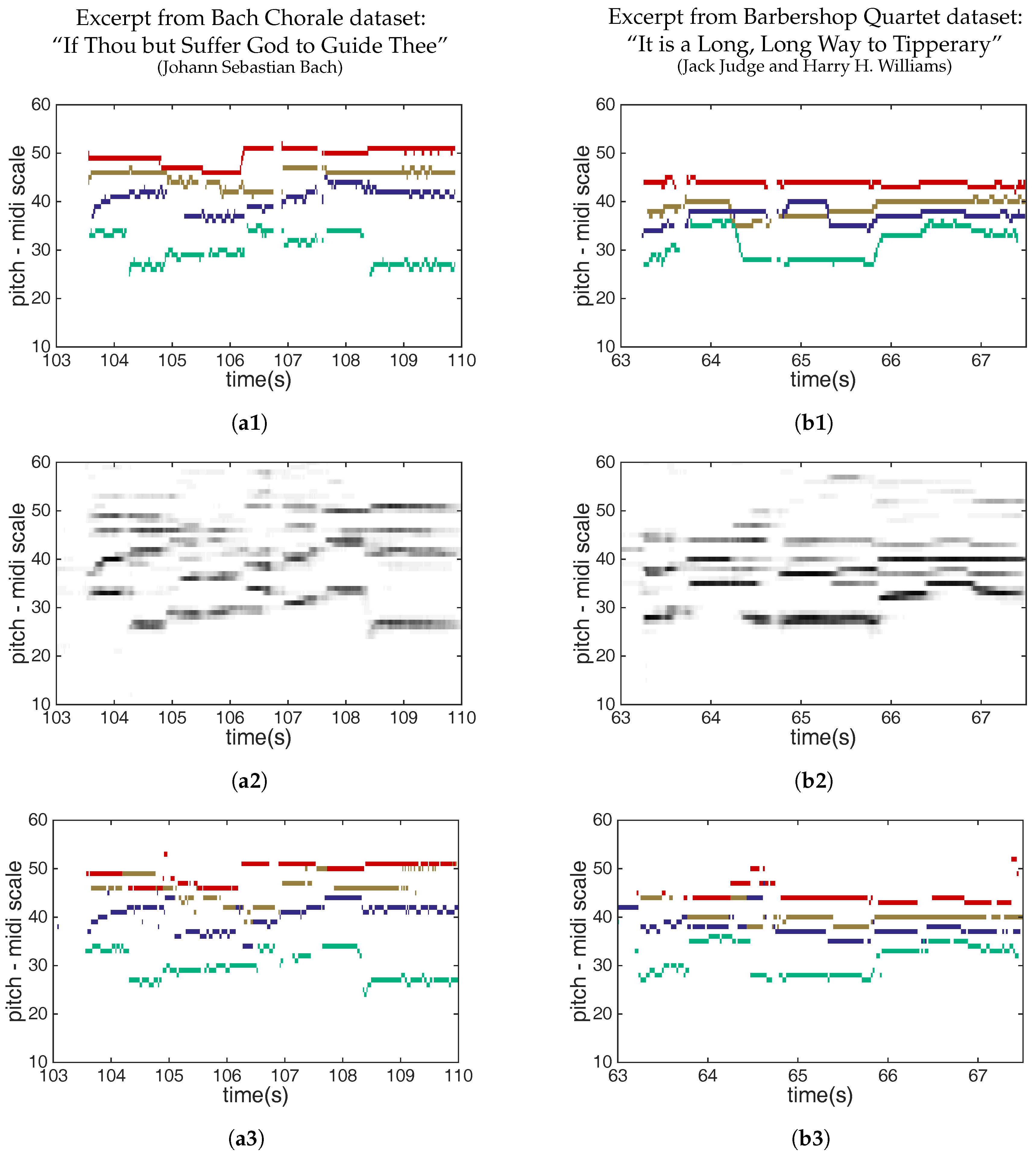
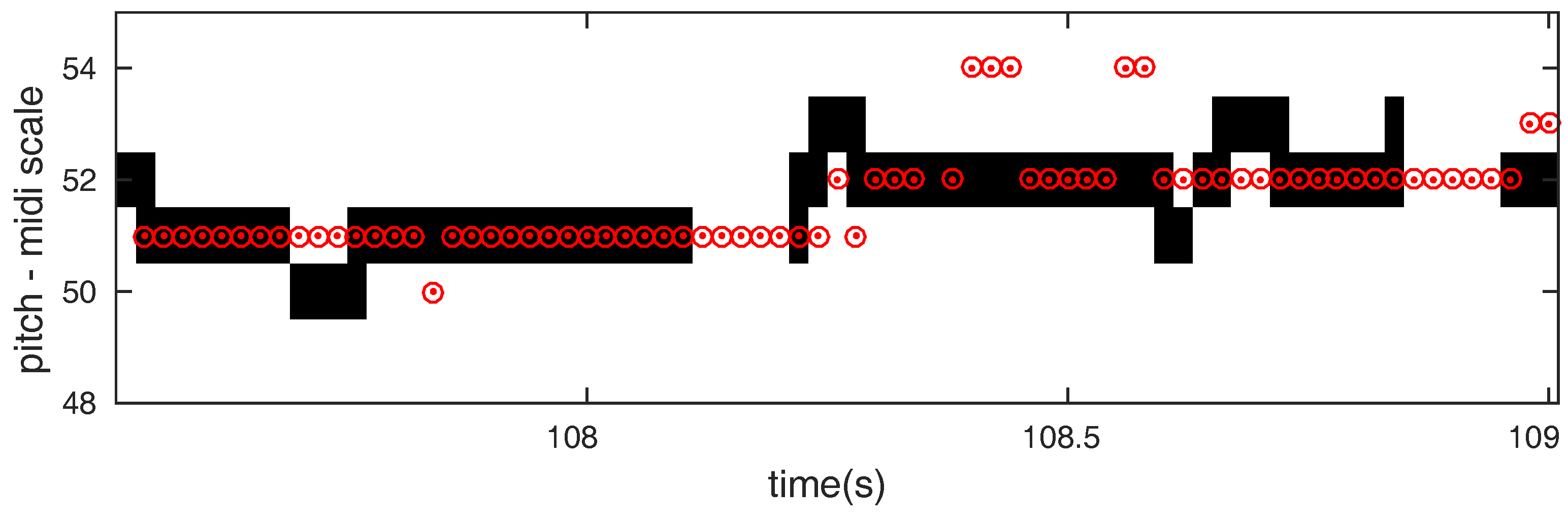
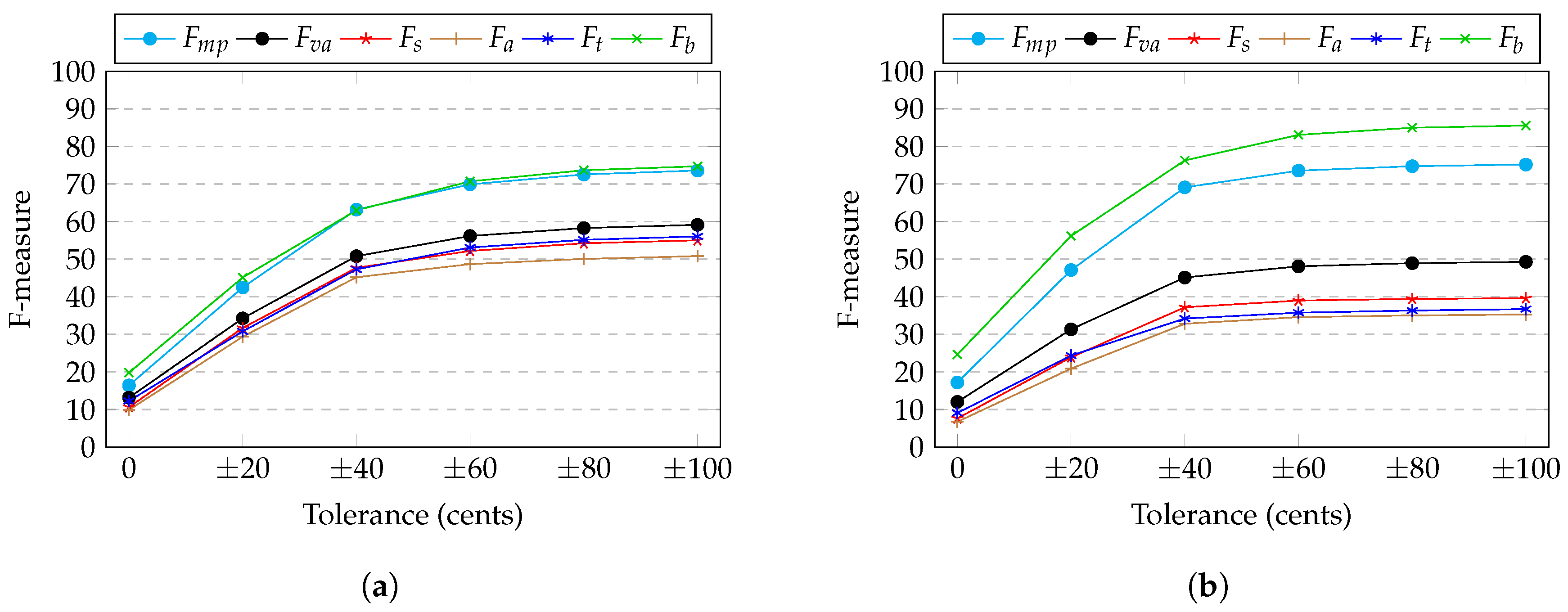
3.4. Results
Twenty-Cent Resolution
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Benetos, E.; Dixon, S.; Giannoulis, D.; Kirchhoff, H.; Klapuri, A. Automatic music transcription: Challenges and future directions. J. Intell. Inf. Syst. 2013, 41, 407–434. [Google Scholar] [CrossRef]
- Li, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar]
- Shashanka, M.; Raj, B.; Smaragdis, P. Probabilistic latent variable models as nonnegative factorizations. Comput. Intell. Neurosci. 2008, 2008, 947438. [Google Scholar] [CrossRef] [PubMed]
- Vincent, E.; Bertin, N.; Badeau, R. Adaptive harmonic spectral decomposition for multiple pitch estimation. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 528–537. [Google Scholar] [CrossRef]
- Kameoka, H.; Nakano, M.; Ochiai, K.; Imoto, Y.; Kashino, K.; Sagayama, S. Constrained and regularized variants of non-negative matrix factorization incorporating music-specific constraints. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 25–30 March 2012; pp. 5365–5368. [Google Scholar]
- Benetos, E.; Dixon, S. Multiple-instrument polyphonic music transcription using a temporally constrained shift-invariant model. J. Acoust. Soc. Am. 2013, 133, 1727–1741. [Google Scholar] [CrossRef] [PubMed]
- Benetos, E.; Weyde, T. An efficient temporally-constrained probabilistic model for multiple-instrument music transcription. In Proceedings of the 16th International Society for Music Information Retrieval Conference, Malaga, Spain, 26–30 October 2015; pp. 701–707. [Google Scholar]
- Fuentes, B.; Badeau, R.; Richard, G. Controlling the convergence rate to help parameter estimation in a PLCA-based model. In Proceedings of the 22nd European Signal Processing Conference, Lisbon, Portugal, 1–5 September 2014; pp. 626–630. [Google Scholar]
- Grindlay, G.; Ellis, D.P.W. Transcribing multi-instrument polyphonic music with hierarchical eigeninstruments. IEEE J. Sel. Top. Signal Process. 2011, 5, 1159–1169. [Google Scholar] [CrossRef]
- Mysore, G.J.; Smaragdis, P. Relative pitch estimation of multiple instruments. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 313–316. [Google Scholar]
- Brown, J. Calculation of a constant Q spectral transform. J. Acoust. Soc. Am. 1991, 89, 425–434. [Google Scholar] [CrossRef]
- Benetos, E.; Dixon, S. A Shift-Invariant Latent Variable Model for Automatic Music Transcription. Comput. Music J. 2012, 36, 81–94. [Google Scholar] [CrossRef]
- Fuentes, B.; Badeau, R.; Richard, G. Blind Harmonic Adaptive Decomposition applied to supervised source separation. In Proceedings of the 2012 European Signal Processing Conference, Bucharest, Romania, 27–31 August 2012; pp. 2654–2658. [Google Scholar]
- Benetos, E.; Badeau, R.; Weyde, T.; Richard, G. Template adaptation for improving automatic music transcription. In Proceedings of the 15th International Society for Music Information Retrieval Conference, Taipei, Taiwan, 27–31 October 2014; pp. 175–180. [Google Scholar]
- O’Hanlon, K.; Nagano, H.; Keriven, N.; Plumbley, M.D. Non-negative group sparsity with subspace note modelling for polyphonic transcription. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 530–542. [Google Scholar] [CrossRef]
- Sigtia, S.; Benetos, E.; Dixon, S. An end-to-end neural network for polyphonic piano music transcription. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 927–939. [Google Scholar] [CrossRef]
- Kelz, R.; Dorfer, M.; Korzeniowski, F.; Böck, S.; Arzt, A.; Widmer, G. On the potential of simple framewise approaches to piano transcription. In Proceedings of the 17th International Society for Music Information Retrieval Conference, New York, NY, USA, 7–11 August 2016; pp. 475–481. [Google Scholar]
- Thickstun, J.; Harchaoui, Z.; Kakade, S. Learning features of music from scratch. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Bittner, R.M.; McFee, B.; Salamon, J.; Li, P.; Bello, J.P. Deep salience representations for F0 estimation in polyphonic music. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October 2017; pp. 63–70. [Google Scholar]
- Bohak, C.; Marolt, M. Transcription of polyphonic vocal music with a repetitive melodic structure. J. Audio Eng. Soc. 2016, 64, 664–672. [Google Scholar] [CrossRef]
- Schramm, R.; Benetos, E. Automatic transcription of a cappella recordings from multiple singers. In Proceedings of the AES International Conference on Semantic Audio, Erlangen, Germany, 22–24 June 2017. [Google Scholar]
- Bay, M.; Ehmann, A.F.; Beauchamp, J.W.; Smaragdis, P.; Downie, J.S. Second fiddle is important too: Pitch tracking individual voices in polyphonic music. In Proceedings of the 13th International Society for Music Information Retrieval Conference, Porto, Portugal, 8–12 October 2012; pp. 319–324. [Google Scholar]
- Duan, Z.; Han, J.; Pardo, B. Multi-pitch streaming of harmonic sound mixtures. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 138–150. [Google Scholar] [CrossRef]
- Ryynanen, M.P.; Klapuri, A. Polyphonic music transcription using note event modeling. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 16 October 2005; pp. 319–322. [Google Scholar]
- Cambouropoulos, E. Voice and stream: Perceptual and computational modeling of voice separation. Music Percept. Interdiscip. J. 2008, 26, 75–94. [Google Scholar] [CrossRef]
- Huron, D. Tone and voice: A derivation of the rules of voice-leading from perceptual principles. Music Percept. 2001, 19, 1–64. [Google Scholar] [CrossRef]
- Tymoczko, D. Scale theory, serial theory and voice leading. Music Anal. 2008, 27, 1–49. [Google Scholar] [CrossRef]
- Temperley, D. A probabilistic model of melody perception. Cogn. Sci. 2008, 32, 418–444. [Google Scholar] [CrossRef] [PubMed]
- Karydis, I.; Nanopoulos, A.; Papadopoulos, A.; Cambouropoulos, E.; Manolopoulos, Y. Horizontal and vertical integration/segregation in auditory streaming: A voice separation algorithm for symbolic musical data. In Proceedings of the Proceedings 4th Sound and Music Computing Conference (SMC’2007), Lefkada, Greece, 11–13 July 2007; pp. 299–306. [Google Scholar]
- Kilian, J.; Hoos, H. Voice separation-a local optimization approach. In Proceedings of the 3rd International Conference on Music Information Retrieval, Paris, France, 13–17 October 2002. [Google Scholar]
- Kirlin, P.B.; Utgoff, P.E. VOISE: Learning to segregate voices in explicit and implicit polyphony. In Proceedings of the 6th International Conference on Music Information Retrieval, London, UK, 11–15 September 2005; pp. 552–557. [Google Scholar]
- Guiomard-Kagan, N.; Giraud, M.; Groult, R.; Levé, F. Improving voice separation by better connecting contigs. In Proceedings of the 17th International Society for Music Information Retrieval Conference, New York, NY, USA, 7–11 August 2016; pp. 164–170. [Google Scholar]
- Gray, P.; Bunescu, R. A neural greedy model for voice separation in symbolic music. In Proceedings of the 17th International Society for Music Information Retrieval Conference, New York, NY, USA, 7–11 August 2016; pp. 782–788. [Google Scholar]
- Chew, E.; Wu, X. Separating voices in polyphonic music: A contig mapping approach. In Proceedings of the Computer Music Modeling and Retrieval, Esbjerg, Denmark, 26–29 May 2004; pp. 1–20. [Google Scholar]
- de Valk, R.; Weyde, T. Bringing ‘musicque into the tableture’: Machine-learning models for polyphonic transcription of 16th-century lute tablature. Early Music 2015, 43, 563–576. [Google Scholar] [CrossRef]
- Duane, B.; Pardo, B. Streaming from MIDI using constraint satisfaction optimization and sequence alignment. In Proceedings of the International Computer Music Conference, Montreal, QC, Canada, 16–21 August 2009; pp. 1–8. [Google Scholar]
- McLeod, A.; Steedman, M. HMM-Based Voice Separation of MIDI Performance. J. New Music Res. 2016, 45, 17–26. [Google Scholar] [CrossRef]
- Schramm, R.; McLeod, A.; Steedman, M.; Benetos, E. Multi-pitch detection and voice assignment for a cappella recordings of multiple singers. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–28 October 2017; pp. 552–559. [Google Scholar]
- Schörkhuber, C.; Klapuri, A.; Holighaus, N.; Dörfler, M. A matlab toolbox for efficient perfect reconstruction time-frequency transforms with log-frequency resolution. In Proceedings of the AES 53rd Conference on Semantic Audio, London, UK, 26–29 January 2014. [Google Scholar]
- Benetos, E.; Holzapfel, A. Automatic transcription of Turkish microtonal music. J. Acoust. Soc. Am. 2015, 138, 2118–2130. [Google Scholar] [CrossRef] [PubMed]
- Goto, M.; Hashiguchi, H.; Nishimura, T.; Oka, R. RWC music database: Music genre database and musical instrument sound database. In Proceedings of the 5th International Conference on Music Information Retrieval, Barcelona, Spain, 10–14 October 2004; pp. 229–230. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Mauch, M.; Dixon, S. PYIN: A fundamental frequency estimator using probabilistic threshold distributions. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 659–663. [Google Scholar]
- De Andrade Scatolini, C.; Richard, G.; Fuentes, B. Multipitch estimation using a PLCA-based model: Impact of partial user annotation. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Queensland, Australia, 19–24 April 2015; pp. 186–190. [Google Scholar]
- Goto, M. A real-time music-scene-description system: Predominant-F0 estimation for detecting melody and bass lines in real-world audio signals. Speech Commun. 2004, 43, 311–329. [Google Scholar] [CrossRef]
- Kameoka, H.; Nishimoto, T.; Sagayama, S. A multipitch analyzer based on harmonic temporal structured clustering. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 982–994. [Google Scholar] [CrossRef]
- Kirchhoff, H.; Dixon, S.; Klapuri, A. Missing template estimation for user-assisted music transcription. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 26–30. [Google Scholar]
- Viterbi, A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory 1967, 13, 260–269. [Google Scholar] [CrossRef]
- Klapuri, A. Multiple fundamental frequency estimation by summing harmonic amplitudes. In Proceedings of the 7th International Conference on Music Information Retrieval, Victoria, BC, Canada, 8–12 October 2006. [Google Scholar]
- Salamon, J.; Gomez, E. Melody extraction from polyphonic music signals using pitch contour characteristics. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1759–1770. [Google Scholar] [CrossRef]
- Pertusa, A.; Iñesta, J.M. Efficient methods for joint estimation of multiple fundamental frequencies in music signals. EURASIP J. Adv. Signal Process. 2012. [Google Scholar] [CrossRef]
- Giannoulis, D.; Benetos, E.; Klapuri, A.; Plumbley, M.D. Improving instrument recognition in polyphonic music through system integration. In Proceedings of the 39th International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 5222–5226. [Google Scholar]
- Bay, M.; Ehmann, A.F.; Downie, J.S. Evaluation of multiple-F0 estimation and tracking systems. In Proceedings of the 10th International Society for Music Information Retrieval Conference, Kobe, Japan, 26–30 October 2009; pp. 315–320. [Google Scholar]
- Bogdanov, D.; Wack, N.; Gómez, E.; Gulati, S.; Herrera, P.; Mayor, O.; Roma, G.; Salamon, J.; Zapata, J.; Serra, X. Essentia: An Audio Analysis Library for Music Information Retrieval. In Proceedings of the 14th International Society for Music Information Retrieval Conference, Curitiba, Brazil, 4–8 November 2013. [Google Scholar]
| Model | Bach Chorales | ||||
|---|---|---|---|---|---|
| Klapuri [49] | 28.12 (4.38) | 24.23 (10.28) | 22.98 (11.85) | 29.35 (12.43) | 35.92 (10.97) |
| Salamon and Gomez [50] | 24.83 (5.31) | 30.03 (12.63) | 25.24 (10.92) | 21.09 (9.91) | 22.95 (9.30) |
| Vincent et al. [4] | 18.30 (4.87) | 13.43 (7.03) | 15.52 (6.50) | 17.14 (6.77) | 27.10 (8.44) |
| Pertusa and Iñesta [51] | 44.05 (4.60) | 40.18 (11.28) | 43.34 (7.38) | 41.54 (7.02) | 50.56 (6.16) |
| Schramm and Benetos [21] | 20.31 (3.40) | 20.42 (5.36) | 21.27 (4.75) | 14.49 (1.37) | 25.05 (2.12) |
| VOCAL4-MP | 21.84 (9.37) | 12.99 (11.23) | 10.27 (10.13) | 22.72 (6.72) | 41.37 (9.41) |
| VOCAL4-VA | 56.49 (10.48) | 52.37 (12.92) | 49.13 (11.22) | 53.10 (11.71) | 71.38 (6.06) |
| Model | Barbershop Quartets | ||||
| Klapuri [49] | 20.90 (5.79) | 2.53 (4.82) | 29.02 (13.25) | 7.94 (7.48) | 44.09 (14.26) |
| Salamon and Gomez [50] | 20.38 (6.61) | 11.14 (10.27) | 35.14 (14.04) | 8.44 (8.22) | 26.81 (13.69) |
| Vincent et al. [4] | 19.13 (8.52) | 10.20 (8.25) | 17.97 (9.03) | 15.93 (8.85) | 32.41 (12.41) |
| Pertusa and Iñesta [51] | 37.19 (8.62) | 30.68 (13.94) | 36.15 (11.70) | 29.15 (13.90) | 52.78 (10.37) |
| Schramm and Benetos [21] | 23.98 (4.34) | 24.45 (6.36) | 31.61 (6.79) | 13.55 (2.18) | 26.34 (2.03) |
| VOCAL4-MP | 18.35 (7.56) | 2.40 (5.54) | 10.56 (13.92) | 16.61 (7.31) | 43.85 (3.46) |
| VOCAL4-VA | 49.06 (14.65) | 41.78 (18.78) | 34.62 (16.29) | 35.59 (16.93) | 84.25 (6.58) |
| Model | Bach Chorales | Barbershop Quartets |
|---|---|---|
| Klapuri [49] | 54.62 (3.00) | 48.24 (4.50) |
| Salamon and Gomez [50] | 49.52 (5.18) | 45.22 (6.94) |
| Vincent et al. [4] | 53.58 (6.27) | 51.04 (8.52) |
| Pertusa and Iñesta [51] | 67.19 (3.82) | 63.85 (6.69) |
| Schramm and Benetos [21] | 71.03 (3.33) | 70.84 (6.17) |
| VOCAL4-MP | 63.05 (3.12) | 59.09 (5.07) |
| VOCAL4-VA | 71.76 (3.51) | 75.70 (6.18) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McLeod, A.; Schramm, R.; Steedman, M.; Benetos, E. Automatic Transcription of Polyphonic Vocal Music. Appl. Sci. 2017, 7, 1285. https://doi.org/10.3390/app7121285
McLeod A, Schramm R, Steedman M, Benetos E. Automatic Transcription of Polyphonic Vocal Music. Applied Sciences. 2017; 7(12):1285. https://doi.org/10.3390/app7121285
Chicago/Turabian StyleMcLeod, Andrew, Rodrigo Schramm, Mark Steedman, and Emmanouil Benetos. 2017. "Automatic Transcription of Polyphonic Vocal Music" Applied Sciences 7, no. 12: 1285. https://doi.org/10.3390/app7121285
APA StyleMcLeod, A., Schramm, R., Steedman, M., & Benetos, E. (2017). Automatic Transcription of Polyphonic Vocal Music. Applied Sciences, 7(12), 1285. https://doi.org/10.3390/app7121285