Precision Obtained Using an Artificial Neural Network for Predicting the Material Removal Rate in Ultrasonic Machining
Abstract
Featured Application
Abstract
1. Introduction
2. Review of Our Earlier Research Work
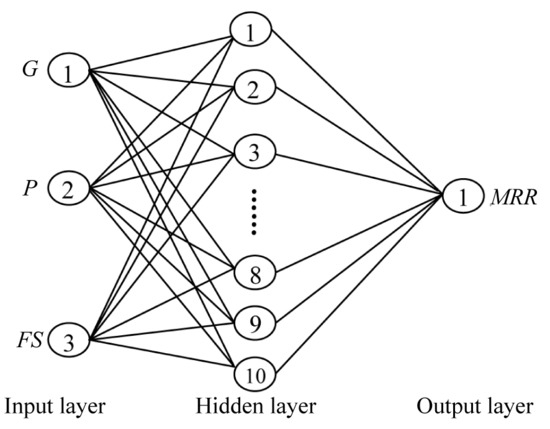
3. Neural Network Modelling Method
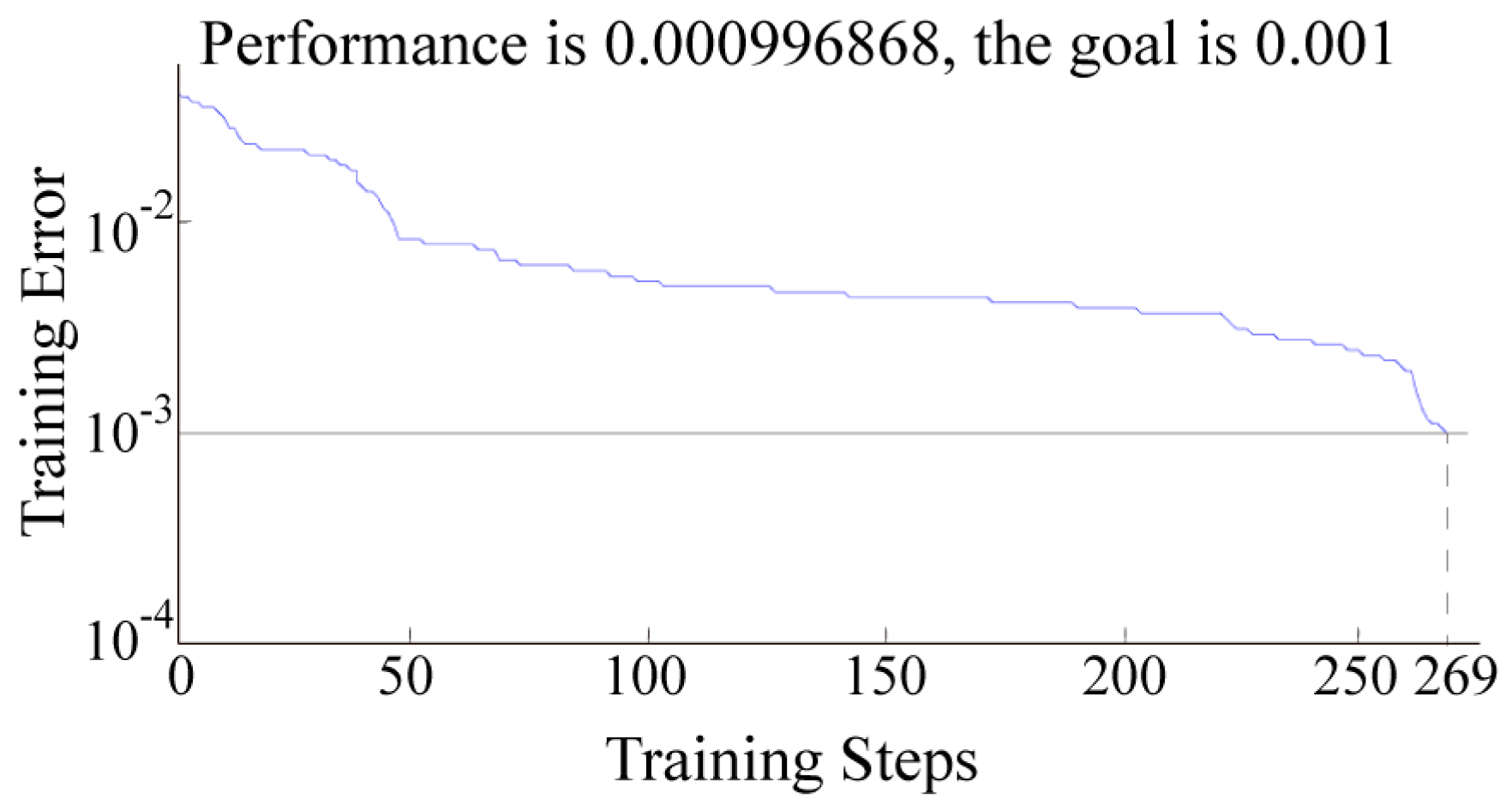
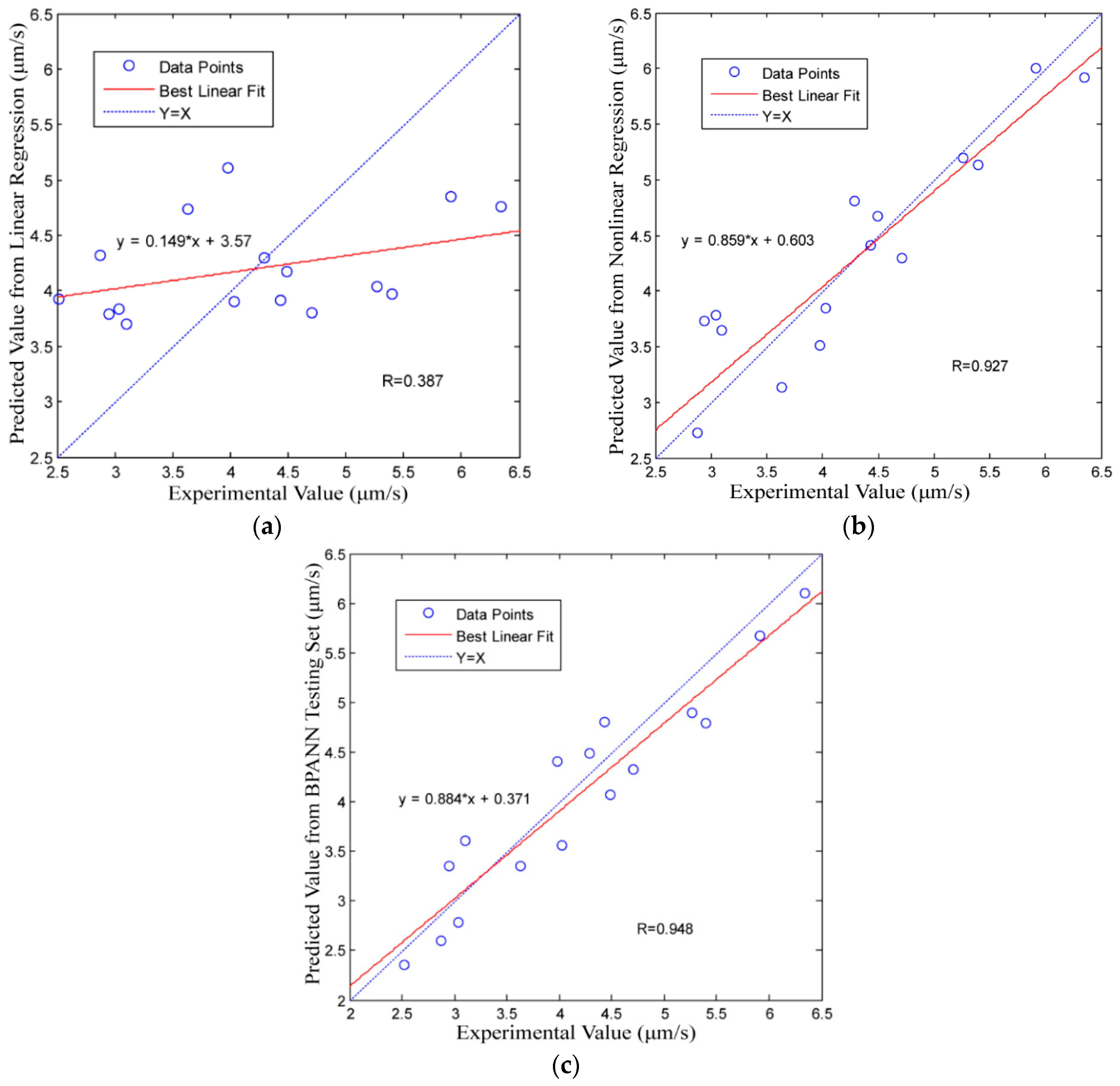
4. Results and Discussion
5. Conclusions
- (1)
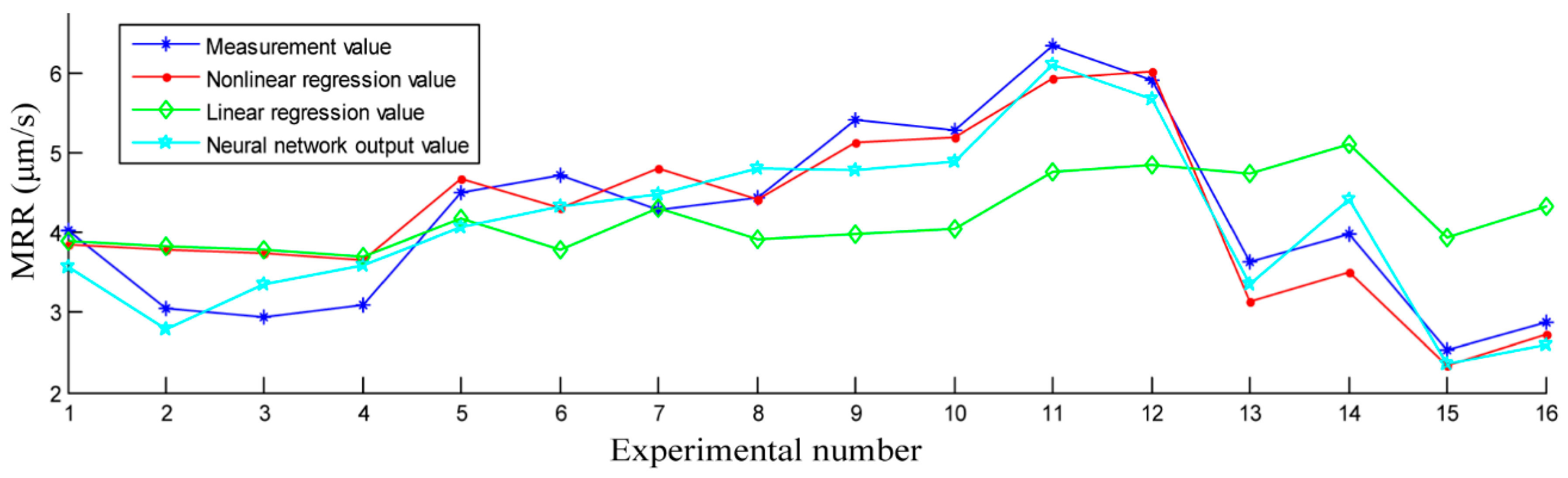
- The BPANN model proposed in this study and the improved nonlinear regression model established in our earlier research are useful for predicting the MRR in the USM process, but the results of the present study demonstrate that the BPANN model provides the best results and requires no explicit mathematical function.
- (2)
- The method employing ANNs proposed in this study for predicting the MRR in USM can be considered as a guide for modelling complex general machining problems without explicit mathematical functions.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Symbolic Definition of the BPANN | |||
| Definition | Symbol | ||
| Input vector of the BPANN | Pk = (a1, a2, …, an) | ||
| where n represents the number of input vectors of the BPANN | |||
| Target vector of the BPANN | Tk = (y1, y2, …, yq) | ||
| where q represents the number of target vectors of the BPANN | |||
| Input vector of the middle layer unit | Sk = (s1, s2, …, sp) | ||
| Output vector of the middle layer unit | Bk = (b1, b2, …, bp) | ||
| where p represents the number of vectors of the middle layer unit | |||
| Input vector of the output layer unit | Lk = (l1, l2, …, lq) | ||
| Output vector of the output layer unit | Ck = (c1, c2, …, cq) | ||
| where the number of vectors of the output layer unit is equal to that of the target vectors of the ANN | |||
| Connection weight of the input layer to the middle layer | wij, i = 1, 2, …, n, j = 1, 2, …, p | ||
| Connection weight of the middle layer to the output layer | vjt, j = 1, 2, …, p, t = 1, 2, …, q | ||
| Output threshold of each unit in the middle layer | θj, j = 1, 2, …, p | ||
| Output threshold of each unit in the output layer | γt, t = 1, 2, …, q | ||
| Parameter k | k = 1, 2, …, m | ||
| where m represents the number of parameters k | |||
| Learning Steps of the BPANN | |||
| Step | Description | ||
| 1 | Initialize and subsequently assign a random value within the interval (−1, 1) to each wij, vjt, θj and γt. | ||
| 2 | Randomly select and apply a set of input and target vectors (i.e., Pk and Tk) to the network. | ||
| 3 | Calculate the input and output value sj and bj of each unit in the middle layer by the transfer function according to the formula . | ||
| 4 | Calculate the input and output value lt and ct of each unit in the output layer by the transfer function according to the formula . | ||
| 5 | Calculate the generalized error of each unit of the output layer according to the formula . | ||
| 6 | Calculate the generalized error of each unit of the middle layer according to the formula . | ||
| 7 | Modify the connection weights vjt and the thresholds γt according to formulas . | ||
| 8 | Modify the connection weights wij and the thresholds θj according to formulas . | ||
| 9 | Randomly select and apply the next learning sample vectors to the network and return to Step 3 until the completion of m training samples. | ||
| 10 | Re-select a set of input and target sample vectors from m study samples and return to Step 3 until the network global error E is less than a pre-set minimum value, i.e., the network converges. Go to Step 11. If the number of training steps is greater than the pre-set value, the network cannot converge. | ||
| 11 | End. | ||
Appendix B
References
- Zhang, Y.M.; Yang, S.; Evans, J.R.G. Revisiting Hume-Rothery’s Rules with artificial neural networks. Acta Mater. 2008, 56, 1094–1105. [Google Scholar] [CrossRef]
- Akhlaghi, F.; Khakbiz, M.; Rezaii Bazazz, A. Evolution of the size distribution of Al–B4C nano-composite powders during mechanical milling: A comparison of experimental results with artificial neural networks and multiple linear regression models. Neural Comput. Appl. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y. Applications of Artificial Neural Networks (ANNs) in Several Different Materials Research Fields; Queen Mary, University of London: London, UK, 2010. [Google Scholar]
- Bhosale, S.B.; Pawade, R.S.; Brahmankar, P.K. Effect of process parameters on MRR, TWR and surface topography in ultrasonic machining of alumina-zirconia ceramic composite. Ceram. Int. 2014, 40, 12831–12836. [Google Scholar] [CrossRef]
- Zhong, G.; Xu, J.; Wu, Y.; Yang, S. Statistical Analyses and Regression Modeling for Influence of Process Parameters on Material Removal Rate in Ultrasonic Machining. Glob. J. Technol. Optim. 2015, 6, 1–6. [Google Scholar]
- Nath, C.; Lim, G.C.; Zheng, H.Y. Influence of the material removal mechanisms on hole integrity in ultrasonic machining of structural ceramics. Ultrasonics 2012, 52, 605–613. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, N.; Abdo1, B.M.; Darwish, S.; Moiduddin, K.; Pervaiz, S.; Alahmari, A.M.; Naveed, M. Electron beam melting of titanium alloy and surface finish improvement through rotary ultrasonic machining. Int. J. Adv. Manuf. Technol. 2017, 4, 1–13. [Google Scholar] [CrossRef]
- Jüschke, M.; Koch, C. Model processes and cavitation indicators for a quantitative description of an ultrasonic cleaning vessel: Part I: Experimental results. Ultrason. Sonochem. 2012, 19, 787–795. [Google Scholar] [CrossRef] [PubMed]
- Abhishek, R.K.; Datta, S.; Biswa, B.; Mahapatra, S. Machining performance optimization for electro-discharge machining of Inconel 601, 625, 718 and 825: An integrated optimization route combining satisfaction function, fuzzy inference system and Taguchi approach. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3499–3527. [Google Scholar]
- Thoe, T.B.; Aspinwall, D.K.; Wise, M.L.H. Review on ultrasonic machining. Int. J. Mach. Tools Manuf. 1998, 38, 239–255. [Google Scholar] [CrossRef]
- Xu, J. Multi-Objective Optimization Research of Precision Turning Process Parameters; Nanjing Agricultural University: Nanjing, China, 2016. [Google Scholar]
- Singh, R.; Khamba, J.S. Investigation for ultrasonic machining of titanium and its alloys. J. Mater. Process. Technol. 2007, 183, 363–367. [Google Scholar] [CrossRef]
- Kasman, S. Impact of parameters on the process response: A Taguchi orthogonal analysis for laser engraving. Measurement 2013, 46, 2577–2584. [Google Scholar] [CrossRef]
- Kivak, T.; Samtas, G.; Cicek, A. Taguchi method based optimisation of drilling parameters in drilling of AISI 316 steel with PVD monolayer and multilayer coated HSS drills. Measurement 2012, 45, 1547–1557. [Google Scholar] [CrossRef]
- Siddiquee, A.N.; Khan, Z.A.; Goel, P. Mukesh Kumar, Gaurav Agarwal, Noor Zaman Khan, Optimization of Deep Drilling Process Parameters of AISI 321 Steel using Taguchi Method. Procedia Mater. Sci. 2014, 6, 1217–1225. [Google Scholar] [CrossRef]
- Zhong, G. Ternary Regression Modeling Analysis of NC Ultrasonic Machining Efficiency. Appl. Mech. Mater. 2010, 37–38, 1388–1392. [Google Scholar] [CrossRef]
- Asilturk, I.; Akkus, H. Determining the effect of cutting parameters on surface roughness in hard turning using the Taguchi method. Measurement 2011, 44, 1697–1704. [Google Scholar] [CrossRef]
- Zhong, G.; Vaezi, M.; Liu, P.; Pan, L.; Yang, S. Characterization approach on the extrusion process of bioceramics for the 3D printing of bone tissue engineering scaffolds. Ceram. Int. 2017, 43, 13860–13868. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, D. Investigation into the shrinkage in Z-direction of components manufactured by selective laser melting (SLM). Int. J. Adv. Manuf. Technol. 2017, 90, 2913–2923. [Google Scholar] [CrossRef]
- Esteban, L.G.; Fernández, F.G.; de Palacios, P. MOE prediction in Abies pinsapo Boiss. timber: Application of an artificial neural network using non-destructive testing. Comput. Struct. 2009, 87, 1360–1365. [Google Scholar] [CrossRef]
- García-Iruela, A.; Fernandez, F.G.; Esteban, L.G.; de Palacios, P.; Simon, C.; Arriaga, F. Comparison of modelling using regression techniques and an artificial neural network for obtaining the static modulus of elasticity of Pinus radiata D. Don. timber by ultrasound. Compos. Part B 2016, 96, 112–118. [Google Scholar] [CrossRef]
- Valls, J.M.; Galvan, I.M.; Isasi, P. Lazy learning in radial basis neural networks: A way of achieving more accurate models. Neural Process. Lett. 2004, 20, 105–124. [Google Scholar] [CrossRef]
- Gaja, H.; Liou, F. Defect classification of laser metal deposition using logistic regression and artificial neural networks for pattern recognition. Int. J. Adv. Manuf. Technol. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Zhong, G.; Wang, Y. NC Ultrasonic Machining Efficiency: Neural Network-Based Modeling and Simulation. Adv. Mater. Res. 2011, 291, 406–410. [Google Scholar] [CrossRef]
- Zhong, G.; Kang, M. Modeling and Simulation for Effect in Numerical Controlled Ultrasonic Machining Based on Artificial Neural Network. China Acad. J. Syst. Simul. 2007, 19, 1620–1623. [Google Scholar]
- Zhong, G.; Kang, M. Performance Analysis on Numerical Controlled Ultrasonic Machining Based on BP Artificial Neural Network. China Acad. J. Electromach. Mould 2007, 4, 37–40. [Google Scholar]
- Zhong, G.; Wang, C.; Yang, S.; Zheng, E.; Ge, Y. Position geometric error modeling, identification and compensation for large 5-axis machining center prototype. Int. J. Mach. Tools Manuf. 2015, 89, 142–150. [Google Scholar] [CrossRef]
- Lee, J.H.; Liu, Y.; Yang, S.-H. Accuracy improvement of miniaturized machine tool: Geometric error modeling and compensation. Int. J. Mach. Tools Manuf. 2006, 46, 1508–1516. [Google Scholar] [CrossRef]
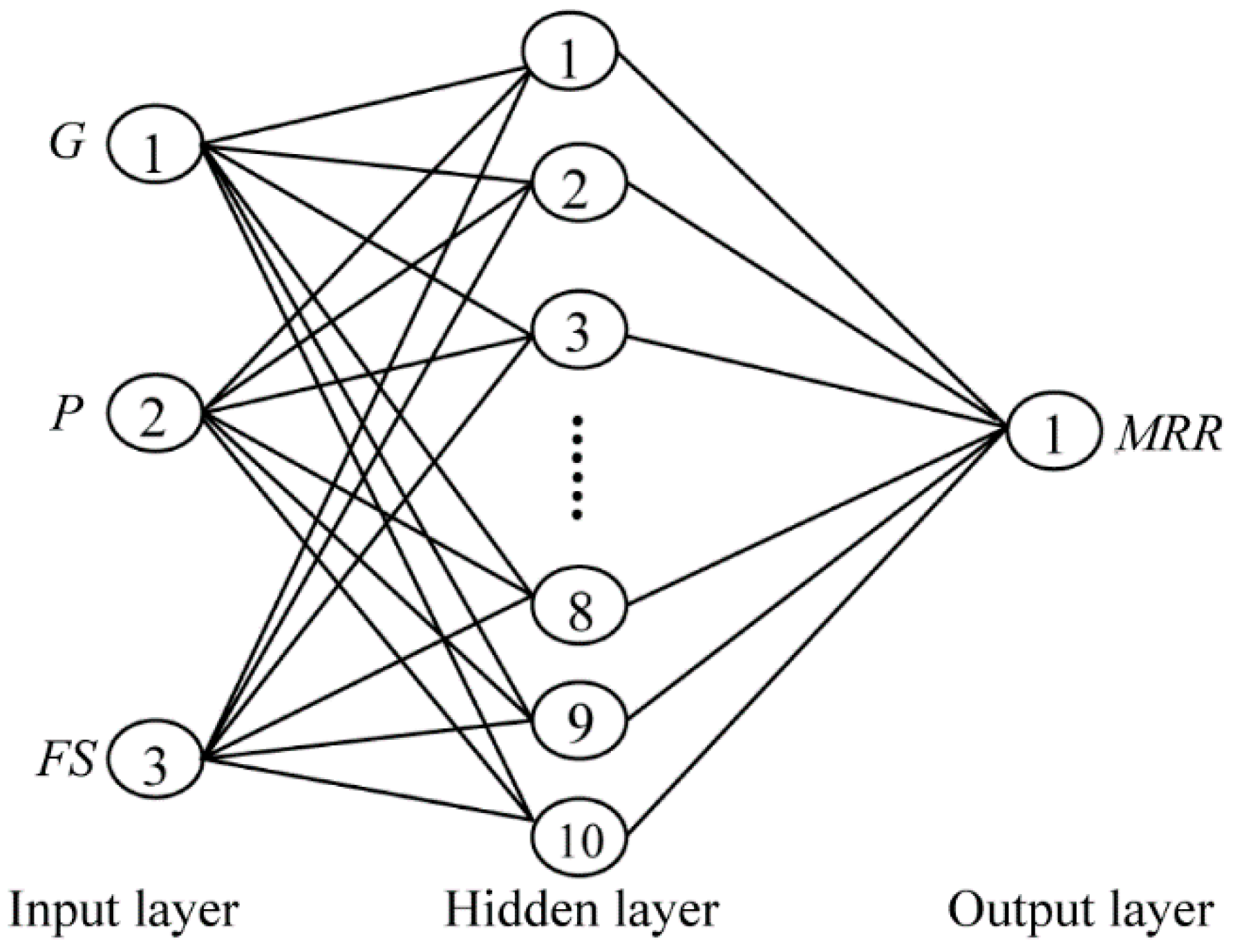
| Research Detail | Description | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Experimental USM apparatus | 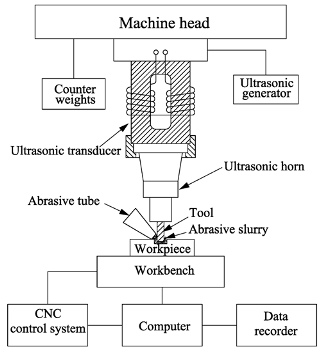 | Primary components consist of an ultrasonic machine tool, multi-axis computer numerical control (CNC) system, ultrasonic generator and data recorder. The unit was employed to perform a series of experiments based on the Taguchi L16 orthogonal array. To reduce the measurement error, each experiment was conducted twice. | |||||||
| Processed workpiece | 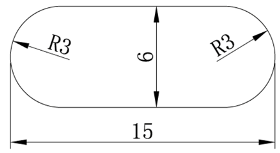 | Workpiece material: soda-lime glass Shape: round head slot Plane dimension: 15 mm × 6 mm Number of reciprocating processing: 20 times. | |||||||
| Fixed factors | Ultrasonic frequency | 20.12 kHz | |||||||
| Ultrasonic amplitude | 12 μm | ||||||||
| Oscillating current | 300 mA | ||||||||
| Abrasive slurry ingredients and concentration | Silicon carbide mixed with water in a 1:3 ratio | ||||||||
| Length of ultrasonic horn | 150 mm | ||||||||
| Diameter of the tool | 6 mm | ||||||||
| Control factors | Symbol | Parameters | Levels | ||||||
| 1 | 2 | 3 | 4 | ||||||
| G | Abrasive granularity (mesh) | 320 | 240 | 120 | 80 | ||||
| P | Feed pressure (N) | 20 | 30 | 40 | 50 | ||||
| FS | Feed speed (mm/s) | 1.32 | 2.08 | 2.94 | 3.62 | ||||
| Process response | Material removal rate (MRR) | Because the plane dimension of the workpiece is certain, the MRR is calculated as follows: where D (um) is the processing depth, measured using a digital display depth micrometre with a resolution of 0.001 mm, and T (s) is the processing time, recorded by the data recorder. | |||||||
| Intuitive analysis | 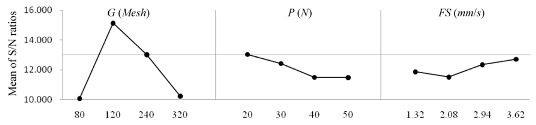 | The value of G exhibits an obvious and nonlinear behaviour. | |||||||
| ANOVA analysis | 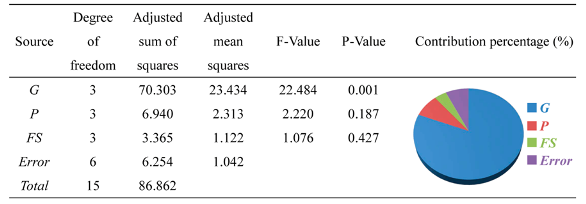 | The effect of G was significant. | |||||||
| Regression models | Linear and nonlinear regression models given by Equations (3) and (4), respectively, in this study. | ||||||||
| Comparison of the modelling precision with 8 new experimental conditions | 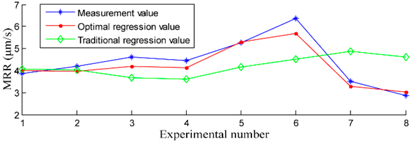 | The MRR values obtained from the nonlinear regression equation are in good agreement with the measured MRR values. | |||||||
| Three Modelling Methods | M | B | R | R2 |
|---|---|---|---|---|
| (a) Conventional linear regression model | 0.149 | 3.57 | 0.387 | 0.150 |
| (b) Improved nonlinear regression model | 0.859 | 0.603 | 0.927 | 0.859 |
| (c) Back-propagation artificial neural network model | 0.884 | 0.371 | 0.948 | 0.899 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, G.; Kang, M.; Yang, S. Precision Obtained Using an Artificial Neural Network for Predicting the Material Removal Rate in Ultrasonic Machining. Appl. Sci. 2017, 7, 1268. https://doi.org/10.3390/app7121268
Zhong G, Kang M, Yang S. Precision Obtained Using an Artificial Neural Network for Predicting the Material Removal Rate in Ultrasonic Machining. Applied Sciences. 2017; 7(12):1268. https://doi.org/10.3390/app7121268
Chicago/Turabian StyleZhong, Gaoyan, Min Kang, and Shoufeng Yang. 2017. "Precision Obtained Using an Artificial Neural Network for Predicting the Material Removal Rate in Ultrasonic Machining" Applied Sciences 7, no. 12: 1268. https://doi.org/10.3390/app7121268
APA StyleZhong, G., Kang, M., & Yang, S. (2017). Precision Obtained Using an Artificial Neural Network for Predicting the Material Removal Rate in Ultrasonic Machining. Applied Sciences, 7(12), 1268. https://doi.org/10.3390/app7121268