Free Vibration Analysis of Functionally Graded Porous Doubly-Curved Shells Based on the First-Order Shear Deformation Theory
Abstract
:1. Introduction
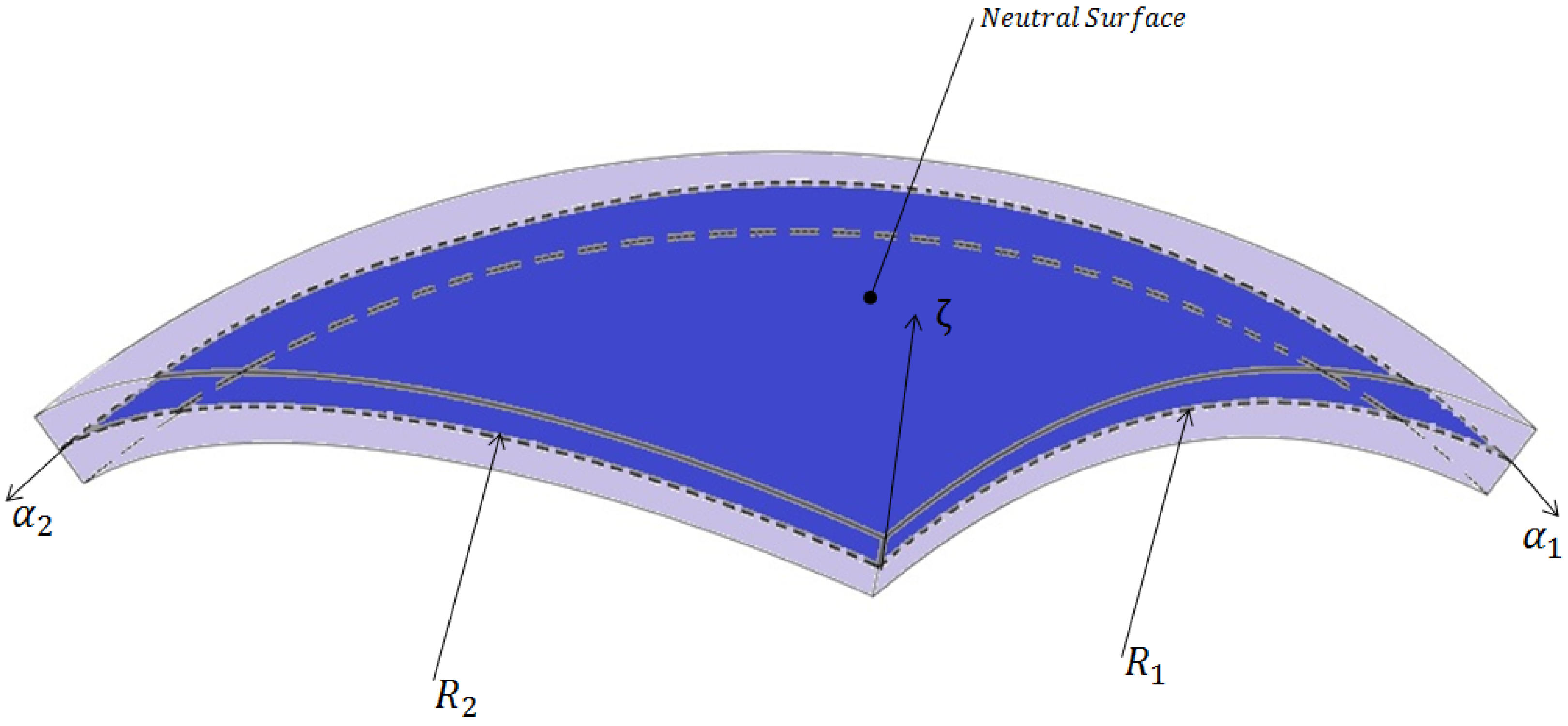
2. Brief Review of the Curvilinear Coordinate System
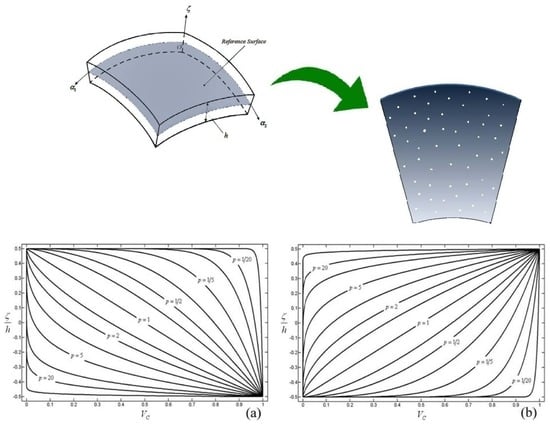
3. Functionally Graded Materials
4. Mathematical Modeling
5. Solution Procedure
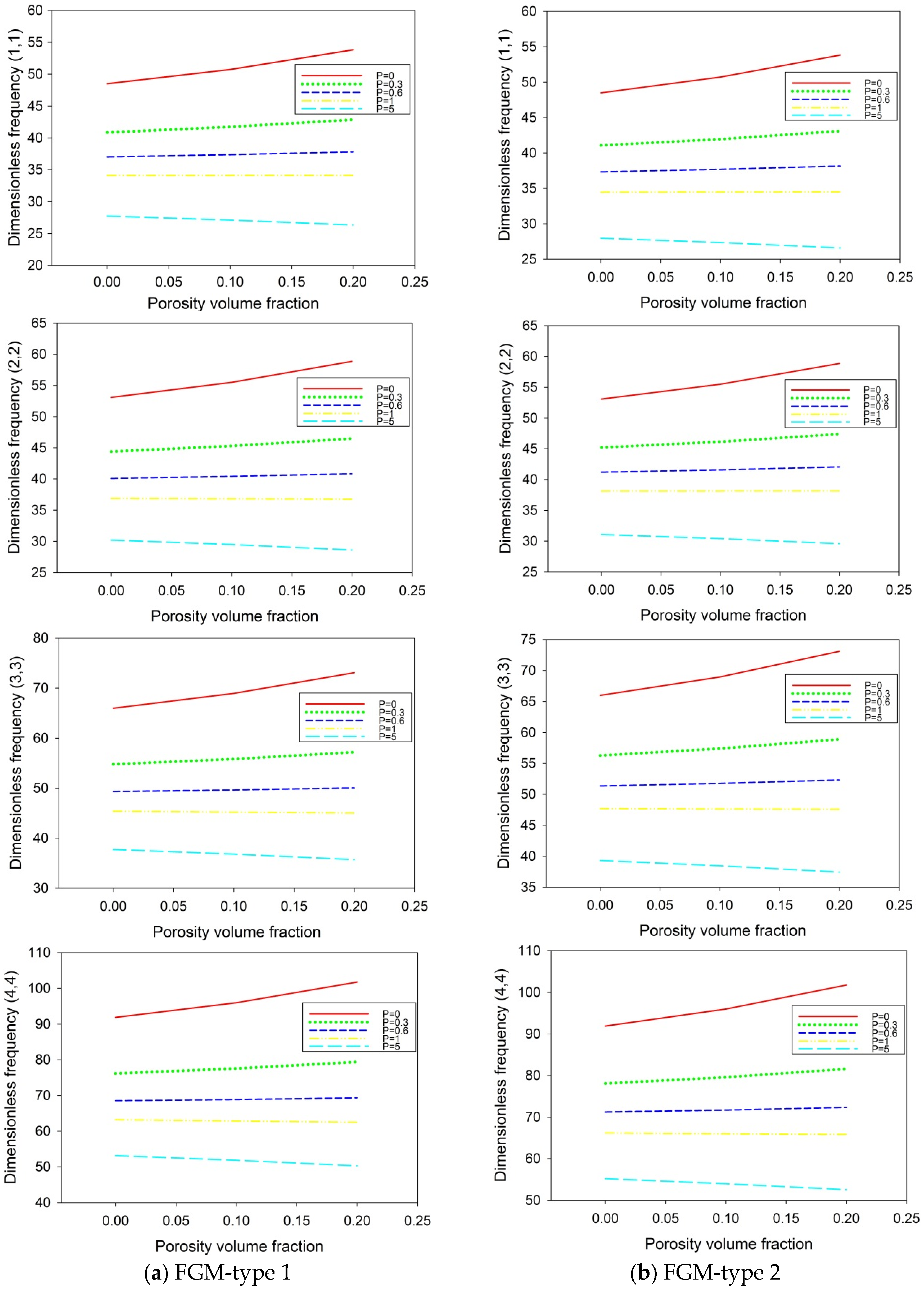
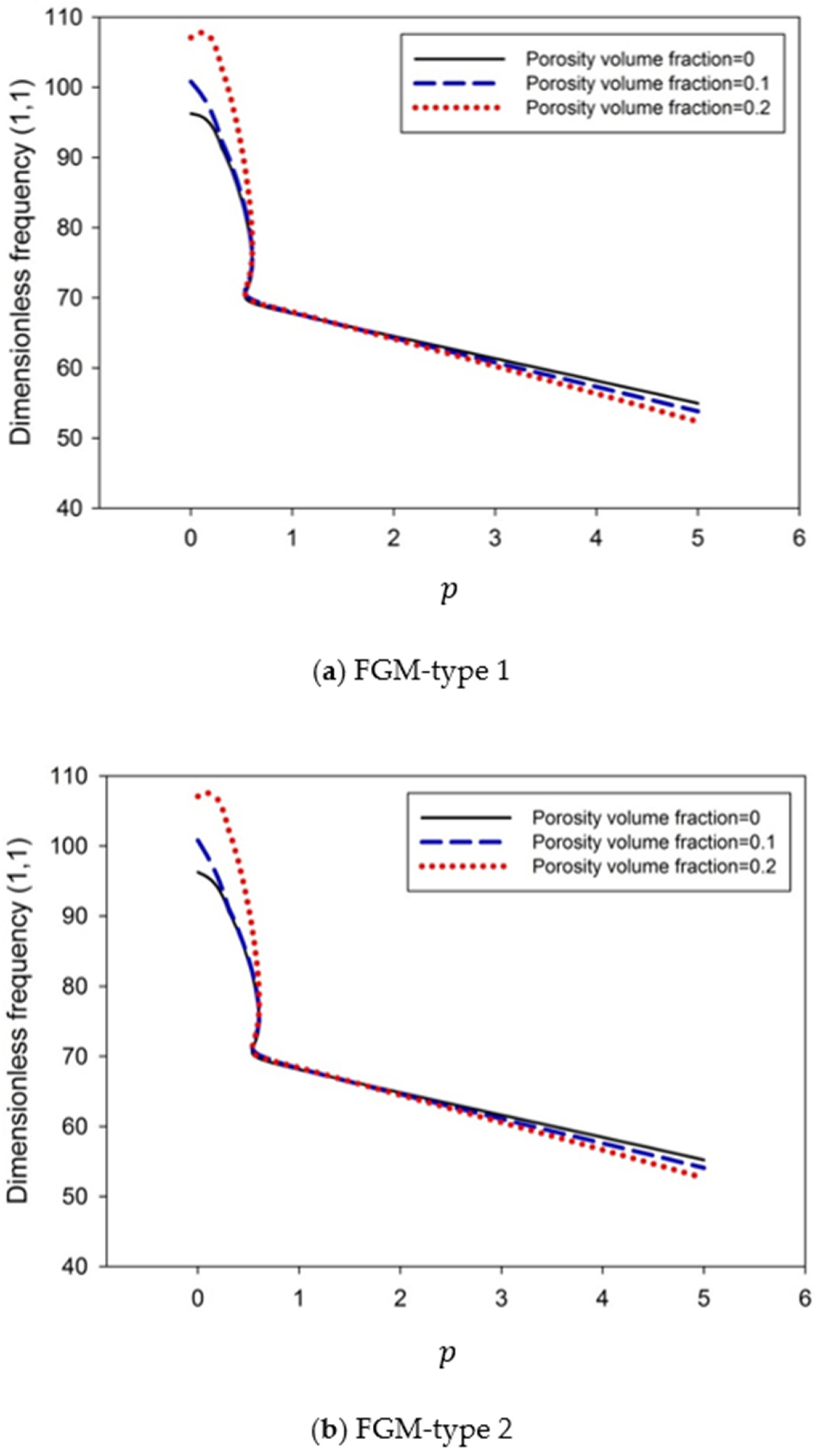
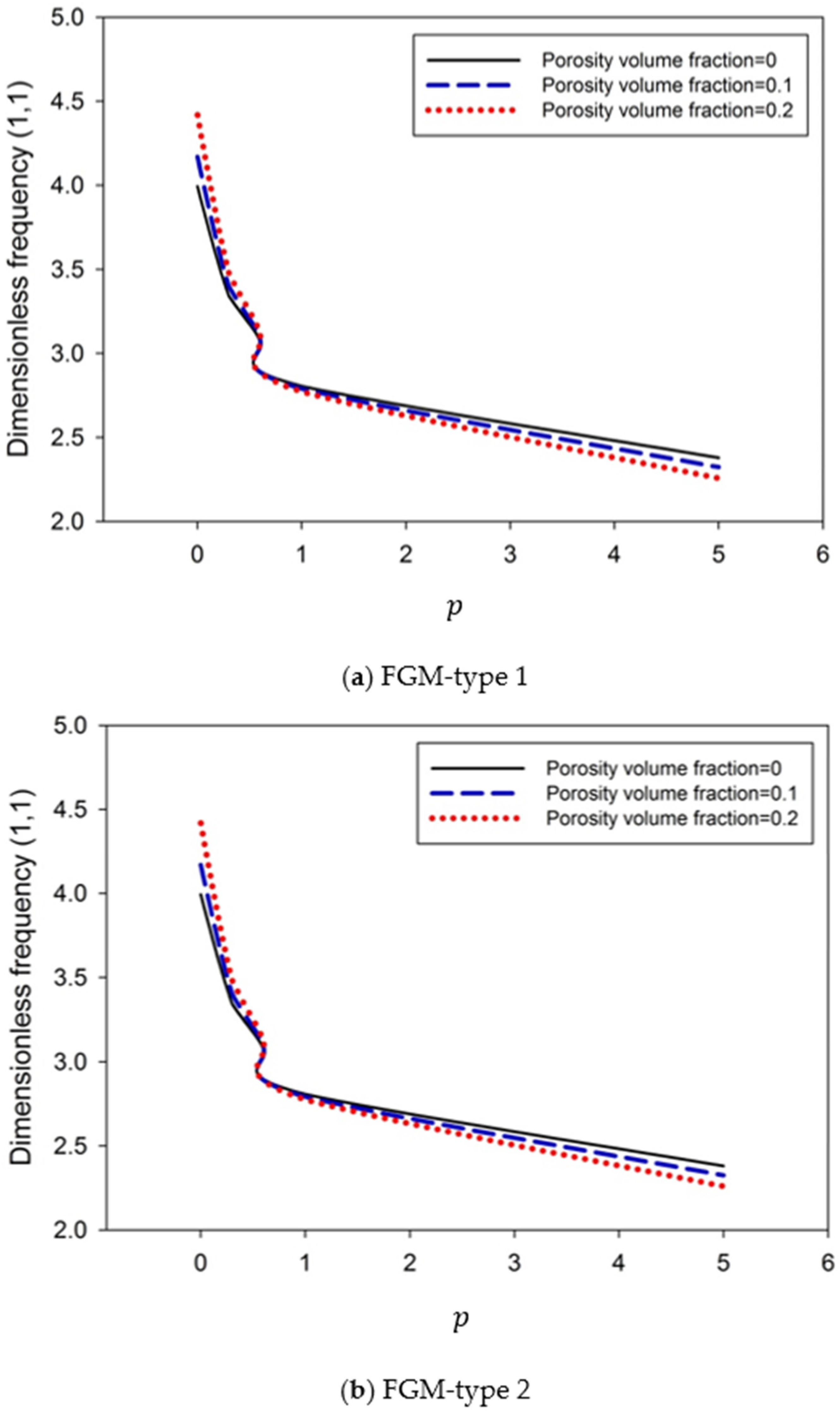
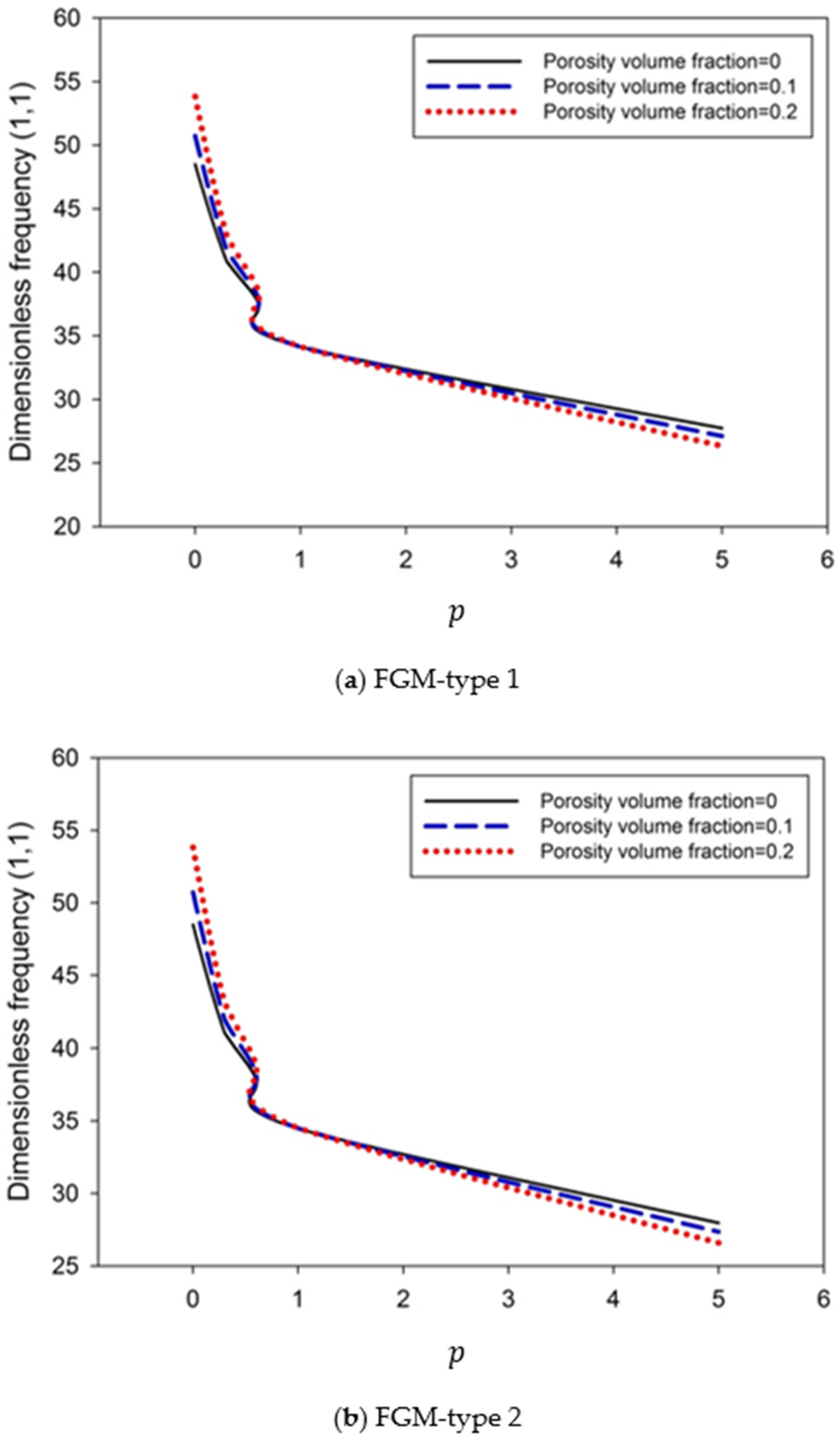
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Niino, M.; Hirai, T.; Watanabe, R. The functionally gradient materials. J. Jpn. Soc. Comp. Mater. 1987, 13, 257. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Chaikittiratana, A. An analytical investigation on free vibration of FGM doubly curved shallow shells with stiffeners under thermal environment. Aerosp. Sci. Technol. 2015, 40, 181–190. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Free vibrations of free-form doubly-curved shells made of functionally graded materials using higher-order equivalent single layer theories. Compos. Part B Eng. 2014, 67, 490–509. [Google Scholar] [CrossRef]
- Kiani, Y.; Akbarzadeh, A.H.; Chen, Z.T.; Eslami, M.R. Static and dynamic analysis of an FGM doubly curved panel resting on the Pasternak-type elastic foundation. Compos. Struct. 2012, 94, 2474–2484. [Google Scholar] [CrossRef]
- Kiani, Y.; Sadighi, M.; Eslami, M. Dynamic analysis and active control of smart doubly curved FGM panels. Compos. Struct. 2013, 102, 205–216. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Farsangi, M.A.A. An analytical solution for dynamic behavior of thick doubly curved functionally graded smart panels. Compos. Struct. 2014, 107, 88–102. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Shafiei, N.; Kazemi, M. Buckling analysis on the bi-dimensional functionally graded porous tapered nano-/micro-scale beams. Aerosp. Sci. Technol. 2017, 66, 1–11. [Google Scholar] [CrossRef]
- Shafiei, N.; Kazemi, M. Nonlinear buckling of functionally graded nano-/micro-scaled porous beams. Compos. Struct. 2017, 178, 483–492. [Google Scholar] [CrossRef]
- Shahverdi, H.; Barati, M.R. Vibration analysis of porous functionally graded nanoplates. Int. J. Eng. Sci. 2017, 120, 82–99. [Google Scholar] [CrossRef]
- Tornabene, F. Free vibrations of anisotropic doubly-curved shells and panels of revolution with a free-form meridian resting on Winkler–Pasternak elastic foundations. Compos. Struct. 2011, 94, 186–206. [Google Scholar] [CrossRef]
- Tornabene, F.; Liverani, A.; Caligiana, G. FGM and laminated doubly curved shells and panels of revolution with a free-form meridian: A 2-D GDQ solution for free vibrations. Int. J. Mech. Sci. 2011, 53, 446–470. [Google Scholar] [CrossRef]
- Tornabene, F.; Liverani, A.; Caligiana, G. General anisotropic doubly-curved shell theory: A differential quadrature solution for free vibrations of shells and panels of revolution with a free-form meridian. J. Sound Vib. 2012, 331, 4848–4869. [Google Scholar] [CrossRef]
- Viola, E.; Tornabene, F.; Fantuzzi, N. Static analysis of completely doubly-curved laminated shells and panels using general higher-order shear deformation theories. Compos. Struct. 2013, 101, 59–93. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E.; Fantuzzi, N. General higher-order equivalent single layer theory for free vibrations of doubly-curved laminated composite shells and panels. Compos. Struct. 2013, 104, 94–117. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The local GDQ method applied to general higher-order theories of doubly-curved laminated composite shells and panels: The free vibration analysis. Compos. Struct. 2014, 116, 637–660. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Accurate inter-laminar recovery for plates and doubly-curved shells with variable radii of curvature using layer-wise theories. Compos. Struct. 2015, 124, 368–393. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Neves, A.M.A.; Ferreira, A.J.M. MLSDQ based on RBFs for the free vibrations of laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 99, 30–47. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. A New Doubly-Curved Shell Element for the Free Vibrations of Arbitrarily Shaped Laminated Structures Based on Weak Formulation Isogeometric Analysis. Compos. Struct. 2017, 171, 429–461. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E.; Reddy, J.N. A Numerical Investigation on the Natural Frequencies of FGM Sandwich Shells with Variable Thickness by the Local Generalized Differential Quadrature Method. Appl. Sci. 2017, 7, 131. [Google Scholar] [CrossRef]
- Amabili, M. A new nonlinear higher-order shear deformation theory with thickness variation for large-amplitude vibrations of laminated doubly curved shells. J. Sound Vib. 2013, 332, 4620–4640. [Google Scholar] [CrossRef]
- Amabili, M. A new third-order shear deformation theory with non-linearities in shear for static and dynamic analysis of laminated doubly curved shells. Compos. Struct. 2015, 128, 260–273. [Google Scholar] [CrossRef]
- Amabili, M. Non-linearities in rotation and thickness deformation in a new third-order thickness deformation theory for static and dynamic analysis of isotropic and laminated doubly curved shells. Int. J. Nonlinear Mech. 2015, 69, 109–128. [Google Scholar] [CrossRef]
- Amabili, M. A non-linear higher-order thickness stretching and shear deformation theory for large-amplitude vibrations of laminated doubly curved shells. Int. J. Nonlinear Mech. 2014, 58, 57–75. [Google Scholar] [CrossRef]
- Amabili, M.; Reddy, J.N. A new non-linear higher-order shear deformation theory for large-amplitude vibrations of laminated doubly curved shells. Int. J. Nonlinear Mech. 2010, 45, 409–418. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Fadaee, M.; Atashipour, S.; Hosseini-Hashemi, S. Free vibration analysis of Lévy-type functionally graded spherical shell panel using a new exact closed-form solution. Int. J. Mech. Sci. 2013, 77, 227–238. [Google Scholar] [CrossRef]
- Khare, R.K.; Kant, T.; Garg, A.K. Free vibration of composite and sandwich laminates with a higher-order facet shell element. Compos. Struct. 2004, 65, 405–418. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Gangadhara Prusty, B.; Kelly, D.W.; Hoffman, M. Free vibration analysis of layered functionally graded beams with experimental validation. Mater. Design 2012, 36, 182–190. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Ungbhakorn, V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp. Sci. Technol. 2014, 32, 111–120. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Chaikittiratana, A. Flexural vibration of imperfect functionally graded beams based on Timoshenko beam theory: Chebyshev collocation method. Meccanica 2015, 50, 1331–1342. [Google Scholar] [CrossRef]
- Shafiei, N.; Mirjavadi, S.S.; Afshari, B.M.; Rabby, S.; Kazemi, M. Vibration of two-dimensional imperfect functionally graded (2D-FG) porous nano-/micro-beams. Comput. Methods Appl. Mech. Eng. 2017, 322, 615–632. [Google Scholar] [CrossRef]
- Ebraimi, F.; Zia, M. Large amplitude nonlinear vibration analysis of functionally graded Timoshenko beams with porosities. Acta Astronaut. 2015, 116, 117–125. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Generalized exponential, polynomial and trigonometric theories for vibration and stability analysis of porous FG sandwich beams resting on elastic foundations. Compos. Part B Eng. 2017, in press. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Leissa, A.W. Vibration of Shells; Acoustical Society of America: New York, NY, USA, 1993. [Google Scholar]
- Tornabene, F.; Fantuzzi, N. Mechanics of Laminated Composite Doubly-Curved Shell Structures; Esculapio: Bologna, Italy, 2014. [Google Scholar]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale Approach for Three-Phase CNT/Polymer/Fiber Laminated Nanocomposite Structures. Polym. Compos. 2017, in press. [Google Scholar] [CrossRef]


| Material | Reference | |||
|---|---|---|---|---|
| 201.04 | 0.3262 | 8166 | [27,36,38] | |
| 349.55 | 0.24 | 3800 | [27,36,38] |
| Mode () | Frequency | ||
|---|---|---|---|
| Present Study | Fadaee et al. [28] | Khare et al. [29] | |
| (1,1) | 0.52692 | 0.52864 | 0.50211 |
| (2,1) | 0.58120 | 0.58954 | 0.56247 |
| (1,2) | 0.58120 | 0.58954 | 0.56248 |
| (2,2) | 0.66757 | 0.68370 | 0.65706 |
| (3,1) | 0.73173 | 0.75974 | 0.73915 |
| (1,3) | 0.73173 | 0.75974 | 0.74035 |
| (3,2) | 0.87284 | 0.88680 | 0.86359 |
| (2,3) | 0.87284 | 0.88680 | 0.86360 |
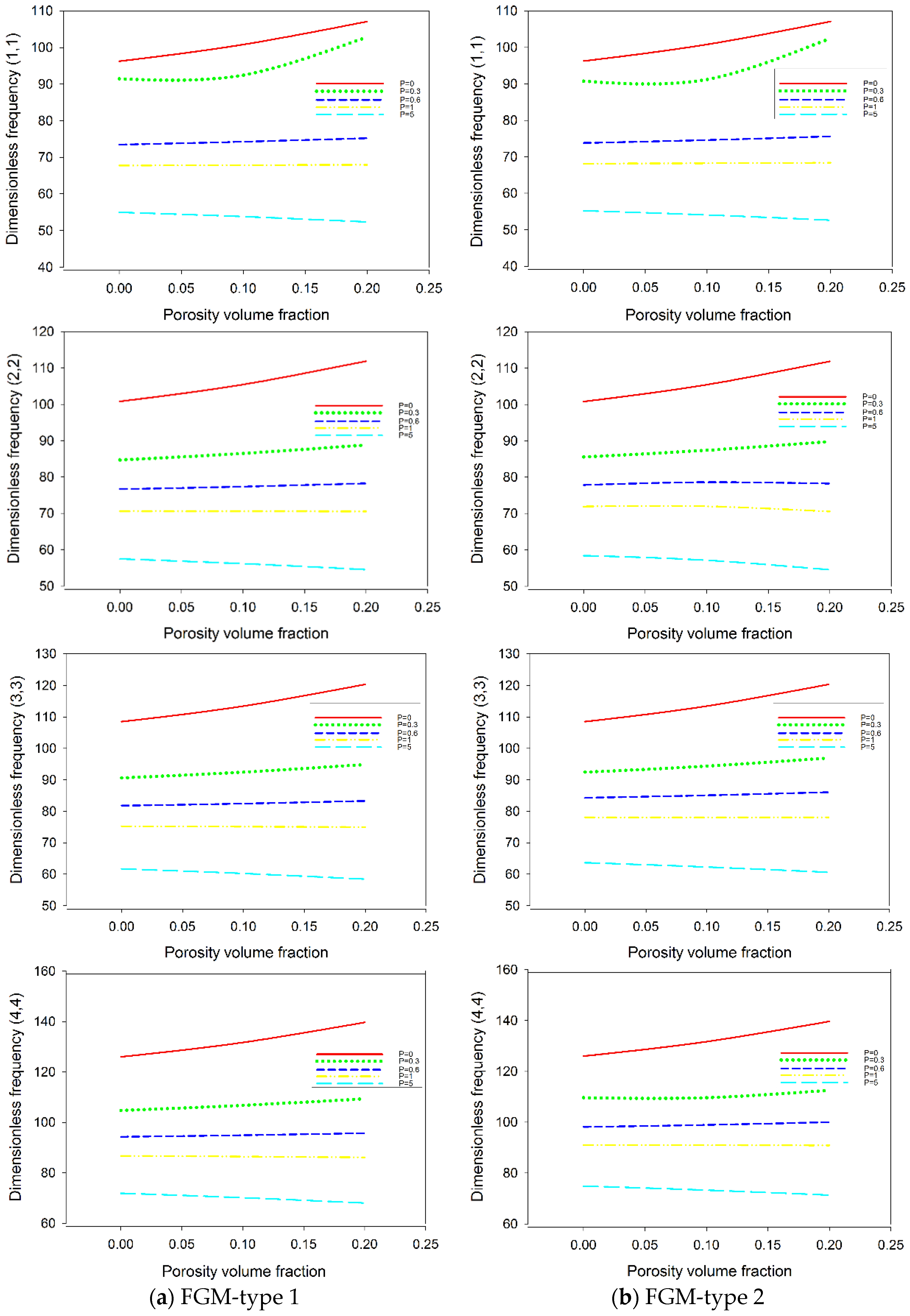
| FGM-Type 1 Power-Law Distribution | ||||||
| Porosity | Mode | |||||
| () | (1,1) | 96.2515 | 91.4707 | 73.5029 | 67.7563 | 54.9591 |
| (2,2) | 100.8020 | 84.7121 | 76.6455 | 70.5771 | 57.4624 | |
| (3,3) | 108.5000 | 90.6464 | 81.7889 | 75.2368 | 61.6982 | |
| (4,4) | 126.0190 | 104.7290 | 94.2881 | 86.7258 | 71.8939 | |
| () | (1,1) | 100.8150 | 92.4828 | 74.2942 | 67.8636 | 53.7906 |
| (2,2) | 105.4450 | 86.5088 | 77.3459 | 70.5635 | 56.1427 | |
| (3,3) | 113.4500 | 92.4888 | 82.4393 | 75.1182 | 60.2263 | |
| (4,4) | 131.7140 | 106.7500 | 94.9017 | 86.4443 | 70.1336 | |
| () | (1,1) | 107.0910 | 102.8620 | 75.2655 | 67.9668 | 52.3336 |
| (2,2) | 111.8720 | 88.8384 | 78.2284 | 70.5396 | 54.5219 | |
| (3,3) | 120.3260 | 94.8992 | 83.2761 | 74.9779 | 58.4334 | |
| (4,4) | 139.6680 | 109.4300 | 95.7237 | 86.1258 | 68.0135 | |
| FGM-type 2 Power-law distribution | ||||||
| Porosity | Mode | |||||
| () | (1,1) | 96.2515 | 90.7627 | 73.8184 | 68.1096 | 55.2069 |
| (2,2) | 100.8020 | 85.5775 | 77.8421 | 71.9234 | 58.4065 | |
| (3,3) | 108.5000 | 92.4549 | 84.2883 | 78.0465 | 63.6580 | |
| (4,4) | 126.0190 | 109.6880 | 98.1258 | 91.0358 | 74.8731 | |
| () | (1,1) | 100.8150 | 91.2313 | 74.6290 | 68.2372 | 54.0529 |
| (2,2) | 105.4450 | 87.4252 | 78.6036 | 71.9729 | 57.1317 | |
| (3,3) | 113.4500 | 94.4013 | 85.0632 | 78.0563 | 62.2761 | |
| (4,4) | 131.7140 | 109.6880 | 98.9337 | 90.9554 | 73.2497 | |
| () | (1,1) | 107.0910 | 102.4517 | 75.6247 | 68.3659 | 52.6147 |
| (2,2) | 111.8720 | 89.8218 | 78.2284 | 70.5396 | 54.5219 | |
| (3,3) | 120.3260 | 96.9495 | 86.0617 | 78.0819 | 60.6011 | |
| (4,4) | 139.6680 | 112.580 | 100.0080 | 90.8967 | 71.3080 | |
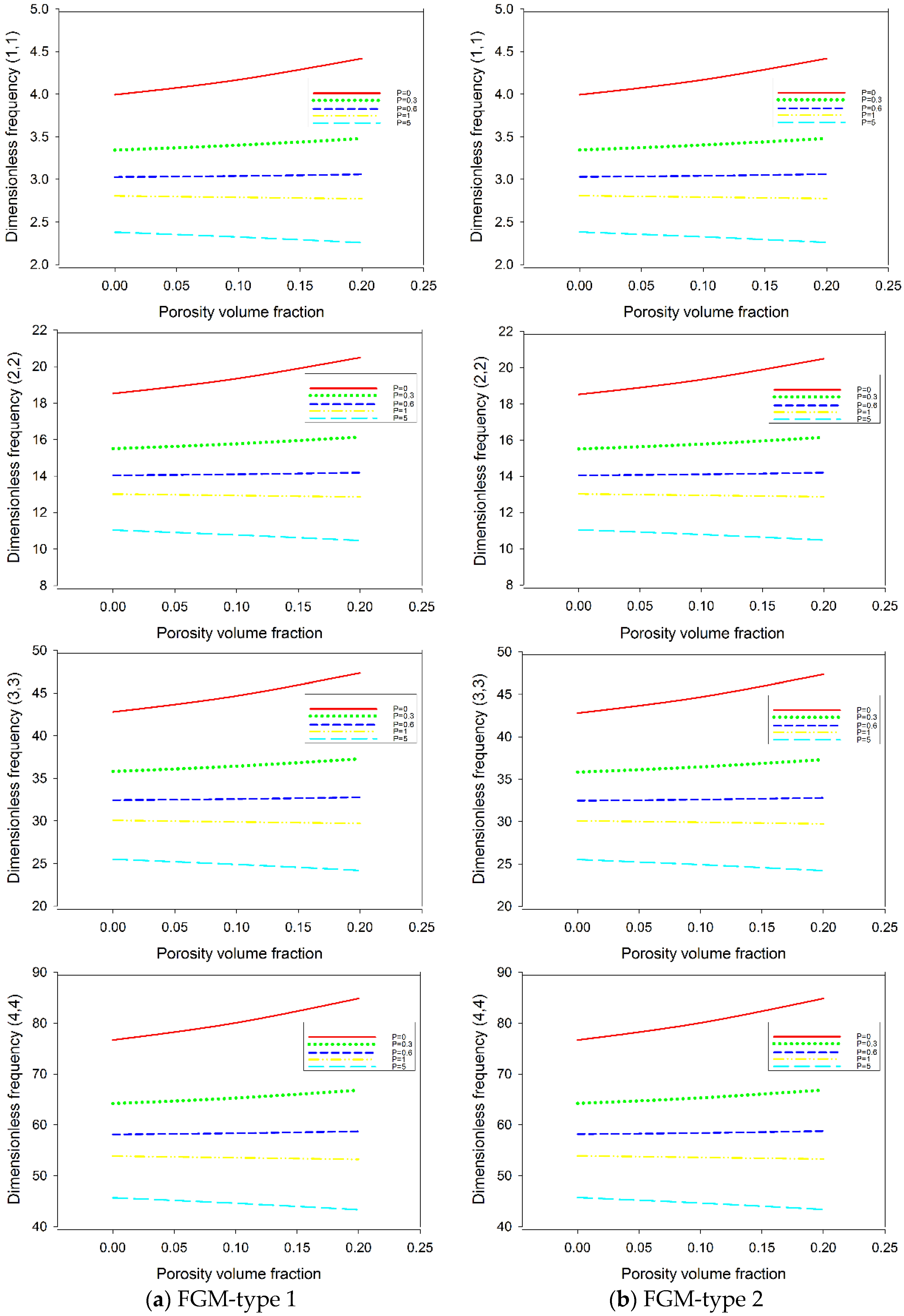
| FGM-1 Power-Law Distribution | ||||||
| Porosity | Mode | |||||
| () | (1,1) | 3.9944 | 3.3438 | 3.0276 | 2.8052 | 2.3793 |
| (2,2) | 18.5237 | 15.5060 | 14.0398 | 13.0083 | 11.0330 | |
| (3,3) | 42.7974 | 35.8247 | 32.4370 | 30.0536 | 25.4874 | |
| (4,4) | 76.6832 | 64.1885 | 58.1186 | 53.8474 | 45.6605 | |
| () | (1,1) | 4.1700 | 3.4012 | 3.0393 | 2.7886 | 2.3225 |
| (2,2) | 19.3382 | 15.7725 | 14.0941 | 12.9312 | 10.7696 | |
| (3,3) | 44.6804 | 36.4414 | 32.5633 | 29.8764 | 24.8799 | |
| (4,4) | 80.0601 | 65.2962 | 58.3473 | 53.5324 | 44.5732 | |
| () | (1,1) | 4.41884 | 3.4809 | 3.05829 | 2.7712 | 2.2566 |
| (2,2) | 20.4929 | 16.1423 | 14.1826 | 12.8511 | 10.4639 | |
| (3,3) | 47.3497 | 37.2966 | 32.769 | 29.6925 | 24.1744 | |
| (4,4) | 84.8460 | 66.8307 | 58.7183 | 53.2052 | 43.3115 | |
| FGM-2 Power-law distribution | ||||||
| Porosity | Mode | |||||
| () | (1,1) | 3.9944 | 3.3452 | 3.0297 | 2.8076 | 2.3810 |
| (2,2) | 18.5237 | 15.5136 | 14.0507 | 13.0208 | 11.0420 | |
| (3,3) | 42.7974 | 35.8428 | 32.4627 | 30.0831 | 25.5091 | |
| (4,4) | 76.6832 | 64.2209 | 58.1647 | 53.9003 | 45.6995 | |
| () | (1,1) | 4.1700 | 3.40289 | 3.04161 | 2.79127 | 2.32458 |
| (2,2) | 19.3382 | 15.7814 | 14.1061 | 12.9450 | 10.7798 | |
| (3,3) | 44.6804 | 36.4616 | 32.5917 | 29.9089 | 24.9039 | |
| (4,4) | 80.0601 | 65.3321 | 58.3983 | 53.5908 | 44.6171 | |
| () | (1,1) | 4.41884 | 3.4828 | 3.0610 | 2.7743 | 2.2590 |
| (2,2) | 20.4929 | 16.1518 | 14.1962 | 12.8666 | 10.4754 | |
| (3,3) | 47.3497 | 37.3192 | 32.8007 | 29.7287 | 24.2014 | |
| (4,4) | 84.8460 | 66.8714 | 58.7752 | 53.2703 | 43.3601 | |
| FGM-1 Power-Law Distribution | ||||||
| Porosity | Mode | |||||
| () | (1,1) | 48.4942 | 40.8660 | 37.0253 | 34.1183 | 27.7268 |
| (2,2) | 53.0808 | 44.3991 | 40.0824 | 36.8778 | 30.1956 | |
| (3,3) | 65.9875 | 54.7970 | 49.3207 | 45.3731 | 37.7164 | |
| (4,4) | 91.8995 | 76.1928 | 68.5752 | 63.1903 | 53.1539 | |
| () | (1,1) | 50.7297 | 41.7402 | 37.3740 | 34.1238 | 27.0979 |
| (2,2) | 55.500 | 45.3040 | 40.4061 | 36.8257 | 29.4760 | |
| (3,3) | 68.9586 | 55.8377 | 49.6220 | 45.2055 | 36.7869 | |
| (4,4) | 95.9954 | 77.5601 | 68.8955 | 62.8567 | 51.8369 | |
| () | (1,1) | 53.8218 | 42.8723 | 37.8124 | 34.1267 | 26.3250 |
| (2,2) | 58.8601 | 46.4870 | 40.8218 | 36.7640 | 28.5992 | |
| (3,3) | 73.1141 | 57.2240 | 50.0319 | 45.0178 | 35.6715 | |
| (4,4) | 101.7600 | 79.4159 | 69.3675 | 62.4923 | 50.2788 | |
| FGM-2 Power-law distribution | ||||||
| Porosity | Mode | |||||
| () | (1,1) | 48.4942 | 41.0805 | 37.3222 | 34.4526 | 27.9614 |
| (2,2) | 53.0808 | 45.2115 | 41.2050 | 38.1398 | 31.0770 | |
| (3,3) | 65.9875 | 56.2839 | 51.3764 | 47.6810 | 39.3077 | |
| (4,4) | 91.8995 | 78.1084 | 71.2254 | 66.1625 | 55.1808 | |
| () | (1,1) | 50.7297 | 41.9677 | 37.6866 | 34.4744 | 27.3442 |
| (2,2) | 55.500 | 46.1629 | 41.5841 | 38.1448 | 30.3976 | |
| (3,3) | 68.9586 | 57.4109 | 51.7815 | 47.6209 | 38.4507 | |
| (4,4) | 95.9954 | 79.5895 | 71.6842 | 65.9730 | 53.9575 | |
| () | (1,1) | 53.8218 | 43.1169 | 38.1453 | 34.4984 | 26.5867 |
| (2,2) | 58.8601 | 47.4074 | 42.0719 | 38.1571 | 29.5735 | |
| (3,3) | 73.1141 | 58.9107 | 52.3262 | 47.5720 | 37.4298 | |
| (4,4) | 101.760 | 81.5943 | 72.3353 | 65.7942 | 52.5205 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare Jouneghani, F.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Free Vibration Analysis of Functionally Graded Porous Doubly-Curved Shells Based on the First-Order Shear Deformation Theory. Appl. Sci. 2017, 7, 1252. https://doi.org/10.3390/app7121252
Zare Jouneghani F, Dimitri R, Bacciocchi M, Tornabene F. Free Vibration Analysis of Functionally Graded Porous Doubly-Curved Shells Based on the First-Order Shear Deformation Theory. Applied Sciences. 2017; 7(12):1252. https://doi.org/10.3390/app7121252
Chicago/Turabian StyleZare Jouneghani, Farajollah, Rossana Dimitri, Michele Bacciocchi, and Francesco Tornabene. 2017. "Free Vibration Analysis of Functionally Graded Porous Doubly-Curved Shells Based on the First-Order Shear Deformation Theory" Applied Sciences 7, no. 12: 1252. https://doi.org/10.3390/app7121252
APA StyleZare Jouneghani, F., Dimitri, R., Bacciocchi, M., & Tornabene, F. (2017). Free Vibration Analysis of Functionally Graded Porous Doubly-Curved Shells Based on the First-Order Shear Deformation Theory. Applied Sciences, 7(12), 1252. https://doi.org/10.3390/app7121252