Atmospheric Attenuation Correction Based on a Constant Reference for High-Precision Infrared Radiometry
Abstract
1. Introduction
2. High Dynamic Infrared (IR) Radiometry Based on a Constant Reference
2.1. High-Speed Calibration
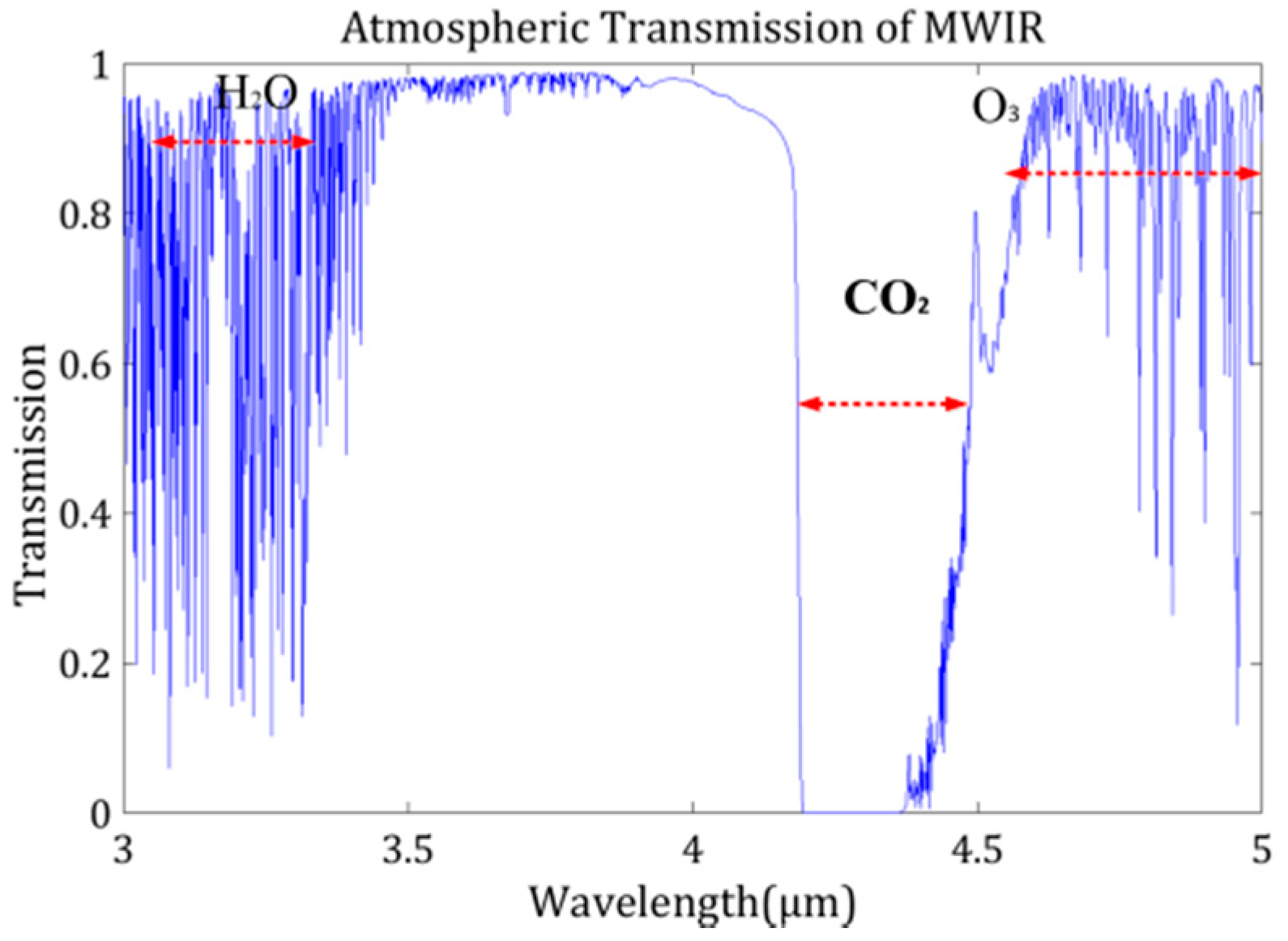
2.2. Atmospheric Transmittance Correction Based on a Constant Reference
3. Experimental Results
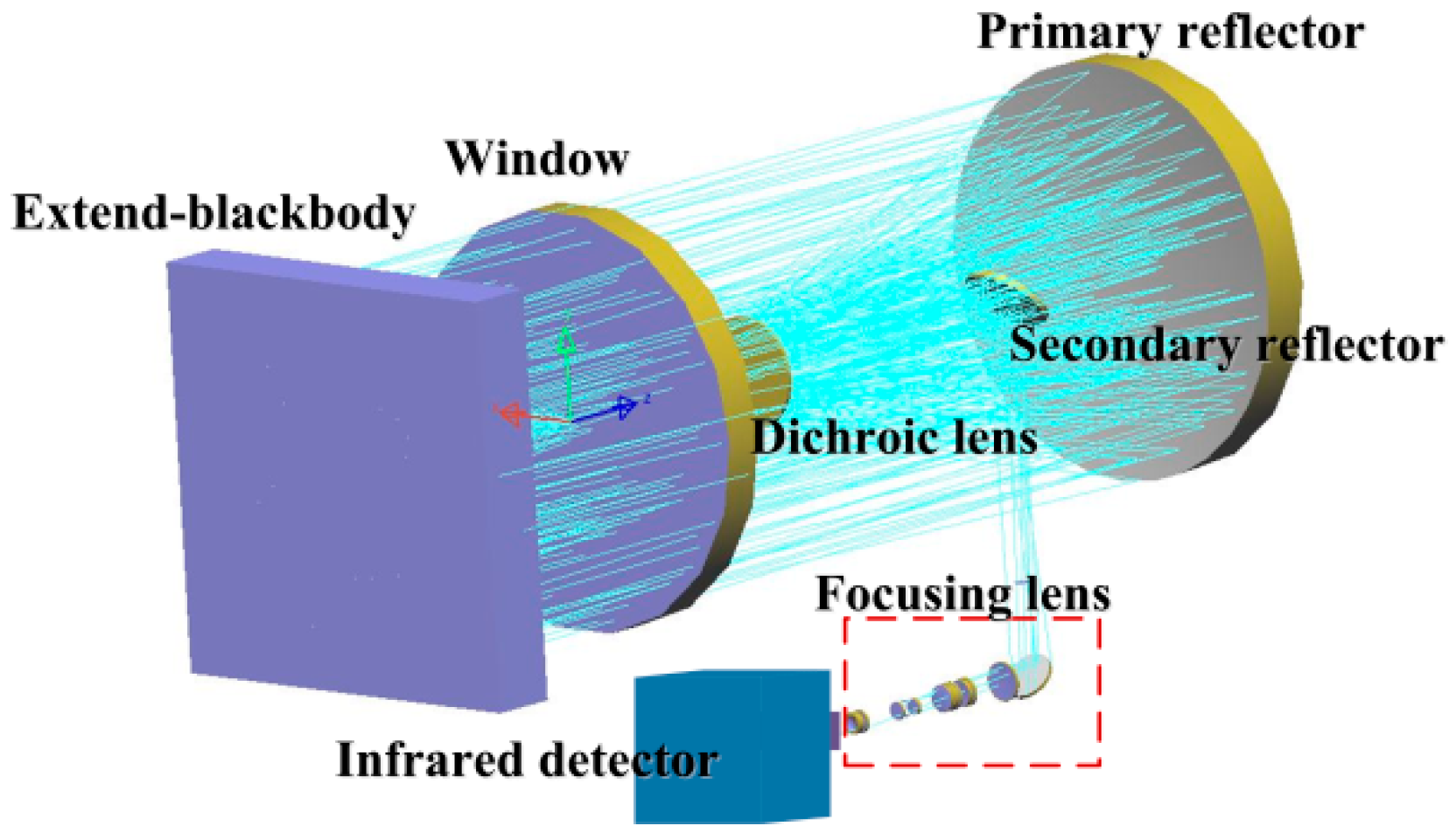
3.1. Experimental Setup
3.2. High-Speed Calibration
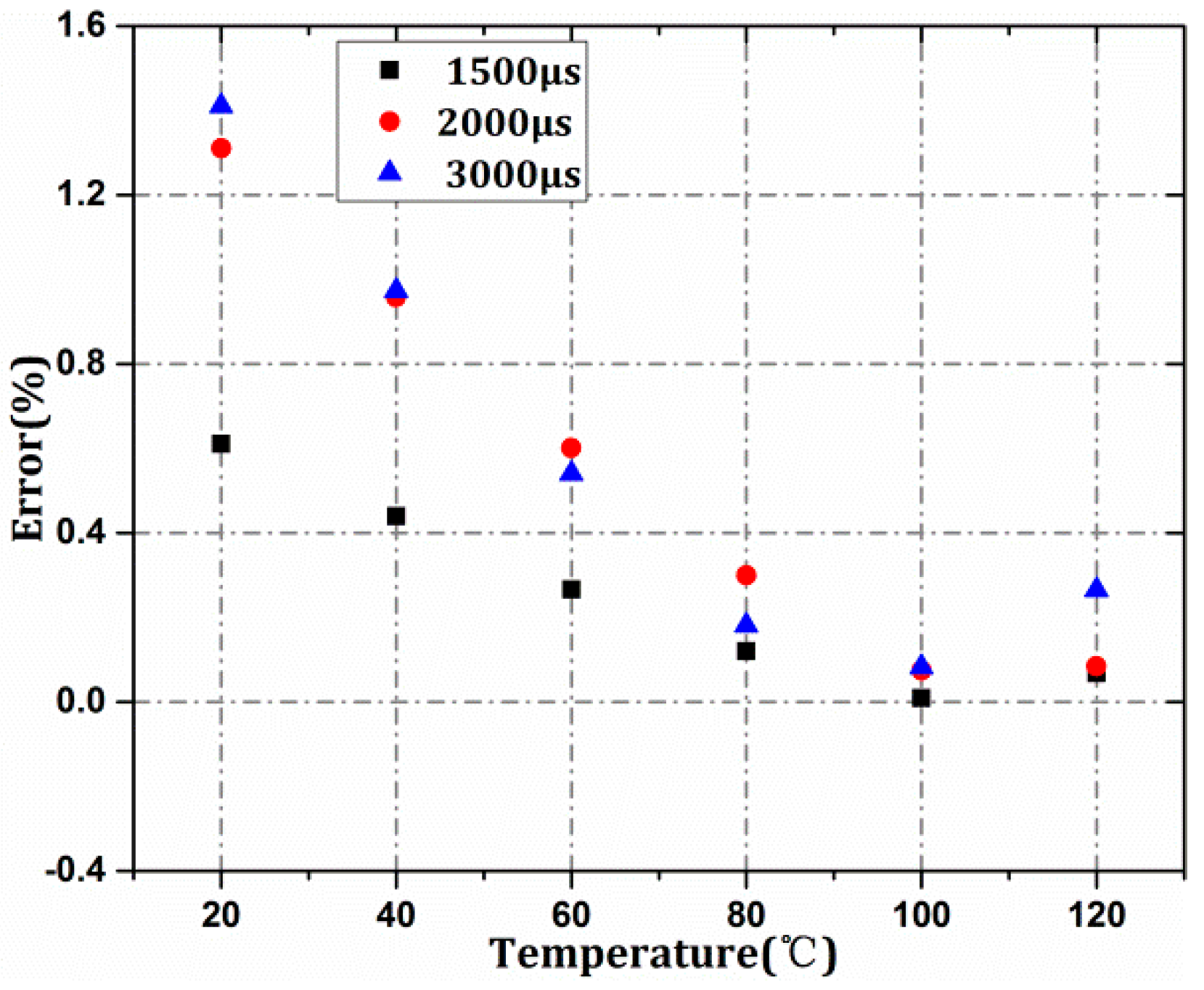
3.3. Atmospheric Transmittance Calculation
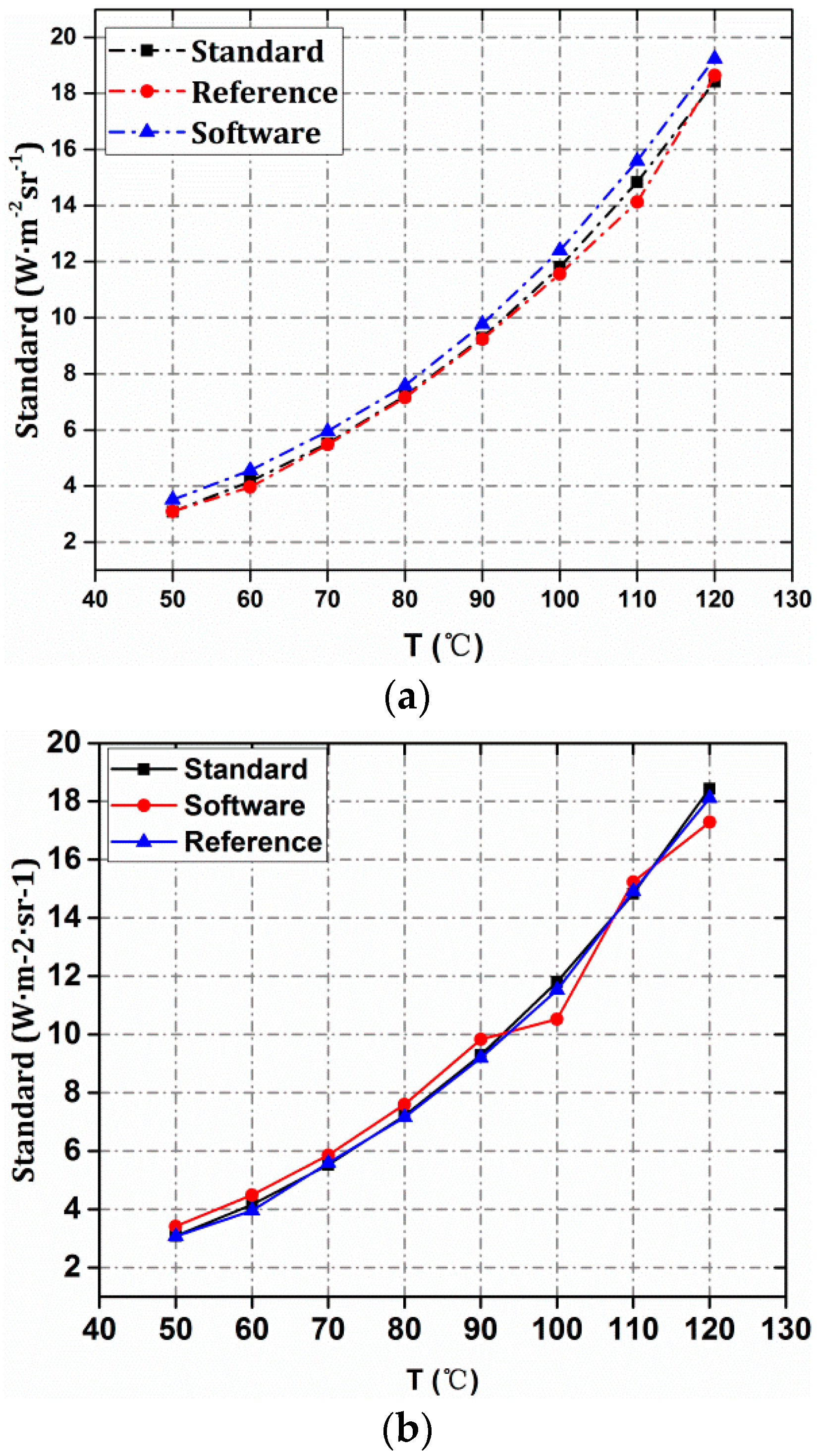
3.4. Radiometry of an IR Target
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Chang, S.; Zhu, W.; Sun, Z. Radiometric calibration method for large aperture infrared system with broad dynamic range. Appl. Opt. 2015, 54, 4659–4666. [Google Scholar]
- Chang, S.; Li, M.; Sun, Z.; Zhang, Y. Method to remove the effect of ambient temperature on radiometric calibration. Appl. Opt. 2014, 53, 6274–6279. [Google Scholar]
- Roney, P.L.; Findlay, F.D.; Blanchard, A.; Cann, M.W.P.; Nicholls, R.W. Atmospheric transmittance in the region near the 4.3-microm band head of CO2. Opt. Lett. 1981, 6, 151–153. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Chen, X.; Rao, R.; Wang, Y.; Yang, P. A moderate-spectral-resolution transmittance model based on fitting the line-by-line calculation. Opt. Express 2007, 15, 8360–8370. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Liu, Y.; Wang, Z.; Cheng, Y.; Gu, Y.; Wen, F. Comparison between infrared and microwave radiometers for retrieving the sea surface temperature. Mar. Sci. Bull. 2007, 11, 3–10. [Google Scholar]
- Wei, H.L.; Chen, X.H.; Zhan, J.; Rao, R. Atmospheric correction in the measurement of infrared radiance. J. Atmos. Environ. Opt. 2007, 2, 472–478. [Google Scholar]
- Han, Y.G.; Xuan, Y.M. Effect of atmospherictransmission on IR radiation feature of target and background. J. Appl. Opt. 2002, 23, 8–11. [Google Scholar]
- Acharya, P.K.; Berk, A.; Anderson, G.P.; Larsen, N.F.; Tsay, S.C.; Stamnes, K.H. MODTRAN4: Multiple scattering and bidirectional reflectance distribution function (BRDF) upgrades to MODTRAN. Proc. SPIE Int. Soc. Opt. Eng. 1999, 3756, 354–362. [Google Scholar]
- Ochs, M.; Schulz, A.; Bauer, H.J. High dynamic range infrared thermography by pixel wise radiometric self-calibration. Infrared Phys. Technol. 2010, 53, 112–119. [Google Scholar] [CrossRef]
- Samantaray, N.; Ruo-berchera, I.; Meda, A.; Genovese, M. Realization of the first sub-shot-noise wide field microscope. Light Sci. Appl. 2017, 6, e17005. [Google Scholar] [CrossRef]
- Zhang, T.S.; Liu, W.Q.; Gao, M.G.; Lu, Y.H.; Liu, J.G.; Liu, C.; Xu, L.; Zhu, J. The study of infrared background radiation of earth and atmosphere by airborne FTIR spectrometer. Spectrosc. Spectr. Anal. 2006, 26, 1018–1021. [Google Scholar]
- Zhu, J.; Liu, W.Q.; Lu, Y.H. Research on radiance measurements of target and background based on FTIR. Infrared Technol. 2004, 26, 52–55. [Google Scholar]
- Wei, H.; Chen, X.; Dai, C. Combined atmospheric radiative transfer (CART) model and its applications. Infrared Laser Eng. 2012, 41, 3360–3366. [Google Scholar]
- Richards, A. Atmospheric effects on infrared imaging systems. Proc. SPIE 2005, 5987, 1–14. [Google Scholar] [CrossRef]
- Yang, T.; Jin, G.F.; Zhu, J. Automated design of freeform imaging systems. Light Sci. Appl. 2017, 6, e17081. [Google Scholar]
- Yan, M.; Luo, P.L.; Iwakuni, K.; Millot, G.; Hänsch, T.W.; Picqué, N. Mid-infrared dual-comb spectroscopy with electro-optic modulators. Light Sci. Appl. 2017, 6, e17076. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN 2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Chen, X.; Wei, H. A Combined atmospheric radiative transfer model (CART): A review and applications. J. Opt. Soc. Korea 2010, 14, 190–198. [Google Scholar] [CrossRef]
- Wang, W.H.; Niu, Z.D.; Chen, Z.P. Research on the operating range of staring IR imaging system in sea-sky background. J. Infrared Millim. Waves 2006, 25, 150–152. [Google Scholar]
- Wei, H.L.; Chen, X.H.; Rao, R.Z. Introduction to the combined atmospheric radiative transfer software CART. J. Atmos. Environ. Opt. 2007, 2, 446–450. [Google Scholar]
- Rodrigo, D.; Tittl, A.; Limaj, O.; de Abajo, F.J.G.; Pruneri, V.; Altug, H. Double-layer graphene for enhanced tunable infrared plasmonics. Light Sci. Appl. 2017, 6, e16277. [Google Scholar] [CrossRef]
- Xu, Q.; Ma, T.; Danesh, M.; Shivananju, B.N.; Gan, S.; Song, J.; Qiu, C.W.; Cheng, H.M.; Ren, W.; Bao, Q. Effects of edge on graphene plasmons as revealed by infrared nanoimaging. Light Sci. Appl. 2017, 6, e16204. [Google Scholar] [CrossRef]


| t/μs | 2000 | 3000 | 3500 |
|---|---|---|---|
| G/DN | 3421 | 5073 | 5896 |
| τ | 0.7924 | 0.8002 | 0.8005 |
| 2000 μs | 3000 μs | ||||
|---|---|---|---|---|---|
| T/°C | Error of Software (%) | Error of Reference (%) | T/°C | Error of Software (%) | Error of Reference (%) |
| 50 | 13.81 | 0.27 | 50 | 10.73 | 0.26 |
| 60 | 9.57 | 4.83 | 60 | 7.84 | 4.89 |
| 70 | 7.77 | 0.84 | 70 | 6.08 | 1.23 |
| 80 | 5.14 | 0.78 | 80 | 5.31 | 0.73 |
| 90 | 5.19 | 0.58 | 90 | 5.83 | 1.02 |
| 100 | 4.96 | 2.11 | 100 | −10.86 | 2.41 |
| 110 | 5.14 | 4.78 | 110 | 2.72 | 0.56 |
| 120RMS | 4.427.63% | 1.172.67% | 120RMS | −6.197.41% | 1.712.12% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Yin, L.; Wang, J.; Li, H. Atmospheric Attenuation Correction Based on a Constant Reference for High-Precision Infrared Radiometry. Appl. Sci. 2017, 7, 1165. https://doi.org/10.3390/app7111165
Huang Z, Yin L, Wang J, Li H. Atmospheric Attenuation Correction Based on a Constant Reference for High-Precision Infrared Radiometry. Applied Sciences. 2017; 7(11):1165. https://doi.org/10.3390/app7111165
Chicago/Turabian StyleHuang, Zhiguo, Limei Yin, Jianli Wang, and Hongzhuang Li. 2017. "Atmospheric Attenuation Correction Based on a Constant Reference for High-Precision Infrared Radiometry" Applied Sciences 7, no. 11: 1165. https://doi.org/10.3390/app7111165
APA StyleHuang, Z., Yin, L., Wang, J., & Li, H. (2017). Atmospheric Attenuation Correction Based on a Constant Reference for High-Precision Infrared Radiometry. Applied Sciences, 7(11), 1165. https://doi.org/10.3390/app7111165





