Impact of Graphene on the Polarizability of a Neighbour Nanoparticle: A Dyadic Green’s Function Study
Abstract
1. Introduction
2. Dyadic Green’s Function for the Electric Field
2.1. Free-Space Dyadic Green’s Function
2.2. Weyl’s or Angular Spectrum Representation of the Dyadic Green’s Function: A Useful Formulation for Interfaces
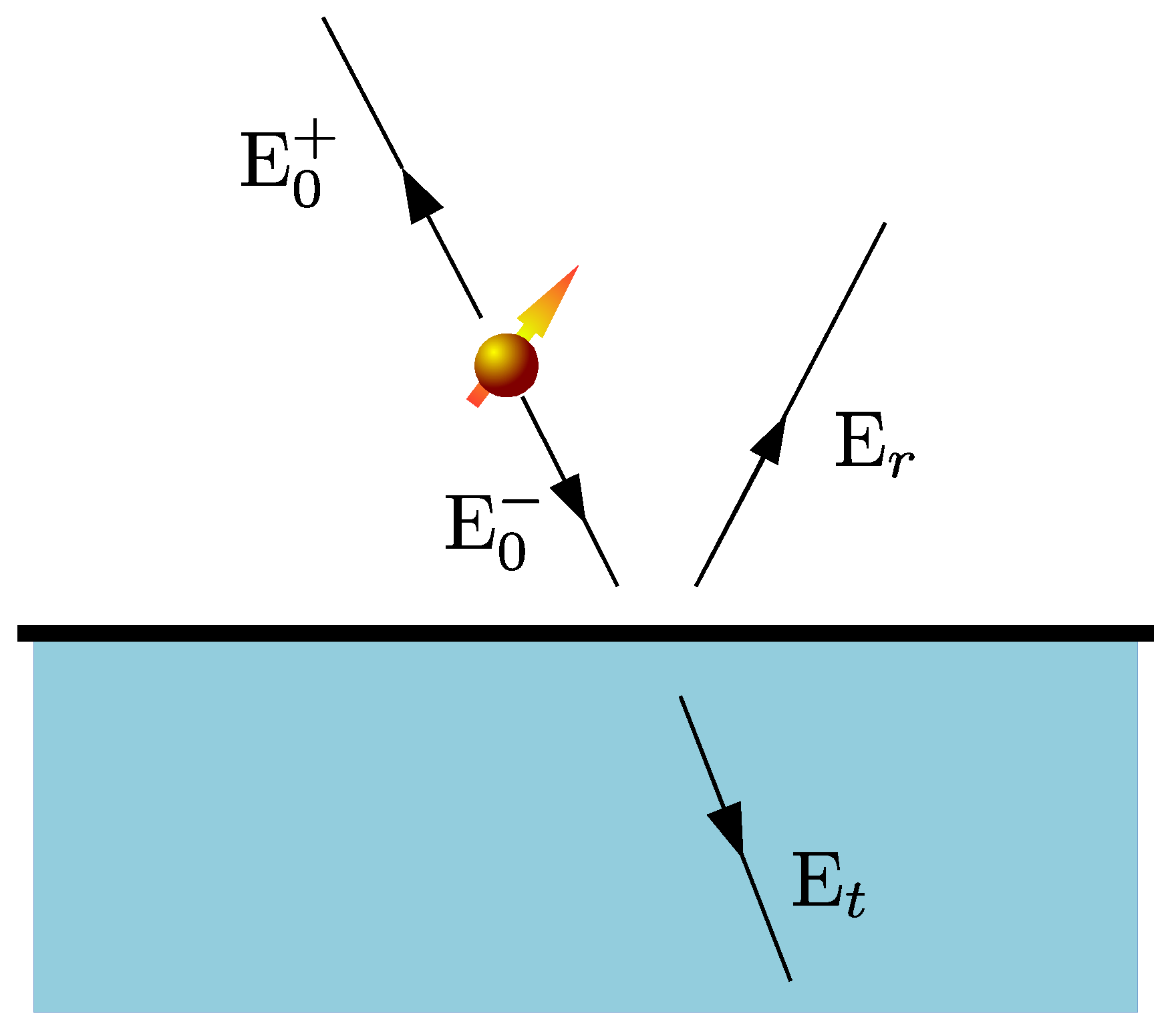
2.3. Source and Scattered Green’s Functions: Scattering at a Planar Interface
3. Renormalization of the Polarizability of a Quantum Emitter Near a Graphene Sheet and a Graphene-Based Grating
3.1. Polarizability of a Quantum Emitter in a Homogeneous Medium
3.2. Polarizability of a Quantum Emitter in Proximity to a Planar Interface
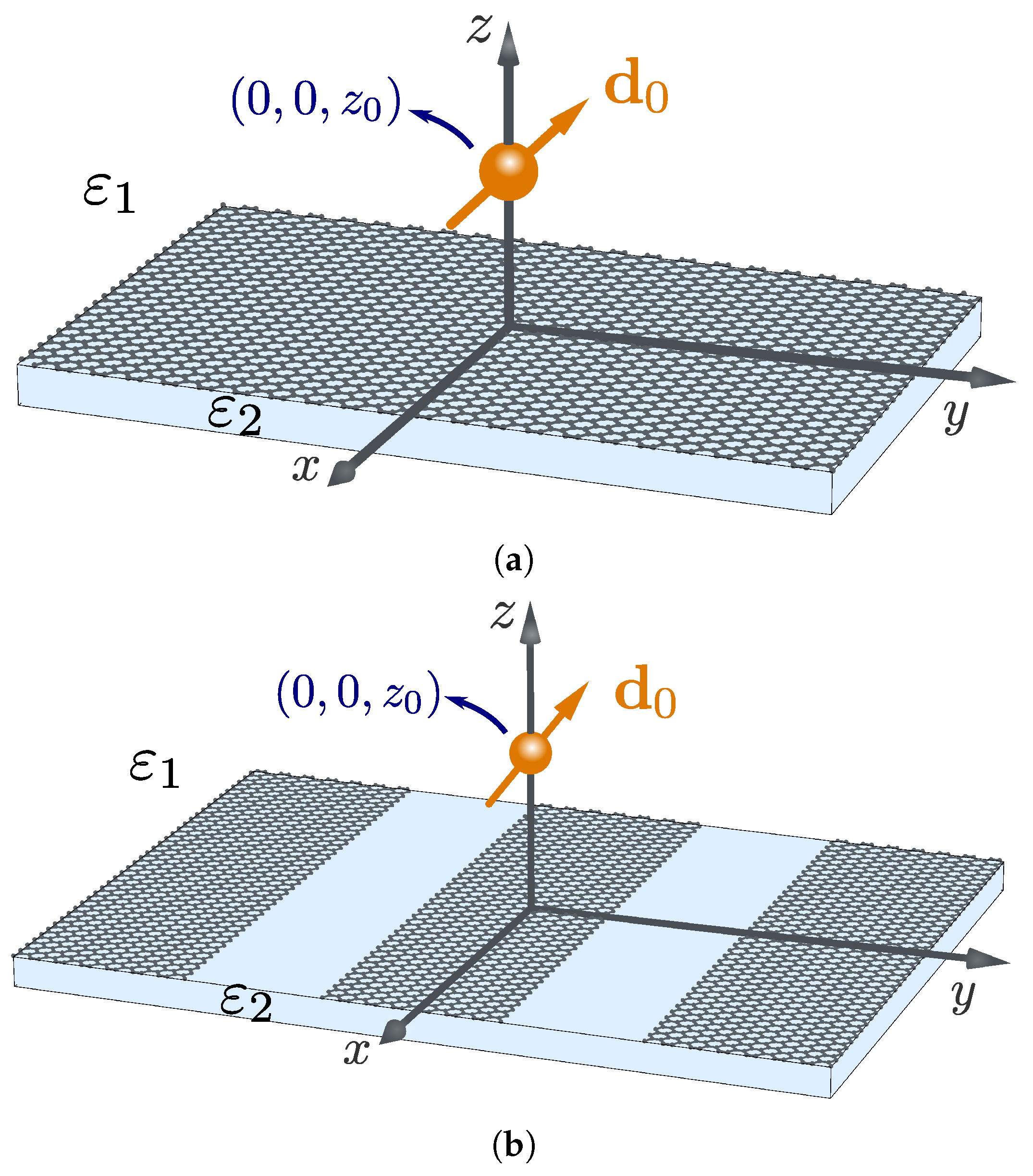
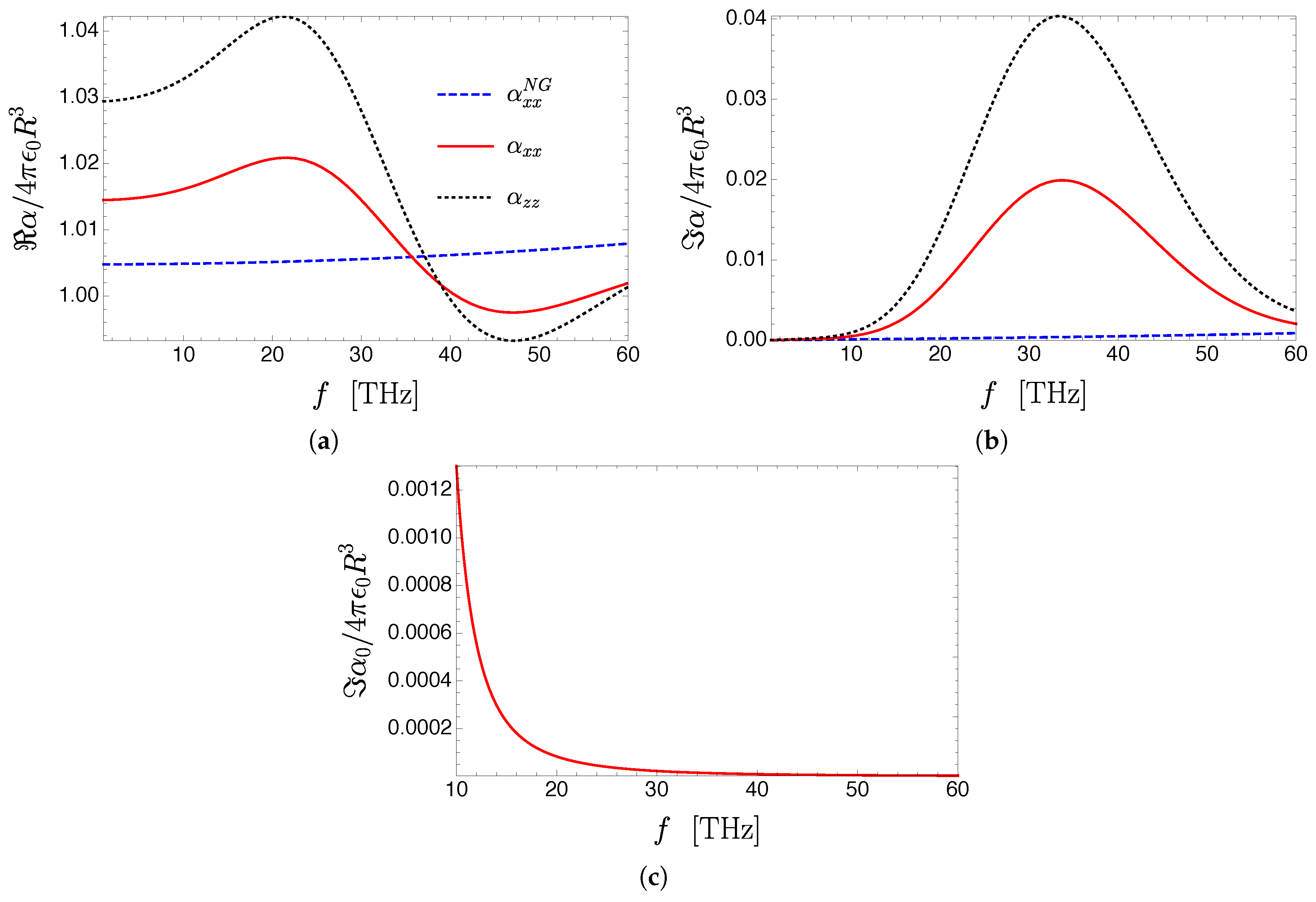
3.3. Renormalized Polarizability of an Isotropic Quantum Emitter Near a Continuous Graphene Sheet
3.4. Renormalized Polarizability of an Isotropic Quantum Emitter Near a Plasmonic Graphene Grating
3.4.1. Optical Properties of a Plasmonic Graphene Grating
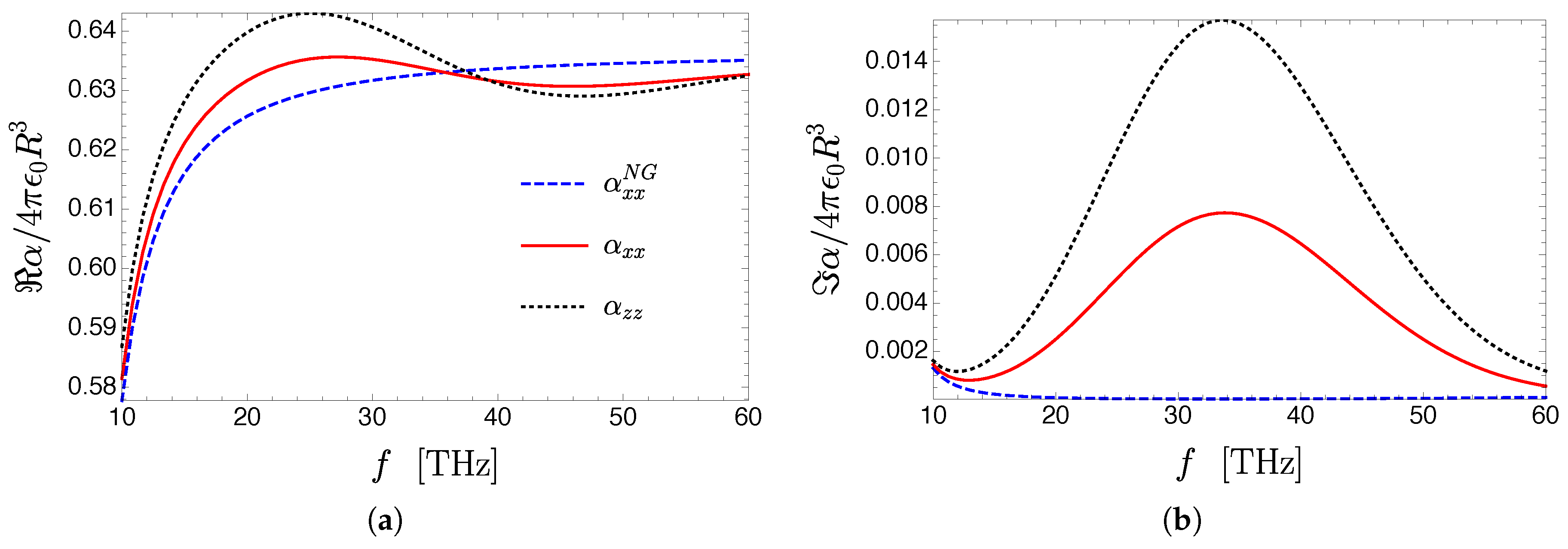
3.4.2. Renormalization of the Polarizability of a Quantum Emitter
4. Extension of the Formalism When the Quantum Emitter Has Both an Electric and a Magnetic Dipole
4.1. Free-Space Electric, Magnetic and Mixed Green’s Functions
4.2. Weyl’s or Angular Spectrum Representation of Magnetic and Mixed Green’s Functions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SNOM | Scanning near-fieldoptical microscope |
| RHS | Right-hand-side |
| NP | Nanoparticle |
| THz | Terahertz |
Appendix A. Derivation of the Wave Equation
Appendix B. Green’s Function for the Helmholtz Equation
References
- Novotny, L.; Hecht, B. Principles of Nano-Optics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Pelton, M.; Bryant, G.W. Introduction to Metal-Nanoparticle Plasmonics; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 5. [Google Scholar]
- Amendola, V.; Pilot, R.; Frasconi, M.; Maragò, O.M.; Iatì, M.A. Surface plasmon resonance in gold nanoparticles: A review. J. Phys. Condens. Matter 2017, 29, 203002. [Google Scholar] [CrossRef] [PubMed]
- Evlyukhin, A.B.; Novikov, S.M.; Zywietz, U.; Eriksen, R.L.; Reinhardt, C.; Bozhevolnyi, S.I.; Chichkov, B.N. Demonstration of Magnetic Dipole Resonances of Dielectric Nanospheres in the Visible Region. Nano Lett. 2012, 12, 3749–3755. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Soshnichenko, A.E.; Evlyukhin, A.B.; Kivshar, Y.S.; Chichkov, B.N. Substrate-Induced Resonant Magnetoelectric Effects for Dielectric Nanoparticles. ACS Photonics 2015, 2, 1423–1428. [Google Scholar] [CrossRef]
- Barnes, W.L. Particle plasmons: Why shape matters. Am. J. Phys. 2016, 84, 593–601. [Google Scholar] [CrossRef]
- Gonçalves, M.R. Plasmonic nanoparticles: fabrication, simulation and experiments. J. Phys. D Appl. Phys. 2014, 47, 213001. [Google Scholar] [CrossRef]
- Slaughter, L.S.; Chang, W.S.; Swanglap, P.; Tcherniak, A.; Khanal, B.P.; Zubarev, E.R.; Link, S. Single-Particle Spectroscopy of Gold Nanorods beyond the Quasi-Static Limit: Varying the Width at Constant Aspect Ratio. J. Phys. Chem. C 2010, 114, 4934–4938. [Google Scholar] [CrossRef]
- Slaughter, L.; Chang, W.S.; Link, S. Characterizing Plasmons in Nanoparticles and Their Assemblies with Single Particle Spectroscopy. J. Phys. Chem. Lett. 2011, 2, 2015–2023. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Łach, G.; De Kieviet, M.; Pachucki, K. One-Loop Dominance in the Imaginary Part of the Polarizability: Application to Blackbody and Noncontact van der Waals Friction. Phys. Rev. Lett. 2015, 114, 043001. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Badioli, M.; Alonso-Gonzalez, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenovic, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 478, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Dai, S.; Fei, Z.; Ma, Q.; Rodin, A.S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Gannett, W.; Regan, W.; Watanabe, K.; et al. Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride. Science 2014, 343, 1125–1129. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Luan, Y.; Scott, M.; Yan, J.; Mandrus, D.; Xu, X.; Fei, Z. Imaging exciton–polariton transport in MoSe2 waveguides. Nat. Photonics 2017, 11, 356–360. [Google Scholar] [CrossRef]
- Joulain, K.; Ben-Abdallah, P.; Chapuis, P.O.; Babuty, A.; De Wilde, Y. Tip-sample electromagnetic interaction in the infrared: Effective polarizabilities, retarded image dipole model and near-field thermal radiation detection. arXiv, 2012; arXiv:physics.optics/1201.4834. [Google Scholar]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.R.; Vasilevskiy, M.I. A Primer on Surface Plasmon-Polaritons in Graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef]
- Sorger, C.; Preu, S.; Schmidt, J.; Winnerl, S.; Bludov, Y.V.; Peres, N.M.R.; Vasilevskiy, M.I.; Weber, H.B. Terahertz response of patterned epitaxial graphene. New J. Phys. 1015, 17, 053045. [Google Scholar] [CrossRef]
- Gonçalves, P.A.D.; Peres, N.M.R. An Introduction to Graphene Plasmonics; World Scientific: Singapore, 2016. [Google Scholar]
- Santos, J.E.; Vasilevskiy, M.I.; Peres, N.M.R.; Smirnov, G.; Bludov, Y.V. Renormalization of nanoparticle polarizability in the vicinity of a graphene-covered interface. Phys. Rev. B 2014, 90, 235420. [Google Scholar] [CrossRef]
- Wind, M.; Vlieger, J.; Bedeaux, D. The polarizability of a truncated sphere on a substrate I. Phys. A Stat. Mech. Appl. 1987, 141, 33–57. [Google Scholar] [CrossRef]
- Hakkarainen, T.; Setälä, T.; Friberg, A.T. Electromagnetic near-field interactions of a dipolar emitter with metal and metamaterial nanoslabs. Phys. Rev. A 2011, 84, 033849. [Google Scholar] [CrossRef]
- Dahan, N.; Greffet, J.J. Enhanced scattering and absorption due to the presence of a particle close to an interface. Opt. Express 2012, 20, A530–A544. [Google Scholar] [CrossRef] [PubMed]
- Evlyukhin, A.B.; Reinhardt, C.; Chichkov, B.N. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation. Phys. Rev. B 2011, 84, 235429. [Google Scholar] [CrossRef]
- Yaghjian, A.D. Electric dyadic Green’s functions in the source region. Proc. IEEE 1980, 68, 248–263. [Google Scholar] [CrossRef]
- Duffy, D.G. Green’s Functions with Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Arnoldus, H.F. Transverse and longitudinal components of the optical self-, near-, middle- and far-field. J. Mod. Opt. 2003, 50, 755–770. [Google Scholar] [CrossRef]
- Frahm, C.P. Some novel delta-function identities. Am. J. Phys. 1983, 51, 826–829. [Google Scholar] [CrossRef]
- Tai, C.T. Dyadic Green Functions in Electromagnetic Theory, 2nd ed.; Institute of Electrical & Electronics Engineers (IEEE): New York, NY, USA, 1994. [Google Scholar]
- Collin, R.E. Field Theory of Guided Waves; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Rothwell, E.J.; Cloud, M.J. Electromagnetics; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Setälä, T.; Kaivola, M.; Friberg, A.T. Decomposition of the point-dipole field into homogeneous and evanescent parts. Phys. Rev. E 1999, 59, 1200–1206. [Google Scholar] [CrossRef]
- Arnoldus, H.F.; Foley, J.T. Transmission of dipole radiation through interfaces and the phenomenon of anti critical angles. J. Opt. Soc. Am. A 2004, 21, 1109–1117. [Google Scholar] [CrossRef]
- Pieplow, G.; Haakh, R.H.; Henkel, C. A Note on longitudinal fields in the Weyl expansion of the electromagnetic Green tensor. Int. J. Mod. Phys. Conf. Ser. 2012, 14, 460–466. [Google Scholar]
- Arnoldus, H.F.; Berg, M.J. Energy transport in the near field of an electric dipole near a layer of material. J. Mod. Opt. 2015, 62, 218–228. [Google Scholar] [CrossRef]
- Bedeaux, D.; Mazur, P. On the critical behaviour of the dielectric constant for a nonpolar fluid. Physica 1973, 67, 23–54. [Google Scholar] [CrossRef]
- Sipe, J. The ATR spectra of multipole surface plasmons. Surf. Sci. 1979, 84, 75–105. [Google Scholar] [CrossRef]
- Sipe, J.E. New Green-function formalism for surface optics. J. Opt. Soc. Am. B 1987, 4, 481–489. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L. Fields radiated by a nanoemitter in a graphene sheet. Phys. Rev. B 2011, 84, 195446. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L. Analytical Expressions for the Electromagnetic Dyadic Green’s Function in Graphene and Thin Layers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 4600611. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Biehs, S.A.; Agarwal, G.S. Large enhancement of Förster resonance energy transfer on graphene platforms. App. Phys. Lett. 2013, 103, 243112. [Google Scholar] [CrossRef]
- Kort-Kamp, W.J.M.; Amorim, B.; Bastos, G.; Pinheiro, F.A.; Rosa, F.S.S.; Peres, N.M.R.; Farina, C. Active magneto-optical control of spontaneous emission in graphene. Phys. Rev. B 2015, 92, 205415. [Google Scholar] [CrossRef]
- Yang, T.R.; Dvoynenko, M.M.; Goncharenko, A.V.; Lozovski, V.Z. An exact solution of the Lippmann–Schwinger equation in one dimension. Am. J. Phys. 2003, 71, 64–71. [Google Scholar] [CrossRef]
- Capolino, F. Theory and Phenomena of Metamaterials; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Meier, M.; Wokaun, A. Enhanced fields on large metal particles: dynamic depolarization. Opt. Lett. 1983, 8, 581–583. [Google Scholar] [CrossRef] [PubMed]
- Ru, E.L.; Etchegoin, P. Principles of Surface Enhanced Raman Spectroscopy and Related Plasmonic Effects; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Carminati, R.; Greffet, J.J.; Henkel, C.; Vigoureux, J. Radiative and non-radiative decay of a single molecule close to a metallic nanoparticle. Opt. Commun. 2006, 261, 368–375. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. Discrete-Dipole Approximation For Scattering Calculations. J. Opt. Soc. Am. A 1994, 11, 1491–1499. [Google Scholar] [CrossRef]
- D’Agostino, S.; Sala, F.D.; Andreani, L. Radiative coupling of high-order plasmonic modes with far-field. Photonics Nanostruct.-Fundam. Appl. 2013, 11, 335–344. [Google Scholar] [CrossRef]
- Stauber, T.; Gómez-Santos, G.; de Abajo, F.J.G. Extraordinary Absorption of Decorated Undoped Graphene. Phys. Rev. Lett. 2014, 112, 077401. [Google Scholar] [CrossRef] [PubMed]
- Bludov, Y.V.; Peres, N.M.R.; Vasilevskiy, M.I. Unusual reflection of electromagnetic radiation from a stack of graphene layers at oblique incidence. J. Opt. 2013, 15, 114004. [Google Scholar] [CrossRef]
- Peres, N.M.R.; Lopes dos Santos, J.M.B.; Stauber, T. Phenomenological study of the electronic transport coefficients of graphene. Phys. Rev. B 2007, 76, 073412. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Guinea, F. Electronic transport in graphene: A semiclassical approach including midgap states. Phys. Rev. B 2007, 76, 205423. [Google Scholar] [CrossRef]
- Haynes, W.M. Handbook of Chemistry and Physics, 93rd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hamma, M.; Miranda, R.P.; Vasilevskiy, M.I.; Zorkani, I. Calculation of the Huang–Rhys parameter in spherical quantum dots: the optical deformation potential effect. J. Phys. Condens. Matter 2007, 19, 346215. [Google Scholar] [CrossRef]
- David, C.; de Abajo, F.J.G. Nonlocal Effects in the Optical Response of Metal Nanoparticles. AIP Conf. Proc. 2010, 1291, 43–45. [Google Scholar]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Size-dependent nonlocal effects in plasmonic semiconductor particles. EPL (Europhys. Lett.) 2017, 119, 17003. [Google Scholar] [CrossRef]
- Vasilevskiy, M.I. Dipolar vibrational modes in spherical semiconductor quantum dots. Phys. Rev. B 2002, 66, 195326. [Google Scholar] [CrossRef]
- Tassin, P.; Koschny, T.; Soukoulis, C.M. Effective material parameter retrieval for thin sheets: Theory and application to graphene, thin silver films, and single-layer metamaterials. Phys. B Condens. Matter 2012, 407, 4062–4065. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, Z.; Zhang, F.; Zhao, Q.; Wei, Z.; Fu, Q.; Li, J.; Gu, C.; Li, H. Tunable mid-infrared coherent perfect absorption in a graphene meta-surface. Sci. Rep. 2015, 5, 13956. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, P.A.D.; Dias, E.J.C.; Bludov, Y.V.; Peres, N.M.R. Modeling the excitation of graphene plasmons in periodic grids of graphene ribbons: An analytical approach. Phys. Rev. B 2016, 94, 195421. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- García-Etxarri, A.; Gómez-Medina, R.; Froufe-Pérez, L.S.; López, C.; Chantada, L.; Scheffold, F.; Aizpurua, J.; Nieto-Vesperinas, M.; Sáenz, J.J. Strong magnetic response of submicron Silicon particles in the infrared. Opt. Express 2011, 19, 4815–4826. [Google Scholar] [CrossRef] [PubMed]
- Desanto, J. Scalar Wave Theory: Green’s Functions and Applications; Springer: Berlin, Germany, 1992. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amorim, B.; Gonçalves, P.A.D.; Vasilevskiy, M.I.; Peres, N.M.R. Impact of Graphene on the Polarizability of a Neighbour Nanoparticle: A Dyadic Green’s Function Study. Appl. Sci. 2017, 7, 1158. https://doi.org/10.3390/app7111158
Amorim B, Gonçalves PAD, Vasilevskiy MI, Peres NMR. Impact of Graphene on the Polarizability of a Neighbour Nanoparticle: A Dyadic Green’s Function Study. Applied Sciences. 2017; 7(11):1158. https://doi.org/10.3390/app7111158
Chicago/Turabian StyleAmorim, B., P. A. D. Gonçalves, M. I. Vasilevskiy, and N. M. R. Peres. 2017. "Impact of Graphene on the Polarizability of a Neighbour Nanoparticle: A Dyadic Green’s Function Study" Applied Sciences 7, no. 11: 1158. https://doi.org/10.3390/app7111158
APA StyleAmorim, B., Gonçalves, P. A. D., Vasilevskiy, M. I., & Peres, N. M. R. (2017). Impact of Graphene on the Polarizability of a Neighbour Nanoparticle: A Dyadic Green’s Function Study. Applied Sciences, 7(11), 1158. https://doi.org/10.3390/app7111158






