Wavenumber-Frequency Analysis of Internal Aerodynamic Noise in Constriction-Expansion Pipe
Abstract
:1. Introduction
2. Theoretical Background
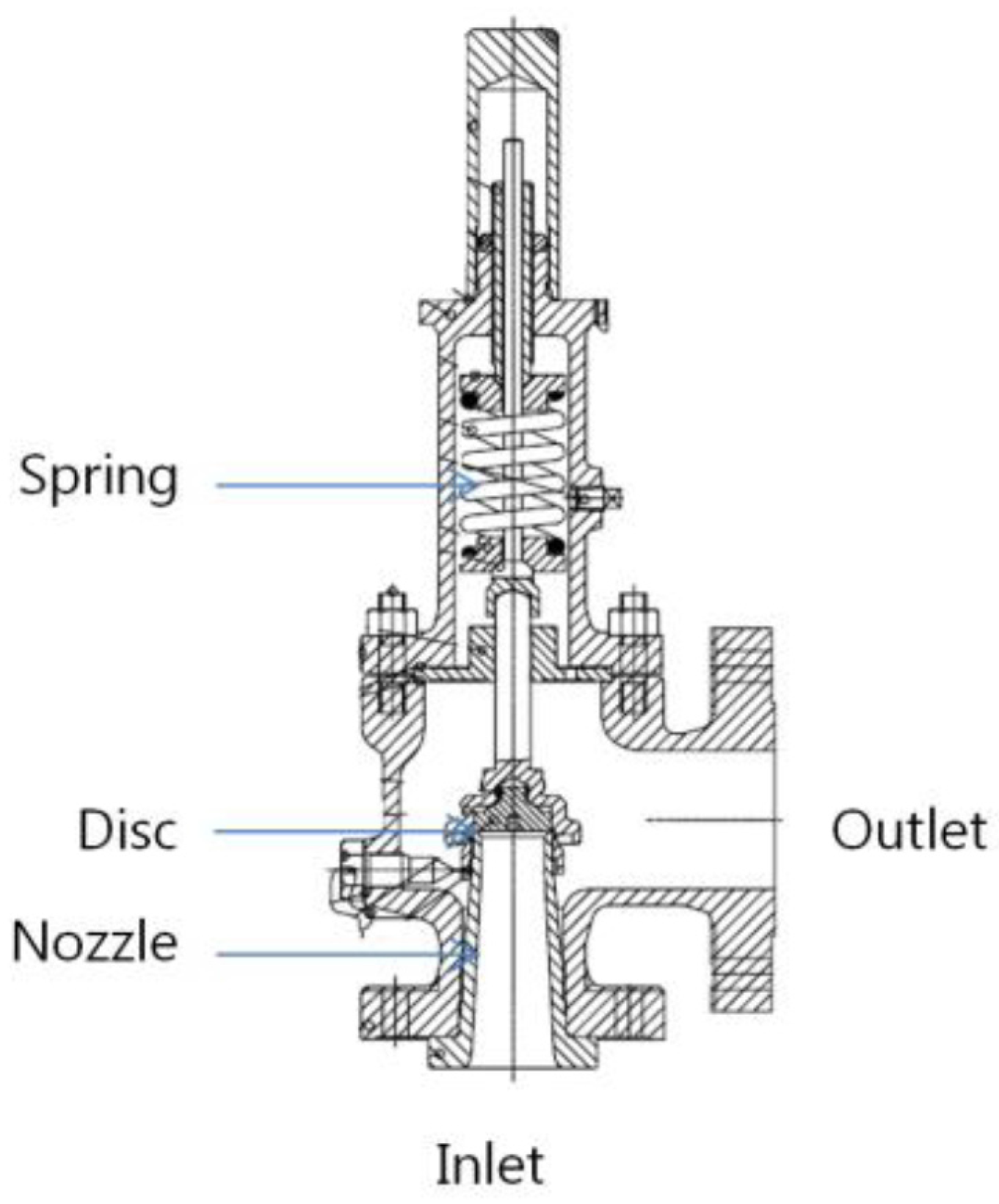
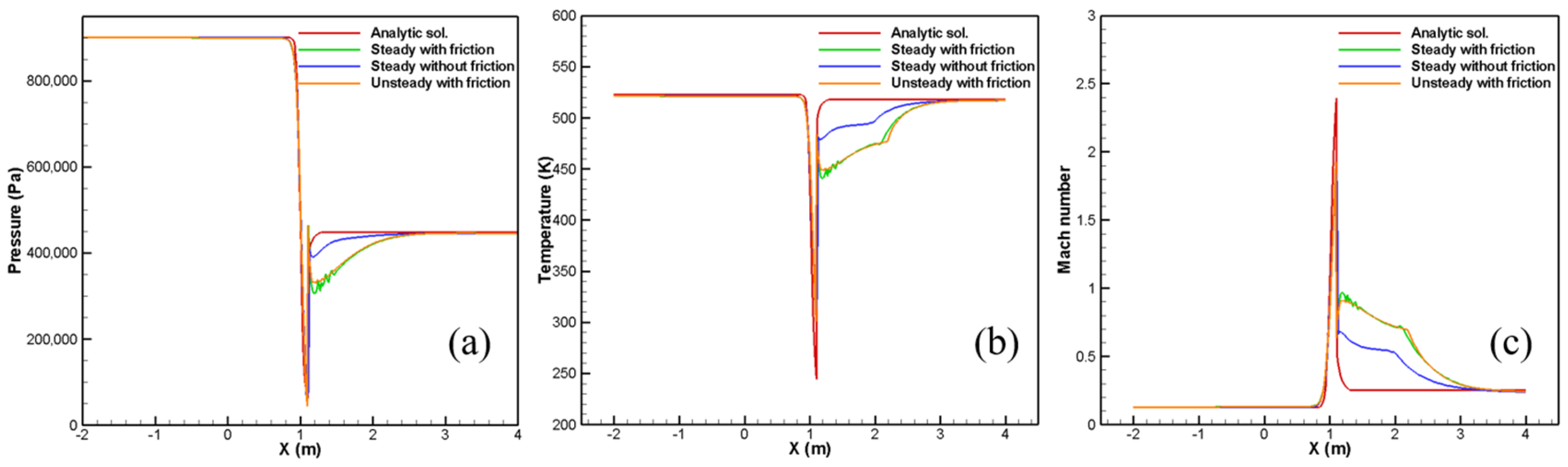
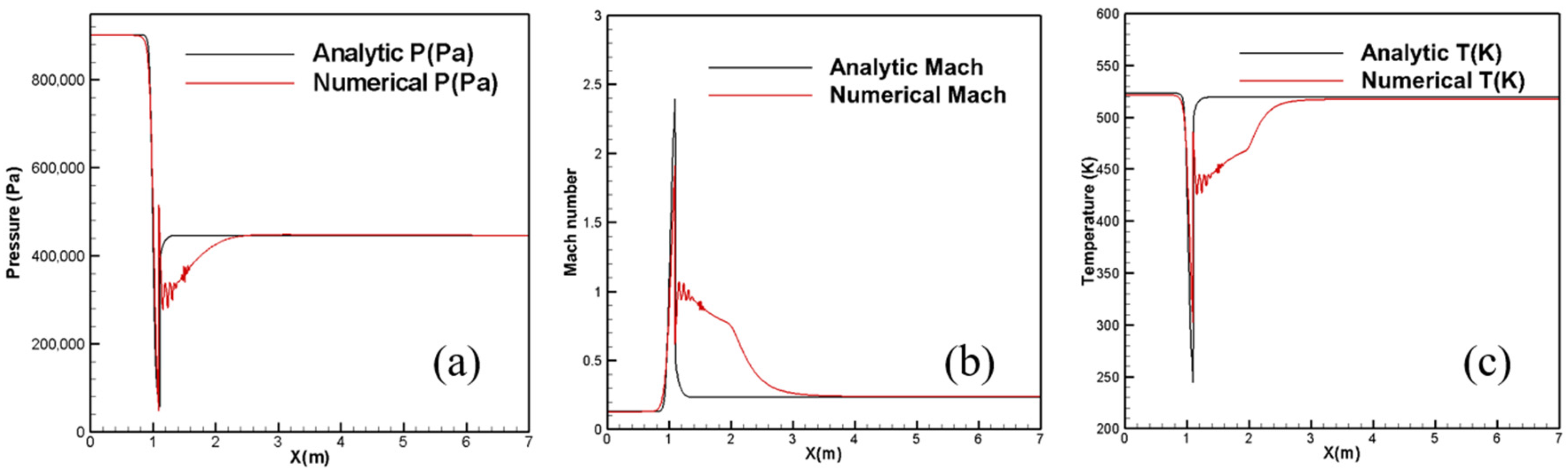
2.1. Valve Flow and Its Quasi-1D Approximation
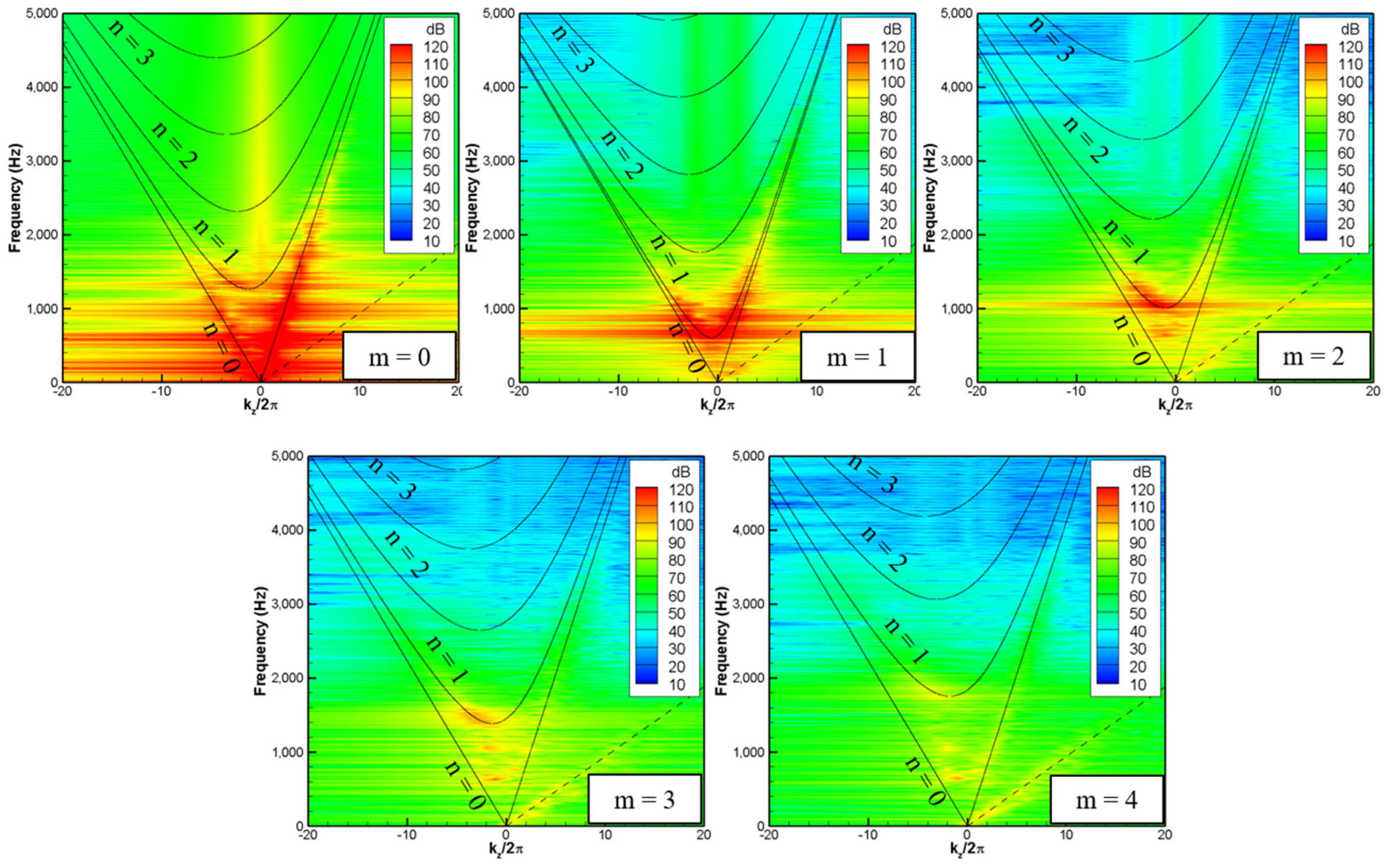
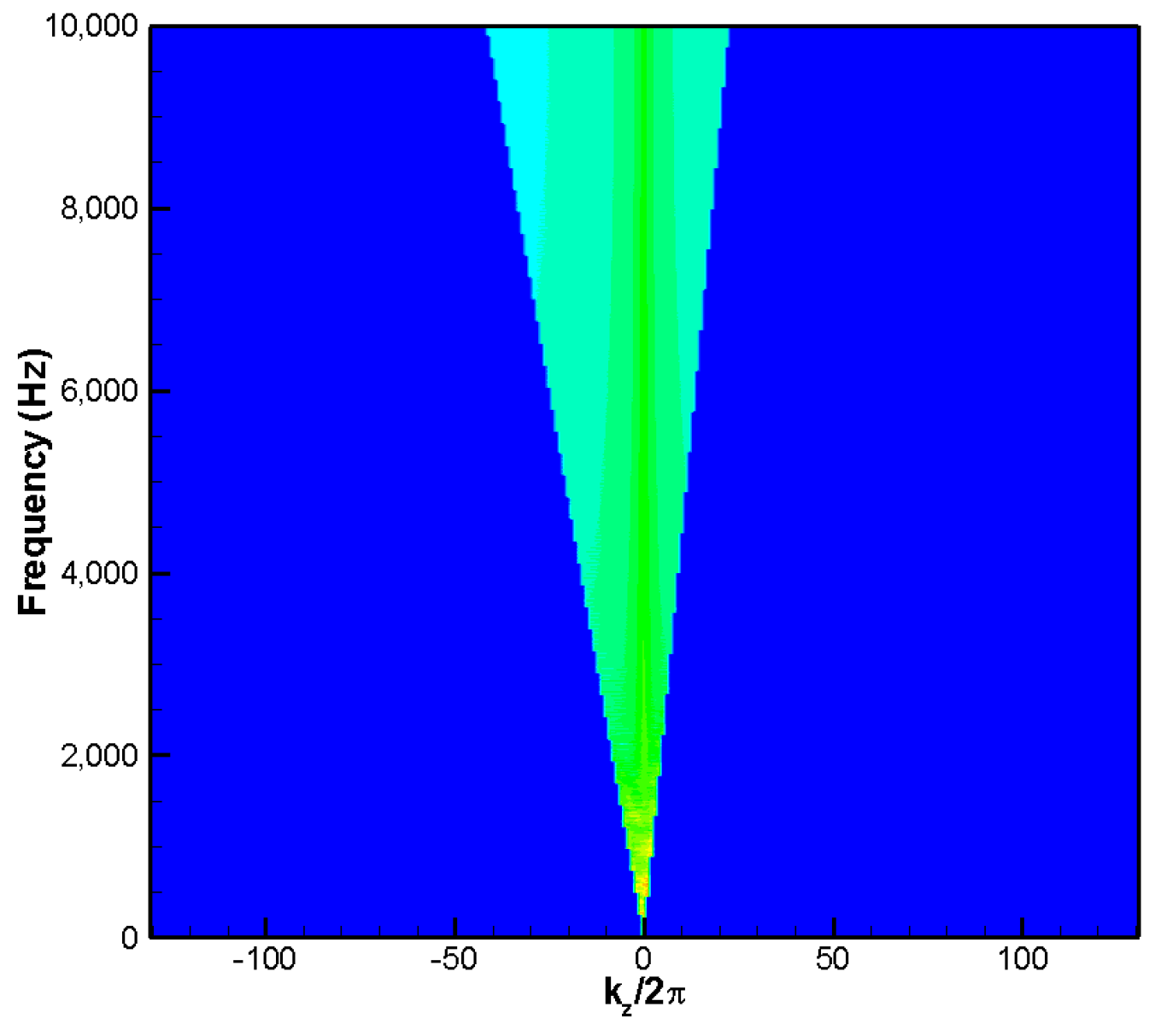
2.2. Wavenumber-Frequency Analysis for Internal Aerodynamic Noise
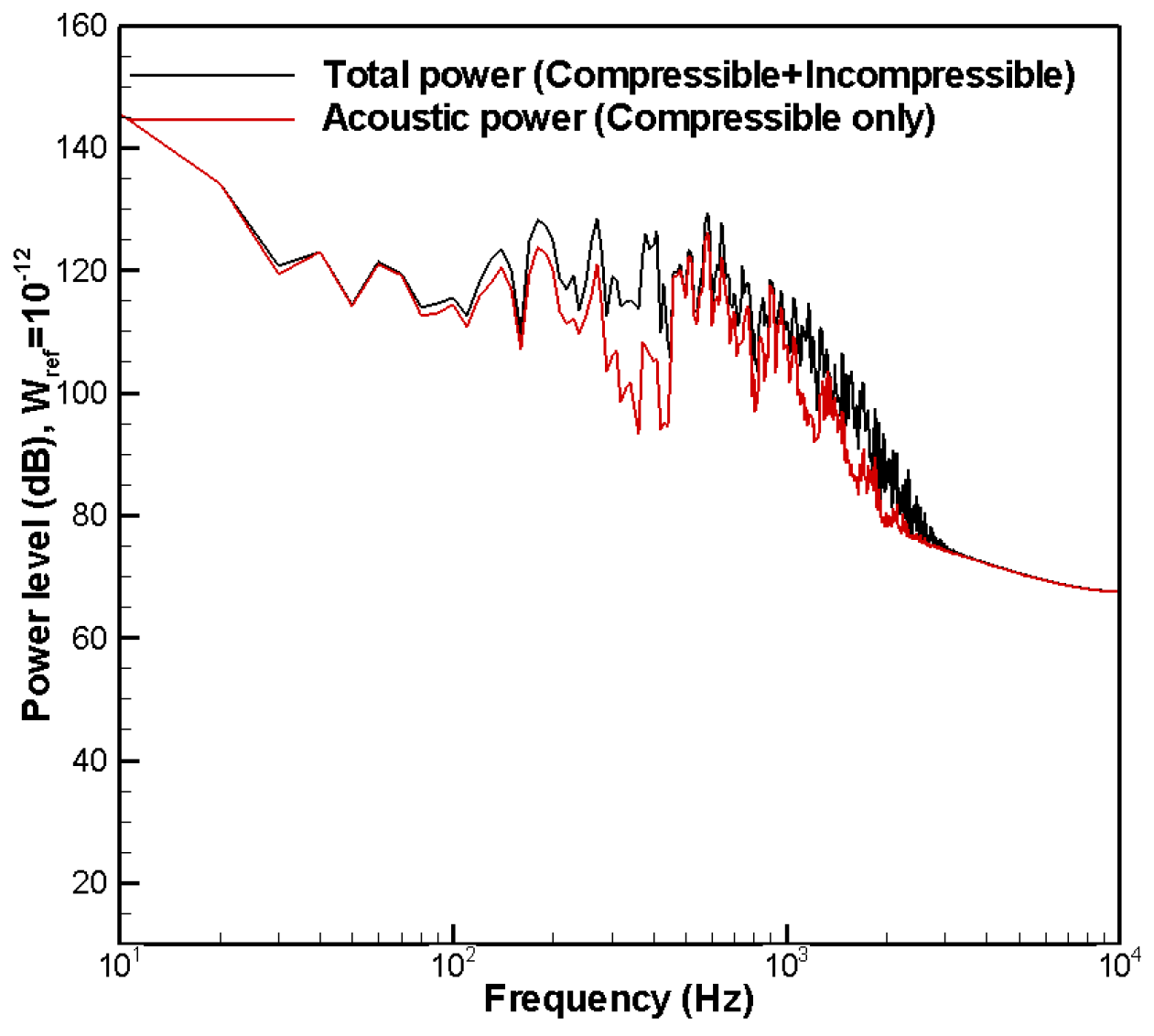
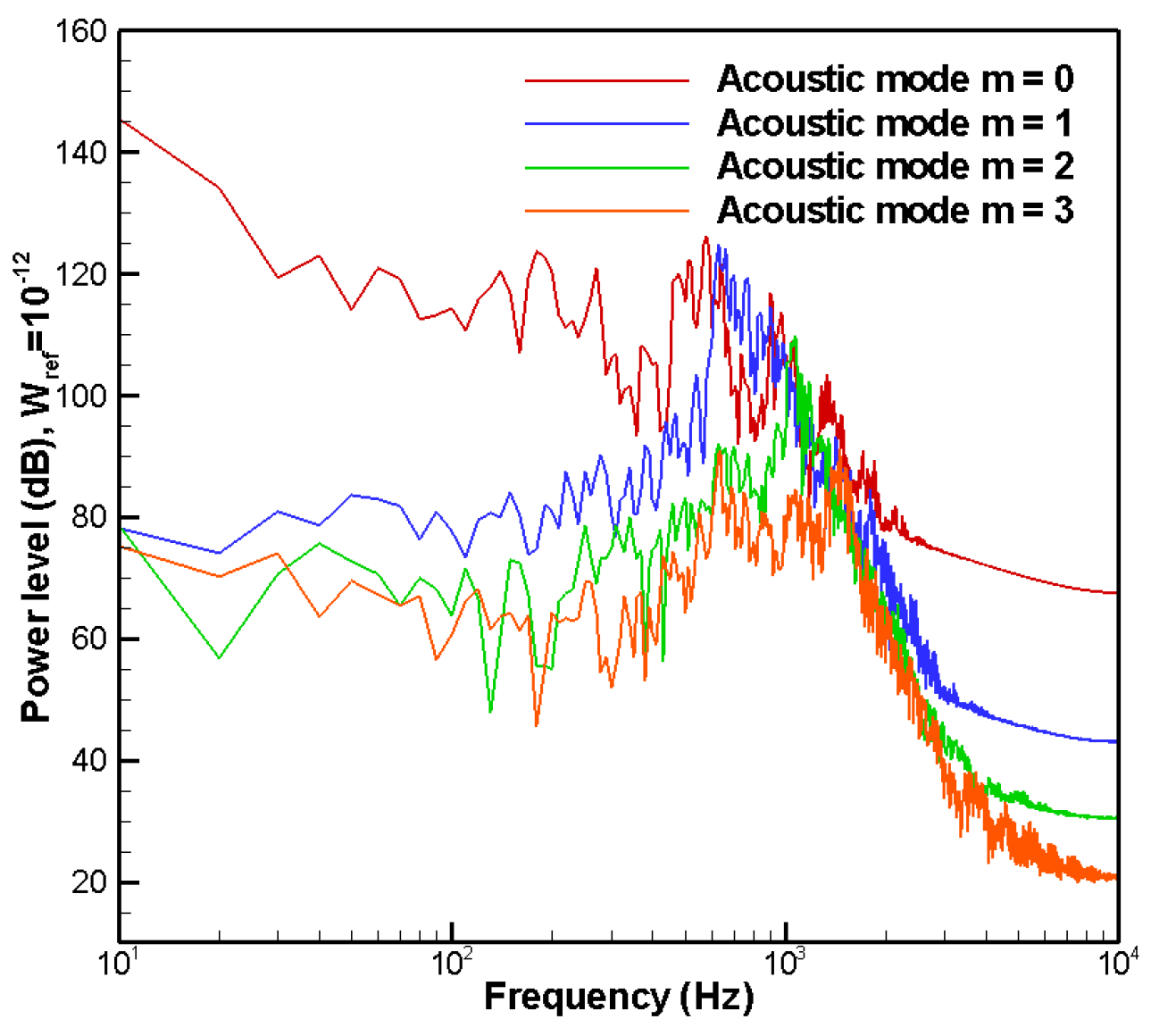
2.3. Acoustic Power Level
3. Governing Equations and Numerical Methods
3.1. Governing Equations
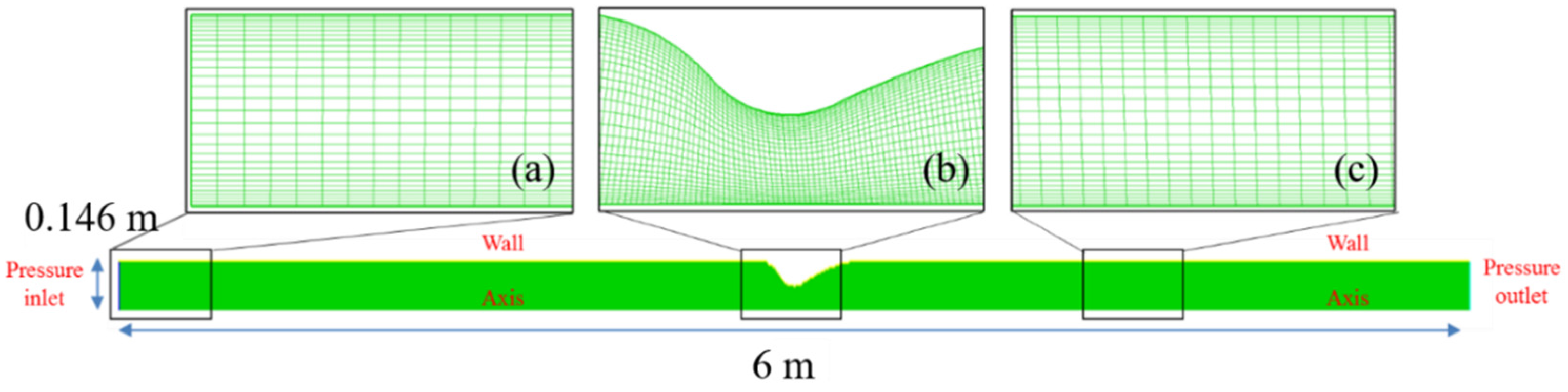
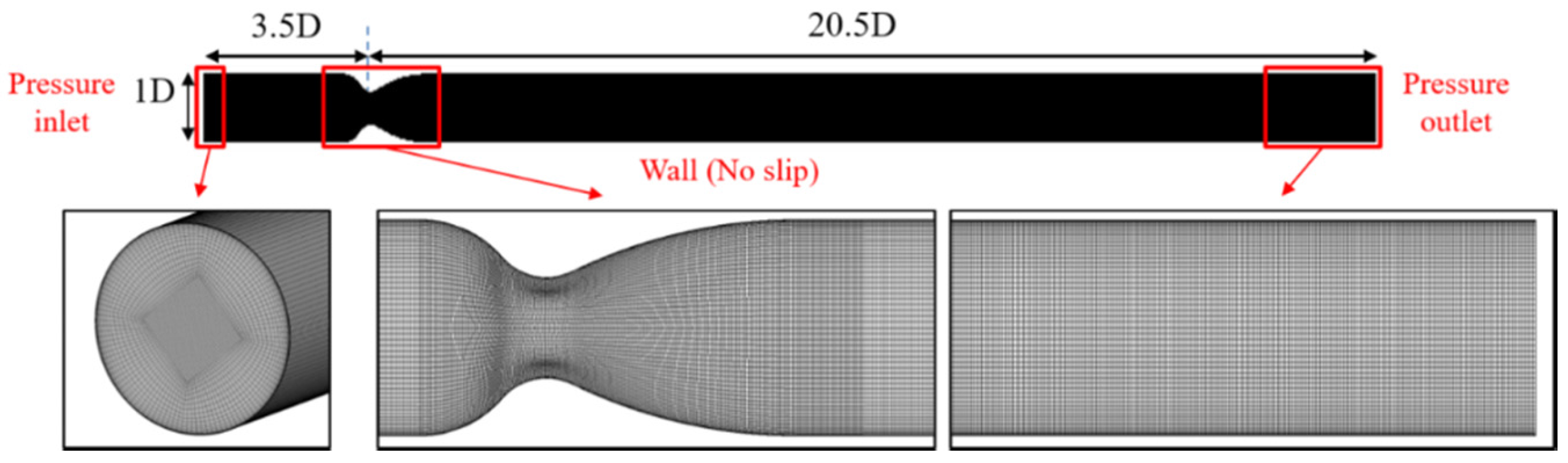
3.2. Numerical Methods
4. Numerical Results
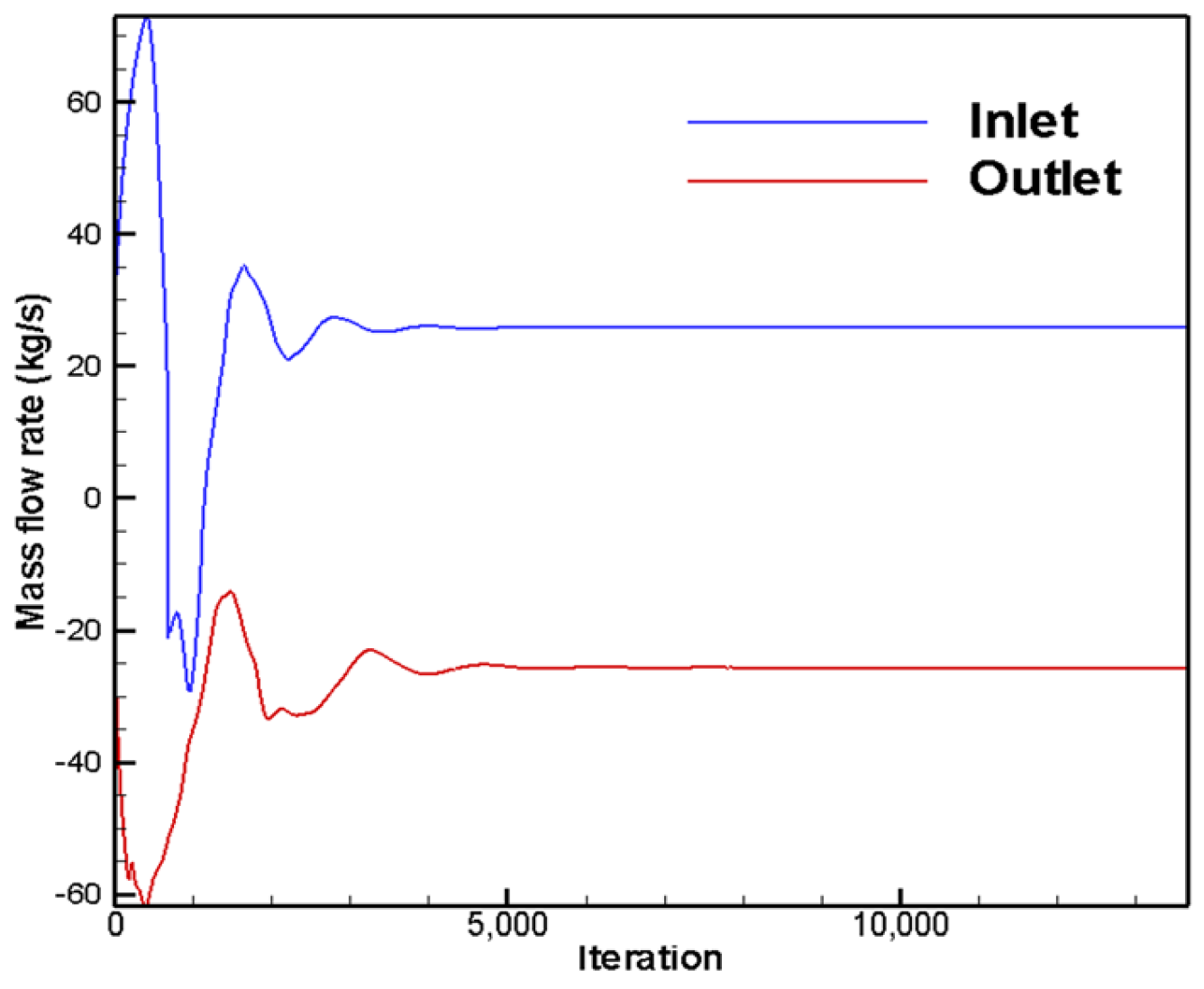
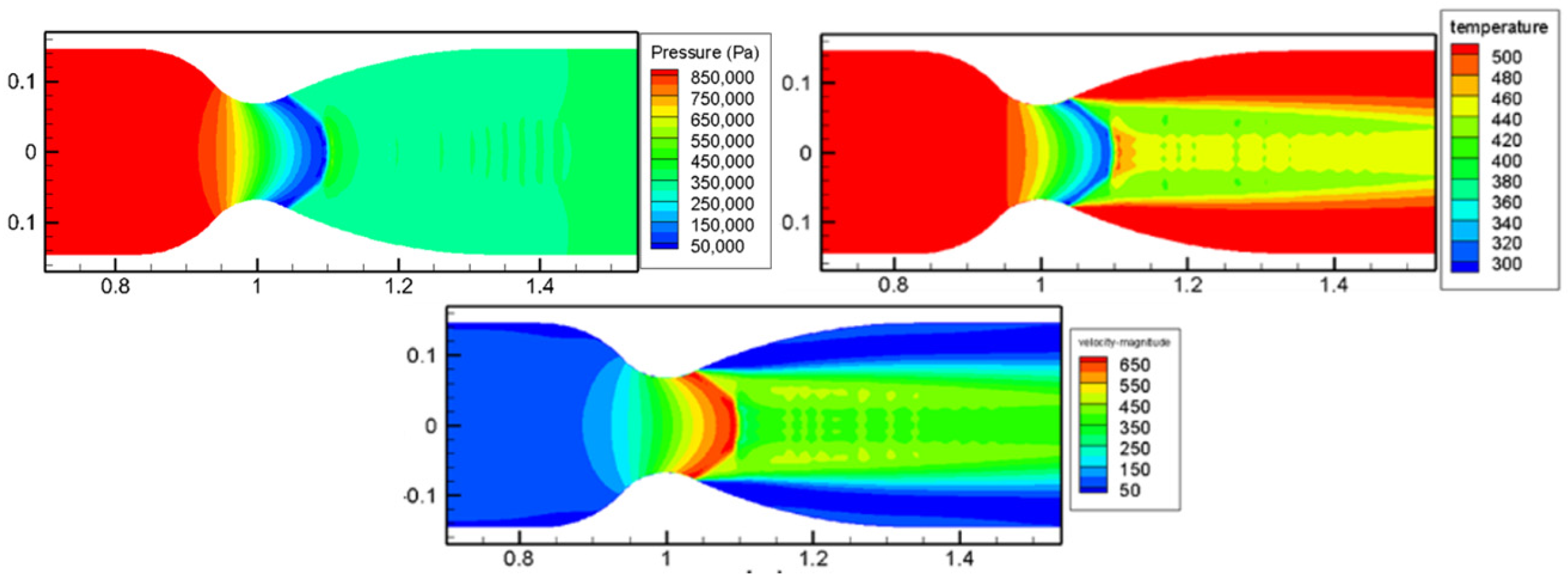
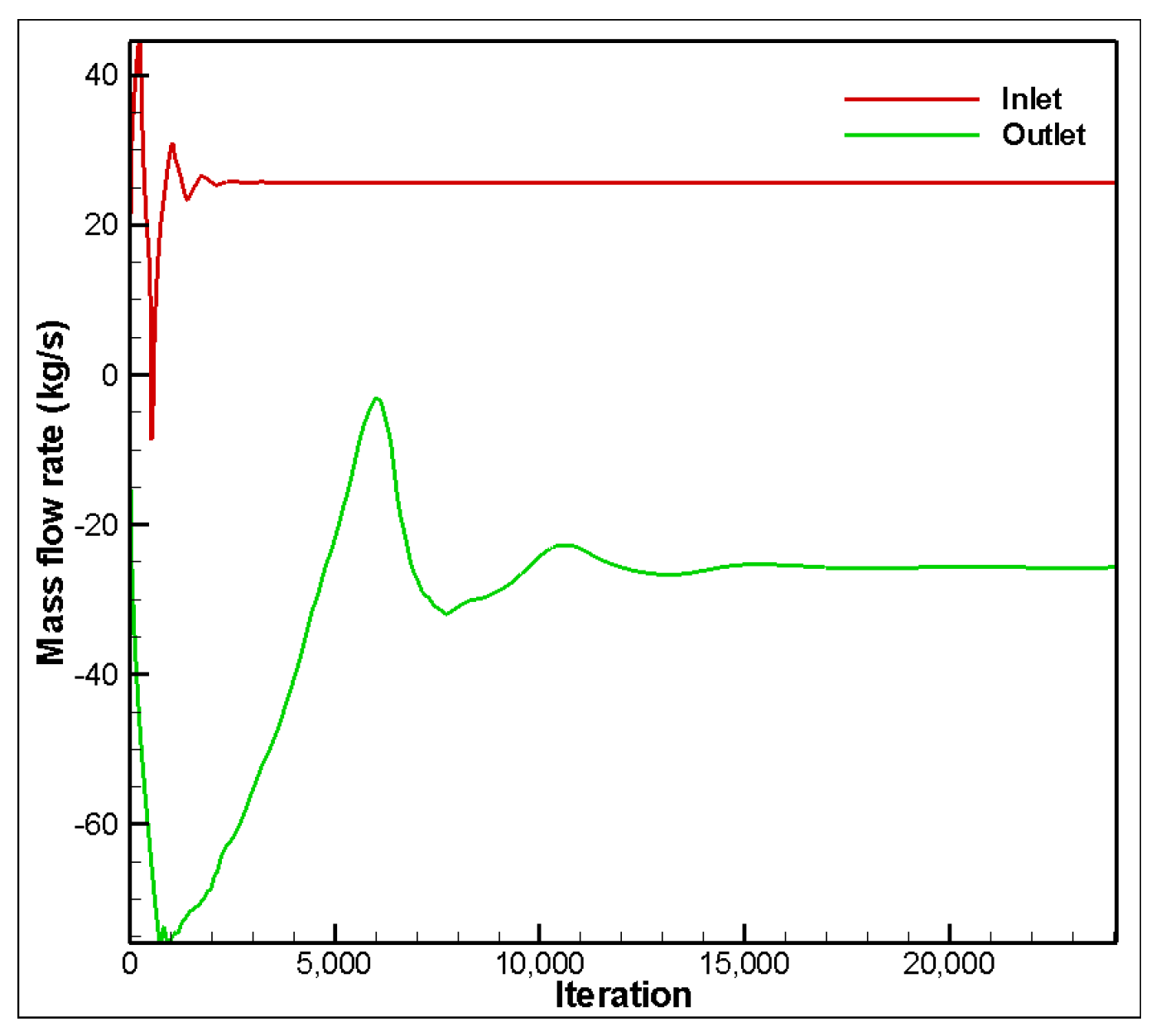
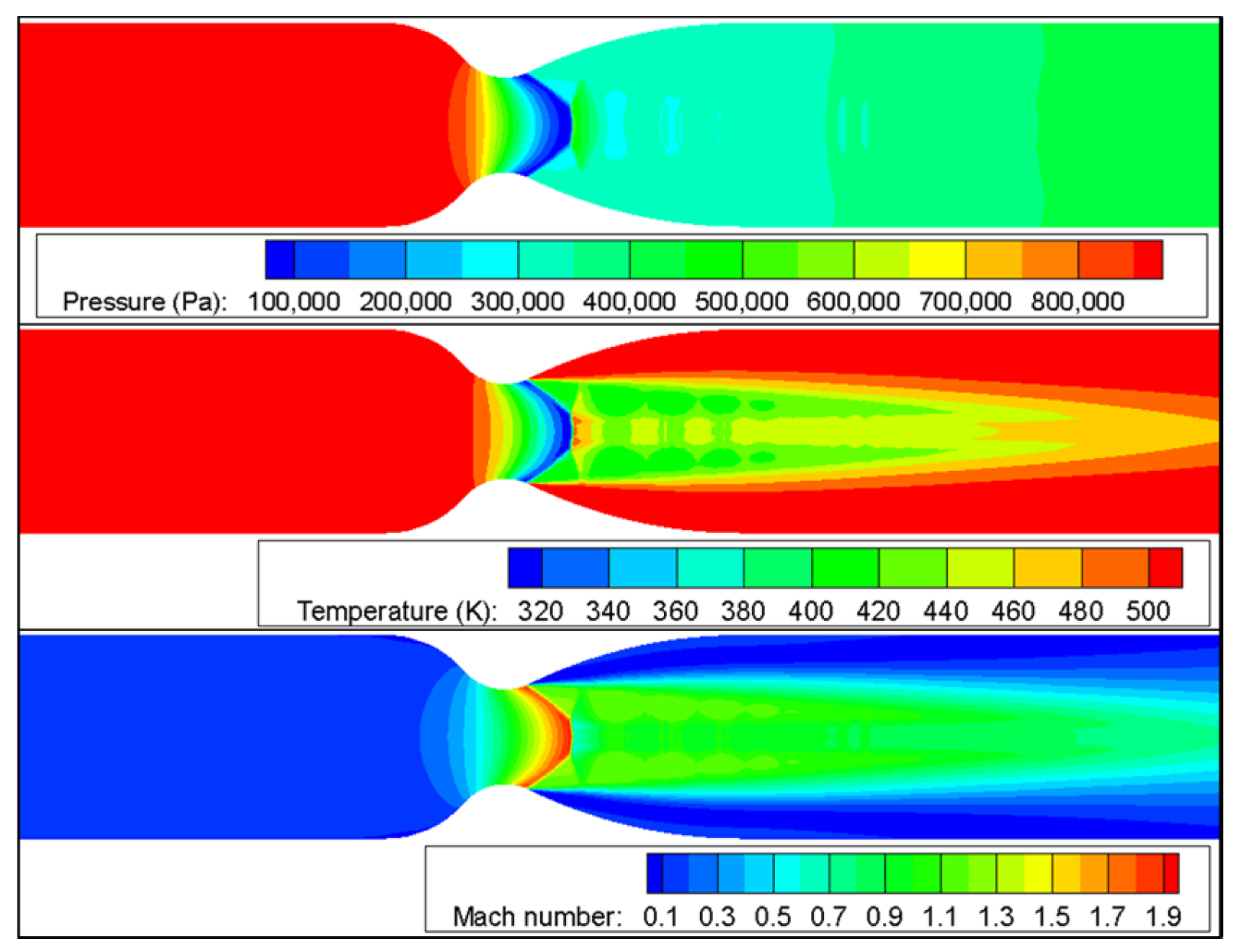
4.1. Axisymmetric Steady Simulation
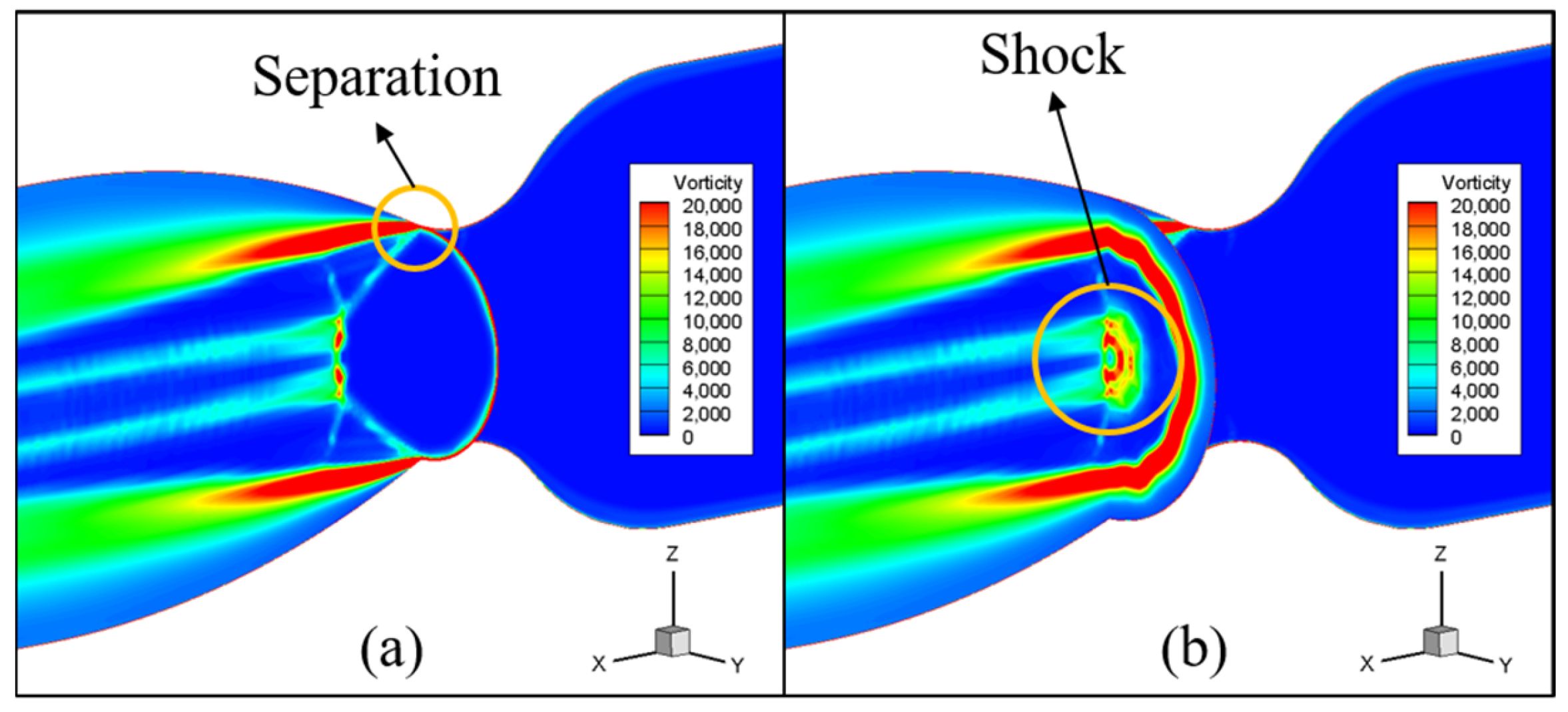
4.2. Three-Dimensional Steady Simulation
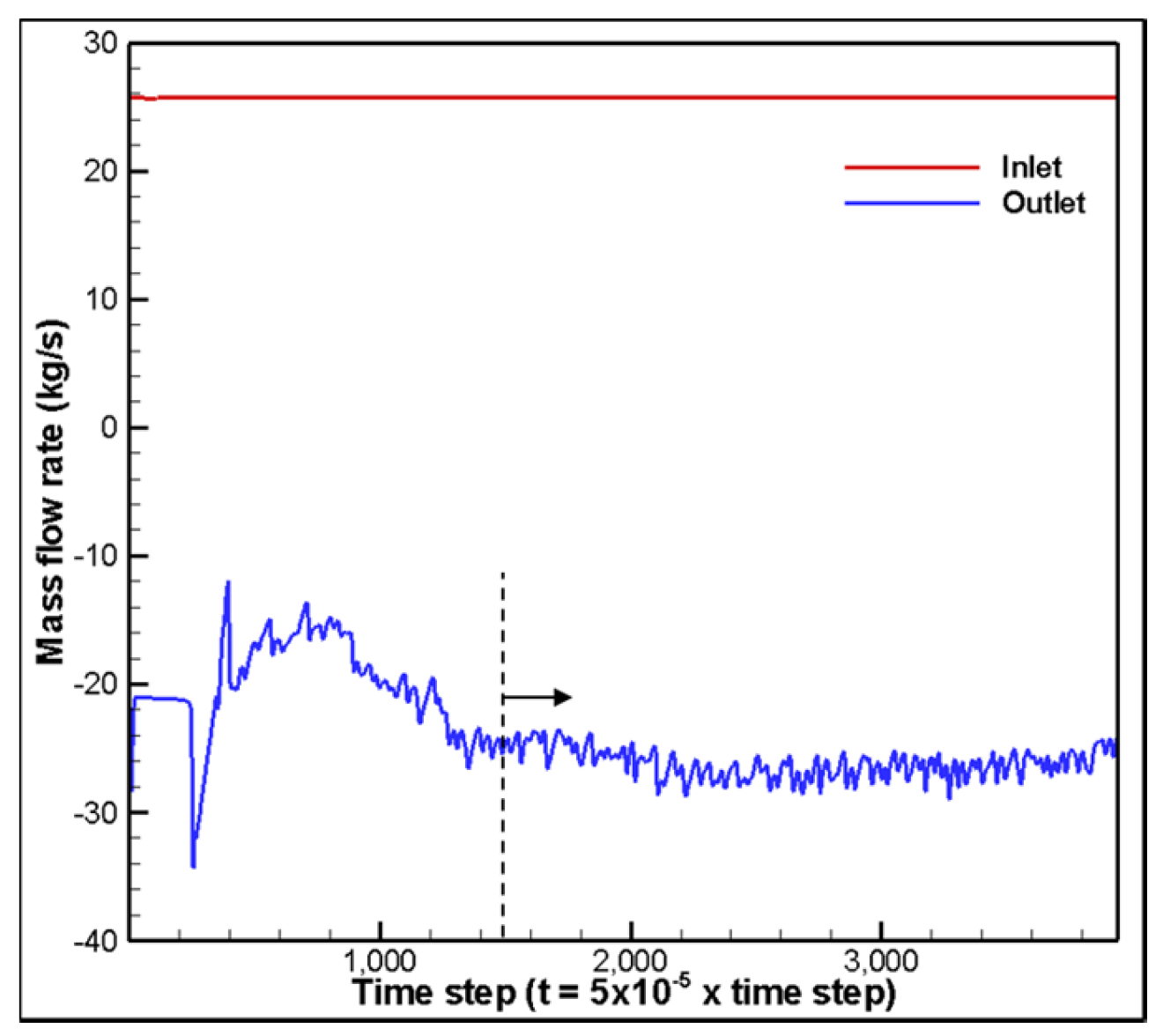
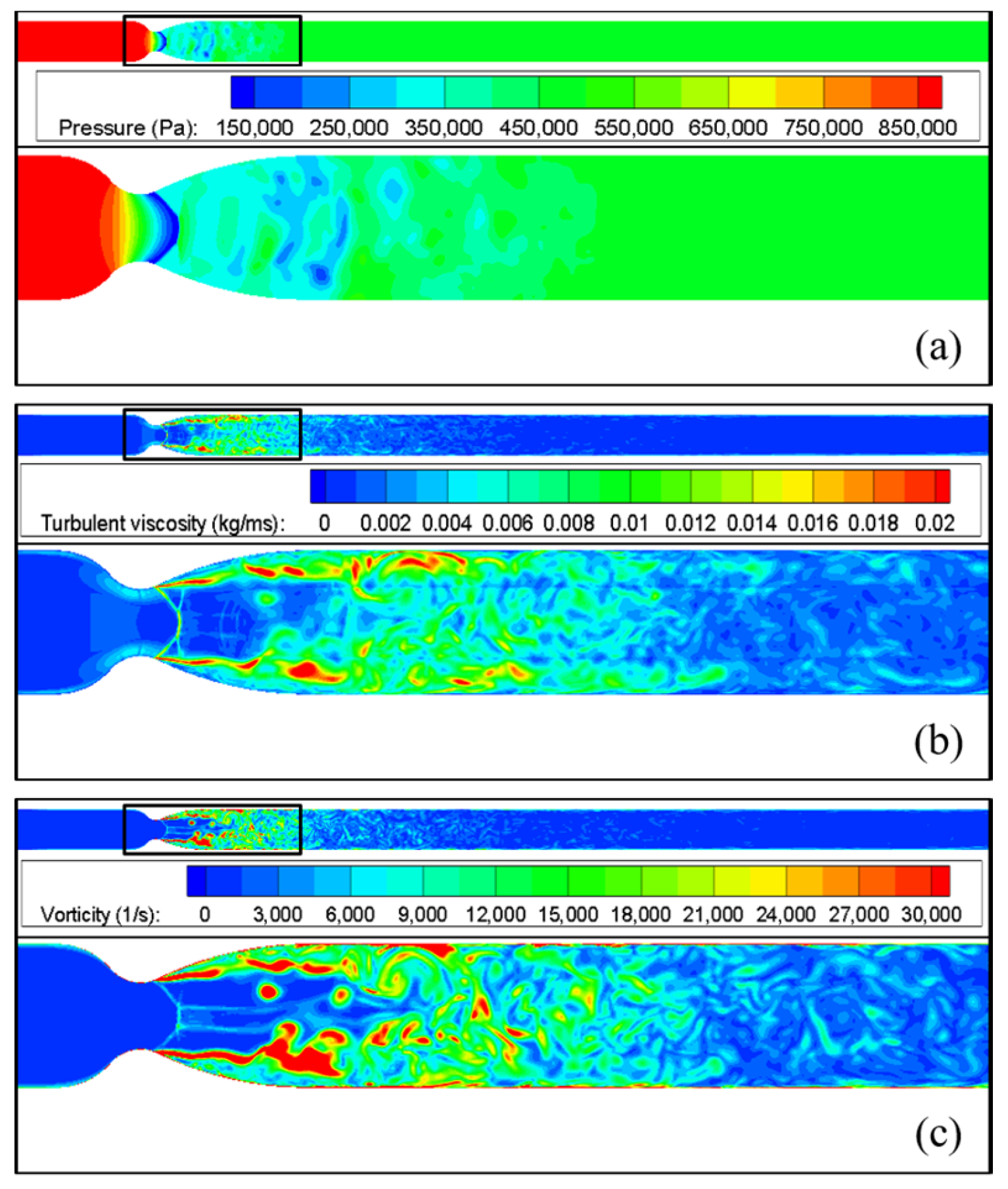
4.3. Three-Dimensional Unsteady Simulation
4.4. Wavenumber-Frequency Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Carucci, V.A.; Mueller, R.T. Acoustically Induced Piping Vibration in High Capacity Pressure Reducing Systems; ASME 82-WA/PVP-8; The American Society of Mechanical Engineers: New York, NY, USA, 1982. [Google Scholar]
- Eisinger, F.L. Designing Piping Systems against Acoustically-Induced Structural Fatigue; ASME 1996, PVP-328; The American Society of Mechanical Engineers: New York, NY, USA, 1996. [Google Scholar]
- Veritas, D.N. L-002 Piping System Layout, Design and Structural Analysis, 3rd ed.; NORSOK Standard: Lysaker, Norway, 2009. [Google Scholar]
- Bruce, R.D.; Bommer, A.S.; LePage, T.E. Solving acoustic-induced vibration problems in the design stage. Sound Vib. 2013, 47, 8–11. [Google Scholar]
- Energy Institute. Guidelines for the Avoidance of Vibration Induced Fatigue Failure in Process Pipework, 2nd ed.; Energy Institute: London, UK, 2008. [Google Scholar]
- API Standard 521. Guide for Pressure Relieving and Depressuring System, 4th ed.; American Petroleum Institute (API): Washington, DC, USA, 1997. [Google Scholar]
- IEC 60534-8-3. Noise Considerations—Control Valve Aerodynamic Noise Prediction Method; The International Electrotechnical Commision (IEC): Geneva, Switzerland, 2010. [Google Scholar]
- Agar, M.; Ancian, L. Acoustic-Induced Vibration: A New Methodology for Improved Piping Design Practice. In Proceedings of the Offshore Technology Conference Asia, Kuala Lumpur, Malaysia, 22–25 March 2016. [Google Scholar]
- White, F.M. Fluid Mechanics, 6th ed.; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Blake, W.K. Mechanics of Flow-Induced Sound and Vibration Volume 1: General Concepts and Elementary Source; Academic Press: New York, NY, USA, 1986. [Google Scholar]
- Park, K.A.; Choi, Y.M.; Choi, H.M.; Cha, T.S.; Yoon, B.H. The evaluation of critical pressure ratios of sonic nozzles at low Reynolds numbers. Flow Meas. Instrum. 2001, 12, 37–41. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; Tata McGraw-Hill Education: New York, NY, USA, 2010; pp. 543–573. [Google Scholar]
- Van Herpe, F.; Baresh, D.; Lafon, P.; Bordji, M. Wavenumber-frequency analysis of the wall pressure fluctuations in the wake of a car side mirror. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA, 5–8 June 2011; pp. 3823–3839. [Google Scholar]
- Munjal, M.L. Acoustics of Ducts and Mufflers, 2nd ed.; John Wiley & Sons: Chichester, UK, 2014; pp. 2–20. [Google Scholar]
- Cowling, J. Acoustic and Turbulence/Flow Induced Vibration in Piping Systems: A Real Problem for LNG Facilities; Perth Convention and Exhibition Centre: Houston, TX, USA, 2016. [Google Scholar]
| Acoustic Power Level, Lw (dB) | |
|---|---|
| Carucci et al. (1982) | 163.24 |
| Eisinger et al. (1996) | 167.85 |
| Riegel et al. (2007) | 169.69 |
| CSTI (2013) | 169.85 |
| Present study | 146.32 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.-S.; Ku, G.-r.; Lee, S.-J.; Park, S.-G.; Cheong, C. Wavenumber-Frequency Analysis of Internal Aerodynamic Noise in Constriction-Expansion Pipe. Appl. Sci. 2017, 7, 1137. https://doi.org/10.3390/app7111137
Kim K-S, Ku G-r, Lee S-J, Park S-G, Cheong C. Wavenumber-Frequency Analysis of Internal Aerodynamic Noise in Constriction-Expansion Pipe. Applied Sciences. 2017; 7(11):1137. https://doi.org/10.3390/app7111137
Chicago/Turabian StyleKim, Kuk-Su, Ga-ram Ku, Song-June Lee, Sung-Gun Park, and Cheolung Cheong. 2017. "Wavenumber-Frequency Analysis of Internal Aerodynamic Noise in Constriction-Expansion Pipe" Applied Sciences 7, no. 11: 1137. https://doi.org/10.3390/app7111137
APA StyleKim, K.-S., Ku, G.-r., Lee, S.-J., Park, S.-G., & Cheong, C. (2017). Wavenumber-Frequency Analysis of Internal Aerodynamic Noise in Constriction-Expansion Pipe. Applied Sciences, 7(11), 1137. https://doi.org/10.3390/app7111137





