Tire-Pavement Friction Characteristics with Elastic Properties of Asphalt Pavements
Abstract
:1. Introduction
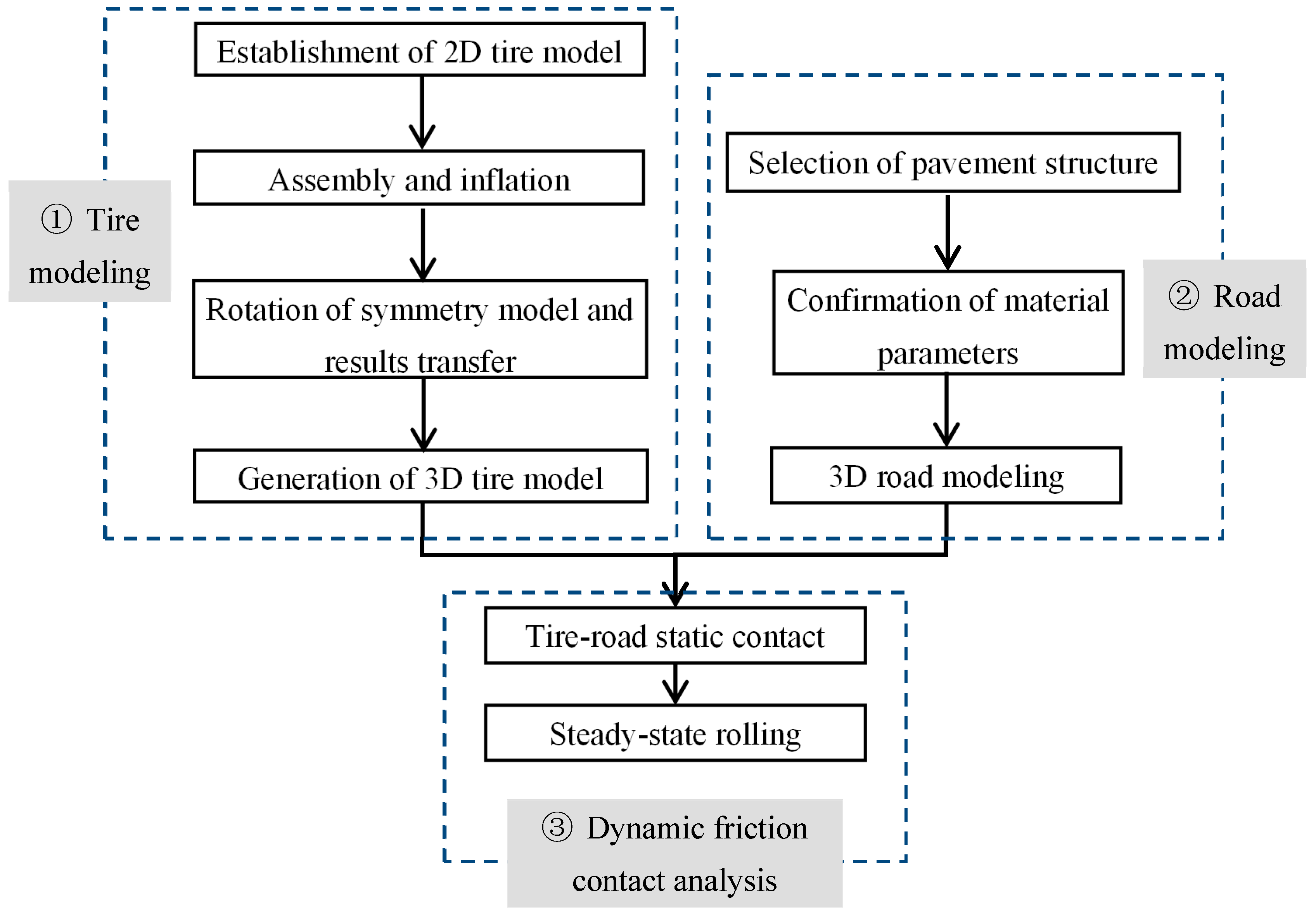
2. Establishment of Tire-Pavement Frictional Contact Simulation Model
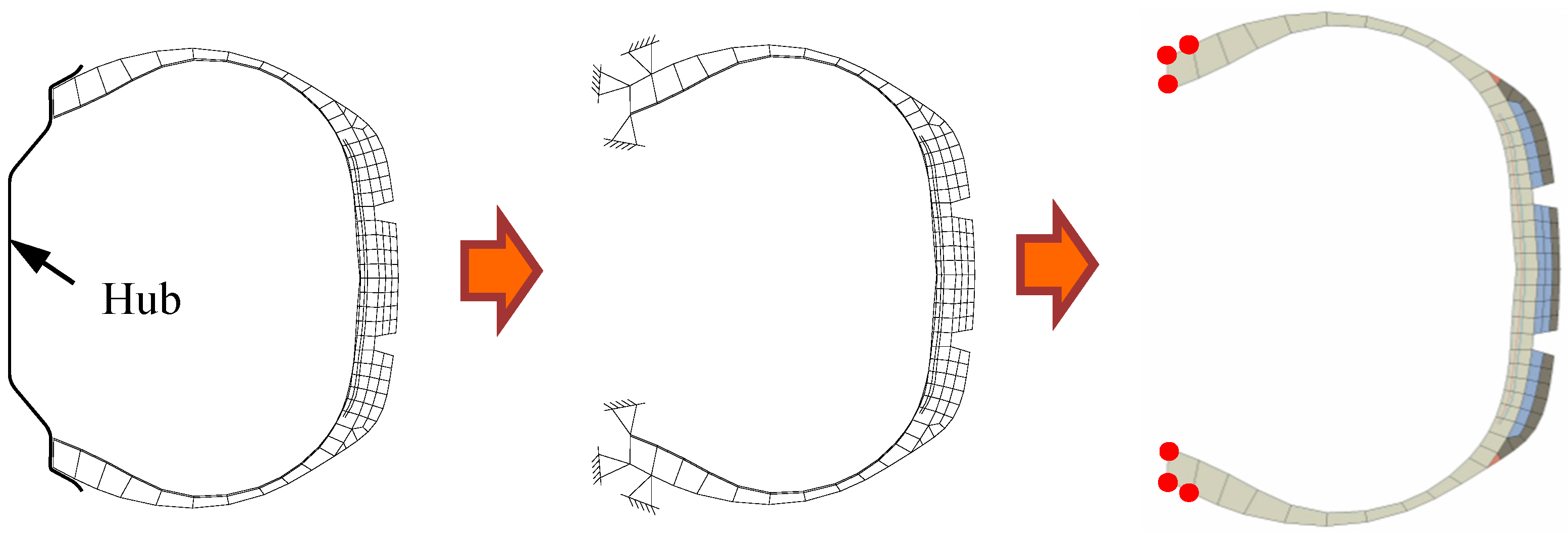
2.1. Establishment of 3D Model for Grooving Radial Tires
- Reduce the poor shape of the cross-sectional element;
- Simplify the contact constraint between the bead chafer and the wheel hub (see Figure 3 for details. Next, simplify the wheel hub as a rigid constraint element, which shares a node with the tire bead);
- Use the rebar elements to simulate the tire’s steel cord and inner liners.
2.2. Pavement Structure Modeling
2.2.1. Pavement Structure Setting
2.2.2. Design of Road Pavement Materials
2.3. Tire-Flexible Pavement Frictional Contact Simulation
2.3.1. Definition of the Tire-Pavement Frictional Contact in ABAQUS
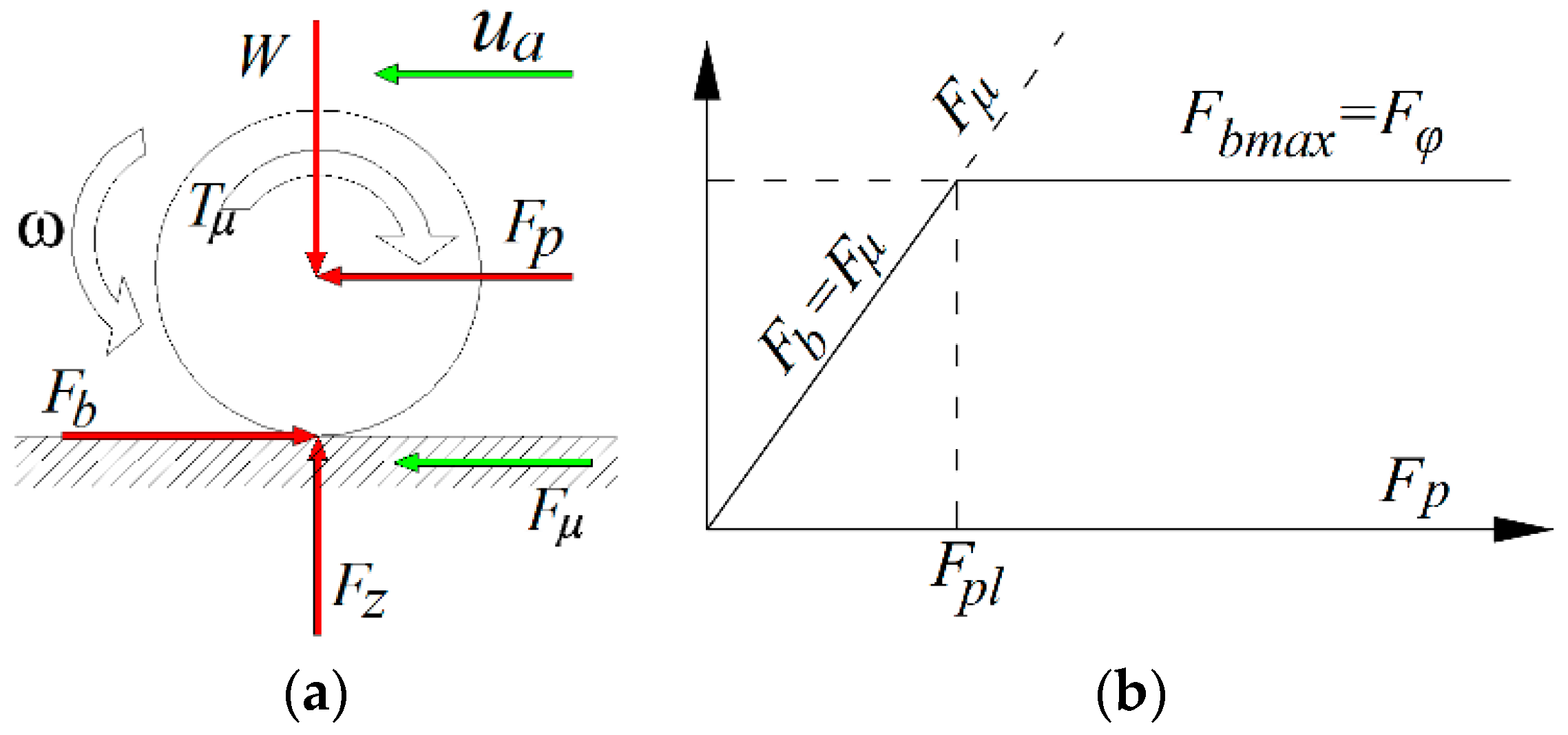
- ωw—the rotational angular velocity of the wheel hub; rad/s
- reff—the effective radius of the wheel; m
- ua—the actual longitudinal velocity of the tire; m/s
- F—the tangential force between tire and pavement contact
- N—the normal force, perpendicular to the contact between tire and pavement
- Fx—the horizontal braking force of the pavement against the tire at the contact region
- Fz—the upper load borne by the tires
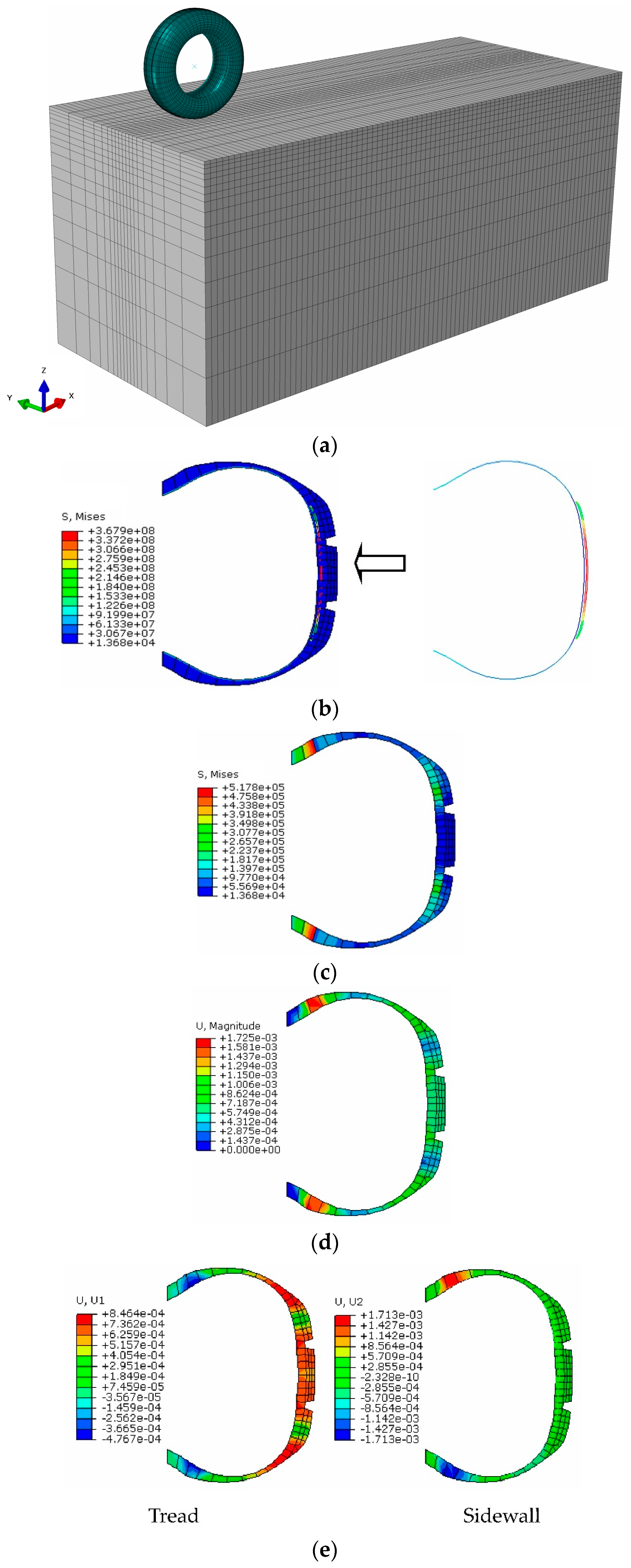
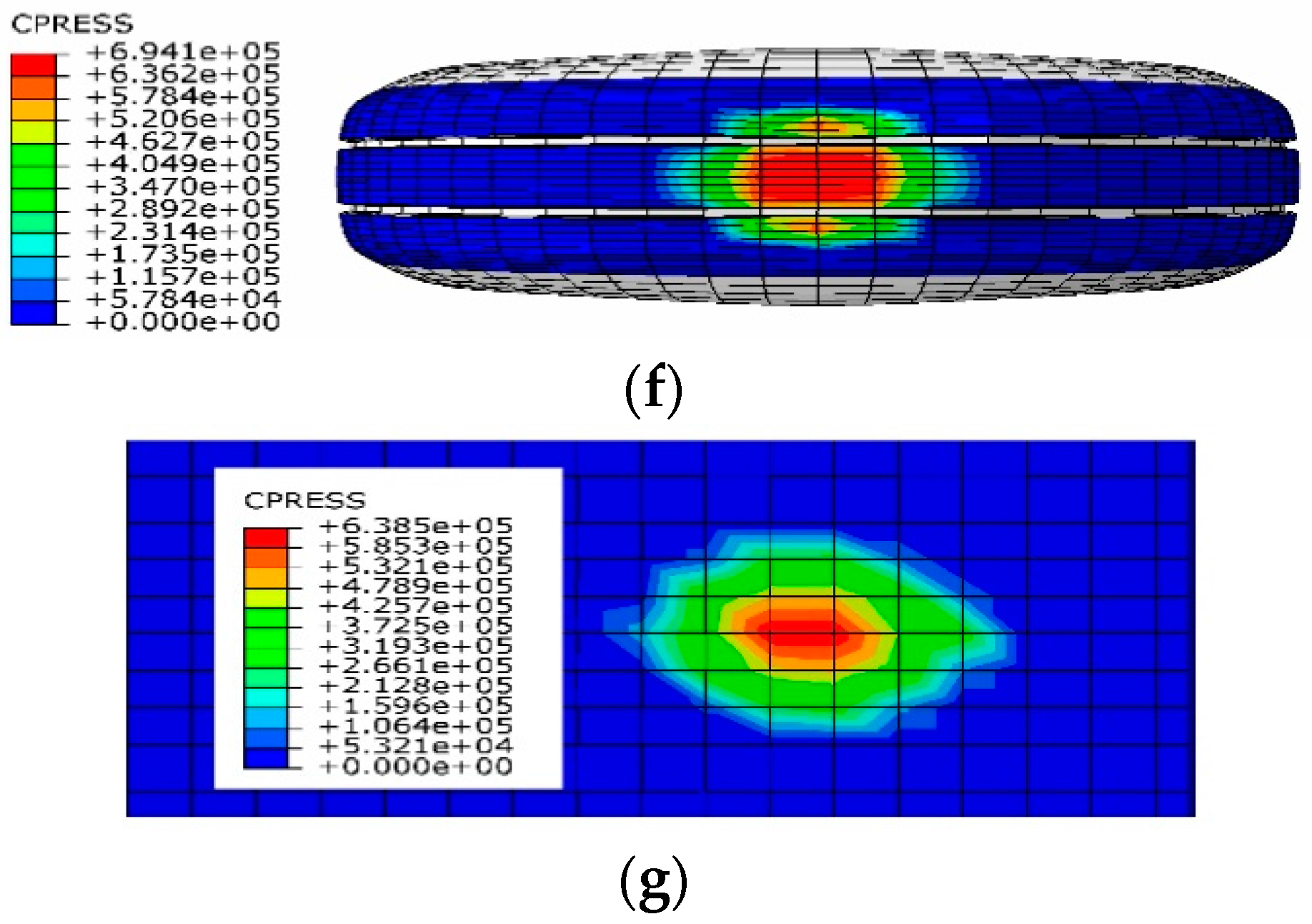
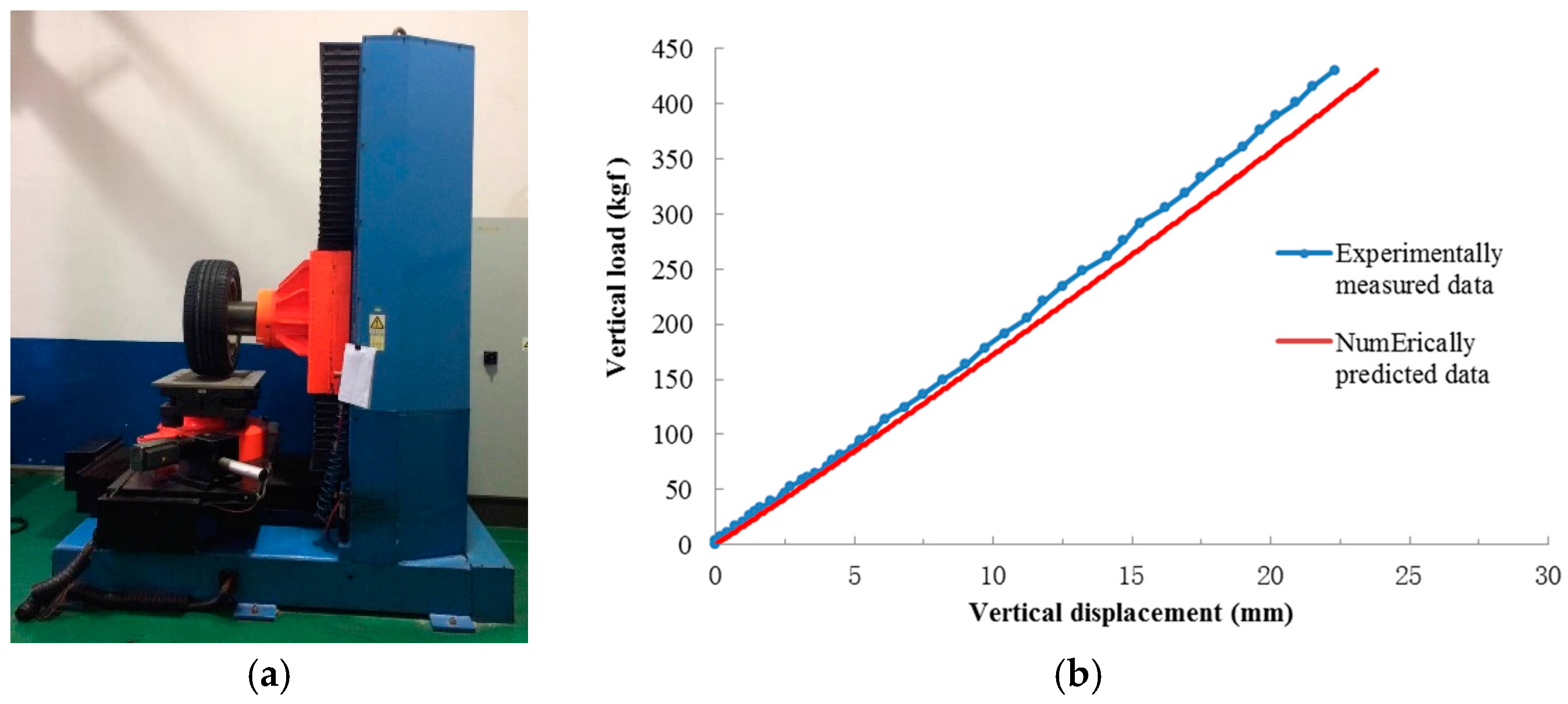
2.3.2. Validation of the 3D Model of Pneumatic Tire-Asphalt Pavement Contact
3. Simulation Analysis of Tire-Asphalt Pavement Frictional Contact
3.1. Simulation Conditions Design of the Tire-Asphalt Pavement Frictional Contact
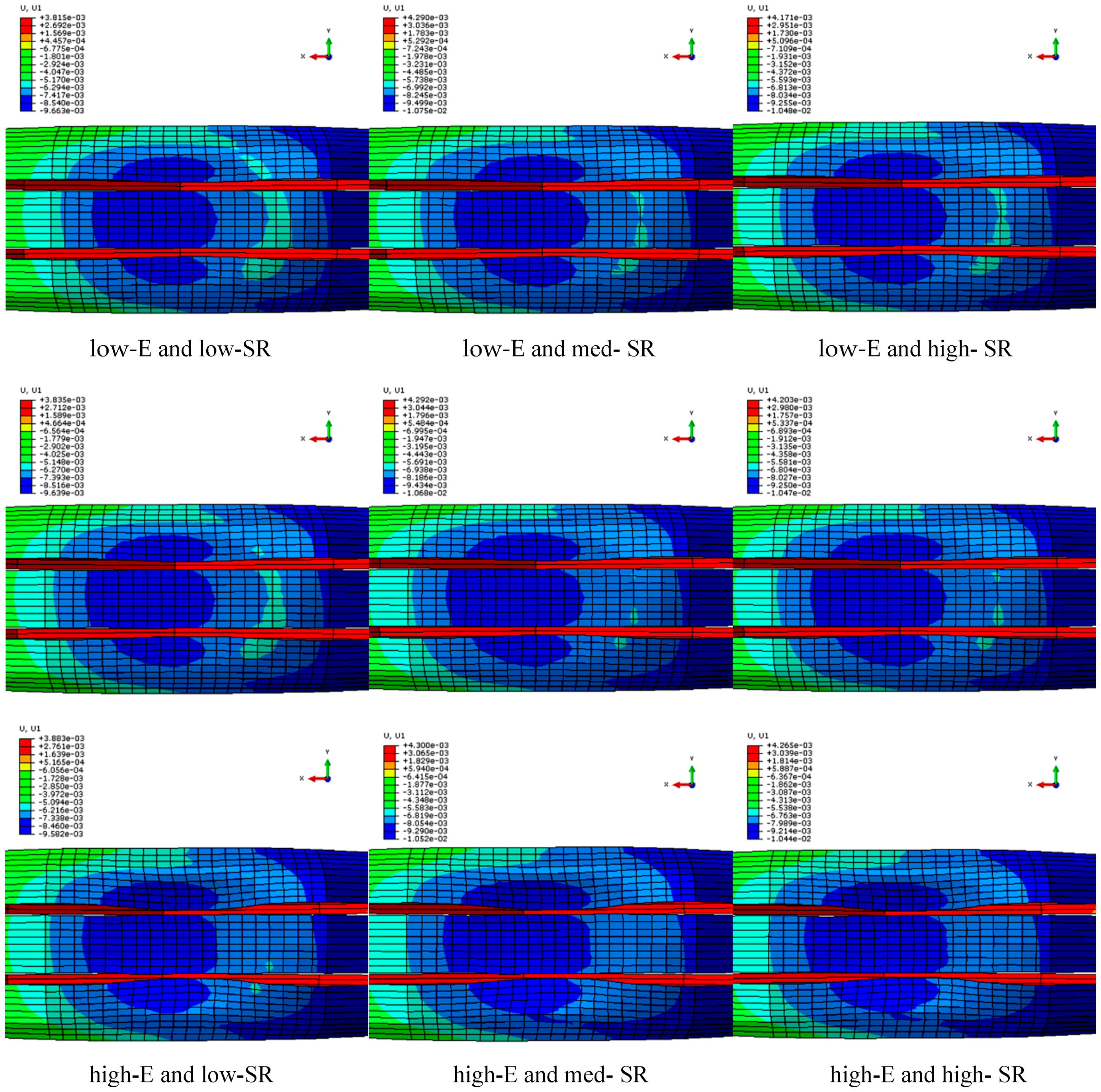
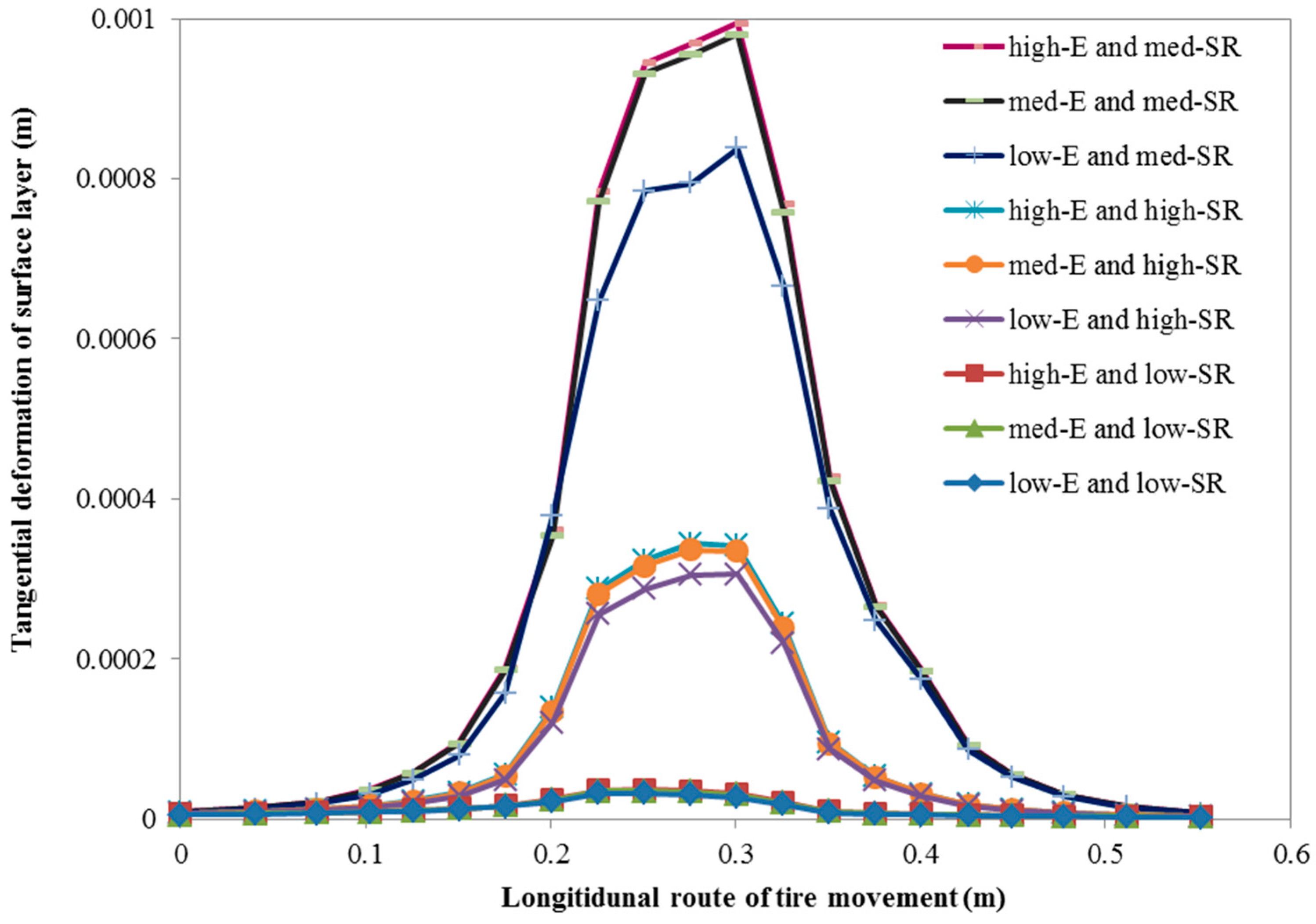
3.2. Tread Deformation
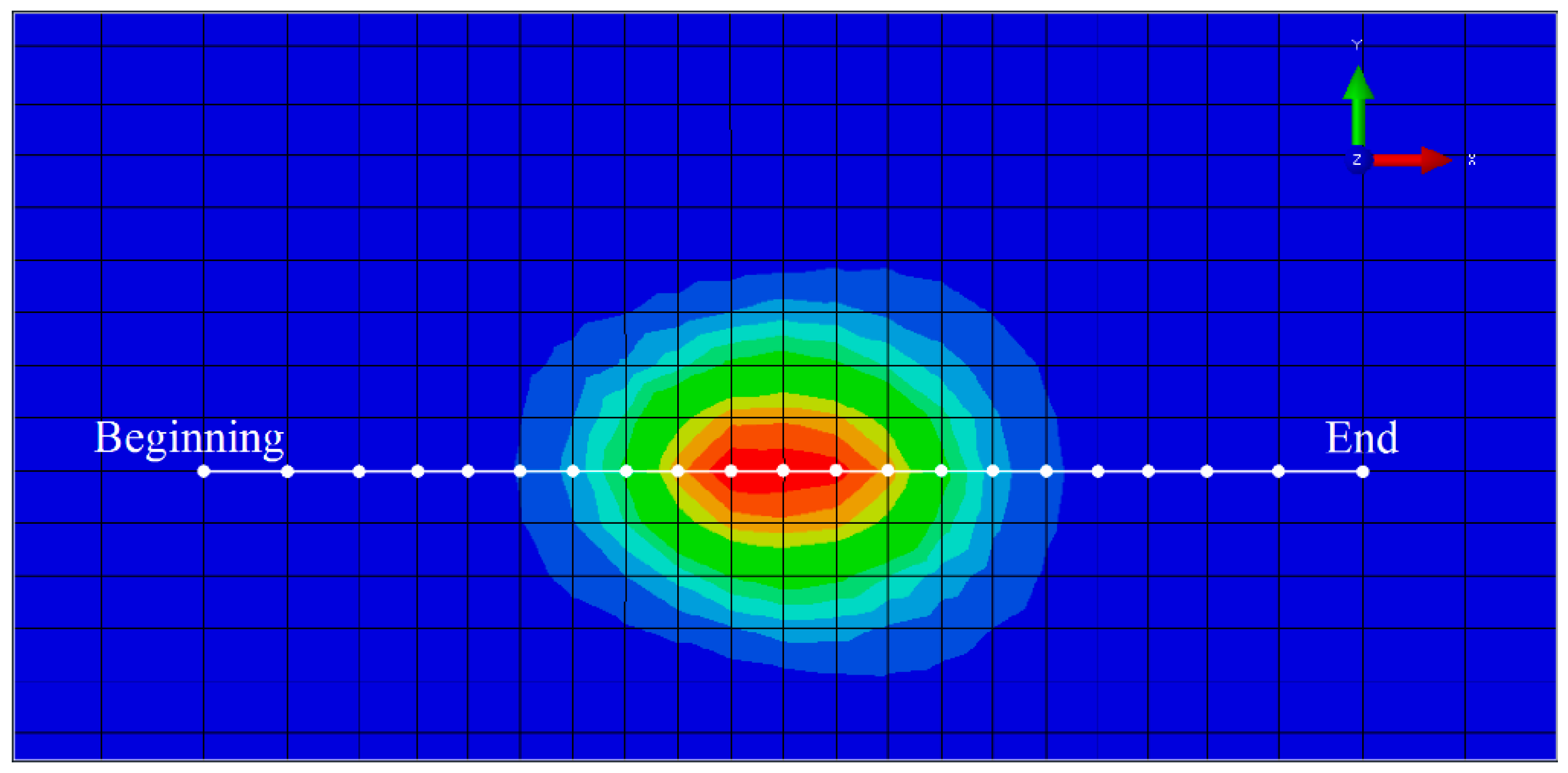
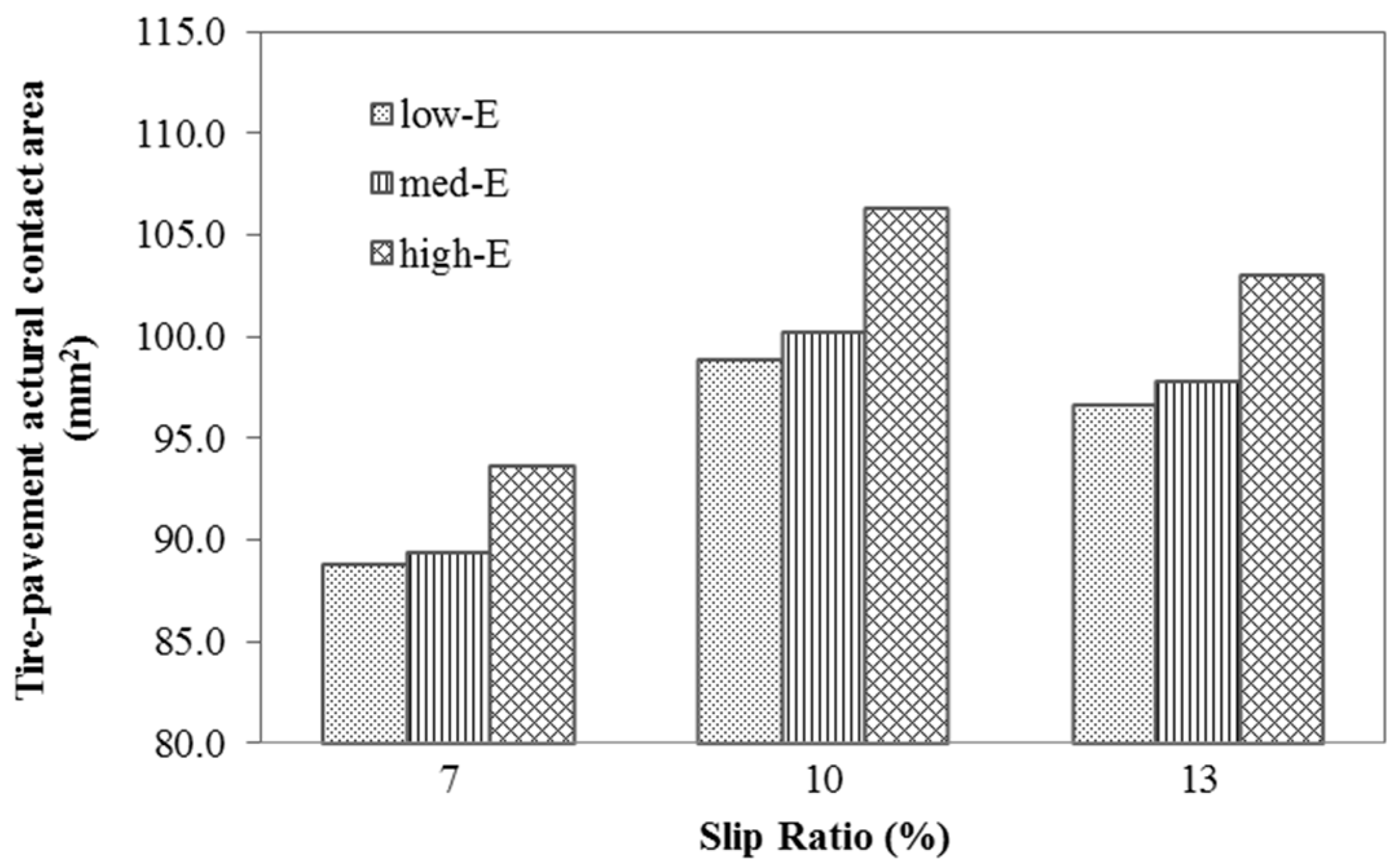
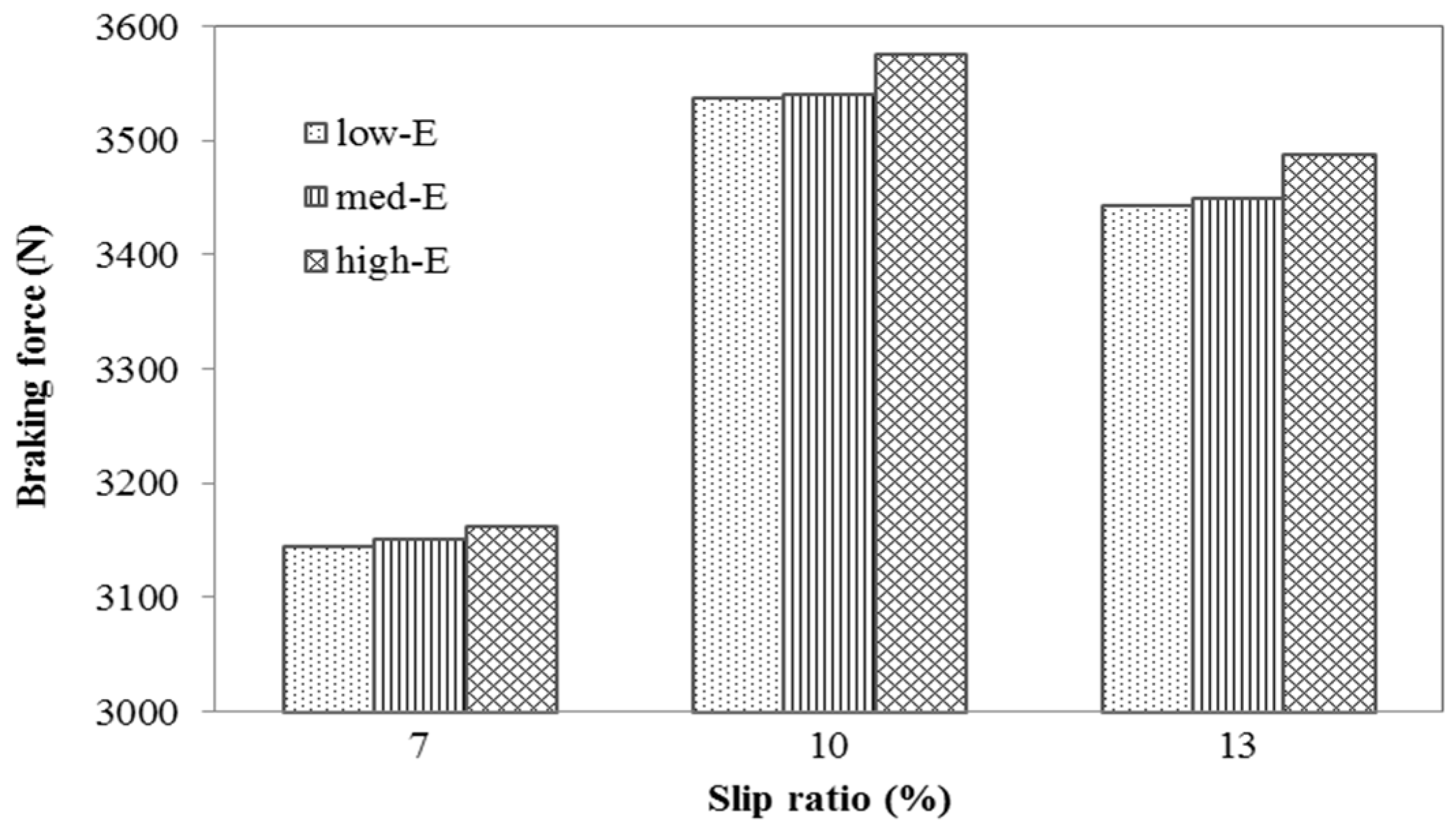
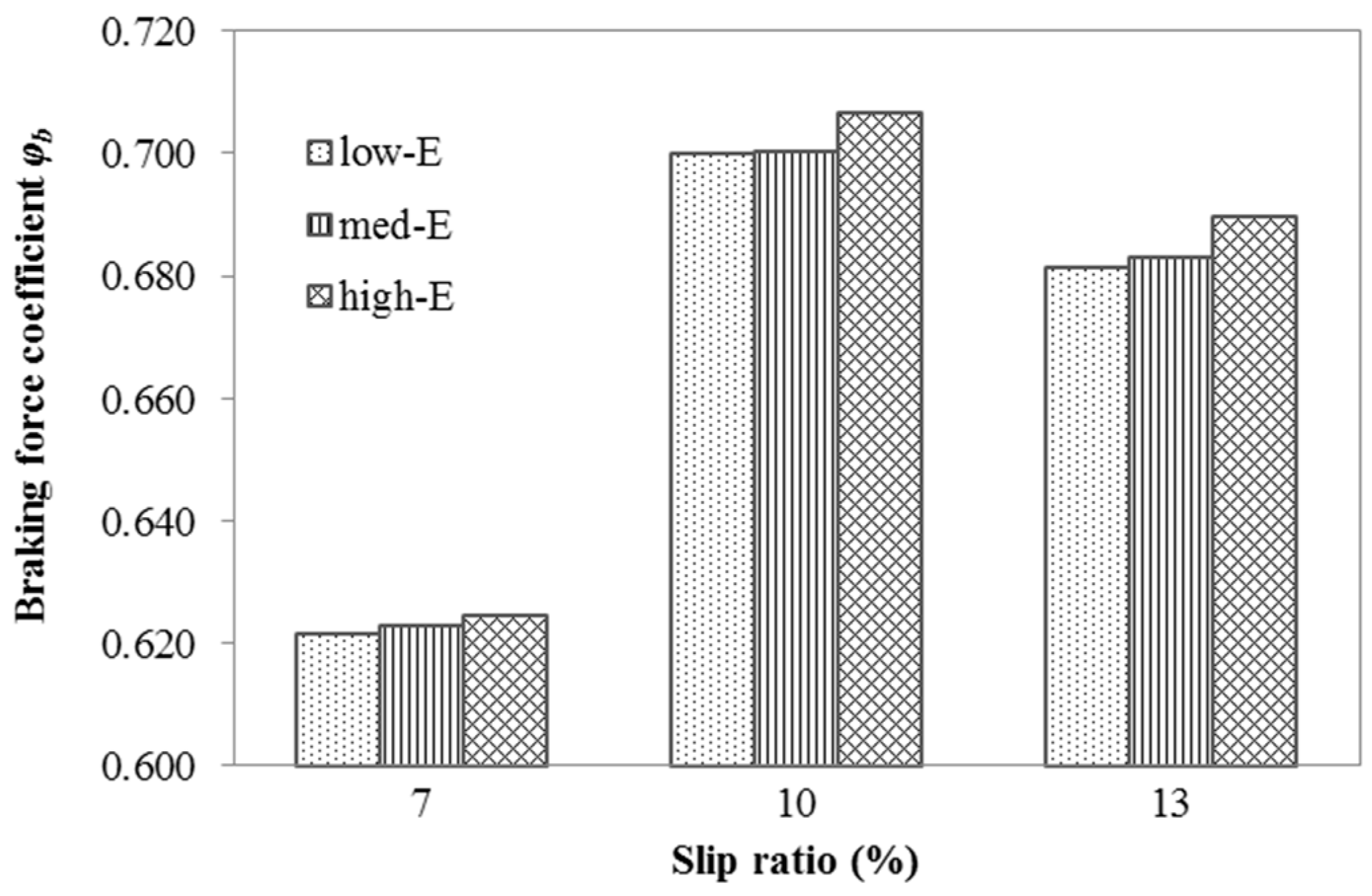
3.3. Pavement Braking Effect
4. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Henry, J.J. Evaluation of Pavement Friction Characteristics (A Synthesis of Highway Practice); NCHRP Synthesis No. 291; National Cooperative Highway Research Program; Transportation Research Board: Washington, DC, USA, 2000. [Google Scholar]
- Horne, W.B.; Dreher, R.C. Phenomena of Pneumatic Tire Hydroplaning; NASA TN D-2056; National Aeronautics and Space Administration: Washington, DC, USA, 1963. [Google Scholar]
- Martin, C.S. Hydrodynamics of Tire Hydroplaning; Final Rep. Project B-608; Georgia Institute of Technology: Atlanta, GA, USA, 1966. [Google Scholar]
- Eshel, A.A. Study of Tires on a Wet Runway; Rep. No. RR67-24; Ampex Corp.: Redwood City, CA, USA, 1967. [Google Scholar]
- Tsakonas, S.; Henry, C.J.; Jacobs, W.R. Hydrodynamics of Aircraft Tire Hydroplaning; NASA CR-1125; National Aeronautics and Space Administration: Washington, DC, USA, 1968. [Google Scholar]
- Horne, W.B.; Yager, T.J.; Ivey, D.L. Recent Studies to Investigate Effects of Tire Footprint Aspect Ratio on Dynamic Hydroplaning Speed; Pottinger, M.G., Yager, T.J., Eds.; The Tire Pavement Interface, ASTM STP 929; ASTM: Philadelphia, PA, USA, 1986; pp. 26–46. [Google Scholar]
- Ong, G.P.; Fwa, T.F. Wet-pavement hydroplaning risk and skid resistance: Modeling. J. Transp. Eng. 2007, 133, 590–598. [Google Scholar] [CrossRef]
- Fwa, T.F.; Ong, G.P. Wet-pavement hydroplaning risk and skid resistance: Analysis. J. Transp. Eng. 2008, 134, 182–190. [Google Scholar] [CrossRef]
- Ong, G.P.; Fwa, T.F. Modeling skid resistance of commercial trucks on highways. J. Transp. Eng. 2010, 136, 510–517. [Google Scholar] [CrossRef]
- Fwa, T.F.; Pasindu, H.R.; Ong, G.P. Critical rut depth for pavement maintenance based on vehicle skidding and hydroplaning consideration. J. Transp. Eng. 2012, 138, 423–429. [Google Scholar] [CrossRef]
- Grosch, K.A. The relation between the friction and viscoelastic properties of rubber. Proc. R. Soc. Lond. Ser. A 1962, 274, 21–39. [Google Scholar] [CrossRef]
- Srirangam, S.K.; Anupam, K.; Scarpas, A.; Kösters, A. Influence of tire temperature increase on friction measurements-I: Laboratory tests and finite element modeling aspects. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Anupam, K.; Srirangam, S.K.; Scarpas, A.; Kasbergen, C. Influence of temperature on the tire-pavement friction-II: Analyses. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Forster, S.W. Pavement Microtexture and Its Relation to Skid Resistance; 151B164; Transportation Research Record; Transportation Research Board: Washington, DC, USA, 1990. [Google Scholar]
- Sengoz, B.; Onsori, A.; Topal, A. Effect of aggregate shape on the surface properties of flexible pavement. KSCE J. Civ. Eng. 2014, 18, 1364–1371. [Google Scholar] [CrossRef]
- Kane, M.; Rado, Z.; Timmons, A. Exploring the texture–friction relationship: From texture empirical decomposition to pavement friction. Int. J. Pavement Eng. 2015, 16, 919–928. [Google Scholar] [CrossRef]
- Srirangam, S.K.; Anupam, K.; Scarpas, A.; Kasbergen, C. Development of a thermomechanical tyre–pavement interaction model. Int. J. Pavement Eng. 2015, 16, 721–729. [Google Scholar] [CrossRef]
- Wang, C.T.; Yao, Z.Q.; Chen, M. Vehicle Tribology; Shanghai Jiaotong University Press: Shanghai, China, 2002; pp. 400–423. [Google Scholar]
- Zhuang, J. Vehicle-Terramechanics; China Machine Press: Beijing, China, 1986. [Google Scholar]
- Wang, L.X.; Wang, H.Y. Vehicle Dynamics; National Defence Industry Press: Beijing, China, 2008. [Google Scholar]
- You, Z.; Adhikari, S.; Kutay, M.E. Dynamic modulus simulation of the asphalt concrete using the X-ray computed tomography images. Mater. Struct. 2009, 42, 617–630. [Google Scholar] [CrossRef]
- Goh, S.W.; You, Z.; Williams, R.C.; Li, X. Preliminary dynamic modulus criteria of HMA for field rutting of asphalt pavements: Michigan’s experience. J. Transp. Eng. 2011, 137, 37–45. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Stanciulescu, I. Effect of surface friction on tire-pavement contact stress during vehicle maneuvering. J. Eng. Mech. 2014, 140, 04014001. [Google Scholar] [CrossRef]
- Zhou, C. Study on Application Technology of Rubber Particle Asphalt Mixture in Ice and Snow Region. Ph.D. Thesis, Harbin University of Industry, Harbin, China, 2006. [Google Scholar]
- Wang, X. The Apply Technology of the Crumb Rubber in the Asphalt and Mixture; China Communications Press: Beijing, China, 2008; pp. 167–197. [Google Scholar]
- Yao, L. Research on Key Technology of Granulated Crumb Rubber Anti-ice Asphalt Pavement. Ph.D. Thesis, Chang’an Universtity, Xi’an, China, 2012. [Google Scholar]
- Yu, M.; Wu, G. Research on the mix design of dry process crumb rubber modified asphalt mixture. J. Build. Mater. 2014, 17, 100–105. [Google Scholar]
- Yu, M.; Wu, G.; Zhou, J.; Easa, S. Proposed compaction procedure for dry process crumb rubber modified asphalt mixtures using air void content and expansion ratio. J. Test. Eval. 2014, 42, 328–338. [Google Scholar] [CrossRef]
- Yu, M. Study on the Dry Process Crumb Rubber Modified Anti-Skid Layer Based on the Tire-Road Coupling. Ph.D. Thesis, Chongqing Jiaotong Universtity, Chongqing, China, 2014. [Google Scholar]
- Kogbara, R.B.; Masad, E.A.; Kassem, E.; Scarpas, A.T.; Anupam, K. A state-of-the-art review of parameters influencing measurement and modeling of skid resistance of asphalt pavements. Constr. Build. Mater. 2017, 133, 330–339. [Google Scholar] [CrossRef]
- Najafi, S.; Flintsch, G.W.; Medina, A. Linking roadway crashes and tire-pavement friction: A case study. Int. J. Pavement Eng. 2017, 18, 119–127. [Google Scholar] [CrossRef]
- Koishi, M.; Kabe, K.; Shiratori, M. Tire cornering simulation using explicit finite element analysis code. J. Appl. Polym. Sci. 2000, 78, 1566–1572. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, F.; Huang, X.; Li, L. Constitutive model of rubber materials. Rubber Ind. 2006, 53, 119–125. [Google Scholar]
- Wang, Y.; Li, X.; Huang, Y. Selection for constitutive model in rubber calculation. The chemical industry and engineering society of China. In Proceedings of the 4th Seminar China Rubber Products, Zhuzhou, Hunan, China, 17 November 2007; pp. 443–449. [Google Scholar]
- Liu, Y.; You, Z.P.; Yao, H. An idealized discrete element model for pavement-wheel interaction. J. Mar. Sci. Technol. 2015, 23, 339–343. [Google Scholar]
- Judge, A.W. Automobile engines. In Theory, Design, Construction, Operation, Testing and Maintenance; Hervey Press: Hervey, Australia, 2008. [Google Scholar]
| Material Parameters | Neo-Hooken Model Parameters in ABAQUS | Tensile Modulus/MPa | Tensile Strength/MPa | Elongation Ratio/% | Permanent Deformation/% | |||
|---|---|---|---|---|---|---|---|---|
| C10 (kPa) | C01 (kPa) | D1 (kPa) | M100 | M300 | Tb | Eb | Ps | |
| Tread | 835 | 0 | 0 | 2.5 | 9.9 | 19.1 | 544 | 15 |
| Sidewall | 1000 | 0 | 0 | 2.3 | 9.3 | 15.1 | 450 | 10 |
| Tire Section | Young’s Modulus (GPa) | Poisson’s Ratio (−) | Density (g/cm3) | Area per Bar (mm2) | Spacing (mm) | Orientation Angle (°) |
|---|---|---|---|---|---|---|
| Tread | From Lab test | 0.45 | 1.12 | - | - | - |
| Sidewall | 1.15 | |||||
| Belt-1 | 172.2 | 0.3 | 5900 | 0.212 | 1.16 | 70 |
| Belt-2 | 110 | |||||
| Carcass | 9.9 | 0.3 | 1500 | 0.421 | 1.00 | 0 |
| Pavement Structure | Layer Thickness (cm) | Elasticity Modulus (MPa) | Poisson’s Ratio | Density (g/cm3) | |
|---|---|---|---|---|---|
| Surface course | 4 | 1480 (without crumb rubber, low-E) | 0.35 | 2.474 | |
| 1265 (with 4% crumb rubber, med-E) | 0.40 | 2.420 | |||
| 886 (with 5.5% crumb rubber, high-E) | 0.40 | 2.387 | |||
| Leveling course | 6 | 1100 | 0.35 | 2.432 | |
| Asphalt base course | 8 | 1000 | 0.35 | 2.471 | |
| Cement-stabilized Macadam Base Course | 18 | 1500 | 0.25 | 2.056 | |
| Lime-fly ash Soil Cushion | 31 | 750 | 0.25 | 1.924 | |
| Subgrade | 500 | 35 | 0.35 | 1.918 |
| Tire Pressure (kPa) | Applied Load (N) | Experimentally Measured Data | Numerically Simulated Results | ||||
|---|---|---|---|---|---|---|---|
| Length (L) (mm) | Width (W) (mm) | Area (cm2) | Length (L) (mm) | Width (W) (mm) | Area (cm2) | ||
| 200 | 2200 | 125.0 | 102.5 | 104.0 | 119.3 | 99.7 | 98.5 |
| 220 | 3200 | 147.6 | 106.1 | 135.0 | 142.1 | 103.6 | 128.6 |
| Pavement Types | Slip Ratio (%) | ||
|---|---|---|---|
| 7 | 10 | 14 | |
| low-E | low-SR | med-SR | high-SR |
| med-E | low-SR | med-SR | high-SR |
| high-E | low-SR | med-SR | high-SR |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Wu, G.; Kong, L.; Tang, Y. Tire-Pavement Friction Characteristics with Elastic Properties of Asphalt Pavements. Appl. Sci. 2017, 7, 1123. https://doi.org/10.3390/app7111123
Yu M, Wu G, Kong L, Tang Y. Tire-Pavement Friction Characteristics with Elastic Properties of Asphalt Pavements. Applied Sciences. 2017; 7(11):1123. https://doi.org/10.3390/app7111123
Chicago/Turabian StyleYu, Miao, Guoxiong Wu, Lingyun Kong, and Yu Tang. 2017. "Tire-Pavement Friction Characteristics with Elastic Properties of Asphalt Pavements" Applied Sciences 7, no. 11: 1123. https://doi.org/10.3390/app7111123
APA StyleYu, M., Wu, G., Kong, L., & Tang, Y. (2017). Tire-Pavement Friction Characteristics with Elastic Properties of Asphalt Pavements. Applied Sciences, 7(11), 1123. https://doi.org/10.3390/app7111123





