Soil Dynamic Constitutive Model for Characterizing the Nonlinear-Hysteretic Response
Abstract
:1. Introduction
2. Nonlinear-Hysteretic Constitutive Model
3. Explicit Formula for the Characterization of the Nonlinear Response
4. Discussion
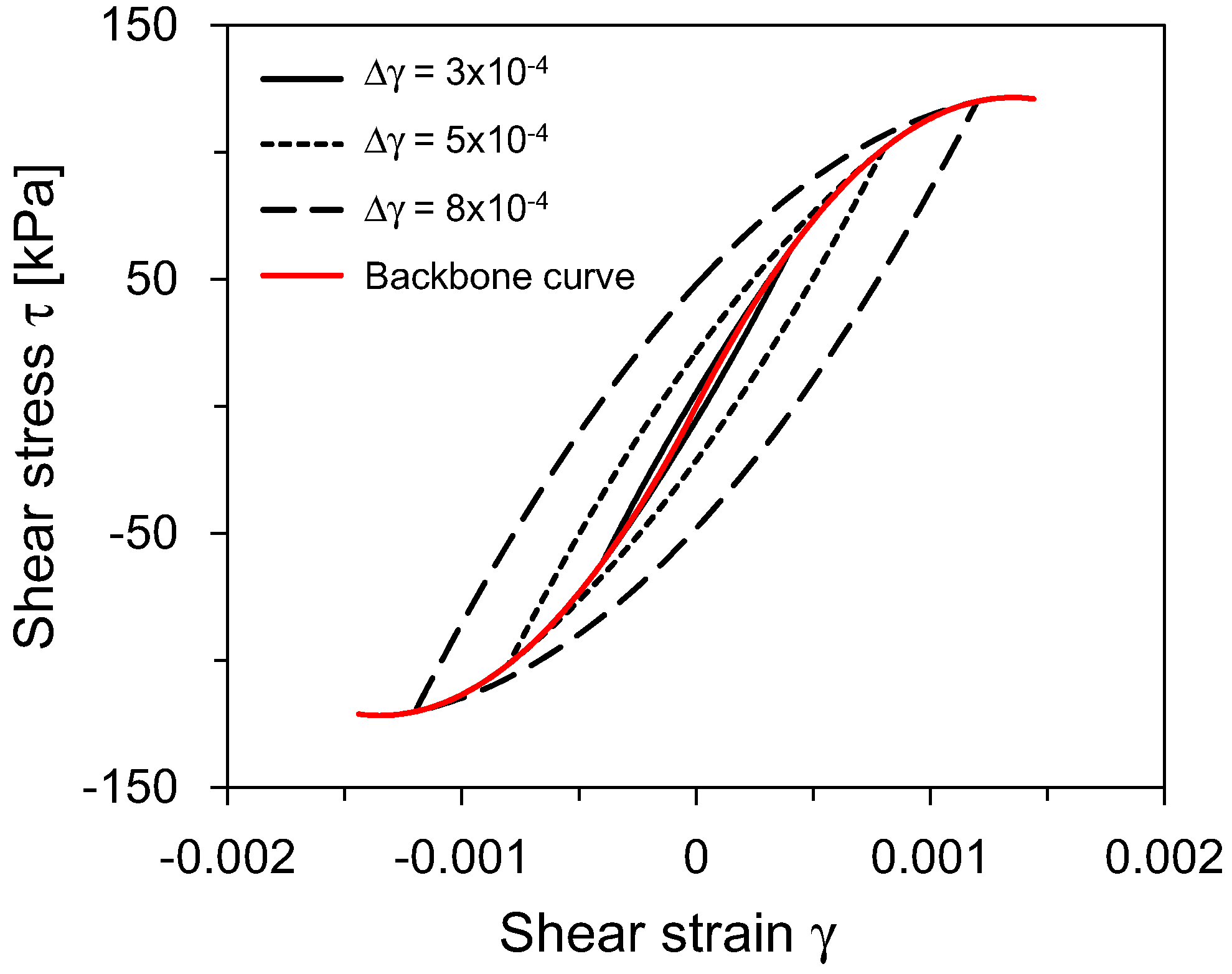
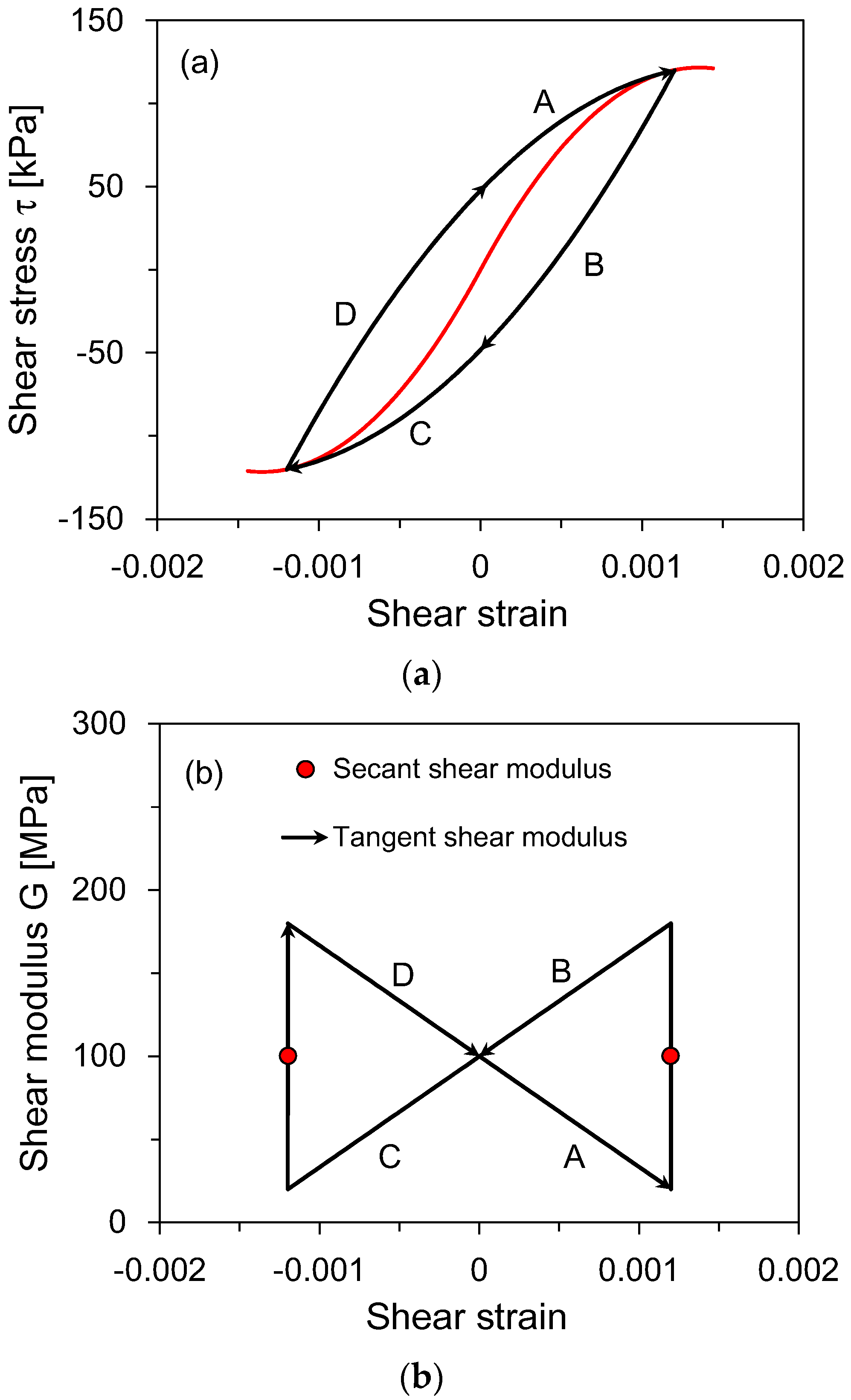
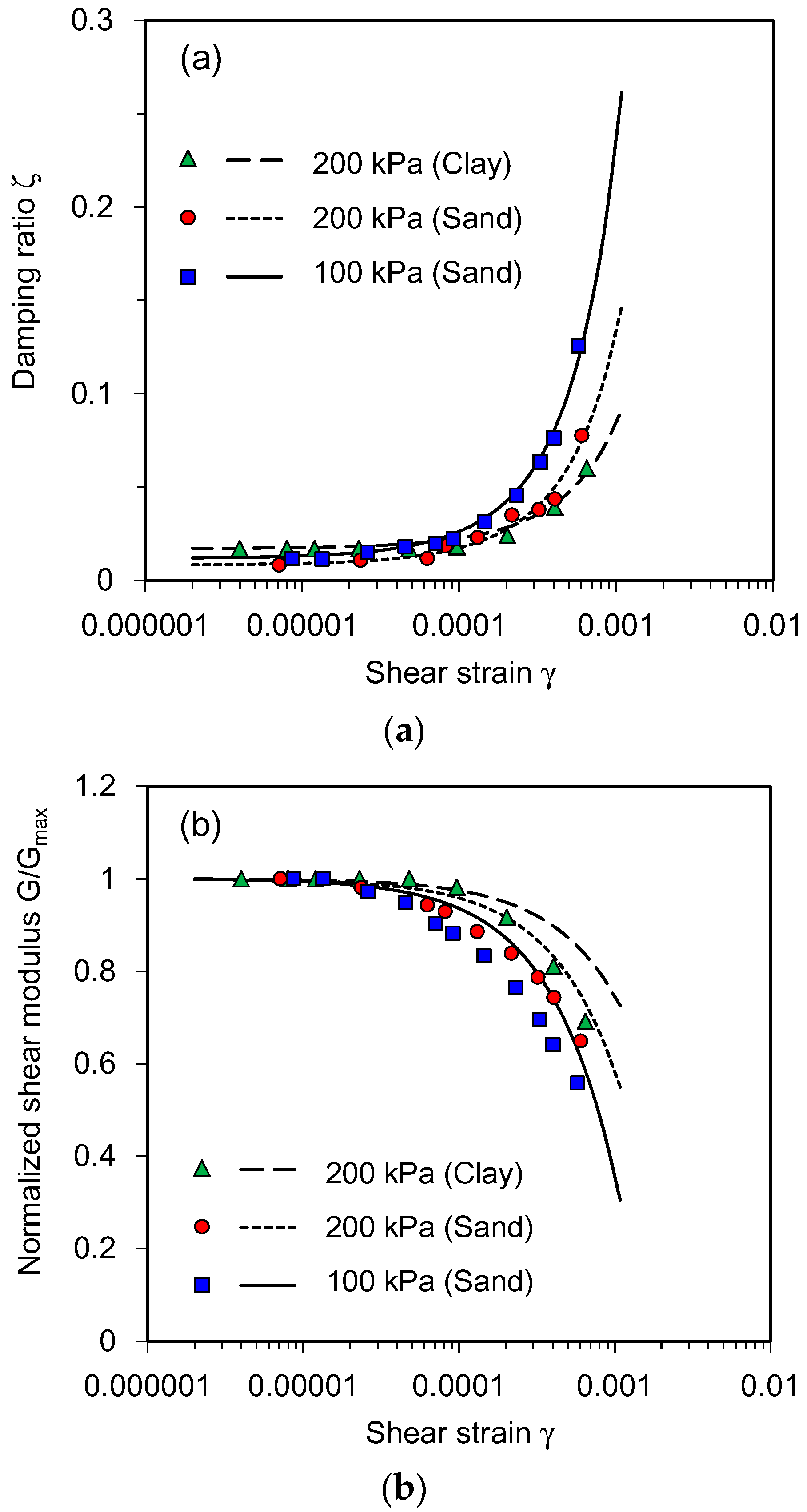
4.1. Examples
4.2. Is the Linear Characteristic Equation Valid for Data Interpretation?
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Martin, P.P.; Seed, H.B. One-dimensional dynamic ground response analyses. J. Geotech. Eng. Div. 1982, 108, 935–952. [Google Scholar] [CrossRef]
- Muravskii, G.; Frydman, S. Site response analysis using a non-linear hysteretic model. Soil Dyn. Earthq. Eng. 1998, 17, 227–238. [Google Scholar] [CrossRef]
- Pavlenko, O.V.; Irikura, K. Types of elastic nonlinearity of sedimentary soils. Geophys. Res. Lett. 2002, 29, 36-31–36-34. [Google Scholar] [CrossRef]
- Hartzell, S.; Bonilla, L.F.; Williams, R.A. Prediction of Nonlinear Soil Effects. Bull. Seismol. Soc. Am. 2004, 94, 1609–1629. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Park, D. Viscous damping formulation and high frequency motion propagation in non-linear site response analysis. Soil Dyn. Earthq. Eng. 2002, 22, 611–624. [Google Scholar] [CrossRef]
- Prévost, J.H.; Abdel-Ghaffar, A.M.; Elgamal, A.W.M. Nonlinear Hysteretic Dynamic Response of Soil Systems. J. Eng. Mech. 1985, 111, 696–713. [Google Scholar] [CrossRef]
- Kondner, R.L. Hyperbolic Stress-Strain Response: Cohesive Soils. J. Geotech. Eng. Div. 1963, 89, 115–143. [Google Scholar]
- Duncan, J.M.; Chang, C.Y. Non-linear analysis of stress and strain in soils. J. Soil Mech. Found. Div. 1970, 96, 1629–1653. [Google Scholar]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2001. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943.
- Hardin, B.O.; Drnecivh, V.P. Shear modulus and damping in soils: Design equation and curve. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar]
- Zhang, J.; Andrus, R.D.; Juang, C.H. Normalized Shear Modulus and Material Damping Ratio Relationships. J. Geotech. Geoenviron. Eng. 2005, 131, 453–464. [Google Scholar] [CrossRef]
- Assimaki, D.; Kausel, E.; Whittle, A. Model for Dynamic Shear Modulus and Damping for Granular Soils. J. Geotech. Geoenviron. Eng. 2000, 126, 859–869. [Google Scholar] [CrossRef]
- Pyke, R. Nonlinear soil models for irregular cyclic loadings. J. Geotech. Eng. 1979, 105, 715–725. [Google Scholar]
- Chiang, D.-Y. The generalized Masing models for deteriorating hysteresis and cyclic plasticity. Appl. Math. Model. 1999, 23, 847–863. [Google Scholar] [CrossRef]
- Muravskii, G. On description of hysteretic behaviour of materials. Int. J. Solids Struct. 2005, 42, 2625–2644. [Google Scholar] [CrossRef]
- Iwan, W.D. A Distributed-Element Model for Hysteresis and Its Steady-State Dynamic Response. J. Appl. Mech. 1966, 33, 893–900. [Google Scholar] [CrossRef]
- Bolton, M.D.; Wilson, J.M.R. An experimental and theoretical comparison between static and dynamic torsional soil tests. Géotechnique 1989, 39, 585–599. [Google Scholar] [CrossRef]
- Matasović, N.; Vucetic, M. Cyclic Characterization of Liquefiable Sands. J. Geotech. Eng. 1993, 119, 1805–1822. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Park, D. Non-linear one-dimensional seismic ground motion propagation in the Mississippi embayment. Eng. Geol. 2001, 62, 185–206. [Google Scholar] [CrossRef]
- Brinkgreve, R.B. Selection of soil models and parameters for geotechnical engineering application. In Soil Constitutive Models: Evaluation, Selection, and Calibration; Yamamuro, J.A., Kaliakin, V.N., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 69–98. [Google Scholar]
- Holcomb, D.J. Memory, relaxation, and microfracturing in dilatant rock. J. Geophys. Res. Solid Earth 1981, 86, 6235–6248. [Google Scholar] [CrossRef]
- Kadish, A.; Johnson, P.A.; Zinszner, B. Evaluating hysteresis in earth materials under dynamic resonance. J. Geophys. Res. 1996, 101, 25139–25147. [Google Scholar] [CrossRef]
- Guyer, R.A.; Johnson, P.A. Nonlinear mesoscopic elasticity: Evidence for a new class of materials. Phys. Today 1999, 52, 30–36. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Johnson, P.A. Dynamic nonlinear elasticity in geomaterials. Rivista del Nuovo Cimento 2001, 24, 1–46. [Google Scholar]
- Johnson, P.A.; Jia, X. Nonlinear dynamics, granular media and dynamic earthquake triggering. Nature 2005, 437, 871–874. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.A.; Zinszner, B.; Rasolofosaon, P.; Cohen-Tenoudji, F.; Van Den Abeele, K. Dynamic measurements of the nonlinear elastic parameter α in rock under varying conditions. J. Geophys. Res. Solid Earth 2004, 109, B02202. [Google Scholar] [CrossRef]
- Orban, F. Damping of materials and members in structures. J. Phys. Conf. Ser. 2011, 268, 012022. [Google Scholar] [CrossRef]
- Chong, S.-H.; Santamarina, J.C. Soil Compressibility Models for a Wide Stress Range. J. Geotech. Geoenviron. Eng. 2016, 142, 06016003. [Google Scholar] [CrossRef]
- Chong, S.H. The Effect of Subsurface Mass Loss on the Response of Shallow Foundations; Georgia Institute of Technology: Atlanta, GA, USA, 2014. [Google Scholar]
- Kim, D.S. Deformational Characteristics of Soils at Small to Intermediate Strains from Cyclic Tests. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 1991. [Google Scholar]
- McCall, K.R.; Guyer, R.A. Equation of state and wave propagation in hysteretic nonlinear elastic materials. J. Geophys. Res. Solid Earth 1994, 99, 23887–23897. [Google Scholar] [CrossRef]
- Nazarov, V.E.; Kiyashko, S.B. Modified Davidenkov hysteresis and the propagation of sawtooth waves in polycrystals with hysteresis loss saturation. Phys. Metals Metallogr. 2016, 117, 766–771. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chong, S.-H. Soil Dynamic Constitutive Model for Characterizing the Nonlinear-Hysteretic Response. Appl. Sci. 2017, 7, 1110. https://doi.org/10.3390/app7111110
Chong S-H. Soil Dynamic Constitutive Model for Characterizing the Nonlinear-Hysteretic Response. Applied Sciences. 2017; 7(11):1110. https://doi.org/10.3390/app7111110
Chicago/Turabian StyleChong, Song-Hun. 2017. "Soil Dynamic Constitutive Model for Characterizing the Nonlinear-Hysteretic Response" Applied Sciences 7, no. 11: 1110. https://doi.org/10.3390/app7111110
APA StyleChong, S.-H. (2017). Soil Dynamic Constitutive Model for Characterizing the Nonlinear-Hysteretic Response. Applied Sciences, 7(11), 1110. https://doi.org/10.3390/app7111110



