Strong Aftershock Study Based on Coulomb Stress Triggering—A Case Study on the 2016 Ecuador Mw 7.8 Earthquake
Abstract
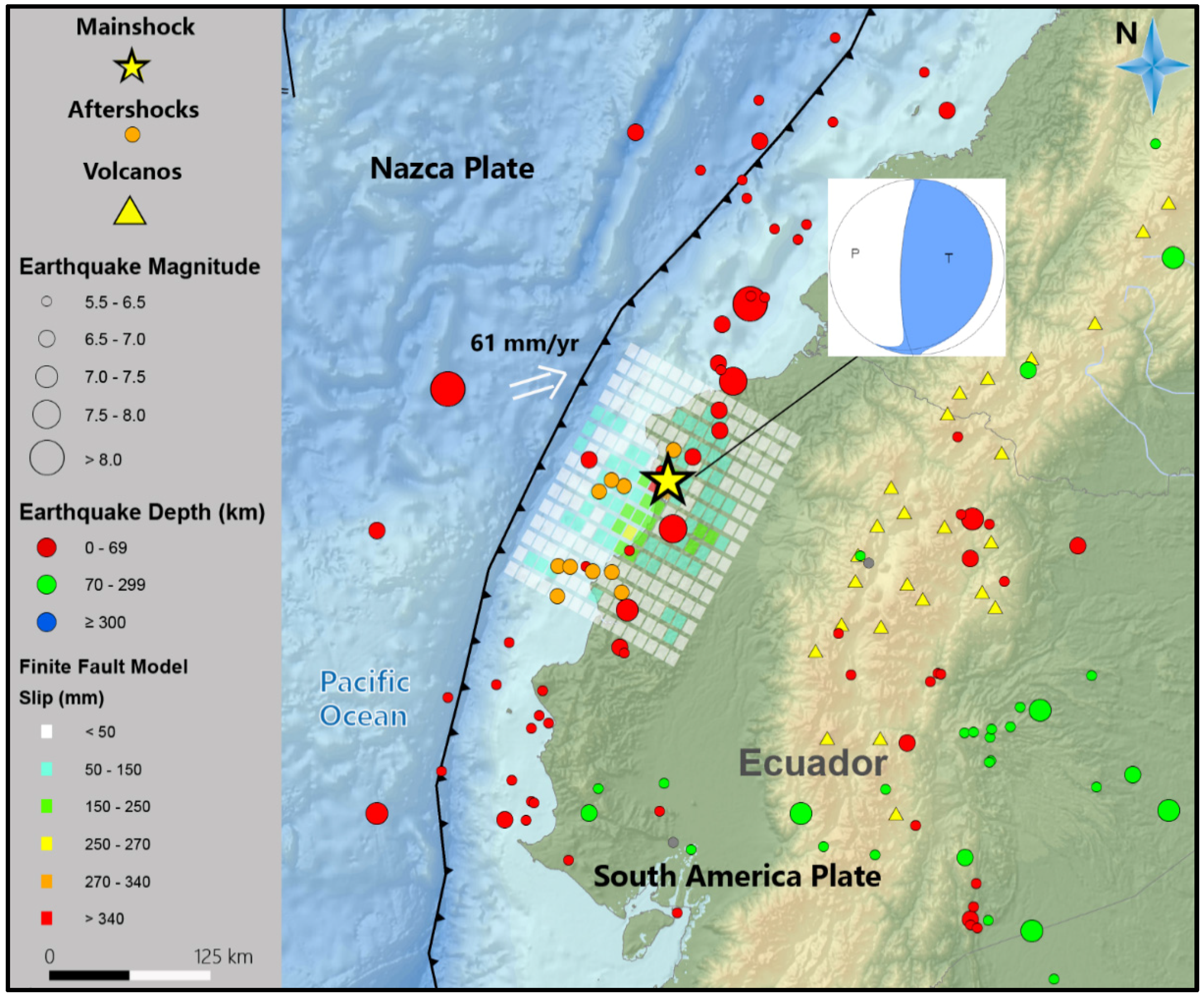
:1. Introduction
2. The Coulomb Stress Triggering Hypothesis
2.1. Coulomb Failure Criterion
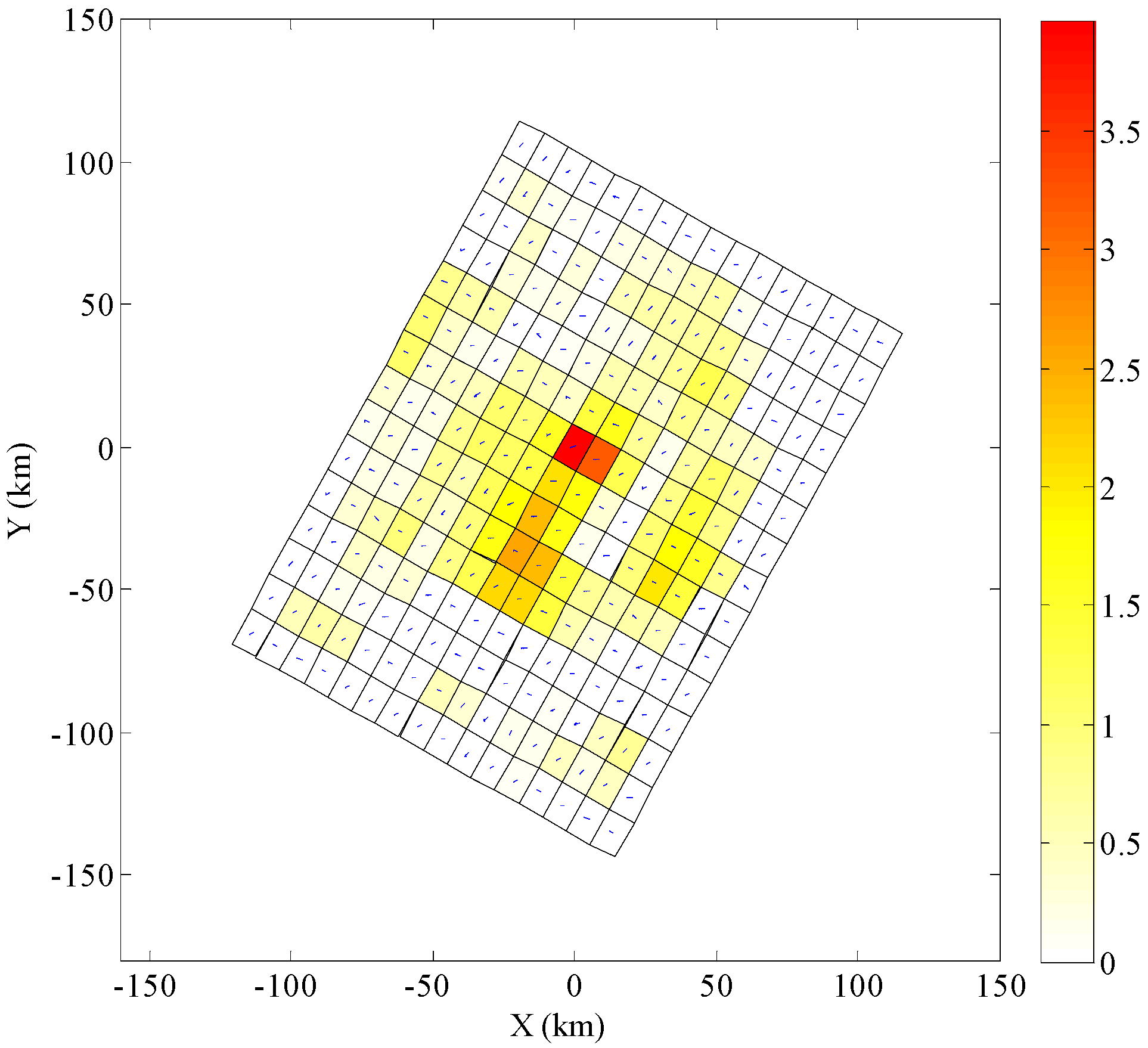
2.2. Finite Fault Model
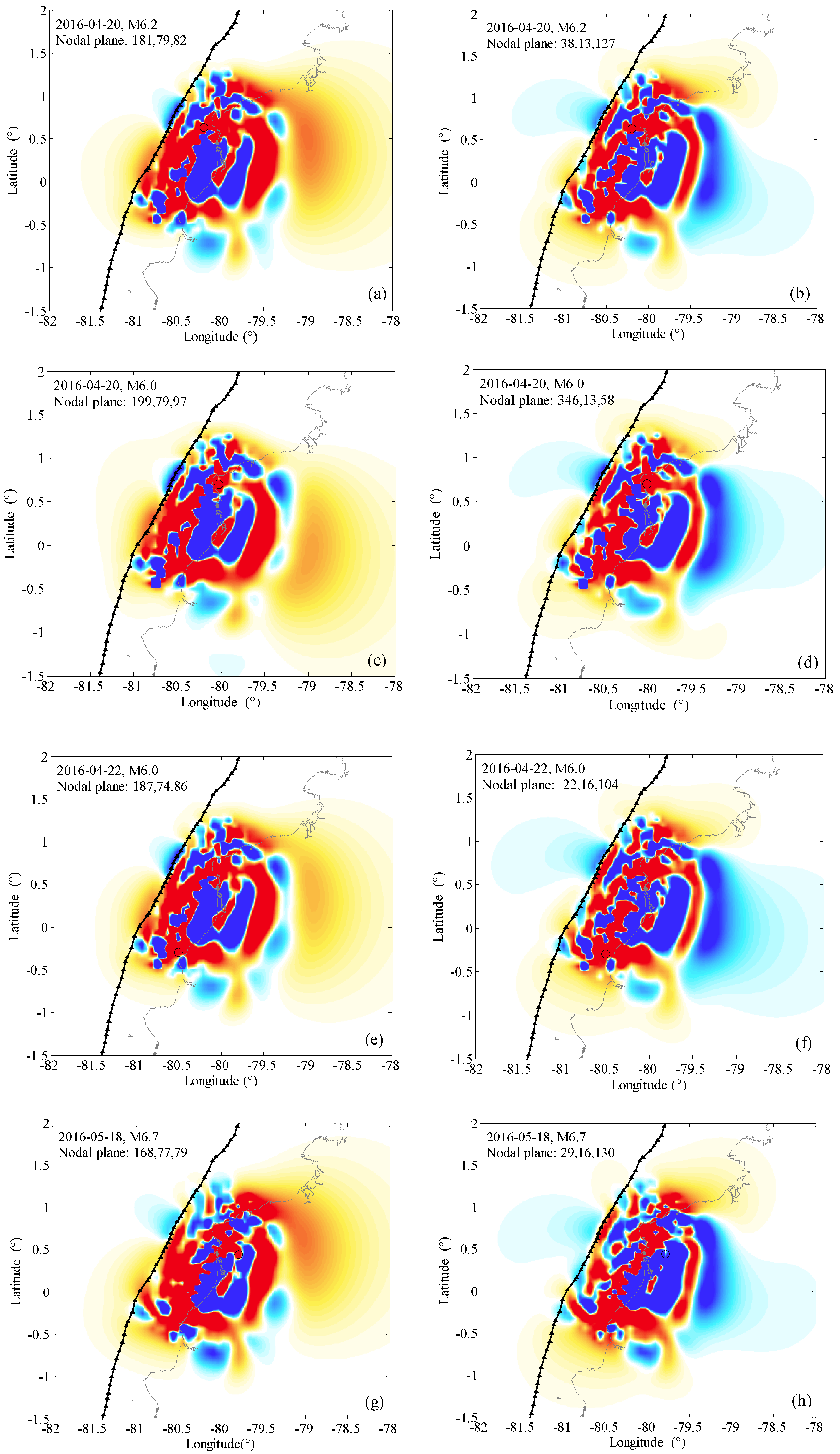
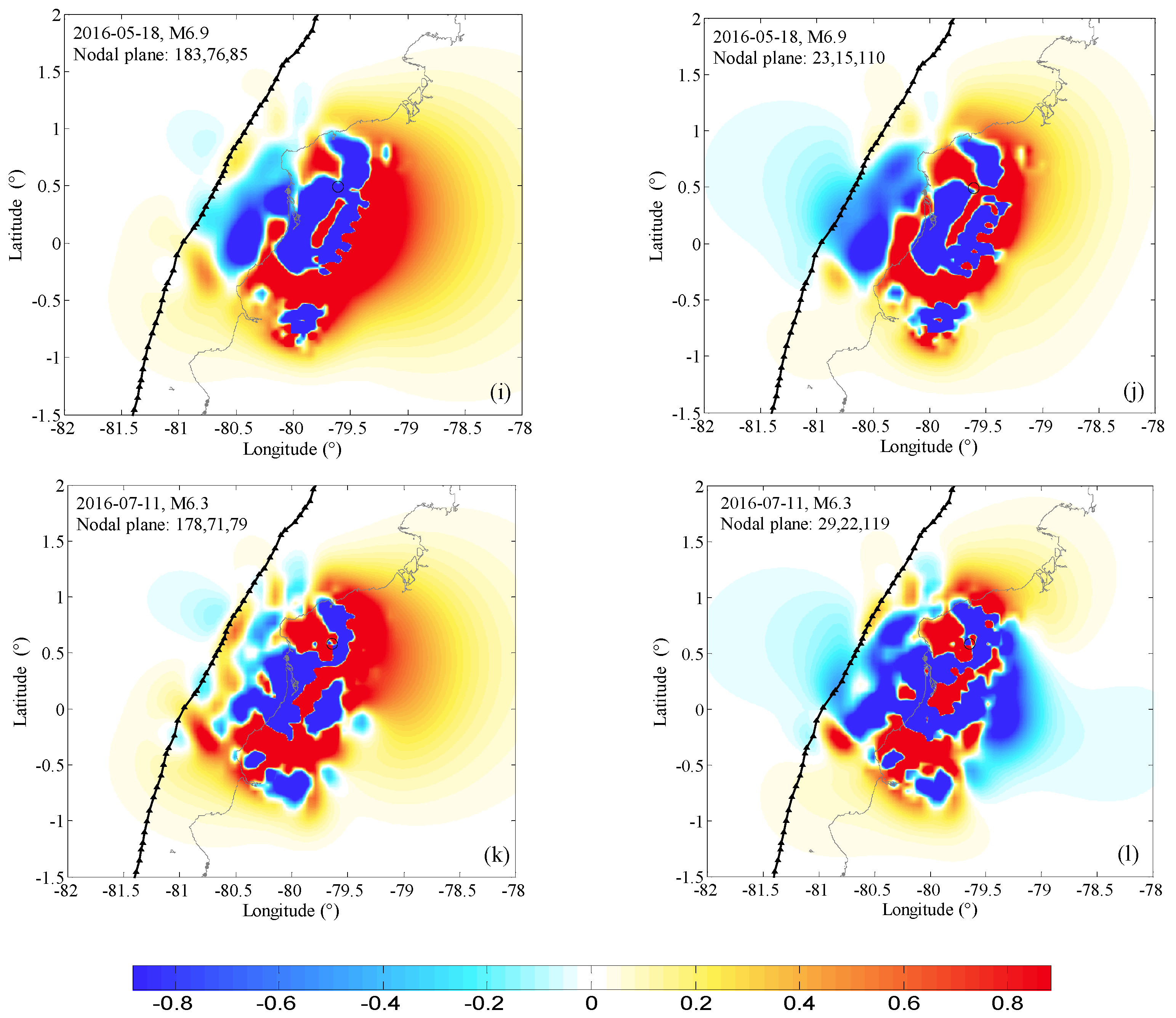
3. Coulomb Stress Changes Computed on Nodal Planes
4. Coulomb Stress Changes Computed in the Focal Source
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- M 7.8–27 km SSE of Muisne, Ecuador. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us20005j32#impact (accessed on 16 Apirl 2016).
- Tucker, B.; Erdik, M.; Hwang, C. Issues in Urban Earthquake Risk, NATO ASI Series, Series E. Appl. Sci. 1994, 271, 21–33. [Google Scholar]
- M 7.8–27 km SSE of Muisne, Ecuador Tectonic Summary. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us20005j32#executive (accessed on 16 Apirl 2016).
- Sumy, D.F.; Sumy, D.S.; Cochran, E.S.; Keranen, K.M.; Wei, M.; Abers, G.A. Observations of static Coulomb stress triggering of the November 2011 M 5.7 Oklahoma earthquake sequence. J. Geophys. Res. Solid Earth 2014, 119, 1904–1923. [Google Scholar] [CrossRef]
- Steacy, S.; Jiménez, A.; Holden, C. Stress triggering and the Canterbury earthquake sequence. Geophys. J. Int. 2013, 196, 473–480. [Google Scholar] [CrossRef]
- Yeo, K.B.; Choong, W.H.; Hau, W.Y. Prediction of Propeller Blade Stress Distribution Through FEA. Appl. Sci. 2014, 14, 3054. [Google Scholar]
- Reasenberg, P.A.; Simpson, R.W. Response of Regional Seismicity to the Static Stress Change Produced by the Loma Prieta Earthquake. Science 1992, 255, 1687. [Google Scholar] [CrossRef] [PubMed]
- King, G.C.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Juan, J.S.-T.; Chen, Y.-C.; Guo, S. Fault-Tolerant Visual Secret Sharing Schemes without Pixel Expansion. Appl. Sci. 2016, 6, 18. [Google Scholar] [CrossRef]
- Meier, M.A.; Werner, M.J.; Woessner, J.; Wiemer, S. A search for evidence of secondary static stress triggering during the 1992 Mw 7.3 Landers, California, earthquake sequence. J. Geophys. Res. Solid Earth 2014, 119, 3354–3370. [Google Scholar] [CrossRef]
- Stein, R.S.; King, G.C.; Lin, J. Stress triggering of the 1994 M = 6.7 Northridge, California, earthquake by its predecessors. Science 1994, 265, 1432–1435. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Sykes, L.R. Evolution of the stress field in southern California and triggering of moderate-size earthquakes: A 200-year perspective. J. Geophys. Res. Solid Earth 1997, 102, 9859–9886. [Google Scholar] [CrossRef]
- Papadimitriou, E.E. Mode of strong earthquake recurrence in the central Ionian Islands (Greece): Possible triggering due to Coulomb stress changes generated by the occurrence of previous strong shocks. Bull. Seismol. Soc. Am. 2002, 92, 3293–3308. [Google Scholar] [CrossRef]
- Nostro, C.; Chiaraluce, L.; Cocco, M.; Baumont, D.; Scotti, O. Coulomb stress changes caused by repeated normal faulting earthquakes during the 1997 Umbria-Marche (central Italy) seismic sequence. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Stein, R.S.; Barka, A.A.; Dieterich, J.H. Progressive failure on the North Anatolian fault since 1939 by earthquake stress triggering. Geophys. J. Int. 1997, 128, 594–604. [Google Scholar] [CrossRef]
- Wu, J.; Lei, D.; Cai, Y.; Li, H. Stress Triggering of the 2012 Sumatra Mw 8.2 Earthquake by the 2012 Sumatra Mw 8.6 Earthquake. Electron. J. Geotech. Eng. 2015, 20, 7. [Google Scholar]
- Pollitz, F.F.; Banerjee, P.; Burgmann, R.; Hashimoto, M.; Choosakul, N. Stress changes along the Sunda trench following the 26 December 2004 Sumatra—Andaman and 28 March 2005 Nias earthquakes. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Wiseman, K.; Bürgmann, R. Stress and seismicity changes on the Sunda megathrust preceding the 2007 Mw 8.4 earthquake. Bull. Seismol. Soc. Am. 2011, 101, 313–326. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Reasenberg, P.A.; Dieterich, J.H.; Yoshida, A. Stress transferred by the 1995 Mw = 6.9 Kobe, Japan, shock: Effect on aftershocks and future earthquake probabilities. J. Geophys. Res. Solid Earth 1998, 103, 24543–24565. [Google Scholar] [CrossRef]
- Jianchao, W.; Yueqiang, Q.; Dongning, L. Coulomb Stress Triggering of the Japan Kyushu M 7.0 Earthquake on 15 April 2016. Electron. J. Geotech. Eng. 2016, 21, 5429–5439. [Google Scholar]
- Toda, S.; Stein, R.S.; Lin, J. Widespread seismicity excitation throughout central Japan following the 2011 M = 9.0 Tohoku earthquake and its interpretation by Coulomb stress transfer. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Enescu, B.; Aoi, S.; Toda, S.; Suzuki, W.; Obara, K.; Shiomi, K.; Takeda, T. Stress perturbations and seismic response associated with the 2011 M 9.0 Tohoku-oki earthquake in and around the Tokai seismic gap, central Japan. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Ishibe, T.; Shimazaki, K.; Satake, K.; Tsuruoka, H. Change in seismicity beneath the Tokyo metropolitan area due to the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 731–735. [Google Scholar] [CrossRef]
- Takeo, I.; Kenji, S.; Shin’ichi, S.; Kunihiko, S.; Hiroshi, T.; Yusuke, Y.; Shigeki, N.; Naoshi, H. Correlation between Coulomb stress imparted by the 2011 Tohoku-Oki earthquake and seismicity rate change in Kanto, Japan. Geophys. J. Int. 2015, 201, 112–134. [Google Scholar]
- Mayorga, E.F.; Sánchez, J.J. Modelling of Coulomb stress changes during the great (Mw = 8.8) 1906 Colombia-Ecuador earthquake. J. S. Am. Earth Sci. 2016, 70, 268–278. [Google Scholar] [CrossRef]
- Ryder, I.; Rietbrock, A.; Kelson, K.; Bürgmann, R.; Floyd, M.; Socquet, A.; Vigny, C.; Carrizo, D. Large extensional aftershocks in the continental forearc triggered by the 2010 Maule earthquake, Chile. Geophys. J. Int. 2012, 188, 879–890. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Harris, R.A. Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. Solid Earth 1998, 103, 24347–24358. [Google Scholar] [CrossRef]
- Stein, R.S.; Lisowski, M. The 1979 Homestead Valley earthquake sequence, California: Control of aftershocks and postseismic deformation. J. Geophys. Res. Solid Earth 1983, 88, 6477–6490. [Google Scholar] [CrossRef]
- Oppenheimer, D.H.; Reasenberg, P.A.; Simpson, R.W. Fault plane solutions for the 1984 Morgan Hill, California, earthquake sequence: Evidence for the state of stress on the Calaveras fault. J. Geophys. Res. Solid Earth 1988, 93, 9007–9026. [Google Scholar] [CrossRef]
- Shawn, L.; Robert, R.; Helen, N.; William, S. Global Positioning System measurements of deformations associated with the 1987 Superstition Hills earthquake: Evidence for conjugate faulting. J. Geophys. Res. Solid Earth 1992, 97, 4885–4902. [Google Scholar]
- Preliminary Finite Fault Results for the 16 April 2016 Mw 7.8 28 km SSE of Muisne, Ecuador Earthquake (Version 1). Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us20005j32#finite-fault (accessed on 16 Apirl 2016).
- Shao, G.; Li, X.; Ji, C.; Maeda, T. Focal mechanism and slip history of the 2011 Mw 9.1 off the Pacific coast of Tohoku Earthquake, constrained with teleseismic body and surface waves. Earth Planets Space 2011, 63, 559–564. [Google Scholar] [CrossRef]
- Ji, C.; Helmberger, D.V.; Wald, D.J.; Ma, K.-F. Slip history and dynamic implications of the 1999 Chi-Chi, Taiwan, earthquake. J. Geophy. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Ji, C.; Wald, D.J.; Helmberger, D.V. Source description of the 1999 Hector Mine, California, earthquake, part I: Wavelet domain inversion theory and resolution analysis. Bull. Seismol. Soc. Am. 2002, 92, 1192–1207. [Google Scholar] [CrossRef]
- Ma, K.-F.; Chan, C.-H.; Stein, R.S. Response of seismicity to Coulomb stress triggers and shadows of the 1999 Mw = 7.6 Chi-Chi, Taiwan, earthquake. Bull. Seismol. Soc. Am. 2005, 110. [Google Scholar] [CrossRef]
- Woessner, J.; Jónsson, S.; Sudhaus, H.; Baumann, C. Reliability of Coulomb stress changes inferred from correlated uncertainties of finite-fault source models. Bull. Seismol. Soc. Am. 2012, 117. [Google Scholar] [CrossRef]
- Wu, J.; Hu, Q.; Li, W.; Lei, D. Study on Coulomb Stress Triggering of the April 2015 M 7.8 Nepal Earthquake Sequence. Int. J. Geophys. 2016, 2016. [Google Scholar] [CrossRef]
- Sudhaus, H.; Sigurjón, J. Improved source modelling through combined use of InSAR and GPS under consideration of correlated data errors: Application to the June 2000 Kleifarvatn earthquake, Iceland. Geophys. J. Int. 2009, 176, 389–404. [Google Scholar] [CrossRef]
| Date | Aftershock | Latitude Longitude | Depth (km) | Strike Dip Rake (°) | Stress Change (Bar) | ||
|---|---|---|---|---|---|---|---|
| Shear | Normal | Coulomb | |||||
| 20 April | M 6.2 | 0.639 80.210 | 11.5 | 181,79,82 | 6.458 | 2.766 | 7.564 |
| 38,13,127 | 6.477 | −0.260 | 6.373 | ||||
| 20 April | M 6.0 | 0.708 80.035 | 11.0 | 199,79,97 | 3.006 | −2.104 | 2.164 |
| 346,13,58 | 3.015 | 0.119 | 3.062 | ||||
| 22 April | M 6.0 | 0.292 80.504 | 11.5 | 187,74,86 | 2.022 | 3.688 | 3.497 |
| 22,16,104 | 2.041 | −0.485 | 1.847 | ||||
| 18 May | M 6.7 | 0.426 79.790 | 16.0 | 168,77,79 | −2.249 | 13.871 | 3.299 |
| 29,16,130 | −2.175 | 5.837 | 0.159 | ||||
| 18 May | M 6.9 | 0.495 79.616 | 35.5 | 183,76,85 | −1.711 | −1.149 | −2.170 |
| 23,15,110 | −1.739 | 6.251 | 0.762 | ||||
| 11 July | M 6.3 | 0.581 79.638 | 25.5 | 178,71,79 | −1.465 | 1.030 | 1.053 |
| 29,22,119 | −1.449 | −1.123 | 1.898 | ||||
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Cai, Y.; Li, W.; Feng, Q. Strong Aftershock Study Based on Coulomb Stress Triggering—A Case Study on the 2016 Ecuador Mw 7.8 Earthquake. Appl. Sci. 2017, 7, 88. https://doi.org/10.3390/app7010088
Wu J, Cai Y, Li W, Feng Q. Strong Aftershock Study Based on Coulomb Stress Triggering—A Case Study on the 2016 Ecuador Mw 7.8 Earthquake. Applied Sciences. 2017; 7(1):88. https://doi.org/10.3390/app7010088
Chicago/Turabian StyleWu, Jianchao, Yongjian Cai, Weijie Li, and Qian Feng. 2017. "Strong Aftershock Study Based on Coulomb Stress Triggering—A Case Study on the 2016 Ecuador Mw 7.8 Earthquake" Applied Sciences 7, no. 1: 88. https://doi.org/10.3390/app7010088
APA StyleWu, J., Cai, Y., Li, W., & Feng, Q. (2017). Strong Aftershock Study Based on Coulomb Stress Triggering—A Case Study on the 2016 Ecuador Mw 7.8 Earthquake. Applied Sciences, 7(1), 88. https://doi.org/10.3390/app7010088







