Design and Optimization of a Lorentz-Force-Driven Planar Motor
Abstract
:1. Introduction
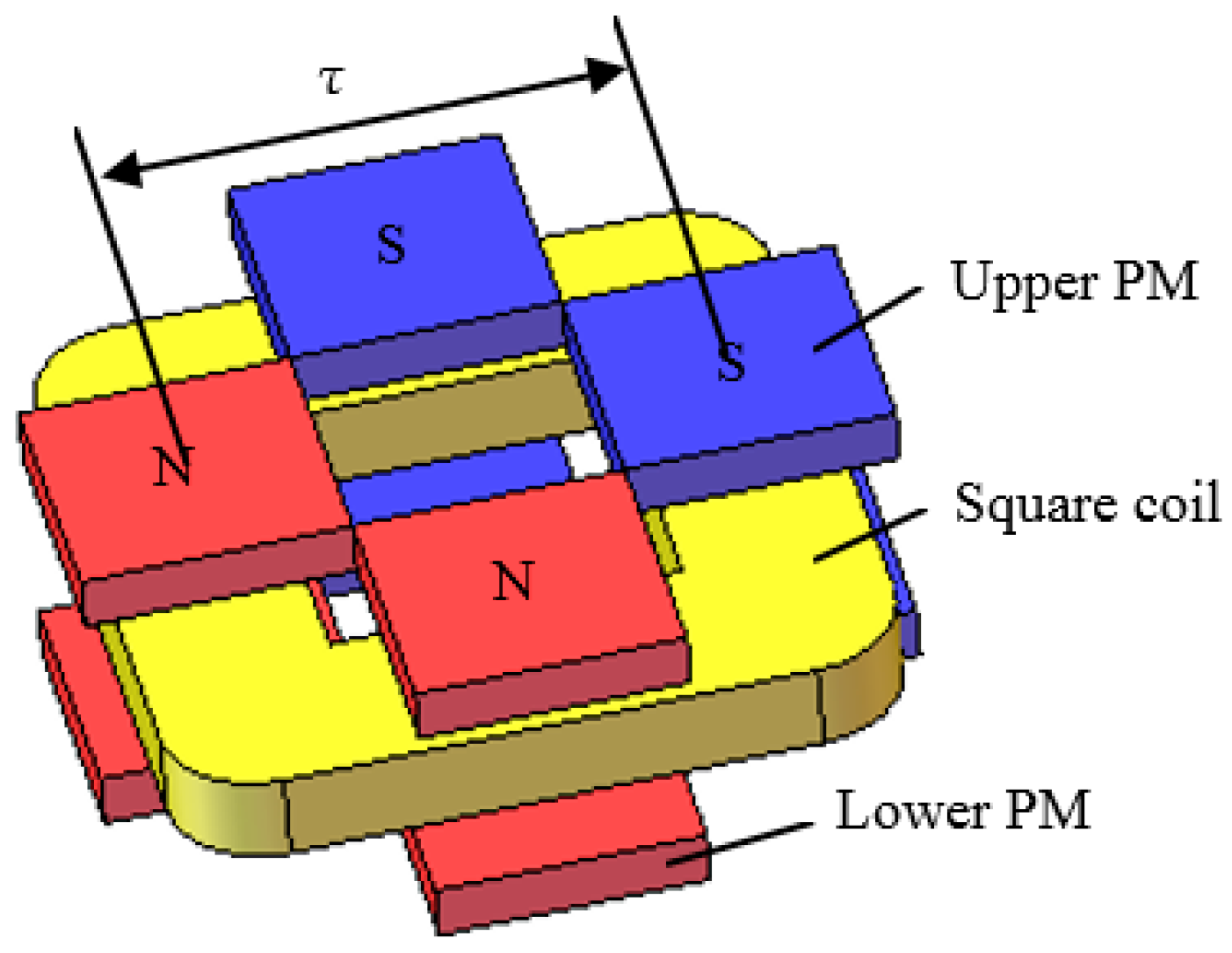
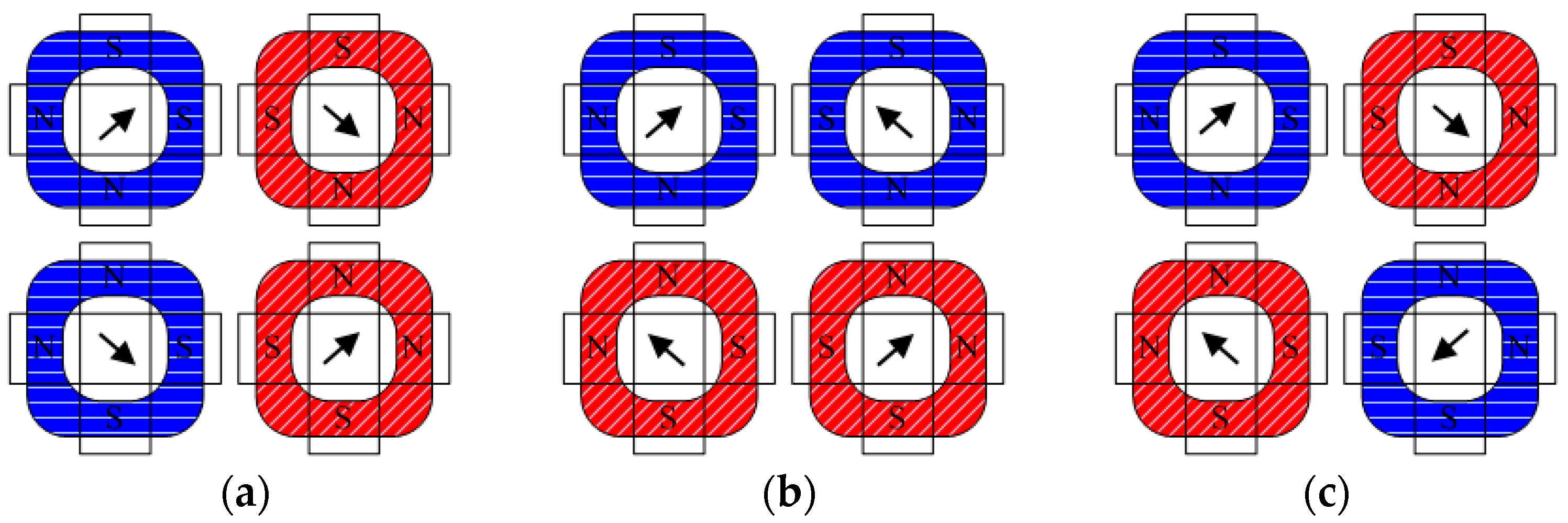
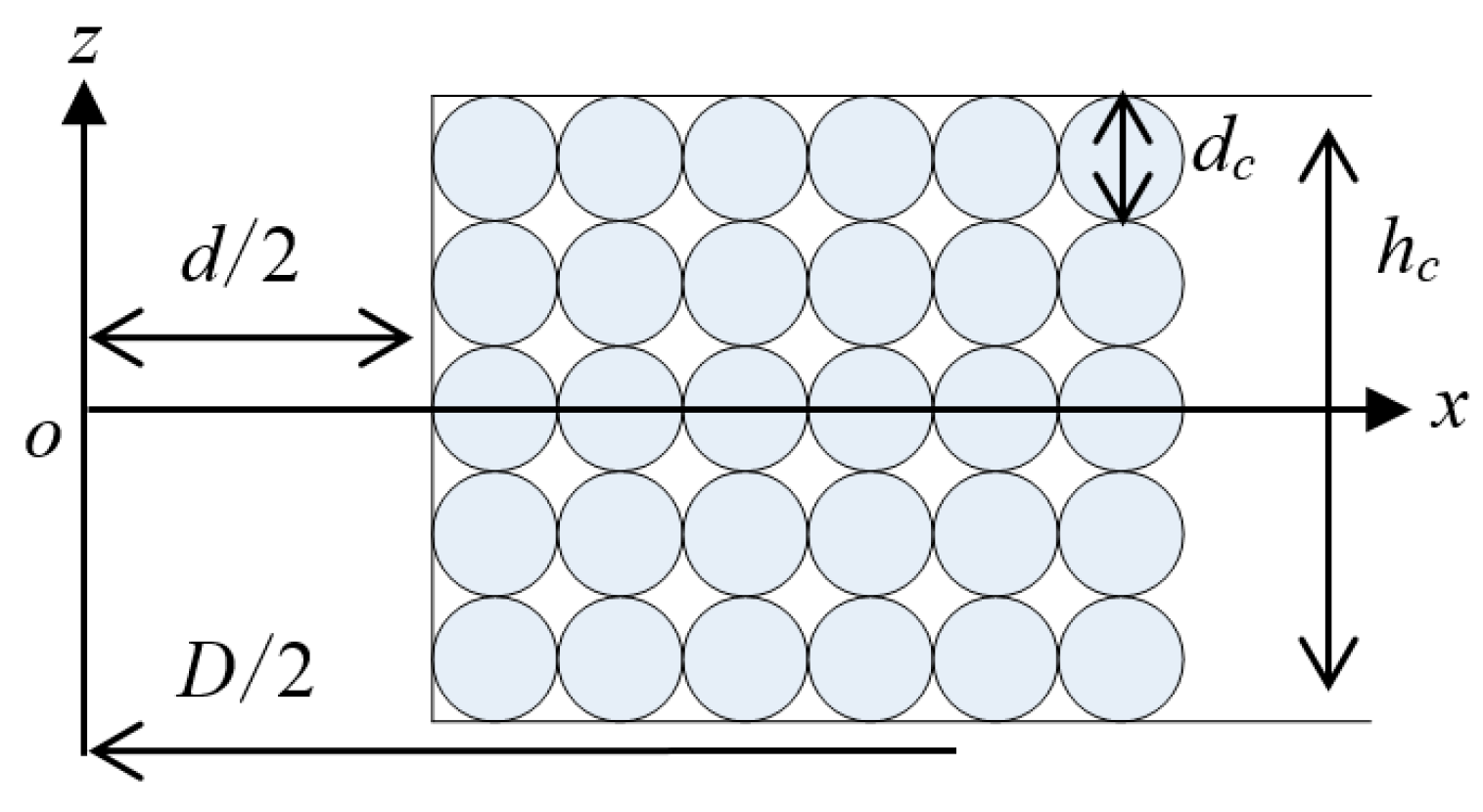
2. Structure and Working Principle
- The working principle is the same as voice coil motors, which is based on the Lorentz force. Compared with three-phase planar motors, with the proposed motor it is easier to achieve high-precision positioning.
- There is no electrical connection and cable disturbance in the moving parts due to the moving-magnet scheme. Additionally, the temperature rise of the motor can be easily controlled because the heat source is in the stator.
- There is no cogging force and force ripple for this slotless motor with air-core coils, which is beneficial for servo performance improvement.
3. Modeling and Design Optimization
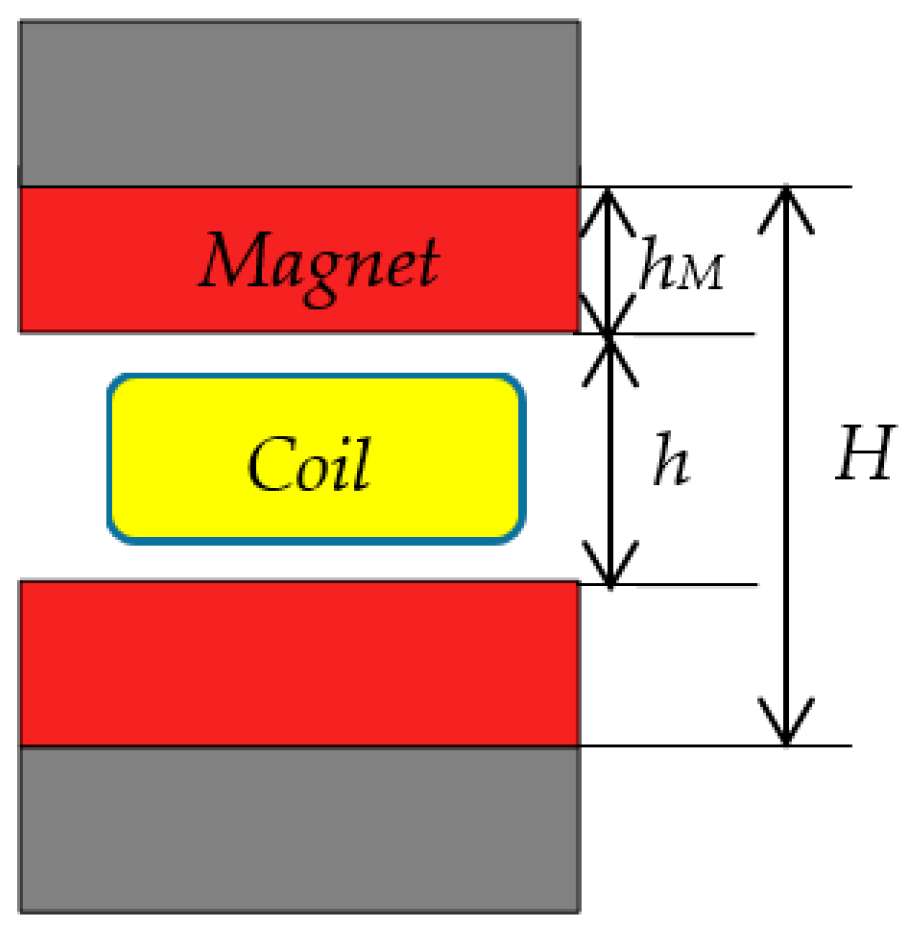
3.1. Magnetic Field and Electromagnetic Force Expression
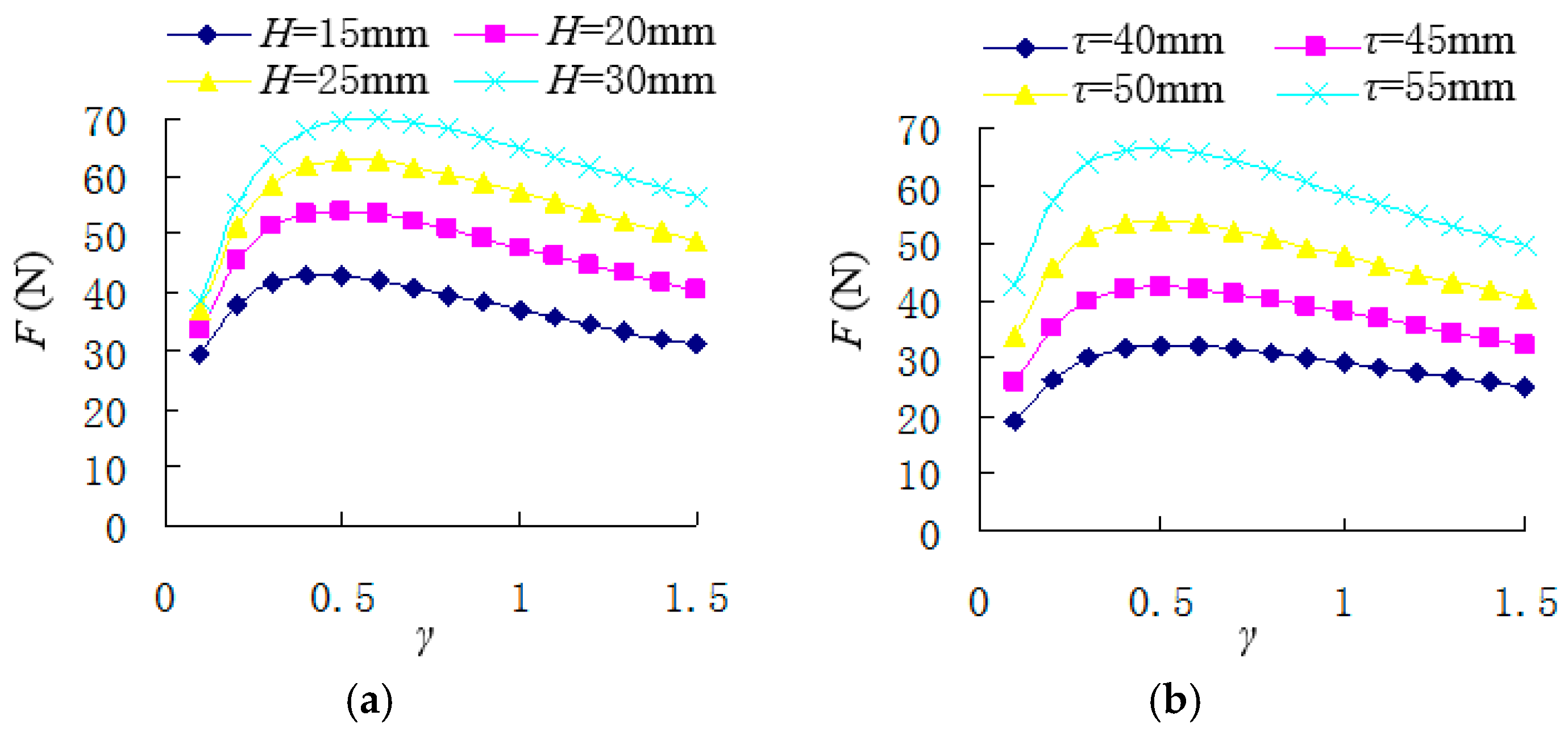
3.2. Optimization Design
3.2.1. Motor force
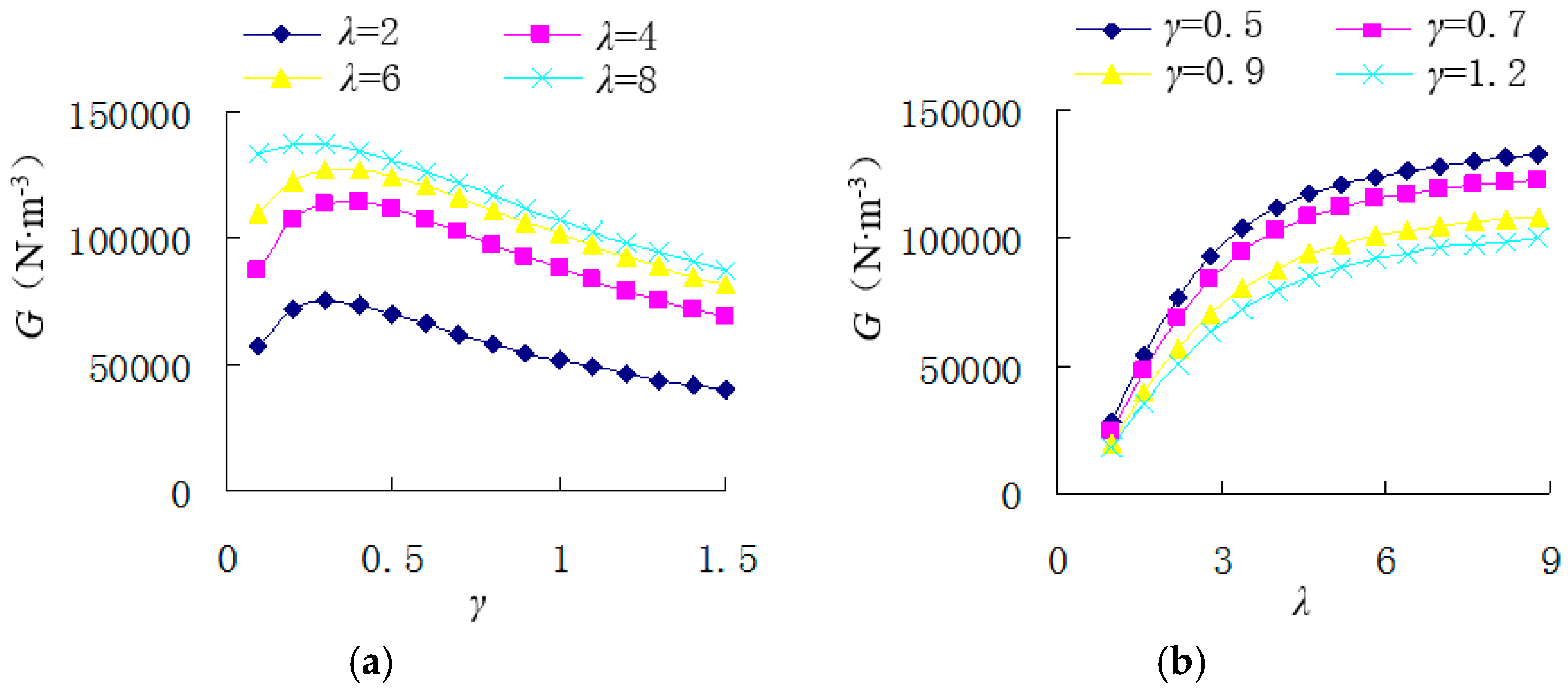
3.2.2. Force Density
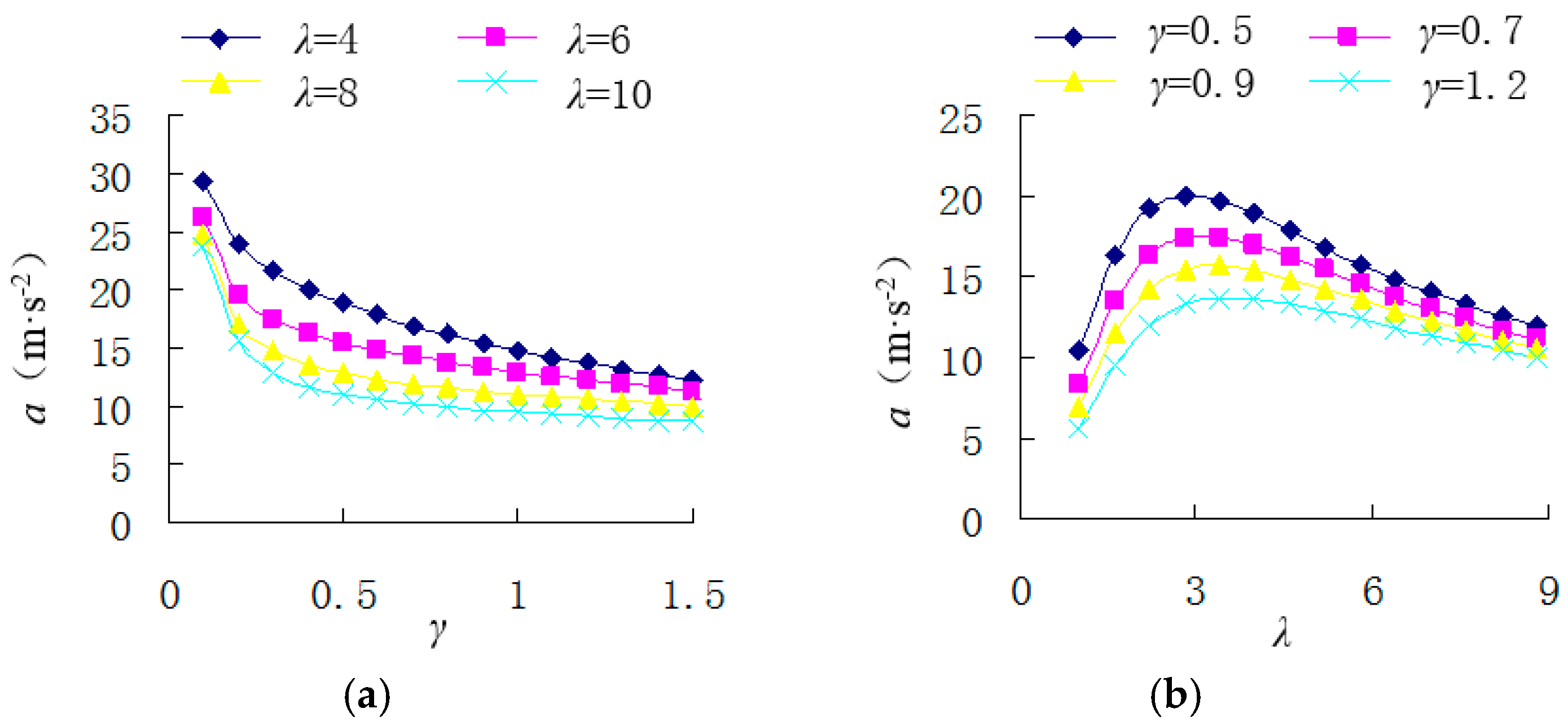
3.2.3. Acceleration
4. Prototype Experiment and Results
4.1. Resistance and Inductance Test
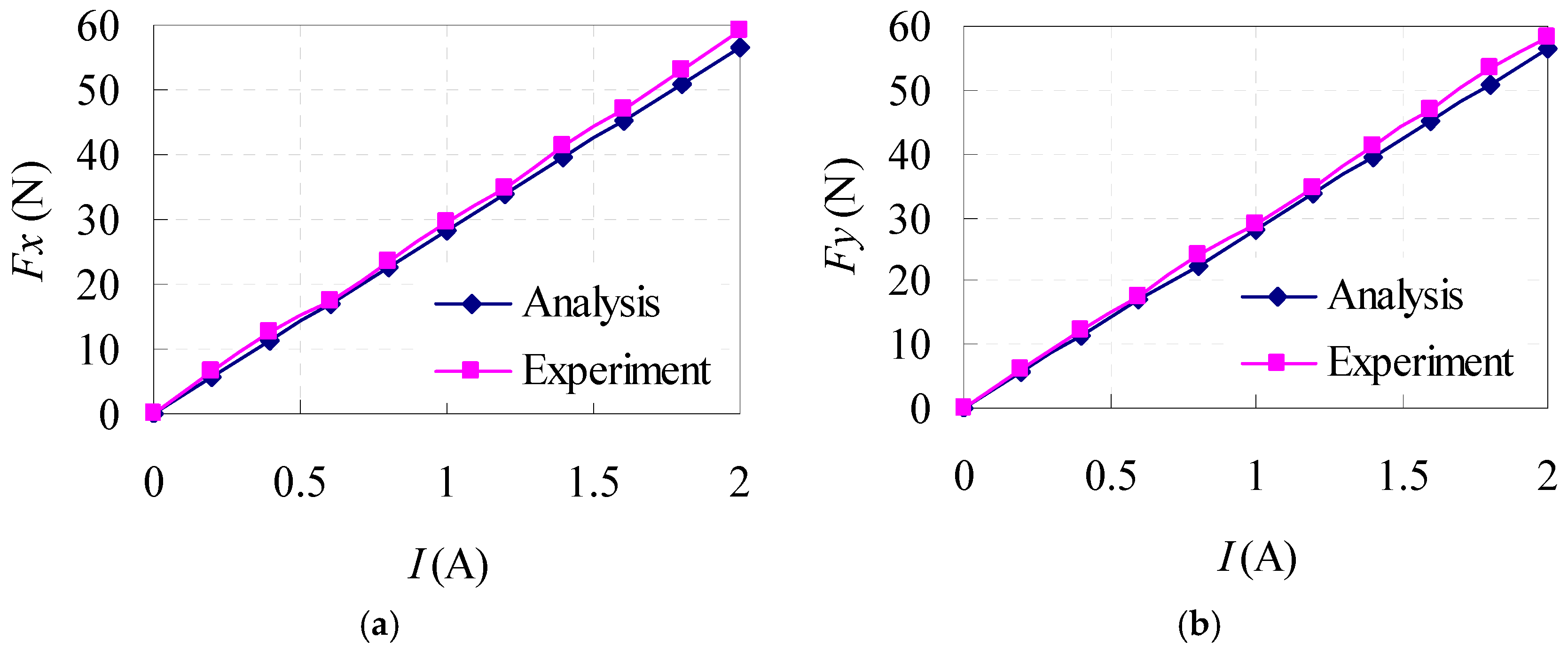
4.2. Motor Force Test
5. Conclusions
- Based on a certain height and pole pitch for the planar motor, the force reaches its maximum value when the ratio between the permanent thickness and the total air-gap length is around 0.5 (i.e., γ = 0.5).
- The force density first increases and then decreases with the increase of parameter γ when parameter λ is constant, but the acceleration will gradually decrease. On the contrary, the acceleration first increases and then decreases with the increase of parameter λ when parameter γ is constant, but the force density will gradually increase. Therefore, the reasonable value range for the parameter γ is between 0.4 and 0.6 to balance the force, the force density, and the acceleration. A larger value of parameter γ will cause the decrease of force density and acceleration, but a smaller value of parameter γ will cause the decrease of force.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kou, B.Q.; Zhang, H.; Li, L.Y. Analysis and design of a novel 3-DOF Lorentz-force-driven DC planar motor. IEEE Trans. Magn. 2011, 47, 2118–2126. [Google Scholar]
- Kuo, S.K.; Menq, C.H. Modeling and control of a six-axis precision motion control stage. IEEE/ASME Trans. Mechatron. 2005, 10, 50–59. [Google Scholar] [CrossRef]
- Verma, S.; Kim, W.J.; Gu, J. Six-axis nanopositioning device with precision magnetic levitation technology. IEEE/ASME Trans. Mechatron. 2004, 9, 384–391. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Menq, C.H. Six-axis magnetic levitation and motion control. IEEE/ASME Trans. Robot. 2007, 23, 196–205. [Google Scholar] [CrossRef]
- Dejima, S.; Gao, W.; Shimizu, H.; Kiyono, S.; Tomita, Y. Precision positioning of a five degree-of-freedom planar motion stage. Mechatronics 2005, 15, 969–987. [Google Scholar] [CrossRef]
- Holmesa, M.; Hockena, R.; Trumperb, D. The long-range scanning stage: A novel platform for scanned-probe microscopy. Precis. Eng. 2000, 24, 191–209. [Google Scholar] [CrossRef]
- Snitka, V. Ultrasonic actuators for nanometer positioning. Ultrasonics 2000, 38, 20–25. [Google Scholar] [CrossRef]
- Chu, X.C.; Wang, J.W.; Yuan, S.M.; Li, L.T.; Cui, H.C. A screw-thread-type ultrasonic actuator based on a langevin piezoelectric vibrator. Rev. Sci. Instrum. 2014, 85, 065002. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Chen, W.S.; Feng, P.L.; Liu, J.K. A linear piezoelectric actuator using the first-order bending modes. Ceram. Int. 2013, 39, S681–S684. [Google Scholar] [CrossRef]
- Chen, M.Y.; Wang, M.J.; Fu, L.C. Dual-axis maglev guiding system modeling and controller design for wafer transportation. In Proceedings of the Conference on Decision & Control, Phoenix, AZ, USA, 7–10 December 1999.
- Chen, M.Y.; Wang, M.J.; Fu, L.C. A novel dual-axis repulsive maglev guiding system with permanent magnet: Modeling and controller design. IEEE/ASME Trans. Mechatron. 2003, 8, 77–86. [Google Scholar] [CrossRef]
- Sawyer, B.A. Magnetic Positioning Device. US Patent 3,376,578, 22 July 1968. [Google Scholar]
- Pelta, E.R. Two-axis sawyer motor for motion systems. IEEE Control Syst. Mag. 1987, 7, 20–24. [Google Scholar] [CrossRef]
- Pan, J.F.; Cheung, N.C.; Gan, W.C.; Zhao, S.W. A novel planar switched reluctance motor for industrial applications. IEEE Trans. Magn. 2006, 42, 2836–2839. [Google Scholar] [CrossRef]
- Pan, J.F.; Cheung, N.C.; Yang, J. High-precision position control of a novel planar switched reluctance motor. IEEE Trans. Ind. Electron. 2005, 52, 1644–1652. [Google Scholar] [CrossRef]
- Fujii, N.; Fujitake, M. Two-dimensional drive characteristics by circular-shaped motor. IEEE Trans. Ind. Electron. 1999, 35, 803–809. [Google Scholar] [CrossRef]
- Kim, W.J.; Trumper, D.L. High-precision magnetic levitation stage for photolithography. Precis. Eng. 1998, 22, 66–77. [Google Scholar] [CrossRef]
- Cho, H.S.; Jung, H.K. Analysis and design of synchronous permanent-magnet planar motors. IEEE Trans. Energy Convers. 2002, 17, 492–499. [Google Scholar] [CrossRef]
- Jansen, J.W.; van Lierop, C.M.M.; Lomonova, E.A.; Vandenput, A.J.A. Modeling of magnetically levitated planar actuators with moving magnets. IEEE Trans. Magn. 2007, 43, 15–25. [Google Scholar] [CrossRef]
- Lei, J.; Luo, X.; Chen, X.; Yan, T. Modeling and analysis of a 3-DOF Lorentz-force-driven planar motion stage for nanopositioning. Mechatronics 2010, 20, 553–565. [Google Scholar] [CrossRef]
- Kim, W.J.; Verma, S.; Shakir, H. Design and precision construction of novel magnetic-levitation-based multi-axis nanoscale positioning systems. Precis. Eng. 2007, 31, 337–350. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, B.Q.; Zhang, H.L.; Jin, Y.X. A three-degree-of-freedom short-stroke Lorentz-force-driven planar motor using a Halbach permanent-magnet array with unequal thickness. IEEE Trans. Ind. Electron. 2015, 62, 3640–3650. [Google Scholar] [CrossRef]
- Choi, Y.M.; Gweon, D.G. A high-precision dual-servo stage using Halbach linear active magnetic bearings. IEEE/ASME Trans. Mechatron. 2011, 16, 925–931. [Google Scholar] [CrossRef]
- Chen, M.Y.; Lin, T.B.; Huang, S.K.; Fu, L.C. Design and experiment of a macro-micro planar maglev positioning system. IEEE Trans. Ind. Electron. 2012, 59, 4128–4139. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V.; Depollier, C. Analytical calculation of the magnetic field created by permanent magnet rings. IEEE Trans. Magn. 2008, 44, 1982–1989. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V.; Depollier, C. Permanent magnet couplings: Field and torque three-dimensional expressions based on the coulombian model. IEEE Trans. Magn. 2009, 45, 1950–1958. [Google Scholar] [CrossRef]





| Item | Symbol | Value | Unit |
|---|---|---|---|
| inner width | d | 35.76 | mm |
| outer width | D | 71.28 | mm |
| thickness | hc | 9.60 | mm |
| wire diameter | dc | 0.76 | mm |
| conductor diameter | dc1 | 0.71 | mm |
| number of turns | N | 276 | - |
| Coil | Value | Unit |
|---|---|---|
| A | 2.341 | Ω |
| B | 2.348 | Ω |
| C | 2.350 | Ω |
| D | 2.349 | Ω |
| Coil | Value | Unit |
|---|---|---|
| A | 4.593 | mH |
| B | 4.595 | mH |
| C | 4.592 | mH |
| D | 4.572 | mH |
| Item | Symbol | Value | Unit |
|---|---|---|---|
| Magnet type | - | N38 | - |
| Magnet thickness | hM | 5.5 | mm |
| Pole pitch | τ | 54 | mm |
| Total air-gap length | h | 13 | mm |
| Main coefficient 1 | λ | 4.15 | - |
| Main coefficient 2 | γ | 0.42 | - |
| Pole-arc coefficient | αi | 0.515 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Kou, B. Design and Optimization of a Lorentz-Force-Driven Planar Motor. Appl. Sci. 2017, 7, 7. https://doi.org/10.3390/app7010007
Zhang H, Kou B. Design and Optimization of a Lorentz-Force-Driven Planar Motor. Applied Sciences. 2017; 7(1):7. https://doi.org/10.3390/app7010007
Chicago/Turabian StyleZhang, He, and Baoquan Kou. 2017. "Design and Optimization of a Lorentz-Force-Driven Planar Motor" Applied Sciences 7, no. 1: 7. https://doi.org/10.3390/app7010007
APA StyleZhang, H., & Kou, B. (2017). Design and Optimization of a Lorentz-Force-Driven Planar Motor. Applied Sciences, 7(1), 7. https://doi.org/10.3390/app7010007





