Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation
Abstract
:1. Introduction
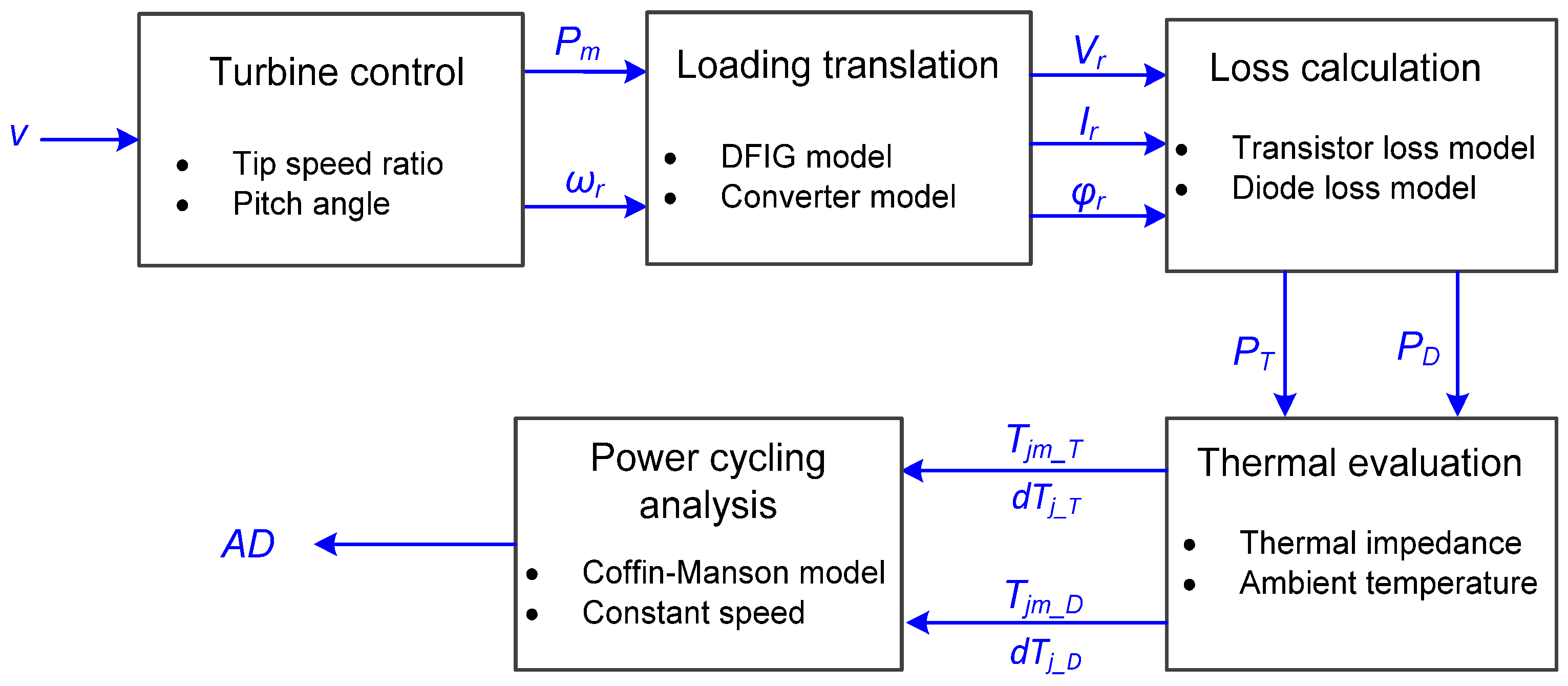
2. Wake Effect and Lifetime Estimation in DFIG Wind Farm
2.1. DFIG Wind Turbine and MPPT Method
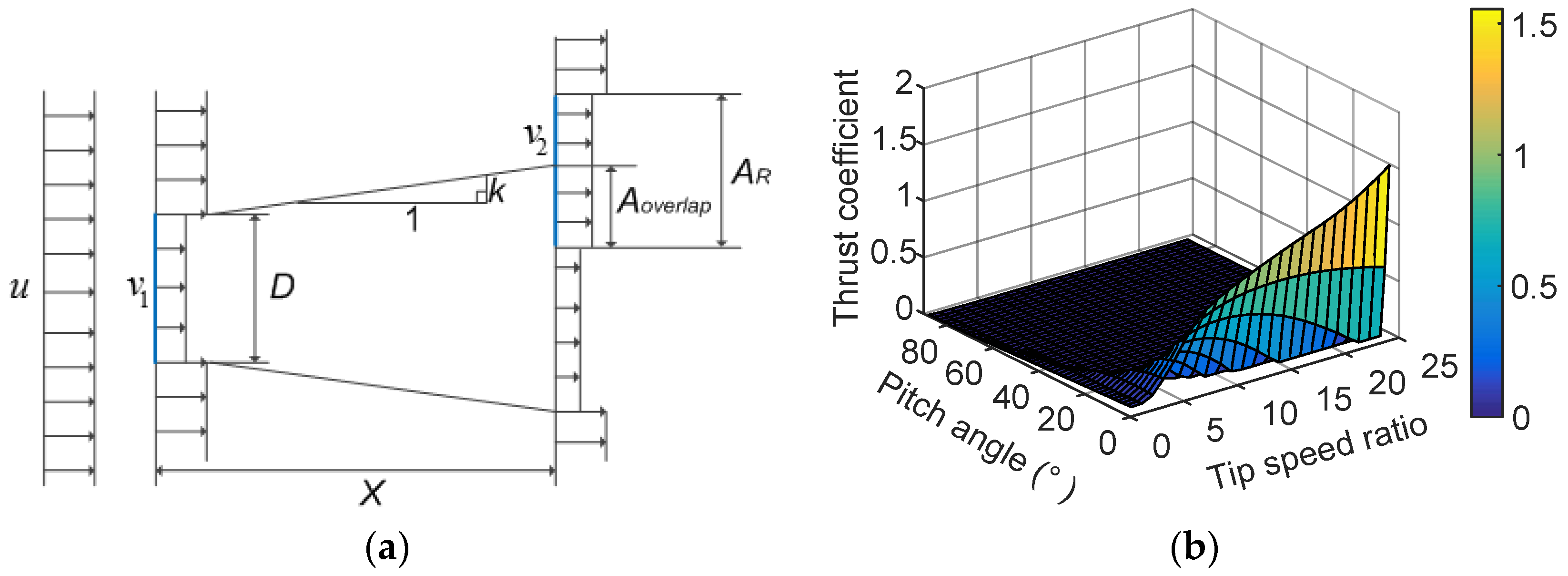
2.2. Katic Wake Model
2.3. Lifetime Estimation of the Power Converter
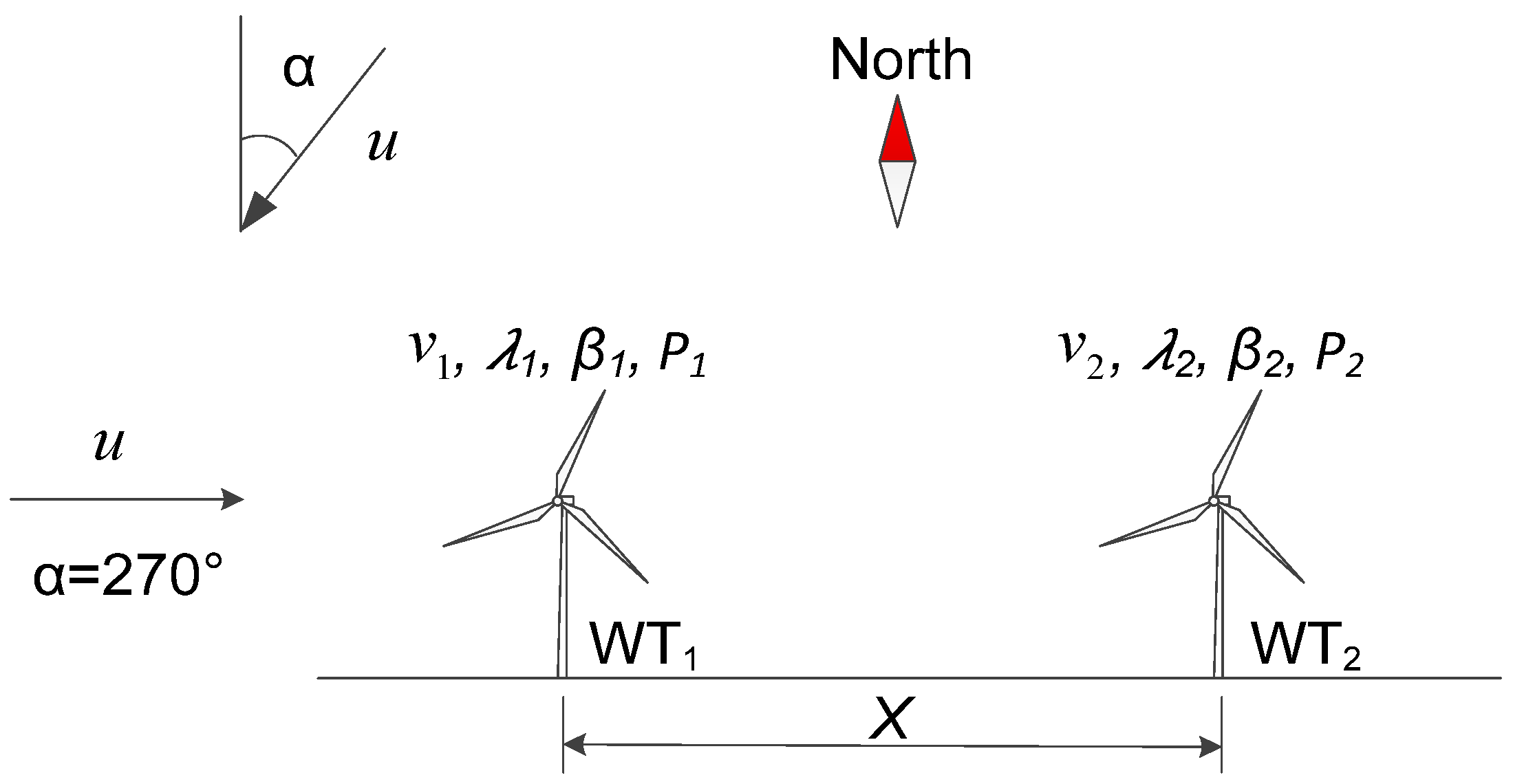
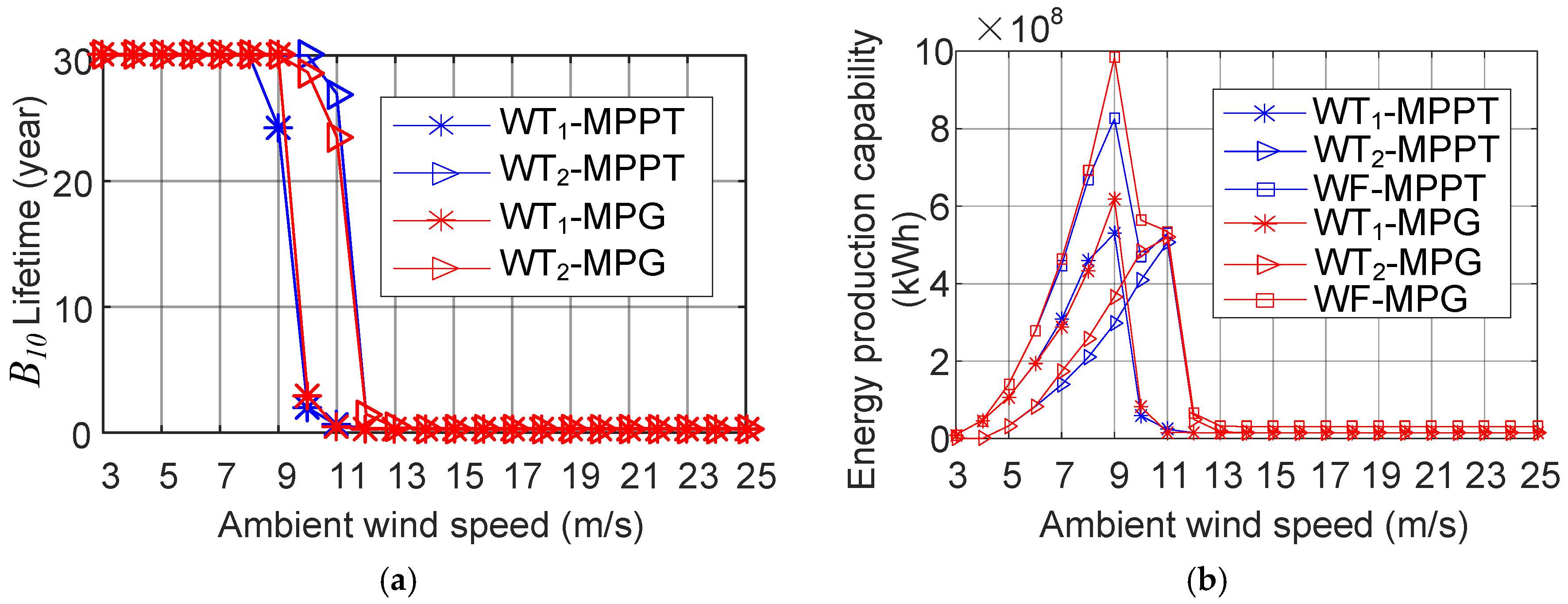
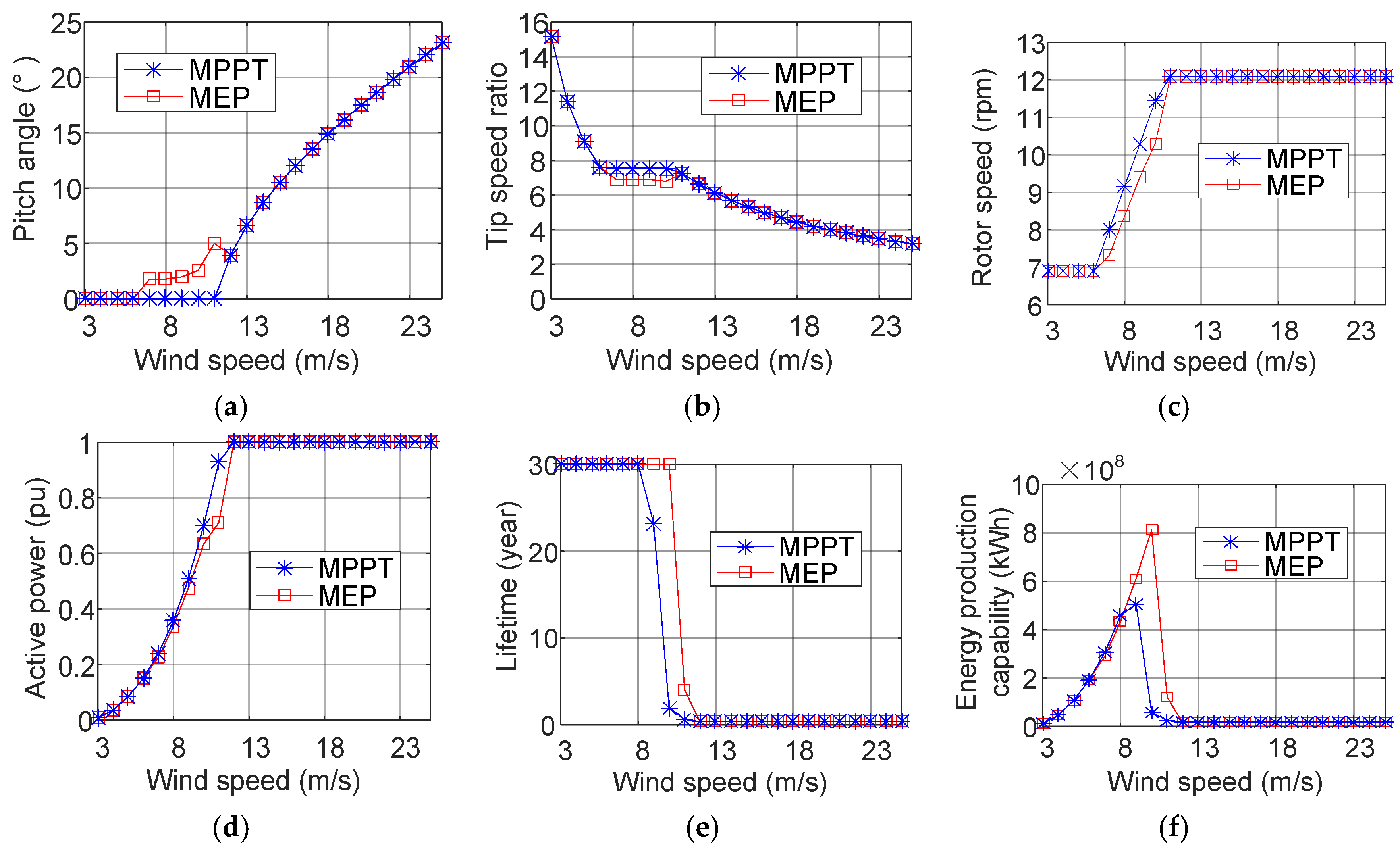
3. Comparison of Power Generation of Wind Farm between MPPT and MPG
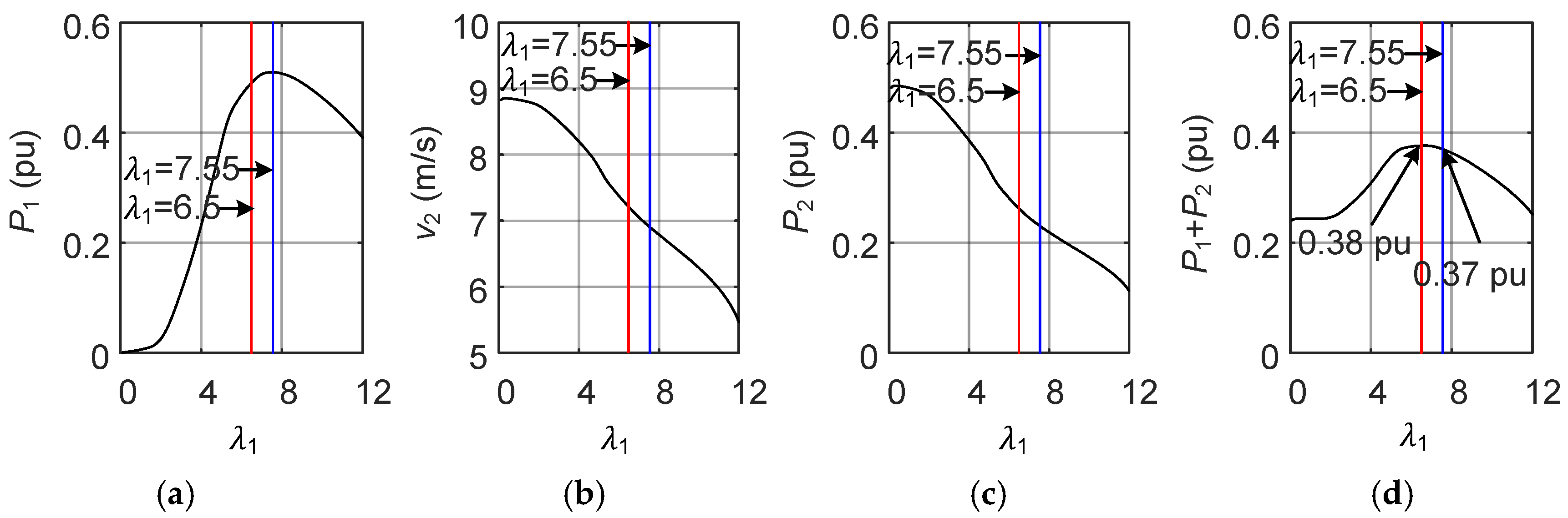
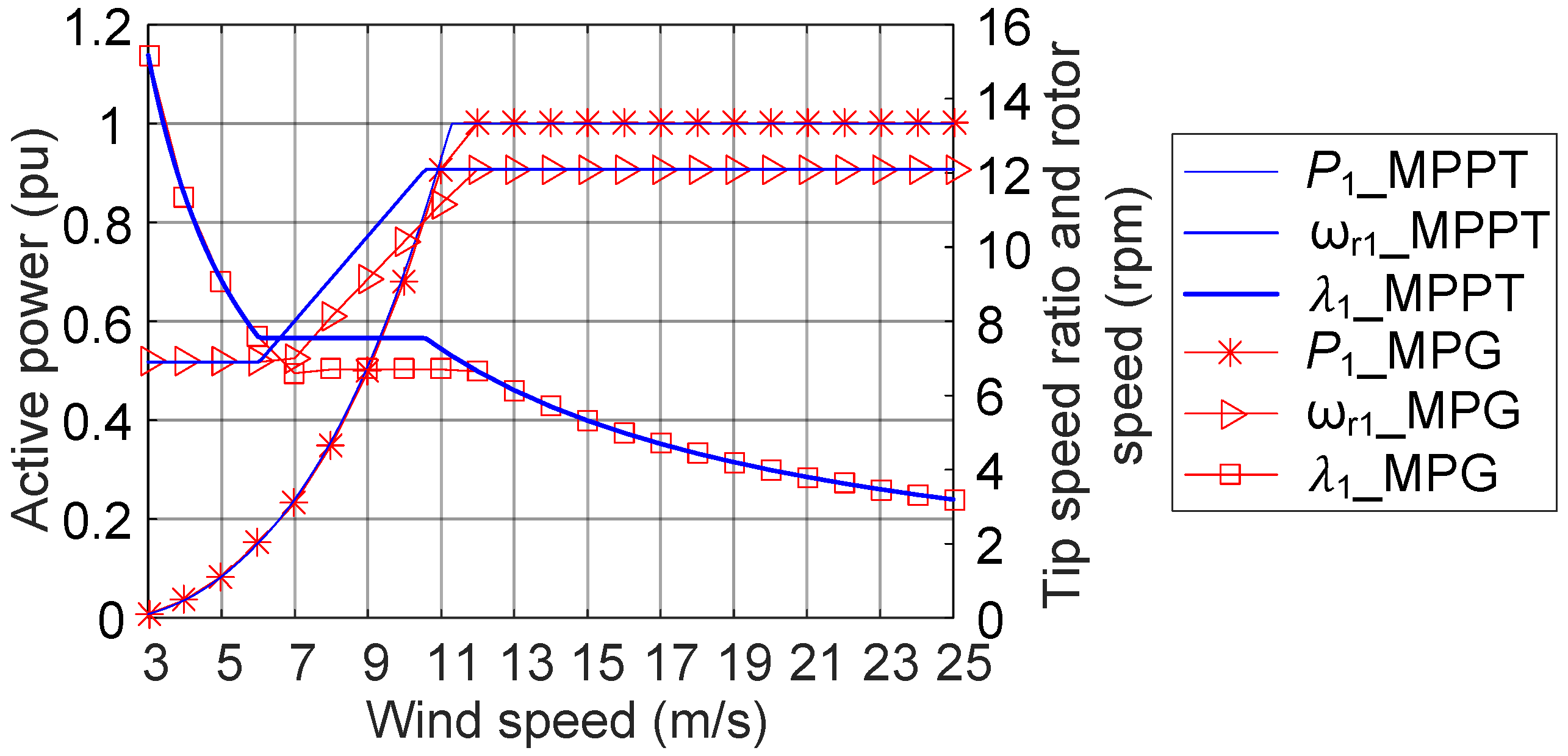
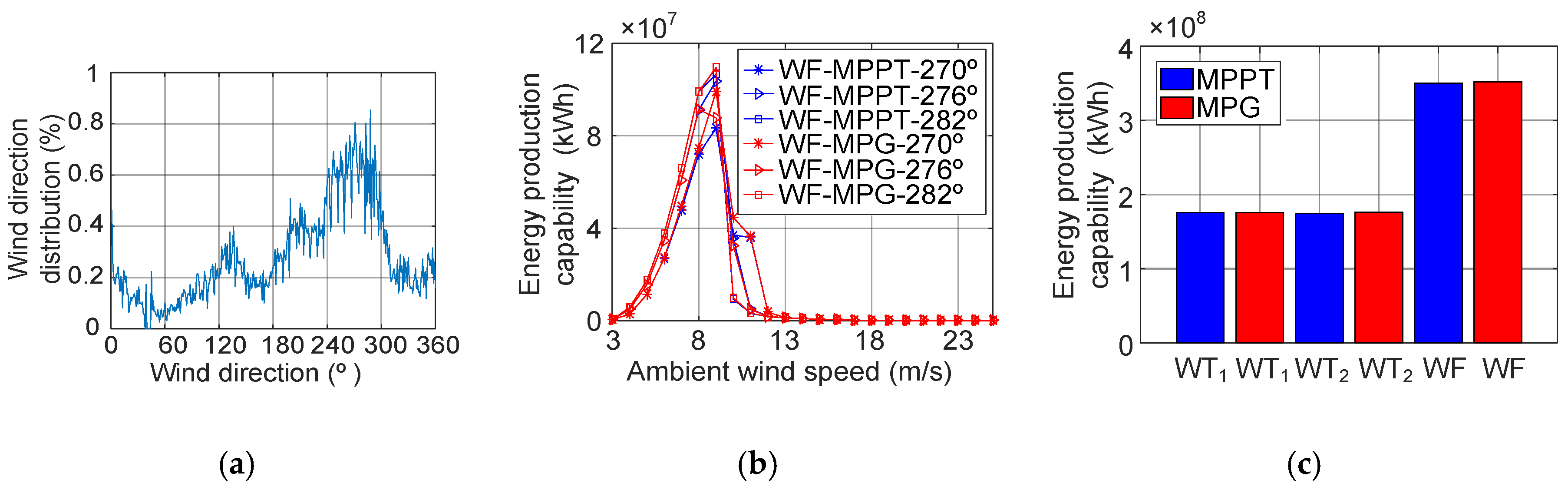
3.1. Optimal Tip Speed Ratio Selection at 270° Wind Direction
3.2. Optimal Pitch Angle and Tip Speed Ratio Selection at 270° Wind Direction
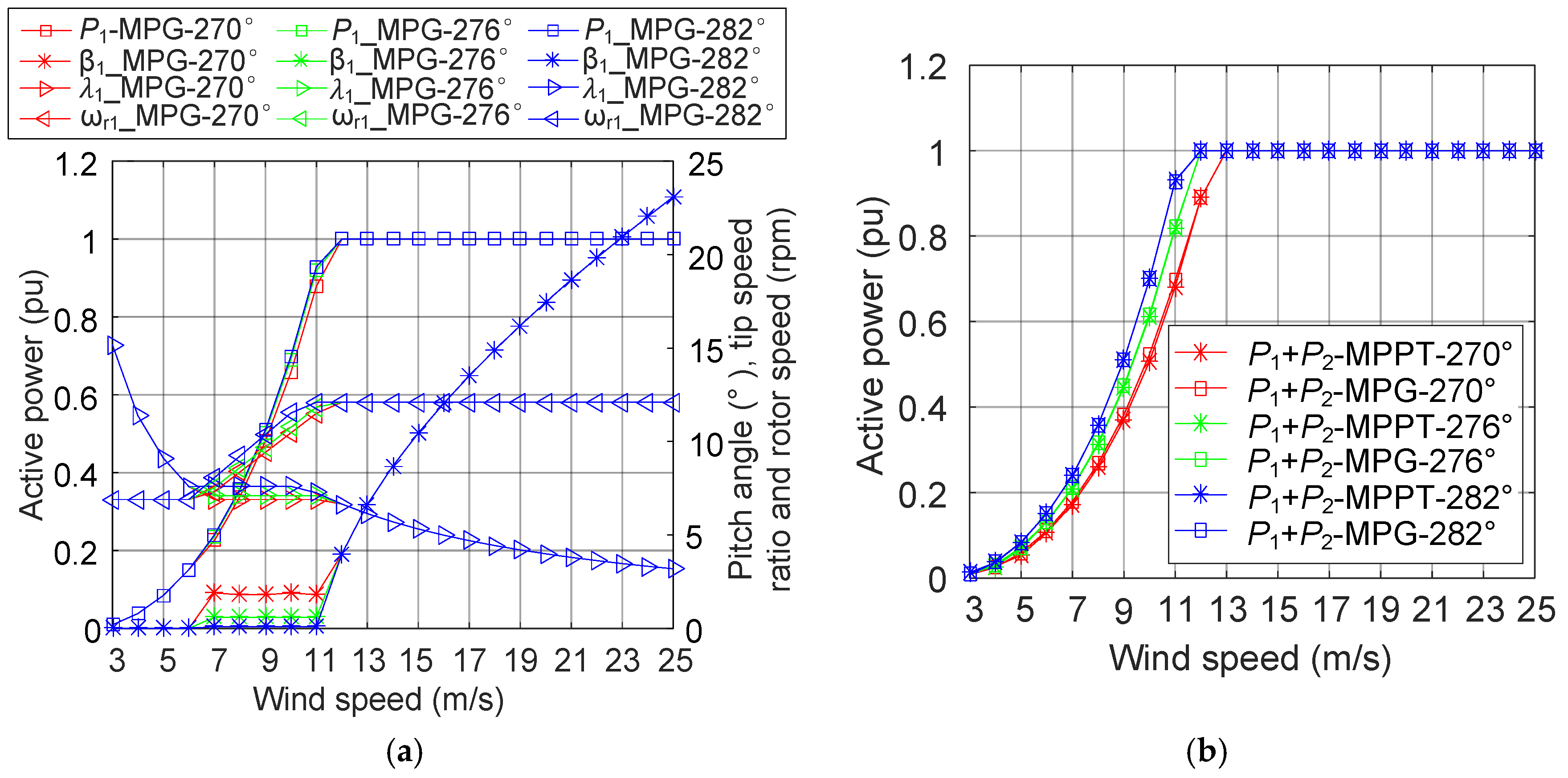
3.3. Optimal Pitch Angle and Tip Speed Ratio Selection at Various Wind Directions
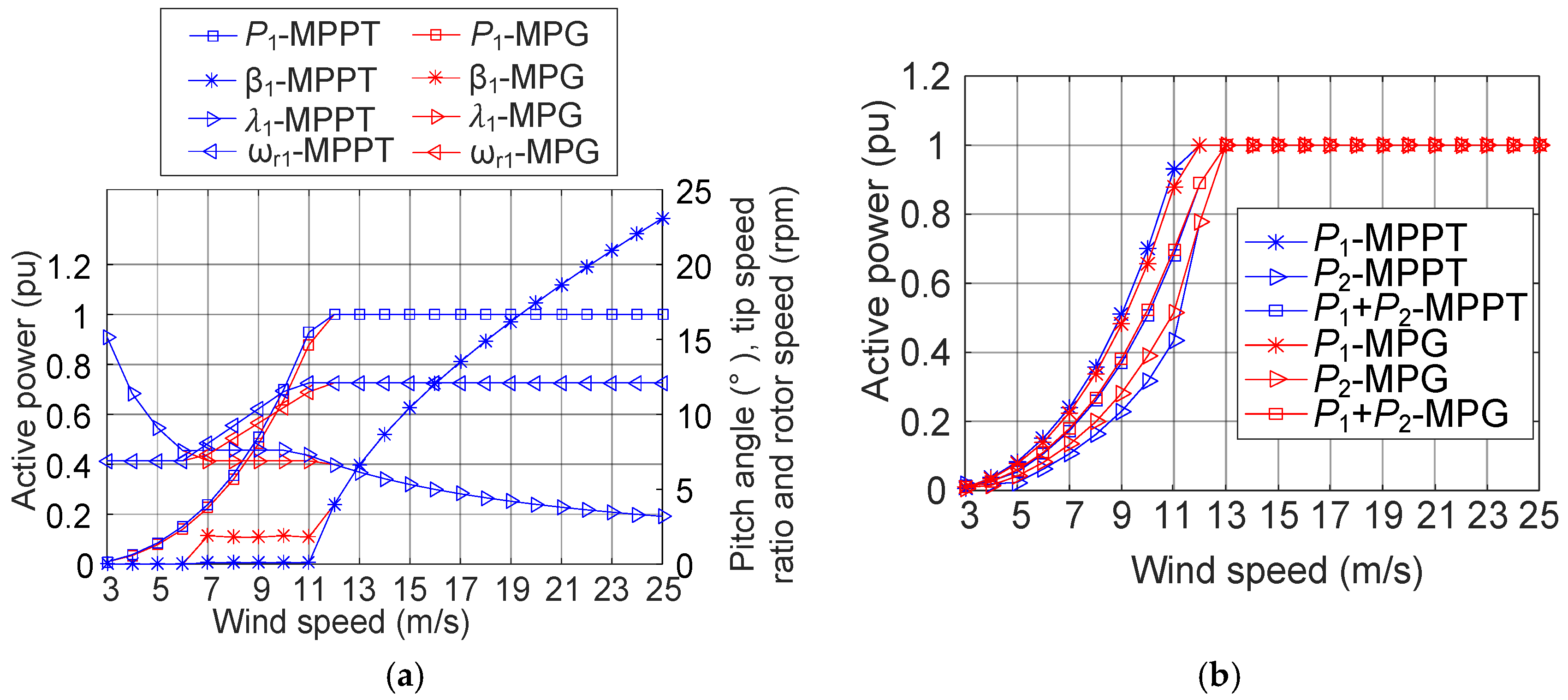
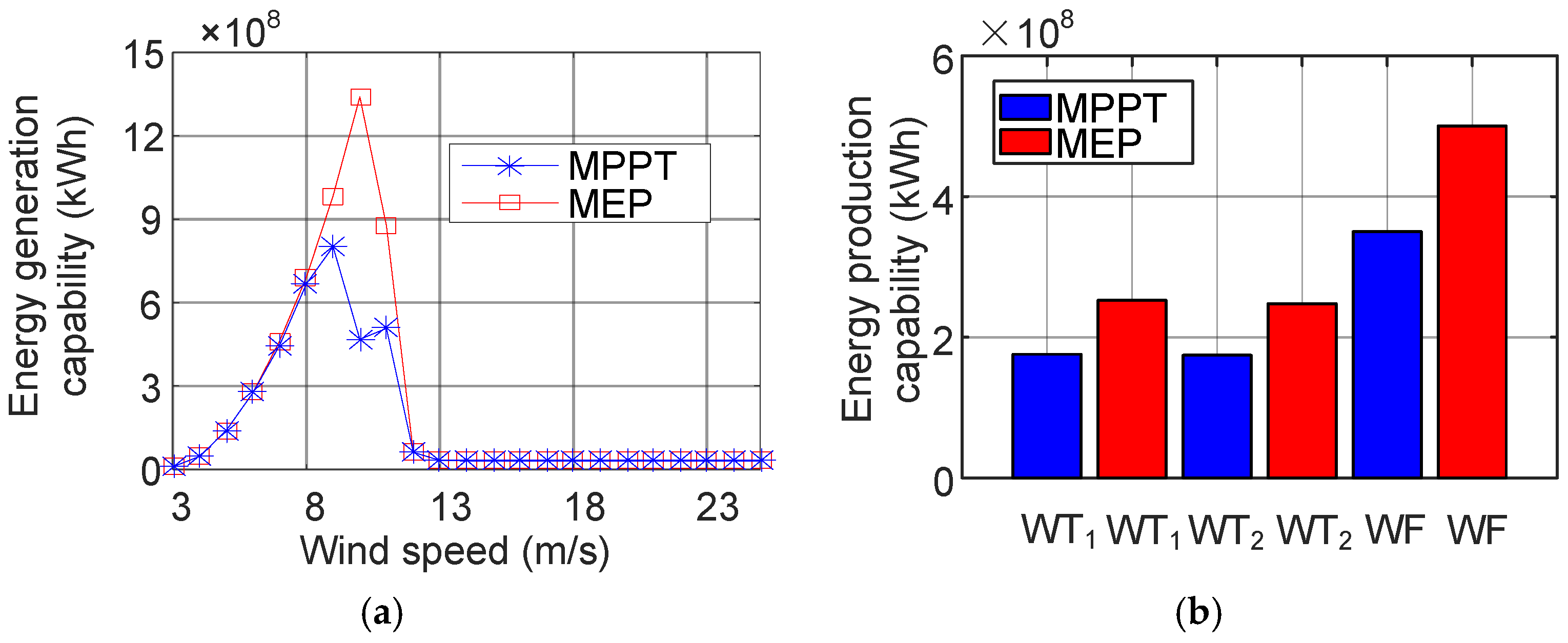
4. Energy Production of Wind Farm According to MPPT and MPG
5. Maximize Energy Production of Wind Farm
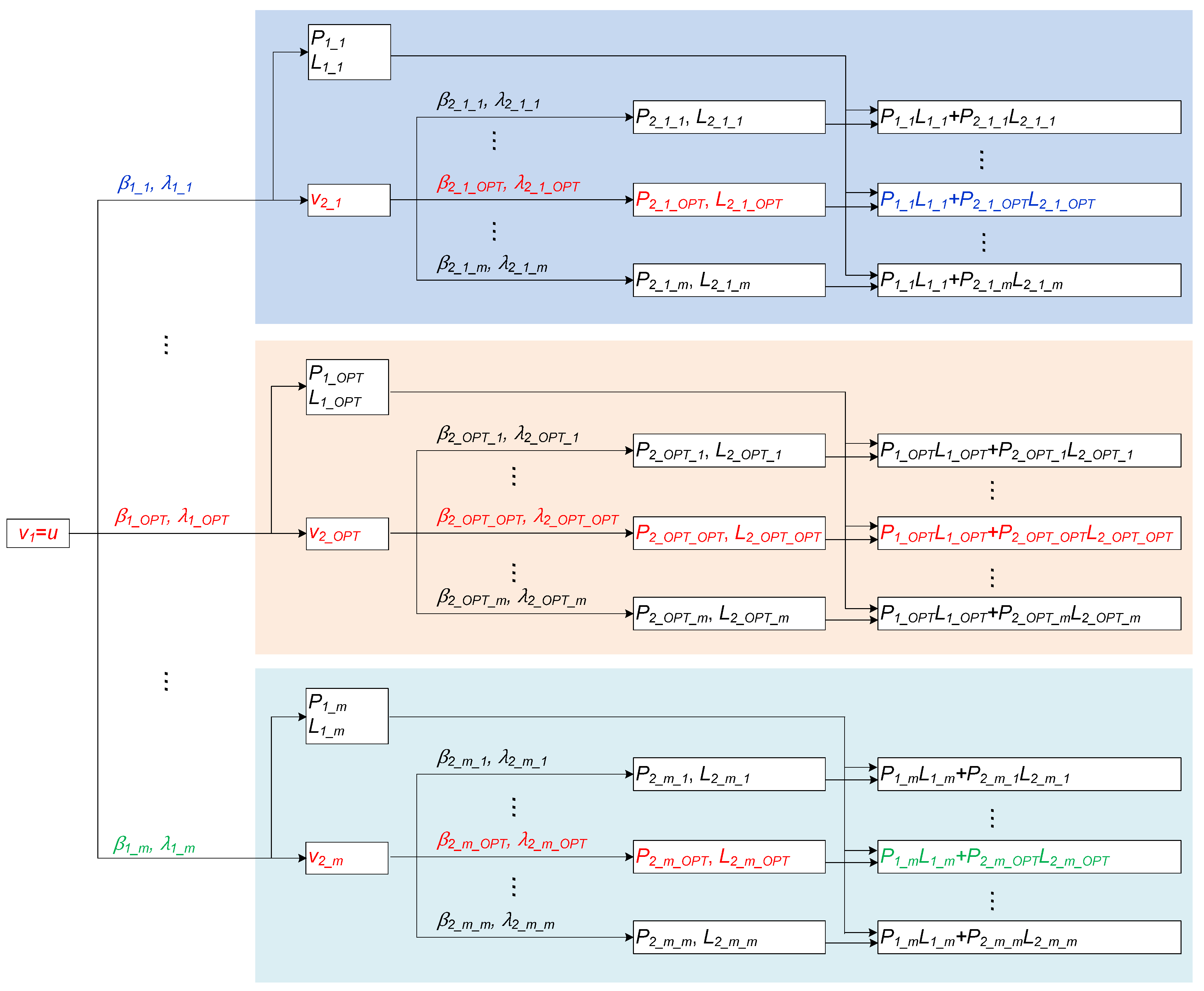
5.1. Optimization Method
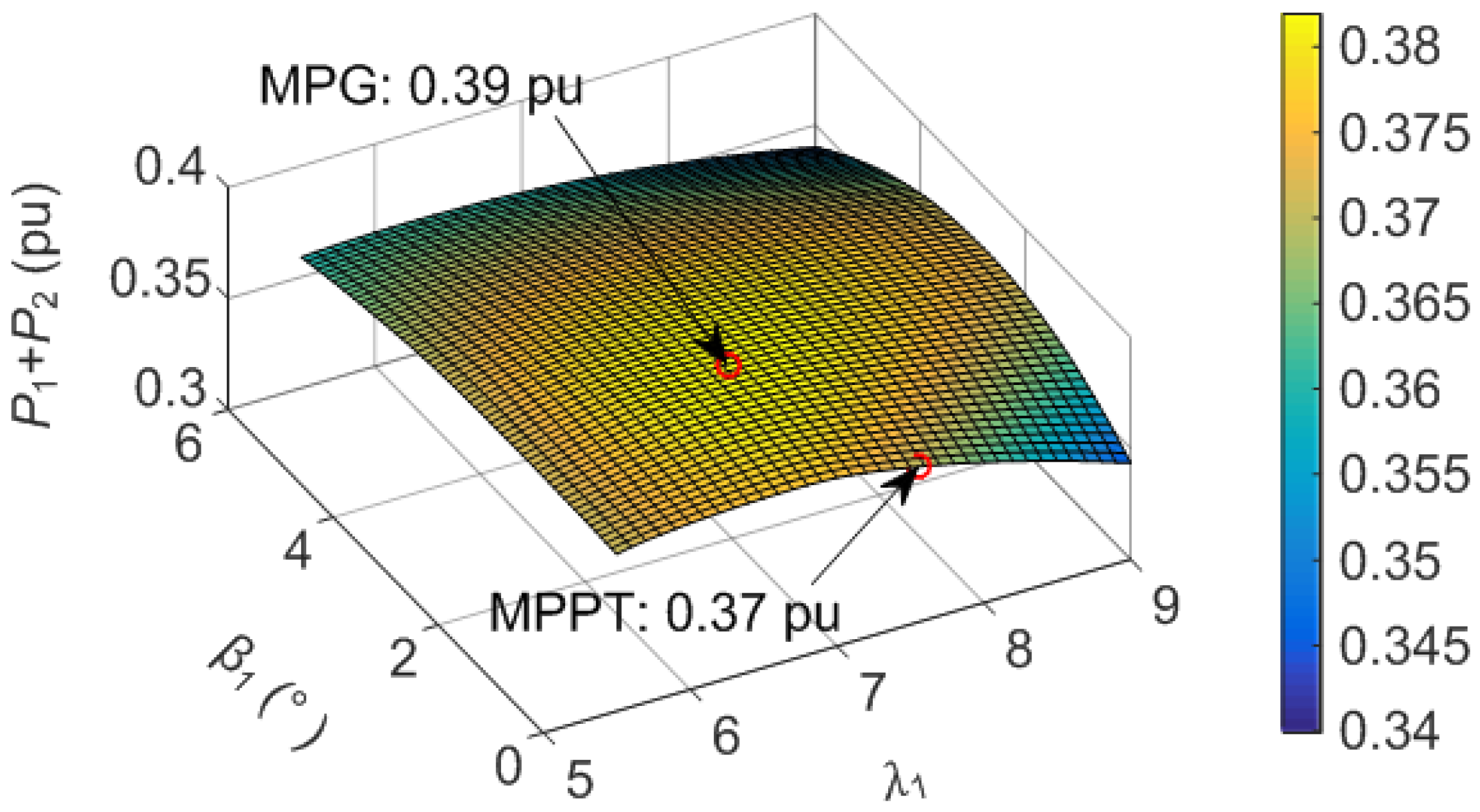
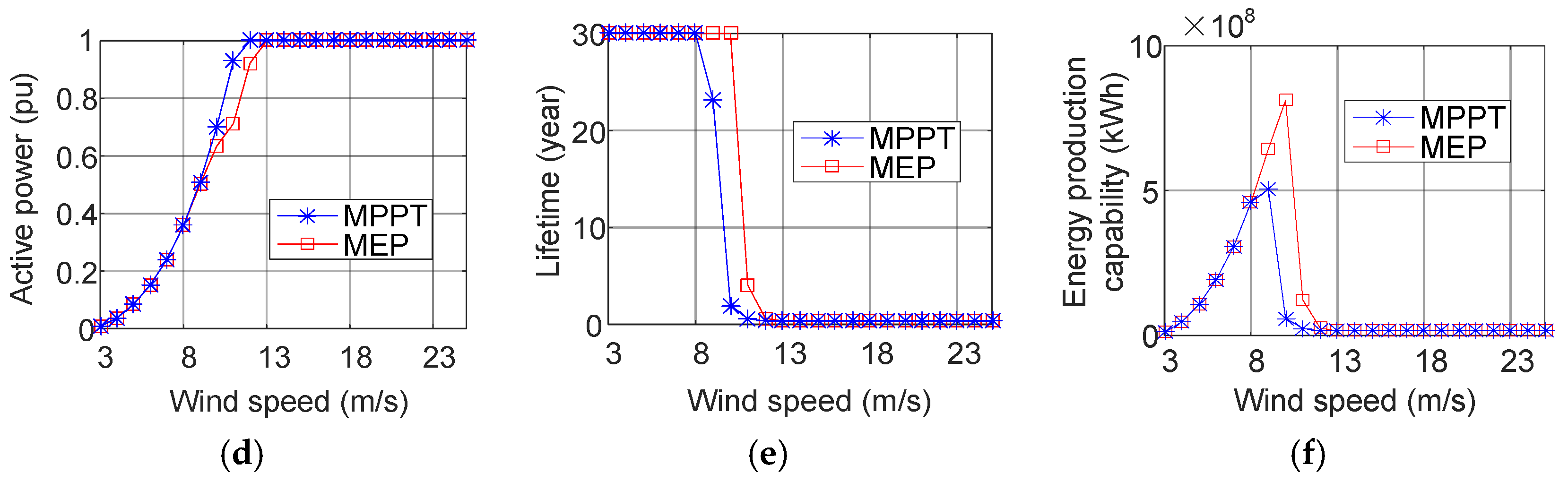
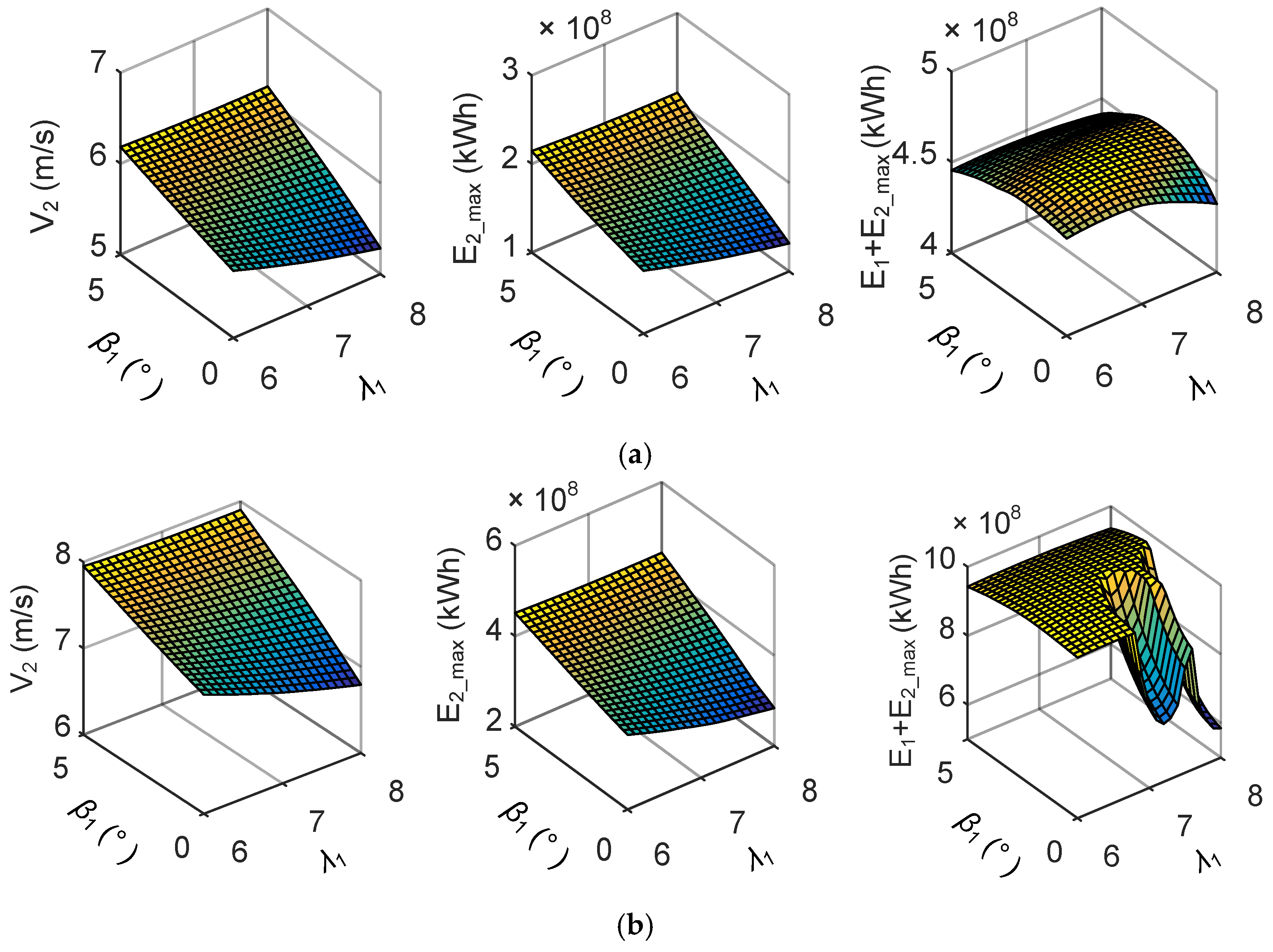
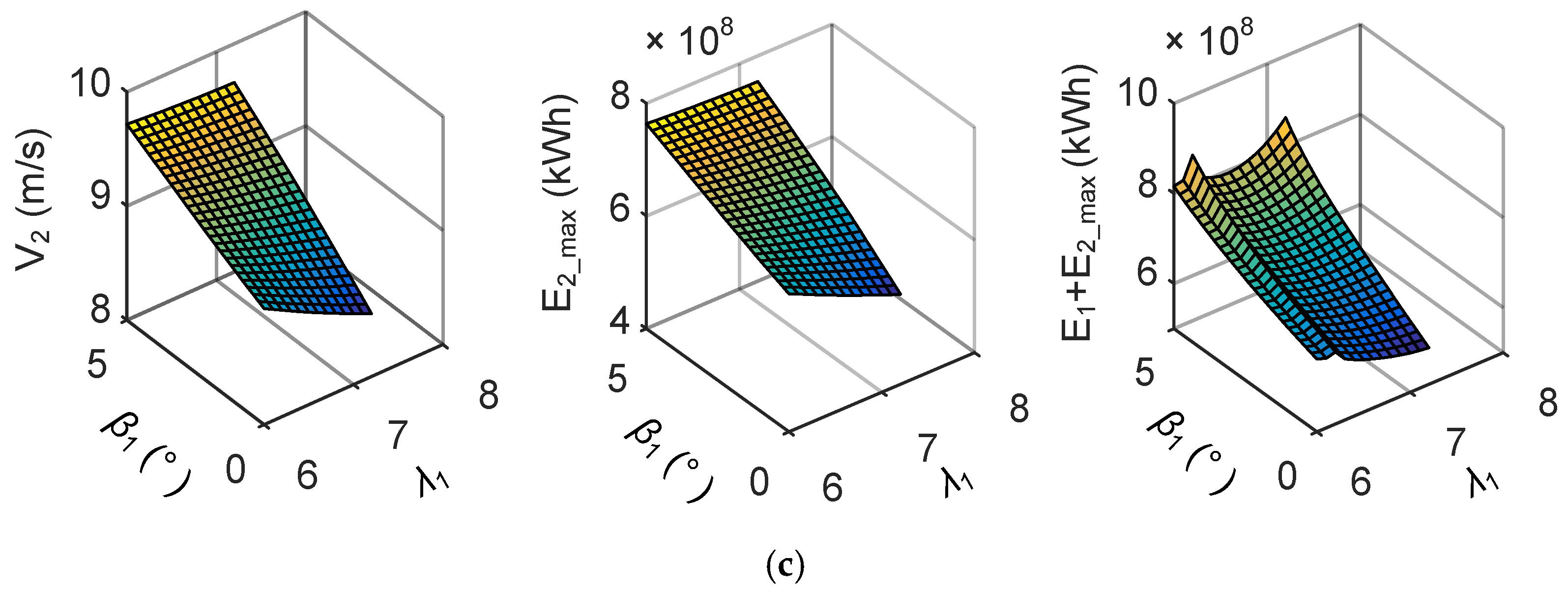
5.2. Optimization for WT2
5.3. Optimization of WT1
5.4. Optimized Energy Production of the Wind Farm
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blaabjerg, F.; Ma, K. Future on power electronics for wind turbine systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Chung, H.S.; Wang, H.; Blaabjerg, F.; Pecht, M. Reliability of Power Electronic Converter Systems; Institution of Engineering and Technology: Stevenage, UK, 2015. [Google Scholar]
- Zhou, D.; Blaabjerg, F.; Lau, M.; Tonnes, M. Optimized reactive power flow of DFIG power converters for better reliability performance considering grid codes. IEEE Trans. Ind. Electron. 2015, 62, 1552–1562. [Google Scholar] [CrossRef]
- Hahn, B.; Durstewitz, M.; Rohrig, K. Reliability of Wind Turbines, Experiences of 15 Years with 1500 WTs. ISET, 2007. Available online: http://renknownet2.iwes.fraunhofer.de/pages/wind_energy/data/2006-02-09Reliability.pdf (accessed on 9 February 2006).
- Electronic Components and Systems (ECS) Division. Handbook for Robustness Validation of Automotive Electrical/Electronic Modules; ZVEL: Berlin, Germany, 2008. [Google Scholar]
- Hirschmann, D.; Tissen, D.; Schroder, S.; De Doncker, R.W. Inverter design for hybrid electrical vehicles considering mission profiles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 7–9 September 2005; pp. 1–6.
- Busca, C.; Teodorescu, R.; Blaabjerg, F.; Munk-Nielsen, S.; Helle, L.; Abeyasekera, T.; Rodriguez, P. An overview of the reliability prediction related aspects of high power IGBTs in wind power applications. Microelectron. Reliab. 2011, 51, 1903–1907. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Richardeau, F.; Pham, T.T.L. Reliability calculation of multilevel converters: Theory and applications. IEEE Trans. Ind. Electron. 2013, 60, 4225–4233. [Google Scholar] [CrossRef]
- Behjati, H.; Davoudi, A. Reliability analysis framework for structural redundancy in power semiconductors. IEEE Trans. Ind. Electron. 2013, 60, 4376–4386. [Google Scholar] [CrossRef]
- ABB Application Note. Load-Cycling Capability of HiPak IGBT Modules. Available online: https://library.e.abb.com/public/1f4fb71e0af3356883257c8d00443ca1/Load-cycling%20capability%20of%20HiPak_5SYA%202043-04.pdf (accessed on 4 February 2014).
- Wintrich, A.; Nicolai, U.; Tursky, W.; Reimann, T. Application Manual Power Semiconductors; ISLE Verlag: Ilmenau, Germany, 2011. [Google Scholar]
- Scheuermann, U.; Schmidt, R. A new lifetime model for advanced power modules with sintered chips and optimized Al wire bonds. In Proceedings of the PCIM, Nuremberg, Germany, 14–16 May 2013; pp. 810–813.
- Krohn, S.; Morthorst, P.E.; Awerbuch, S. The Economics of Wind Energy Euro. Wind Energy Association (EWEA), Technical Report, Brussels, Belgium, March 2009. Available online: http://www.ewea.org/fileadmin/ewea_documents/documents/publications/reports/Economics_of_Wind_Main_Report_FINAL-lr.pdf (accessed on 16 March 2009).
- Barthelmie, R.J.; Folkerts, L.; Larsen, G.C.; Rados, K.; Pryor, S.C.; Frandsen, S.T.; Lange, B.; Schepers, G. Comparison of wake model simulations with offshore wind turbine wake profiles measured by Sodar. J. Atmos. Ocean. Technol. 2006, 23, 888–901. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Teeuwisse, F.W.; van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw control using a parametric model for wake effects—A CFD simulation study. Wind Energy 2014, 19, 95–114. [Google Scholar] [CrossRef]
- Serrano González, J.; Burgos Payán, M.; Riquelme Santos, J.; González Rodríguez, Á.G. Maximizing the overall production of wind farms by setting the individual operating point of wind turbines. Renew. Energy 2015, 80, 219–229. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Hansen, K.; Frandsen, S.T.; Rathmann, O.; Schepers, J.G.; Schlez, W.; Phillips, J.; Rados, K.; Zervos, A.; Politis, E.S.; et al. Chaviaropoulos, Modelling and measuring flow and wind turbine wakes in large wind farms offshore. Wind Energy 2009, 12, 431–444. [Google Scholar] [CrossRef]
- Duckworth, A.; Barthelmie, R.J. Investigation and validation of wind turbine wake models. Wind Eng. 2008, 32, 459–475. [Google Scholar] [CrossRef]
- Tian, J.; Su, C.; Soltani, M.; Chen, Z. Active power dispatch method for a wind farm central controller considering wake effect. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 30 October–1 November 2014; pp. 5450–5456.
- Marden, J.R.; Ruben, S.D.; Pao, L.Y. A model-free approach to wind farm control using game theoretic methods. IEEE Trans. Control Syst. Technol. 2013, 21, 1207–1214. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Dam, F.C.; Wingerden, J.W. A model-free distributed approach for wind plant control. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 628–633.
- Duong, M.Q.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. Pitch angle control using hybrid controller for all operating regions of SCIG wind turbine system. Renew. Energy 2014, 70, 197–203. [Google Scholar] [CrossRef]
- Duong, M.Q.; Grimaccia, F.; Leva, S.; Mussetta, M.; Le, K.H. Improving transient stability in a gride-connected squirrel-cage induction generator wind turbine system using a fuzzy logic controller. Energies 2015, 8, 6328–6349. [Google Scholar] [CrossRef]
- Shariatpanah, H.; Fadaeinedjad, R.; Rashidinejad, M. A new model for PMSG-based wind turbine with Yaw control. IEEE Trans. Energy Convers. 2013, 28, 929–937. [Google Scholar] [CrossRef]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; Wiley: Seoul, Korea, 2011; pp. 34–35. [Google Scholar]
- Muyeen, S.M.; Takahashi, R.; Murata, T.; Tamura, J. A variable speed wind turbine control strategy to meet wind farm grid code requirements. IEEE Trans. Power Syst. 2010, 25, 331–340. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Katic, I.; Højstrup, D.; Jensen, N.O. A sample model for cluster efficiency. In Proceedings of the European Wind Energy Association Conference, Rome, Italy, 7–9 October 1986; pp. 407–410.
- Jensen, N.O. A Note on Wind Generator Interaction; Technical Report Risø-M-2411; Risø National Laboratory: Roskilde, Denmark, 1984. [Google Scholar]
- Mortensen, N.G.; Heathfield, D.N.; Myllerup, L.; Landberg, L.; Rathmann, O. Wind Atlas Analysis and Application Program: WAsP 8 Help Facility; Risø National Laboratory: Roskilde, Denmark, 2005. [Google Scholar]
- Tian, J.; Zhou, D.; Su, C.; Chen, Z.; Blaabjerg, F. Reactive Power Dispatch Method in Wind Farms to Improve the Lifetime of Power Converter Considering Wake Effect. IEEE Trans. Sustain. Energy 2016. [Google Scholar] [CrossRef]
- Tian, J.; Su, C.; Chen, Z. Reactive Power Capability of the Wind Turbine with Doubly Fed Induction Generator. In Proceedings of the 39th IEEE Industrial Electronics Society Conference, Vienna, Austria, 10–13 November 2013; pp. 5310–5315.
- Zhou, D.; Blaabjerg, F.; Franke, T.; Tonnes, M.; Lau, M. Comparison of wind power converter reliability with low-speed and medium-speed permanent-magnet synchronous generators. IEEE Trans. Ind. Electron. 2015, 62, 6575–6584. [Google Scholar] [CrossRef]
- Amro, R.; Lutz, J.; Lindemann, A. Power cycling with high temperature swing of discrete components based on different technologies. In Proceedings of the PESC, Aachen, Germany, 20–26 June 2004; pp. 2593–2598.
- Yildirim, H.C.; Marquis, G.; Barsoum, Z. Fatigue assessment of high frequency mechanical impact (HFMI)-improved fillet welds by local approaches. Int. J. Fatigue 2013, 52, 57–67. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Rated Power | 5 MW |
| Rotor Diameter | 126 m |
| Cut-in, Rated, Cut-out Wind Speed | 3 m/s, 11.4 m/s, 25 m/s |
| Min. and Max. Rotor Speed | 6.9 rpm, 12.1 rpm |
| Gearbox Ratio | 97:1 |
| Number of Pole-pairs | 3 |
| Synchronous Frequency | 50 Hz |
| Electrical Generator Efficiency | 94.4% |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Zhou, D.; Su, C.; Blaabjerg, F.; Chen, Z. Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation. Appl. Sci. 2017, 7, 65. https://doi.org/10.3390/app7010065
Tian J, Zhou D, Su C, Blaabjerg F, Chen Z. Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation. Applied Sciences. 2017; 7(1):65. https://doi.org/10.3390/app7010065
Chicago/Turabian StyleTian, Jie, Dao Zhou, Chi Su, Frede Blaabjerg, and Zhe Chen. 2017. "Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation" Applied Sciences 7, no. 1: 65. https://doi.org/10.3390/app7010065
APA StyleTian, J., Zhou, D., Su, C., Blaabjerg, F., & Chen, Z. (2017). Optimal Control to Increase Energy Production of Wind Farm Considering Wake Effect and Lifetime Estimation. Applied Sciences, 7(1), 65. https://doi.org/10.3390/app7010065









