Abstract
Description of the physical behavior of electric guitars is still not very widespread in the scientific literature. In particular, the physical models describing a nonlinear behavior of pickups still requires some refinements. The study presented in this paper is focused on nonlinear modeling of the pickups. Two main issues are raised. First, is the currently most used nonlinear model (a Hammerstein model) sufficient for the complex nonlinear behavior of the pickup? In other words, would a more complex model, such as a Generalized Hammerstein that can deal better with the nonlinear memory, yield better results? The second troublesome issue is how to measure the nonlinear behavior of a pickup correctly. A specific experimental set-up allowing for driving the pickup in a controlled way (string displacement perpendicular to the pickup) and to separate the nonlinear model of the pickup from other nonlinearities in the measurement chain is proposed. Thanks to this experimental set-up, a Generalized Hammerstein model of the pickup is estimated for frequency range 15–500 Hz and the results are compared with a simple Hammerstein model. A comparison with experimental results shows that both models succeed in describing the pickup when used in realistic conditions.
1. Introduction
Physical modeling and synthesis of musical instruments has been an active research field for the last few decades [1,2] including a guitar and an electric guitar [3,4,5,6,7,8,9]. One of the most important elements of an electric guitar is a pickup, a sensor that captures the string vibrations and translates them into an electric signal [10]. It is basically composed of a set of permanent magnets surrounded by an electric coil. A ferromagnetic string vibrating in the vicinity of the pickup results in a variation of the magnetic flux through the coil. According to Faraday’s law, an electrical voltage is then induced across the coil.
A few models of pickup are available in the literature. Some of them are based on integral equations leading to the variation of magnetic flux at the coil location [11]. These models principally show, first, that vertical oscillations of the guitar strings produce a stronger effect than horizontal ones and, second, that there is a noticeable distortion of the electric signal generated by both oscillations. An overview of the modeling issues related to magnetic pickups is available in [12]. It concerns effects of both pickup position and pickup width on the pickup timbre, as well as the effect of the pickup internal impedance. In [12], the magneto-electric conversion done by the pickup is modeled using static nonlinearity followed by a simple derivative (Figure 1). The static nonlinearity represents the nonlinear relationship between the string displacement and the magnetic flux, which can be evaluated using computer simulations and implemented as an exponential or N-th order polynomial [13]. A slightly different but very powerful approach based on physical-laws and on the framework of port Hamiltonian systems is used in [14,15] to model an electro-mechanical piano (including a pickup).

Figure 1.
Nonlinear system usually used to model nonlinearities of a guitar pickup [12].
On the other hand, studies on nonlinear modeling have led to many nonparametric nonlinear models, discussed in Section 2, that have evolved through the last few decades. One of them, a Generalized Hammerstein model, has proved to be useful in modeling nonlinear systems with no physical knowledge of the system [16,17,18].
The goal of this paper is to proceed with the identification of pickup linearities based on a Generalized Hammerstein representation of the pickup. For this purpose, a specific experimental set-up is used to drive the pickup in a controlled way, and a technique is carried out to get rid of nonlinearities due to the driver. One of the aims of this study is to find out if it is meaningful, or not, to use a simple Hammerstein structure given in Figure 1, as it is usually done in modeling the pickup nonlinearities [11,12,13], or if a more complex model, such as the Generalized Hammerstein one, is necessary. The answer is given through the measurement provided in Section 4 and Section 5, and a comparison between theoretical and experimental results in the case of a realistic use of the pickup is given in Section 6.
2. Nonlinear Models
Study of a nonlinear physical system, such as a guitar pickup, usually begins with a basic model based on a memory-less polynomial representation [11,12,13]. As demands for better physical description increase, more and more complicated nonlinear models are proposed and used. The main criteria for these models are low complexity together with a high ability to predict the systems output. If both criteria are fulfilled, the model can be successfully used for simulation.
When dealing with modeling of nonlinear systems, two different methodological approaches are usually considered. The first approach studies the physical causes of the nonlinear phenomena and the model is derived purely from the physical laws governing the behavior of the system. These laws can then be used for the derivation of a theoretical nonlinear model of the system [14]. In the second approach, little, or even no physical properties are known. The system is said to be a black box and a generic nonlinear model is used for nonlinear system identification. Among many methods available in the literature [19], the class of Volterra-Series models and block-oriented models [20,21] have drawn a particular attention in the field of audio, musical instruments, and digital effects [18,22,23,24,25,26].
Probably the best known block-oriented nonlinear model is the Hammerstein model combining two elements in series: a static nonlinear system and a linear filter [27,28,29]. This kind of model has been, up to today, applied to guitar pickups in [12,13]. The Hammerstein model is then often preferred because of its simpler structure and lower computational cost.
On the other hand, the Volterra series representation is usually considered to be more effective but less practical due to the highly complex calculation of multidimensional kernels [30,31,32,33]. A Generalized Hammerstein model [16,17,18] represents a very good compromise between the complexity and the efficacy. It is made up of N parallel branches, with each branch consisting of a linear filter preceded by an N-th order power static nonlinear function, for . The output of such a model to any input is governed by the following equation
where is the inverse Fourier transform of and where stands for convolution. Note that the Generalized Hammerstein model is functionally equivalent to a Chebyshev polynomial-based model [34] successfully applied in e.g., [35,36].
To estimate the filters , we need to estimate m Higher Harmonic Frequency Responses (HHFRs) between the input and the output noted as , m referring to the number of each HHFR. We use a procedure based on the Synchronized Swept-Sine technique [37].
3. Synchronized Swept-Sine Technique
The synchronized swept-sine is generated using [37]
where
and where and are initial and final frequency, respectively, and T is duration of the swept-sine. Note that the definition of the exponential swept-sine (Equation (2)) does not contain the "" term contrary to the usual definition [16,38]. The original definition [38] led to a good estimation of amplitudes of Higher Harmonic Frequency Responses (HHFRs), but the phases of HHFRs have been estimated poorly. A restriction of the parameters , , and T in order to synchronize the swept-sine signal has been proposed in [16], avoiding the problem of poor phase estimation and allowing an estimation of the filters of the Generalized Hammerstein model. A similar approach has been proposed in [17]. It has been shown, in [37], that in removing the "" term from the original definition, the synchronized swept-sine becomes suitable for estimation of the HHFRs without any need of correction or restriction of the parameters , , and T.
The method, originally developed by Angelo Farina [38], consists of de-convolving the measured signals with a so-called inverse filter as
where is the acquired response of the nonlinear system (displacement or voltage signal) to the synchronized swept-sine. The Fourier transform of inverse filter can be either calculated numerically from the generated signal , or an analytical formula derived in [37],
can be used. The impulse response then consists of time-delayed higher harmonic impulse responses, separated by time delays
m being the order of the higher harmonic.
Finally, to get the Higher Harmonic Frequency Responses (HHFRs), the time-delayed higher harmonic impulse responses are windowed from and Fourier Transformed to obtain
x and u denoting input and output.
4. Measurement of the Pickup Nonlinearities
The first goal of this paper is to identify the pickup in terms of the Generalized Hammerstein model (Figure 2). Since the pickup is an electromagnetic transducer that converts string vibration into an electrical output signal, its experimental characterization is not straightforward. Usually, when measuring a linear or a nonlinear device, excitation signal is a controlled one (impulses, swept-sine, pseudo-random sequences) so that output signal can be used to identify the system in terms of a frequency response function (FRF) for a linear system, or in terms of a set of describing functions when dealing with a nonlinear system. For a pickup, the excitation signal is the displacement of a plucked string exhibiting a multi-modal and non stationary behavior. Such an excitation is useful for a study in real conditions [39] but can hardly be used to get an FRF or to identify nonlinearities.
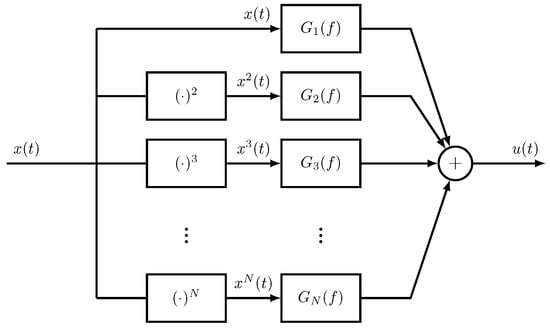
Figure 2.
Generalized Hammerstein model for identifying the nonlinearities of the pickup; and represent the displacement of the guitar string and the output voltage of the pickup, respectively.
To control the string displacement, we use the system shown in Figure 3. A sample of a guitar string (steel, low E-string, diameter 1.42 mm) is glued on a non-magnetic rigid support, itself fixed to a shaker which imposes a string displacement perpendicular to the pickup [40]. The rigid connection between the string sample, rigid support and the shaker ensures a piston-like motion. An mu-metal shielding covers the shaker in order to limit its electromagnetic radiation. The pickup under test (SSL-5 single-Coil pickup, Seymour Duncan, Santa Barbara, CA, USA) is set on a precision movement device, which allows for adjusting the distance at rest between the string and the magnet. For this experiment, is set to = 5 mm, corresponding approximately to the distance set on a real guitar.
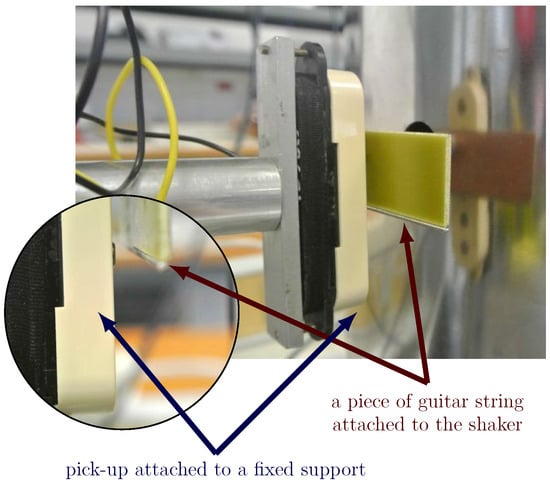
Figure 3.
Measurement device used to characterize the nonlinearities of the pickup. A sample of a guitar string is glued on a non-magnetic rigid support, itself fixed to a shaker. An mu-metal shielding covers the shaker in order to limit its electromagnetic radiation.
The shaker is driven by a Synchronized Swept Sine signal [37] so that the nonlinearities of the whole system, that is, the shaker and the pickup in series can be easily identified using a Generalized Hammerstein model [16].
To protect the shaker from a possible destruction due to excessive displacement or current, the frequency range is furthermore limited to the span 15–500 Hz. The excitation signal is pre-filtered using a linear filter so as to obtain a displacement whose amplitude is almost constant over the frequency span. The peak amplitude is set here to 1 mm. The displacement of the string portion (that is, the displacement of the shaker) is measured by means of a single-point vibrometer (OFV-503 and OFV-505, Polytec, Irvine, CA, USA), pointing at a piece of reflective tape glued to the string support. The electrical output of the pickup is then connected to an acquisition card that exhibits a high input impedance (470 kΩ). Consequently, the measured output voltage corresponds to the open-circuit voltage that does not take into account the effect of pickup output impedance.
The Higher Harmonic Frequency Responses (HHFRs) for both the string displacement and for the pickup output voltage calculated using the Synchronized Swept Sine method [37] are given in Figure 4. The noise level of the measurement is visible on the first HHFR (blue line) at frequencies higher than the highest excitation frequency (500 Hz), giving at least 60 dB signal-to-noise ratio (SNR) for the displacement measurement and 80 dB SNR for the voltage measurement.
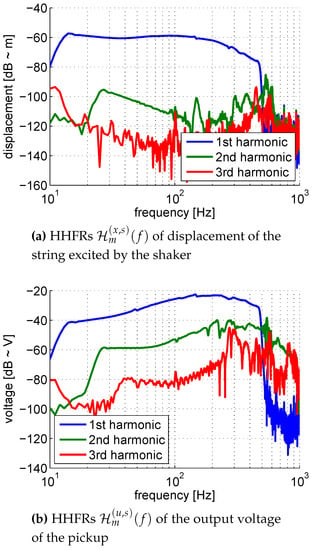
Figure 4.
First three Higher Harmonic Frequency Responses (HHFRs) of (a) displacement of the string excited by the shaker and (b) the output voltage of the pickup.
The fundamental harmonic of the string displacement (Figure 4a) is not flat despite the pre-filtering and the second harmonic reaches dB relative to fundamental harmonic. It is thus rather difficult, or almost impossible, to estimate which part of the HHFRs of the pickup output voltage (Figure 4b) is due to the pickup behavior and which part is due to the shaker behavior.
To overcome this problem, we use a technique presented in [41] and detailed in the Appendix A. Thanks to this technique, a nonlinear system can be identified in terms of an N-th order Generalized Hammerstein model (Figure 2), even if it is preceded by another unknown nonlinear system.
For the pickup under test, a fifth order Generalized Hammerstein model, the magnitude values of which are depicted in Figure 5, is identified using this technique. The order of the model is chosen as a compromise between the sufficient number of branches of the Generalized Hammerstein model (to be able to reproduce the nonlinear effect correctly) and the noise level.
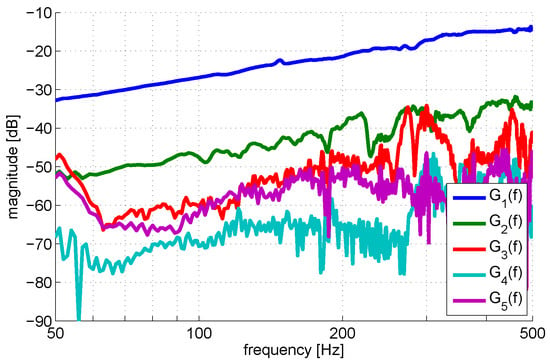
Figure 5.
Magnitude values of the estimated filters of the Generalized Hammerstein model (Figure 2) of the pickup.
5. Nonlinear Parametric Model of the Pickup
Observing the estimated filters of the Generalized Hammerstein model depicted in Figure 5, one can note that the dependence on frequency for all filters is approximately 6 dB/oct. Such a slope corresponds to in the frequency domain or to a simple derivative in the time domain.
It is thus tempting to fit all the filter responses with a function in order to replace each branch of the Generalized Hammerstein model by a multiplicative coefficient in series with a derivative function . A fit of the first two filters and (magnitude and phase), obtained using linear regression of absolute values within the frequency range 15-500 Hz, is depicted in Figure 6 and Figure 7. It is interesting to note that the estimated phases of both filters are very close to within the whole frequency range.
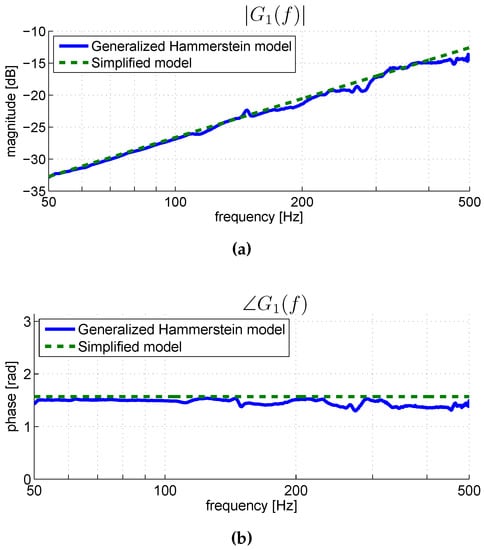
Figure 6.
Modulus (a) and phase (b) of the first filter of the identified Generalized Hammerstein model of the pickup under test (blue solid line) and the equivalent frequency response of the simplified Hammerstein model followed by a differentiator (green dashed line).
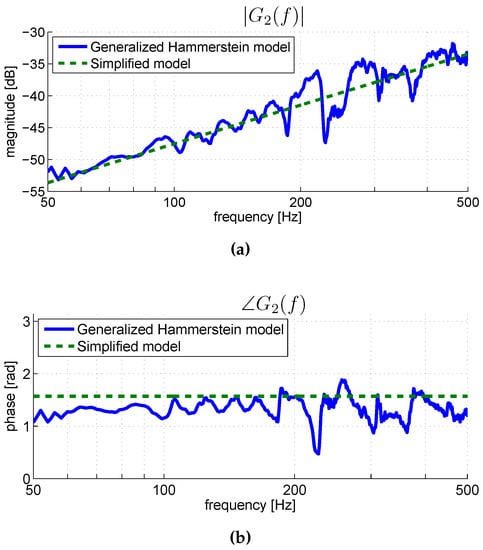
Figure 7.
Modulus (a) and phase (b) of the first filter of the identified Generalized Hammerstein model of the pickup under test (blue solid line) and the equivalent frequency response of the simplified Hammerstein model followed by a differentiator (green dashed line).
Fixing the phase of all of the estimated filters to and parameterizing the absolute value by (resulting coefficient of the linear regression), we can write the following relation
This relation being a time derivative of a Taylor series, we can simplify the Generalized Hammerstein model to a Hammerstein model consisting of a static nonlinearity followed by a linear filter (Figure 1). In this particular case, the static nonlinearity is represented by a simple Taylor series with coefficients , and the linear filter is represented by a time domain derivative, as shown in Figure 1. This result tends to confirm the model previously proposed by [12]. The fitted coefficients for the pickup under test are given in Table 1, and the corresponding input–output characteristic is depicted in Figure 8.

Table 1.
Coefficients of the estimated parametric Hammerstein model.
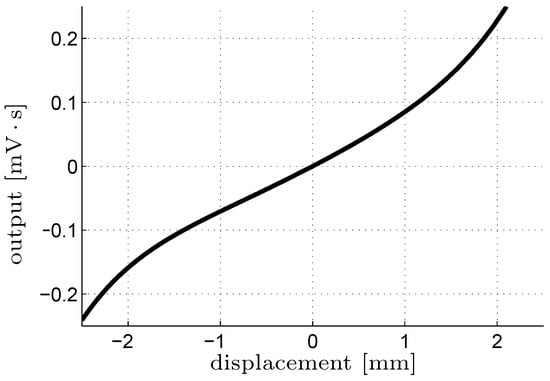
Figure 8.
Input–output graph of the static nonlinearity (power series development with coefficients given in Table 1).
6. Model vs. Real Guitar-String Signal
To test the validity of the identified Hammerstein model, we set up a different experiment corresponding to a realistic use of the pickup. For that purpose, we use a lab guitar prototype [40]. A guitar string is fixed on an wooden beam. The string is tuned as open low E ( = 82 Hz). The pickup under test is set on a mechanical arm on which some precision movement pieces are fixed. Thanks to this system, the pickup position under the string can be adjusted along the three axes. For this experiment, the pickup is set at 1/4 of the total length of the string corresponding approximately to the neck position on a real guitar, and the distance at rest between the string and the pickup is set at 5 mm. A detail of the experiment is shown in Figure 9.

Figure 9.
Picture of the second experiment in which the pickup is placed under a vibrating string.
The string is struck using an impact hammer. A single-point vibrometer (OFV-503 and OFV-505, Polytec, Irvine, CA, USA) pointing at a piece of reflective tape glued to the string and located above the pickup allows the measurement of the string displacement in the vertical plane. Temporal evolution of both string displacement and pickup output voltage are recorded simultaneously and depicted in Figure 10 and Figure 11. A zoom on a few periods of both experimental signals is given for three different time lags along the time-varying response. As expected, the string displacement is distorted just after the excitation (Figure 10—zoom to t = 1.3 s). It becomes less and less distorted as the harmonics of higher orders fade with time (Figure 10—zoom to t = 22 s). The output signal of the pickup exhibits the same kind of behavior with time. One can notice that the output voltage is more distorted due to pickup nonlinearities.
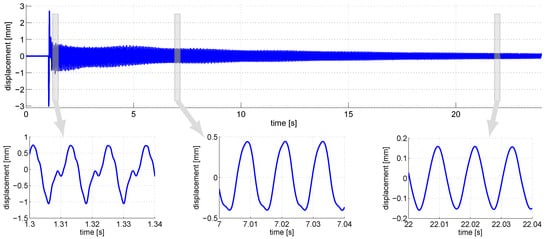
Figure 10.
Recorded signals of the vibrating string.
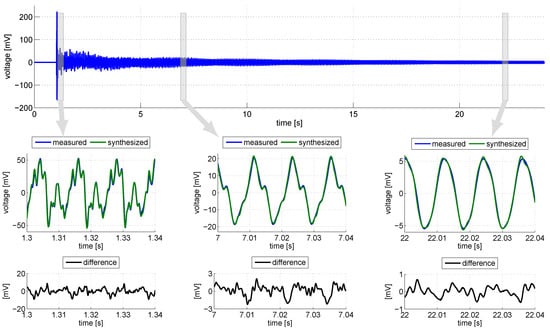
Figure 11.
Recorded and synthesized signals of the voltage from the pickup.
The displacement signal measured with the vibrometer is then used as the input of estimated parametric Hammerstein model of the pickup and both the measured and the synthesized pickup outputs are compared on the same graph (Figure 11). The difference between estimated and experimental signals is plotted on Figure 11, showing that the model succeeds in describing the nonlinear behavior of the pickup when used in realistic conditions.
7. Discussion
The results presented in this paper show that a simple Hammerstein model seems to be sufficient for the pickup modeling and that using a Generalized Hammerstein model is not necessary. However, several hypotheses have been put forward, simplifying the problem that might be at the origin of small differences between the measured and modeled pickup outputs compared in Figure 10 and Figure 11.
First, the frequency range of the excitation signal is limited to 15–500 Hz due to the capacities of the shaker. Using a larger frequency range might have been beneficial. The nonlinearities of the pickup may differ at higher frequencies, and thus, in such a case, a complete Hammerstein Generalized model might be useful. A supplementary study would be necessary to draw a meaningful conclusion.
Next, in the first experimental setup used for the model identification, the movement of the rigid string attached to the shaker exhibits only z-axis polarization, whereas it is known that the string being played by a guitar player exhibits rather an ellipsoid type motion in both y- and z-directions [42,43]. A hammer-like impact, used in the second experiment for the synthesis, has been used to excite the string in order to approach the z-axis motion of the string in the comparative measurements whose results are provided in Figure 10 and Figure 11. Note that, even if the real movement of the string is important in both y- and z-directions [44,45], and it has been shown that the pickup behavior is mainly influenced by the z-axis contribution [8,40]. Moreover, the piece of the rigid string attached to the shaker is of finite length and does not exhibit any deformation compared to a string attached on the guitar.
Even though these phenomena have been neglected, the results presented in this paper show a very good agreement between the output predicted by the model and the output obtained from the experimental measurement.
8. Conclusions
Physical modeling of musical instruments is still a challenge for not only physicists, acousticians, and instrument makers, but also for engineers from the digital audio community. An electric guitar is not an exception.
This paper focuses on nonlinear modeling of a pickup of an electric guitar capturing vibrations of ferromagnetic steel strings. Two main issues are raised: how we should proceed to measure the nonlinear properties of the pickup and what model we should use. An experimental set-up, in which a piece of steel string is attached to a shaker, is proposed. It allows for driving the pickup by shaker vibrations in a controlled way (string displacement perpendicular to the pickup). The shaker is driven by a Synchronized Swept Sine signal and a Generalized Hammerstein model of the pickup is estimated. Next, a simple Hammerstein model, usually used to represent pickup nonlinearities, is derived from the Generalized Hammerstein model and the validity of the Hammerstein model is verified for a pickup operating in a realistic way with a string excited by a hammer-like impact. Even if the experimental bench for model identification has a limited working frequency range (15–500 Hz), the estimated Hammerstein model precisely predicts the signal output.
In future work, the model can be used to synthesize different kinds of existing pickups (single coil pickups, humbuckers). However, two important questions need to be answered: is the Hammerstein model sufficient for all the single coil pickups on the market, and, if yes, would their corresponding coefficients differ? Is the conclusion of this work also valid for other types of pickup such as humbuckers? Moreover, a focus on a larger frequency excitation range might bring more insight on whether a Generalized Hammerstein model would be more beneficial over a simple Hammerstein model.
The results of this study shows that the Generalized Hammerstein model does not bring much more complementary information in a low-frequency range (15–500 Hz) and that the simple Hammerstein model is a very good compromise between precision and complexity.
Acknowledgments
This research was funded by the Region Pays de la Loire within the Le Mans Acoustic Project. The paper is an extended version of [46], and the winner of the best paper award.
Author Contributions
Antonin Novak, Leo Guadagnin, Bertrand Lihoreau, Pierrick Lotton, Emmanuel Brasseur, and Laurent Simon conceived and designed the experiments; Antonin Novak performed the experiments, Antonin Novak, Leo Guadagnin, Bertrand Lihoreau, Pierrick Lotton, Emmanuel Brasseur, and Laurent Simon analyzed the data; and Antonin Novak wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Since the measurement technique described in this paper uses a shaker as the excitation device to create the displacement of the guitar string, the nonlinearities caused by the shaker must be taken into account. The problem is depicted in Figure A1 in which the first nonlinear system (NLS) (NL) represents the shaker and the second NLS (NL) represents the pickup under test.
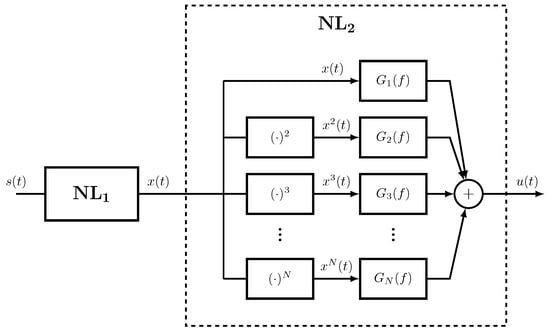
Figure A1.
Two dynamic nonlinear systems in series; the first one represents the shaker, and the second one, represented by a Generalized Hammerstein model, is the pickup under test.
The excitation swept-sine signal (Equation (2)) is the input of the first NLS. The displacement is the output of the first NLS and the input of the second NLS. The voltage is the output of the second NLS. Consequently, may be seen as the output of the whole system for the input signal .
The method presented in [41] then allows the identification of the second NLS. The identification of the system is equivalent to estimating the linear filters , , from the measured signals and . The identification process is based on the off-line estimation of both the HHFRs between and , and the HHFRs between and , for , M being the total number of harmonics taken into account. We recall that, given an input signal and an output signal of an NLS, the HHFR may be seen as the contribution, in both amplitude and phase, of the m-th harmonic at the output, for a sine at frequency f at the input, as
First, the HHFRs and are estimated using the synchronized swept sine method described in Section 4. Next, the displacement signal , already distorted by the shaker (NL), is taken to the powers of n and HHFRs for are calculated.
The HHFRs of the output signal result in the combination of all HHFRs after filtering by filters . The relationship between the HHFRs , and the linear filters can indeed be written in a matrix form as [41]
Equation (A2) can then be solved for unknown by using a square matrix inversion in the case , or by using a pseudo-inversion in the case . The number of harmonics M chosen for the estimation of HHFRs must be equal to or greater than the number of the branches N of the Generalized Hammerstein model. The matrix (pseudo)-inversion must be computed for each frequency f separately.
References
- Smith, J.O. Physical modeling synthesis update. Comput. Music J. 1996, 20, 44–56. [Google Scholar] [CrossRef]
- Välimäki, V.; Pakarinen, J.; Erkut, C.; Karjalainen, M. Discrete-time modelling of musical instruments. Rep. Prog. Phys. 2005, 69, 1. [Google Scholar] [CrossRef]
- Välimäki, V.; Huopaniemi, J.; Karjalainen, M.; Jánosy, Z. Physical Modeling of Plucked String Instruments with Application to Real-Time Sound Synthesis. J. Audio Eng. Soc. 1996, 44, 331–353. [Google Scholar]
- Laurson, M.; Erkut, C.; Välimäki, V.; Kuuskankare, M. Methods for modeling realistic playing in acoustic guitar synthesis. Comput. Music J. 2001, 25, 38–49. [Google Scholar] [CrossRef]
- Evangelista, G.; Eckerholm, F. Player–instrument interaction models for digital waveguide synthesis of guitar: Touch and collisions. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 822–832. [Google Scholar] [CrossRef]
- Karjalainen, M.; Mäki-Patola, T.; Kanerva, A.; Huovilainen, A. Virtual air guitar. J. Audio Eng. Soc. 2006, 54, 964–980. [Google Scholar]
- Karjalainen, M.; Penttinen, H.; Valimaki, V. Acoustic sound from the electric guitar using DSP techniques. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’00), Istanbul, Turkey, 5–9 June 2000; Volume 2, pp. II773–II776.
- Paté, A.; Le Carrou, J.L.; Fabre, B. Predicting the decay time of solid body electric guitar tones. J. Acoust. Soc. Am. 2014, 135, 3045–3055. [Google Scholar] [CrossRef] [PubMed]
- Bilbao, S.; Torin, A.; Chatziioannou, V. Numerical modeling of collisions in musical instruments. Acta Acust. Acust. 2015, 101, 155–173. [Google Scholar] [CrossRef]
- Hunter, D. The Guitar Pickup Handbook: The Start of Your Sound; Hal Leonard Corporation: Milwaukee, WI, USA, 2008. [Google Scholar]
- Horton, N.G.; Moore, T.R. Modeling the magnetic pickup of an electric guitar. Am. J. Phys. 2009, 77, 144–150. [Google Scholar] [CrossRef]
- Paiva, R.C.; Pakarinen, J.; Välimäki, V. Acoustics and modeling of pickups. J. Audio Eng. Soc. 2012, 60, 768–782. [Google Scholar]
- Remaggi, L.; Gabrielli, L.; de Paiva, R.; Välimäki, V.; Squartini, S. A pickup model for the Clavinet. In Proceedings of the 15th International Conference on Digital Audio Effects (DAFx-12), York, UK, 17–21 September 2012.
- Falaize, A.; Hélie, T. Guaranteed-passive simulation of an electro-mechanical piano: A port-Hamiltonian approach. In Proceedings of the 18th International Conference on Digital Audio Effects (DAFx-15), Trondheim, Norway, 30 November–3 December 2015.
- Falaize, A.; Hélie, T. Passive simulation of the nonlinear port-Hamiltonian modeling of a Rhodes Piano. J. Sound Vib. 2017, 390, 289–309. [Google Scholar] [CrossRef]
- Novak, A.; Simon, L.; Kadlec, F.; Lotton, P. Nonlinear system identification using exponential swept-sine signal. IEEE Trans. Instrum. Meas. 2010, 59, 2220–2229. [Google Scholar] [CrossRef]
- Rébillat, M.; Hennequin, R.; Corteel, E.; Katz, B.F. Identification of cascade of Hammerstein models for the description of nonlinearities in vibrating devices. J. Sound Vib. 2011, 330, 1018–1038. [Google Scholar] [CrossRef]
- Tronchin, L. The emulation of nonlinear time-invariant audio systems with memory by means of Volterra series. J. Audio Eng. Soc. 2013, 60, 984–996. [Google Scholar]
- Pearson, R.K. Discrete-Time Dynamic Models; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Schetzen, M. The Volterra and Wiener Theories of Nonlinear Systems; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Rugh, W.J. Nonlinear System Theory; Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
- Eichas, F.; Möller, S.; Zölzer, U. Block-Oriented Modeling of Distortion Audio Effects Using Iterative minimization External Link. In Proceedings of the 18th International Conference on Digital Audio Effects (DAFx-15), Trondheim, Norway, 30 November–3 December 2015.
- Yeh, D.T.; Abel, J.S.; Smith, J.O. Simplified, physically-informed models of distortion and overdrive guitar effects pedals. In Proceedings of the 10th International Conference on Digital Audio Effects (DAFx-07), Bordeaux, France, 10–15 September 2007; pp. 10–14.
- Eichas, F.; Fink, M.; Holters, M.; Zölzer, U. Physical Modeling of the MXR Phase 90 Guitar Effect Pedal. In Proceedings of the 17th International Conference on Digital Audio Effects (DAFx-14), Erlangen, Germany, 1–5 September 2014; pp. 153–158.
- Kaizer, A.J. Modeling of the nonlinear response of an electrodynamic loudspeaker by a Volterra series expansion. J. Audio Eng. Soc. 1987, 35, 421–433. [Google Scholar]
- Agerkvist, F.T. Volterra Series Based Distortion Effect. In Proceedings of the AES 120th Convention, San Francisco, CA, USA, 4–7 November 2010.
- Ll-Duwaish, H.; Karim, M.N. A new method for the identification of Hammerstein model. Automatica 1997, 33, 1871–1875. [Google Scholar] [CrossRef]
- Koukoulas, P.; Kalouptsidis, N. Blind identification of second order Hammerstein series. Signal Process. 2003, 83, 213–234. [Google Scholar] [CrossRef]
- Chan, K.H.; Bao, J.; Whiten, W.J. Identification of MIMO Hammerstein systems using cardinal spline functions. J. Process Control 2006, 16, 659–670. [Google Scholar] [CrossRef]
- Hélie, T. Volterra series and state transformation for real-time simulations of audio circuits including saturations: Application to the Moog ladder filter. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 747–759. [Google Scholar] [CrossRef]
- Panicker, T.M.; Mathew, V. Parallel-cascade realizations and approximations of truncated Volterra systems. IEEE Trans. Signal Process. 1998, 46, 2829–2832. [Google Scholar] [CrossRef]
- Ji, W.; Gan, W.S. Identification of a parametric loudspeaker system using an adaptive Volterra filter. Appl. Acoust. 2012, 73, 1251–1262. [Google Scholar] [CrossRef]
- Mirri, D.; Luculano, G.; Filicori, F.; Pasini, G.; Vannini, G.; Gabriella, G.P. A modified Volterra series approach for nonlinear dynamic systems modeling. IEEE Trans. Circuits Syst. I 2002, 49, 1118–1128. [Google Scholar] [CrossRef]
- Novak, A.; Simon, L.; Lotton, P.; Gilbert, J. Chebyshev model and synchronized swept sine method in nonlinear audio effect modeling. In Proceedings of the 13th International Conference on Digital Audio Effects (DAFx-10), Graz, Austria, 6–10 September 2010.
- Oksanen, S.; Välimäki, V. Modeling of the carbon microphone nonlinearity for a vintage telephone sound effect. In Proceedings of the 14th International Conference on Digital Audio Effects (DAFx-11), Paris, France, 19–23 September 2011.
- Bank, B. Computationally Efficient Nonlinear Chebyshev Models Using Common-Pole Parallel Filters with the Application to Loudspeaker Modeling. In Proceedings of the AES 130th Convention, London, UK, 13–16 May 2011.
- Novak, A.; Lotton, P.; Simon, L. Synchronized Swept-Sine: Theory, Application, and Implementation. J. Audio Eng. Soc. 2015, 63, 786–798. [Google Scholar] [CrossRef]
- Farina, A.; Bellini, A.; Armelloni, E. Non-Linear Convolution: A New Approach for the Auralization of Distorting Systems. In Proceedings of the AES 110th Convention, Amsterdam, The Netherlands, 12–15 May 2001.
- Mustonen, M.; Kartofelev, D.; Stulov, A.; Välimäki, V. Experimental verification of pickup nonlinearity. In Proceedings of the International Symposium on Musical Acoustics (ISMA 2014), Le Mans, France, 7–12 July 2014; Volume 1.
- Lotton, P.; Lihoreau, B.; Brasseur, E. Experimental Study of a Guitar Pickup. In Proceedings of the International Symposium on Musical Acoustics (ISMA 2014), Le Mans, France, 7–12 July 2014; Volume 1.
- Novak, A.; Maillou, B.; Lotton, P.; Simon, L. Nonparametric identification of nonlinear systems in series. IEEE Trans. Instrum. Meas. 2014, 63, 2044–2051. [Google Scholar] [CrossRef]
- Woodhouse, J. Plucked guitar transients: Comparison of measurements and synthesis. Acta Acust. 2004, 90, 945–965. [Google Scholar]
- Pàmies-Vilà, M.; Kubilay, I.A.; Kartofelev, D.; Mustonen, M.; Stulov, A.; Välimäki, V. High-speed linecamera measurements of a vibrating string. In Proceedings of the Baltic-Nordic Acoustic Meeting (BNAM), Tallinn, Estonia, 2–4 June 2014; Volume 1.
- Pakarinen, J.; Karjalainen, M. An apparatus for measuring string vibration using electric field sensing. In Proceedings of the Stockholm Music Acoustics Conference, Stockholm, Sweden, 6–9 August 2003; pp. 739–742.
- Kotus, J.; Szczuko, P.; Szczodrak, M.; Czyżewski, A. Application of fast cameras to string vibrations recording. In Proceedings of the IEEE Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznań, Poland, 23–25 September 2015; pp. 104–109.
- Novak, A.; Guadagnin, L.; Lihoreau, B.; Lotton, P.; Brasseur, E.; Simon, L. Non-Linear Identification of an Electric Guitar Pickup. In Proceedings of the 19th International Conference on Digital Audio Effects (DAFx-16), Brno, Czech Republic, 5–9 September 2016.
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).