1. Introduction
Gears and bearings are important components that are commonly used in the rotating machinery parts of trains, ships, and automobile manufacturing, among others. However, gears and bearing are prone to breakdown. Therefore, an unexpected failure may lead to serious project accidents, large economic losses, and even human casualties [
1].
Detecting and diagnosing fault to enhance the safety and reliability of machinery, as well as reduce operation and maintenance costs, are essential and have practical significant because of the effect of unexpected accidents [
2]. Vibration signals can accurately indicate the health conditions of mechanical equipment; hence, these signals are extensively used in fault diagnosis based on artificial methods, such as multinomial logistic regression, wavelet packet transforms (WPT), and support vector machines (SVMs) [
3,
4,
5,
6]. Yuan et al. [
7] selected kurtosis and entropies of the signals as the feature of the input, and put these into the neural network to do fault diagnosis. This work showed that kurtosis and entropies are useful and unique features to classify faults. Jiang et al. [
8] improved SVM, which is included in the fault dictionary category, and proposed a novel approach to diagnose actual analog circuits. Ahcène et al. [
9] used wavelet-packet method to generalize wavelet decomposition for signal analysis. The research showed that the wavelet decomposition was a satisfactory method for analyzing motor faults over load torque or non-stationary signals. Lei et al. [
10] proposed complete ensemble empirical mode decomposition with adaptive noise into application of fault diagnosis in rolling element bearings, where a unique residue was computed after each IMF extraction and used as feature to do diagnosis. Wang et al. [
11] introduced a Bayesian approach based on a linked posterior probability density function of wavelet parameters, and [
12] combined a novel approach to the Gauss–Hermite integration on Bayesian theory to estimate the posterior distribution of wavelet parameters. These signal processing methods based on crucial math analysis are beneficial in feature extraction of fault signals. Shen et al. [
13] presented a model that used empirical mode decomposition (EMD) to select silent features and put these into multi-class transductive SVM (TSVM), thereby obtaining an accuracy of 91.62% in diagnosing the faults of a gear reducer. Feng et al. [
14] proposed a method called Teager energy spectrum to extract the fault induced impulses as features to conduct bearing fault diagnosis, as well as proved the superiority of this method in recognizing transient components in signals and in identifying the characteristic frequency of bearing faults. Cai et al. [
15] introduced a high order spectrum to reconstruct the signals’ power spectrum, and used it to extract fault feature information. This novel method proved to extract more useful feature information than others. The above methods have obtained satisfactory performance. However, some of the methods select features according to the signals statistical properties, such as kurtosis and variance. Sometimes, the researchers also rely on the knowledge about faults, such as the fault characteristic frequency, and extract the related frequency band energy as features, and then establish the relationship between the feature vectors and their labels (fault type or healthy condition). Moreover, the performance of the traditional methods relies heavily on the representability of the features which are usually manually selected.
Nevertheless, the effective diagnosis of the machinery health status based on vibration signals remains a challenge when machinery systems are considerably complex, and sometimes the decision process requires some expertise and signal processing techniques [
16]. Hence, automatically extracting failure features from machine signals without human interference is significant [
17]. Up to date, intelligent methods (e.g., BPNN) have been extensively investigated and used to diagnose faults in rotating machinery [
18,
19]. Liang et al. [
17] combined BPNN with wavelet packet decomposition, where the wavelet packet decomposition coefficients were used to extract eight energy features, and the BPNN was used to do recognition with validation accuracy at 92.5%. Recently, deep-learning methods, such as the DBN–WPT combination, have been determined to overcome the obstacles in fault diagnosis in complex machines [
20,
21,
22]. Deep architectures have been proven to be more effective fault recognition than shallow architecture. However, in these methods, features still need to be selected manually at first and deep models just function as classifiers.
The early vibration signals of gear or bearing fault are often characterized as non-stationary and are well-affected by vibrations from other components in the equipment and transmission path [
23]. This way, the beneficial information of signals is often restricted by other noises or even completely overwhelmed. Obtaining useful information from a signal polluted by noise is essential for effective fault diagnosis methods. However, inadequate denoising or over denoising can distort the original signals, thereby resulting in useless machinery fault diagnosis or reduced recognition rate. Therefore, an efficient denoising technique is required before analyzing the signals for the characteristic fault frequency retrieval. If the components of the signal are known, then optimal filters can be employed for denoising [
24]. Moreover, numerous methods have been developed and applied to the denoising step, such as wavelet transform (WT), ensemble empirical mode decomposition (EEMD), and undecimated discrete wavelet transform (UDWT), among others. Tan et al. [
25] denoised signals with digital wavelet frame (DWF) and performed fault diagnosis based on a stacked autoencoder (SAE). It combined low-level features to form more abstract high-level features to represent data distributed characteristics and obtained accuracy around 99%. Santhana et al. [
26] also proposed a method that combined UDWT and EMD to complete the denoising and diagnosis progress. The UDWT was used to denoise signals and EMD was used to decompose the signals into a number of Intrinsic Mode Functions (IMFs). Even though EMD is an adaptive signal processing method, it suffers from several shortcomings, such as mode-mixing problem that makes analyses of IMFs difficult and empirical. Some fault related signatures may reside in several IMFs, which make the selection/combination of useful IMFs for machine fault feature extraction difficult. Besides, some combinations of the denoising step with the feature extraction and classification step bring more human intervention, such as the base function or other parameters selection affecting the final performance.
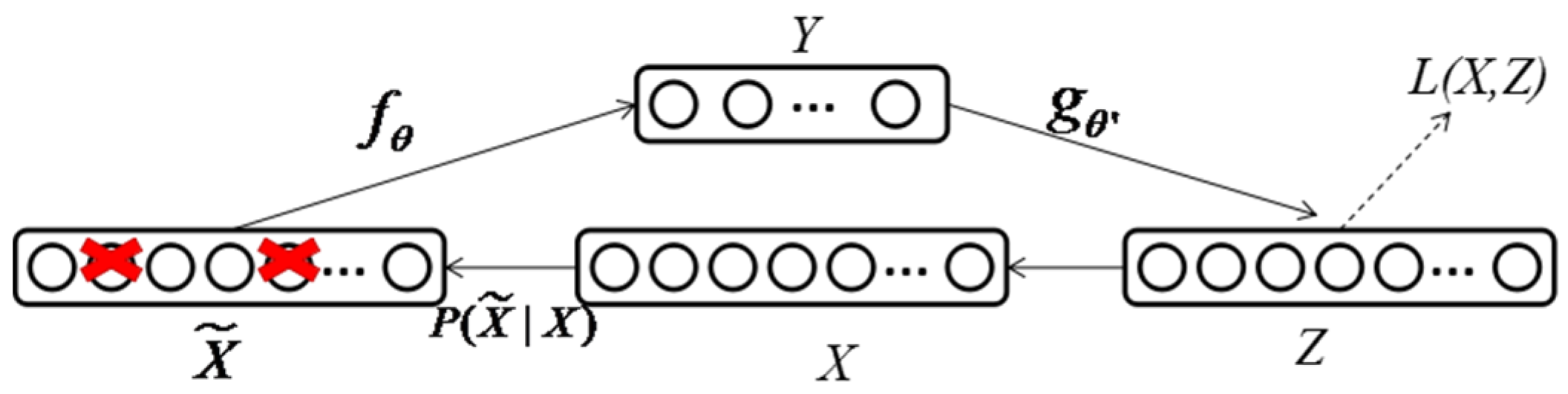
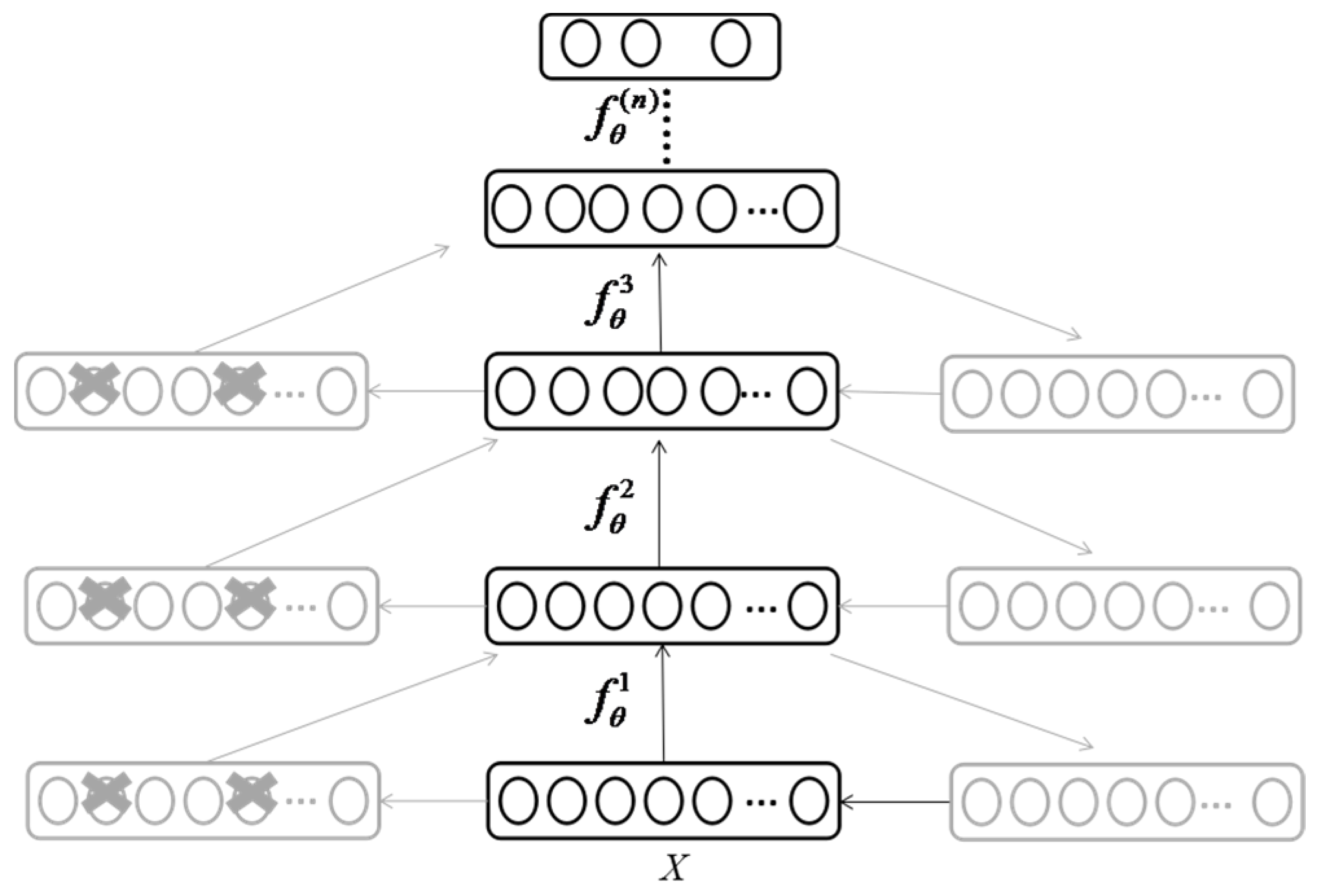
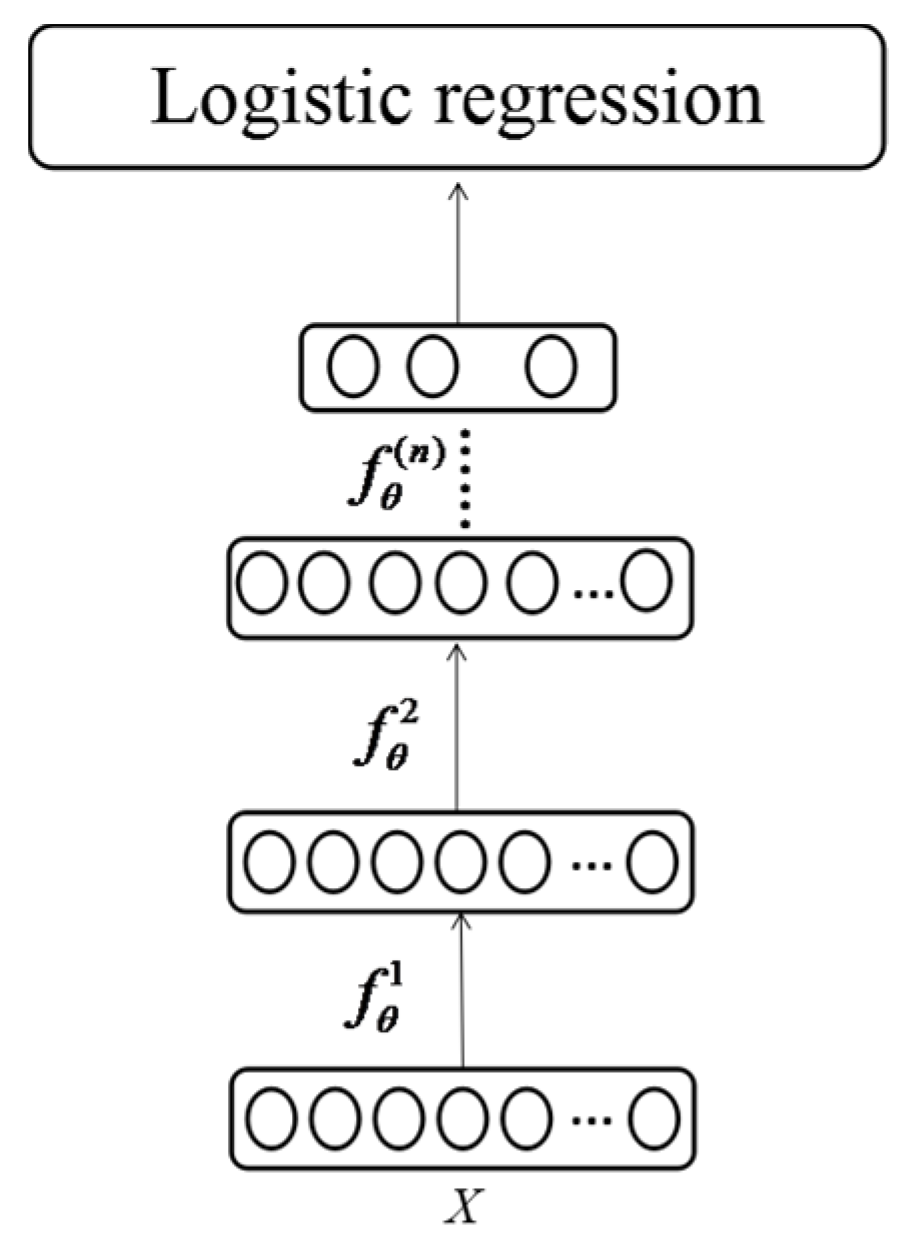
To determine a concise and efficient method that can simultaneously denoise the signals while extracting features, a stacked denoising autoencoder (SDAE) based on a deep network is proposed to construct a fault diagnosis system. SDAE, which was first proposed by Vincent et al., is a stacked neural network comprising several classical denoising autoencoders (DAs) that are trained not to construct their input but rather denoise an artificially corrupted version of their input [
27]. DAs have been previously shown to be competitive to restricted Boltzmann machines, constructive unit of a DBN, and for the unsupervised pre-training of each layer [
28]. Vincent et al. [
29,
30] extended DA with a greedy layer-wise procedure of deep learning algorithm. Pierre et al. [
31] introduced a general mathematical framework for the study of both linear and non-linear autoencoders, thereby enabling the autoencoder to solve additional types of tasks. Thereafter, SDAE has been extensively used in different types of application [
32,
33,
34,
35,
36]. In the field of fault diagnosis, Lin et al. [
37] placed a stacked autoencoder (SAE) into fault diagnosis. However, with an additional independent component analysis (ICA), the diagnosis system became unintelligent and complicated. Natarajan et al. [
38] used DWT to select features as well as denoise the signals in the first step, and put the features into artificial neural network (ANN) to do classification. Wavelet Daubechies-6 was selected for processing 49 signal samples per condition in their work. It is important to select a proper wavelet mother function which should be highly similar to impulses generated by a bearing or gear defect, and to determine a wavelet decomposition level/depth for retaining the resonant frequency band excited by the defect. In general, the performance of DWT processing relies on the selection of wavelet mother function and the depth of wavelet decomposition to obtain the representative features. On the other hand, a proper classifier construction is also needed for the extracted DWT features. The current study proposes a deep-learning-based fault diagnosis method. Accordingly, a deep fault recognizer based on SDAE is used to deal with the random noises of the original signals and extract features to simultaneously perform fault pattern recognition. The SDAE is an integral model, in which the weights of the feature selection part are updated based on the final output every iteration. The proposed method has been empirically shown to avoid obtaining poor convergence, which is typically reached with random initialization [
39]. In addition, the experiment manifests that the SDAE method obtains superior diagnosis performance compared to the DBN methods, particularly in the existing situation of noises.
The remainder of this paper is organized as follows.
Section 2 details the methodology of the traditional SDAE.
Section 3 provides details of the structure and the algorithm of the proposed SDAE based diagnosis system.
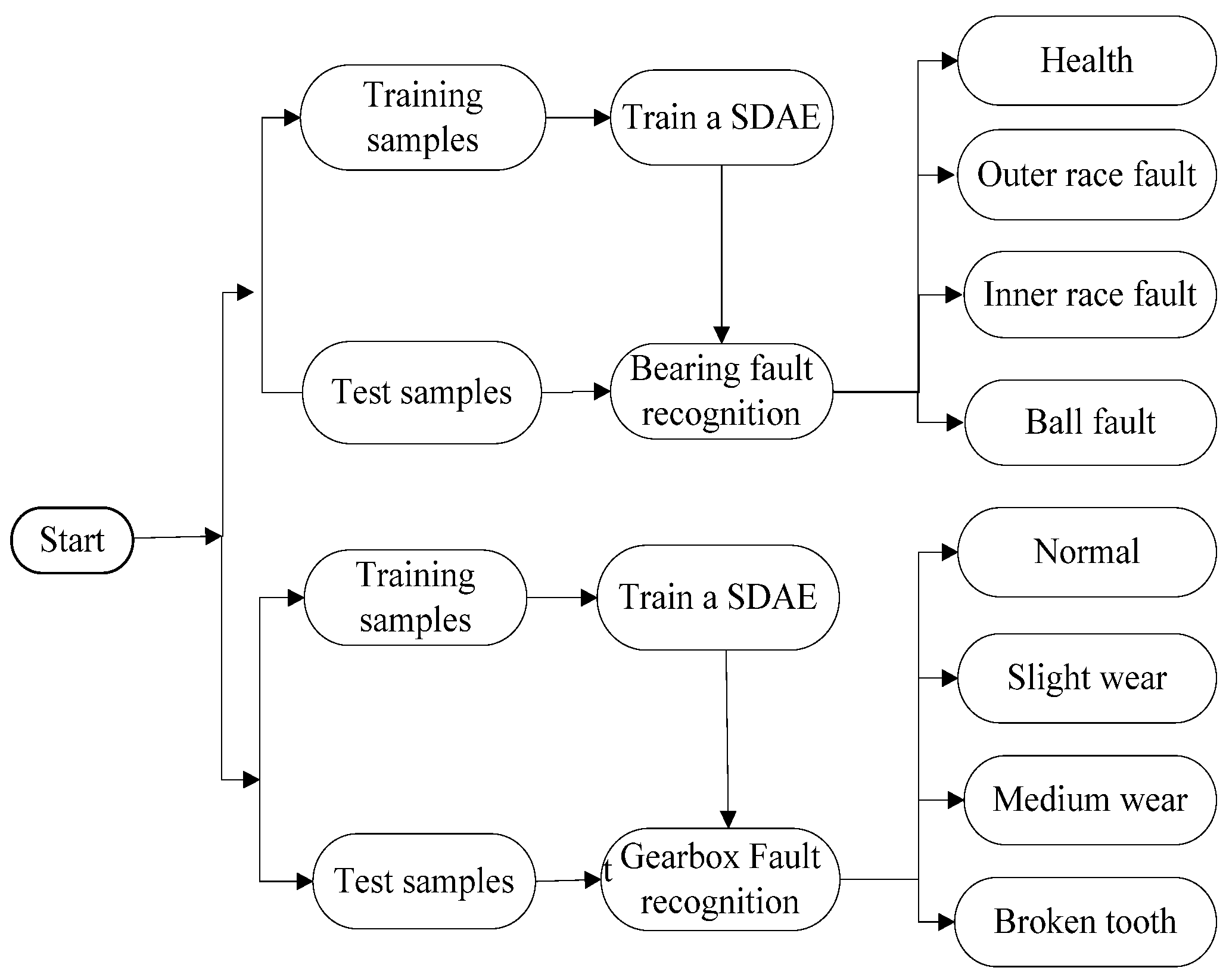
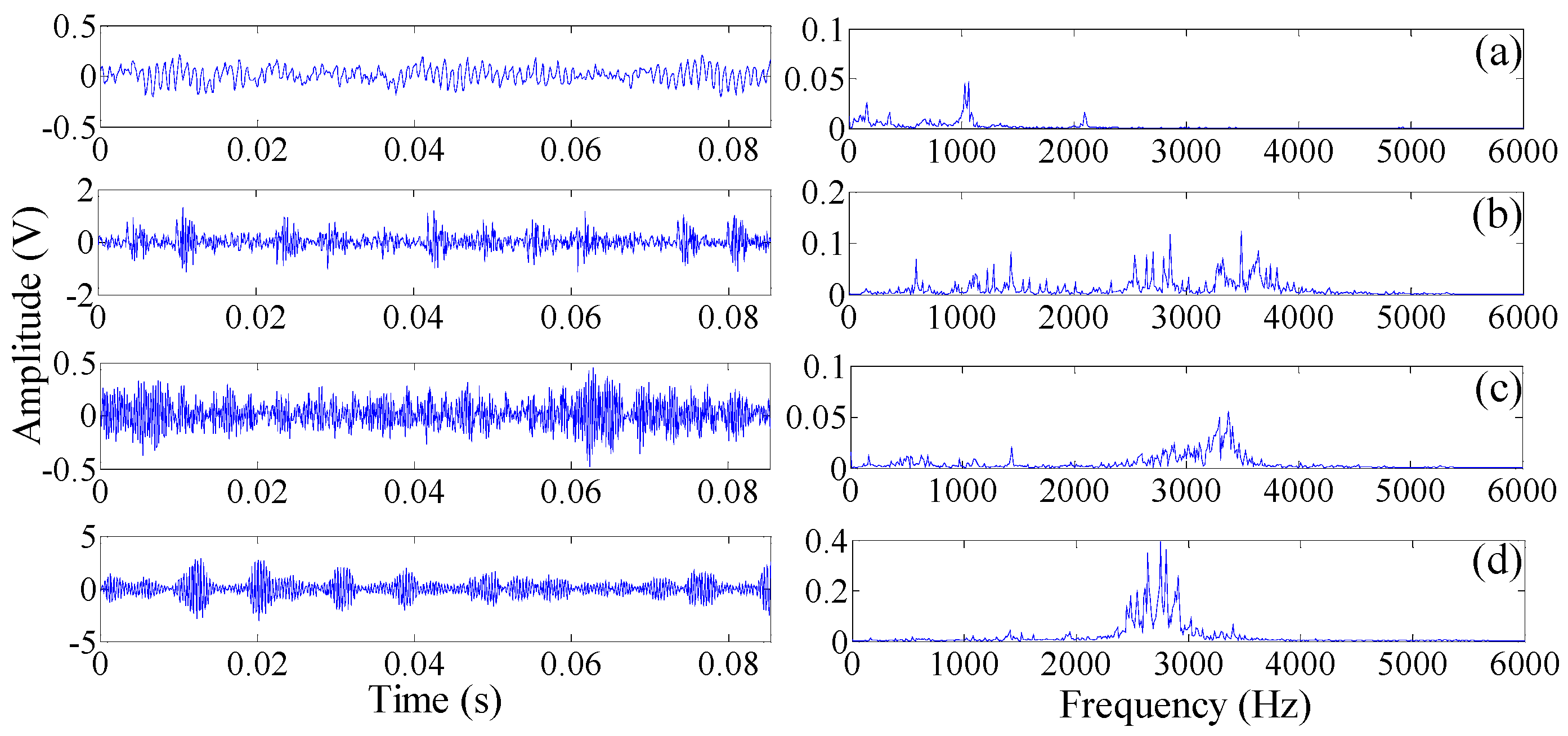
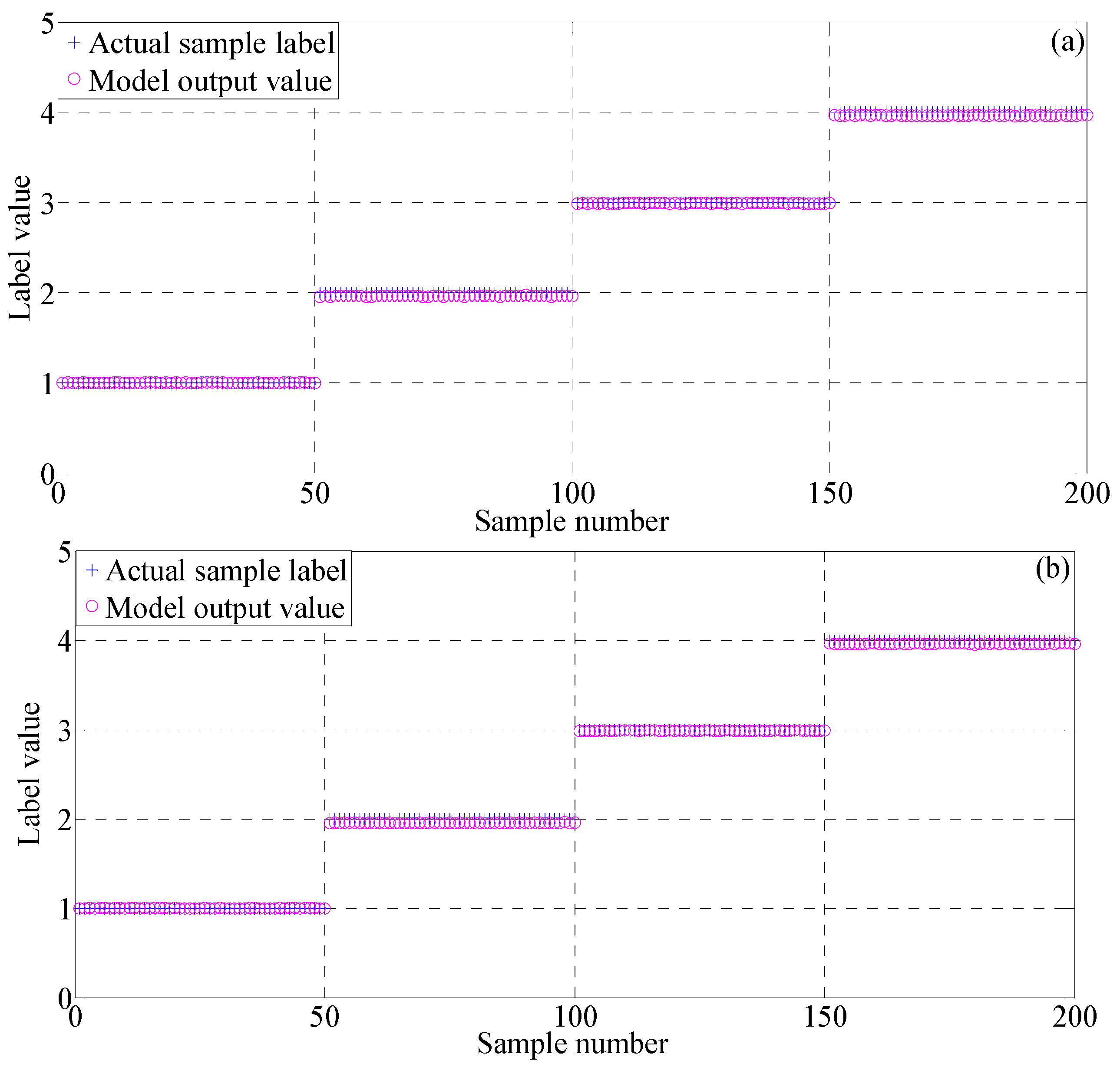
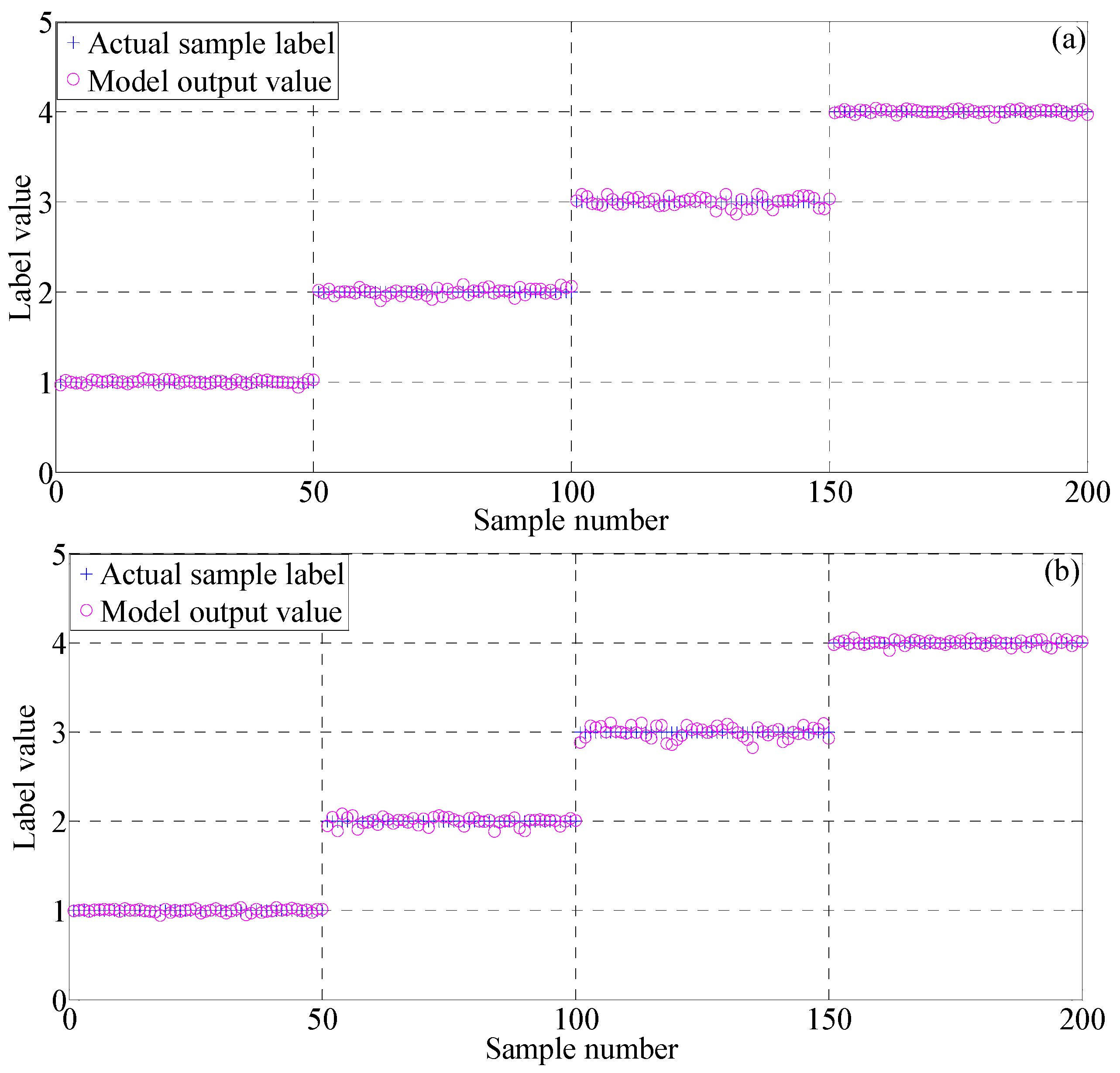
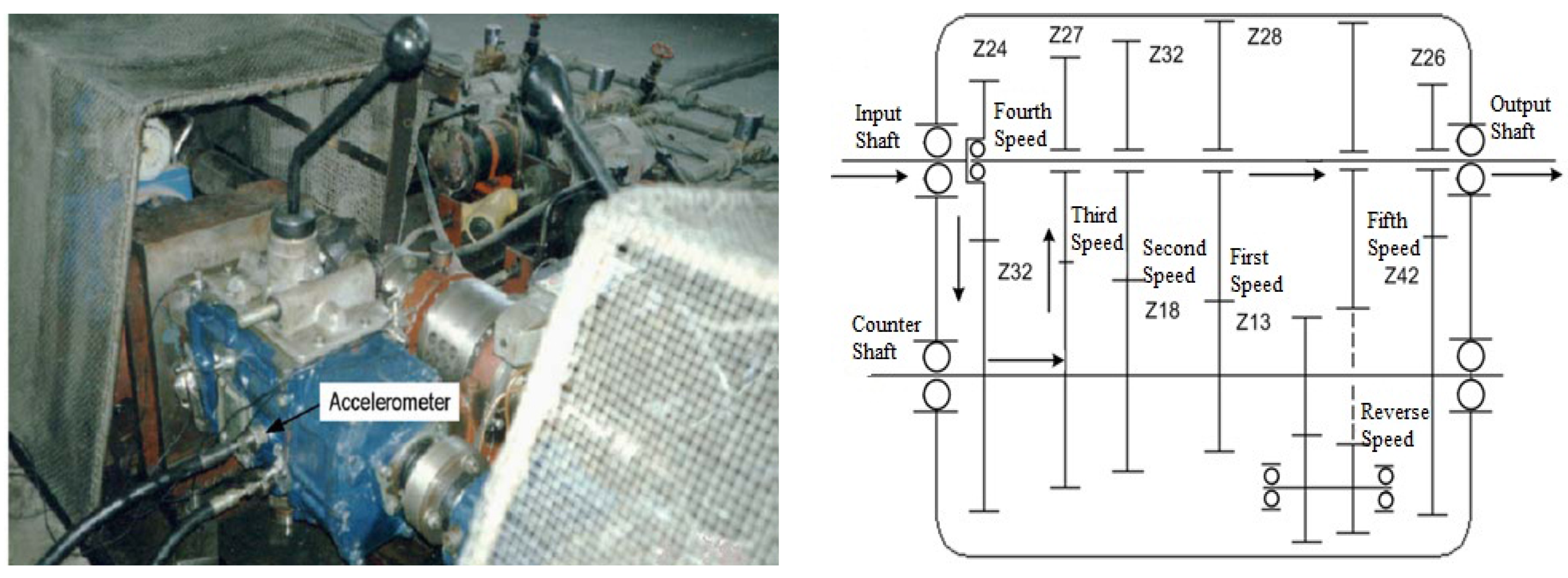
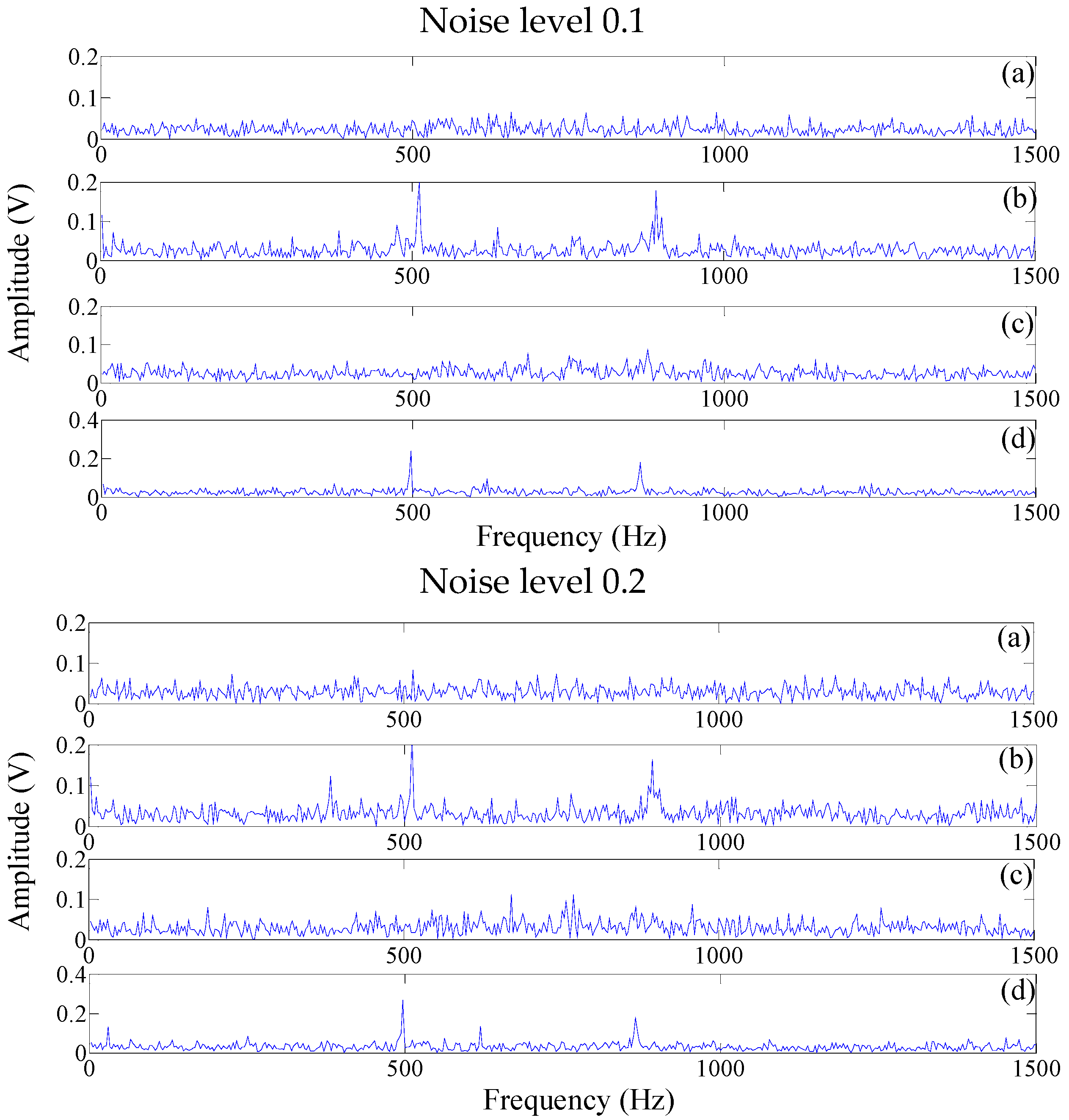
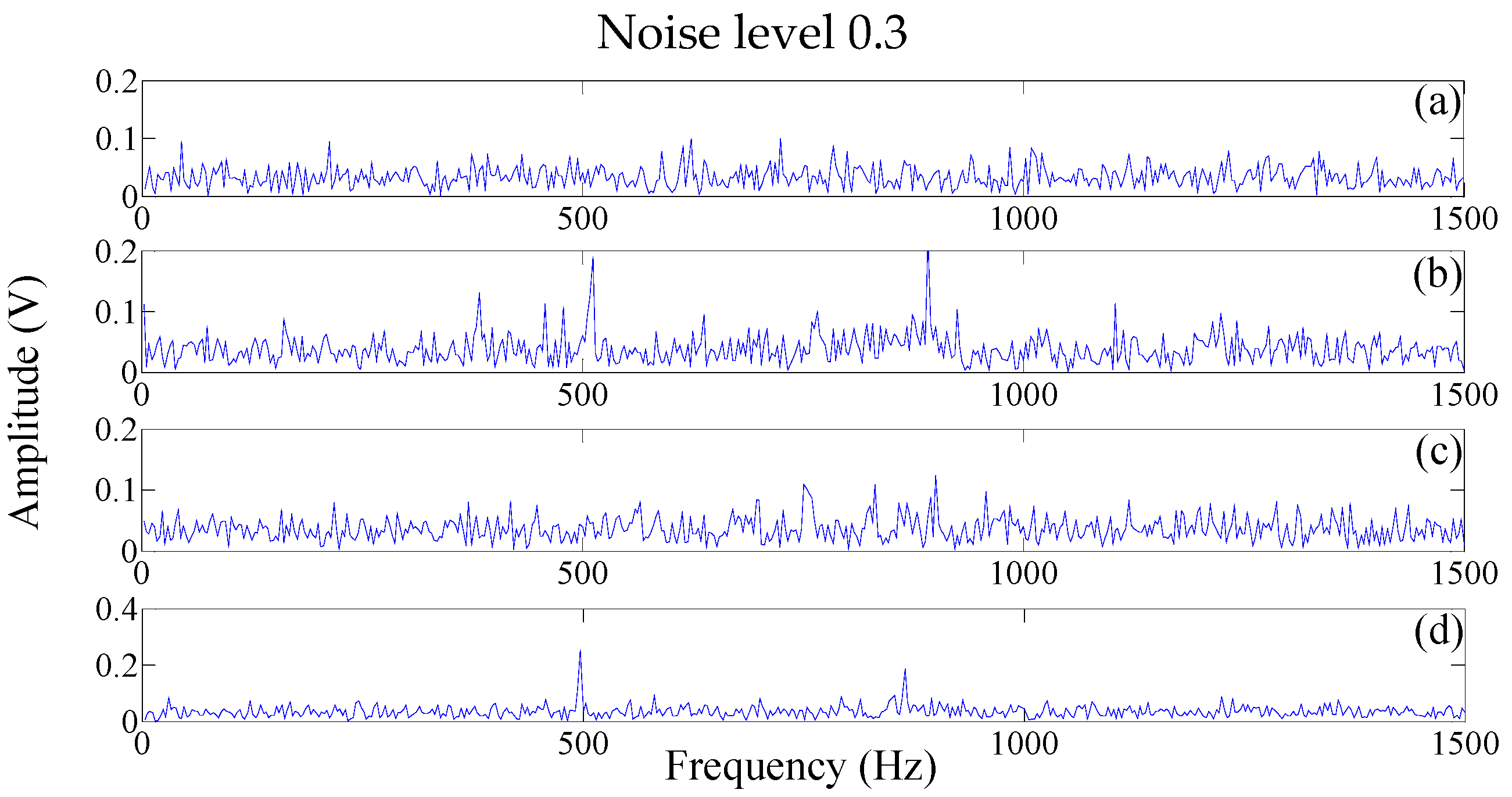
Section 4 validates the effectiveness of the SDAE method on rolling bearing datasets and gearbox dataset. Moreover, this section further tested the advantage of the proposed method through a comparative study between DBN and SDAE on both original datasets, as well as the dataset mixed with artificially white noises. Finally,
Section 5 presents the conclusion.