Strength Correlation and Prediction of Engineered Cementitious Composites with Microwave Properties
Abstract
:1. Introduction
2. Methodologies
2.1. PVA-ECC Specimen Mix Design
2.2. Microwave Near-Field Detecting Technique
2.2.1. Preparation of ECC Specimens for Microwave Measurement
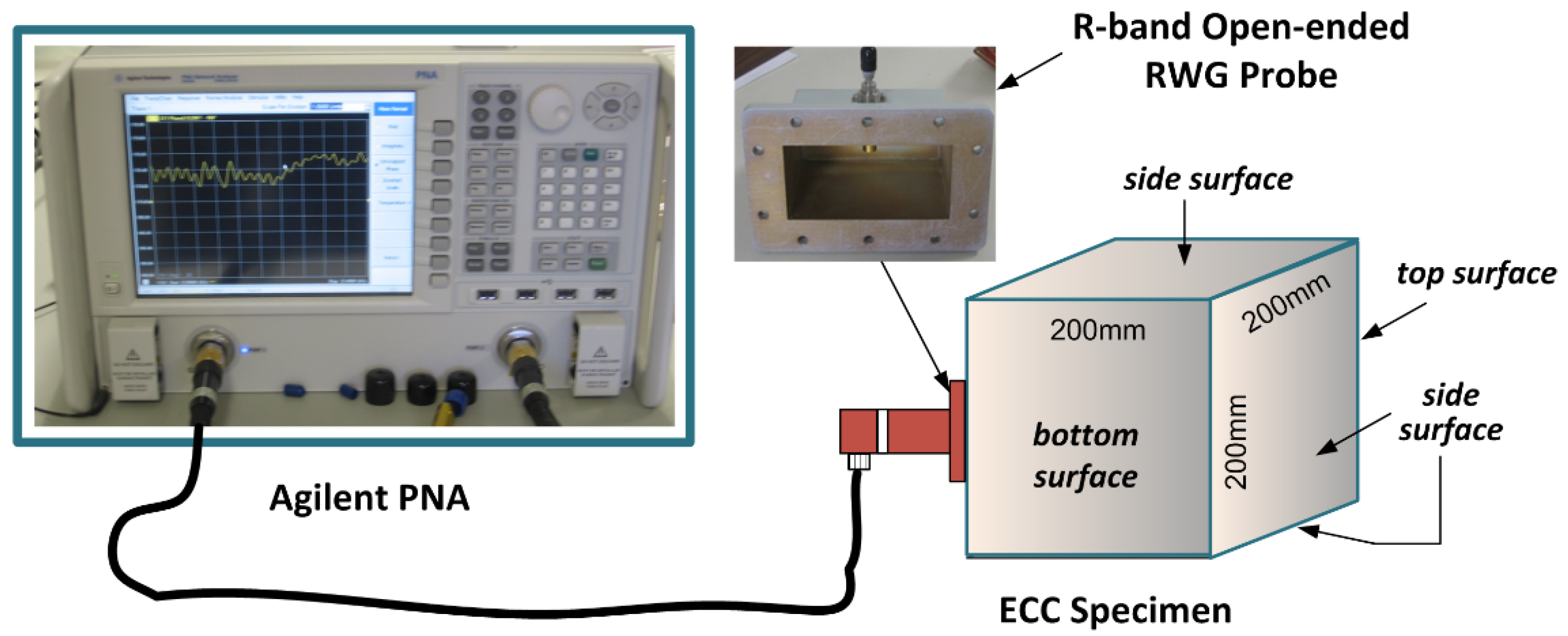
2.2.2. Microwave Measurement Setup
2.2.3. Measurement Techniques
2.3. Mechanical Destructive Compression Test
2.3.1. Preparation of ECC Specimens for Compression Test
2.3.2. Compressive Strength Measurement
3. Experimental Measurements and Results
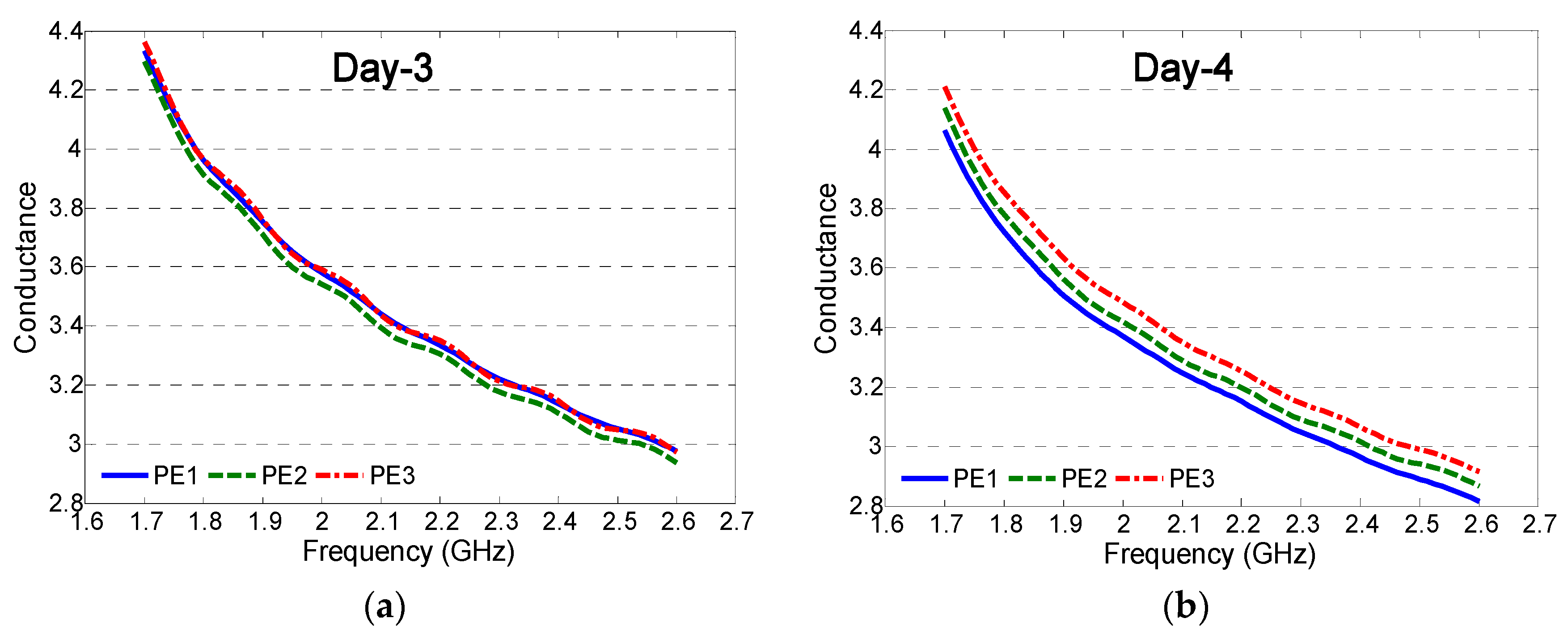
3.1. Electrical Conductance Measurement from Early-Age ECCs
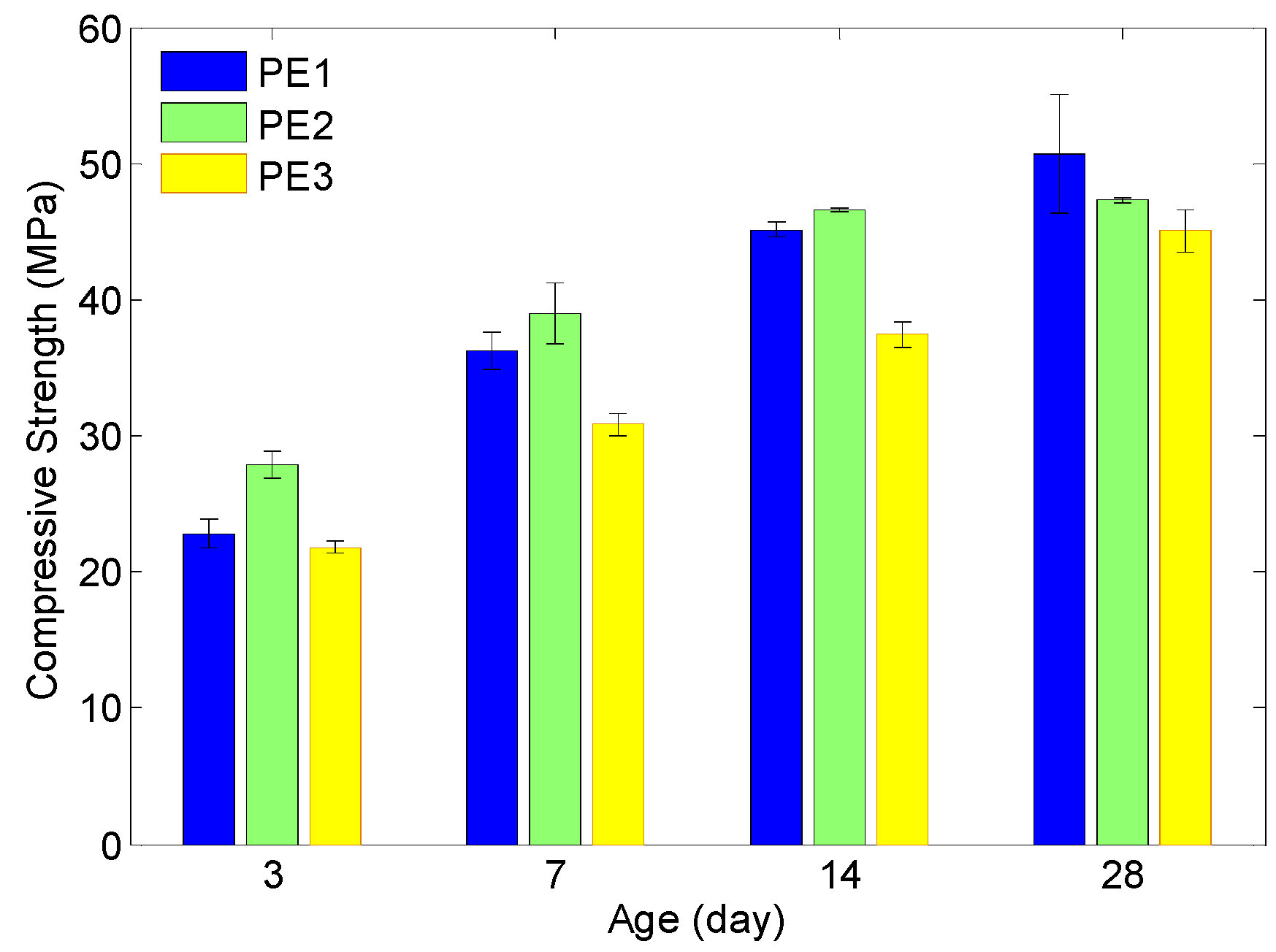
3.2. Mechanical Compression Test Results
4. Mathematical Modelling of Experimental Results
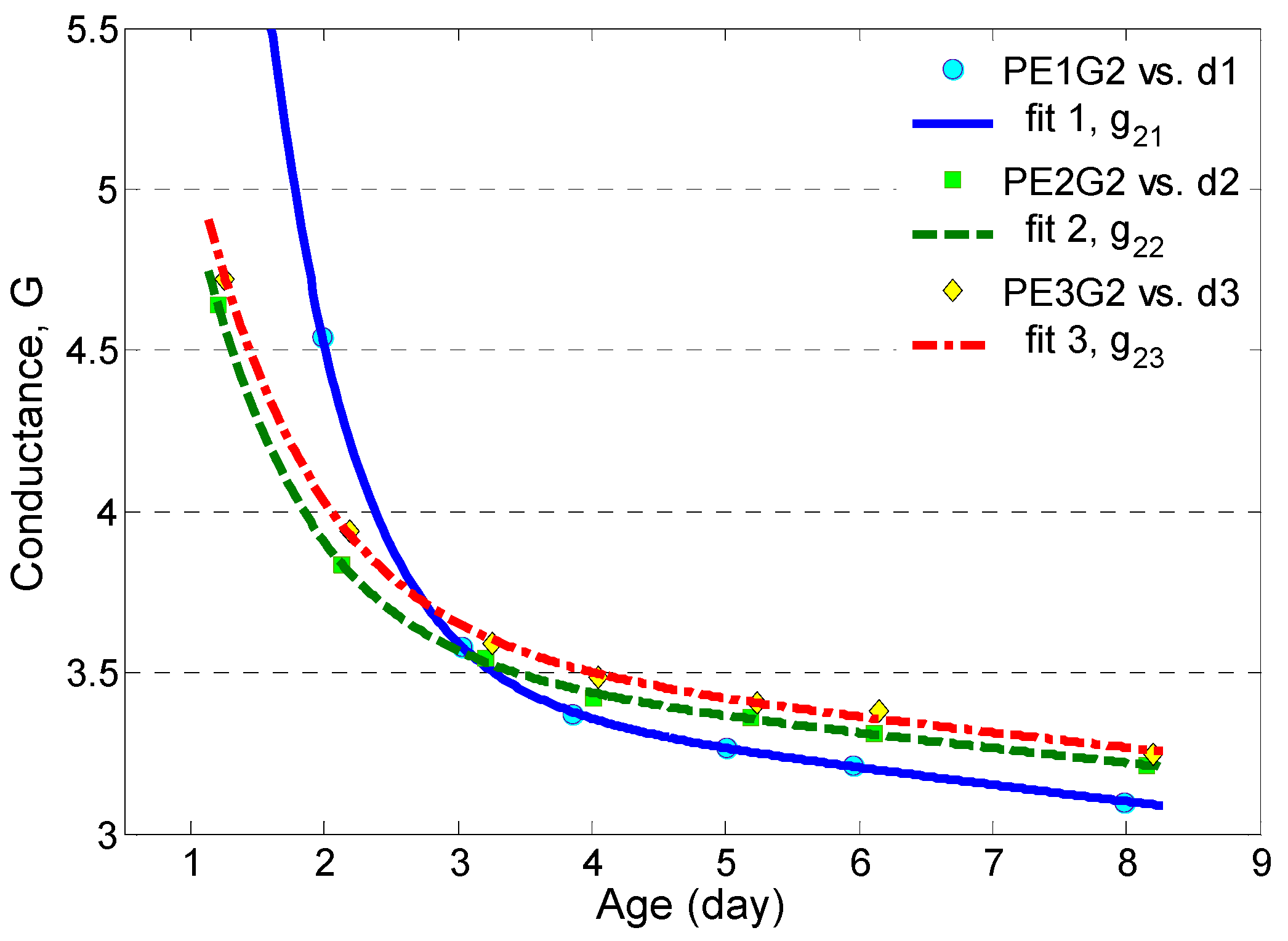
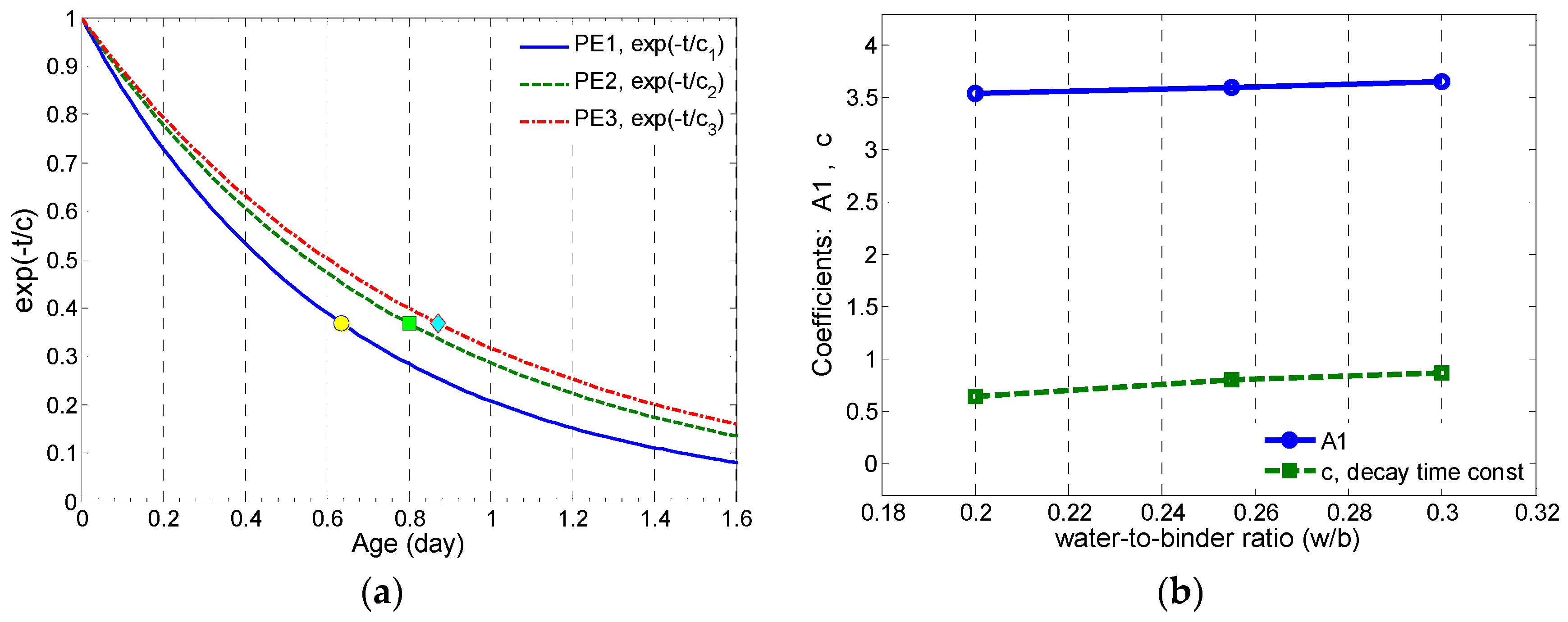
4.1. Microwave Conductance Modelled by Bi-Exponential Regressions
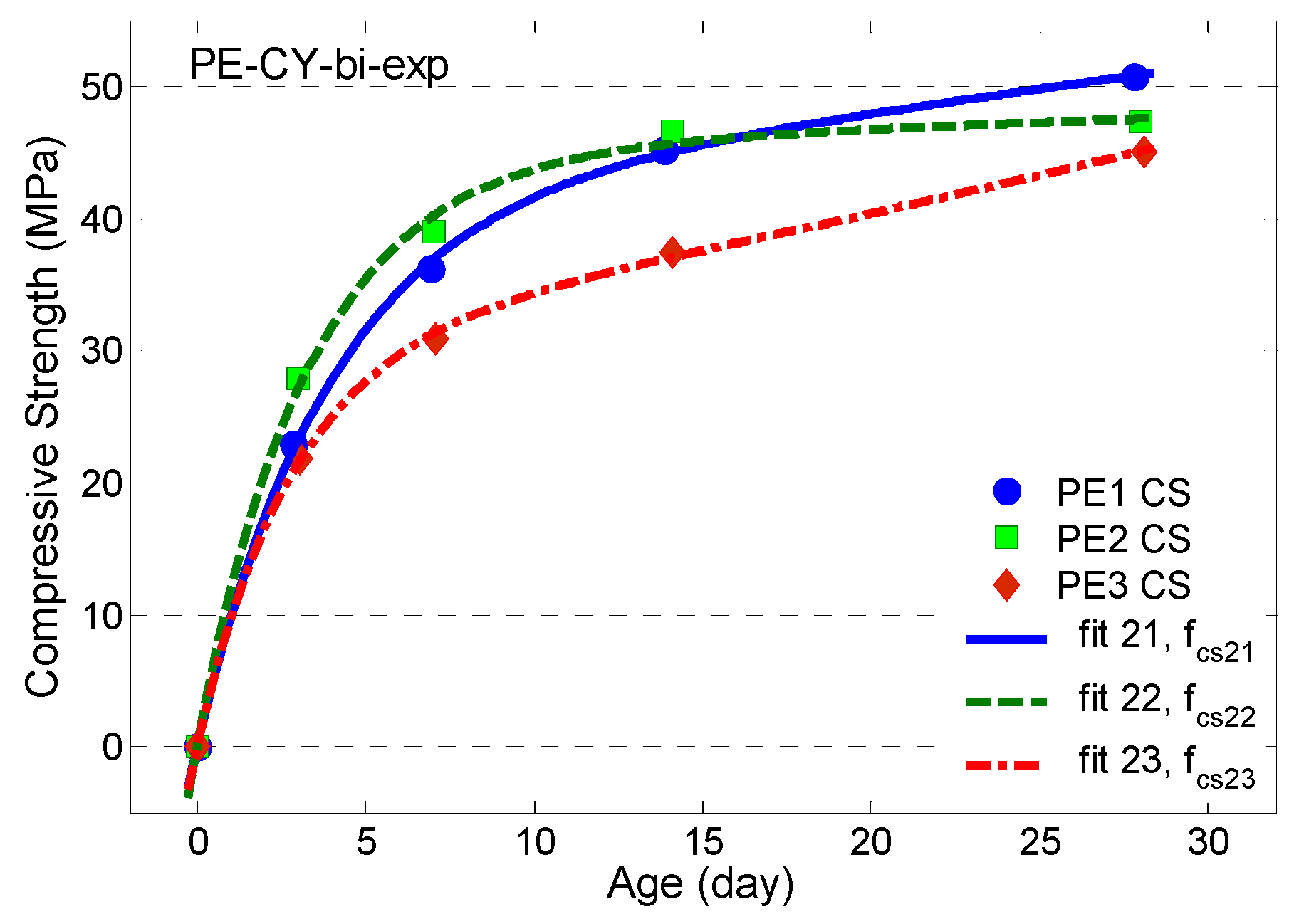
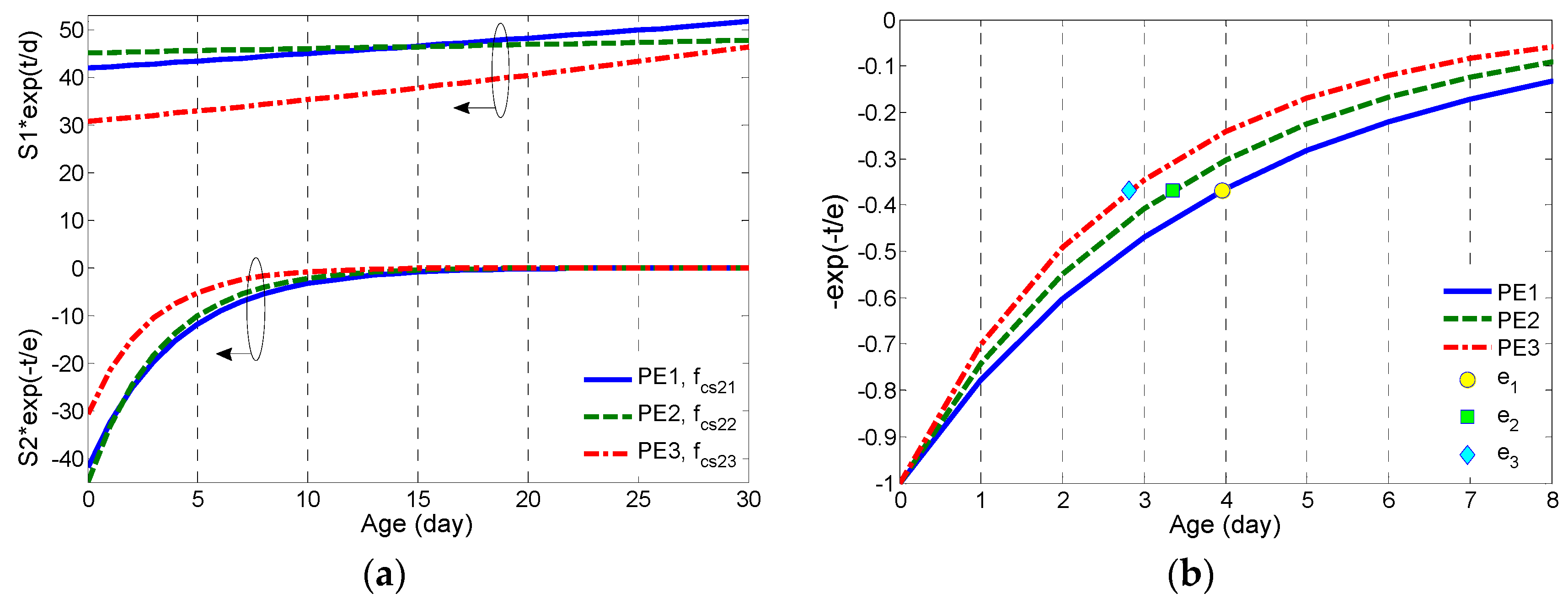
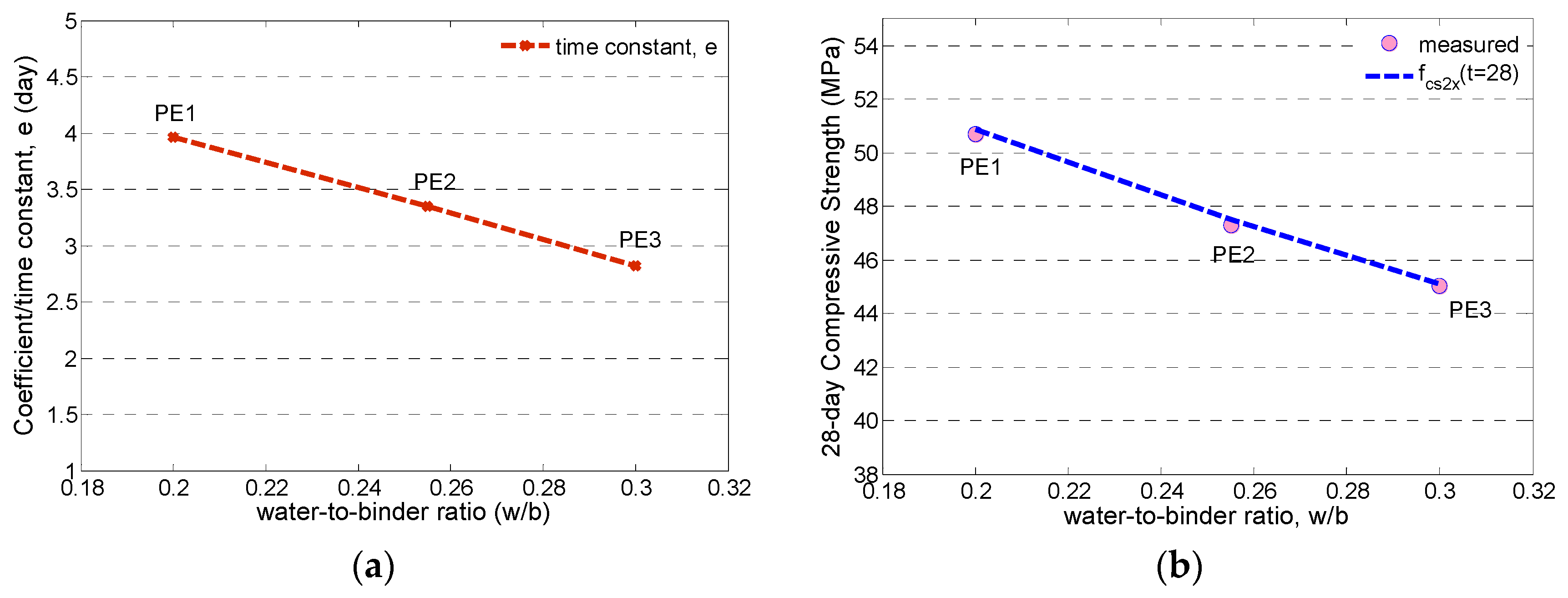
4.2. Compressive Strength Modelled by using Bi-Exponential Regressions
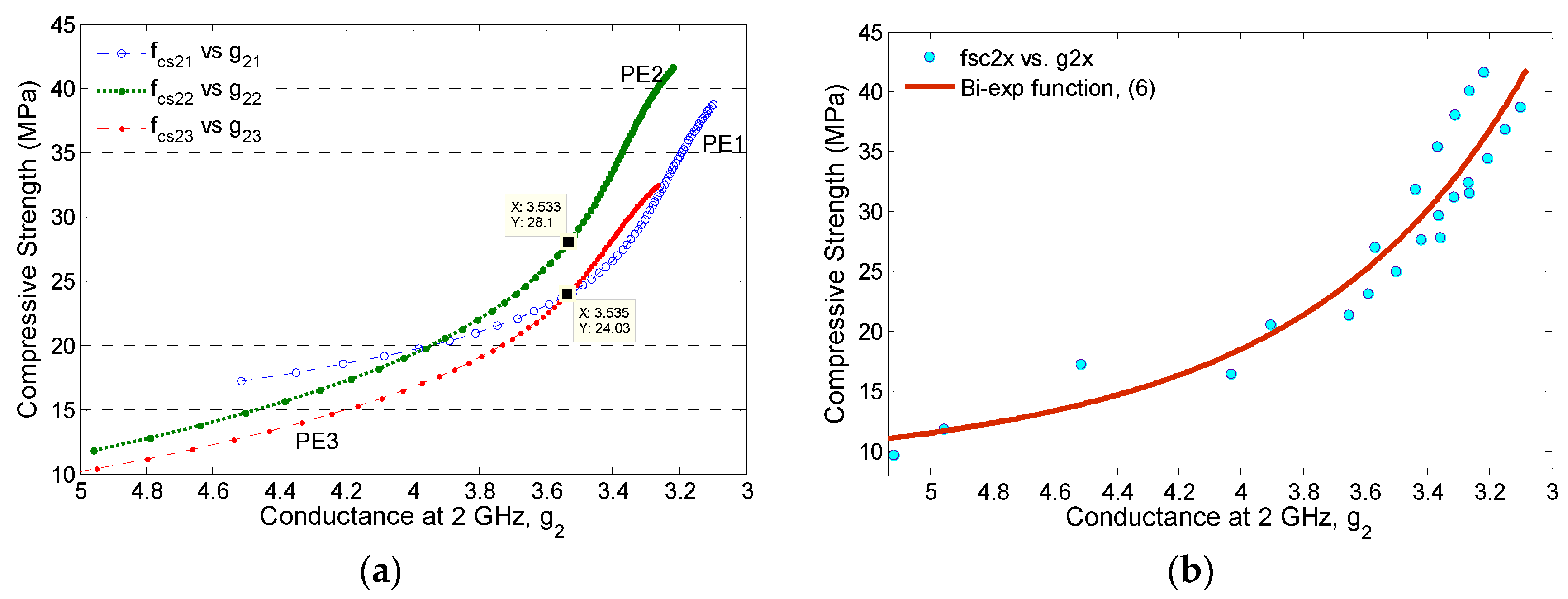
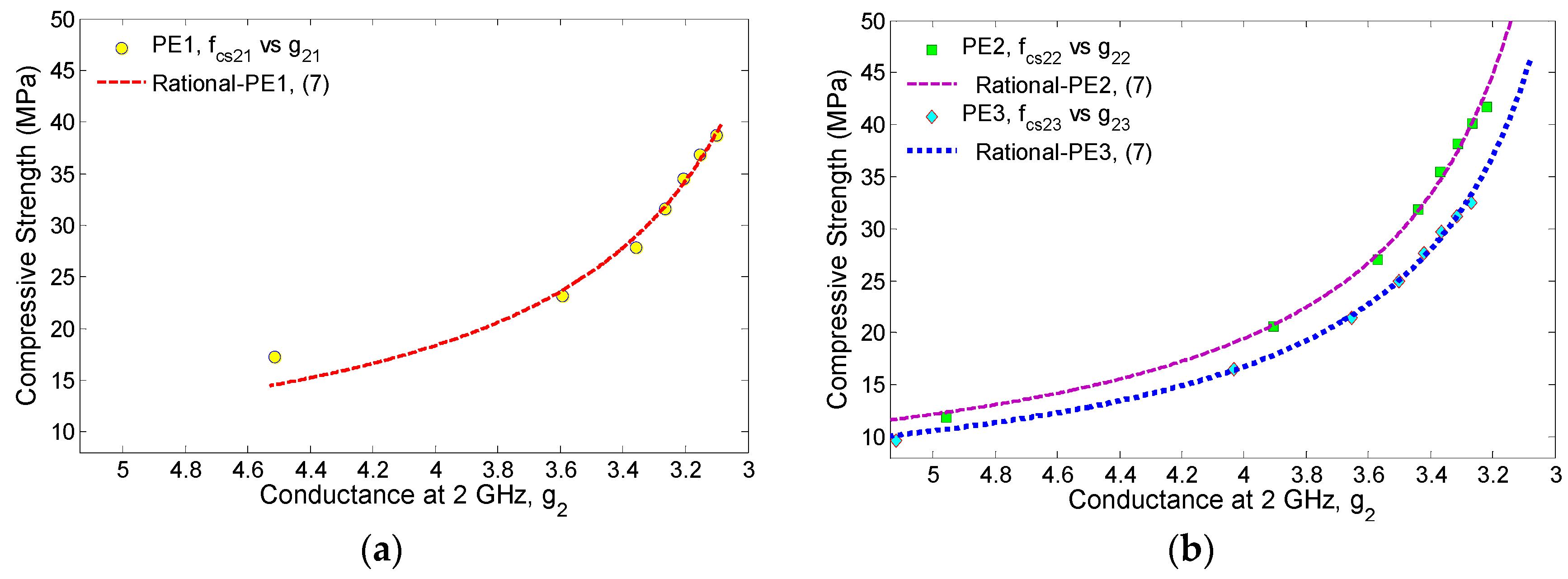
4.3. Correlations between Compressive Strength and Conductance
5. Conclusions
- The decay of conductance at 2 GHz is modelled by using the bi-exponential regression function (4), where the time-constant of the rapid decay term increases as a function of increasing w/b.
- The growth of compressive strength of ECC specimens till 28 days is found to be best fitted by using bi-exponential function (5). The time constant of the rapid growing term decreases as a function of increasing w/b.
- ECC specimens have the general trend—strength develops as a function of decreasing effective conductance. This produced the ability of the microwave technique in monitoring the variation of the liquid phase morphology and pore structure.
- When considering the ECC specimens with similar w/b ratios in the range of 0.20–0.30, a generic model is developed in a bi-exponential form for all ECC specimens as a whole, as given in (6).
- An accurate correlation model for strength–conductance is developed by including w/b as the dependent variable. The rational correlation model effectively emulates the nonlinear evolution of compressive strength with decreasing conductance. Moreover, the two coefficients K and m increase as a linear function of increasing w/b. This makes in situ nondestructive strength predicting and monitoring feasible for concrete infrastructure.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Z.J. Advanced Concrete Technology; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Roller, J.J.; Russell, H.G.; Bruce, R.N.; Hassett, B. Effect of curing temperatures on high strength concrete bridge girders. PCI J. 2003, 48, 72–79. [Google Scholar] [CrossRef]
- Sun, Z.; Voigt, T.; Shah, S.P. Temperature effects on strength evaluation of cement-based materials with ultrasonic wave reflection technique. ACI Mater. J. 2005, 102, 272–278. [Google Scholar]
- Demirboga, R.; Turkmen, I.; Karakoc, M.B. Relationship between ultrasonic velocity and compressive strength for high-volume mineral-admixtured concrete. Cem. Concr. Res. 2004, 34, 2329–2336. [Google Scholar] [CrossRef]
- Gu, H.; Song, G.B.; Dhonde, H.; Mo, Y.L.; Yan, S. Concrete early-age strength monitoring using embedded piezoelectric transducers. Smart Mater. Struct. 2006, 15, 1837–1845. [Google Scholar] [CrossRef]
- Kong, Q.; Feng, Q.; Song, G. Water presence detection in a concrete crack using smart aggregates. Int. J. Smart Nano Mater. 2015, 6, 149–161. [Google Scholar] [CrossRef]
- Qin, L.; Li, Z. Monitoring of cement hydration using embedded piezoelectric transducers. Smart Mater. Struct. 2008, 17, 055005. [Google Scholar] [CrossRef]
- Wang, N.; Shi, Z.; Xiang, H.; Song, G. Modeling on energy harvesting from a railway system using piezoelectric transducers. Smart Mater. Struct. 2015, 24, 105017. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Gallego, A.; Vico, J.M. An acoustic emission energy index for damage evaluation of reinforced concrete slabs under seismic loads. Struct. Health Monit. 2011, 11, 69–81. [Google Scholar] [CrossRef]
- Sagasta, F.; Benavent-Climent, A.; Roldan, A.; Gallego, A. Correlation of plastic strain energy and acoustic emission energy in reinforced concrete structures. Appl. Sci. 2016, 6, 84–98. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, T.; Ma, H.; Li, Z. Monitoring setting and hardening of concrete by active acoustic method: effects of water-to-cement ratio and pozzolanic materials. Constr. Build. Mater. 2015, 88, 118–125. [Google Scholar] [CrossRef]
- McCarter, W.J.; Chrisp, T.M.; Starrs, G.; Blewett, J. Characterization and monitoring of cement-based systems using intrinsic electrical property measurements. Cem. Concr. Res. 2003, 33, 197–206. [Google Scholar] [CrossRef]
- Ferreira, R.M.; Jalali, S. NDT measurements for the prediction of 28-day compressive strength. NDT&E Intern. 2010, 43, 55–61. [Google Scholar]
- Xiao, L.; Li, Z. Early-age hydration of fresh concrete monitored by non-contact electrical resistivity measurement. Cem. Concr. Res. 2008, 38, 312–319. [Google Scholar] [CrossRef]
- Wei, X.; Xiao, L.; Li, Z. Prediction of standard compressive strength of cement by the electrical resistivity measurement. Constr. Build. Mater. 2012, 31, 341–346. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, J.; Li, Z. Study on hydration process of early-age concrete using embedded active acoustic and non-contact complex resistivity methods. Constr. Build. Mater. 2013, 46, 183–192. [Google Scholar] [CrossRef]
- Martinelli, E.; Koenders, E.A.B.; Caggiano, A. A numerical recipe for modelling hydration and heat flow in hardening concrete. Cem. Concr. Compos. 2013, 40, 48–58. [Google Scholar] [CrossRef]
- Bourdi, T.; Rhazi, J.E.; Boone, F.; Ballivy, G. Modelling dielectric-constant values of concrete: An aid to shielding effectiveness prediction and ground-penetrating radar wave technique interpretation. J. Phys. D Appl. Phys. 2012, 45, 405401. [Google Scholar] [CrossRef]
- Buyukozturk, O. Electromagnetic properties of concrete and their significance in nondestructive testing. J. Transp. Res. Board 1997, 1574, 10–17. [Google Scholar] [CrossRef]
- Zoughi, R.; Gray, S.D.; Nowak, P.S. Microwave nondestructive estimation of cement paste compressive strength. ACI Mater. J. 1995, 92, 64–70. [Google Scholar]
- Bois, K.J.; Benally, A.D.; Nowak, P.S.; Zoughi, R. Cure-state monitoring and w/c ratio determination of fresh Portland cement-based materials using near field microwave techniques. IEEE Trans. Instrum. Meas. 1999, 47, 628–637. [Google Scholar] [CrossRef]
- Chung, K.L.; Kharkovsky, S. Monitoring of microwave properties of early-age concrete and mortar specimens. IEEE Trans Instrum. Meas. 2015, 64, 1196–1203. [Google Scholar] [CrossRef]
- Rizzo, P.; Nasrollahi, A.; Deng, W.; Vandenbossche, J.M. Detecting the presence of high water-to-cement ratio in concrete surfaces using highly nonlinear solitary waves. Appl. Sci. 2016, 6, 104–119. [Google Scholar] [CrossRef]
- Li, V.C.; Wu, C.; Wang, S.; Saito, T. Interface tailoring for strain-hardening PVA-ECC. ACI Mater. J. 2002, 99, 463–472. [Google Scholar]
- Li, V.C. Tailoring ECC for special attributes: A Review. J. Concr. Struct. Mater. 2012, 6, 135–144. [Google Scholar] [CrossRef]
- Lim, Y.M.; Li, V.C. Durable repair of aged infrastructures using trapping mechanism of engineered cementitious composites. Cem. Concr. Compos. 1997, 19, 373–385. [Google Scholar] [CrossRef]
- Sobolev, K.; Tabatabai, H.; Zhao, J.; Flores-Vivian, I.; Muzenski, S.; Oliva, M.G.; Rose, J. Superhydrophobic Engineered Cementitious Composites for Highway Bridge Applications: Technology Transfer and Implementation. CFIRE 06-03. National Center for Freight & Infrastructure Research & Education, University of Wisconsin-Madison, 2013. Available online: www.wistrans.org/cfire/ documents/FR_CFIRE0603.pdf (accessed on 18 December 2016).
- Li, X.; Li, M.; Song, G. Energy-dissipating and self-repairing SMA-ECC composites material system. Smart Mater. Struct. 2015, 24, 025024. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, S.; Ye, G.; Copuroglu, O.; Breugel, K.; Li, V.C. Improved fiber distribution and mechanical properities of engineered cementitious composites by adjusting the mixing sequence. Cem. Concr. Compos. 2012, 34, 342–348. [Google Scholar] [CrossRef]
- Agilent Technologies. Specifying Calibration Standards and Kits for Agilent Vector Network Analyzers; Application Note 1287-11; Agilent Technologies, Inc.: Santa Clara, CA, USA, 2010. [Google Scholar]
- Standards Australia. AS-1012.9. Methods of Testing Concrete—Determination of the Compressive Strength of Concrete Specimens; Standards Australia: Sydney, Australia, 2014. [Google Scholar]
- ASTM International. ASTM-C39/C39M-15a. Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- EN1992–1-1. Eurocode 2: Design of Concrete Structures. Part 1–1: General Rules and Rules for Buildings. 2004. Available online: https://law.resource.org/pub/eu/eurocode/en.1992.1.1.2004.pdf (accessed on 18 December 2016).


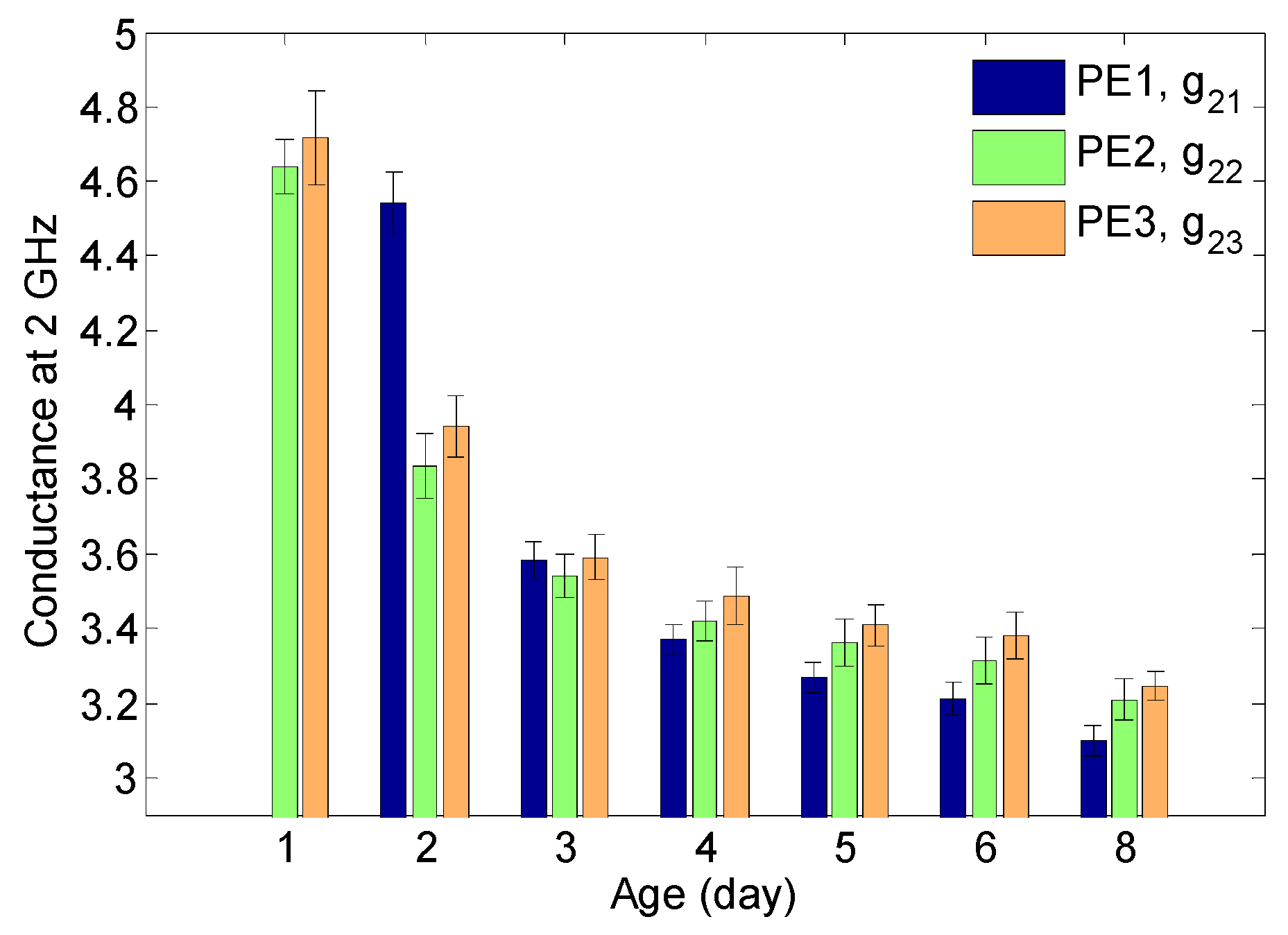
| Fiber | Diameter (µm) | Length (mm) | Tensile Strength (MPa) | Flexural Strength (GPa) | Specific Gravity | Shape | Color |
|---|---|---|---|---|---|---|---|
| PVA | 38 | 8 | 1600 | 40 | 1.3 | straight | white |
| Specimen | Cement | Fly Ash | Sand | Water | w/b | s/b | HRWR | PVA (% Vol) |
|---|---|---|---|---|---|---|---|---|
| PE1 | 1 | 1.2 | 0.8 | 0.440 | 0.200 | 0.364 | 0.028 | 2 |
| PE2(ECC-M45) | 1 | 1.2 | 0.8 | 0.560 | 0.255 | 0.364 | 0.022 | 2 |
| PE3 | 1 | 1.2 | 0.8 | 0.660 | 0.300 | 0.364 | 0.012 | 2 |
| Constituent | PC | FS | FA-F |
|---|---|---|---|
| CaO | 58.1 | - | - |
| SiO2 | 24.7 | 95.6 | 76.3 |
| Al2O3 | 6.4 | 1.9 | 20.2 |
| SO3 | 3.5 | 0.3 | - |
| MgO | 2.4 | - | - |
| FeO | 2.2 | 0.3 | 0.4 |
| TiO2 | - | 0.9 | 0.9 |
| K2O | 0.5 | - | 0.4 |
| LOI | 2.2 | 1.0 | 1.8 |
| Total | 100 | 100 | 100 |
| 2 GHz | w/b | A1 | b | A2 | c | R2 |
|---|---|---|---|---|---|---|
| PE1 (g2,1) | 0.200 | 3.535 | 60.96 | 25.44 | 0.6358 | 0.9999 |
| PE2 (g2,2) | 0.255 | 3.601 | 71.43 | 4.913 | 0.8003 | 0.9997 |
| PE3 (g2,3) | 0.300 | 3.649 | 72.32 | 4.794 | 0.8708 | 0.9993 |
| ECC | w/b | S1 | S2 | d | e | R2 |
|---|---|---|---|---|---|---|
| PE1 (fc1) | 0.200 | 41.9 | −41.82 | 143.947 | 3.960 | 0.9998 |
| PE2 (fc2) | 0.255 | 45.1 | −44.94 | 534.759 | 3.347 | 0.9980 |
| PE3 (fc3) | 0.300 | 30.68 | −30.63 | 72.727 | 2.820 | 0.9996 |
| ECC | w/b | K | m | R2 |
|---|---|---|---|---|
| PE1 (fc1) | 0.200 | 2.274 | 1.196 | 0.9814 |
| PE2 (fc2) | 0.255 | 2.710 | 1.285 | 0.9953 |
| PE3 (fc3) | 0.300 | 3.008 | 1.336 | 0.9979 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, K.L.; Luo, J.; Yuan, L.; Zhang, C.; Qu, C. Strength Correlation and Prediction of Engineered Cementitious Composites with Microwave Properties. Appl. Sci. 2017, 7, 35. https://doi.org/10.3390/app7010035
Chung KL, Luo J, Yuan L, Zhang C, Qu C. Strength Correlation and Prediction of Engineered Cementitious Composites with Microwave Properties. Applied Sciences. 2017; 7(1):35. https://doi.org/10.3390/app7010035
Chicago/Turabian StyleChung, Kwok L., Jianlin Luo, Lei Yuan, Chunwei Zhang, and Chengping Qu. 2017. "Strength Correlation and Prediction of Engineered Cementitious Composites with Microwave Properties" Applied Sciences 7, no. 1: 35. https://doi.org/10.3390/app7010035
APA StyleChung, K. L., Luo, J., Yuan, L., Zhang, C., & Qu, C. (2017). Strength Correlation and Prediction of Engineered Cementitious Composites with Microwave Properties. Applied Sciences, 7(1), 35. https://doi.org/10.3390/app7010035








