A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation
Abstract
:1. Introduction
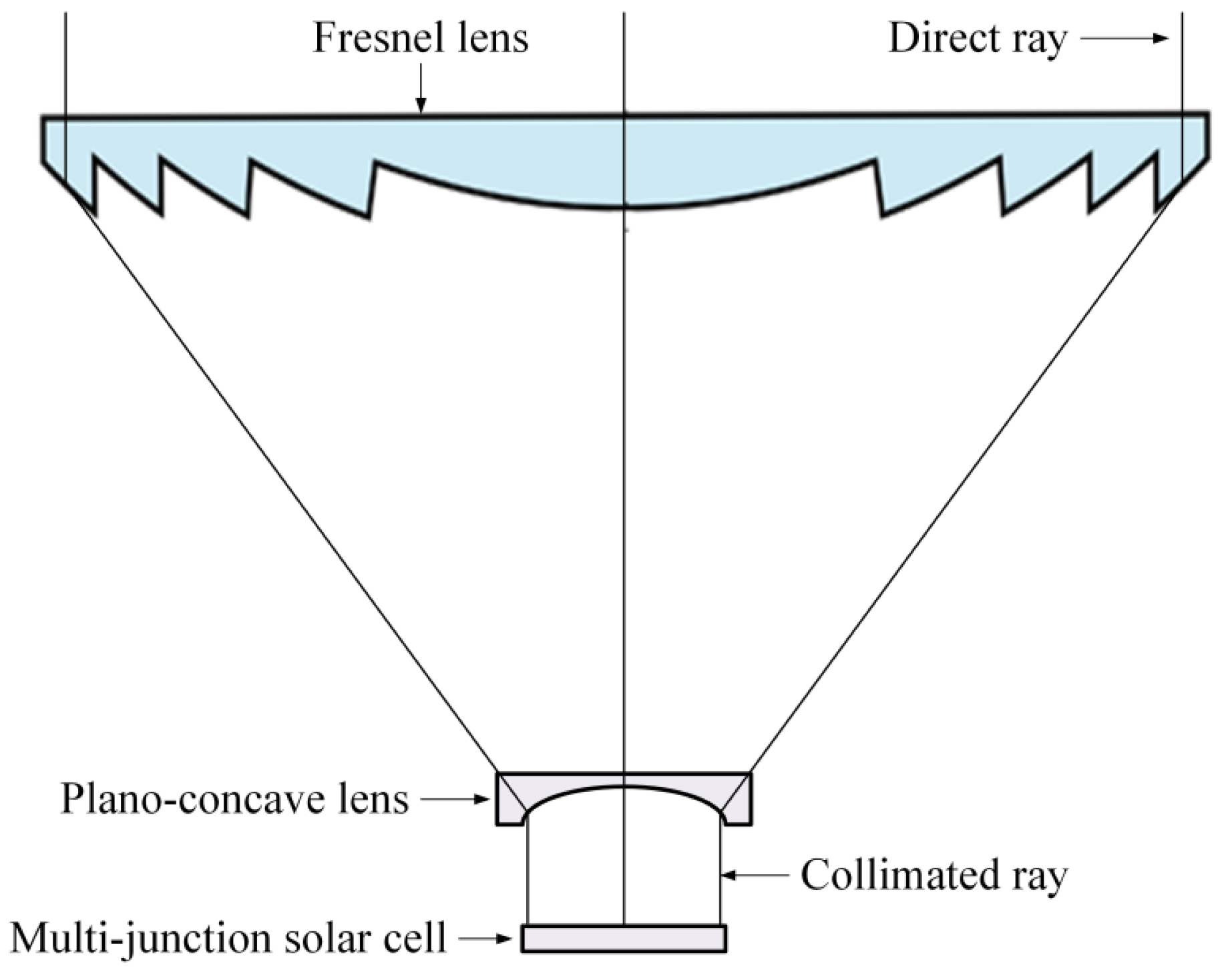
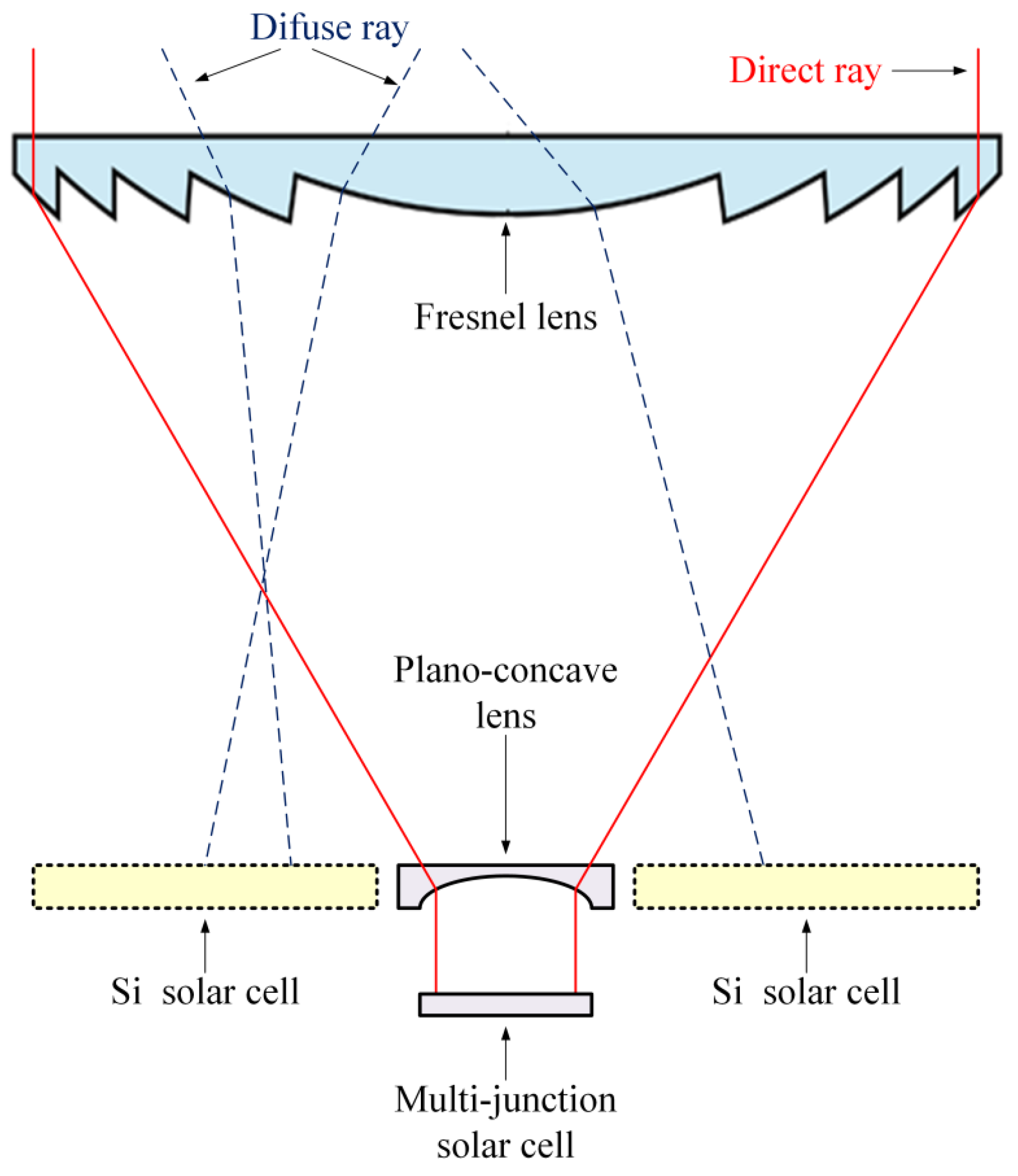
2. The Proposed CPV System
2.1. Improving Irradiance Uniformity
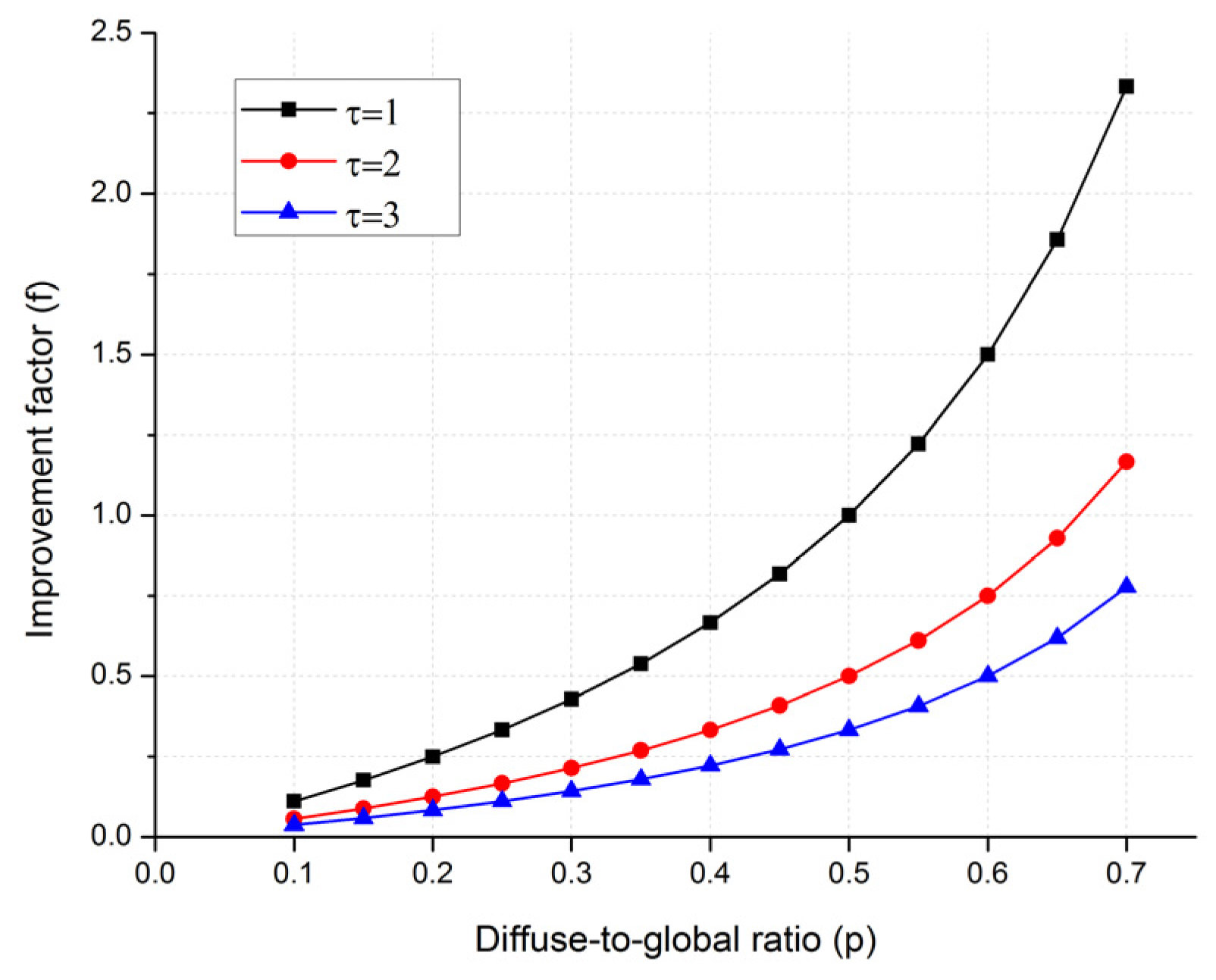
2.2. Capturing Diffuse Solar Radiation
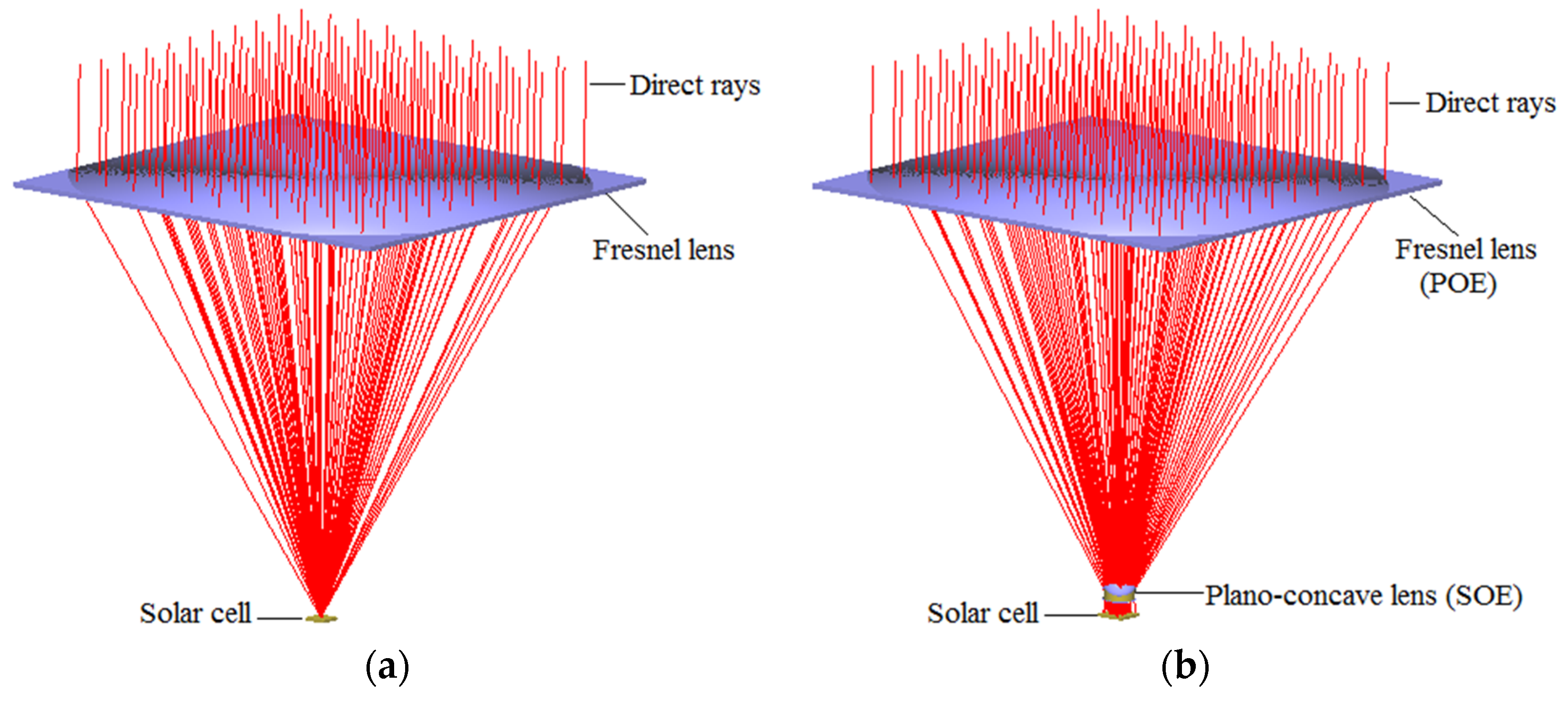
3. Performance Analysis and Simulations
3.1. Irradiance Uniformity vs. Optical Loss
3.1.1. Irradiance Uniformity
3.1.2. Optical Loss
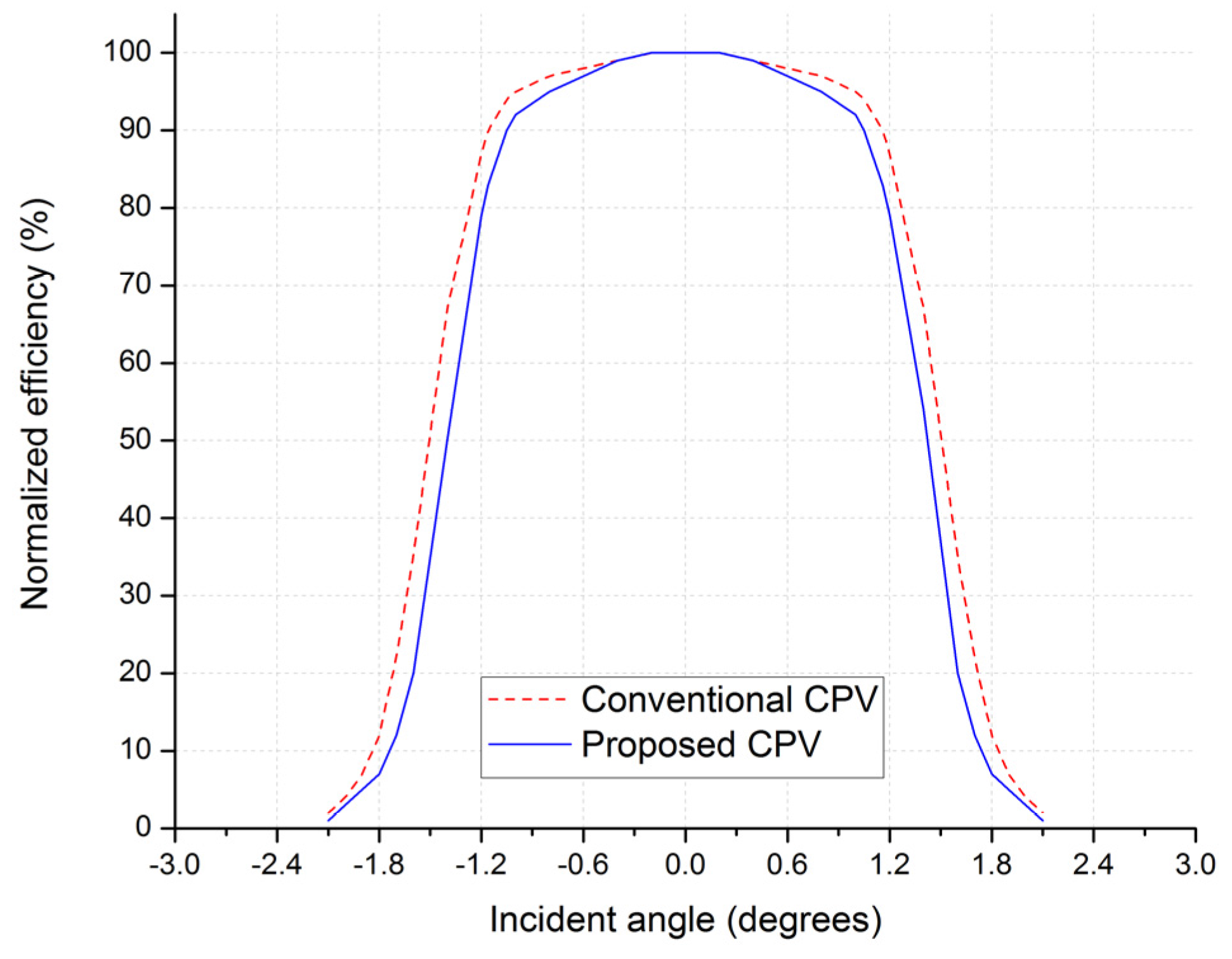
3.1.3. Acceptance Angle
3.1.4. Discussion
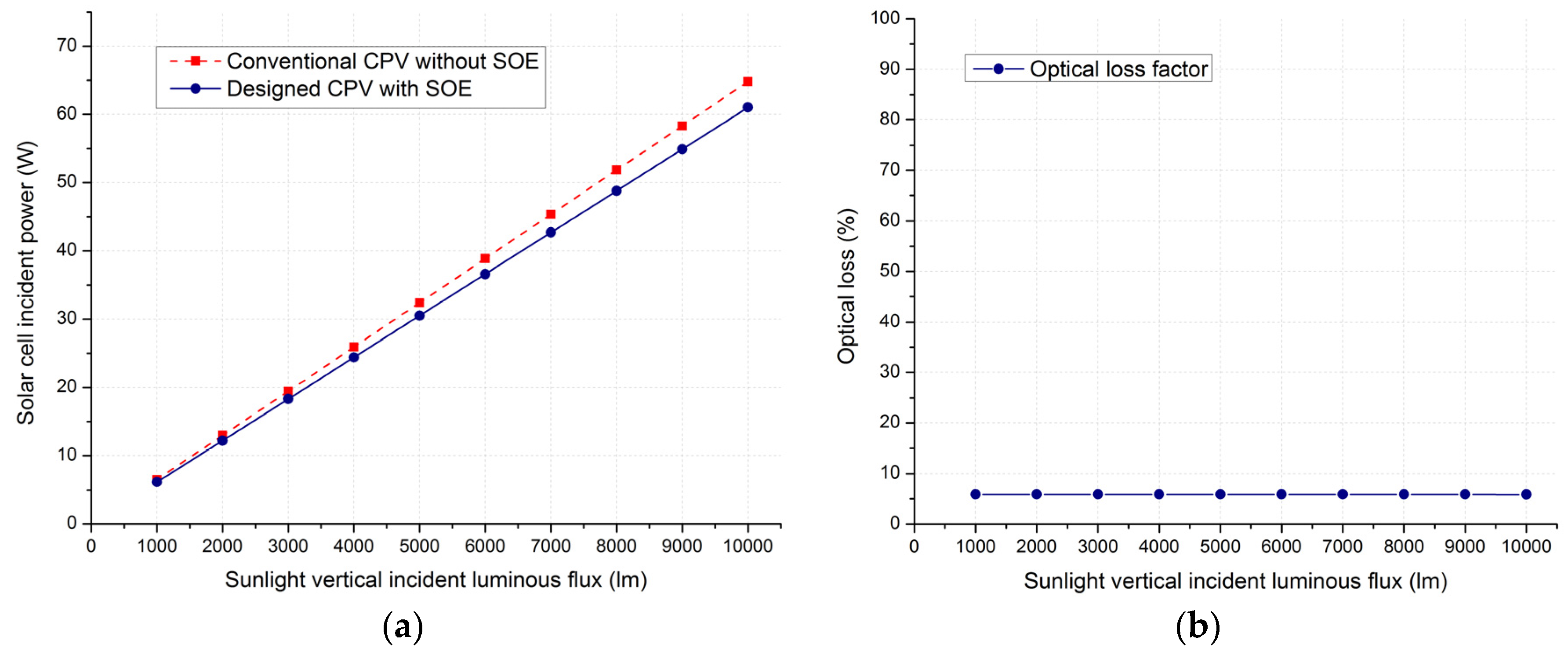
3.2. System Efficiency
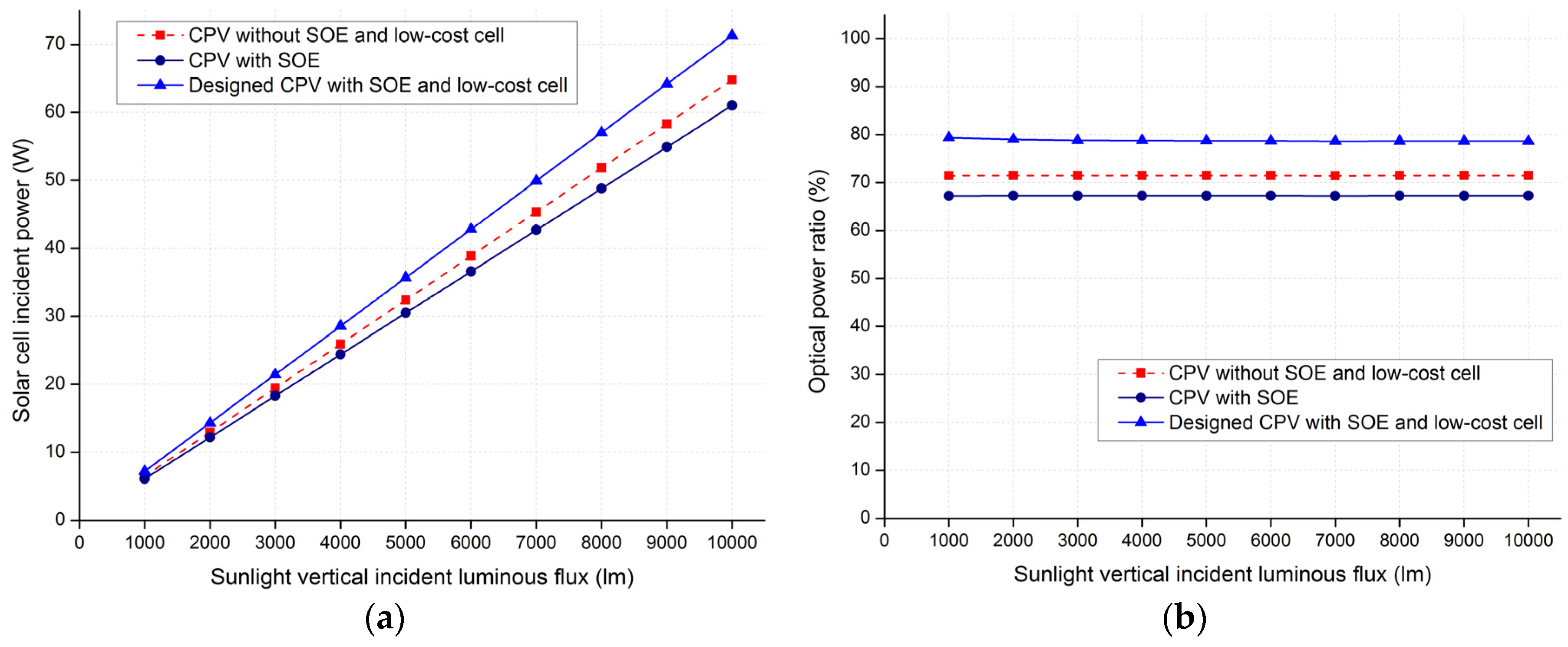
3.2.1. Optical Power Ratio
3.2.2. System Conversion Efficiency
3.2.3. System Cost
3.2.4. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems, 2nd ed.; Academic Press: Millbrae, CA, USA, 2014. [Google Scholar]
- Baig, H.; Heasman, K.C.; Mallick, T.K. Non-uniform illumination in concentrating solar cells. Renew. Sustain. Energy Rev. 2012, 15, 5890–5909. [Google Scholar] [CrossRef]
- Xie, W.T.; Dai, Y.J.; Wang, R.Z.; Sumathy, K. Concentrated solar energy applications using Fresnel lenses: A review. Renew. Sustain. Energy Rev. 2011, 15, 2588–2606. [Google Scholar] [CrossRef]
- Mittelman, G.; Kribus, A.; Mouchtar, O.; Dayan, A. Water desalination with concentrating photovoltaic/thermal (CPVT) systems. Sol. Energy 2009, 83, 1322–1334. [Google Scholar] [CrossRef]
- Fraidenraich, N.; Tiba, C.; Brandão, B.B.; Vilela, O.C. Analytic solutions for the geometric and optical properties of stationary compound parabolic concentrators with fully illuminated inverted V receiver. Sol. Energy 2008, 82, 132–143. [Google Scholar] [CrossRef]
- Krüger, D.; Pandian, Y.; Hennecke, K.; Schmitz, M. Parabolic trough collector testing in the frame of the REACt project. Desalination 2008, 220, 612–618. [Google Scholar] [CrossRef]
- Weber, K.J.; Everett, V.; Deenapanray, P.N.K.; Franklin, E.; Blakers, A.W. Modeling of static concentrator modules incorporating lambertian or v-groove rear reflectors. Sol. Energy Mater. Sol. Cells 2006, 90, 1741–1749. [Google Scholar] [CrossRef]
- Yamada, N.; Kanno, K.; Hayashi, K.; Tokimitsu, T. Performance of see-through prism CPV module for window integrated photovoltaics. Opt. Express 2011, 19, A649–A656. [Google Scholar] [CrossRef] [PubMed]
- Van Sark, W.G.J.H.M.; Barnham, K.W.J.; Slooff, L.H.; Chatten, A.J.; Büchtemann, A.; Meyer, A.; McCormack, S.J.; Koole, R.; Farrell, D.J.; Bose, R.; et al. Luminescent Solar Concentrators—A review of recent results. Opt. Express 2008, 16, 21773–21792. [Google Scholar] [CrossRef] [PubMed]
- Segev, G.; Kribus, A. Performance of CPV modules based on vertical multi-junction cells under non-uniform illumination. Sol. Energy 2013, 88, 120–128. [Google Scholar] [CrossRef]
- Luque, A.; Sala, G.; Arboiro, J.C. Electric and thermal model for non-uniformly illuminated concentration cells. Sol. Energy Mater. Sol. Cells 1998, 51, 269–290. [Google Scholar] [CrossRef]
- Cuevas, A.; Lopez-Romero, S. The combined effect of non-uniform illumination and series resistance on the open-circuit voltage of solar cells. Sol. Cells 1984, 11, 163–173. [Google Scholar] [CrossRef]
- Leutz, R.; Suzuki, A. Nonimaging Fresnel Lenses: Design and Performance of Solar Concentrators; Springer-Verlag: Berlin, Germany; Heidelberg, Germany, 2012. [Google Scholar]
- Winston, R.; Miñano, J.C.; Benítez, P. Nonimaging Optics; Elsevier Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Stefancich, M.; Zayan, A.; Chiesa, M.; Rampino, S.; Roncati, D.; Kimerling, L.; Michel, J. Single element spectral splitting solar concentrator for multiple cells CPV system. Opt. Express 2012, 20, 9004–9018. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, C.; Zayan, A.; Stefancich, M. Three-Dimensional Point-Focus Spectral Splitting Solar Concentrator System. Int. J. Opt. Appl. 2014, 4, 6–11. [Google Scholar]
- Ning, X.; O’Gallagher, J.; Winston, R. Optics of two-stage photovoltaic concentrators with dielectric second stages. Appl. Opt. 1987, 26, 1207–1212. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Xia, X.; Sun, C.; Dai, G. Optimal design of symmetrical two-stage flat reflected concentrator. Sol. Energy 2013, 93, 334–344. [Google Scholar] [CrossRef]
- Benítez, P.; Miñano, J.C.; Zamora, P.; Mohedano, R.; Cvetkovic, A.; Buljan, M.; Chaves, J.; Hernández, M. High performance Fresnel-based photovoltaic concentrator. Opt. Express 2010, 18, A25–A40. [Google Scholar] [CrossRef] [PubMed]
- Miñano, J.C.; Benítez, P.; Zamora, P.; Buljan, M.; Mohedano, R.; Santamaría, A. Free-form optics for Fresnel-lens-based photovoltaic concentrators. Opt. Express 2013, 21, A494–A502. [Google Scholar] [CrossRef] [PubMed]
- Mendes-Lopes, J.; Benítez, P.; Zamora, P.; Miñano, J.C. 9-fold Fresnel–Köhler concentrator with Fresnel lens of variable focal point. Opt. Express 2014, 22, A1153–A1163. [Google Scholar] [CrossRef] [PubMed]
- Miñano, J.C.; Hernández, M.; Benítez, P.; Blen, J.; Dross, O.; Mohedano, R.; Santamaría, A. Free-form integrator array optics. Proc. SPIE 2005. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chiang, H.W. Design of the secondary optical elements for concentrated photovoltaic units with Fresnel lenses. Appl. Sci. 2015, 5, 770–786. [Google Scholar] [CrossRef]
- Ullah, I.; Shin, S. Development of optical fiber-based daylighting system with uniform illumination. J. Opt. Soc. Korea 2012, 16, 247–255. [Google Scholar] [CrossRef]
- Ullah, I.; Shin, S. Uniformly illuminated efficient daylighting system. Smart Grid Renew. Energy 2013, 4, 161–166. [Google Scholar] [CrossRef]
- Ullah, I.; Shin, S. Highly concentrated optical fiber-based daylighting systems for multi-floor office buildings. Energy Build. 2014, 72, 246–261. [Google Scholar] [CrossRef]
- Vu, N.H.; Shin, S. A large-scale daylighting system based on a stepped thickness waveguide. Energies 2016, 9. [Google Scholar] [CrossRef]
- Yamada, N.; Okamoto, K. Experimental measurements of a prototype high-concentration Fresnel lens CPV module for the harvesting of diffuse solar radiation. Opt. Express 2014, 22, A28–A34. [Google Scholar] [CrossRef] [PubMed]
- Benitez, P.; Miñano, J.C.; Alvarez, R. Photovoltaic Concentrator with Auxiliary Cells Collecting Diffuse Radiation. U.S. Patent 2010/0126556 A1, 27 May 2010. [Google Scholar]
- Yamada, N.; Okamoto, K.; Ijiro, T. Feasibility study of harvesting diffuse solar radiation in a high-concentration CPV module for better solar energy conversion. In Proceedings of the 23rd International Photovoltaic Science and Engineering Conference (PVSEC-23), Taiwan, China, 28 October–1 November 2013.
- Leutz, R.; Suzuki, A.; Akisawa, A.; Kashiwagi, T. Developments and designs of solar engineering Fresnel lenses. In Proceedings of Symposium on Energy Engineering (SEE 2000); Project Nerd: Hong Kong, China, 2000; Volume 2, pp. 759–765. [Google Scholar]
- Malacara, D. Optical Shop Testing, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- LightTool v8.2.0. Optical Simulation Tool. Available online: https://optics.synopsys.com/lighttools/ (accessed on 24 May 2016).
- Selimoglu, O.; Turan, R. Exploration of the horizontally staggered light guides for high concentration CPV applications. Opt. Express 2012, 20, 19137–19147. [Google Scholar] [CrossRef] [PubMed]






| Parameter | Value |
|---|---|
| Focal length of the Fresnel lens | 300 mm |
| Size of the Fresnel lens | 300 mm × 300 mm |
| Thickness of the Fresnel lens | 3 mm |
| Material of the Fresnel lens | PMMA 1 |
| Focal length of the plano-concave lens | 25 mm |
| Diameter of the plano-concave lens | 21.5 mm |
| Thickness of the plano-concave lens | 2 mm |
| Material of the plano-concave lens | N-BK7 2 |
| Distance between the POE 3 and SOE 4 | 283 mm |
| Diameter of the multi-junction solar cell | 20 mm |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien, N.X.; Shin, S. A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation. Appl. Sci. 2016, 6, 251. https://doi.org/10.3390/app6090251
Tien NX, Shin S. A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation. Applied Sciences. 2016; 6(9):251. https://doi.org/10.3390/app6090251
Chicago/Turabian StyleTien, Nguyen Xuan, and Seoyong Shin. 2016. "A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation" Applied Sciences 6, no. 9: 251. https://doi.org/10.3390/app6090251
APA StyleTien, N. X., & Shin, S. (2016). A Novel Concentrator Photovoltaic (CPV) System with the Improvement of Irradiance Uniformity and the Capturing of Diffuse Solar Radiation. Applied Sciences, 6(9), 251. https://doi.org/10.3390/app6090251






