Full-Band Quasi-Harmonic Analysis and Synthesis of Musical Instrument Sounds with Adaptive Sinusoids
Abstract
:1. Introduction
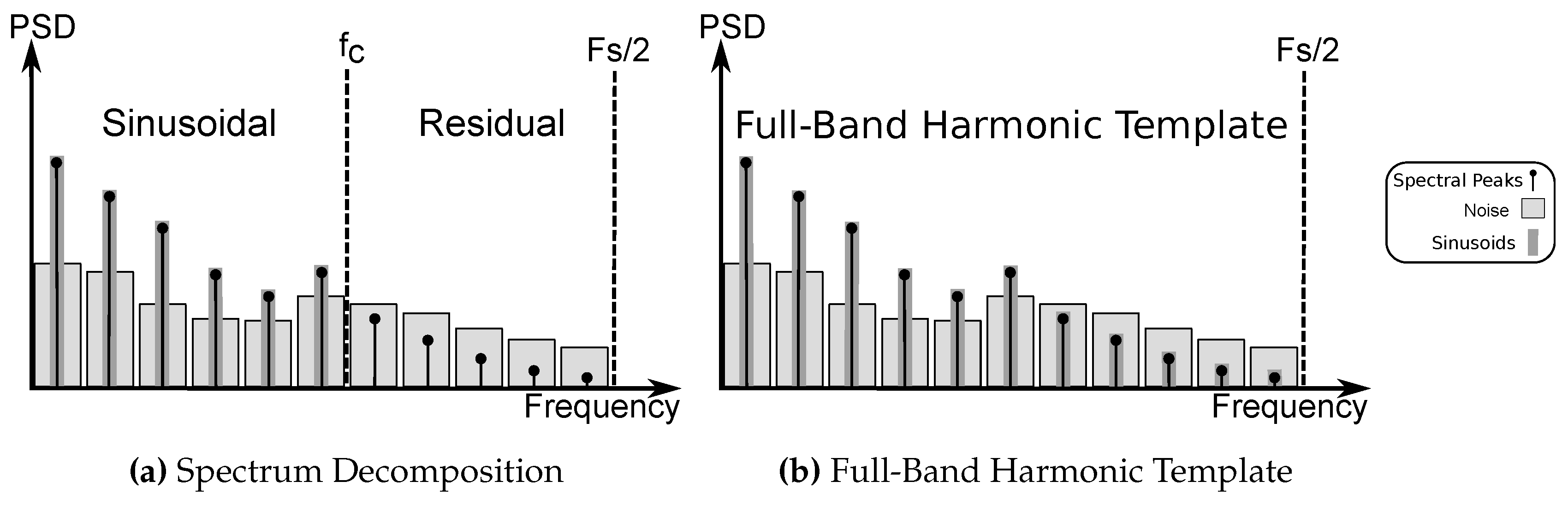
2. Full-Band Modeling
3. Adaptive Sinusoidal Modeling with eaQHM
3.1. The Quasi-Harmonic Model (QHM)
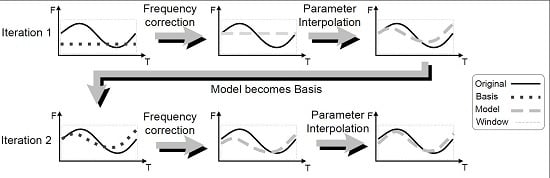
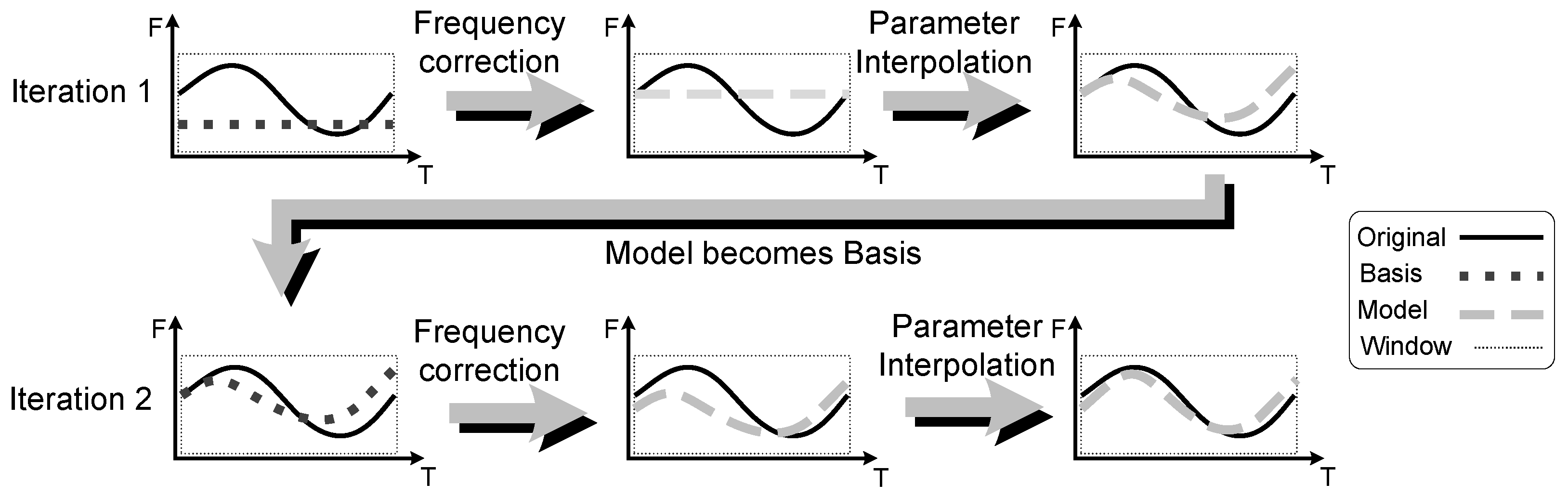
3.2. Parameter Interpolation across Frames
3.3. The Extended Adaptive Quasi-Harmonic Model (eaQHM)
4. Experimental Setup
4.1. The Musical Instrument Sound Dataset
4.2. Analysis Parameters
5. Results and Discussion
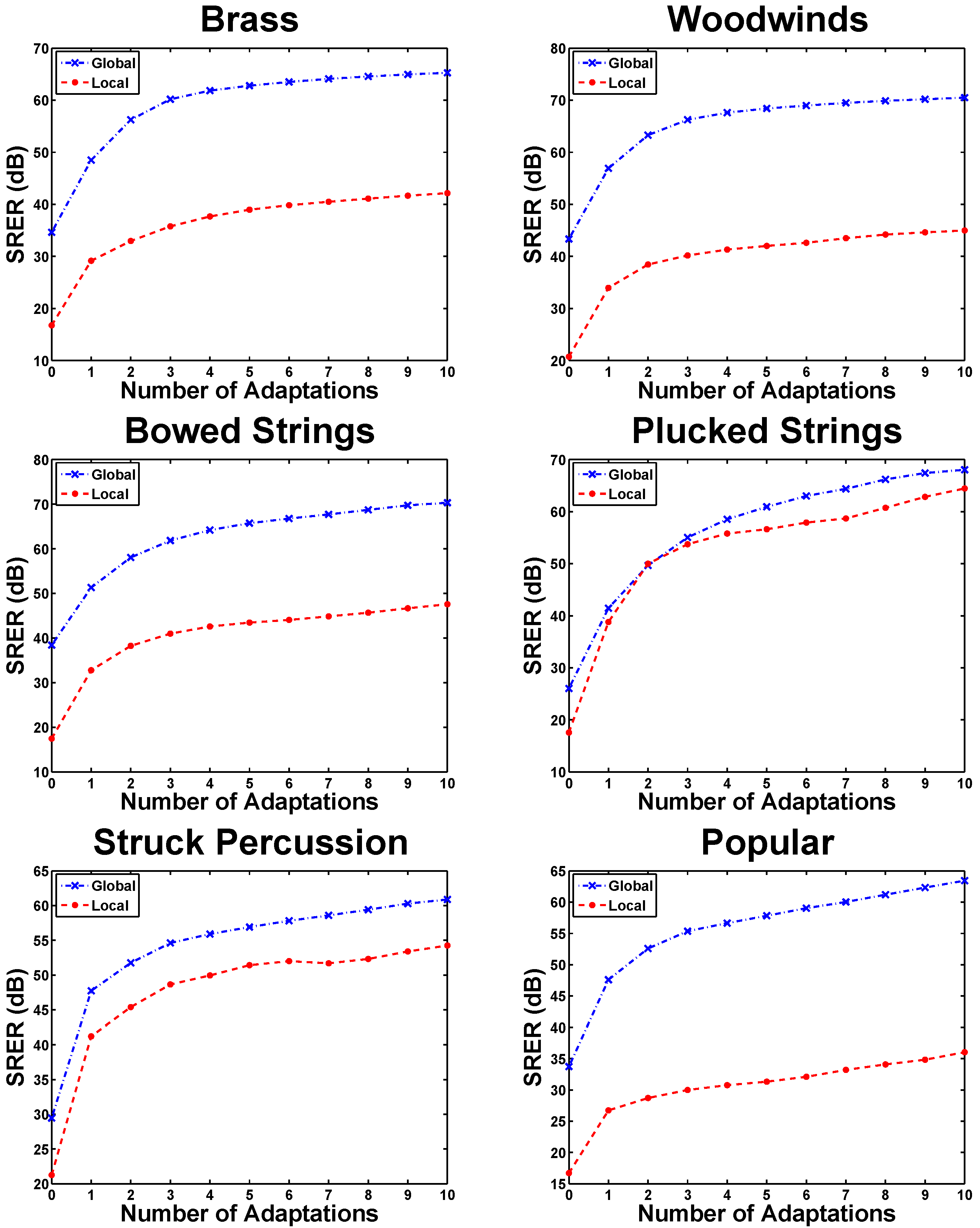
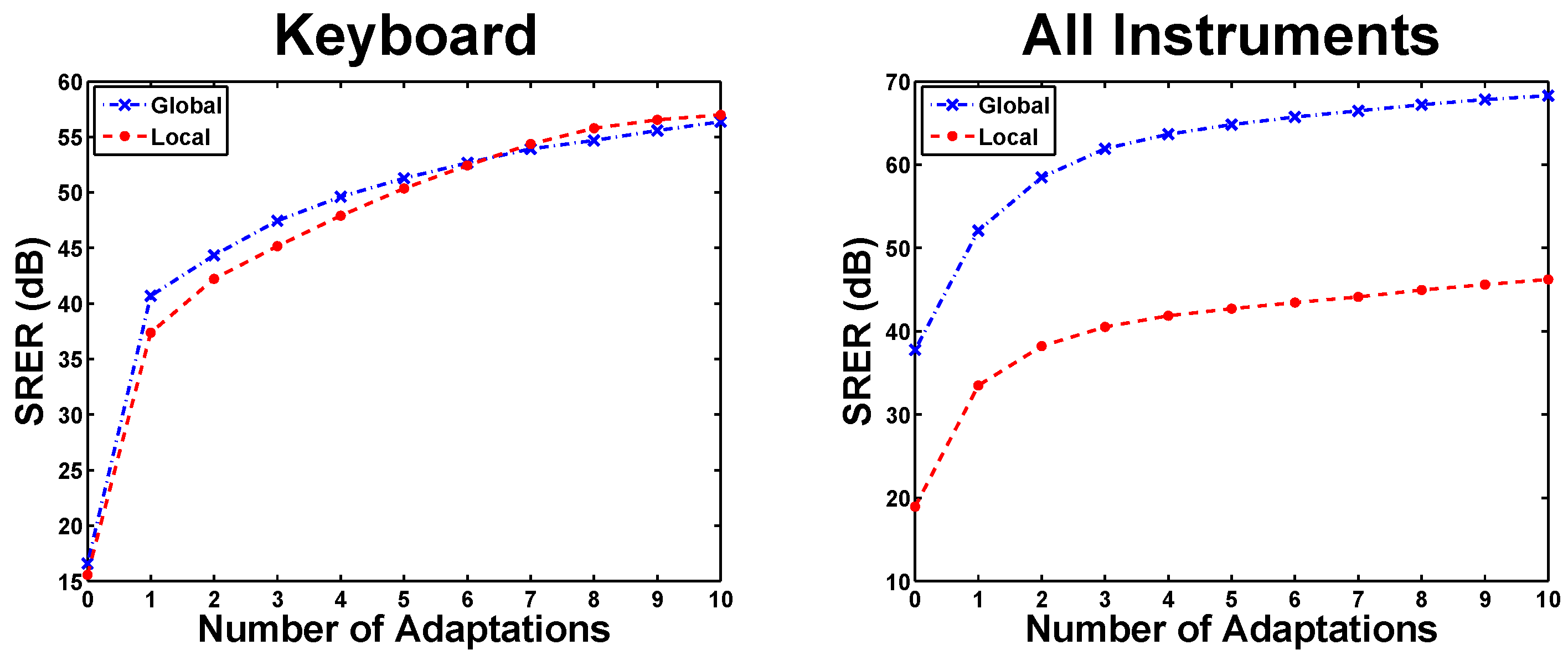
5.1. Adaptation Cycles in eaQHM
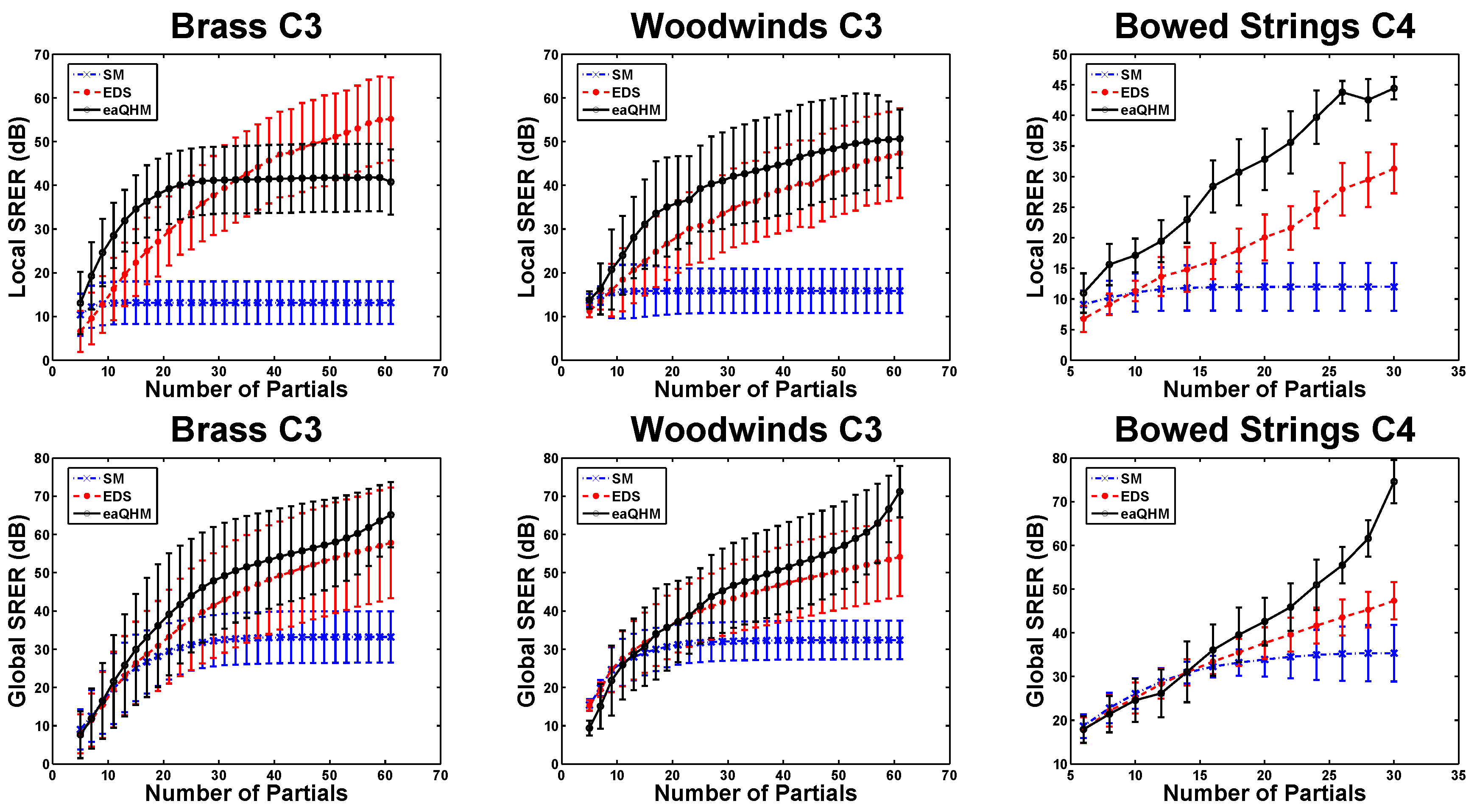
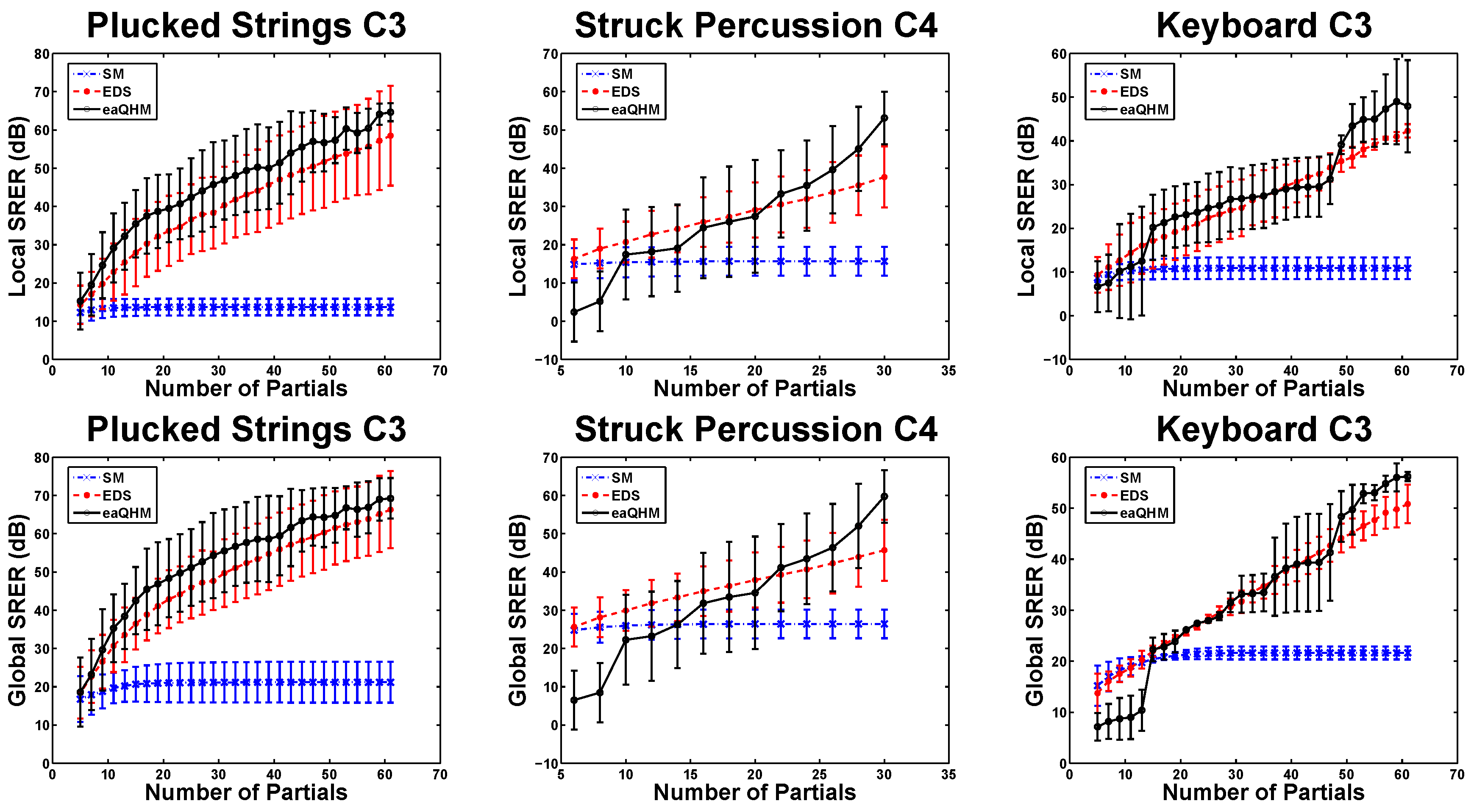
5.2. Experiment 1: Variation Across K (Constant )
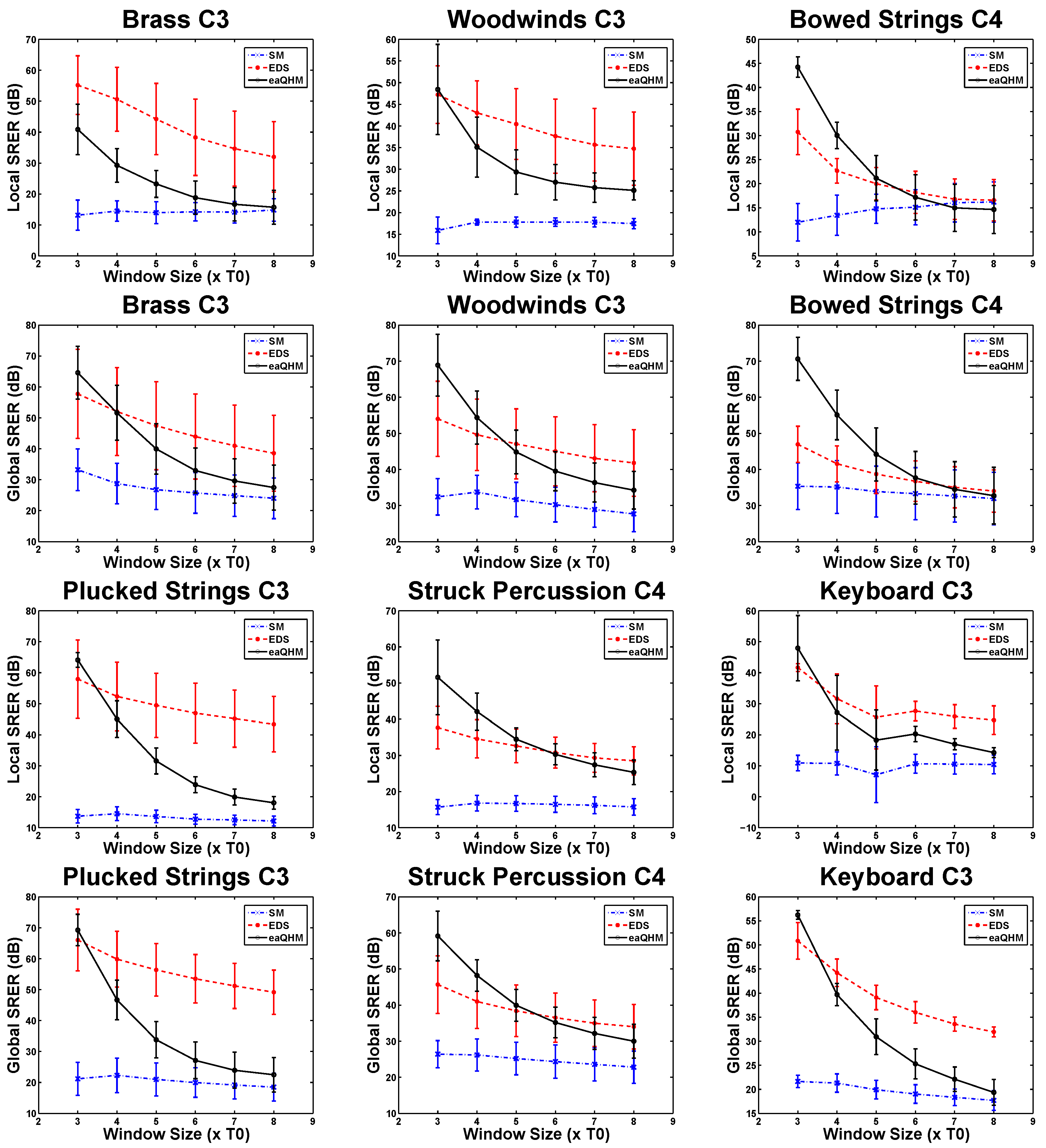
5.3. Experiment 2: Variation Across L (Constant )
5.4. Full-Band Quasi-Harmonic Analysis with AM–FM Sinusoids
5.5. Full-Band Modeling and Quasi-Harmonicity
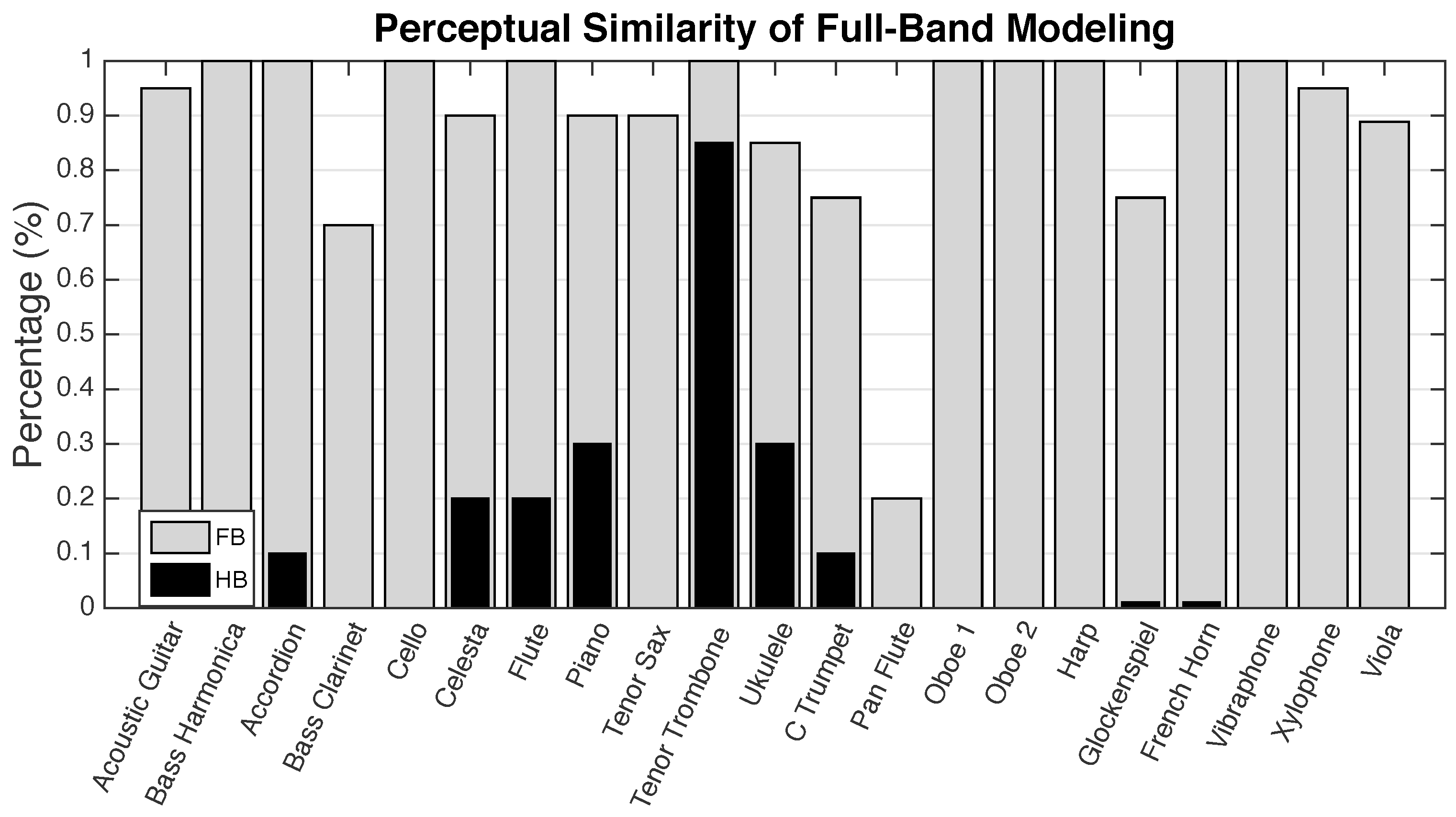
6. Evaluation of Perceptual Transparency with a Listening Test
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Serra, X.; Smith, J.O. Spectral modeling synthesis: A sound analysis/synthesis system based on a deterministic plus stochastic decomposition. Comput. Music J. 1990, 14, 49–56. [Google Scholar] [CrossRef]
- Beauchamp, J.W. Analysis and synthesis of musical instrument sounds. In Analysis, Synthesis, and Perception of Musical Sounds; Beauchamp, J.W., Ed.; Modern Acoustics and Signal Processing; Springer: New York, NY, USA, 2007; pp. 1–89. [Google Scholar]
- Quatieri, T.; McAuley, R. Audio signal processing based on sinusoidal analysis/synthesis. In Applications of Digital Signal Processing to Audio and Acoustics; Kahrs, M., Brandenburg, K., Eds.; Kluwer Academic Publishers: Berlin/Heidelberg, Germany, 2002; Chapter 9; pp. 343–416. [Google Scholar]
- Serra, X.; Bonada, J. Sound Transformations based on the SMS high level attributes. Proc. Digit. Audio Eff. Workshop 1998, 5. Available online: http://mtg.upf.edu/files/publications/dafx98-1.pdf (accessed on 26 April 2016). [Google Scholar]
- Caetano, M.; Rodet, X. Musical Instrument sound morphing guided by perceptually motivated features. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 1666–1675. [Google Scholar] [CrossRef]
- Barbedo, J.; Tzanetakis, G. Musical instrument classification using individual partials. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 111–122. [Google Scholar] [CrossRef]
- Herrera, P.; Bonada, J. Vibrato Extraction and parameterization in the spectral modeling synthesis framework. Proc. Digit. Audio Eff. Workshop 1998, 99. Available online: http://www.mtg.upf.edu/files/publications/dafx98-perfe.pdf (accessed on 26 April 2016). [Google Scholar]
- Glover, J.; Lazzarini, V.; Timoney, J. Real-time detection of musical onsets with linear prediction and sinusoidal modeling. EURASIP J. Adv. Signal Process. 2011. [Google Scholar] [CrossRef]
- Virtanen, T.; Klapuri, A. Separation of harmonic sound sources using sinusoidal modeling. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Istanbul, Turkey, 5–9 June 2000; Volume 2, pp. II765–II768.
- Lagrange, M.; Marchand, S.; Rault, J.B. Long interpolation of audio signals using linear prediction in sinusoidal modeling. J. Audio Eng. Soc. 2005, 53, 891–905. [Google Scholar]
- Hermus, K.; Verhelst, W.; Lemmerling, P.; Wambacq, P.; Huffel, S.V. Perceptual audio modeling with exponentially damped sinusoids. Signal Process. 2005, 85, 163–176. [Google Scholar] [CrossRef]
- Nsabimana, F.; Zolzer, U. Audio signal decomposition for pitch and time scaling. In Proceedings of the International Symposium on Communications, Control, and Signal Processing (ISCCSP), St Julians, Malta, 12–14 March 2008; pp. 1285–1290.
- El-Jaroudi, A.; Makhoul, J. Discrete all-pole modeling. IEEE Trans. Commun. Technol. 1969, 39, 481–488. [Google Scholar] [CrossRef]
- Caetano, M.; Rodet, X. A source-filter model for musical instrument sound transformation. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 137–140.
- Wen, X.; Sandler, M. Source-Filter Modeling in the Sinusoidal Domain. J. Audio Eng. Soc. 2010, 58, 795–808. [Google Scholar]
- Fletcher, N.H.; Rossing, T.D. The Physics of Musical Instruments, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Caetano, M.; Kafentzis, G.P.; Degottex, G.; Mouchtaris, A.; Stylianou, Y. Evaluating how well filtered white noise models the residual from sinusoidal modeling of musical instrument sounds. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 20–23 October 2013; pp. 1–4.
- Bader, R.; Hansen, U. Modeling of musical instruments. In Handbook of Signal Processing in Acoustics; Havelock, D., Kuwano, S., Vorländer, M., Eds.; Springer: New York, NY, USA, 2009; pp. 419–446. [Google Scholar]
- Fletcher, N.H. The nonlinear physics of musical instruments. Rep. Prog. Phys. 1999, 62, 723–764. [Google Scholar] [CrossRef]
- McAulay, R.J.; Quatieri, T.F. Speech analysis/synthesis based on a sinusoidal representation. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 744–754. [Google Scholar] [CrossRef]
- Green, R.A.; Haq, A. B-spline enhanced time-spectrum analysis. Signal Process. 2005, 85, 681–692. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Frequency estimation by two- or three-point interpolated Fourier algorithms based on cosine windows. Signal Process. 2015, 117, 115–125. [Google Scholar] [CrossRef]
- Prudat, Y.; Vesin, J.M. Multi-signal extension of adaptive frequency tracking algorithms. Signal Process. 2009, 89, 96–973. [Google Scholar] [CrossRef]
- Candan, Ç. Fine resolution frequency estimation from three DFT samples: Case of windowed data. Signal Process. 2015, 114, 245–250. [Google Scholar] [CrossRef]
- Röbel, A. Adaptive additive modeling with continuous parameter trajectories. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1440–1453. [Google Scholar] [CrossRef]
- Verma, T.S.; Meng, T.H.Y. Extending spectral modeling synthesis with transient modeling synthesis. Comput. Music J. 2000, 24, 47–59. [Google Scholar] [CrossRef]
- Laurenti, N.; De Poli, G.; Montagner, D. A nonlinear method for stochastic spectrum estimation in the modeling of musical sounds. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 531–541. [Google Scholar] [CrossRef]
- Daudet, L. A review on techniques for the extraction of transients in musical signals. Proc. Int. Symp. Comput. Music Model. Retr. 2006, 3902, 219–232. [Google Scholar]
- Jang, H.; Park, J.S. Multiresolution sinusoidal model with dynamic segmentation for timescale modification of polyphonic audio signals. IEEE Trans. Speech Audio Process. 2005, 13, 254–262. [Google Scholar] [CrossRef]
- Beltrán, J.R.; de León, J.P. Estimation of the instantaneous amplitude and the instantaneous frequency of audio signals using complex wavelets. Signal Process. 2010, 90, 3093–3109. [Google Scholar] [CrossRef]
- Levine, S.N.; Smith, J.O. A compact and malleable sines+transients+noise model for sound. In Analysis, Synthesis, and Perception of Musical Sounds; Beauchamp, J.W., Ed.; Modern Acoustics and Signal Processing; Springer: New York, NY, USA, 2007; pp. 145–174. [Google Scholar]
- Markovsky, I.; Huffel, S.V. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Van Huffel, S.; Park, H.; Rosen, J. Formulation and solution of structured total least norm problems for parameter estimation. IEEE Trans. Signal Process. 1996, 44, 2464–2474. [Google Scholar] [CrossRef]
- Liu, Z.S.; Li, J.; Stoica, P. RELAX-based estimation of damped sinusoidal signal parameters. Signal Process. 1997, 62, 311–321. [Google Scholar] [CrossRef]
- Nieuwenhuijse, J.; Heusens, R.; Deprettere, E.F. Robust exponential modeling of audio signals. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Seattle, WA, USA, 12–15 May 1998; Volume 6, pp. 3581–3584.
- Badeau, R.; Boyer, R.; David, B. EDS Parametric Modeling And Tracking of Audio Signals. In Proceedings of the 5th International Conference on Digital Audio Effects (DAFx), Hambourg, Germany, 26–28 September 2002; pp. 26–28.
- Jensen, J.; Heusdens, R. A comparison of sinusoidal model variants for speech and audio representation. In Proceedings of the 2002 11th European Signal Processing Conference (EUSIPCO), Toulouse, France, 3–6 September 2002; pp. 1–4.
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Fulop, S.A.; Fitz, K. Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications. J. Acoust. Soc. Am. 2006, 119, 360–371. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Bi, G. The reassigned local polynomial periodogram and its properties. Signal Process. 2009, 89, 206–217. [Google Scholar] [CrossRef]
- Girin, L.; Marchand, S.; Di Martino, J.; Röbel, A.; Peeters, G. Comparing the order of a polynomial phase model for the synthesis of quasi-harmonic audio signals. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 19–22 October 2003; pp. 193–196.
- Kafentzis, G.P.; Pantazis, Y.; Rosec, O.; Stylianou, Y. An extension of the adaptive quasi-harmonic model. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech, and Signal Processing, Kyoto, Japan, 25–30 March 2012; pp. 4605–4608.
- Kafentzis, G.P.; Rosec, O.; Stylianou, Y. On the modeling of voiceless stop sounds of speech using adaptive quasi-harmonic models. In Proceedings of the Annual Conference of the International Speech Communication Association (INTERSPEECH), Portland, OR, USA, 9–13 September 2012.
- Pantazis, Y.; Rosec, O.; Stylianou, Y. Adaptive AM–FM signal decomposition with application to speech analysis. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 290–300. [Google Scholar] [CrossRef]
- Degottex, G.; Stylianou, Y. Analysis and synthesis of speech using an adaptive full-band harmonic model. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 2085–2095. [Google Scholar] [CrossRef]
- Caetano, M.; Kafentzis, G.P.; Mouchtaris, A.; Stylianou, Y. Adaptive sinusoidal modeling of percussive musical instrument sounds. In Proceedings of the European Signal Processing Conference (EUSIPCO), Marrakech, Morocco, 9–13 September 2013; pp. 1–5.
- Pantazis, Y.; Rosec, O.; Stylianou, Y. On the Properties of a time-varying quasi-harmonic model of speech. In Proceedings of the Annual Conference of the International Speech Communication Association (INTERSPEECH), Brisbane, Australia, 22–26 September 2008; pp. 1044–1047.
- Smyth, T.; Abel, J.S. Toward an estimation of the clarinet reed pulse from instrument performance. J. Acoust. Soc. Am. 2012, 131, 4799–4810. [Google Scholar] [CrossRef] [PubMed]
- Smyth, T.; Scott, F. Trombone synthesis by model and measurement. EURASIP J. Adv. Signal Process. 2011. [Google Scholar] [CrossRef]
- Brown, J.C. Frequency ratios of spectral components of musical sounds. J. Acoust. Soc. Am. 1996, 99, 1210–1218. [Google Scholar] [CrossRef]
- Borss, C.; Martin, R. On the construction of window functions with constant overlap-add constraint for arbitrary window shifts. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 337–340.
- Camacho, A.; Flory, H.Y. A sawtooth waveform inspired pitch estimator for speech and music. J. Acoust. Soc. Am. 2008, 124, 1638–1652. [Google Scholar] [CrossRef] [PubMed]
- Goto, M.; Hashiguchi, H.; Nishimura, T.; Oka, R. RWC Music Database: Music Genre Database and Musical Instrument Sound Database. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Baltimore,MD, USA, 26–30 October 2003; pp. 229–230. Available online: http://staff.aist.go.jp/m.goto/RWC-MDB/ (accessed on 26 April 2016).
- Vienna Symphonic Library–GmbH. Available online: http://www.vsl.co.at/ (accessed on 26 April 2016).
- Grey, J.M.; Gordon, J.W. Multidimensional perceptual scaling of musical timbre. J. Acoust. Soc. Am. 1977, 61, 1270–1277. [Google Scholar] [CrossRef] [PubMed]
- Krumhansl, C.L. Why is musical timbre so hard to understand? In Structure and Perception of Electroacoustic Sound and Music; Nielzén, S., Olsson, O., Eds.; Excerpta Medica: New York, NY, USA, 1989; pp. 43–54. [Google Scholar]
- McAdams, S.; Giordano, B.L. The perception of musical timbre. In The Oxford Handbook of Music Psychology; Hallam, S., Cross, I., Thaut, M., Eds.; Oxford University Press: New York, NY, USA, 2009; pp. 72–80. [Google Scholar]
- Listening Test. Webpage for the Listening Test. Available online: http://ixion.csd.uoc.gr/kafentz/listest/pmwiki.php?n=Main.JMusLT (accessed on 26 April 2016).
- AdaptiveSinMus. Companion webpage with sound examples. Available online: http://www.csd.uoc.gr/kafentz/listest/pmwiki.php?n=Main.AdaptiveSinMus (accessed on 26 April 2016).

| Family | Musical Instrument Sounds |
|---|---|
| Brass | Bass Trombone (C3 f nv na), Bass Trombone (C3 f stac), Bass Trumpet (C3 f na vib), Cimbasso (C3 f nv na), Cimbasso (C3 f stac), Contrabass Trombone* (C2♯ f stac), Contrabass Tuba (C3 f na), Contrabass Tuba (C3 f stac), Cornet (C4 f), French Horn (C3 f nv na), French Horn (C3 f stac), Piccolo Trumpet (C5 f nv na), Piccolo Trumpet (C5 f stac), Tenor Trombone (C3 f na vib), Tenor Trombone (C3 f nv sa), Tenor Trombone (C3 f stac), C Trumpet (C4 f nv na), C Trumpet (C4 f stac), Tuba (C3 f vib na), Tuba (C3 f stac), Wagner Tuba (C3 f na), Wagner Tuba (C3 f stac) |
| Woodwinds | Alto Flute (C4 f vib na), Bass Clarinet (C3 f na), Bass Clarinet (C3 f sforz), Bass Clarinet (C3 f stac), Bassoon (C3 f na), Bassoon (C3 f stac), Clarinet (C4 f na), Clarinet (C4 f stac), Contra Bassoon* (C2 f stac), Contra Bassoon* (C2 f sforz), English Horn (C4 f na), English Horn (C4 f stac), Flute (C4 f nv na), Flute (C4 f stac), Flute (C4 f tr), Flute (C4 f vib na), Oboe 1 (C4 f stac), Oboe 2 (C4 f nv na), Oboe (C4 f pa), Piccolo Flute (C6♯ f vib sforz), Piccolo Flute (C6 f nv ha ff) |
| Plucked Strings | Cello (C3 f pz vib), Harp (C3 f), Harp (C3 f pdlt), Harp (C3 f mu), Viola (C3 f pz vib), Violin (C4 f pz mu) |
| Bowed Strings | Cello (C3 f vib), Cello (C3 f stac), Viola (C3 f vib), Viola (C4 f stac), Violin (C4 f), Violin (C4♯ ff vib), Violin (C4 f stac) |
| Struck Percussion | Glockenspiel (C4 f), Glockenspiel (C6 f wo), Glockenspiel (C6 f pl), Glockenspiel (C6 f met), Marimba (C4 f), Vibraphone (C4 f ha 0), Vibraphone (C4 f ha fa), Vibraphone (C4 f ha sl), Vibraphone (C4 f med 0), Vibraphone (C4 f med fa), Vibraphone (C4 f med 0 mu), Vibraphone (C4 f med sl), Vibraphone (C4 f so 0), Vibraphone (C4 f so fa), Xylophone (C5 f GA L), Xylophone (C5 met), Xylophone (C5 f HO L), Xylophone (C5 f mP L), Xylophone (C5 f wP L) |
| Bowed Percussion | Vibraphone (C4 f sh vib), Vibraphone (C4 f sh nv), Vibraphone (C4 f lg nv) |
| Popular | Accordion (C3♯ f), Acoustic Guitar (C3 f), Baritone Sax (C3 f), Bass Harmonica (C3♯ f), Chromatic Harmonica (C4 f), Classic Guitar (C3 f), Mandolin (C4 f), Pan Flute (C5 f), Tenor Sax (C3♯ f), Ukulele (C4 f) |
| Keyboard | Celesta (C3 f na nv), Celesta (C3 f stac), Clavinet (C3 f), Piano (C3 f) |
| SRER (eaQHM-EDS) | SRER (eaQHM-SM) | |||
|---|---|---|---|---|
| Family | Local (dB) | Global (dB) | Local (dB) | Global (dB) |
| Brass | −9.4± 7.0 | 12.5 ± 6.8 | 27.3 ± 5.8 | 31.9 ± 4.0 |
| Woodwinds | 7.8 ± 3.9 | 22.0 ± 5.9 | 30.9 ± 7.5 | 36.1 ± 4.7 |
| Bowed Strings | 12.2 ± 4.2 | 24.1 ± 6.7 | 35.0 ± 4.7 | 40.0 ± 4.7 |
| Plucked Strings | 8.3 ± 5.0 | 4.7 ± 3.4 | 49.5 ± 4.3 | 46.6 ± 5.1 |
| Bowed Percussion | −2.7± 2.5 | 16.3 ± 2.2 | 12.7 ± 2.6 | 37.6 ± 3.6 |
| Struck Percussion | 10.5 ± 4.8 | 10.1 ± 2.6 | 28.6 ± 13.3 | 26.0 ± 11.3 |
| Popular | 6.3 ± 3.3 | 11.9 ± 7.0 | 26.5 ± 10.8 | 27.5 ± 11.6 |
| Keyboard | 5.7 ± 3.4 | 5.4 ± 4.3 | 37.0 ± 8.0 | 34.6 ± 2.0 |
| Total | 5.3 ± 2.4 | 13.2 ± 3.3 | 31.0 ± 7.1 | 35.0 ± 5.9 |
| Number of Real Parameters p Per Sinusoid k Per Frame m | |||
|---|---|---|---|
| SM | EDS | eaQHM | |
| Analysis | |||
| Synthesis | |||
| Algorithmic Complexity | |||
|---|---|---|---|
| SM | EDS | eaQHM | |
| Complexity | |||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caetano, M.; Kafentzis, G.P.; Mouchtaris, A.; Stylianou, Y. Full-Band Quasi-Harmonic Analysis and Synthesis of Musical Instrument Sounds with Adaptive Sinusoids. Appl. Sci. 2016, 6, 127. https://doi.org/10.3390/app6050127
Caetano M, Kafentzis GP, Mouchtaris A, Stylianou Y. Full-Band Quasi-Harmonic Analysis and Synthesis of Musical Instrument Sounds with Adaptive Sinusoids. Applied Sciences. 2016; 6(5):127. https://doi.org/10.3390/app6050127
Chicago/Turabian StyleCaetano, Marcelo, George P. Kafentzis, Athanasios Mouchtaris, and Yannis Stylianou. 2016. "Full-Band Quasi-Harmonic Analysis and Synthesis of Musical Instrument Sounds with Adaptive Sinusoids" Applied Sciences 6, no. 5: 127. https://doi.org/10.3390/app6050127
APA StyleCaetano, M., Kafentzis, G. P., Mouchtaris, A., & Stylianou, Y. (2016). Full-Band Quasi-Harmonic Analysis and Synthesis of Musical Instrument Sounds with Adaptive Sinusoids. Applied Sciences, 6(5), 127. https://doi.org/10.3390/app6050127